Abstract
We report the iAMOEBA (i.e. “inexpensive AMOEBA”) classical polarizable water model. iAMOEBA uses a direct approximation to describe electronic polarizability, which reduces the computational cost relative to a fully polarizable model such as AMOEBA. The model is parameterized using ForceBalance, a systematic optimization method that simultaneously utilizes training data from experimental measurements and high-level ab initio calculations. We show that iAMOEBA is a highly accurate model for water in the solid, liquid, and gas phases, with the ability to fully capture the effects of electronic polarization and predict a comprehensive set of water properties beyond the training data set including the phase diagram. The increased accuracy of iAMOEBA over the fully polarizable AMOEBA model demonstrates ForceBalance as a method that allows the researcher to systematically improve empirical models by optimally utilizing the available data.
Keywords: Force field, force matching, AMOEBA, parameterization, optimization, polarizable
INTRODUCTION
Water is a fascinating liquid that possesses many anomalous physical and chemical properties, including the temperature of maximum density, expansion on freezing, unusually large heat capacity, compressibility minimum, and unique solvation properties. The study of how the molecular interactions in water are related to its unique properties is a fundamental and important topic in physical chemistry. A related essential question is how water interacts with solutes such as ions, organic molecules and proteins to form the foundation of biomolecular structure and function, including studies of how proteins fold,1–3 misfold,4–6 undergo conformational change,7–9 and interact with their environments.10–14 For all of these reasons, the study of water interactions has been a highly active field for decades in experimental and theoretical chemistry.15
The theoretical and computational modeling of water allows us to investigate water and aqueous solutions with precise spatial and temporal resolution, providing a helpful complement to experiment. The application of these models has contributed to important progress in our understanding of pure water properties, such as the nature of the hydrogen bonding network and its structural organization,15–18 the transport of hydronium and hydroxide ions,19,20 the mechanism of freezing21 and the surface properties of ice,22 the geometries and binding energies of water clusters in the gas phase,23–26 and the dual phases of liquid water at extremely low temperatures.27–29 However, no current single model is able to capture the full complexity of water and its properties, due to the tradeoff between model complexity and the ability to sample the condensed phase.
For example, some of the most widely used biomolecular force fields – including the popular AMBER30–33 and CHARMM models13,34 – are based on the three-site, pairwise-additive TIP3P water model35 developed for use with Monte Carlo simulations nearly thirty 30 years ago. The computationally tractable TIP3P model allows for long simulation timescales to be reached that are important for extreme regions of water’s phase diagram, or solvation of large biomolecules. The TIP3P model was fitted to the experimental density and heat of vaporization at room temperature and 1 atm pressure, and its validation showed it could predict the isobaric heat capacity quite well at this temperature and pressure – to within 1 J/g °C.36 However, this model often fails on properties outside the ambient conditions for which it was parameterized; for example, the TIP3P model yields a simulated freezing point value of −91 °C, far below the experimental value of 0 °C, and incorrectly predicts the solid phase to be ice II rather than ordinary ice Ih.37–39
The development of water models using only pairwise-additive interactions (such as TIP3P) has significantly benefited from more sophisticated treatments of long-ranged electrostatics, extending the experimental data sets used for parameterization, and adding more interaction sites. For example, the TIP4P/Ew40 and TIP4P/2005 models41 were developed for use with Ewald summation techniques and parameterized using the temperature dependence of the density and heat of vaporization. These models provide agreement with a much broader range of experimental reference data outside of the parameterization data used in model refinement.
There is also a more sophisticated class of water models that move beyond point charges and the pairwise additive approximation by including anisotropic electrostatic multipole interactions and N-body polarization. For example, polarizable models such as SWM-4DP42, TIP4P-FQ43, DPP223, TTM3-F44, and AMOEBA45,46 further improve on the description of many water properties, especially gas-phase properties and the dielectric constant – where additive force fields typically overestimate binding energies of gas-phase clusters and underestimate the dielectric constant in order to capture a larger subset of condensed phase properties. Given the increase in model complexity, polarizable force fields are also more expensive to evaluate, by a factor of at least 2–3.
In all cases the parameterization and validation of a water model is both difficult and time-consuming. Improved methods for building force fields are therefore desirable, for they can be used to improve models in a systematic and reproducible way, and be applied more generally for parameterizing models of other solutes such as drugs, ligands, proteins, lipids, or nucleic acids that are compatible with the water model.
In this Article we report a new classical, flexible, direct polarization water model that is a simplified version of the fully polarizable AMOEBA water model. The direct polarization method determines induced dipole moments directly, based only on the electric field due to static multipoles.47–49 The direct polarization approximation eliminates the self-consistent field step needed to describe mutual polarization and reduces the computational cost; hence we refer to the new model as inexpensive AMOEBA or iAMOEBA. However, neglecting mutual polarization results in a loss of ∼20% of the polarization energy, and that must be recovered through optimization of the model parameters.
Here we use the ForceBalance method50,51 for parameterizing the iAMOEBA model using a combination of experimental data and high-level theoretical calculations. We will describe our choice of reference data and provide a brief overview of the parameterization method. We demonstrate the accuracy of iAMOEBA using a published, comprehensive benchmark of water properties developed by Vega and coworkers36 that covers a wide range of phases and thermodynamic conditions going far beyond the parameterization data set. We provide further discussion on the generality of the parameterization approach explored here for iAMOEBA and its potential for force field development for other liquids, biomolecular solutes and other materials, or for potentials of arbitrary functional form.
THEORY AND METHODS
A. The iAMOEBA Model
The iAMOEBA model described in this work is a direct polarization approximation of the AMOEBA water model developed by Ren and Ponder, and we refer the reader to Ref. 45 for a complete description of the mutually polarizable AMOEBA water model. The iAMOEBA and AMOEBA functional form for water is briefly recapitulated here:
| (1) |
where the first three terms describe the short-range valence interactions (bond stretching, angle bending, Urey-Bradley bond-angle cross term), and the last three terms are the nonbonded van der Waals (vdW) and electrostatic contributions. More specifically, the nuclei are described using classical point particles and the molecular connectivity is fixed; the water molecule is allowed to undergo classical vibrations represented using anharmonic potential functions in the O-H bond length, the H-O-H angle, and the H-H distance (Urey-Bradley interaction). The van der Waals interactions are described using a Halgren buffered 14-7 function that describes dispersion interactions at long range and exchange repulsion at short range. The permanent electrostatic interactions are represented as atomic multipole moments through the quadrupole, requiring the definition of a local coordinate system for each atom.
The main difference between iAMOEBA and AMOEBA is that we evaluate only the direct polarization,47–49,52 and not the full self-consistent mutual polarization. In this approximation, the polarizable dipoles are induced solely by the electric fields from the permanent multipoles. The dipoles are given by:
| (2) |
where αi is the atomic polarizability on site i, Mj =[qj,µj,1,µj,2,µj,3,…]T contains the permanent multipole components on site j, and is the interaction matrix element between site i and j following Stone’s notation.53 The full expressions for the T matrix elements are the same as Equations 2–5 in Ref. 45.
Direct polarization may alternatively be viewed as including three-body polarization interactions, because the interaction of two polarizable sites is further modified by the permanent moments of a third site. By contrast, the mutual scheme in AMOEBA represents the full N-body polarization interaction, in which the polarizable dipoles further induce one another and must be converged self-consistently. Direct polarization provides a model that still captures much of the polarization effects important in the condensed phase at greatly reduced computational cost, as the iterative evaluation of electrostatic energies to achieve self-consistency in polarizable dipoles is avoided entirely. Furthermore, the resulting model no longer requires a convergence tolerance, eliminating the possibility that incompletely converged dipoles might result in nonconservative forces.
As a result, the direct iAMOEBA model speeds up the calculation of energies and gradients by a factor of 1.5 to 6 over the mutual AMOEBA model. These estimates were derived from benchmark calculations using the TINKER and OpenMM software packages (see Supporting Table S1); the precise value depends on the system and simulation settings, notably the self-consistent convergence tolerance for the AMOEBA induced dipoles. Furthermore, the use of extended Lagrangian formalisms54–57 is known to greatly reduce the computational cost of mutual polarization methods, but it requires a careful choice of the fictitious mass parameter for the electronic degrees of freedom58–60; we did not consider the impact of these methods in these timing comparisons.
The more important scientific question is how effectively we can recapture the physical interactions using the approximate polarizable form. In order to address this question, we must reoptimize the 19 independent parameters of the iAMOEBA model: five due to intramolecular vibrations, two for van der Waals interactions, nine for permanent multipoles, and three for electronic polarization. This requires a discussion of the reference data set and the optimization method used to parameterize the model.
B. Reference Data
A significant challenge for model parameterization and validation is the choice of suitable reference data, which can be both experimental and theoretical in origin. For water we are fortunate that both experimental and theoretical reference data are plentiful,61,62 although this is often not the case for less studied materials and compounds. In this work, we apply a systematic and versatile optimization method (ForceBalance)50,51, which allows us to efficiently utilize combinations of experimental and theoretical data. Here we describe the different types of data used to parameterize iAMOEBA, which we summarize in Table 1. Due to the large size of the data set, the files are provided on the Web.63
Table 1.
Data references for parameterization of iAMOEBA (full tables online, Ref 63.) Orange: Condensed phase experimental data, 249 – 373 K (1 atm), 1 – 8000 bar (298 K). Green: Gas phase experimental data. Blue: Theoretical reference data. The objective function is a scaled sum of squared differences between the simulation results and the reference data; the scaling factors (equivalent to inverse weights) are given in the right column.
| Reference Data | Scaling Factor |
|---|---|
| Density ρ | 2 kg m−3 |
| Heat of Vaporization ΔHvap | 5 kJ mol−1 |
| Thermal Expansion Coefficient α | 10−4 K−1 |
| Isothermal Compresibility κT | 10−5 bar−1 |
| Isobaric Heat Capacity cP | 2 kg mol−1 K−1 |
| Dielectric Constant ε(0) | 2 |
| Gas Phase Dipole | 0.2 Debye |
| Gas Phase Quadrupole | 1.0 Debye Å |
| Gas Phase Vibrational Modes | 30 cm−1 |
| Water Dimer CCSD(T)/CBS Binding Energy, RMSD |
1.0 kcal mol−1, 0.1 Å |
| 21 Small Gas Phase Clusters (size 3–6) CCSD(T)/CBS Binding Energy, RMSD |
10.0 kcal mol−1, 2.0 Å |
| 18 Large Gas Phase Clusters (size 8–20) MP2/CBS Binding Energy, RMSD |
100.0 kcal mol−1, 2.0 Å |
| 48,000 MP2/aug-cc-pVTZ Potential Energies and Atomistic Forces |
σ(EQM), σ(FQM) |
Experimental measurements
The dominant paradigm in water model development is to fit the parameters to reproduce a set of experimentally measured condensed phase properties. Generally speaking, a diverse data set over a wide range of thermodynamic conditions improves the domain of applicability of the model, but it also increases the complexity of the optimization problem. In this work, we extend the parameterization data sets used in past studies to include six key experimental properties over a wide range of thermodynamic conditions: density, heat of vaporization, thermal expansion coefficient, isothermal compressibility, isobaric heat capacity, and dielectric constant. These properties are evaluated at 32 temperatures spanning a range of 249.15 – 373.15 K at atmospheric pressure, and 10 pressures from 1 – 8000 bar at 298.15 K. Our liquid simulations for the heat of vaporization were performed at atmospheric pressure rather than the vapor pressure, which introduces a negligible correction term at the temperature range studied. We also include experimentally known properties of the water monomer in the gas phase, in particular its dipole moment, quadrupole moment and vibrational frequencies. All of the experimental reference data, along with the theoretical reference data, is summarized in Table 1; the complete experimental data is provided in Supporting Tables S2 and S3, as well as on the Web.63
Theoretical reference data
In addition to experimental data, highly detailed theoretical calculations also provide valuable reference data for model development. Methods following this approach include potential fitting,64–66 force matching,50,67–69 and relative entropy70,71 methods, and they have found widespread success in building both atomistic and mesoscale (coarse grained) models. The general goal is to reproduce the accuracy of the highly detailed reference levels of theory with a comparatively simple and inexpensive classical model. Quantum chemistry methods such as Møller-Plesset perturbation theory,72 coupled-cluster theory72 and density functional theory73 are examples of reference theories used to develop atomistic models; they are impractical for many condensed-phase applications due to their high cost but provide valuable information on the electronic potential energy surface for smaller systems such as water clusters.
In this work, the theoretical reference data includes energies and gradients calculated at the DB-RIMP274–767heavy-aug-cc-pVTZ77 level of theory for over 48,000 cluster geometries extracted randomly from simulations of liquid water. These geometries are taken from condensed-phase simulations performed using the AMOEBA model at a temperatures ranging from 249.15 – 373.15 K and including cluster sizes ranging from 2 – 22 to minimize finite size effects. The calculations were performed using Q-Chem 4.0.78 We also include the optimal geometries and binding energies of 40 small water clusters ranging from 2 to 20 molecules. We have used the highest available level of theory for each cluster, with some of the largest calculations taken from literature benchmarks,79–84 and include multiple key geometries for the dimer, hexamer, and larger clusters where available. Most of the reference calculations of the binding energy allow the cluster and monomer geometries to fully relax, so our calculations using the model follow the same approach; we include the RMSD of the minimized cluster into the objective function in order to ensure that the iAMOEBA model provides energy-minimized clusters with the correct geometry. We also include ten dimer poses (the “Smith” dimer set)23 where the geometries are not relaxed, and only the interaction energies enter into the objective function. All of the data used in the parameterization of iAMOEBA is available on the Web.63
C. Optimization
Least squares optimization of force fields first began with the Consistent Force Field proposed by Lifson and Warshel in the 1960s.85 Hagler and coworkers first proposed removal of hydrogen vdW sites in order to description of hydrogen bonding.86 Other early efforts extended formal least squares optimization through use of ab initio calculations87 and application to bulk phase crystal modeling.88
ForceBalance50,51 (Figure 1) extends this prior work in several directions, including the ability to use a much larger and more diverse data set which includes experimental liquid phase measurements and ab initio calculations. Here we use ForceBalance to optimize the iAMOEBA parameters. The overall objective function is expressed as a weighted sum of squared residuals over the experimental and theoretical target data sets (weights and data types in Table 1). The exact gradient and approximate Hessian matrix of the objective function is derived from the first derivatives of the properties using the Gauss-Newton approximation. The Levenberg-Marquardt algorithm with an adaptive trust radius is used to perform an iterative minimization of the nonlinear least squares objective function.
Figure 1.
ForceBalance procedure. The calculation begins with an initial set of parameters (lower left), which is used to generate a force field and perform simulations. The objective function is a weighted sum of squared differences between the simulation results and the reference data, plus a regularization term that prevents overfitting. The optimization method updates the parameters in order to minimize the objective function.
There are significant challenges involved in using such a large experimental reference data set in an optimization scheme, because many of these properties are difficult to simulate to convergence for a single set of parameters, let alone fit via a parameter optimization method. Furthermore, computer simulations of condensed-phase properties suffer from statistical errors, and the errors are compounded when estimating the dependence of a particular property on the force field parameters. These difficulties can relegate the researcher to performing manual parameter searches guided by insight and evaluating models by inspection, which gives force field model parameterization some of its reputation as an onerous task or “black art”.
ForceBalance attempts to address these challenges in optimizing parameters to fit complex condensed phase properties. A key aspect of this approach is that we calculate analytic derivatives of the simulated properties with respect to the force field parameters using a new fluctuation formula similar to Hamiltonian Gibbs-Duhem integration.41 In the past, these derivatives have been evaluated by running multiple simulations with different parameter values,40,41 but statistical noise is a major problem. Here we recognize our properties of interest originate from averages and fluctuations in the isothermal-isobaric (NPT) ensemble. For instance, the ensemble average of a generic observable A that does not depend explicitly on the force field parameters (for example, the density or an order parameter) can be expressed as follows:
| (3) |
where A is the observable, r a given molecular configuration in a periodic simulation cell, λ the force field parameter, E the potential energy, β ≡ (kBT)−1 the inverse temperature, kB the Boltzmann constant, T the temperature, P the pressure, V the volume, Q the isothermal-isobaric partition function, and the angle brackets represent an ensemble average in the thermodynamic ensemble of the force field parameterized by λ. In practice, this integral is evaluated numerically using molecular dynamics or Monte Carlo simulation in the NPT ensemble.
Since the expression for A depends on λ only through the potential energy E, we can differentiate Equation 3 and obtain the analytic derivative (Equation 4):
| (4) |
In practice these calculations require the potential energy derivative, which we evaluate by postprocessing the simulation trajectory. This equation may be directly applied to obtain derivatives of ensemble-averaged observables that don’t contain explicit force field parameter dependence, such as the density ρ.
By contrast, the derivative of the enthalpy contains an extra partial derivative term, because the potential energy appears in the integrand:
| (5) |
The derivative of the heat of vaporization ΔHvap is given by subtracting the formulas for the liquid phase and gas phase enthalpies:
| (6) |
where H ≡ E + PV is the enthalpy and the subscripts g and l denote the gas and liquid phases. Here, we have invoked the ideal gas law so that the molecular volume of water vapor does not appear in the expression.
We note the derivative of an ensemble average property resembles a fluctuation property or second-order correlation function; the above equation is derived in a similar manner to the fluctuation formulas for second-order thermodynamic properties like the thermal expansion coefficient, isothermal compressibility, etc. The derivative of nearly any ensemble average property can be evaluated in this fashion, and we also have derived formulas for differentiating fluctuation properties. For example, the derivatives of the thermodynamic fluctuation formulas for the thermal expansion coefficient α, isothermal compressibility κT, isobaric heat capacity cp, and dielectric constant ε(0) resemble third-order fluctuations (Equations 7–10):
| (7) |
| (8) |
| (9) |
| (10) |
Here, M is the total dipole moment of the simulation cell, and the summation goes over the three Cartesian axes. We remark that although we have eliminated the compounded numerical noise from running multiple simulations, the derivative of an ensemble average property is intrinsically more difficult to estimate since it manifests as a fluctuation property, and the derivative of a fluctuation property manifests as a third-order fluctuation.
Finally, the different kinds of experimental and theoretical reference data used for parameterization have different physical units, so they require rescaling factors and weights in order to incorporate all data into an optimization scheme that minimizes a single objective function. The rescaling factor for each property is based on its intrinsic size and uncertainty from the simulation, and their values are given in Table 1.
Regularization
Although we included an unprecedented amount of reference data into our optimization, there is still the danger of overfitting. This arises because all of the simulated quantities emerge from the interactions in the model, which can easily have linear dependencies. Overfitting is treated by regularization, in which parameter values are penalized if they stray too far from their original values. Penalty functions have a natural interpretation in Bayesian statistics because they correspond to the negative logarithm of a prior distribution, analogous to how a potential energy function is the negative logarithm of a Boltzmann distribution.89 For example, a parabolic-shaped penalty function corresponds to a Gaussian prior distribution. The width of the prior distribution (and corresponding strength of the penalty function) represents our expectation of possible parameter values before introducing the parameterization data. The regularized objective function then corresponds to the posterior distribution.
The regularized optimization is more accurately described as performing maximum a posteriori estimation, instead of a formally Bayesian method which samples from the posterior distribution. Another important difference is that the “empirical Bayesian” methods treat the weights for reference data and the prior widths as nuisance parameters and samples over them, whereas we chose the weights and prior widths in this work by examining the physical scale and variability of each quantity. The reason for our approach is twofold. Given the high complexity of evaluating the objective function, a derivative-based optimization with predetermined weights and prior widths was the only feasible option with the current method and available resources. Furthermore, we found that perturbing the weights and prior widths by large amounts (∼50%) had minor effects on the behavior of the final model, but the same could not be said for perturbing force field parameters by a similar amount. In summary, the regularized optimization alleviates the task of manually selecting the highly sensitive force field parameters, but still requires the researcher to qualitatively specify the problem using his/her physical knowledge.
Our optimization was regularized using a Gaussian prior specified in Table 2. This corresponds to a parabolic penalty function in parameter space centered at the original AMOEBA parameter values with the chosen force constants. Since the various iAMOEBA parameters have different physical meanings (e.g. vdW well depth, O-H bond length), each parameter type was assigned its own prior width. We performed the optimization by first fitting only the theoretical data, because this was computationally less expensive. We then included the condensed phase properties and optimized the full objective function until fluctuations from numerical noise prevented further improvement. The full optimization converged to within the statistical error after about 10 nonlinear iterations, though we performed several optimizations with different choices of weights for the reference data and prior widths before arriving at the final answer.
Table 2.
Potential parameters for AMOEBA (Ref. 45) and iAMOEBA (this work). The prior widths are used in regularization.
| Parameter Name | Units | AMOEBA | iAMOEBA | Prior Width |
|---|---|---|---|---|
| O-H Equilibrium Bond Length | Å | 0.9572 | 0.9584 | 0.1 |
| O-H Bond Force Constant | kcal/mol/Å2 | 529.6 | 557.63 | 50 |
| H-O-H Equilibrium Angle | Degree | 108.5 | 106.48 | 5 |
| H-O-H Angle Force Constant | kcal/mol/Å2 | 34.05 | 49.90 | 40 |
| H-H Urey-Bradley Length | Å | 1.5537 | 1.5357 | N/Aa |
| H-H Urey-Bradley Force Constant | kcal/mol/Å2 | 38.25 | −10.31 | 25 |
| Oxygen vdW Sigma | Å | 3.405 | 3.6453 | 0.3 |
| Oxygen vdW Epsilon | kcal/mol | 0.11 | 0.19682 | 0.1 |
| Hydrogen vdW Sigma | Å | 2.655 | 0 | N/Ab |
| Hydrogen vdW Epsilon | kcal/mol | 0.0135 | 0 | N/Ab |
| Hydrogen vdW Reduction Factor | None | 0.91 | 0 | N/Ab |
| Oxygen Charge | e | −0.51966 | −0.59402 | 0.4 |
| Oxygen Dipole Z-component | e bohr | 0.14279 | 0.08848 | 0.1 |
| Oxygen Quadrupole XX-component | e bohr2 | 0.37928 | 0.22618 | 0.2 |
| Oxygen Quadrupole YY-component | e bohr2 | −0.41809 | −0.32244 | 0.2 |
| Oxygen Quadrupole ZZ-component | e bohr2 | 0.03881 | 0.09626 | 0.2 |
| Hydrogen Charge | e | 0.25983 | 0.29701 | 0.4 |
| Hydrogen Dipole X-component | e bohr | −0.03859 | −0.09391 | 0.1 |
| Hydrogen Dipole Z-component | e bohr | −0.05818 | −0.12560 | 0.1 |
| Hydrogen Quadrupole XX-component | e bohr2 | −0.03673 | 0.18754 | 0.2 |
| Hydrogen Quadrupole YY-component | e bohr2 | −0.10739 | 0.02174 | 0.2 |
| Hydrogen Quadrupole XZ-component | e bohr2 | −0.00203 | −0.03635 | 0.2 |
| Hydrogen Quadrupole ZZ-component | e bohr2 | 0.14412 | −0.20928 | 0.2 |
| Oxygen Polarizability | Å3 | 0.837 | 0.80636 | 0.1/0.2c |
| Hydrogen Polarizability | Å3 | 0.496 | 0.50484 | |
| Polarization Damping Factor | Å−1 | 0.39 | 0.23616 | 0.2 |
The Urey-Bradley equilibrium length is determined from the O-H bond length and H-O-H angle parameters using the law of cosines.
iAMOEBA does not contain hydrogen vdW interactions.
The polarizability parameters were optimized in terms of their sum (αo + 2αH, prior width 0.1 Å3) and their ratio (αo/αH, prior width 0.2).
In order to perform the simulations of condensed phase properties, ForceBalance interfaces with existing simulation software. To meet the high requirements for accuracy in the simulated properties, we used a combination of powerful and complementary methods in simulation software and distributed computing. The condensed phase simulations in the optimization used OpenMM,90–92 a GPU-accelerated molecular dynamics software package with an extensively validated implementation of AMOEBA, which provides a speedup of an order of magnitude. At each optimization step, the set of 42 simulations at different phase points is performed simultaneously on multiple GPU clusters; the Work Queue library93–95 allows ForceBalance to act as a distributed computing server and coordinate many OpenMM simulations running on multiple compute nodes in different physical locations. Finally, the data from the finished simulations was analyzed using the multistate Bennett acceptance ratio estimator (MBAR),96,97 which allows each simulation to contribute to the estimated property of the each other simulation. This combination of methods allowed us to optimize the condensed phase properties very accurately. A combination of the OpenMM and TINKER98 software packages were used to evaluate the potential energies, forces, binding energies, and monomer properties for comparison with the ab initio and gas phase reference data. ForceBalance50, TINKER98, OpenMM92, and Work Queue95 are freely available on the Web.
RESULTS
A. iAMOEBA Parameters
Table 2 provides the optimized parameters for the iAMOEBA water model. Parameter files in the TINKER and OpenMM formats are provided on the Web.63 The Gaussian prior widths in Table 2 are given to ForceBalance as inputs for the optimization, and they enter into the objective function as harmonic restraints in the parameter space. Our choices for the prior widths represent our expectation that the parameters should not deviate from the initial AMOEBA values by more than these amounts, though ultimately the deviation in the parameter is also strongly affected by its importance in minimizing the objective function.
The first six rows contain the intramolecular parameters for iAMOEBA. The equilibrium bond length is essentially unchanged from the initial AMOEBA value. The force constants are changed more significantly; the original AMOEBA model reverses the symmetric and antisymmetric vibrational frequency order, and the iAMOEBA parameters restore the correct order. The equilibrium HOH angle parameter is reduced by 2 degrees, which gives energies and atomistic forces in better agreement with ab initio calculations; however, as with all flexible models that lack intramolecular charge transfer, the angle contracts in the liquid phase relative to the gas phase value, in contrast to experimental measurements which indicate an expansion of the angle.99,100 The liquid phase angle of iAMOEBA at room temperature and atmospheric pressure is 103° with a standard deviation of 4°, which is smaller than the value of 105–106° inferred from experiment101 and ab initio molecular dynamics simulation.102 The rationale for choosing an artificially large angle parameter of 108.5° in the original AMOEBA model was to reproduce the correct angle in the liquid phase, which aided in reproducing experimental liquid properties such as the dielectric constant; however, as we will see, iAMOEBA is able to accurately predict a broad range of condensed phase properties despite having a reduced bond angle value in the liquid phase.
The next two rows contain the vdW parameters, followed by twelve rows containing the permanent multipole parameters (only nine of which are independent, due to the constraint of charge neutrality and use of traceless quadrupoles). iAMOEBA has a larger vdW radius and well depth compared to AMOEBA, which is largely due to the vdW interaction sites being removed from hydrogen (see the section on liquid structure for more details). The next twelve rows contain the permanent electrostatic parameters. The charges are increased in magnitude, but the deviations in the higher-order electrostatic parameters show no clear pattern. The hydrogen quadrupole parameters have the most significant deviations with three out of four parameters changing sign from the initial AMOEBA values; this is probably related to alterations in the hydrogen interactions due to removing the vdW interactions, and/or the reduced angle in the condensed phase. Despite the large changes from the AMOEBA parameters, the iAMOEBA model gives very good agreement with the molecular multipole moments at the gas phase optimal geometry (Supporting Table S2).
The polarizability parameters are perhaps the most interesting due to the direct polarization approximation. Direct polarization implies that the atomic polarizabilities are additive and the molecular polarizability is isotropic, unless atomic polarizability tensors are used. While the atomic polarizability is additive with respect to an externally applied electric field, polarization effects become nonadditive for multipole interactions at short range due to iAMOEBA’s use of Thole damping. Our initial parameters were taken to be 80.4% of the AMOEBA values, such that their sum was equal to the molecular polarizability of the AMOEBA model (1.47 Å3). The optimization resulted in parameters that were significantly larger, resulting in a molecular polarizability of 1.82 Å3, or an increase of 23%. This agrees with our intuition that iAMOEBA determines the electronic polarization without any further induction, which would require a stronger response to the permanent multipoles. To compensate for this stronger response, the Thole damping factor is significantly reduced from the value used by AMOEBA, resulting in increased damping at short range.
B. Quality of Fit to Parameterization Data
In this section we analyze the quality of fit that the iAMOEBA model obtains for the parameterization data listed in Table 1. Figure 2 shows the iAMOEBA, AMOEBA, and experimental density as a function of temperature over the temperature range 245 – 373 K at atmospheric pressure. The AMOEBA water model was only fit to the density and heat of vaporization at 25 °C, but yields a temperature of maximum density (TMD) of 20 ± 2 °C, with the overall temperature dependence being approximately correct (blue line). If we use a direct polarization model with the AMOEBA parameters (i.e. turning off the mutual polarization), the result is qualitatively incorrect (dashed green line); the density decreases monotonically with temperature and the heat of vaporization is 5 kJ/mol too low (Supporting Figure S1). Optimizing the parameters of the direct polarization iAMOEBA model using ForceBalance (solid green line) gives a TMD of 4 ± 2 °C that is closer to experiment compared to the original AMOEBA model, and the accuracy of the simulated density agrees with experiment to within 0.3 % over the entire temperature range. Numerical values are given in Table 3.
Figure 2.
Density of liquid water over the temperature range 249 – 373 K at atmospheric pressure. The AMOEBA model from 2003 (blue line) uses mutual polarization. The direct polarization model gives a qualitatively incorrect result if the AMOEBA parameters are used (dashed green line). Optimizing the parameters of the direct polarization model leads to iAMOEBA (solid green line), which reproduces the experimental density and TMD for the whole temperature range.
Table 3.
Experimental and simulation data from different water models. TIP3P and TIP4P/2005 data and percent tolerances for determining the numerical score (% tol. column) are reproduced from Ref. 39. All AMOEBA properties (except for melting properties) and iAMOEBA properties are calculated in this work. Cells with a green background indicate properties that are part of the parameterization data set; they are excluded from the average score for iAMOEBA. The liquid structure was not included in the score; see instead Figure 4. The phase diagram is scored qualitatively following Ref. 39.
| Property | Experiment | % tol. | TIP3P | TIP4P/2005 | AMOEBA | iAMOEBA | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Quantity | Score | Quantity | Score | Quantity | Score | Quantity | Score | |||
| Enthalpy of phase change / kcal mol−1 | ||||||||||
| ΔHmelt | 1.44 | 5 | 0.3 | 0 | 1.16 | 6 | * | 1.19 | 7 | |
| ΔHvap | 10.52 | 2.5 | 10.05 | 8 | 11.99 | 4 | 10.48 | 10 | 10.94 | 8 |
| Critical point properties | ||||||||||
| Tc/K | 647.1 | 2.5 | 578 | 6 | 640 | 10 | 581 (2) | 6 | 622 | 8 |
| ρc/g cm−3 | 0.322 | 2.5 | 0.272 | 4 | 0.337 | 8 | 0.334 | 9 | 0.333 | 9 |
| pc/bar | 220.64 | 5 | 126 | 1 | 146 | 3 | 183 | 7 | 201 | 8 |
| Surface tension / mN m−1 | ||||||||||
| σ300K | 71.73 | 2.5 | 52.3 | 0 | 69.3 | 9 | 64 (4) | 6 | 68.3 (11) | 8 |
| σ450K | 42.88 | 2.5 | 24.7 | 0 | 41.8 | 9 | 32 (2) | 0 | 38.4 (7) | 6 |
| Melting properties | ||||||||||
| Tm/K | 273.15 | 2.5 | 146 | 0 | 252 | 7 | * | 261 (2) | 8 | |
| ρliq/g cm−3 | 0.999 | 0.5 | 1.017 | 6 | 0.993 | 9 | * | 0.999 | 10 | |
| ρsolid/g cm−3 | 0.917 | 0.5 | 0.947 | 3 | 0.921 | 9 | * | 0.929 | 7 | |
| dp/dT (bar K−1) | −137 | 5 | −66 | 0 | −135 | 10 | * | −141 | 10 | |
| Orthobaric densities and TMD | ||||||||||
| TMD/K | 277 | 2.5 | 182 | 0 | 278 | 10 | 292 (2) | 8 | 277 (1) | 10 |
| ρ298K/g cm−3 | 0.997 | 0.5 | 0.98 | 7 | 0.993 | 9 | 1.000 | 9 | 0.997 | 10 |
| ρ400K/g cm−3 | 0.9375 | 0.5 | 0.868 | 0 | 0.93 | 8 | 0.928 | 8 | 0.934 | 9 |
| ρ450K/g cm−3 | 0.8903 | 0.5 | 0.791 | 0 | 0.879 | 7 | 0.858 | 3 | 0.883 | 8 |
| Isothermal compressibility (10−6 / bar) | ||||||||||
| κT [1 bar; 298 K] | 45.3 | 5 | 57.4 | 5 | 46 | 10 | 66 (1) | 1 | 41.1 (4) | 8 |
| κT [1 bar; 360 K] | 47 | 5 | 79.2 | 0 | 50.9 | 8 | 65 (1) | 2 | 45.4 (4) | 9 |
| Gas properties | ||||||||||
| pv [350K] (bar) | 0.417 | 5 | 0.56 | 3 | 0.13 | 0 | 0.43 (5) | 9 | 0.39 (5) | 9 |
| pv [450K] (bar) | 9.32 | 5 | 11.72 | 5 | 4.46 | 0 | 17.3 (1) | 0 | 9.8 (1) | 9 |
| B2 [450K] (cm3 mol−1) | −238 | 5 | −476 | 0 | −635 | 0 | −214 | 8 | −269 | 7 |
| Heat capacity at constant pressure / cal mol−1 K−1 | ||||||||||
| Cp [liq 298 K; 1 bar] | 18 | 5 | 18.74 | 9 | 21.1 | 7 | 21.3 | 6 | 18.0 (2) | 10 |
| Cp [ice 250 K; 1 bar] | 8.3 | 5 | * | 0 | 14 | 0 | 9.4 (7) | 7 | 8.5 (1) | 10 |
| Static dielectric constant | ||||||||||
| ε [liq; 298 K] | 78.5 | 5 | 94 | 6 | 58 | 5 | 81.4 (14) | 9 | 80.7 (11) | 9 |
| ε [Ih; 240 K] | 107 | 5 | 19 | 0 | 53 | 0 | * | 96 (3) | 8 | |
| Ratio | 1.36 | 5 | 0.2 | 0 | 0.91 | 3 | * | 1.19 (4) | 8 | |
| Tm-TMD-Tc ratios | ||||||||||
| Tm[Ih]/Tc | 0.422 | 5 | 0.253 | 2 | 0.394 | 9 | * | 0.416 | 10 | |
| TMD/Tc | 0.428 | 5 | 0.315 | 5 | 0.434 | 10 | 0.503 | 6 | 0.445 | 9 |
| TMD-Tm (K) | 3.85 | 5 | 36 | 4 | 26 | 6 | * | 18 | 7 | |
| Densities of ice polymorphs / g cm−3 | ||||||||||
| ρ[Ih 250 K; 1 bar] | 0.92 | 0.5 | * | 0 | 0.921 | 10 | 0.894 | 4 | 0.930 | 8 |
| ρ[II 123 K; 1 bar] | 1.19 | 0.5 | 1.219 | 5 | 1.199 | 8 | 1.211 | 6 | 1.180 | 8 |
| ρ[V 223 K; 5.3 kbar] | 1.283 | 0.5 | * | 0 | 1.272 | 8 | 1.277 | 9 | 1.263 | 7 |
| ρ[VI 225 K; 11 kbar] | 1.373 | 0.5 | 1.366 | 9 | 1.38 | 9 | 1.384 | 8 | 1.364 | 9 |
| EOS high pressure | ||||||||||
| ρ[373 K; 10 kbar] | 1.201 | 0.5 | 1.211 | 8 | 1.204 | 10 | 1.246 | 3 | 1.189 | 8 |
| ρ[373 K; 20 kbar] | 1.322 | 0.5 | 1.34 | 7 | 1.321 | 10 | 1.373 | 2 | 1.303 | 7 |
| Self-diffusion coefficient / cm2 s−1 | ||||||||||
| ln D278K | −11.24 | 0.5 | −10.2 | 0 | −11.27 | 9 | −11.68 | 2 | −11.15 | 8 |
| ln D298K | −10.68 | 0.5 | −9.81 | 0 | −10.79 | 8 | −10.82 | 7 | −10.58 | 8 |
| ln D318K | −10.24 | 0.5 | −9.67 | 0 | −10.39 | 7 | −10.45 | 6 | −10.19 | 9 |
| Ea/kJ mol−1 | 18.4 | 5 | 9.7 | 1 | 16.2 | 8 | 19.6 | 9 | 18.8 | 10 |
| Shear viscosity / mPa s | ||||||||||
| η[1 bar; 298 K] | 0.896 | 5 | 0.321 | 0 | 0.855 | 9 | 1.08 (5) | 6 | 0.85 (2) | 9 |
| η[1 bar; 373 K] | 0.284 | 5 | 0.165 | 2 | 0.289 | 10 | 0.25 (2) | 8 | 0.28 (2) | 10 |
| Orientational relaxation time / ps | ||||||||||
| τ2HH[1 bar; 298 K] | 2.36 | 5 | 0.8 | 0 | 2.3 | 9 | 1.94 (2) | 6 | 2.41 | 10 |
| Structure | ||||||||||
| χ2(F(Q)) | 0 | 5 | * | 4 | 8.5 | 8 | * | * | ||
| χ2(overall) | 0 | 5 | * | 4 | 14.8 | 7 | * | * | ||
| Phase diagram | N/A | N/A | 2 | 8 | 8 | |||||
| Overall score (out of 10) | 2.6 | 7.1 | 5.9 | 8.4 | ||||||
We also used the second-order thermodynamic properties of water to parameterize iAMOEBA, which include the thermal expansion coefficient, isothermal compressibility, isobaric heat capacity and dielectric constant. Their temperature dependence is shown in Supporting Figures S2–S5. At 25 °C the simulated values for second-order properties agree with experiment to within 10%, but the deviations become slightly more significant at the temperature extremes. The isothermal compressibility is too low across the entire temperature range, which we were not able to improve further.
Figure 3 illustrates the quality of fit for the ab initio data for a representative water cluster from the liquid. The MP2 and iAMOEBA forces are shown using blue and gold vectors, respectively. The strongest components of the force are often in the intramolecular degrees of freedom, which reflects the fact that forces tend to be stronger along degrees of freedom with higher force constants. This demonstrates the importance of explicitly looking at intermolecular forces, which we have done here by equally partitioning the force contribution into an atomistic, net force, and net torque component following Ref. 67.
Figure 3.
Illustration of iAMOEBA fit to theoretical data. The atomistic forces from the QM reference method (blue) and iAMOEBA model (yellow) are shown for a representative configuration of a water 7-mer extracted from the liquid. The relative RMS force error is 24% over all configurations. Inset: Scatter plot of cluster relative potential energies. Blue color indicates a higher density of points; diagonal line indicates zero error.
The RMS error of the iAMOEBA atomistic forces relative to the MP2 values is 24% (statistical error <1%) for all 2400 clusters of this size in the data set; the errors in the intermolecular forces and torques are 32 and 33%, respectively. By comparison, the AMOEBA model has atomistic / net force / net torque errors of 37% / 31% / 23%, and the flexible TIP3P model has much larger errors of 43% / 61% / 66%. This comparison indicates that polarizable force fields may be more appropriate for describing intermolecular interactions, since the pairwise-additive force fields are mainly designed to recapitulate bulk properties. The AMOEBA and iAMOEBA models perform comparably at predicting the intermolecular forces from this data set; although AMOEBA performs slightly better for torques, the force errors of 24–37% for both models are still somewhat large. We remark that it is possible to match the ab initio forces to 10–15% error if we had solely focused on force matching without any other reference data, but this could worsen the overall accuracy of the model for describing the condensed phase properties of water (see Discussion section).
Supporting Figures S6–S7 shows the quality of fit for the binding energies of geometry-optimized clusters on a linear and log scale. iAMOEBA finds a 5.09 kcal/mol binding energy for the dimer, while AMOEBA yields 4.98 kcal/mol relative to the experimental value of 4.99 kcal/mol. For larger clusters, iAMOEBA systematically underestimates the binding energies, slightly more than AMOEBA. This indicates that mutual polarization likely plays an important role in obtaining a size-consistent description of cluster binding energies. We remark that AMOEBA does a very good job at predicting the ab initio binding energies for all of the clusters, despite having been parameterized using only a subset of the dimer and hexamer conformations. iAMOEBA and AMOEBA are both able to accurately reproduce the optimal structures of the water clusters; the RMSDs to the reference QM-optimized structures are below 0.15 Å for all of the clusters in the parameterization data set; in particular, the RMSD of the iAMOEBA-minimized water dimer is 0.043 Å. The O-O distance of the water dimer is 2.836 Å in iAMOEBA, which is shorter than the values of 2.912 Å and 2.892 Å from the QM-optimized structure and AMOEBA. The flap angle between the O-O vector and the H-O-H bisector vector of the acceptor molecule is 54.9 degrees from iAMOEBA, compared to 55.2 degrees from the QM-optimized structure and 57.2 degrees from AMOEBA.
While it is possible to obtain a more precise fit to the ab initio data, the utility of this data set is to ensure that the potential energy surface is qualitatively correct; the main goal is to accurately reproduce the experimental condensed phase properties. We return to this parameterization decision in the Discussion section.
C. Model Testing and Validation
The predictive power of the iAMOEBA model is tested using properties outside of the fitting set (Table 3, uncolored cells). All validation properties were computed using the TINKER molecular dynamics software,98 which provides a reference implementation of iAMOEBA. Here we include a comprehensive test set of properties taken from Ref. 36, which provides a scoring system on a ten-point scale derived from the accuracy of the model prediction relative to specified tolerance thresholds. The properties include thermodynamic and kinetic properties at a wide range of conditions, most of which are outside our parameterization data set; they cover the solid, liquid, and gas phases of water, focusing mainly on the liquid but also emphasizing reproducibility of the ice phases. The average of all property scores gives an overall score of the model from 0 – 10, which gives a general sense of the water model quality at a glance. To ensure a fair comparison, our average score excludes all properties that were used in the parameterization (highlighted in green in Table 3). We calculated an overall score of 8.4 out of 10 for iAMOEBA because of its excellent agreement for all of the tested properties. Furthermore, the liquid properties calculated using iAMOEBA compare favorably with a collection of well-established42,44,108 and newly developed103,107 polarizable water models in the literature (Table 4).
Table 4.
Properties of water calculated using several polarizable models and compared to experimental measurements. Liquid bulk properties are measured at 298 K, 1 bar; TMD and Tm are measured at 1 bar, and Tc is determined for the critical pressure of the model. Numbers in parentheses indicate the statistical error in terms of the least significant digit, where available. AMOEBA and iAMOEBA properties were calculated in this work. SWM4-DP and SWM6 properties are from Reference 103, except for the melting point37 and critical point104 of SWM4-DP. TTM3-F properties are from References 44,105,106. GCPM properties are from References 107,108. BK3 properties are from Reference 107.
| Property | Experiment | AMOEBA | SWM4-NDP | TTM3-F | GCPM | SWM6 | BK3 | iAMOEBA |
|---|---|---|---|---|---|---|---|---|
| ρ / g cm−3 | 0.997 | 1.000 | 0.994 (2) | 0.994 | 1.007 | 0.996 (2) | 0.9974 (2) | 0.997 |
| ΔHvap / kcal mol−1 | 10.52 | 10.48 | 10.44 | 11.4 | 11.30 | 10.52 | 10.94 | 10.94 |
| α / 10−4 K−1 | 2.56 | 1.9 (6) | 4.2 | 3.01 (8) | 2.5 (1) | |||
| κT / 10−6 bar−1 | 45.3 | 66 (1) | 44.4 (7) | 41.1 (4) | ||||
| Cp / cal mol−1 K−1 | 18.0 | 21.3 (5) | 22.5 | 22.0 (2) | 18.0 (2) | |||
| ε(0) | 78.5 | 81.4 (14) | 78.0 (14) | 67.7 | 84 | 78.1 (28) | 79 (3) | 80.7 (11) |
| D0 / 10−5 cm2 s−1 | −10.68 | 2.0 | 2.85 (28) | 2.37 | 2.26 | 2.14 (19) | 2.28 (4) | 2.54 (2) |
| η / mPa s | 0.896 | 1.08 (5) | 0.66 (9) | 0.87 (12) | 0.95 (1) | 0.85 (2) | ||
| TMD / K | 277 | 292 (2) | < 220 | 255 | 235 | 275 (3) | 277 (1) | |
| Tm / K | 273.15 | < 120 | 248 (2) | 250 (3) | 261 (2) | |||
| Tc / K | 647.1 | 581 (2) | 576 | 642 | 629 (5) | 622 |
Liquid phase thermodynamic properties
These properties include the density, thermal expansion coefficient, isothermal compressibility, and isobaric heat capacity; they are so categorized by their derivation from the thermodynamic ensemble as equilibrium averages and fluctuations from equilibrium. We expect iAMOEBA to reproduce these properties reasonably well because they were already included as part of the parameterization data set (though not at the same thermodynamic conditions). The density of liquid iAMOEBA water agrees with experiment to within the simulation uncertainty (roughly 0.3%) for thermodynamic conditions ranging from 249.15 – 373.15 K and up to 1 kbar. Small deviations of up to one percent are observed at very high temperatures (450 K) and pressures (10 kbar). The heat of vaporization is 10.94(1) kcal mol−1 at 298.15 K, which is higher than the experimental value of 10.52 kcal mol−1; the temperature trend also has a larger slope compared to experiment. This insufficiency is due to well-known quantum nuclear effects on the heat capacity, since at lower temperatures the faster vibrational degrees of freedom are frozen out.
The fluctuation properties also show good trends with experiment though they are less accurate, similar to what we found for the parameterization data set for these same properties. The isothermal compressibility is 10% too low at 298 K, and the error increases with lower temperatures; there exists a shallow minimum in the compressibility at 301 – 317 K, which is near the experimental value of 319 K. The isobaric heat capacity agrees very well with experiment at 298 K, but the heat capacity drops with temperature too quickly; again, this is likely due to nuclear quantum effects. The temperature trends of the heat capacity and enthalpy of vaporization can be brought into closer agreement with experiment by applying quantum vibrational corrections,40 but we decided not to apply these corrections due to their large impact on the absolute value of the heat capacity.
Liquid phase kinetic properties
Kinetic properties constitute an important test for iAMOEBA, particularly because no kinetic properties were fitted. We calculated the self-diffusion constant corrected for finite size effects,109 the shear viscosity, and the orientational relaxation time at different temperatures. The self-diffusion constant for iAMOEBA at 298 K, 1 atm is 2.54(2) × 10−9 m2 s−1 (experiment: 2.30) and the temperature trend shows excellent agreement with experiment as shown by the activation energy from the Arrhenius rate law (Supporting Figure S8). The shear viscosity and orientational relaxation times also show very good agreement with experiment.
The infrared (IR) spectrum of water contains a wealth of information on the kinetic properties. In Figure 4, we show the calculated IR spectrum from iAMOEBA and the experimental IR spectrum on an arbitrary intensity scale. We also included the predictions from the TTM3-F model,44 which was parameterized to reproduce the IR spectrum of water, and the flexible SPC/Fw model.110 The spectra were generated by applying the quantum harmonic approximation to the Fourier-transformed dipole autocorrelation function of a classical MD trajectory. The peaks around 3500 cm−1 and 1650 cm−1 correspond to vibrations of the O-H bond and the H-O-H angle, respectively; both TTM3-F and iAMOEBA predict the correct frequency shift from the gas phase values, but iAMOEBA and SPC/Fw do not predict the correct relative intensities. This is almost certainly due to the absence of intramolecular charge transfer111 (also known as charge flux52,112) in the functional forms of iAMOEBA and SPC/Fw, which is required for a proper description of the dipole moment surface and which is included in the TTM3-F model. iAMOEBA and SPC/Fw both predict a slight splitting of the 3500 cm−1 peak corresponding to the symmetric and antisymmetric stretch frequencies; we postulate that including intramolecular charge transfer terms would broaden these peaks and lead to better agreement with experiment. Another promising route toward quantitative reproduction of the IR spectrum would be to account for nuclear quantum effects explicitly by reparameterizing the model for path integral molecular dynamics simulations.113,114 The peaks below 1000 cm−1 correspond to librational and slower degrees of freedom. Here, both iAMOEBA and TTM3-F present a low-frequency shoulder below 300 cm−1, whereas the SPC/Fw spectrum does not present this feature; this is thought to be a characteristic of polarizable water models, but more analysis is needed in order to establish this link.
Figure 4.
IR spectra of liquid water, measured using experiment and calculated using the SPC/Fw, TTM3-F, and iAMOEBA models. Experimental and TTM3-F data taken from Ref. 115. Gray bars represent gas phase vibrational frequencies from experiment. Inset: Magnification of the far IR region (< 1000 wavenumber).
Liquid structure
The partial radial distribution functions (RDFs) are an important indicator of liquid structure and connections to X-ray and neutron liquid diffraction.28,116–119 For water, the oxygen-oxygen RDF, gOO(r), is especially well captured in an X-ray scattering experiment due to oxygen’s high atomic number relative to hydrogen. Figure 5, left panel, shows the gOO(r) of water from iAMOEBA (green) along with an experimentally derived RDF from X-ray scattering data taken by Hura and coworkers at the Advanced Light Source (ALS, black).116 The agreement with experiment is good to within the distribution of past experimental derivations from X-ray and neutron diffraction data (Supporting Figure S9). The O-H and H-H RDFs are provided in Supporting Figures S10 and S11 and compared to experimentally derived gOH(r) and gHH(r) from neutron scattering data.118 Figure 5, right panel, compares the simulated X-ray scattering intensity from iAMOEBA and the ALS experimental data; the comparison is again favorable across all momentum transfer vectors, under assumptions of the electron density derived from the modified atomic form factors developed in Ref. 116. Both real-space and momentum-space comparisons indicate that iAMOEBA reproduces the structure of water at room temperature very accurately. Since we did not follow the exact procedure in Ref. 120 for quantifying the accuracy of the structure, this property was not included in the overall numerical score.
Figure 5.
O-O radial distribution function (left) and X-ray scattering intensity (right) from ALS X-ray data (black line), the final iAMOEBA model (green line), and an intermediate version of the model with hydrogen vdW interaction sites (blue dotted line). The model with hydrogen vdW interactions deviates significantly from experiment in the low-Q region of the intensity plot.
During the optimization, we monitored the gOO(r) and X-ray intensity plot for agreement with experiment, though we did not explicitly include it in the optimization. In an intermediate stage of the optimization, we found that our model was performing poorly for the liquid structure prediction (blue dotted line) with significant deficiencies in the low-Q region of the X-ray intensity plot. After trying a number of modifications, we found that the agreement with experiment was completely recovered by eliminating the vdW interactions involving hydrogen; thus, the final iAMOEBA model has spherically symmetric vdW interactions centered on oxygen. Interestingly, while the choice of vdW functional form has a significant impact on the agreement with liquid structure, other properties were found to be in equally good agreement with experimental data whether hydrogen van der Waals interactions were included or not included.
Vapor and critical properties
The vapor and critical properties include the heat of vaporization, the vapor pressure, the surface tension, and the critical point; none of these properties were included in the optimization. These properties are very important tests for a polarizable model because the dipole moment of water molecules differs significantly between the vapor and liquid phases.102,121,122 By contrast, nonpolarizable water models have a fixed molecular dipole moment that is parameterized to the liquid phase value in order to reasonably reproduce liquid properties. One consequence is that the fixed charge models overestimate the attraction between water molecules in the gas phase. These errors are demonstrated by the second virial coefficient and the vapor pressure, where nonpolarizable models significantly underestimate the experimental value.
We calculated the second virial coefficient and the liquid-vapor coexistence line of iAMOEBA up to the critical point. The calculated critical properties are in good agreement with experiment; the critical temperature and pressure are underestimated by a few percent. The vapor pressures and second virial coefficient also have good agreement with experiment. The accuracy of iAMOEBA exceeds AMOEBA in the neighborhood of the critical point; this is because iAMOEBA was explicitly optimized to reproduce densities at higher temperatures.104 In general, the vapor and critical properties confirm that iAMOEBA with its direct polarization approximation is a highly viable model for water.
Ice, melting properties and phase diagram
The melting point of ordinary ice (ice Ih) in the iAMOEBA model is calculated using direct coexistence simulation to be 261 ± 2 K at 1 atm, 12 degrees below the experimental value of 273.15 K (Figure 6). The enthalpy of melting is about 15% lower than the experimental value. The agreement with experiment is very good in the context of comparing with other models; however, there is a temperature gap of 16 K between the freezing point and the TMD (experimental gap 4K). The overestimation of the TMD-Tm difference is a consistent trend across classical water models37–39 although promising results have been obtained using force-matching on configurations sampled from both water and ice.123 Since isotope effects are known to significantly affect the freezing point of water, it remains to be seen whether nuclear quantum effects can provide a further improved description of this important property.
Figure 6.
Determination of the iAMOEBA melting point by direct coexistence simulation. The initial configuration contains equal parts ice Ih and liquid water. Simulations run at temperatures below the freezing point of the model turned to ice (top), while simulations above the freezing point turned to liquid (bottom).
Water also forms many high-density ice polymorphs at high pressure; they constitute an interesting test for iAMOEBA because we did not include any ice properties in the reference data. However, the diverse geometries of hydrogen bonding networks in different phases of ice show the versatility of water hydrogen bonding networks in different configurations, and we expect the ab initio calculations helped to serve as a guide in parameter space for describing these interactions correctly. The tests focus on the stable, crystalline, proton-disordered ice polymorphs; this rules out metastable ice phases (IV, XII) and extremely high-pressure phases (> 100 kbar) where the individual water molecules dissociate. This leaves us with ices II, III, V, VI and VII. iAMOEBA generally predicts the densities of the ice phases to be in generally good agreement with experiment, although there is a small systematic underestimation of roughly 1%.
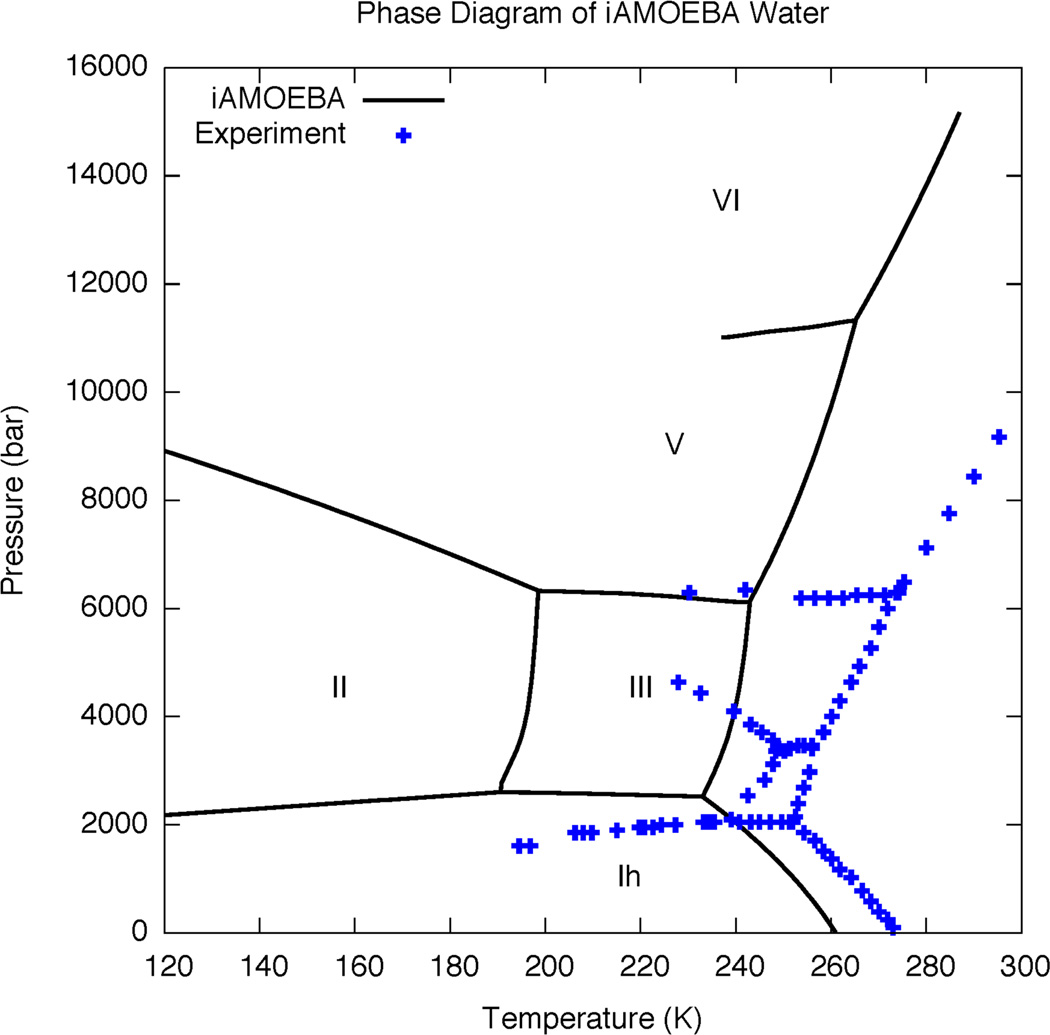
The phase diagram shows the phase with the lowest free energy at different thermodynamic conditions, with each line on the diagram indicating a coexistence line between two phases. Figure 7 shows the phase diagram of the iAMOEBA water model compared to experiment, which represents the first time the calculated phase diagram has been shown for any polarizable water model. To calculate the phase diagram, we first determined the melting point of each phase of ice using direct coexistence simulations with the liquid39 (Supporting Figure S13). Following this, we numerically integrated the Clapeyron equation to provide the melting curves.36,38,124 Two melting curves meet at a triple point, from which we integrated the Clapeyron equation to obtain the solid-solid coexistence lines; we continued to propagate solid-solid coexistence lines from triple points and arrived at the phase diagram shown in Figure 7. The qualitative structure of the phase diagram is correct, with ice phases Ih, II, III, V and VI all appearing in the correct relative positions. This is a surprisingly difficult test for water models; to date, the only models that are known to reproduce the qualitative structure of the phase diagram are those that adopt the TIP4P functional form. By contrast, the TIP3P and TIP5P models predict qualitatively incorrect phase diagrams, in which ordinary ice only exists under large tensions (negative pressures).38 In the low pressure region (< 2500 bar), our calculated phase diagram is quantitatively accurate; the melting point is consistently underestimated by 12–15 degrees, and the slope of the melting curve and the Ih-III transition pressure is correct to within 200 bar (10% of the total pressure). However, at higher pressures, the slopes of the melting curves are too high, and the solid-solid coexistence lines are also predicted to be too high. Following the scoring system in Ref. 36, we assigned 8 points out of 10 for the phase diagram, based on the observation that four phases of ice appeared in the correct relative positions.
Figure 7.
Phase diagram of iAMOEBA water model compared to experiment (blue crosses). Experimental data adapted from Ref. 38.
Dielectric properties
The dielectric constant should be a property for which polarizable models perform well due to their focus on properly describing the molecular electrostatics. Our simulated value for the dielectric constant agrees with experiment with a value of 81 ± 1 at 298 K (experiment: 78.3), and the trend is correct across the entire temperature range although we overestimate the experimental value by 2–3. Polarizable models also allow us to calculate the dielectric constant of ice, where the water molecules are expected to have a larger dipole moment than the liquid. We calculated the dielectric constant of ice Ih using the electrostatic switching method125 and found that iAMOEBA correctly predicts a higher dielectric constant in ice Ih compared to the liquid, although the ratio is a bit lower than the experimental value (Table 3); this is where full mutual polarization may be important. Non-polarizable models, on the other hand, incorrectly predict the ratio to be less than one, largely due to their fixed dipole moment.38
The gas phase dipole moment of the iAMOEBA water molecule is 1.86 D; the dipole increases to 2.78 D in the liquid at 298 K with full width at half maximum (FWHM) of 0.25 D, and increases even further to 2.90 D in ice 240 K with a somewhat narrower FWHM (0.16 D). Although the molecular dipole moment in the condensed phase cannot be directly measured, literature estimates based on ab initio calculations102,122,126 and experimental measurements121,127 suggest values of 2.3 – 3.1 D, indicating that the direct polarization approximation correctly describes the average dipole moment in the various phases. Moreover, the iAMOEBA liquid phase dipole moment agrees very closely with AMOEBA, which also predicts a value of 2.78 D; this hints that the agreement may go beyond simple coincidence, especially given the important relationships between the liquid phase dipole moment and other, experimentally observable liquid properties.
DISCUSSION
Water models can be derived from experimental data, ab initio quantum chemistry, or a combination of the two. Since the condensed phase is an emergent property of the microscopic interactions, it is certainly desirable to derive a model entirely based on ab initio quantum chemistry, and indeed water models have been successfully developed following this approach.51,110,123,128 The main drawback is that agreement with experimental condensed phase values is not guaranteed due to assumptions in the functional form of the classical model, integrating the equations of motion using Newtonian dynamics, approximations in the reference ab initio theory, or incomplete sampling of the thermodynamic ensemble of either the model or the reference theory.129 In a compromise approach, the model parameters can be further modified to match the experimental properties, but this must be done carefully in order to preserve agreement with the theoretical data, which may be representative of important molecular interactions when solutes are introduced. By contrast, water models that are solely fitted to a subset of experimental properties can have significant predictive power, although most ab initio results are poorly predicted, some condensed phase properties are predicted more accurately than others, and the models can sometimes fail outside their parameterization range. Here we addressed this challenge by including a wide range of experimental and ab initio reference data simultaneously using the ForceBalance method to optimize the iAMOEBA model.
We validated the iAMOEBA model using a scoring scheme developed by Vega and coworkers that evaluates the predictive power of a model against an experimental data set that covers thermodynamic and kinetic data over much of water’s phase diagram. iAMOEBA based on the direct polarization approximation receives an overall score of 8.4 out of 10 because of its excellent agreement for all of the tested properties. We caution that a single numerical score is not sufficient to fully assess a model for a particular application; rather, the primary utility of the undertaking advocated in Ref. 36 is the wide range of properties investigated to provide a complete characterization of the iAMOEBA model.
Fixed charge pairwise additive models such as TIP3P earned a score of 2.7 while TIP4P/2005 earned a score of 7.2. TIP4P/2005, a model by Vega and coworkers using Ewald long-range electrostatics in similar fashion to the TIP4P-Ew model, achieves remarkable accuracy for many properties (e.g. the critical temperature) and sacrifices accuracy for other properties (e.g. the critical pressure). One possible interpretation is that the properties for which TIP4P/2005 gives poor agreement are fundamental limitations of non-polarizable models. Therefore, properties that are thought to require an explicit polarization treatment would include the dielectric constant of ice, the IR spectrum, the vapor pressure, and the critical pressure. The iAMOEBA model in fact is qualitatively superior to the fixed charge models on these properties, showing the importance of polarization.
While vapor properties are an important test of polarization effects where iAMOEBA performs well, these effects can have far-reaching implications beyond the gas phase. For instance, water molecules in biological settings such as protein active sites, membrane channels, and the coordination spheres of ions experience significantly different electric fields compared to the bulk liquid. While direct polarization clearly provides a better description compared to non-polarizable models, its appropriateness for describing interactions with solute molecules, in particular ionic species, is an important open question; answering this question would require the development of force fields with direct and mutual polarization for these solute species with the parameterization conditions held constant.
CONCLUSION
In this work we presented the iAMOEBA polarizable water model, which uses the direct polarization approximation. Compared to the AMOEBA model, iAMOEBA is simpler and computationally more efficient because it does not require a self-consistent solution for the induced dipoles. We confirmed the viability of the direct polarization approximation and established iAMOEBA as a highly accurate model with broad predictive power and applicability. We used the ForceBalance method to optimize the parameters, which allowed us to utilize a diverse data set with elements from experimental measurements and high-level theoretical calculations. The iAMOEBA model was tested against an extensive benchmark set of water properties and found to accurately describe many aspects of the vapor, liquid, and ice phases.
The improved accuracy of iAMOEBA over AMOEBA for many properties illustrates the advances in methodology and computation over the past ten years; ForceBalance allows us to systematically optimize many parameters using a much larger and more diverse set of gas and condensed phase properties compared to previous methods. By combining GPU acceleration with distributed computing tools, we are able to perform simulations over a wide range of conditions rather than a single thermodynamic phase point. In the future, we postulate that kinetic properties can be differentiated in our optimization framework using a path integral approach in a similar manner to how thermodynamic properties are differentiated through the use of configuration integrals.
Our work has important implications for the fundamental understanding of molecular interactions in water and for the construction of molecular models in general. By building realistic but approximate models, we learn about which microscopic interactions are truly important for describing the properties of interest, and which other neglected interactions (in this case mutual polarization) can be effectively captured by other terms. For example, the main lesson from this work is that an appropriately parameterized direct polarization model is capable of capturing the effect of mutual polarization for a very wide range of water properties. Another major lesson is the role of model parameterization in establishing this understanding. For most practical problems it is impossible to explore the entire parameter space, so we can only provide a lower bound on the accuracy of the empirical model using the most accurate parameters we can find. Thus, the model must be parameterized carefully before drawing conclusions about the upper bound of its descriptive capability. Thinking along these lines, the optimization approach outlined here can be easily applied to AMOEBA to further increase its accuracy for water properties and explore the aspects of mutual polarization which cannot be recovered through the direct approximation.
In terms of practical application, iAMOEBA is faster than AMOEBA (Supporting Table S1) and does not compromise on the accuracy of water properties. The behavior of water at interfaces and in confined spaces is a highly active area of research where iAMOEBA can generate quantitatively accurate predictions at a reduced computational cost. Furthermore, the iAMOEBA water model lays the groundwork for analogous inexpensive polarizable models for solutes and biomolecules; while iAMOEBA is still more expensive than simple fixed point charge models (roughly 3–6 times the computational cost of TIP3P), it represents a significant increase in efficiency over AMOEBA. The accuracy of a future iAMOEBA model for solutes remains to be seen, but the success of the present work is encouraging. The possibility of developing a hybrid model using a combination of iAMOEBA water and mutually polarizable solutes is also promising, since most of the computational cost in typical biomolecular simulations comes from the solvent degrees of freedom.
Supplementary Material
ACKNOWLEDGEMENTS
We are thankful for the assistance of Douglas Thain, Dinesh Rajan and Li Yu in their dependable support and improvement of the Work Queue library. THG thanks Martin Head-Gordon for insightful discussions that helped to inspire the idea for this project. LPW thanks William Swope, Julia Rice and Sotiris Xantheas for helpful discussions in building the theoretical reference data set for this project. We also thank the anonymous referees for their constructive comments.
LPW gratefully acknowledges support from the SimBios program, funded through the NIH Roadmap for Medical Research Grant U54 GM072970.
JWP would like to acknowledge support from NSF CHE-1152823 from the National Science Foundation Division of Chemistry.
PR acknowledges support by the Robert A. Welch Foundation (F-1691).
This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number OCI-1053575; the majority of GPU hours were provided by the Stampede supercomputer under XSEDE grant MCB100057.
This research used resources from the Keeneland Computing Facility at the Georgia Institute of Technology, which is supported by the National Science Foundation under Contract OCI-0910735.
The authors acknowledge the following award for providing computing resources that have contributed to the research results reported within this paper: MRI-R2: Acquisition of a Hybrid CPU/GPU and Visualization Cluster for Multidisciplinary Studies in Transport Physics with Uncertainty Quantification (NSF Award Number 0960306). This award is funded under the American Recovery and Reinvestment Act of 2009 (Public Law 111-5).
Footnotes
SUPPORTING INFORMATION
Computational details, further characterization of the iAMEOBA model and experimental data used in parameterization. This information is available free of charge via the Internet at http://pubs.acs.org.
REFERENCES
- 1.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. Science. 2011;334:517. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 2.Simmerling C, Strockbine B, Roitberg AE. J. Am. Chem. Soc. 2002;124:11258. doi: 10.1021/ja0273851. [DOI] [PubMed] [Google Scholar]
- 3.Snow CD, Nguyen N, Pande VS, Gruebele M. Nature. 2002;420:102. doi: 10.1038/nature01160. [DOI] [PubMed] [Google Scholar]
- 4.Baumketner A, Shea J-E. J. Mol. Biol. 2006;362:567. doi: 10.1016/j.jmb.2006.07.032. [DOI] [PubMed] [Google Scholar]
- 5.Kelley NW, Huang X, Tam S, Spiess C, Frydman J, Pande VS. J. Mol. Biol. 2009;388:919. doi: 10.1016/j.jmb.2009.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lin Y-S, Bowman GR, Beauchamp KA, Pande VS. Biophys. J. 2012;102:315. doi: 10.1016/j.bpj.2011.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ball KA, Phillips AH, Nerenberg PS, Fawzi NL, Wemmer DE, Head-Gordon T. Biochemistry. 2011;50:7612. doi: 10.1021/bi200732x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fawzi NL, Phillips AH, Ruscio JZ, Doucleff M, Wemmer DE, Head-Gordon T. J. Am. Chem. Soc. 2008;130:6145. doi: 10.1021/ja710366c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gnanakaran S, Garcia AE. Proteins. 2005;59:773. doi: 10.1002/prot.20439. [DOI] [PubMed] [Google Scholar]
- 10.Bizzarri AR, Cannistraro S. J. Phys. Chem. B. 2002;106:6617. [Google Scholar]
- 11.Fujitani H, Tanida Y, Ito M, Jayachandran G, Snow CD, Shirts MR, Sorin EJ, Pande VS. J. Chem. Phys. 2005;123 doi: 10.1063/1.1999637. [DOI] [PubMed] [Google Scholar]
- 12.Grubmuller H, Heymann B, Tavan P. Science. 1996;271:997. doi: 10.1126/science.271.5251.997. [DOI] [PubMed] [Google Scholar]
- 13.Pastor RW, MacKerell AD., Jr. J. Phys. Chem. Lett. 2011;2:1526. doi: 10.1021/jz200167q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang L, Berne BJ, Friesner RA. Proc. Nat. Acad. Sci. USA. 2011;108:1326. doi: 10.1073/pnas.1016793108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Clark GNI, Cappa CD, Smith JD, Saykally RJ, Head-Gordon T. Mol. Phys. 2010;108:1415. [Google Scholar]
- 16.Eaves JD, Loparo JJ, Fecko CJ, Roberts ST, Tokmakoff A, Geissler PL. Proc. Nat. Acad. Sci. USA. 2005;102:13019. doi: 10.1073/pnas.0505125102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Luzar A, Chandler D. Phys. Rev. Lett. 1996;76:928. doi: 10.1103/PhysRevLett.76.928. [DOI] [PubMed] [Google Scholar]
- 18.Rahman A, Stillinger FH. J. Chem. Phys. 1971;55:3336. [Google Scholar]
- 19.Roberts ST, Petersen PB, Ramasesha K, Tokmakoff A, Ufimtsev IS, Martinez TJ. Proc. Nat. Acad. Sci. USA. 2009;106:15154. doi: 10.1073/pnas.0901571106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ufimtsev IS, Kalinichev AG, Martinez TJ, Kirkpatrick RJ. Chem. Phys. Lett. 2007;442:128. [Google Scholar]
- 21.Matsumoto M, Saito S, Ohmine I. Nature. 2002;416:409. doi: 10.1038/416409a. [DOI] [PubMed] [Google Scholar]
- 22.Materer N, Starke U, Barbieri A, VanHove MA, Somorjai GA, Kroes GJ, Minot C. Surf. Sci. 1997;381:190. [Google Scholar]
- 23.Kumar R, Wang F-F, Jenness GR, Jordan KD. J. Chem. Phys. 2010;132 doi: 10.1063/1.3276460. [DOI] [PubMed] [Google Scholar]
- 24.Lambrecht DS, Clark GNI, Head-Gordon T, Head-Gordon M. J. Phys. Chem. A. 2011;115:5928. doi: 10.1021/jp110334w. [DOI] [PubMed] [Google Scholar]
- 25.Liu K, Cruzan JD, Saykally RJ. Science. 1996;271:929. doi: 10.1126/science.271.5245.59. [DOI] [PubMed] [Google Scholar]
- 26.Xantheas SS, Burnham CJ, Harrison RJ. J. Chem. Phys. 2002;116:1493. [Google Scholar]
- 27.Abascal JLF, Vega C. J. Chem. Phys. 2010;133 doi: 10.1063/1.3506860. [DOI] [PubMed] [Google Scholar]
- 28.Clark GNI, Hura GL, Teixeira J, Soper AK, Head-Gordon T. Proc. Nat. Acad. Sci. USA. 2010;107:14003. doi: 10.1073/pnas.1006599107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Soper AK, Teixeira J, Head-Gordon T. Proc. Nat. Acad. Sci. USA. 2010;107:E44. doi: 10.1073/pnas.0912158107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Proteins. 2006;65:712. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kollman PA. Acc. Chem. Res. 1996;29:461. [Google Scholar]
- 32.Lindorff-Larsen K, Piana S, Palmo K, Maragakis P, Klepeis JL, Dror RO, shaw DE. Proteins. 2010;78:1950. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang JM, Wolf RM, Caldwell JW, Kollman PA, Case DA. J. Comput. Chem. 2004;25:1157. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- 34.Best RB, Zhu X, Shim J, Lopes PEM, Mittal J, Feig M, MacKerell AD., Jr. J. Chem. Theory Comput. 2012;8:3257. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926. [Google Scholar]
- 36.Vega C, Abascal JLF. Phys. Chem. Chem. Phys. 2011;13:19663. doi: 10.1039/c1cp22168j. [DOI] [PubMed] [Google Scholar]
- 37.Kiss PT, Bertsyk P, Baranyai A. J. Chem. Phys. 2012;137 doi: 10.1063/1.4767063. [DOI] [PubMed] [Google Scholar]
- 38.Vega C, Abascal JLF, Conde MM, Aragones JL. Faraday Discuss. 2009;141:251. doi: 10.1039/b805531a. [DOI] [PubMed] [Google Scholar]
- 39.Vega C, Sanz E, Abascal JLF. J. Chem. Phys. 2005;122 doi: 10.1063/1.1931662. [DOI] [PubMed] [Google Scholar]
- 40.Horn HW, Swope WC, Pitera JW, Madura JD, Dick TJ, Hura GL, Head-Gordon T. J. Chem. Phys. 2004;120:9665. doi: 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- 41.Abascal JLF, Vega C. J. Chem. Phys. 2005;123 doi: 10.1063/1.2121687. [DOI] [PubMed] [Google Scholar]
- 42.Lamoureux G, MacKerell AD, Roux B. J. Chem. Phys. 2003;119:5185. doi: 10.1063/5.0019987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Rick SW, Stuart SJ, Berne BJ. J. Chem. Phys. 1994;101:6141. [Google Scholar]
- 44.Fanourgakis GS, Xantheas SS. J. Chem. Phys. 2008;128 doi: 10.1063/1.2837299. [DOI] [PubMed] [Google Scholar]
- 45.Ren PY, Ponder JW. J. Phys. Chem. B. 2003;107:5933. [Google Scholar]
- 46.Ren PY, Ponder JW. J. Phys. Chem. B. 2004;108:13427. [Google Scholar]
- 47.Ferenczy GG, Reynolds CA. J. Phys. Chem. A. 2001;105:11470. [Google Scholar]
- 48.Ren PY, Ponder JW. J. Comput. Chem. 2002;23:1497. doi: 10.1002/jcc.10127. [DOI] [PubMed] [Google Scholar]
- 49.Straatsma TP, McCammon JA. Mol. Simulat. 1990;5:181. [Google Scholar]
- 50.Wang L-P. [accessed 2013 March 24];ForceBalance : Systematic Force Field Optimization. Available from: https://simtk.org/home/forcebalance/
- 51.Wang L-P, Chen J, Van Voorhis T. J. Chem. Theory Comput. 2013;9:452. doi: 10.1021/ct300826t. [DOI] [PubMed] [Google Scholar]
- 52.Palmo K, Krimm S. Chem. Phys. Lett. 2004;395:133. [Google Scholar]
- 53.Stone AJ. The theory of intermolecular forces. Oxford ; New York: Clarendon Press ; Oxford University Press; 1996. Oxford. [Google Scholar]
- 54.Toukmaji A, Sagui C, Board J, Darden T. J. Chem. Phys. 2000;113:10913. [Google Scholar]
- 55.Car R, Parrinello M. Phys. Rev. Lett. 1985;55:2471. doi: 10.1103/PhysRevLett.55.2471. [DOI] [PubMed] [Google Scholar]
- 56.Lamoureux G, Roux B. J. Chem. Phys. 2003;119:3025. [Google Scholar]
- 57.Vanbelle D, Froeyen M, Lippens G, Wodak SJ. Mol. Phys. 1992;77:239. [Google Scholar]
- 58.Genzer J, Kolafa J. J. Mol. Liq. 2004;109:63. [Google Scholar]
- 59.Kuo IFW, Mundy CJ, McGrath MJ, Siepmann JI. J. Chem. Theory Comput. 2006;2:1274. doi: 10.1021/ct6001913. [DOI] [PubMed] [Google Scholar]
- 60.Ong SW, Tok ES, Kang HC. Phys. Chem. Chem. Phys. 2010;12:14960. doi: 10.1039/c0cp00411a. [DOI] [PubMed] [Google Scholar]
- 61.Wagner W, Pruss A. J. Phys. Chem. Ref. Data. 2002;31:387. [Google Scholar]
- 62.Kell GS. J. Chem. Eng. Data. 1975;20:97. [Google Scholar]
- 63.Wang L-P. [accessed 2013 March 24];iAMOEBA parameter file and data repository. Available from: https://simtk.org/home/iamoeba.
- 64.Banks JL, Kaminski GA, Zhou RH, Mainz DT, Berne BJ, Friesner RA. J. Chem. Phys. 1999;110:741. [Google Scholar]
- 65.Brommer P, Gaehler F. Modell. Simul. Mater. Sci. Eng. 2007;15:295. [Google Scholar]
- 66.Liu YP, Kim K, Berne BJ, Friesner RA, Rick SW. J. Chem. Phys. 1998;108:4739. [Google Scholar]
- 67.Akin-Ojo O, Song Y, Wang F. J. Chem. Phys. 2008;129 doi: 10.1063/1.2965882. [DOI] [PubMed] [Google Scholar]
- 68.Ercolessi F, Adams JB. Europhys. Lett. 1994;26:583. [Google Scholar]
- 69.Izvekov S, Parrinello M, Burnham CJ, Voth GA. J. Chem. Phys. 2004;120:10896. doi: 10.1063/1.1739396. [DOI] [PubMed] [Google Scholar]
- 70.Shell MS. J. Chem. Phys. 2008;129 doi: 10.1063/1.2992060. [DOI] [PubMed] [Google Scholar]
- 71.Wu D, Kofke DA. J. Chem. Phys. 2005;123 doi: 10.1063/1.2011391. [DOI] [PubMed] [Google Scholar]
- 72.Szabo A, Ostlund NS. Modern Quantum Chemistry. Dover; 1996. [Google Scholar]
- 73.Parr RG, Yang W. Density-Functional Theory of Atoms and Molecules. Oxford University Press; 1989. [Google Scholar]
- 74.Distasio RA, Jr., Steele RP, Head-Gordon M. Mol. Phys. 2007;105:2731. [Google Scholar]
- 75.Steele RP, DiStasio RA, Jr., Head-Gordon M. J. Chem. Theory Comput. 2009;5:1560. doi: 10.1021/ct900058p. [DOI] [PubMed] [Google Scholar]
- 76.Steele RP, DiStasio RA, Jr., Shao Y, Kong J, Head-Gordon M. J. Chem. Phys. 2006;125 doi: 10.1063/1.2234371. [DOI] [PubMed] [Google Scholar]
- 77.Dunning TH. J. Chem. Phys. 1989;90:1007. [Google Scholar]
- 78.Shao Y, Molnar LF, Jung Y, Kussmann J, Ochsenfeld C, Brown ST, Gilbert ATB, Slipchenko LV, Levchenko SV, O'Neill DP, DiStasio RA, Jr., Lochan RC, Wang T, Beran GJO, Besley NA, Herbert JM, Lin CY, Van Voorhis T, Chien SH, Sodt A, Steele RP, Rassolov VA, Maslen PE, Korambath PP, Adamson RD, Austin B, Baker J, Byrd EFC, Dachsel H, Doerksen RJ, Dreuw A, Dunietz BD, Dutoi AD, Furlani TR, Gwaltney SR, Heyden A, Hirata S, Hsu C-P, Kedziora G, Khalliulin RZ, Klunzinger P, Lee AM, Lee MS, Liang W, Lotan I, Nair N, Peters B, Proynov EI, Pieniazek PA, Rhee YM, Ritchie J, Rosta E, Sherrill CD, Simmonett AC, Subotnik JE, Woodcock HL, III, Zhang W, Bell AT, Chakraborty AK, Chipman DM, Keil FJ, Warshel A, Hehre WJ, Schaefer HF, III, Kong J, Krylov AI, Gill PMW, Head-Gordon M. Phys. Chem. Chem. Phys. 2006;8:3172. doi: 10.1039/b517914a. [DOI] [PubMed] [Google Scholar]
- 79.Yoo S, Apra E, Zeng XC, Xantheas SS. J. Phys. Chem. Lett. 2010;1:3122. [Google Scholar]
- 80.Bates DM, Tschumper GS. J. Phys. Chem. A. 2009;113:3555. doi: 10.1021/jp8105919. [DOI] [PubMed] [Google Scholar]
- 81.Bulusu S, Yoo S, Apra E, Xantheas S, Zeng XC. J. Phys. Chem. A. 2006;110:11781. doi: 10.1021/jp0655726. [DOI] [PubMed] [Google Scholar]
- 82.Fanourgakis GS, Apra E, Xantheas SS. J. Chem. Phys. 2004;121:2655. doi: 10.1063/1.1767519. [DOI] [PubMed] [Google Scholar]
- 83.Lagutschenkov A, Fanourgakis GS, Niedner-Schatteburg G, Xantheas SS. J. Chem. Phys. 2005;122 doi: 10.1063/1.1899583. [DOI] [PubMed] [Google Scholar]
- 84.Xantheas SS, Apra E. J. Chem. Phys. 2004;120:823. doi: 10.1063/1.1626624. [DOI] [PubMed] [Google Scholar]
- 85.Lifson S, Warshel A. J. Chem. Phys. 1968;49:5116. [Google Scholar]
- 86.Hagler AT, Huler E, Lifson S. J. Am. Chem. Soc. 1974;96:5319. doi: 10.1021/ja00824a004. [DOI] [PubMed] [Google Scholar]
- 87.Maple JR, Hwang MJ, Stockfisch TP, Dinur U, Waldman M, Ewig CS, Hagler AT. J. Comput. Chem. 1994;15:162. [Google Scholar]
- 88.Williams DE. Topics Curr. Phys. 1981;26:3. [Google Scholar]
- 89.Liu P, Shi Q, Daume H, III, Voth GA. J. Chem. Phys. 2008;129 doi: 10.1063/1.3033218. [DOI] [PubMed] [Google Scholar]
- 90.Eastman P, Friedrichs MS, Chodera JD, Radmer RJ, Bruns CM, Ku JP, Beauchamp KA, Lane TJ, Wang L-P, Shukla D, Tye T, Houston M, Stich T, Klein C, Shirts MR, Pande VS. J. Chem. Theory Comput. 2013;9:461. doi: 10.1021/ct300857j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Eastman P, Pande VS. Comput. Sci. Eng. 2010;12:34. doi: 10.1109/MCSE.2010.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Pande VS, Eastman P. [accessed 2013 March 24];OpenMM. Available from: https://simtk.org/home/openmm.
- 93.Abdul-Wahid B, Yu L, Rajan D, Feng H, Darve E, Thain D, Izaguirre JA. IEEE International Conference on e-Science. 2012 doi: 10.1109/eScience.2012.6404429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Bui P, Rajan D, Abdul-Wahid B, Izaguirre JA, Thain D. Workshop on Python for High Performance and Scientific Computing (PyHPC) 2011 [Google Scholar]
- 95.Thain D. [accessed 2013 March 24];Work Queue: A Scalable Master/Worker Framework. Available from: http://www3.nd.edu/~ccl/software/workqueue/
- 96.Shirts MR, Chodera JD. J. Chem. Phys. 2008;129 doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Shirts MR, Chodera JD. [accessed 2013 March 24];A Python implementation of the multistate Bennett acceptance ratio (MBAR) Available from: https://simtk.org/home/pymbar.
- 98.Ponder JW. [accessed 2013 March 24];TINKER Molecular Modeling Package. Available from: http://dasher.wustl.edu/ffe/
- 99.Burnham CJ, Xantheas SS. J. Chem. Phys. 2002;116:5115. [Google Scholar]
- 100.Fanourgakis GS, Xantheas SS. J. Chem. Phys. 2006;124 doi: 10.1063/1.2193151. [DOI] [PubMed] [Google Scholar]
- 101.Ichikawa K, Kameda Y, Yamaguchi T, Wakita H, Misawa M. Mol. Phys. 1991;73:79. [Google Scholar]
- 102.Silvestrelli PL, Parrinello M. Phys. Rev. Lett. 1999;82:3308. doi: 10.1103/PhysRevLett.77.3149. [DOI] [PubMed] [Google Scholar]
- 103.Yu W, Lopes PEM, Roux B, MacKerell AD., Jr. J. Chem. Phys. 2013;138 doi: 10.1063/1.4774577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Kiss PT, Baranyai A. J. Chem. Phys. 2012;137 doi: 10.1063/1.4767064. [DOI] [PubMed] [Google Scholar]
- 105.Imoto S, Xantheas SS, Saito S. J. Chem. Phys. 2013;138 doi: 10.1063/1.4789951. [DOI] [PubMed] [Google Scholar]
- 106.Yoo S, Xantheas SS. J. Chem. Phys. 2011;134 doi: 10.1063/1.3573375. [DOI] [PubMed] [Google Scholar]
- 107.Kiss PT, Baranyai A. The Journal of Chemical Physics. 2013;138:204507. doi: 10.1063/1.4807600. [DOI] [PubMed] [Google Scholar]
- 108.Paricaud P, Predota M, Chialvo AA, Cummings PT. J. Chem. Phys. 2005;122 doi: 10.1063/1.1940033. [DOI] [PubMed] [Google Scholar]
- 109.Yeh IC, Hummer G. J. Phys. Chem. B. 2004;108:15873. [Google Scholar]
- 110.Wu YJ, Tepper HL, Voth GA. J. Chem. Phys. 2006;124 doi: 10.1063/1.2136877. [DOI] [PubMed] [Google Scholar]
- 111.Chen J, Martinez TJ. Chem. Phys. Lett. 2007;438:315. [Google Scholar]
- 112.Mannfors B, Palmo K, Krimm S. J. Phys. Chem. A. 2008;112:12667. doi: 10.1021/jp806948w. [DOI] [PubMed] [Google Scholar]
- 113.Liu J, Miller WH, Paesani F, Zhang W, Case DA. J. Chem. Phys. 2009;131 doi: 10.1063/1.3254372. [DOI] [PubMed] [Google Scholar]
- 114.Paesani F, Iuchi S, Voth GA. J. Chem. Phys. 2007;127 doi: 10.1063/1.2759484. [DOI] [PubMed] [Google Scholar]
- 115.Liu J, Miller WH, Fanourgakis GS, Xantheas SS, Imoto S, Saito S. J. Chem. Phys. 2011;135 doi: 10.1063/1.3670960. [DOI] [PubMed] [Google Scholar]
- 116.Hura G, Sorenson JM, Glaeser RM, Head-Gordon T. J. Chem. Phys. 2000;113:9140. [Google Scholar]
- 117.Soper AK. Chem. Phys. 2000;258:121. [Google Scholar]
- 118.Soper AK. J. Phys.-Condens. Mat. 2007;19 [Google Scholar]
- 119.Soper AK, Phillips MG. Chem. Phys. 1986;107:47. [Google Scholar]
- 120.Pusztai L, Pizio O, Sokolowski S. J. Chem. Phys. 2008;129 doi: 10.1063/1.2976578. [DOI] [PubMed] [Google Scholar]
- 121.Badyal YS, Saboungi ML, Price DL, Shastri SD, Haeffner DR, Soper AK. J. Chem. Phys. 2000;112:9206. [Google Scholar]
- 122.Gregory JK, Clary DC, Liu K, Brown MG, Saykally RJ. Science. 1997;275:814. doi: 10.1126/science.275.5301.814. [DOI] [PubMed] [Google Scholar]
- 123.Pinnick ER, Erramilli S, Wang F. J. Chem. Phys. 2012;137 doi: 10.1063/1.4731693. [DOI] [PubMed] [Google Scholar]
- 124.Habershon S, Manolopoulos DE. Phys. Chem. Chem. Phys. 2011;13:19714. doi: 10.1039/c1cp21520e. [DOI] [PubMed] [Google Scholar]
- 125.Lindberg GE, Wang F. J. Phys. Chem. B. 2008;112:6436. doi: 10.1021/jp800736t. [DOI] [PubMed] [Google Scholar]
- 126.Batista ER, Xantheas SS, Jonsson H. J. Chem. Phys. 1999;111:6011. [Google Scholar]
- 127.Gubskaya AV, Kusalik PG. J. Chem. Phys. 2002;117:5290. [Google Scholar]
- 128.Akin-Ojo O, Wang F. J. Comput. Chem. 2011;32:453. doi: 10.1002/jcc.21634. [DOI] [PubMed] [Google Scholar]
- 129.Wang L-P, Van Voorhis T. J. Chem. Phys. 2010;133 doi: 10.1063/1.3519043. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.