The pH dependence of staphylococcal nuclease stability is incompatible with a three-state denaturation model

Abstract

Six single substitution mutations, V66F, V66G, V66N, V66Q, V66S, V66T, and V66Y, were made in the background of a highly stable triple mutant (P117G, H124L, and S128A) of staphylococcal nuclease. The thermodynamic stabilities of wild type staphylococcal nuclease, of the stable triple mutant and of its six variants were determined by guanidine hydrochloride denaturation in thirteen different buffers spanning the pH range 4.5 to 10.2. Within experimental error the values of ΔG_H2O and m_GuHCl for the various proteins measured over this wide range of pH maintain a constant offset from one another, tracing a series of approximately parallel curves. This data offers an independent means of determining the error of stabilities and slopes determined by guanidine hydrochloride denaturations and shows that previous error estimates are accurate. More importantly, this behavior cannot be reconciled with a three-state denaturation model for staphylococcal nuclease. The large variations in m_GuHCl observed in these mutants must therefore arise from other causes.

We have published a number of studies [1–9] examining the effects of burying in the hydrophobic core residues which are normally ionized at neutral pH. These substitutions were done originally at position 66 of staphylococcal nuclease, a protein much used as a model system to study protein stability. The free energy differences between the native and denatured states of these proteins were examined as a function of pH to determine the apparent pK_a values of the ionizable groups in the denatured and native states. To extend the pH range over which protein stability could be measured, we made these mutations in a background of three other stabilizing mutations.

Because analysis of the pH dependence of stability to extract apparent pKa values makes assumptions about the denaturation processes used to measure stability, it was of interest to examine the effects of pH on the stability of variants with substitutions other than ionizable groups at hydrophobic core positions. We focused on a highly stable variant of staphylococcal nuclease engineered with three stabilizing mutations. A set of control proteins were made with a number of other non-ionizable mutations at position 66, and we examined how their energetics varied with pH. We report here the results of our study and the surprising conclusion that mutants with widely varying stabilities and differing values of m_GuHCl appear to have very similar denatured states, a result in conflict with much of the literature regarding staphylococcal nuclease.

There is good evidence that some mutants of nuclease, most notably the V66W variant, have a well-populated equilibrium unfolding intermediate [10–22]. Some have argued most or all nuclease mutants as well as wild-type denature via an intermediate [23, 24], meaning that a three-state model should be used to analyze the data rather than the two-state model commonly used. If wild-type and the many other mutants of nuclease characterized over the years do in fact denature via an intermediate state, a failure to take this into account in the analysis could lead to large errors in the apparent stabilities relative to the true free energy difference between the native state and the denatured states and could account for the variation in m_GuHCl between various substitution mutants of the protein.

Further complicating matters, Bolen’s group has proposed that neither a simple two or three state model fully explains the data for wild-type nuclease and the majority of mutants that have been studied [22, 25]. They argue for the variable two state model proposed by Shortle [26, 27], in which the character of the denatured state changes with mutation, denaturant concentration, or temperature. However, they point out several disagreements between this model and experimental data [21, 22, 25].

Experimental Procedures

Mutagenesis and protein expression

Since the stability of nuclease is too low to give reliable data at extremes of pH, the mutants were made in a GLA background. GLA is a hyperstable variant of nuclease that contains the mutations P117G, H124L, and S129A [28]. Originally, Shortle’s group cloned nuclease [29] from the Foggi strain of Staphylococcus aureus, which differs from the nuclease in the V8 strain at position 124, which is L in V8 and H in the Foggi strain. Therefore either one of these residues at 124 might be regarded as wild type.

All mutations were introduced into the DNA sequence of GLA nuclease in a M13 vector using the method of Kunkel [30]. Protein expression and purification was carried out as previously described [31]. Final dialysis was against a 100 mM NaCl, 25mM sodium phosphate buffer, pH 7.0. Purity was verified by SDS-PAGE. Typical protein yields were in the range of 5–15 mg of at least 98% pure protein.

Preparation of buffers

The mutants were first titrated with 6M GuHCl that was buffered using pH 7.0 25mM sodium phosphate, 100 mM NaCl. After determining that the mutant proteins in the GLA background had a stability of that of the corresponding mutant in the wild-type background plus 3.3 kcal/mol (the difference between the stabilities of GLA and wild-type), they were then titrated with guanidine hydrochloride in other buffers over a wide range of pH.

The buffer used for pH values ranging from around 4.5 to 7.8 consisted of 25mM bis-tris-propane (1,3-bis(tris[hydroxymethyl]methylamino)propane, Sigma) brought to the correct pH with acetic acid. Initially stock solutions of buffer were made at 100 mM concentration. These stock solutions were then diluted to 25 mM and the pH of the dilute solution was checked at the concentration intended for actual use. The buffer used for pH values ranging from around 7.9 to 9.7 consisted of 25mM bis-tris-propane brought to the correct pH with phosphoric acid. The buffer used for pH values ranging from around 9.2 to 10.2 consisted of 25mM ethanolamine from Sigma brought to the correct pH with hydrochloric acid. It should be noted that, in contrast to our regular procedure, no NaCl was added to the buffer. All buffers were filtered with Corning disposable sterile bottle top filters with a 0.22 micron cellulose acetate membrane to remove any suspended particles. The pH of the buffers was checked with a Beckman 39536 glass body combination calomel electrode and Orion model 720A pH meter with a resolution of 0.001 pH units.

Preparation of buffered guanidine hydrochloride

6.00 M guanidine hydrochloride (GuHCl, Gibco Ultrapure grade) was prepared over the same range of pH at matching pH values for each 0.025 M buffered solution. GuHCl was added to a carefully weighed volume of the 100 mM stock buffer solution and an appropriate amount of water to bring the solution to approximately 25mM buffer and 6M GuHCl. The pH was first checked to see that it matched the original buffer. The density of the resulting buffered GuHCl solution was then checked and adjusted if necessary by adding either 25mM buffer or GuHCl as appropriate to bring the concentration to ~6 M. Final adjustments were made by comparing the refractive index of the 25 mM buffer to that of the guanidine solution [32], using a Bausch & Laumb model 33-45-58 refractometer. In the case of buffered solutions at pH values 5.5 and less, the GuHCl concentration of the final solution was checked using density measurements alone due to difficulties with measuring the refractive index in those buffer systems. A comparison of density measurement with refractive index measurement at other pHs showed that the two different methods led to [GuHCl] within 0.02 M of each other.

Titration of proteins

The mutant proteins were titrated with buffered 6.00 M GuHCl as generally described previously [33]. The shifting of pH values during protein titration was measured as the 6.00M GuHCl/0.025M buffer solution was added to a quartz cuvette containing 3mL of 0.025M buffer plus 25μg of wild type protein. Protein was added by weighing out a stock solution of protein of known concentration previously prepared in 25mM sodium phosphate, 100 mM NaCl, pH 7.0. The volume of protein in phosphate/NaCl buffer added to each 3ml of buffer was on the order of 15–30μl. This simulated protein titration was carried out with the Beckman 39536 glass body combination calomel electrode in place and the stir bar spinning. The guanidine hydrochloride solution was added incrementally until the final concentration of GuHCl within the cuvette was in excess of 2M. Fluorescence was also measured and compared to an identical setup minus the pH electrode in order to ensure that complete mixing was taking place inside the cuvette. The pH of the solution in the cuvette was checked with a Beckman 39536 glass body combination calomel electrode. The pH of the buffer plus GuHCl solution in the cuvette was also monitored for a mock titration in each buffer to in order to observe any pH shifting which might occur.

In preparation for titration an aliquot of the concentrated protein stock was placed in a corresponding buffer for which the pH has previously been brought to ±0.02 pH units of the corresponding 6.00 M GuHCl/25mM buffer system.

It has been pointed out that guanidine hydrochloride solution interferes with the measurement of pH by a glass electrode [34]. This effect is correctable but is in fact quite small, only ~0.1–0.2 pH units in the useful range of 0 M through 2 M guanidine hydrochloride. This is unlikely to produce significant changes in the interpretation of results, so no correction to pH values was made.

Results

We examined the pH dependence of the stability of wild-type staphylococcal nuclease (WT) and the stabilized triple mutant P117G, H124L, and S128A (GLA, also referred to as PHS in some previous publications) [28]. Six single substitution mutations were also made in the GLA background, V66F, V66G, V66N, V66Q, V66S, V66T, and V66Y. Where space allows, each mutant has been identified by these standard one letter code abbreviations and the notation/GLA is used to indicate that this mutation is in the GLA background. In other places, a shorthand notation is used to denote mutations to conserve space. In this shorthand, each mutation is assumed to be in the GLA background and is referred to simply by the one letter code of the side chain substituted for valine 66. For example, the notation “G” refers to the mutant V66G/GLA.

Guanidine hydrochloride titrations were performed at thirteen different pH values ranging from ~4.5 to ~10.2. No single buffering system can buffer over the entire range of pH studied. Past work in our laboratory at pH 7 has used 25 mM sodium phosphate buffer, and the results of the guanidine hydrochloride and thermal denaturations in this standard buffer are shown in Table 1. The error estimates are based on the standard deviation of repeated denaturation experiments performed upon wild-type staphylococcal nuclease [35].

Table 1.

Guanidine hydrochloride parameters of mutants in pH 7.0 phosphate buffer.

Mutant	ΔGH20a	Cmb	mGuHClc
GLA	8.8	1.53	5.76
V66F/GLA	8.2	1.47	5.62
V66N/GLA	4.6	0.70	6.57
V66Q/GLA	4.5	0.67	6.68
V66S/GLA	5.7	0.97	5.92
V66T/GLA	7.1	1.24	5.75
V66Y/GLA	8.2	1.41	5.82
WT	5.3	0.82	6.44

^aFree energy difference between native and denatured states in the absence of denaturant. Units of kcal/mol. Error estimated to be ±0.1 kcal/mol.

^bMidpoint concentration (concentration of guanidine hydrochloride at which half of the protein is denatured) in units of molar. Error estimated to be ±0.01 M.

^cSlope value (change in free energy with respect to change in guanidine hydrochloride concentration) in units of kcal·mol⁻¹·M⁻¹. Error is estimated to be ±0.11 kcal·mol⁻¹·M⁻¹.

The first experiments to extend the pH range were done with a bis-tris-propane/phosphate buffer system. Although suitable at slightly basic pH values, it was discovered that at lower pH values the bis-tris-propane/phosphate buffer system allowed the pH to vary during the titration. In order to prevent this several other buffer systems were evaluated. It was determined that by using acetate as the counterion for bis-tris-propane, instead of phosphate, the pH fluctuations at low pH were minimized.

In some other buffers tested the formation of a white precipitate occurred at high GuHCl concentrations. Presumably this is due to the buffers used, as this phenomenon does not occur in our standard phosphate buffer. The precipitate is possibly an aggregate of denatured protein that is not soluble in certain buffers. The data reported in this study only used buffers in which this phenomenon did not occur.

In the end, three different buffer systems were used and were shown to give similar protein stabilities at overlapping pH values. At the transition between buffer systems data was collected at similar pH for both buffer systems. At low pH values (4.5, 5.0, 5.5, 6.0, 6.5, 7.0, and 7.8) the buffer system used was 25mM bis-tris-propane/acetic acid. At slightly basic pH values (7.9, 8.3, and 9.7) 0.25mM bis-tris-propane/phosphoric acid was used as the buffering system. At high pH values (9.2, 9.7, and 10.2) ethanolamine/hydrochloric acid was used to buffer the titrations. The pK_a values of acetic acid and ethanolamine are 4.75 and 9.5 respectively. Bis-tris-propane has pK_as at 6.8 and 9.0. The pK_a of phosphoric acid that is relevant here is 7.21. No corrections were made to the pH values obtained in the presence of guanidine hydrochloride. Another observation of note was that some of the mutants, especially those with stability higher than 5 kcal/mol, required longer equilibration times than habitually used. Lastly, as described in the experimental procedures, there were often pronounced slopes to the native and denatured baselines, particularly at extremes of pH. This required the use of non-linear regression to fit the data using the procedure of Santoro and Bolen [36]. For the sake of consistency this procedure was used at all pH values. As we have previously shown at pH 7, where there are minimal baseline slopes, the Santoro and Bolen fitting procedure gives results that are experimentally indistinguishable from our normal fitting procedure, which assumes horizontal baselines [35].

In Tables 2, 3, and 4 are compiled, respectively, the free energies of unfolding (ΔG_H2O), midpoint (C_m), and slope values (m_GuHCl) determined over a wide range of pH values. The values of ΔG_H2O and m_GuHCl as a function of pH are shown in Figures 1a and 2a respectively. Units and error estimates are identical to those in Table 1. The fitted values for the slope of the native and denatured baselines are available in supplementary materials.

Table 2.

Free energy of unfolding at zero denaturant concentration (ΔG_H2O) of mutants in various buffers. Units of kcal/mol.

Buffera	pH	GLA	F	G	N	Q	S	T	Y	WT
A	4.5	7.7	7.3	3.2	3.1	3.0	4.7	6.2	7.2	3.1
A	5.0	8.4	8.0	4.2	4.2	4.0	5.6	6.9	8.1	4.2
A	5.5	8.0	7.7	3.9	3.9	3.9	5.3	6.5	7.7	4.2
A	6.0	8.1	7.9	4.2	4.1	ND	5.4	6.6	7.9	4.7
A	6.5	8.2	8.1	4.2	4.3	4.3	5.5	6.8	8.2	5.0
A	7.0	8.4	8.2	4.3	4.3	4.3	5.7	6.8	8.2	5.5
A	7.8	8.4	8.3	ND	4.3	4.4	5.7	6.9	8.3	5.4
B	7.9	8.6	8.5	4.4	4.5	4.4	5.5	7.0	8.3	5.5
B	8.3	8.7	8.7	4.3	4.3	4.4	5.5	6.6	8.4	5.5
C	9.2	8.1	8.3	4.1	3.9	4.1	5.2	6.7	7.8	5.3
B	9.7	ND	7.7	4.1	3.9	3.9	5.2	6.4	ND	ND
C	9.7	7.8	7.5	4.0	3.8	3.9	5.0	6.3	7.4	5.2
C	10.2	7.3	7.0	2.9	3.0	2.9	4.2	5.4	6.2	3.9

^aBuffer A indicates 25mM bis-tris-propane/acetic acid, Buffer B indicates 25mM bis-tris-propane/phosphoric acid, Buffer C indicates 25mM ethanolamine/hydrochloric acid. ND indicates that a denaturation was not determined in that particular buffer for that particular mutant.

Table 3.

Midpoint concentration (C_m) of mutants in various buffers. Units of M.

Buffera	pH	GLA	F	G	N	Q	S	T	Y	WT
A	4.5	1.40	1.37	0.52	0.52	0.49	0.80	1.11	1.30	0.54
A	5.0	1.52	1.47	0.66	0.67	0.63	0.93	1.23	1.41	0.71
A	5.5	1.43	1.39	0.60	0.60	0.57	0.86	1.15	1.34	0.67
A	6.0	1.46	1.41	0.63	0.62	ND	0.88	1.18	1.36	0.74
A	6.5	1.51	1.46	0.66	0.67	0.65	0.94	1.24	1.40	0.81
A	7.0	1.54	1.48	0.69	0.69	0.66	0.95	1.26	1.42	0.85
A	7.8	1.55	1.49	ND	0.68	0.67	0.96	1.27	1.42	0.86
B	7.9	1.58	1.55	0.69	0.74	0.67	1.00	1.30	1.46	0.90
B	8.3	1.57	1.53	0.68	0.73	0.68	1.02	1.20	1.44	0.89
C	9.2	1.48	1.49	0.64	0.66	0.61	0.90	1.21	1.33	0.81
B	9.7	ND	1.36	0.57	0.59	0.61	0.83	1.12	ND	ND
C	9.7	1.36	1.30	0.60	0.55	0.61	0.80	1.08	1.19	0.77
C	10.2	1.18	1.12	0.44	0.40	0.40	0.64	0.90	0.96	0.52

^aBuffer A indicates 25mM bis-tris-propane/acetic acid, Buffer B indicates 25mM bis-tris-propane/phosphoric acid, Buffer C indicates 25mM ethanolamine/hydrochloric acid. ND indicates that a denaturation was not determined in that particular buffer for that particular mutant.

Table 4.

Slope (m_GuHCl) of mutants in various buffers. Units of kcal·mol⁻¹·M⁻¹.

Buffera	pH	GLA	F	G	N	Q	S	T	Y	WT
A	4.5	5.47	5.36	6.17	6.02	6.14	5.88	5.57	5.50	5.74
A	5.0	5.50	5.42	6.44	6.27	6.36	6.08	5.60	5.71	5.96
A	5.5	5.61	5.55	6.60	6.60	6.71	6.15	5.63	5.79	6.29
A	6.0	5.55	5.63	6.56	6.61	ND	6.19	5.57	5.82	6.39
A	6.5	5.44	5.54	6.42	6.38	6.58	5.90	5.51	5.85	6.21
A	7.0	5.44	5.51	6.20	6.26	6.56	5.93	5.43	5.76	6.45
A	7.8	5.43	5.56	ND	6.22	6.52	5.93	5.41	5.85	6.29
B	7.9	5.43	5.47	6.34	6.05	6.49	5.54	5.35	5.67	6.18
B	8.3	5.54	5.65	6.36	5.90	6.55	5.37	5.47	5.82	6.20
C	9.2	5.47	5.61	6.49	5.98	6.71	5.81	5.52	5.86	6.56
B	9.7	ND	5.67	7.15	6.63	6.37	6.23	5.67	ND	ND
C	9.7	5.71	5.76	6.74	6.91	6.37	6.26	5.82	6.20	6.74
C	10.2	6.23	6.24	6.73	7.60	7.33	6.56	6.06	6.49	7.56

^aBuffer A indicates 25mM bis-tris-propane/acetic acid, Buffer B indicates 25mM bis-tris-propane/phosphoric acid, Buffer C indicates 25mM ethanolamine/hydrochloric acid. ND indicates that a denaturation was not determined in that particular buffer for that particular mutant.

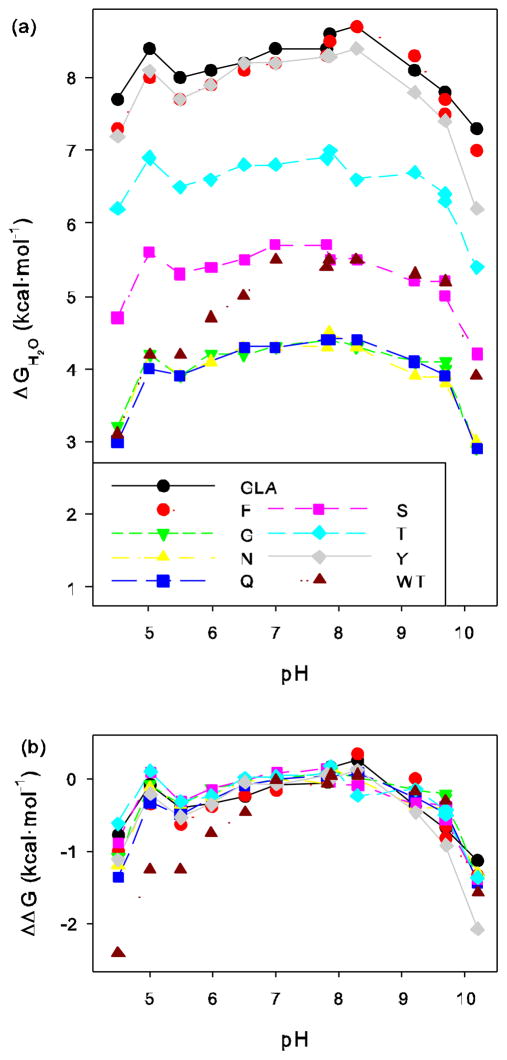
Figure 1.

(a) Free energy of unfolding, ΔG_H2O, of wild-type staphylococcal nuclease and various mutants in a GLA background obtained through fluorescence monitored GuHCl titrations at different pHs. (b) Difference in ΔG_H2O at each pH relative to average value of ΔG_H2O over a neutral pH range.

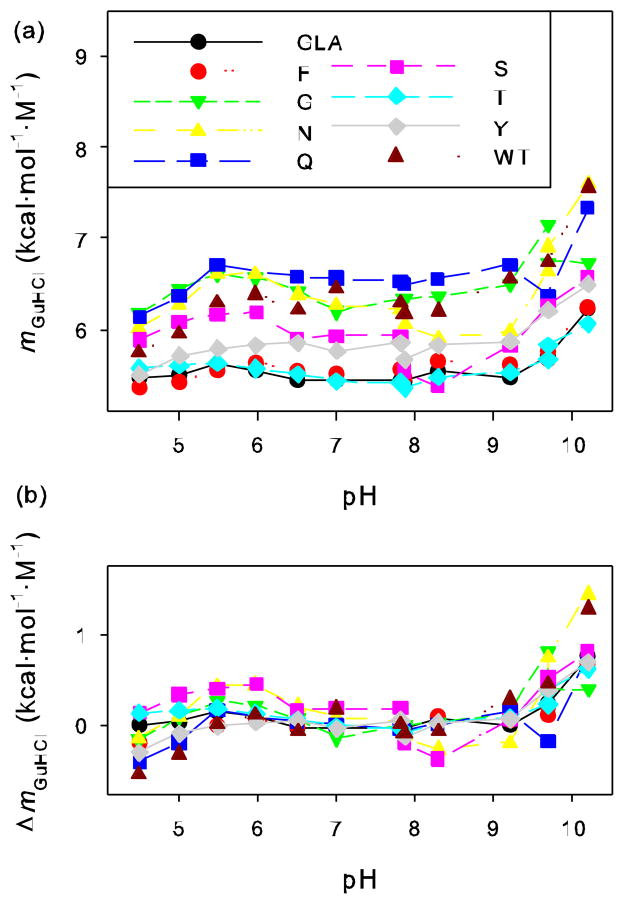
Figure 2.

(a) The rate of change of free energy with respect to GuHCl concentration (m_GuHCl or d(ΔG)/d[GuHCl]) of wild-type staphylococcal nuclease and various mutants in a GLA background obtained from fluorescence monitored GuHCl titrations at different pHs. (b) Difference in m_GuHCl at each pH relative to average value of m_GuHCl over neutral pH range.

As seen in these tables and graphs, V66Q/GLA appeared to have stability characteristics similar to V66N/GLA. Both of these proteins were confirmed to be the correct mutants using ion electro-spray mass spectrometry, showing that they differ by 14 atomic mass units, exactly the difference expected from the difference of a methylene unit.

To compare the variability of ΔG_H2O and m_GuHCl across the range of pH, the values were normalized. First, the average of ΔG_H2O and m_GuHCl was calculated over the range of pH 6.5 to 8.3 for GLA and each mutant. For wild-type, with an additional histidine ionizing, the averages were calculated over the range 7.0 to 8.3. (Normalization against the average over these pH values was chosen since no ionizable groups are expected to titrate in this range and abrupt changes in ΔG_H2O and m_GuHCl are not occurring, but similar results, not shown, are found when normalizing to the values at pH 7.0 or the average of all values from all pHs.) The differences between the values of ΔG_H2O and m_GuHCl for each protein at each pH and the values of ΔG_H2O and m_GuHCl averaged over the neutral pH range for that same protein were then calculated. These normalized values of ΔΔG_H2O and Δm_GuHCl are plotted as a function of pH in Figures 1b and 2b respectively.

Discussion

As in our previous studies of the effects of pH upon the stability of substitution at position 66 with ionizable side chains, the non-ionizable mutations examined here were made in a version of staphylococcal nuclease with three stabilizing mutations. The additional stability afforded by these three substitutions allows the determination of the free energy difference between the native and denatured states over a broad range of pH, even for substitutions at position 66 that move the folding equilibrium strongly in the direction of the unfolded state. To facilitate comparison to the many mutants of staphylococcal nuclease previously examined, the effects of pH upon the stability of wild-type were also determined.

Changes in pH alter the stability of all of these proteins in a very similar pattern, with two prominent exceptions: the stability of wild-type protein at low pH and the stability of mutant V66Y/GLA at high pH (Table 2 and in Figure 1a). Both of these exceptions are easily rationalized. The wild type protein differs from all the other proteins by one ionizable residue, H124, which is substituted with the stabilizing, non-ionizable side chain leucine in all the other proteins studied. The imidazole side chain begins to protonate as the pH drops and this ionization event evidently destabilizes the native state relative to the denatured state [37]. As discussed in our earlier work concerning ionization effects on stability [1, 3], the first point at slightly below pH 7 where the shape of the curve begins to diverge from the others corresponds to the pK_a of the side chain in the denatured state. The second point at about pH 5.5 where it begins to parallel the other curves again roughly corresponds to the pK_a of the side chain in the native state. Both of these approximate pK_a values seem reasonable, with the apparent denatured state pK_a being similar to that found for histidine in short peptides and the shift in pK_a for the native state being proportional to the observed destabilization of approximately 1.5 kcal/mol and consistent with the known pK_a of this residue [37, 38]. The second exception of V66Y/GLA is similarly explained. While we have referred to the substitutions made here at position 66 as non-ionizable, that is not strictly correct for tyrosine, which deprotonates at high pH. Ionization of a buried side chain will destabilize the native state relative to the denatured state, precisely what was observed with the V66Y/GLA variant starting at pH 9.7 where the tyrosine is partially deprotonated in the denatured state. In this case, the stabilities were not measured at high enough pH to be able to see the curve again begin to parallel the others as the deprotonation of the side chain, shifted to a much higher pKa, occurs in native state.

These two explicable exceptions aside, it is remarkable how closely the stability values track with each other across a wide range of pH. This is most apparent after the stability values are normalized relative to the average stability near neutral pH (Figure 1b). It appears that most of the variability between the curves traced can be attributed to experimental error.

Our standard error estimates are based on the reproducibility of many runs of wild-type protein [35] under standard conditions (25 mM phosphate, 100 mM NaCl, pH 7.0), which may or may not be applicable over a wide range of pH values. As described in Results, the difference between the value of ΔG_H2O and m_GuHCl at each pH and the value of ΔG_H2O and m_GuHCl over the range from 6.5 to 8.3 was calculated. (Because wild-type begins to diverge somewhat from the other proteins at pH 6.5, presumably as H124 begins to titrate, the values from 7.0 to 8.3 were averaged instead.) As the plot of these normalized values in Figures 1b and 2b show, both ΔΔG_H2O and Δm_GuHCl have a very narrow range of variability at any given pH.

The values cluster quite tightly in the neutral range, but diverge more at the extremes of pH. This subjective observation from the figures is made more quantitative by determining the standard deviation of ΔΔG_H2O and Δm_GuHCl at each pH value, as summarized in Table 5. This tests the hypothesis that the values of ΔG_H2O and m_GuHCl are in fact perfectly correlated between protein variants and the values of ΔΔG_H2O and Δm_GuHCl are identical for all proteins at each pH value. If this hypothesis is correct, the standard deviation of ΔΔG_H2O and Δm_GuHCl should be explained solely by experimental error. There are two exceptions to this assumption. Because wild-type and V66Y/GLA diverge from the other stability curves as ionizable groups unique to those proteins titrate, we excluded from the calculation of standard deviation the values of ΔΔG_H2O and Δm_GuHCl at pH 6.5 and below for wild-type and for pH 9.7 and above for V66Y/GLA, i.e. the pHs over which those groups are titrating. There is a slight increase in the standard deviations at extremes of pH, where stabilities are changing more rapidly with pH and the native baseline is often very difficult to fit accurately because of general protein instability. There are two values that go into each calculation, the average value over the neutral pH range and the value at each pH. The errors calculated here should be equal to the square root of the sum of the squares of the error in each contributing value. If we assume that the error in each contributing value is the same, the overall average standard deviation turns out to be 0.087 kcal/mol for ΔG_H2O and, for m_GuHCl, 0.115 kcal·mol⁻¹·M⁻¹. These standard deviations are quite similar to the 0.096 kcal/mol and 0.116 kcal·mol⁻¹·M⁻¹ estimated from the reproducibility of wild-type data [35]. In other words, within experimental error, the values of ΔG_H2O track parallel curves for all the different proteins, as do the values of m_GuHCl.

Table 5.

Averages and standard deviations for normalized stability (ΔΔG_H2O) and slope (Δm_GuHCl) in various buffers.

Buffera	pH	ΔΔGH2O		ΔmGuHCl
		Average	Std. Dev.	Average	Std. Dev.
A	4.5	−1.010	0.224	−0.109	0.183
A	5.0	−0.129	0.156	0.046	0.161
A	5.5	−0.432	0.108	0.204	0.155
A	6.0	−0.272	0.094	0.211	0.163
A	6.5	−0.097	0.089	0.078	0.076
A	7.0	−0.037	0.068	0.030	0.100
A	7.8	0.001	0.065	0.033	0.070
B	7.9	0.074	0.073	−0.083	0.056
B	8.3	0.047	0.163	−0.045	0.153
C	9.2	−0.260	0.139	0.079	0.119
B	9.7	−0.435	0.132	0.327	0.313
C	9.7	−0.519	0.170	0.353	0.253
C	10.2	−1.364	0.115	0.853	0.321

^aBuffer A indicates 25mM bis-tris-propane/acetic acid, Buffer B indicates 25mM bis-tris-propane/phosphoric acid, Buffer C indicates 25mM ethanolamine/hydrochloric acid.

Detailed analysis of stability versus pH is not our main interest here, but one feature of these curves bears specific mention. All the proteins show a small, but significant, increase in stability as the pH falls from 5.5 to 5.0. This increase would be tempting to wave aside as experimental error if a single protein had been examined, but must be taken at face value given its occurrence in every protein. The logical explanation for this behavior is that, as some group protonates, the protonation either removes a destabilizing interaction from the native state or introduces one to the denatured state. Although we have no direct evidence, we lean toward the former interpretation and would not be surprised if the protonation of aspartate 21, a key side chain in the active site, previously shown by us to be greatly stabilizing when mutated to asparagine [28, 39], were responsible. The pK_a of D21 measured with NMR spectroscopy is 6.5, reasonably consistent with protonation of this side chain becoming complete in the range of pH where this increase in stability was observed [4].

While it is interesting to speculate on the causes of why the curves of stability versus pH have the specific shape they do, this is not the most important observation to be made. Rather, the fact that these curves are, within experimental error, superimposable is an observation with several interesting implications about the denaturation of staphylococcal nuclease. To discuss this point we must first consider how variation in pH can cause a change in protein stability. The most significant contribution comes from differences in H⁺ binding/release between the folded and the denatured forms of the protein. For example, at low pH H⁺ are bound preferentially to the unfolded form because the pK_a values of Asp and Glu residues tend to be higher in the unfolded state than in the native one. But there are also physical forces that are responsible for the variation of stability as a function of pH. At low pH, many groups are protonated, becoming either neutral or positively charged. At high pH, many groups are deprotonated, becoming either neutral or negatively charged. This predominance of either positive or negative charge removes favorable electrostatic interactions that would normally stabilize the native state and introduces strong electrostatic repulsions that are minimized in the unfolded state.

Coulomb interactions, both favorable and unfavorable, are primarily responsible for these effects because they are responsible for differences in pK_a values in the folded and unfolded forms of the protein. A favorable interaction between basic and acidic groups shifts the pK_a higher and lower respectively. Two negatively charged groups brought into proximity with one another will cause a higher than normal pK_a and the interaction of two positively charged groups will cause a lower than normal pK_a. This has implications for our understanding of the nature of nuclease’s unfolding reaction, which we will return to after a brief discussion of alternative hypotheses about how that unfolding occurs.

There is evidence that at least some staphylococcal nuclease mutants unfold by a three-state mechanism with a significantly populated intermediate [10–14, 17, 19, 20, 23, 40, 41]. Of particular relevance to the results presented here, Fink’s laboratory demonstrated that nuclease has a compact unfolding intermediate significantly populated at low pH or high ionic strength [42–45]. Others have argued that rather than a three-state model with a true intermediate, nuclease unfolds in a variable two-state fashion, where the amount of residual structure present in the denatured state changes as a function of temperature and denaturant concentration [22, 25, 46]. Regardless of whether a true intermediate is formed or whether there are differing amounts of residual structure in the denatured state, both of these possible unfolding mechanisms raise a troubling question. If the unfolding of nuclease does not follow a true two-state unfolding mechanism, does the application of the two-state model to analyze the data introduce significant error? Previously, we have shown that thermal unfolding of wild-type and ninety-seven mutants were experimentally indistinguishable, whether followed by tryptophan fluorescence or by CD at 222 nm [47]. We interpreted this agreement in results from these two very different probes as indication of a two-state denaturation or an intermediate that nearly completely lacks helical structure. More recently, we have analyzed the results of 106 guanidine hydrochloride denaturations of wild-type staphylococcal nuclease carried out at pH 7.0 over the course of twenty years. As we showed, a three-state unfolding, even if the two denatured states are indistinguishable by tryptophan fluorescence has a characteristic signature. We found no sign of this signature [35]. Nevertheless, these are indirect proofs and further exploration of this important question for this well used protein is warranted.

The mutants studied here are of widely varying stabilities, with over 4 kcal/mol separating the least stable from the most stable (Table 1). This means that at the same pH and guanidine hydrochloride concentration there is an approximate 1000 fold difference in the folding equilibrium constant. To achieve the same ratio of folded to unfolded protein at a particular guanidine hydrochloride concentration for any two mutants would require them to be at very different pH values. If three-state unfolding is occurring, in order for the two-state model to give consistently similar behavior across a wide range of pH, the intermediate and the unfolded state would have to have essentially identical stability dependence upon pH. Although it is theoretically possible that the relative stabilities of the transition between the native and intermediate states and the intermediate and fully denatured state might vary in perfect lockstep, it seems extraordinarily unlikely it should do so, especially for all the mutant proteins examined here and in light of their very different overall stabilities.

If it were true, interactions between charged groups would have to perturb their pK_a values, as discussed above. Recall that the system is responding in readily observable ways to differences in a single ionizable group, as shown by the overall change in stability with pH or the behavior of wild-type at low pH or tyrosine at high pH. If there is no difference in stability dependence upon pH between two putative unfolded states, this means there is no difference in pK_a values or in the interactions of the electrostatically charged groups in these two denatured states, which leads one to wonder if there is any functionally significant difference between them.

Similarly, if there are variable amounts of structure in the unfolded state, it would appear there is no experimentally significant difference in the electrostatic interactions in the different mutants at different pH values or guanidine hydrochloride concentrations. Let us suppose that the native state breaks down to a more compact denatured state that then transitions to a more fully unfolded state more closely approximating a random coil. It seems likely that there is much greater scope for electrostatic interactions, favorable or unfavorable, in the more compact state. Some of the less mutants cause the denatured state to become populated at low denaturant concentrations or near neutral pH. Similar levels of denatured state are only achieved in the more stable mutants, or the stabilized wild-type, at extremes of pH or much higher concentrations of denaturant. Is it reasonable to expect the compact form of the denatured state to be populated in exactly the same amount under these widely varying conditions? Not unless, just as in the case with a well-populated equilibrium intermediate, unless every factor affecting stability, whether it is the mutation itself, the pH, the ionic strength, or the concentration of denaturant affects the relative stability of the native state and the transitions in the denatured state in exactly the same way. Otherwise, one would expect to see the relative stabilities of various mutants change as a function of pH. And, we do not observe such behavior. This does not mean that the denatured state is not variable. Indeed, we find Bolen’s evidence for this convincing. But it argues that these changes are not energetically significant and analysis in terms of a simple two-state model does not introduce inaccuracies. This is a qualitative argument, but it can be made more quantitatively with regard to the pH dependence of m_GuHCl.

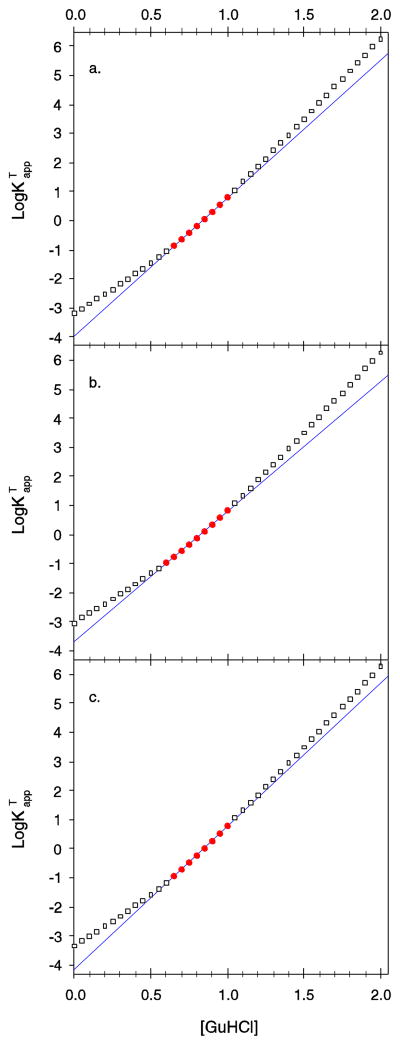
Staphylococcal nuclease is notorious for the large changes in m_GuHCl that are observed upon mutation. It has been argued that the changes in m_GuHCl for nuclease mutants may be attributable to the presence of a three-state unfolding mechanism and the incorrect assumption of a two-state process [24]. Previously, we have laid out the mathematical model for the three-state denaturation of nuclease where the native state is in a two-state equilibrium with an intermediate denatured state, D₁, which is in turn in a two-state equilibrium with a more fully unfolded denatured state, D₂ [35]. In this model D₁ and D₂ are indistinguishable by the tryptophan fluorescence probe of structure. Using this model, we have calculated the overall, or total, equilibrium between the native state and both denatured states in several circumstances and show the results of these simulations in Figure 3.

Figure 3.

Simulation of three-state unfolding, N ⇌ D₁ ⇌ D₂, where the postulated denatured states D₁ and D₂ are indistinguishable by the spectroscopic probe showing how the apparent values of m_GuHCl that result from a two-state fit can change dramatically. Points are ${\text{logK}}_{\text{app}}^{\text{T}}(\text{N}\rightleftharpoons {\text{D}}_1+{\text{D}}_2)$ versus [GuHCl] calculated using a three-state model [35]. The solid line is the apparent stwo-state least square fit of ${\text{logK}}_{\text{app}}^{\text{T}}$ versus [GuHCl] in the region where 1 > logK_app > - 1. Points used in the regression are shown by filled circles. Outside this experimentally accessible region the calculated ${\text{logK}}_{\text{app}}^{\text{T}}$ values are shown by hollow squares. (a) The first transition between N and D₁ is assumed to be two-state with values for $m_{\text{GuHCl}}^{\text{a}}$ of 4.3 kcal·mol⁻¹·M⁻¹ and $\mathrm{\Delta }{\text{G}}_{{\text{H}}_2\text{O}}^{\text{a}}$ of 4 kcal·mol⁻¹. The second transition between D₁ and D₂ was assigned values for $m_{\text{GuHCl}}^{\text{b}}$ of 2.9 kcal·mol⁻¹·M⁻¹ and of 2 kcal·mol⁻¹ for $\mathrm{\Delta }{\text{G}}_{{\text{H}}_2\text{O}}^{\text{b}}$. The apparent value of ΔG_H2O and m_GuHCl from the two-state fit are 5.33 kcal·mol⁻¹ and 6.38 kcal·mol⁻¹·M⁻¹ respectively. (b) $m_{\text{GuHCl}}^{\text{a}}$ and $m_{\text{GuHCl}}^{\text{a}}$ are unchanged. $\mathrm{\Delta }{\text{G}}_{{\text{H}}_2\text{O}}^{\text{a}}$ is assumed to be 3.8 kcal·mol⁻¹ and $\mathrm{\Delta }{\text{G}}_{{\text{H}}_2\text{O}}^{\text{b}}$ is assumed to be 2.2 kcal·mol⁻¹. The apparent value of ΔG_H2O and m_GuHCl from the two-state fit are 4.95 kcal·mol⁻¹ and 6.03 kcal·mol⁻¹·M⁻¹ respectively, much less than in panel a. (c) $m_{\text{GuHCl}}^{\text{a}}$ and $m_{\text{GuHCl}}^{\text{b}}$ are unchanged. $\mathrm{\Delta }{\text{G}}_{{\text{H}}_2\text{O}}^{\text{a}}$ is assumed to be 4.2 kcal·mol⁻¹ and $\mathrm{\Delta }{\text{G}}_{{\text{H}}_2\text{O}}^{\text{b}}$ is assumed to be 1.8 kcal·mol⁻¹. The apparent value of ΔG_H2O and m_GuHCl from the two-state fit are 5.58 kcal·mol⁻¹ and 6.61 kcal·mol⁻¹·M⁻¹ respectively, much more than in panel a.

This argument for changes in m_GuHCl being caused by a three-state unfolding process supposes the protein is unfolding in such a way that D₁ and D₂ are comparable in stability in the experimentally accessible region for equilibrium measurements (Figure 3a) and a mutation is made that perturbs the stability of either the D₁ or D₂ state slightly more than the other. This either shifts the denaturation to have more D₁ and less D₂ (Figure 3b) or to a situation where N denatures to mostly D₂ and very little D₁ (Figure 3c). Either possibility will cause the fit of the two-state model to the underlying three-state reality to change dramatically, giving very different values of ${\text{K}}_{\text{app}}^{\text{T}}$ and $m_{\text{GuHCl}}^{\text{T}}$. Note that in every case, the slope of the two transitions in the three-state reality was not varied, nevertheless the apparent slope value changed greatly. In all cases, the true values of ${\text{K}}_{\text{app}}^{\text{T}}$ and $m_{\text{GuHCl}}^{\text{T}}$, represented by the hollow squares, diverge substantially from the two state least square fit to the experimentally accessible data, but the least square fit to that experimentally accessible data is excellent. This, it has been argued, is the explanation for why staphylococcal nuclease shows large changes in slope upon mutation and the values for nuclease stability and m_GuHCl are unreliable. If this were correct, it would be a serious problem for any use of staphylococcal nuclease as a model of protein folding.

The results presented here are not consistent with this argument. The values of m_GuHCl for the various proteins cover a fairly wide range, and the value of m_GuHCl for any given protein varies significantly with pH. However, the difference in slope between any given pair of proteins is fairly constant, with the two lines traced as a function of pH having a regular offset. This is seen in Figure 2b, where the values of Δm_GuHCl are well superimposed. Again, it is theoretically possible that the changes in slope concomitant with changes in pH are due to changes in the relative stability of two different denatured states, as illustrated in Figure 3. But, again, this would require that the stabilities of these two denatured states vary in a similar fashion for all the protein variants, which is so improbable as to be dismissed.

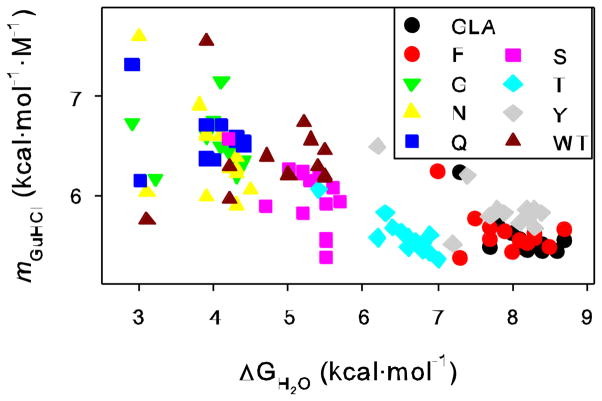
There is a second argument against the three-state model as a source of slope variation. In Figure 4 we plot the value of m_GuHCl versus ΔG_H2O for all the proteins at all the pH values. There is a clear tendency for these two values to be inversely correlated. In other words, the more stable the protein, the lower the slope. This is true whether comparing completely different proteins, mutants of a certain protein, or examining the behavior of any given protein as a function of pH. Elsewhere [35] we have shown as a mathematical consequence of the three-state model that higher slopes tend to be associated with more stable proteins and this is also seen in the simulations of Figure 3. The opposite is found here. Higher slopes can be accomplished in a less stable protein via a three-state mechanism, but only if the stability of both the D₁ and D₂ states drop relative to the native state, and the D₁ stability must drop more. This is difficult to rationalize in any physical model for these states we envision. These stability changes would have to occur for all the protein variants examined here in a very similar fashion, but at very different pH values and guanidine hydrochloride concentrations, since less stable variants would have to populate D₁ at generally more neutral pH values and lower concentrations of guanidine hydrochloride. Occam’s razor would argue that a simpler two-state denaturation, with no significantly populated intermediates, is the favored interpretation.

Figure 4.

Plot of ΔG_H2O vs. m_GuHCl for each protein variant at each pH.

Lastly, we point out that we have determined pK_a values of a variety of individual mutant side chains in nuclease by rigorous analysis of the pH dependence of stabilities [1–3, 48]. These stabilities were determined using a two-state analysis. Subsequently, the pK_a values for some of these side chains were determined by NMR and in some cases potentiometry [3, 49]. The values from each method of analysis agree well. If two-state analysis of staphylococcal nuclease denaturation data was incorrect, the pK_a values calculated from the energetic linkage would have been significantly different from those more directly measured.

Conclusions

The differences in the stability of the various staphylococcal nuclease mutants examined here vary so little across a wide range of pH that they are difficult to reconcile with the proposal that the equilibrium unfolding mechanism for these variants or wild-type is three-state. This difficulty becomes an impossible stretch when the parallel curves traced by the m_GuHCl values across this pH range are considered. The large differences in the absolute values of m_GuHCl for the various mutants and the simultaneous invariance of their relative values are quite remarkable and quite incompatible with the ways that a three-state mechanism would alter the m_GuHCl values coming from a two-state fit. It is clear that analysis of denaturation data for staphylococcal nuclease wild-type and most mutants with a two-state model is entirely appropriate and yields thermodynamic values that are very low in error. There does not appear to be, in other words, a significantly populated equilibrium unfolding intermediate.

More broadly, the results presented here are not just evidence against the three-state model. They are also evidence that the changes in m_GuHCl values observed upon mutation are consistent in a way that was not anticipated. Another commonly advanced explanation for mutationally caused change in slope is that it is due to change in the denatured state solvent accessible surface area. Although we have not fully explored this idea here, the fact that the relative differences between m_GuHCl values of mutants are invariant as conditions are altered in ways that are known to change the size and character of the denatured state significantly is noteworthy. As will be discussed in future publications, our results here imply that this explanation of changes in m_GuHCl also falls short and that other means of altering m_GuHCl are at work as well.

Highlights.

• Six single mutations were made in a highly stable triple mutant of nuclease.

• Stabilities were measured in 13 buffers ranging over pH 4.50 to 10.19.

• m_GuHCl AND ΔG_H2O vary widely with pH, but differences between mutants do not.

• Therefore, most nuclease mutants do not denature by a three-state mechanism.

• Changes in m_GuHCl upon mutation do not arise from a three-state mechanism.