Mesoscopic modeling as a starting point for computational analyses of cystic fibrosis as a systemic disease

Abstract

Probably the most prominent expectation associated with systems biology is the computational support of personalized medicine and predictive health. At least some of this anticipated support is envisioned in the form of disease simulators that will take hundreds of personalized biomarker data as input and allow the physician to explore and optimize possible treatment regimens on a computer before the best treatment is applied to the actual patient in a custom-tailored manner. The key prerequisites for such simulators are mathematical and computational models that not only manage the input data and implement the general physiological and pathological principles of organ systems but also integrate the myriads of details that affect their functionality to a significant degree. Obviously, the construction of such models is an overwhelming task that suggests the long-tern development of hierarchical or telescopic approaches representing the physiology of organs and their diseases, first coarsely and over time with increased granularity.

This article illustrates the rudiments of such a strategy in the context of cystic fibrosis (CF) of the lung. The starting point is a very simplistic, generic model of inflammation, which has been shown to capture the principles of infection, trauma, and sepsis surprisingly well. The adaptation of this model to CF contains as variables healthy and damaged cells, as well as different classes of interacting cytokines and infectious microbes that are affected by mucus formation, which is the hallmark symptom of the disease [1]. The simple model represents the overall dynamics of the disease progression, including so-called acute pulmonary exacerbations, quite well, but of course does not provide much detail regarding the specific processes underlying the disease. In order to launch the next level of modeling with finer granularity, it is desirable to determine which components of the coarse model contribute most to the disease dynamics. The article introduces for this purpose the concept of module gains or ModGains, which quantify the sensitivity of key disease variables in the higher-level system. In reality, these variables represent complex modules at the next level of granularity, and the computation of ModGains therefore allows an importance ranking of variables that should be replaced with more detailed models. The "hot-swapping" of such detailed modules for former variables is greatly facilitated by the architecture and implementation of the overarching, coarse model structure, which is here formulated with methods of Biochemical Systems Theory (BST).

Introduction

Until the turn of the century, biomathematics by and large lived in the shadows of experimental biology. Data were scarce, and while computational methods were rapidly improving, they were not really up to the task of analyzing biological systems of a realistic size. The situation started to change over the past decade, which witnessed unparalleled advancements in high-throughput molecular biology, as well as in computer science. The former all the sudden began to offer more data than had been thought possible merely a decade ago, while the latter put new, powerful computational options at the disposal of most users of personal computers. These options triggered a change in the way we began to think about systems analyses, because it became possible to replace targeted mathematical analyses of system features with large-scale simulation methods that readily swept entire domains of relevant parameter spaces. These changes immediately suggested the feasibility of corresponding increases in the scope of analyzable systems, from the original models of small, relatively well characterized systems to much larger, less-defined systems . It became feasible to look at genomes and flux-balance models of entire cells [3], and systems models based on proteomes and metabolomes now appear to be coming within reach.

The careful analysis of many small models in the past offered the opportunity to develop general and specific methods and strategies for assessing biological systems, from stability and sensitivity analyses to targeted manipulations and optimization. Among the analyses, one of the most challenging tasks has been the estimation of parameter values [4–6]. Many methods were developed over the years, yet parameter estimation remains to be a daunting task [7]. Directly tied to this task, yet often ignored, has been the deeper question of which mathematical representations are best suited for describing the processes governing biological systems [8]. One reason that these tasks were even addressable in the past was a relatively low level of expectation: If a model reflected the overall trends in often scarce and noisy datasets, one felt justified to declare success. After all, the data were usually too coarse to distinguish alternative candidate models. A second reason for the success of small-scale analyses was the relative homogeneity of the analyzed systems. If a model described biochemical pathways or the signal transduction in neurons, biochemistry and kinetics, or neuroscience and the insights of Hodgkin and Huxley, offered at least default information for getting started and setting up appropriate models.

While entering the realm of much larger dynamic models, the implicit assumption is often that the degree of difficulty associated with the various required tasks scales linearly and that the same technical issues and challenges continue to dominate the modeling task. The reality is sometimes different. With respect to parameter and structure identification issues, the experimental community is beginning to generate much better and more comprehensive data for some aspects of systems than ever before. At the same time, the level of expectation has risen tremendously, and only a very accurate fit to most if not all data available is sometimes seen as acceptable. Along with these changes within the modeling landscape, parameter estimation is no longer necessarily the only or even most challenging bottleneck. Instead, larger, heterogeneous systems require us to ask how even to get started with the development of a complex model? Are we allowed to ignore components even if they are known to exist? How do we identify appropriate functions? How “good” does a “good” fit have to be [7]? These are complicated questions, because nature does not provide us with guidelines toward their answers, and appropriate interaction diagrams, describing functions, and parameter values must be obtained from the new types of observation data through reverse engineering methods, which are notoriously difficult, especially if the mathematical structure of the functions is a priori not known [9, 10].

This article mainly focuses on the question of how to get started with the design of a model. The context is the task of initiating the modeling a complex systemic disease, cystic fibrosis (CF), with the ultimate goal of understanding how the different components of the disease contribute to its severity. In the distant future, such an understanding could lead to a disease simulator that permits personalization and the exploration of treatment options.

It is evident that it is much too difficult to set up a comprehensive model of a complex disease system from scratch in one stroke. A natural strategy, which is sketched out here, is therefore to develop an initial, relatively simplistic model, based on literature information, to analyze its high-level features, and to determine through an adaptation of sensitivity analysis where the next level of refinements and improvements might be most beneficial. The description of this strategy is rather preliminary in specifics, and the article is therefore more strategic and educational than a true advance with respect to our understanding of CF [11].

A starting model of a simplified, coarse type may be called mesoscopic. It is neither a fully mechanistic model nor a black-box model, but resides somewhere in between [12], and could be what Noble Laureate Sidney Brenner called a middle-out model (cited in [13]). As was discussed elsewhere in a different context [14], a mesoscopic model permits extensions in two directions. First, it allows an initial assessment of the role and importance of each component contributing to a complex system like a disease and constitutes a foundation for larger and more refined models that might ultimately lead to the construction of comprehensive health and disease simulators. Second, a mesoscopic model facilitates further size reduction and abstraction toward the discovery of design and operating principles fundamentally governing the functionality and interactions of the processes governing the disease [15–18].

Case Study: Developing an initial understanding of CF of the lung

Cystic Fibrosis (CF) is a complex and systemic disease that affects several organs and leads to a drastic reduction in life span [19, 20]. It ranks among the most common lethal genetic diseases in Caucasians. No cure for the disease is known, and while the treatment of sequelae has extended the life expectancy of CF patients substantially, it has not succeeded in bringing the expected life span of a CF patient up to par with individuals without the disease.

Most of the morbidity and mortality associated with CF are attributable to a progressive loss of lung function, which is due to chronic inflammation, recurring and/or persistent infections, and a heightened susceptibility to damage from oxidative stress. This unfortunate trend of diminished lung capacity is not linear and not even monotonic. Instead, it typically consists of iterated cycles of acute infections and recovery phases, which are collectively called acute pulmonary exacerbations (APEs) [21, 22]. Their hallmark characteristics are an increased bacterial burden and acute inflammation [23], which is caused or worsened by increased oxidative stress and accompanied by strong interactions between pro- and anti-inflammatory cytokines [24]. The current treatments of APEs consist of antibiotics and anti-inflammatory drugs, as well as physical or chemical airway clearance with inhalers, vibrating chest vests, and bronchodilators [25, 26]. While APEs can be controlled to some degree, patients with CF or other lung impairments usually do not regain the level of lung function they had before the episode and instead often experience a certain degree of irreversible damage to their lungs [27, 28]. As a consequence, the progression of this aspect of CF is a complicated series of APEs and recovery phases as it is sketched qualitatively in Fig. 1.

Fig. 1.

Qualitative clinical observation indicates an iterated loss of lung function (blue) in CF patients, which generically occurs in a non-monotonic fashion characterized by acute pulmonary exacerbations (APEs). Even with aggressive treatment, the patient typically does not recover fully from an APE, and the result is a negative trend (red dotted line) in lung function over time and a resultant reduced life expectancy.

At this point, no treatment administered in response to the onset of an APE is sufficient for restoring lung function completely. An effective strategy, which is yet to be developed but appears likely to be effective, would consist of preempting APEs altogether. Such a strategy would require two components. First, biomarkers must be collected during APE episodes and, maybe more importantly, between and especially just before such episodes. These biomarkers would presumably be genomic, proteomic, metabolomic, and physiological, and should also include samples of bacteria and possibly fungi, which inhabit the lung of CF patients. Second, it is to be expected that these biomarker datasets are quite large, thus posing a substantial challenge of analysis and interpretation, and suggesting computational analysis. For instance, it is a priori not evident which biomarkers are causative, symptomatic, coincidental, or operate within their range of normal variation.

The reason for this uncertainty is that CF of the lung constitutes a complex disease system that consists of numerous components, which in many cases are still only incompletely characterized, function at different time scales and organizational levels, and interact in nonlinear ways that are difficult to intuit. One set of components consists of different host cells, which are continuously affected by the disease. An important driver of the disease symptoms is the mucus that covers the lung epithelium and provides a fertile breeding ground for invading bacteria and fungi [1, 29]. These mircoorganisms form a further set of contributors to the disease. It is at this point unclear how many different species or strains of bacteria may be present simultaneously in a heterogeneous, patient-age-dependent metapopulation inside the lung [20, 30–33]. Yet another set of contributors contains various types of cytokines, whose role it is to attack invading bacteria and control inflammation events [24]. Under normal conditions, cytokines are maintained in a finely tuned and delicately balanced system of pro- and anti-inflammatory molecular species that is robust to bacterial attacks, cell damage, infection and inflammation, as well as other perturbations. However, once this complex system becomes unbalanced, it is sometimes difficult to control. In favorable cases it may regulate itself, but it may also enter a sometimes fatal phenomenon called a cytokine storm [34], in which some cytokines reach 1,000 times their normal concentrations. Further contributors to CF are reactive oxygen species (ROS), which alter the inter- and intra-cellular milieu, may trigger signaling events and immune responses, and can generally move the homeostatic system of the lung to a state of allostasis, that is, an altered steady state that is prone to a variety of problems [35].

The size and complexity of the CF disease system suggests the use of computational modeling tools that have the potential of storing, integrating, and interpreting large sets of heterogeneous data and nonlinear interactions. Interestingly, while many mathematical models have addressed bacterial dynamics, oxidative stress, and cell population dynamics in different species, the literature is essentially devoid of models that shed light on the CF lung as an "ecological disease system" [36, 37]. In response to this paucity of baseline models, this article describes a possible first phase of the development of a coarse preliminary model that describes the overall dynamics of lung cells, bacteria, cytokines, and mucus. The mesoscopic model is very simplistic, yet capable of representing hallmark observations of the CF lung at a high level. Specifically, APEs arise from the dynamics of the model as emergent properties.

The process of designing this model is recaptured in the following. It begins with a generic model of inflammation [38–40], which is adapted to the specifics of CF. This derivative model represents the interactions and overall dynamics of the main contributors to CF. It is diagnosed and tested with simulations against qualitative data and then subjected to a variation of sensitivity analysis that permits the assessment of the significance of the various contributing factors associated with the disease. As an illustrative example demonstrating how a mesoscopic model may be extended, the single population of bacteria is "telescopically" expanded into a small, generic three-species metapopulation that allows the investigation of different sensitivities of microbial species to antibiotic treatment. It is furthermore shown how the model can be reduced for the exploration of its design features.

The mesoscopic strategy resembles conceptually a modeling approach that was proposed in biomechanics, where one begins with a macroscopic, high-level model of locomotion or some other phenomenon of interest and subsequently embeds increasingly finer-grained models into these first models [41]. In this biomechanical context, the high-level models are called templates. They help the modeler organize anchors, which are more complex models representing anatomical and physiological features in a detailed fashion and can be incorporated into the template models in a natural manner.

Two aspects of this approach are noteworthy. First, it is feasible to use information of almost any degree of granularity. And second, once the template has been established and coarsely validated, the anchor models can be "hot-swapped," as a computer hardware scientist might say: while keeping the context the same, individual components can be replaced with new or refined components, without substantially disturbing overall functioning.

The telescopic moving between levels of organization is particularly convenient when a canonical modeling framework is chosen for the system representation. A canonical model is derived from strict model construction rules and uses the same type of approximation for all processes involved [42, 43]. Notably, linear models are canonical, because all processes are represented with linear functions. Among the nonlinear canonical models, which are better suited in biology, Lotka-Volterra (LV) [44–46] models and models of Biochemical Systems Theory (BST) are most prominent [47–50]. In the case of LV, all processes are represented by binary terms, that is, of simple products of interacting components, plus one linear term. BST is used here and described in the following section.

Model Design

Biochemical Systems Theory (BST)

The core feature of BST is the representation of all processes with products of power-law functions [47–50]. Thus, if a process involves the two variables X and Y, the representation of this process always has the format αX^gY^h. Here, the parameter α is a non-negative rate constant that quantifies the turnover rate of the process, while g and h are real-valued kinetic orders that signify the strength of the effect that a variable has on the process. A positive kinetic order represents a positive (activating or augmenting) effect, while a negative value means a negative (inhibiting or diminishing) affect. A kinetic order of 0 effectively eliminates the influence of the variable on the process. The formulation of processes with power-law functions is the direct consequence of a Taylor linearization, which is executed in a logarithmic space [47].

BST models have received a lot of attention, because they are easy to set up as default models and offer immediate analyzability. This ease of getting started is especially valuable in the context of systems whose governing processes or mechanisms are ill characterized [43, 51]. As an example, the processes of transcription and translation consist of complicated amalgamations of mechanistic steps at the molecular level, and a detailed physical representation would be very difficult to construct. Also, it would not necessarily be needed, for instance, in a model focusing on metabolic events in response to altered gene expression. In a much coarser fashion, by contrast, the information flow from changes in gene expression to changes in enzymatic activities could be represented with a simple function.

A particularly interesting feature of the modeling strategy in BST is its telescopic property: No matter what the level of modeling, the process descriptions are always in the same format [52]. Thus, a complicated process at a low level may be approximated with a power-law term and included into a higher-order model without destroying its mathematical structure. While this telescopic property has been realized for a long time, it has seldom been used explicitly in model generation. A later section of this article will demonstrate this property in the context of CF.

An interesting mixture of LV and BST models is the representation of growth phenomena, which are of interest here, due to the involvement of bacteria. A typical starting point is the logistic function, which is a special case of both frameworks. Expressed as a differential equation, this function has the format

$$\frac{dN}{dt}=rN-\frac{r}{K}{N}^2$$ (1)

[53]. Using this function as a starting point, BST allows changes in the exponents as well as modulators that affect growth (r N) or the limitation in growth, as it is expressed in the negative term [54]. For instance, the positive effect of pro-inflammatory cytokines, P, on the removal of bacteria can directly be included as

$$\frac{dN}{dt}=rN-\alpha \frac{r}{K}{N}^2{P}^g,$$ (2)

where α and g are parameters characterizing the features of the effect.

From a Generic Inflammation Model to a Coarse Model of CF

Vodovotz and colleagues suggested a series of relatively simple models for understanding generic inflammation processes [38–40]. The basic concept is shown in Fig. 2. Pathogens trigger the production of both, pro- and anti-inflammatory cytokines. The pro-inflammatory cytokines can cause tissue damage or dysfunction, which stimulates further inflammation by means of a "danger signal." Under normal circumstances, the inflammation leads to control of the pathogens. It also triggers the production of anti-inflammatory cytokines, which help reduce the inflammation.

Fig. 2.

The role of pathogens in inflammation, which here is vastly abstracted for mathematical modeling purposes. Green arrows: induction; blunted red lines: suppression. The initiating stimulus, i.e., a pathogen, stimulates both pro- and anti-inflammatory pathways, although with different strengths. Pro-inflammatory agents (e.g., TNFα) can cause tissue damage or dysfunction, which in turn stimulates further inflammation through the release of “danger signals.” Adapted from [32].

In contrast to constructing a model for CF from scratch, it is relatively easy to adapt the generic inflammation model (Fig. 2), set up a coarse CF diagram (Fig. 3), and convert this diagram into a mathematical model in a symbolic format, that is, without the specification of parameter values [11]. In addition to bacteria (B), pro- and anti-inflammatory cytokines (P and A, respectively), and damaged cells (D), it is useful to introduce healthy cells (H), as an indicator of lung function, and mucus (M), which in some sense is the immediate cause of symptoms in CF sufferers. All variables represent dynamic pools that continuously receive replenishing material and lose material through degradation or transport out of the pool (blue arrows in Fig. 3). These in- and effluxes may be large or small and are affected by other components of the system. Of particular importance are the activating (green) and inhibiting (red signals) that functionally connect the pools. For instance, the green arrow from P to the production arrow of A indicates that P triggers the generation of anti-inflammatory cytokines. CF is modeled as an indicator variable that is either present (1; CF patient) or absent (0; healthy subject) and directly affects the dynamics of mucus. The bacterial population has the potential of growing, and its dynamics is affected by mucus, which provides substrate and protection but also impedes bacterial growth due to its viscosity. The bacteria are assumed to contribute to the formation of mucus. If an effect like this activation turns out to be negligible, it is easily removed by setting the corresponding parameter to 0. The remaining interactions correspond to those in the generic inflammation model (Fig. 2).

Fig. 3.

Components and regulatory interactions in the preliminary “template” model. Adapted from [47].

Parameter Values

While BST facilitates the rather straightforward creation of a symbolic model from an interaction diagram as in Fig. 3, the determination of suitable parameter values is, as almost always, a significant challenge [5]. Indeed, some aspects of this step are much harder than, for instance, for purely metabolic models, while others are easier. The more difficult aspects derive from the fact that the modeled effects are in most cases aggregations of several processes that are often ill defined. An example is the effect of cytokines on healthy cells. First, there are several classes of cytokines, each with their own roles and efficacies. Second, their effects on cells may be multifold and not necessarily direct but involve many components of the immune system (see later). Finally, the aggregated processes involved here have seldom been quantified in experiments, let alone in situ. As a consequence, a high percentage of parameter values cannot be found in the literature directly, although clinical and biochemical data may provide ranges, time scales, or general trends. A possible approach to identifying parameter values in such a situation is a large-scale Monte-Carlo situation, where parameter values are randomly chosen from generous ranges, and the output simulations are filtered against observation data or even qualitative expectations (e.g., [55, 56]).

In the present case, the estimation task is to some degree made easier by the fact that our expectations must obviously be lower than for a well-characterized pathway model. Indeed, it should be clear that we can, at best, obtain coarse trends in outputs, rather than numerically precise predictions regarding concentrations or the efficacy of a particular treatment.

BST ameliorates the estimation task due to the fact that all its parameters have a clear interpretation. Kinetic orders quantify the strength or significance of a variable in a given process, as discussed before, and experience with a wide variety of systems has shown that positive kinetic orders seldom exceed a value of 2, while negative kinetic orders are usually between 0 and −1 (see Chapter 5 of [49]). Furthermore, variables subject to transport often have a kinetic order of 1, while substrates of enzyme-catalyzed reactions typically have a kinetic order between 0 and 1, and close to 0.5, if the nominal concentration of the substrate is similar to the K_M of a Michaelis-Menten-type reaction. While not hard and definite, these guidelines permit an initial, coarse assignment of kinetic orders. The rate constants are more variable, but some guidelines for their determination exist as well. In the simplest case, where a BST equation, say for variable X_i, contains only one positive and one negative term, the ratio of the rate constants is directly associated with the steady-state value of X_i [49]. Furthermore, the magnitudes of the two rate constants are directly related to the time unit used: If all terms in the entire system are multiplied by the same positive factor τ, the system runs τ times as fast as before, while leaving the system dynamics otherwise unaffected. In other words, τ merely changes the labels along the x-axis of time course output.

Using these guidelines, an initial model for CF may have the following form:

$$Ḃ=(B^{0.8}{M}^{1.2}-0.8B^{1.2}{P}^{0.1})·M^{-2.4}Ṗ=20B^{0.2}{D}^{0.4}{A}^{-0.1}-50P^{0.5}Ȧ=15B^{0.1}{P}^{0.1}-12A^{0.5}Ḣ=500-40H^{0.3}{P}^{0.2}{A}^{-0.2}Ḋ=40H^{0.3}{P}^{0.2}{A}^{-0.2}-5DṀ=0.16·2^{CF}{B}^{0.25}-0.15M^{2-CF}$$ (3)

The Appendix contains a system file that may be copied directly into the freeware PLAS [57], which is ideal for exploratory analyses of power-law systems. One notes that the effects of CF are implemented as powers. This strategy provides a simple means of switching between the absence (0) and presence (1) of the disease without entirely eliminating the corresponding terms. It also preserves the format of a so-called S-system within BST [49, 50], which permits a variety analyses, for instance, with respect to the steady state and to limit cycle oscillations (see later).

The equations can be used to compute the steady state, which in this case would even be possible with algebraic means [58]. The steady-state values critically depend on the indicator variable CF, which may be 0 or 1. They are given in Table 1. These values are typically taken as initial values for dynamic simulations.

Table 1.

Steady-state values of system variables for healthy individuals (CF=0) and CF sufferers (CF = 1)

	CF = 0	CF = 1
B	1.383617	1278.037
P	6.091615	64.7532
A	2.393149	15.04461
M	1.075577	12.75542
H	2431.41	1713.089
D	100	100

The particular values in Table 1 do not mean all that much per se, except that they constitute the baseline for further analyses. Each value may refer to some unit that is not specified here. For instance, B could be the number of bacteria in units of 1 million. As an alternative to accepting these arbitrary units, one could divide all variables in the differential equations by their steady-state values, which would result in a reference steady state consisting of 1's. Subsequently, all numerical results would be in the format of percent or fold changes. The time unit is similarly unspecified; with the above settings, it could correspond to days. For CF = 1, the "normal" bacterial load and the amount of mucus are substantially higher than for CF = 0. Also, with these settings, the number of healthy cells is already compromised for CF = 1.

Results

Simulations

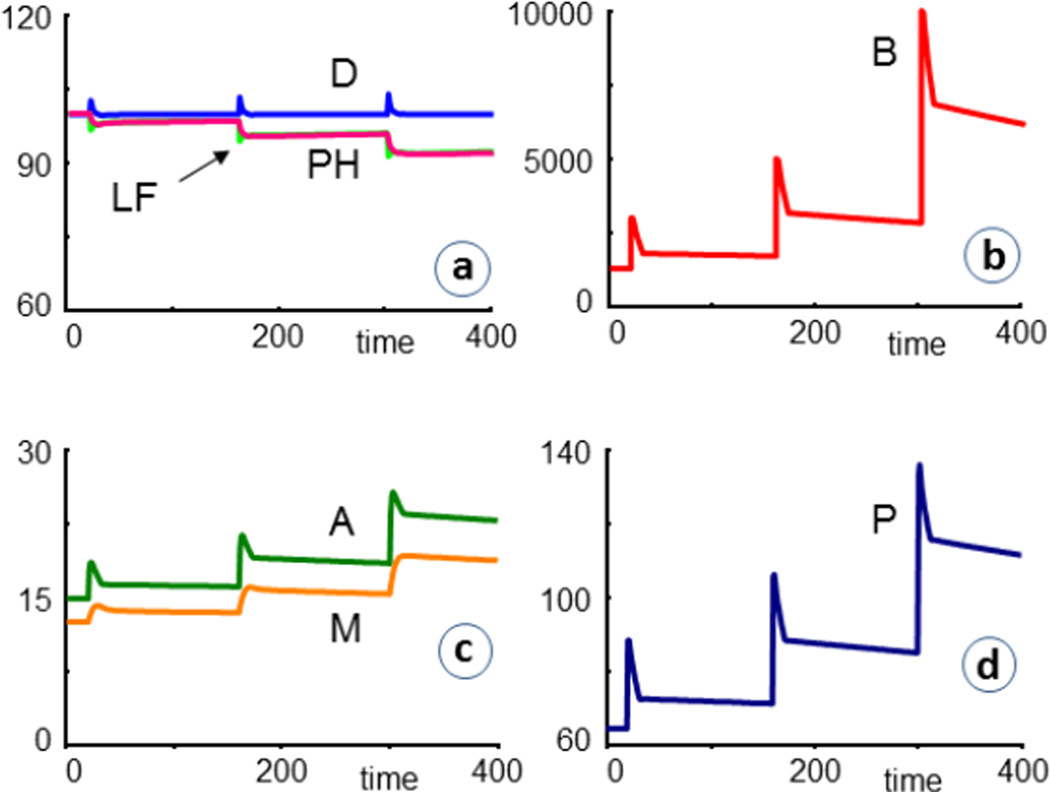
Most results consist of comparative simulations that contrast CF = 1 with CF = 0, or assess CF patients under different infection and treatment scenarios. The first typical set of simulations concerns repeated bacterial infections. As a specific scenario for illustration, we reset the bacteria at times t = 20, 160, and 300 to values of 3000, 5000, and 10,000, respectively. For CF = 0 (healthy), the infections are cleared out quite readily (Fig. 4). In these figures, PH is the percentage of healthy cells left, in comparison to the initial value. LF is another measure of lung function, which for these simplified simulation scenarios is defined as the ratio of healthy to diseased cells, scaled by initial values; thus $\mathrm{L}\mathrm{F}(\mathrm{t})=100·\frac{\mathrm{H}(\mathrm{t})/\mathrm{D}(\mathrm{t})}{\mathrm{H}(0)/\mathrm{D}(0)}$

Fig. 4.

In simulations of healthy individuals (CF = 0), repeated infections are readily cleared, even without the use of antibiotics. Most labels refer to dependent variables in the model (Fig. 3). PH denotes the percent healthy cells left, in comparison to the initial value. LF is a measure of lung function, which here is defined as the ratio of healthy to diseased cells, scaled by initial values; thus LF =100*[H(t)/D(t)] / [H(0)/D(0)].

The same series of infections has a drastically different outcome if CF patients are affected and not treated. As a default, we assume that the model has the same structure and parameter values as for healthy individuals, except for CF = 1, which leads to the steady-state values in Table 1 that are used as initial values. Mucus and cytokine concentrations increase, with P clearly outpacing A, although the system responds much stronger in the production of A, which thereby dampens the infection effects. Nonetheless, the percentage of remaining healthy cells (PH) and the lung function (LF) are significantly reduced after each infection event, thereby leading to a pattern of APEs that is similar to the clinical observations shown in Fig. 1. The model result is somewhat simpler, presumably because the model does not account for delays and secondary effects of the infection.

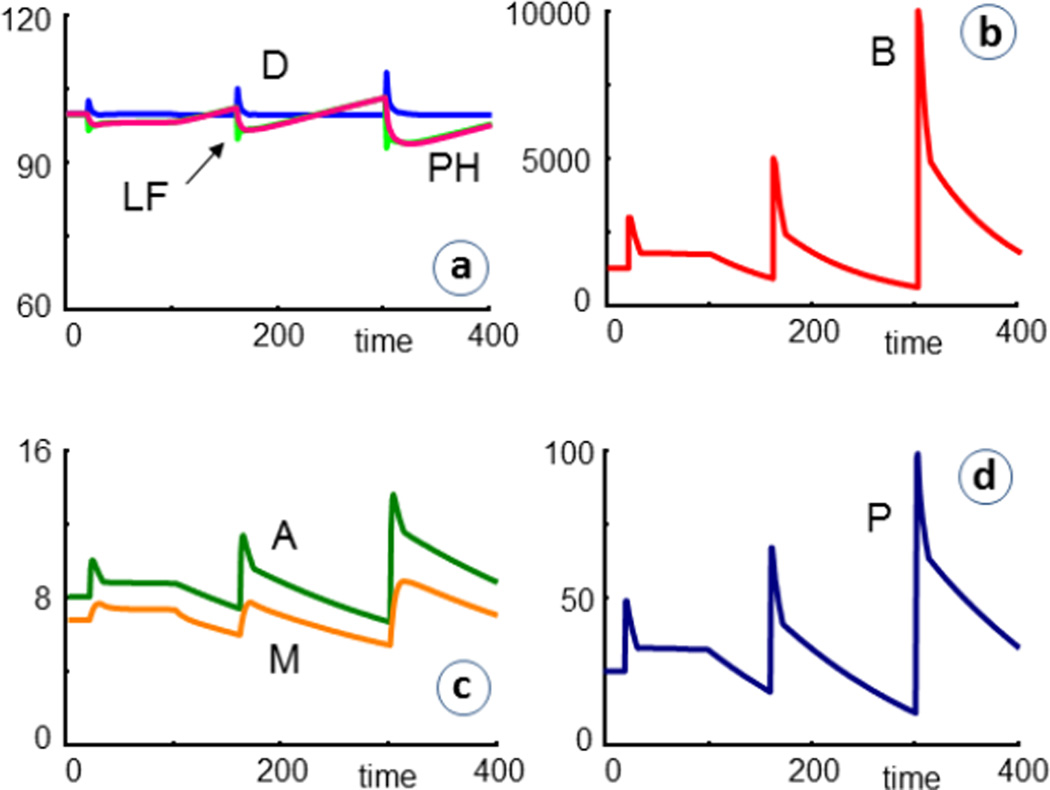
The situation is improved when each infection is followed by an antibacterial treatment, which is here implemented as beginning two days after infection and lasting for ten days in each case. The treatment is taken into account by the inclusion of the term (AB+1) in the degradation term of the equation of bacteria. Under normal conditions, AB = 0, but during treatment, AB is set to a positive value, which reflects the efficacy of the drug. In the example shown in Fig. 6, AB = 5. One can see that bacteria are killed, although not completely, and that the number of healthy cells and the lung function do not decrease quite as rapidly as before (Fig. 5). For drugs such as penicillin, which prevent cell wall formation rather than killing bacteria, a corresponding term with a negative kinetic order could be included in the bacterial production term. It is also possible to model increased drug resistance by reducing this value over time.

Fig. 6.

Simulation results of cystic fibrosis patients (CF = 1) that are repeatedly infected and receive antibiotics for ten days, starting shortly after each infection (AB = 5 during time periods 22–32, 162–172, 302–312). The bacterial load is substantially decreased, but the percentage of remaining healthy cells (PH) and the lung function (LF) at t = 400 are not all that much improved (PH = 92.2 with antibiotics versus 90.6 without). For an antibiotic with doubled efficacy (AB = 10), the trends are very similar, and the final the value is PH = 94.2.

Fig. 5.

In contrast to healthy individuals (see Fig. 4), simulations suggest that cystic fibrosis patients (CF = 1) may have problems with repeated infections. For instance, if no antibiotics are given (the situation shown here), the percentage of remaining healthy cells (PH) and the lung function (LF) decrease slightly after every infection, thereby resembling a pattern of APEs as it was shown in Fig. 1. The APEs in the model show less of an undershoot, presumably because the model does not account for sufficient details, such as secondary problems and delays between infection and effective host responses.

A different common treatment of CF is the removal of mucus by means of saline inhalations and a vibrating chest vest that loosens the mucus and helps the patient cough it up [25, 26]. A possible means of accounting for this treatment is the inclusion of a term like −0.1·B·CV or −0.1·M·CV into the equations for bacteria and mucus, respectively. Without the vest, CV = 0, while application of the vest corresponds to CV= 1. For the patient's comfort, the treatment is in reality applied intermittently, once or a few times per day, and this regimen could be modeled in the same fashion. As a simplification, we here consider the vest application as a continuous treatment. Fig. 7 shows results where CV is permanently set to 1, starting at t = 100.

Fig. 7.

Simulation results of cystic fibrosis patients (CF = 1) that are repeatedly infected and treated with antibiotics, as in the simulations depicted in Fig. 6. In addition, the patients receive continuous chest vest treatment (CV = 1), starting at t = 100, as explained in the text. Reflecting clinical experience, the treatment is quite effective.

Anti-inflammatory treatment could be modeled with the addition of material to the equation of A. Different degrees of CF severity, for instance, as the consequence of different mutations, or of successful gene therapy, could be modeled with a fractional value of CF between 0 and 1.

Sensitivity Analysis with Respect to Dependent Variables

Sensitivity analysis addresses the effects of changes in parameter values on some features of a system, such as its steady-state values or fluxes. In BST, the relative effects of changes in (constant) independent variables on the system are called logarithmic gains [59]. Here we use a variation of gain analysis to explore the effect of changes in dependent variables on the system, with the goal of identifying where future model expansions, in particular, the replacement of a variable with a subsystem or module, might be most beneficial. One could call these sensitivities module gains or ModGains, because they quantify the relative effects of changes in dependent variables, which in reality represent modules, on the system. This ModGain assessment may be executed in a simple manner. Namely, one eliminates one differential equation at a time and replaces it with a constant value of the corresponding variable; typically, this value is the steady-state value. As the variable is now de facto independent, the logarithmic gain of the system to a change in this variable quantifies this effect. Table 2 shows the percent change in the steady-state value of each systems variable in response to a 1% increase in a dependent systems variable that is set constant at its steady state. While this analysis appears to be the first explicit definition and use of ModGains, the principal ideas behind this concept are quite natural and presumably have been used many times before.

Table 2.

ModGains of systems variables with respect to other dependent variables^*

Altered Variable	% Response in B	% Response in P	% Response in A	% Response in M	% Response in H	% Response in D
B	-	0.34615	0.26923	0.25000	−0.05128	0.00000
P	−1.00000	-	0.00000	−0.25000	−0.66667	0.00000
A	0.14286	−0.14286	-	0.03571	0.76190	0.00000
M	2.76106	0.95575	0.74336	-	−0.14159	0.00000

^*Induced changes in H and D seem unrealistic and are therefore omitted.

Of particular interest in Table 2 are the effects of the various alterations on the number of healthy cells (H), which one may expect to correlate with lung function. Increases in B, P, or M lead to decreases in healthy cells, while an increase in anti-inflammatory cytokines leads to an increase in lung function, which makes intuitive sense. Studying the ModGains with respect to a constant D or H is not realistic, as the numbers of damaged or healthy cells cannot really be controlled directly. One notices in the table that all ModGains associated with D are zero. This result is a consequence of the fact that the input to H is considered constant in the model and must be balanced, at steady state, by the flux between H and D, which in turn must match the efflux from D.

Strictly speaking, the ModGains with respect to dependent variables are infinitesimal quantities. However, they do project trends for moderately small changes appropriately. For instance, if B is set to a constant value that is increased by 10% above its steady state, the results in Table 2 project H to decrease by 0.05128-10%; that is, from 1713.1 to 1704.3. In a corresponding simulation, H decreases to 1704.736.

Replacing a Variable with a Module

Simulations with the model indicate, not surprisingly, that killing bacteria, reducing mucus, or administering anti-inflammatory therapy is beneficial, as measured by the number of remaining healthy cells in the model. At the same time, it is known that these three target variables are in reality much more complicated. Mucus consists of complicated, cross-linked polymers that are subjected to a complex formation and degradation dynamics [29]. Cytokines do not exist in just two classes, as portrayed in the model, but in numerous types, which are not even always cleanly classifiable as pro- or anti-inflammatory . Bacteria and fungi inhabiting the CF lung often live in complex metapopulations that are ill understood [60].

As an example for how to expand the model to another level, consider the dynamics of bacteria in the CF model. It is given by the equation

$$Ḃ=(B^{0.8}{M}^{1.2}-0.8B^{1.2}{P}^{0.1})·M^{-2.4}.$$ (4)

If we consider mucus and pro-inflammatory cytokines constant at their initial values (12.76 and 64.75, respectively), the equation reduces to the quasi-logistic representation that motivated this particular component of the model, namely

$$Ḃ=0.047B^{0.8}-0.0027B^{1.2}$$ (5)

(see Eq. 2). In an ideal situation, this equation would be parameterized from direct measurements in situ, in an animal or cell culture model, or in vitro. Constrained by the overall shape of this population growth dynamics, imagine that the population actually consists of a metapopulation composed of three interacting species, as shown in Fig. 8. These interactions may be activating or inhibiting, as different species often share metabolic activities and energy metabolism while, at the same time, competing for the same space and resources.

Fig. 8.

Assumed interaction network within a bacterial metapopulation with three species. Blue arrows represent replication and death, while red and green arrows indicate influences that reduce or augment another population, respectively.

It is straightforward to set up describing symbolic equations, for instance, in the format of a Lotka-Volterra or BST model [43]. The parameters would ideally be measured directly from the dynamics of the bacterial populations. Here, we just choose parameter values such that the overall population size resembles the dynamics of B in the original model. This choice is by no means unique, and it is in fact possible to select parameter values that render B and the sum of B₁, B₂ and B₃ more similar (see Appendix). For illustration purposes, these differences are immaterial. The equations used for this illustration are

$${Ḃ}_1=0.01B_1-1.2\times {10}^{-5}{B}_1^2-6.0\times {10}^{-6}{B}_1{B}_3{Ḃ}_2=0.03B_2^{0.8}+1.75\times {10}^{-5}{B}_1{B}_2-0.002B_2^{1.2}-2.0\times {10}^{-5}{B}_2{B}_3{Ḃ}_3=0.06B_3^{0.5}-2.0\times {10}^{-9}{B}_3^3$$ (6)

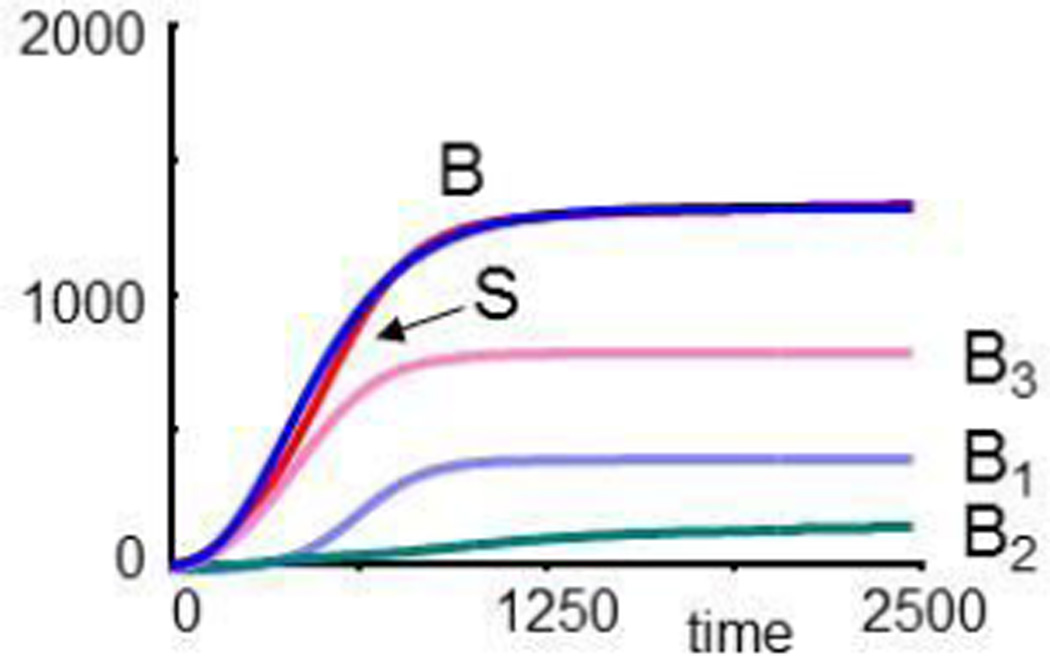
where each term on the right-hand sides corresponds to an arrow in Fig. 8. Starting with small population sizes, all three populations grow and reach a steady state, and their sum S reaches the same final value as B in the original CF model (Fig. 9a).

Fig. 9.

Dynamics of a simulated bacterial metapopulation with three species, as sketched in Fig. 8. Panel (a) compares the population growth of each species and their sum, S, with the overall growth curve of bacteria, B, in the CF model. Panel (b) shows that the populations recover, if 99% of all three species are eradicated. In panel (c), B₁ is entirely eliminated at t = 5000, while B₂ and B₃ are reduced to 1% each. B₂ assumes a lower level than before. In panel (d), the formerly most prevalent species, B₃, is eliminated at t = 5000. Surprisingly, the formerly “weak” population B₂ grows immensely.

It is easy to simulate with these equations how the metapopulation responds to antibiotics. For instance, even if 99% of all bacteria are killed at t = 3,000, the populations readily recover and approach the same steady state as before (Fig. 9b). The outcome is much more difficult to predict if the treatment actually eradicates one of the populations. As a first example, suppose the least prevalent population (B₂) is eliminated at t = 5,500, while B₁ and B₃ are both reduced to 1% each. B₁ and B₃ quickly recover, with a profile similar to the original one including B₂ (not shown). If B₁ is wiped out, with 1% of B₂ and B₃ remaining, B₂ assumes an even lower level as before (4.4, as opposed to 16.7), while B₃ fully recovers (Fig. 9c). Intriguingly, if the most prevalent population (B₃) is eliminated at t = 5,500, while B₁ and B₂ are reduced to 1% each, B₁ attains a steady state at about 830, as opposed to its earlier level of about 340, while the formerly rarest species (B₂) shoots up to almost 60,000 units (Fig. 9d). Thus, differential killing of subpopulations may have drastic, unpredictable, and undesirable effects. It may be one of the reasons that the prevalence of bacterial species changes dramatically over the age of CF sufferers, with Staphylococcus aureus dominating in young individuals and Pseudomonas aeruginosa in mid-age individuals with CF [20, 30–33, 61].

Slightly different interaction patterns among the bacterial populations may enable damped or sustained oscillations. For instance, the three populations, scaled to average levels of about 1 and represented by the following equations

$${Ḃ}_1=0.035(B_2-B_1^{0.1}){Ḃ}_2=0.035(B_1^{-0.5}{B}_2^{0.2}-B_2^{0.1}){Ḃ}_3=0.8(B_2^{-0.2}{B}_3-B_1{B}_3^2)$$ (7)

with initial conditions B₁ = B₃ = 1, B₂ = 1.2, oscillate in a sustained pattern (Fig. 10). Similar to a sine-cosine oscillator, this pattern changes with initial conditions. Many other oscillations, including limit cycle oscillations, would be possible.

Fig. 10.

Three bacterial populations oscillate without external triggers. The system is described by Eq. (7).

Analyses and Expansions of the Mesoscopic Model

It would be appealing to construct a generic flow chart showing the different directions in which a mesoscopic may be taken. However, while about every modeler has reduced or expanded an initial model, the specifics of the process depend highly on the particular model and the questions asked. Some guidelines may be given nevertheless. For instance, the selection of a variable to be expanded into a module could be based on the following arguments. If the variable's ModGains are small in magnitude, and if its dynamic range is small, an expansion into a module, while possibly leading to new insights, is not likely to change the overall dynamics of the system much. As an example, the concentrations of physiological metabolites in blood serum are very tightly controlled, so that wide variations are by and large unrealistic, expect for the most pathological conditions.

By contrast, bacterial counts in the CF lung must be expected to change dramatically, and combined with even modest ModGains these changes will presumably perturb the system substantially. If large changes in a variable are likely, one might perform initial tests of its amplifying or attenuating role by setting the variable constant at different values throughout its expected range and computing the steady-state in each case. One could furthermore reset the variable from its normal to a different value within its expected range and study the ensuing transients. In reality, the system, including the variable of interest, would of course respond to these changes, but this type of analysis nevertheless sheds some light on consequences of perturbations in the variable. It may also foretell to some degree how the module, represented by the variable, might affect the system. As a variation of resetting the variable step by step, the variable of interest could also be dynamically varied, either in a monotonic or a periodic fashion. This strategy, and especially the use of sinusoidal input perturbations, is a standard procedure in linear systems analysis [62]. As another variation, one could study two or more variables simultaneously, especially if they are closely interacting, such as the two variables P and A, which represent pro- and anti-inflammatory cytokines (see below).

Once a variable has been selected for expansion into a module, it might be instructive to isolate it from the rest of the system, develop a representation of the module, and diagnose and analyze it, before it is returned to supplant one or more variables in the original system. For instance, P and A could be replaced with a larger model describing a more comprehensive cytokine interaction network (Fig. 11) that represents the system of host defenses against the fungus C. albicans [63], which often leads to chronic colonization in CF patients [64]. While the overall dynamics of the extended network model might be similar to the simple mesoscopic model, the more detailed model allows the more targeted testing of specific anti-inflammatory treatments.

Fig. 11.

Host defense system against the fungus C. albicans. The response is governed by a network of cytokine (blue) and chemokine (red) production processes, that are triggered in response to the pathogen, B, which interacts with an epithelial cell (blue box surrounding B). The cell releases interleukin IL-8 which, in turn, recruits circulating neutrophils (N). Once activated by different interleukins and cytokines, such as GM-CSF and G-CSF, neutrophils produce TNFα and other cytokines and effect changes in epithelial gene transcription. CCL20 and β-defensin 2 activate dendritic cells (D) and, together with TGFβ, IL-1β and IL-6, lead to the induction of T-cell differentiation to the Th1 phenotype. CCL20 and β-defensin 2 also recruit T_reg-cells that counteract the Th17 response. Finally, infected epithelial cells produce cytokines, such as IL-19, IL-20 and IL-24, which function in an autocrine fashion. Adapted from [54].

Similar to the expansion of P and A, the dynamics of mucus and its interactions with other components of the model could be investigated. Clearly, mucus is a major contributor to the negative symptoms of CF, and specific insights in the formation and natural or treatment-induced dissolution or removal of mucus could lead to new control options for the disease.

A different type of a relatively direct extension is the inclusion of new variables, such as neutrophils, which play an important role in CF but are not even mentioned in the original model [65, 66]. A much more complicated extension would elevate the simple ODE system to a model accounting for spatial features. Depending on the scale of such a model, partial differential equations could be beneficial, but it seems more likely that spatial features would require rule-based or agent-based models [67, 68].

Finally, instead of expanding the system, one could study the natural design of the system and explore the repertoire of its possible dynamic responses. As an example, consider again P and A. These two variables affect each other's dynamics, and one might ask whether this interaction could constitute a stable limit cycle. Indeed, by isolating P and A, along with the interactions between them, from all other variables and processes, one can study different types of oscillations. As an illustration, recall that P activates the production of A, and that A inhibits the production of P (Fig. 3). Let's suppose that P could also activate its own production, directly or indirectly through a network as shown in Fig. 11. Describing equations, scaled to values of P and A around 1, could be

$$Ṗ=0.1(1+\mu )(A^{-0.15}{P}^{0.4}-P^{0.2})Ȧ=0.1(P-A^{0.2})$$ (8)

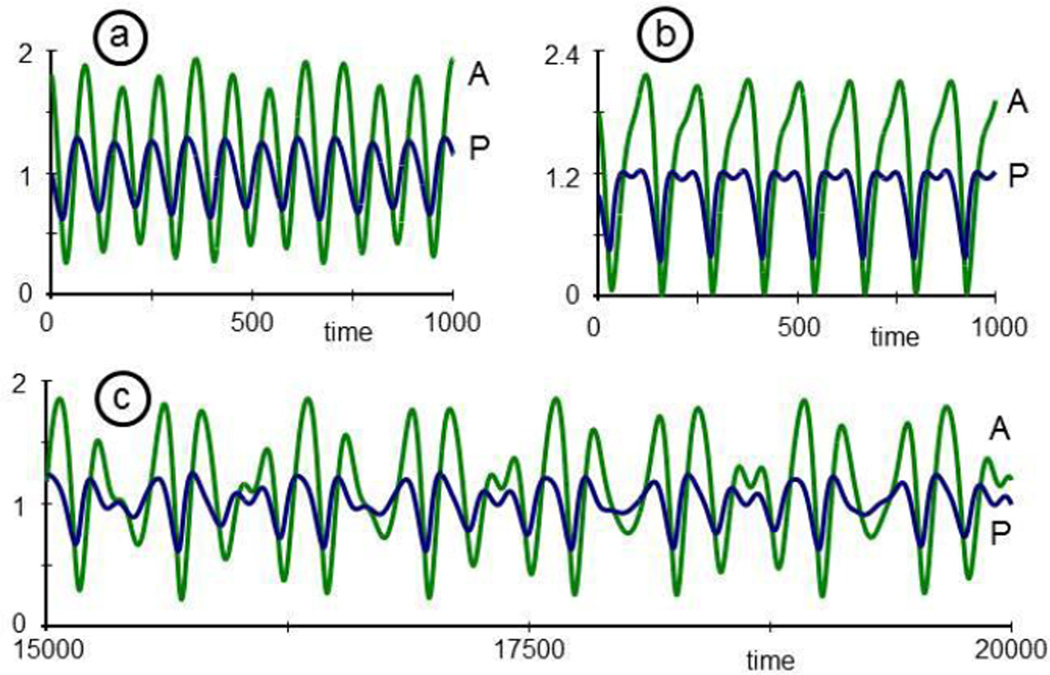
These equations, while not overly complicated, permit interesting responses (for a theoretical background see [69, 70]). In particular, if the parameter µ, affecting the speed of the dynamics of P is negative (e.g., µ = −0.2), the P-A system has a steady state that is stable to moderate perturbations (Fig. 12a; here P(0) = 1, A(0) = 1.8). However, if µ exceeds a bifurcation point at 1 and becomes slightly positive, P and A form a stable limit cycle that oscillates in a sustained manner and tolerates small perturbations (Fig. 12b; µ = 0.04).

Fig. 12.

Depending on small changes in the parameter µ, the two-variable cytokine system in Eq. (8) exhibits oscillations that are damped (panel a; µ = −0.2) or constitute a stable limit cycle (panel b; µ= 0.04).

It is known that limit cycles, perturbed by periodic functions with just the right frequency, may become chaotic [71]. Indeed, if the periodic bacterial populations in Eq. (7) affect the dynamics of P, the combined bacterial-cytokine system responds in a very complicated manner (Fig. 13) that, depending on parameter settings, could be chaotic. The specific equations used to generate this figure, including a tunable parameter q, are

$$Ṗ=0.1(1+0.04)(A^{-0.15}{P}^{0.4}+q{B}_3-P^{0.2}-q)Ȧ=0.1(P-A^{0.2})$$ (9)

For q = 0.001, the effect of the bacteria on the system is negligible, and the oscillations are essentially the same as in Fig. 12b (not shown). For q = 0.01, the oscillations are no longer regular (Fig. 13a), and for q = 0.2, the system shows double oscillations in P (Fig. 13b) and larger amplitudes than before. Finally, for a small window of values in between, e.g., for q = 0.08, the oscillations become rather erratic, and further tests would need to show whether this behavior is truly chaotic (Fig. 13c). The phase plane, which plots P against A, for t = 0, ..., 5000 illustrates this behavior in a different fashion (Fig. 14).

Fig. 13.

If the limit cycle oscillation of the two-cytokine system (Eq. 8) is perturbed by the oscillatory bacterial population B₃ (see Eqs. (7) and (9)), the oscillations in P and A can become irregular (panels a and b) and possibly chaotic (panel c).

Fig. 14.

The phase-plane representation of P against A shows the irregularities of the population sizes in Fig. 13c in a different manner. The plot resembles a Rössler band [71].

Discussion and Conclusions

It is impossible to construct a complex disease model from scratch in a single stroke. As an alternative, one might begin with a mesoscopic model that contains the main contributors to the disease, as well as their interactions. A model at this coarse scale permits a relatively easy and undistracted first exploration of intervention options, an also an assessment of the importance of any of the dependent variables, which in reality represent sub-systems at a lower level of biological organization.

This article outlined the construction of a mesoscopic model within the context of cystic fibrosis (CF). The process started with a generic inflammation model from the literature and demonstrated that it is beneficial to use a canonical nonlinear modeling framework, such as Biochemical Systems Theory (BST), for the model design process. In particular, BST permits the setting up of initial equations even if the mechanisms governing the system are only vaguely characterized. Furthermore, BST offers guidelines regarding the determination of parameter values, which are directly based on the strengths of the effects that are represented by these parameters.

As the simulation analysis demonstrated, even the coarse mesoscopic model is capable of generating interesting insights and, for instance, reflects acute pulmonary exacerbations (Figs. 1 and 4–7). Beyond numerical simulations, the model may be used to rank the effects of model features on the system. Of special interest here were the effects of specific dependent variables on other dependent variables. Commonly, sensitivity analysis is used to study such effects with respect to changes in constant, independent variables or parameters, but it was shown here that fixing a dependent variable at its steady-state values allows the exploration of its importance. This exploration is useful, because the dependent variables of a mesoscopic model often represent sub-systems in a coarse manner. Thus, if the effects of changes in a dependent variable are minor or even negligible, it may not be necessary to replace this variable with a fully developed module. On the other hand, if small changes in the dependent variable cause major changes in some of the system features, it might be useful, if not necessary, to study which lower-level processes govern the dynamics of this variable.

In one example shown here, the originally single bacterial pool was replaced with a metapopulation of three species, and it was shown that certain interactions among these species can lead to distinct sensitivities to antibiotics. This information may be used to understand otherwise unexplainable responses of the mesoscopic model to some antibiotic treatments but not others. It was also shown how the analysis of isolated variables permits the exploration of the dynamic repertoire of the system.

The use of mesoscopic models is particularly useful for educational purposes [11, 72]. Whereas the burden of setting up a much more comprehensive model can be too complicated and confusing for a student or newcomer, it is relatively easy to explain the rationale of a mesoscopic model, and surprisingly little background is needed to start developing a feel for a more realistic system, such as a disease even if, or just because, the system has been so much simplified that its logic and structure are easier to intuit. Once a novice has been afforded the basic tools of model analysis, it is only a small step to discuss limitations and expansions of the model, as well as strategies for fine-tuning the model and making it more realistic.

Highlights.

Disease modeling requires complex computational models that cannot be constructed in a single stroke.

The article proposes mesoscopic modeling as a means of initiating the design of disease models.

The steps of mesoscopic model design are illustrated in the context of cystic fibrosis.

The mesoscopic model allows high-level analyses, including the importance ranking of disease drivers.

It is shown how a model variable may be telescopically expanded into a dynamic sub-system.

Appendix

1. PLAS Model Implementation of the Original System (Eq. 3)

The following script may be copied directly into the freeware PLAS [57], which allows simulations and other analyses in a very easy fashion. Shown is the scenario of repeated infections in a CF patient treated with antibiotics (Fig. 6).

Mesoscopic CF Model
B' = (B^0.8 M^1.2 - 0.8 B^1.2 P^.1 (AB+1)) * M^-2.4
P' = 20 B^0.2 D^0.4 A^-0.1 - 50 P^0.5
A' = 15 B^0.1 P^0.1 - 12 A^0.5
H' = 500 - 40 H^0.3 P^0.2 A^-0.2
D' = 40 H^0.3 P^0.2 A^-0.2 - 5 D
M' = 0.16 B^0.25 2^CF - 0.15 M^(2-1*CF)

CF = 1

B = 1278.037
P = 64.7532
A = 15.04461
H0 = 1713.089
D0 = 100
M = 12.75542

H=H0
D = D0
LF = 100*((H/D)/(H0/D0))
PH = 100*H/H0

AB = 0
@ 20 B = 3000
@ 22 AB = 5
@ 32 AB = 0
@ 160 B = 5000
@ 162 AB = 5
@ 172 AB = 0
@ 300 B = 10000
@ 302 AB = 5
@ 312 AB = 0

!! B P A D M H LF PH

t0 = 0
tf = 400
hr = 1

An introductory tutorial to the freeware PLAS can be downloaded from http://www.bst.bme.gatech.edu/software.php.

2. Alternative Equations for a Bacterial Metapopulation

The following implementation of the three-species metapopulation of bacteria matches the dynamics of the bacterial pool B in the original model even better than the implementation in the text (Fig. A1):

$${Ḃ}_1=0.01B_1-2.0\times {10}^{-5}{B}_1^2-2.3\times {10}^{-6}{B}_1{B}_3{Ḃ}_2=0.02B_2^{0.8}+1.5\times {10}^{-5}{B}_1{B}_2-0.002B_2^{1.2}-1.0\times {10}^{-5}{B}_2{B}_3{Ḃ}_3=0.09B_3^{0.5}-5.0\times {10}^{-9}{B}_3^3$$ (A1)

Fig. A1.

The dynamics of the metapopulation with species B₁, B₂ and B₃, as described with Eq. (A1), has a very similar dynamic as the bacterial population B of the original mesoscopic model.