Working Memory Inefficiency: Minimal Information is Utilized in Visual Recognition Tasks

Abstract

Can people make perfect use of task-relevant information in working memory (WM)? Specifically, when questioned about an item in an array that does not happen to be in WM, can participants take into account other items that are in WM, eliminating them as response candidates? To address this question, an ideal-responder model that assumes perfect use of items in a capacity-limited WM was tested against a minimal-responder model that assumes use of only information about the queried item. Three different WM tasks were adopted: change detection, identity recognition, and location recognition. The change-detection task produced benchmark WM results. The two novel tasks showed that only the minimal responder model provided convergence with this benchmark. This finding was replicable even when the change-detection task was replaced by a feature-switch detection task. Thus, it appears that people do not make full use of information in WM.

After the field of cognitive psychology superseded the behaviorist approach in the 1950s, researchers started to study mental processes that could not be directly observed. One key to transforming the unobservable into the measurable was in assumptions about the processes. Some fundamental assumptions, however, are still made through introspection or subjective reasoning, without empirical test. An assumption we examine pertains to working memory (WM), the small amount of information that is held in mind at once and, in particular, how efficiently WM information can be used. Studies of visual WM may be especially useful to address this issue. In a typical visual WM task, a spatial array of unique objects is followed by a recognition probe for one specific object or its location. We will examine one question of efficiency: whether a recognition judgment querying the characteristics of a particular item in an array can be guided by a process of elimination of other relevant items present in WM.

Visual WM refers to visual information that can be actively maintained and processed by attention over a short period of time. The capacity of visual WM has been intensively studied in recent years (e.g., Awh, Barton, & Vogel, 2007; Bays & Husain, 2008; Cowan, 2001; Luck & Vogel, 1997; Rouder, et al., 2008; Song & Jiang, 2006; Vogel, Woodman, & Luck, 2001; Zhang & Luck, 2008). Behavioral, electrophysiological and neural imaging data have consistently indicated that people at best can remember about 3~4 identifiable objects from a brief glance of a scene (Cowan, 2001; Luck & Vogel, 1997; McCollough, Machizawa, & Vogel, 2007; Todd & Marois, 2004). However, it is still unclear how people use WM representations to make responses in a WM task.

One idea about WM efficiency is that an observer is capable of making full use of task-related WM to achieve perfect performance, which is called the ideal-responder model in this paper. It includes the assumption that a limited number of items can be present in WM at once, but also the assumption that the information that is present in WM will be used whenever it is relevant to the task. A manifestation of this idea is seen in Alvarez & Thompson (2009). They assessed participants’ object-based visual WM capacity with a four-alternative-forced-choice, cued-recognition task, in which the observer was cued to recognize either the location or the color feature of a critical item that was no longer in sight, by selecting one of four options. In their Equation 2 (p. 148), Alvarez and Thompson assumed that if the critical item had been encoded into visual WM, the observer should be able to recognize one of its features; if the critical item was not in WM, the observer would first eliminate from the option set the features of items that were remembered, and then guess the critical feature by randomly picking one out of the remaining options. For example, suppose that there are four visual items, A, B, C, and D, to be remembered and an observer remembers only A and B. When the observer is prompted to recognize the location of item C, the ideal-responder model, Alvarez and Thompson presumed, would predict that the probability of a successful guess is 50% because the observer is supposed to eliminate the location features of items A and B from the four options in the first place and then choose at random the location of either C or D.

A contrasting assumption is seen in the model of Zhang and Luck (2009, p. 425). Also with a forced-choice cued-recognition visual WM task, but with an option set of 180 choices, they assumed that if the critical item is unavailable in WM, the response will be a random guess among all options. The idea that information of non-critical items is useless in WM during the responding process is what we term the minimal-responder model. Given the huge option size in Zhang and Luck’s WM tasks, the two theoretically distinct models make little quantitative difference in predicting the successful guessing rate. However, for Alvarez and Thompson’s (2009) WM task, with two of four items in WM but the probed item not represented, the minimal-responder model would predict a 25% successful guessing rate when the probed item is not in WM, in contrast to the 50% rate in the ideal-responder model. According to the minimal-responder model, WM cannot sustain the eliminating processes that an ideal responder is supposed to do. Instead, a minimal responder would ignore memory of items A and B before making one random choice out of four options.

As there is little research in the literature on responder efficiency with WM, the current paper seeks to fill the gap by testing side-by-side the ideal-responder model and the minimal-responder model. Here is a simple rationale for such a test. Each observer’s WM is assessed separately by three models, including a benchmark model, an ideal-responder model, and a minimal-responder model. Out of the two competing responder models, the one that yields a WM estimate consistent with that from the benchmark model is considered the valid model.

Benchmark Model from Cowan (2001)

The benchmark model, theoretically neutral to the two possible responding processes, is a capacity model (Cowan, 2001). It is a conventional model for measuring object-based WM capacity. The model applies to a change-detection task in which an array of items is followed by a single probe item to be judged the same as the item from the corresponding location in the array, or changed. Because the probe item provides the location information, the task requires only memory of the other feature of the item from that location in the array.

Within this model from Cowan (2001), it takes two steps to obtain a WM estimate. Step 1 is to measure accuracy (proportion correct) in both change and no-change trials. Step 2 is to compute K, the number of objects in WM, based on these accuracies.

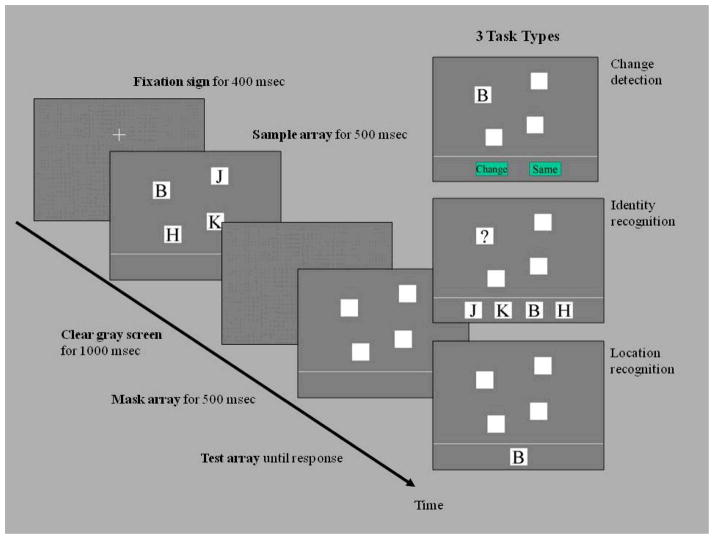
In the present research, each trial includes an array of letters, with no repetitions within an array (Figure 1), followed by a probe item. The probe in this task is a letter at a location of one of the array items (termed the critical item) and, in the change-detection task of Experiment 1, it either is the same as the critical item or is a letter not found in the array. A correct response to a change trial is considered a hit and the proportion correct of change trials is taken as an estimate of the probability of a hit, namely, the hit rate (hr), whereas a correct response to a no-change trial is a correct rejection and the proportion correct of no-change trials, an estimate of the probability of a correct rejection, i.e., the correct rejection rate (cr).

Figure 1.

Schematic illustration of the experimental procedure for the three WM tasks. In the change-detection task, on a change trial in Experiment 1, the B in the probe display would be replaced with an item that had not appeared in the array, such as T; on a change trial in Experiment 2, the B would be replaced instead with an item that had appeared in the array, such as H.

In Step 2, the model is constructed to estimate items in WM by making three assumptions. First, the representation of any item in the sample array is either present in or absent from WM. Second, if the critical item has been encoded in WM, the probability of a correct response should be 1, as detection of the change is certain upon comparing the critical item with the probe item in WM. Third, if the critical item has not been encoded into WM, a correct response may still occur, but only by random guessing.

As first described by Cowan (2001), these assumptions lead to a formula for K that we term the benchmark formula, the derivation of which is reproduced in Appendix A and shown there as Equation 3:

$$K=N\times (hr+cr-1)$$

Presumably, K increases as a function of set size N until the participant’s capacity is reached, after which the function becomes asymptotic. It is assumed that the performance in each trial is independent and identically distributed and the frequencies of hits and correct rejections are distributed as conditionally independent binomials (Rouder, et al., 2008).

Although considered to be just a first approximation of WM capacity, our benchmark model has been shown to be an excellent estimate of the object-based WM that is (1) limited to 3–4 items in adults (Cowan, 2001), (2) consistent with other neural imaging and psychophysiological indexes of WM capacity (Todd & Marois, 2004; Vogel & Machlzawa, 2004) and (3) able to survive selective influence on the guessing biases (Rouder, et al., 2008). Most important to our current goal, the change-detection task that the model is built upon is neutral to the two possible responding processes. Unlike a forced-choice cued-recognition task, the change-detection task does not make remembering non-critical items beneficial to the performance. In the change-detection task, there are no options to eliminate and the probe item never changes into a non-critical item. Therefore, the change-detection task coupled with the model of Cowan (2001) is adopted as a benchmark measurement of WM to distinguish the two competing responder models.

In our study, two forced-choice cued recognition tasks and the change-detection task were interwoven into a single test session. As shown in Figure 1, any trial of the three tasks consisted of a sample array, a delay interval, a mask array, and a test array. No difference between the three tasks could be perceived until the test array came up, so that the participant had no information to encode the stimuli differently across tasks. In the change-detection task, a probe item was given in the test array, whose identity, compared to that of the critical item, awaited a change-or-no-change judgment by the participant. In the identity-recognition task, the location of a probe item was given and the participant was asked to recognize the identity of the critical item. Similarly, in the location-recognition task, the identity of a probe item was given and the participant was asked to recognize the location of the critical item. The assumption underlying our approach is that the estimate of the number of items in WM should not depend on what kind of probe task is presented, given that the task is unknown until after the retention interval.

Here is the detailed rationale for our experimental design. Given that the three tasks were indistinguishable during encoding, the amount of visual information loaded into WM should be equivalent across task types. The change-detection task coupled with the model of Cowan (2001) yielded a benchmark WM measure, which was denoted as K_{c_det}, with a subscript c for Cowan’s model and det for the change-detection task. In parallel, a recognition task coupled with two responder models produced responder-model-specific WM measures. With a denotation rule similar to K_{c_det}, K_{i_iden} denoted the visual WM measure by the identity-recognition task coupled with the ideal-responder model; K_{i_loc} by the location-recognition task with the ideal-responder model, K_{m_iden} by the identity-recognition task with the minimal-responder model and K_{m_loc} by the location-recognition task with the minimal-responder model. The criterion of our test was that whichever model that generates WM estimates consistent with the benchmark K_{c_det} would be the valid one.

The reason we included both identity and location recognition tasks was to monitor whether the identity and location features of our visual stimuli are well bound, which is indicated by how closely the performances in the two feature recognition tasks match each other. An object-based WM measure, like that of Cowan (2001), is justified only if the visual stimuli are familiar and with all features well integrated (Alvarez & Cavanagh, 2004; Chen, 2009; Davis & Holmes, 2005; Eng, Chen & Jiang, 2005).

Ideal-Responder and Minimal-Responder Models

The main theoretical issue under consideration here is whether participants use all of the information presumably available in WM as in what we will call the ideal-responder model, or whether they only use the minimally necessary information. Models distinguishing these possibilities are developed in Appendix A and can be easily explained by example. Consider the identity recognition trial shown in Figure 1 (with the probe as in the middle panel of the figure). The task is to decide whether the probed location of the studied array contained a J, K, B, or H. According to either model, this question can be answered correctly if the location of B is stored in WM. The issue distinguishing the models is what happens if B is not stored. According to the ideal-responder model, other choices can be ruled out if their locations are known. For example, if a participant knows the location of K, he or she knows that this location differs from the probed location, ruling out K as a response option. If the locations of J, K, and H were all stored in WM, then they all could be ruled out as response options and the participant would answer correctly by the process of elimination. According to the minimal-responder model, in contrast, none of this inferential process is applied and, instead, the participant either knows the probed location and responds correctly, or else guesses randomly among the choices. Likewise, in the location recognition procedure, according to the ideal-responder model, the participant is able to rule out incorrect choices if those items are present in WM; whereas, according to the minimal-responder model, the participant either knows the location of the probed letter or guesses randomly among the location choices. Behaving according to the minimal responder model would be expected to be quite possibly less effortful, but less accurate than the ideal-responder model.

Testable Predictions

The models, as detailed in Appendix A, lead to the following mutually exclusive predictions.

• Prediction 1: if K_{c_det}=K_{i_iden}=K_{i_loc}, the ideal-responder model would be shown to be valid.

• Prediction 2: if K_{c_det}=K_{m_iden}=K_{m_loc}, the minimal-responder model would be shown to be valid.

• Prediction 3: if K_{c_det} ≠ K_{i_iden}=K_{i_loc} and K_{c_det} ≠ K_{m_iden}=K_{m_loc,} both of the two responder models would be shown to be invalid.

• Prediction 4: if K_{i_iden} ≠ K_{i_loc} and/or K_{m_iden} ≠ K_{m_loc,} the features of our visual stimuli would not be well-bound, so that the test of the models would be inconclusive.

We rely upon conventional inferential statistics to establish differences between estimates but we use judgment to decide when different estimates are close enough to be considered the same for theoretical purposes. It is our belief that the outcome was too simple and straightforward to benefit from sophisticated statistical model-fitting. We present two experiments with slightly different change-detection tasks, leading to the same conclusion.

Experiment 1

Method

Design

In the experiment, a condition was a unique combination of one of 4 array sizes (3, 4, 5, or 6 letters) and one of 3 task types (change detection, identity recognition, or location recognition). It thus formed 12 conditions and each condition had 40 trials, totaling 480 trials in the test session. The change-detection task had an equal number of change trials and no-change trials, but the participants were not informed of the frequency of two types of trials. The presented order of all trials was randomized over 12 conditions.

Participants

15 undergraduates (9 females and 6 males, aged 18–25 years old) from introductory psychology courses at University of Missouri-Columbia participated in the experiment in exchange for course credit. They were native speakers of English, with normal hearing and normal or corrected-to-normal vision.

Apparatus & stimuli

The WM tasks were programmed with E-prime software (Schneider, Eschman, & Zuccolotto, 2002) and administered on personal computers equipped with a 15-inch CRT monitor, loudspeaker and mouse-pointing device in quiet, private booths.

To ensure high familiarity and high feature integrity, English consonants were adopted as stimuli. A set of seven English consonants, including B, G, H, K, N, J, and T, were chosen to form a visual stimulus pool. In each trial, the sample array included a random subset of 3 to 6 items without repetition from the stimulus pool. One of them was assigned to be the critical item, which would be probed for change-detection, identity recognition, or location recognition.

As shown in Figure 1, the displays of the sample and test arrays had the computer screen area divided by a white horizontal line into a stimulus area (30×20 cm, above the line) and a response area (30×4 cm, below the line). Within the stimulus area, each item contained a black English consonant filling up a 2.5×2.5 cm white box (about 3° × 3° visual angle, given the viewing distance of 50 cm). All items were displayed on a gray background and pseudo-randomly distributed within a 27×15 cm area (about 30° × 17° visual angle) that was centered in the stimulus area. The minimal side-to-side distance among items was about 2° of visual angle. Each quadrant of the stimulus area had no more than two items at any time. The response area was always blank during the display of a sample array, but showed option buttons for the response during the display of a test array.

Procedure

Each participant was tested separately in a quiet booth equipped with a 15-inch CRT monitor. First came a practice session, during which the experimenter made sure the participant understood the three WM tasks and monitored the participant while carrying out two practice trials for each task. The order of the practice tasks was random for each participant. The participants were told to bring out their best performance but nothing about the two possible responding strategies.

After the practice, the participant was left alone to complete the test. To initiate a trial, the participant pressed the space bar and a fixation sign was then shown for 400 msec. It was followed by a sample array for 500 msec. The sample array was replaced by a clear gray screen for 1000 msec. Next came a mask array that covered each item in the sample array with a 2.5×2.5 cm white square. The mask array lasted for 500 msec for the purpose of removing any lingering visual sensory memory of the sample array, but without introducing unnecessary interference.

Following the mask array, a test array was shown until the participant made a response. The procedure at the test array varied from task to task (Figure 1). For the change-detection task, all but the probe item were masked by white squares. The probe item could be identical to the critical item in both identity and location or could have changed to a new identity originally not in the sample array. The participant was supposed to mouse click on either the “Change” or “Same” option button in the response area accordingly. For the identity-recognition task, all items in the stimulus area were masked by white squares and the probe item had a black question mark on it. In the response area, all item identities in the sample array were lined up in a random order, from which the participant was supposed to mouse click the identity of the critical item. For the location-recognition task, all items in the stimulus area were masked by white squares and a probe item shown in the response area provided the identity of the critical item. The participant was supposed to mouse click on one of the white squares to indicate the location of the critical item.

Both visual and auditory feedback was provided immediately following the participant’s response. A correct response would release a text message “good job” on the screen and a pleasant chime from the loud speaker; otherwise, a text message “work harder” and a zapping tone were given. The participant was allowed to take breaks between trials as long as needed.

Results

Descriptive statistics

Mean WM estimates of K_{c_det}, K_{i_iden}, K_{i_loc}, K_{m_iden}, and K_{m_loc} appear in Table 1 and mean proportions correct (i.e., estimates of hr, cr, Ac_iden and Ac_loc) appear in Table 2, separately for each set size in both cases. It is noteworthy that Ac_iden and Ac_loc were almost identical in means and standard errors of mean, suggesting that identity and location features of our visual stimuli were integrated so well that recognition of identity almost always led to recognition of location, and vice versa.

Table 1.

Mean estimates of items in working memory in every experimental condition, Experiment 1

Task Type	Array Size
	3	4	5	6
Change Detection (Kc_det)	2.94(0.02)	3.72(0.08)	3.92(0.20)	4.06(0.28)
Ideal Responder, Identity Recognition (Ki_iden)	1.93(0.03)	2.63(0.09)	3.13(0.16)	3.42(0.25)
Ideal Responder, Location Recognition (Ki_loc)	1.95(0.03)	2.69(0.09)	3.18(0.17)	3.47(0.26)
Minimal Responder, Identity Recognition (Km_iden)	2.89(0.04)	3.50(0.13)	3.92(0.20)	4.10(0.31)
Minimal Responder, Location Recognition (Km_loc)	2.92(0.04)	3.59(0.12)	3.97(0.21)	4.16(0.32)

Note. In the subscript, c=Cowan (2001) model, i=ideal-responder model, m=minimal-responder model, det=change-detection task, iden=identity-recognition task, loc=location-recognition task. Standard errors of mean in parentheses.

Table 2.

Proportion correct in every experimental condition, Experiment 1.

Task Type	Array Size
	3	4	5	6
Change Detection, Change Trials (estimates of hr)	0.99(0.01)	0.96(0.02)	0.86(0.03)	0.78(0.05)
Change Detection, No-change Trials (estimates of cr)	0.99(0.00)	0.97(0.01)	0.92(0.01)	0.90(0.02)
Identity Recognition (estimates of Aciden)	0.98(0.01)	0.91(0.02)	0.83(0.03)	0.74(0.04)
Location Recognition (estimates of Acloc)	0.98(0.01)	0.92(0.02)	0.84(0.03)	0.75(0.04)

Note. In the subscript, hr=hit rate, cr=correct rejection rate, Ac = accuracy, iden=identity-recognition task, loc=location-recognition task. Standard errors of mean in parentheses.

Testing predictions

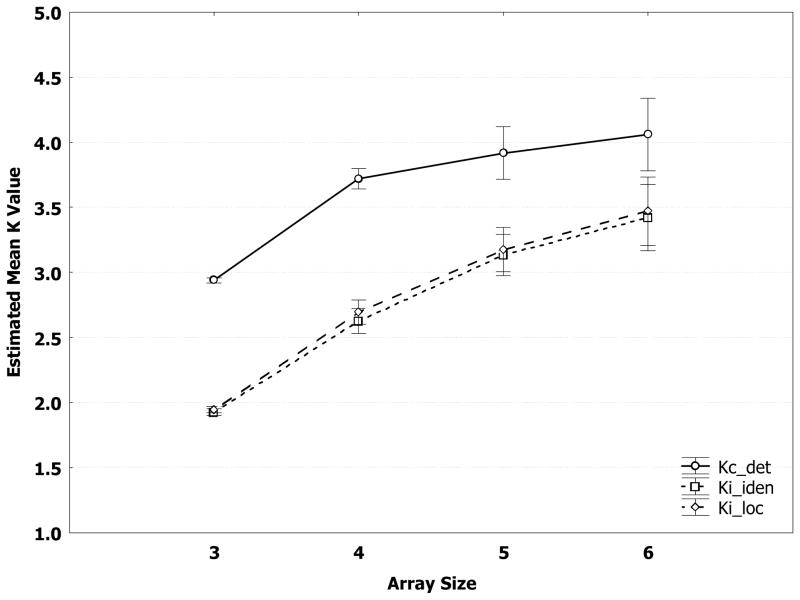
In order to test Prediction 1, values of K_{c_det}, K_{i_iden}, and K_{i_loc} were taken as the measures of items in WM for three different task types (change-detection, identity recognition, and location recognition) and were included as a factor along with array size N in a two-way (3 task types × 4 array sizes) repeated-measures ANOVA. As shown in Figure 2, the result was a significant and fairly large main effect of task type, F(2, 28)=72.08, p<.001, and η_p² = .84. Follow-up post hoc Newman-Keuls tests indicated that the main effect was due to K_{c_det} being significantly greater than either K_{i_iden} or K_{i_loc} (p’s< .001). The main effect of array size was also significant, F(3, 42)=35.11, p<.001, and η_p² = .71, but the interaction between array size and task type was not. In addition, a separate two-way (2 task types × 4 array sizes) repeated-measures ANOVA including only K_{i_iden} and K_{i_loc} produced no significant main effect of task type and no significant interaction between array size and task type, only a significant main effect of array size, F(3,42)= 39.57, p<.001, η_p² = .74. In short, this analysis indicates K_{c_det}>K_{i_iden}=K_{i_loc}, a pattern inconsistent with Prediction 1, suggesting that the ideal-responder model is not supported.

Figure 2.

Mean WM estimates in Experiment 1, K_{c_det}, K_{i_iden}, and K_{i_loc}, as a function of array size and task type. In the subscript, c_det stands for the Cowan model coupled with the change-detection task, i_iden for the ideal-responder model with the identity-recognition task and i_loc for the ideal-responder model with the location-recognition task. The error bars indicate standard errors of the mean.

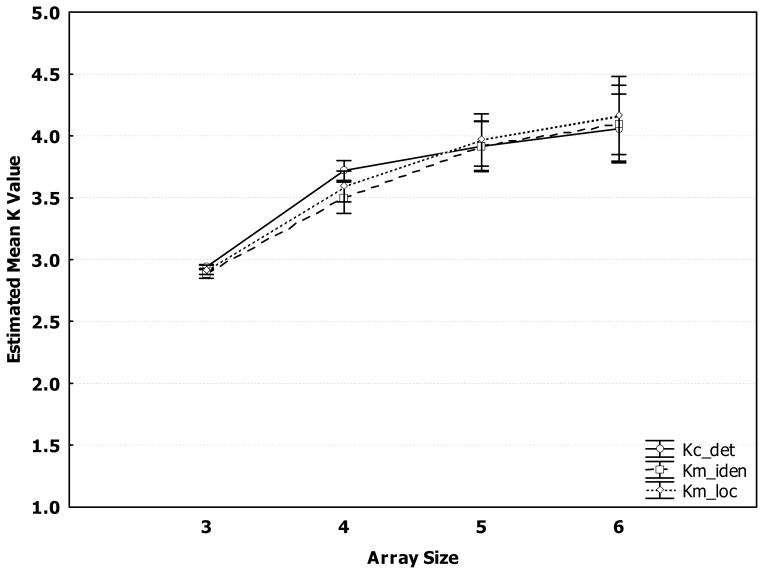
In order to test Prediction 2, similarly, a two-way (3 task types × 4 array sizes) repeated-measures ANOVA was conducted between K_{c_det}, K_{m_iden}, and K_{m_loc}. As illustrated in Figure 3, no significant main effect of task type was found, F(2, 28)=.23, p=.798, η_p² = .02, and there was no interaction between array size and task type either, F(6, 84)=.35, p=.911, η_p² = .02. Only the main effect of array size was significant, F(3, 42)=21.28, p <.001, η_p² = .60. To further compare K_{c_det}, K_{m_iden}, and K_{m_loc} at each array size, a series of post hoc Newman-Keuls tests were conducted, but not a single significant difference among the three K values was found at any array size, with .33 ≤ p’s ≤ 1. In short, this analysis indicates K_{c_det}= K_{m_iden}= K_{m_loc}, an almost perfect confirmation of Prediction 2, suggesting that the minimal-responder model is supported. Furthermore, Prediction 3 and Prediction 4 are directly contradicted by the significant effects that were obtained, so that only Prediction 2 was not contradicted.

Figure 3.

Mean WM estimates in Experiment 1, K_{c_det}, K_{m_iden}, and K_{m_loc} as a function of array size and task type. In the subscript, c_det stands for the Cowan model coupled with the change-detection task, m_iden for the minimal-responder model with the identity-recognition task and m_loc for the minimal-responder model with the location-recognition task. The error bars indicate standard errors of the mean.

Assessment of the pattern of K values

Inasmuch as we varied the array size N from 3 to 6, from below to over the typical WM capacity (Cowan 2001), it should result in a series of K values increasing to asymptote. This way, we can assess whether the K values derived from different models really reflect the number of items loaded into WM, which is supposed to change along an upward asymptotic line with increasing array sizes. Without an array size of 3, K values would align pretty much along a horizontal line with little variance between conditions. It may be important to show the growth of K across set sizes in order to reveal minor inadequacies of the model. For example, participants may make a few errors even at sub-capacity set sizes, possibly due to inattentiveness (Rouder et al., 2008), and it is important to show that these factors are small in the data.

To examine this theoretical prediction, the trajectory of K_{c_det}, K_{m_iden} and K_{m_loc} were analyzed. As Figure 3 shows, the three mean K values all started at about 3 at an array size of 3 and increased gradually with the array size rising. They became asymptotic at about 4 for the array sizes of 5 and 6. This observation was confirmed by the following statistical tests. Three one-way repeated-measures ANOVAs on array size revealed a similar significant main effect of array size, for K_{c_det}, F(3, 42)=11.46, p <.001, η_p² = .45; for K_{m_iden}, F(3, 42)=13.52, p<.001, η_p² = .49, and for K_{m_loc}, F(3, 42)=15.88, p<.001, η_p² = .53. Post hoc Newman-Keuls tests showed significant differences in the K values between N=3 and N=4 (p’s < .001) but no significant difference between N=4 and N=5 (.05 < p’s < .35) and between N=5 and N=6 (.32 ≤ p’s ≤ .50). Given that the upper limit of K values could reach up to the maximum array size of 6, their leveling off at about 4 was not likely a ceiling effect. These findings are consistent with the theoretical predictions and are empirically in line with previous behavioral, electrophysiological and neural imaging data on humans’ visual WM capacity (Cowan, 2001; Luck & Vogel, 1997; McCollough, et al., 2007; Todd & Marois, 2004).

Comparing observed accuracies and predicted accuracies by two responder models

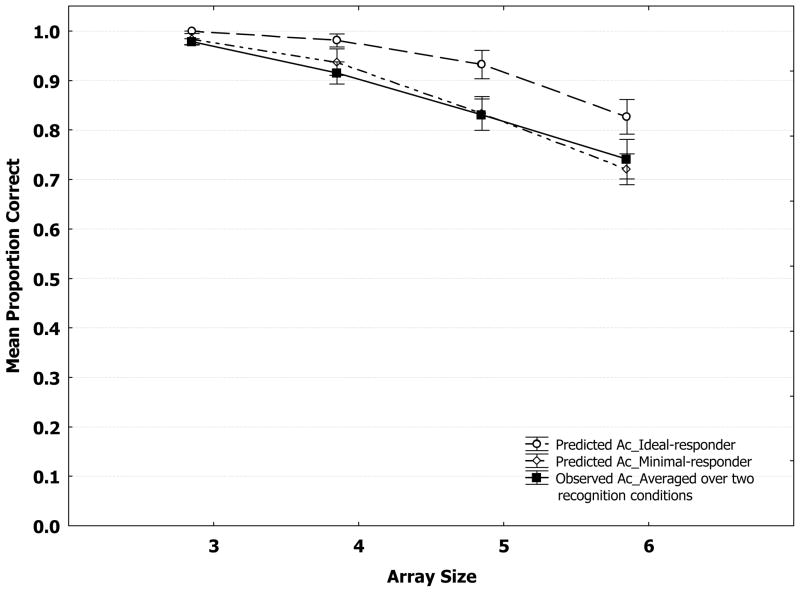
Comparing the observed accuracies with the predicted accuracies by the two responder models in the recognition conditions provides another perspective to assess whether the minimal-responder model fits the data better. The predicted accuracies by the ideal-responder model were derived from Appendix A, Equation 4, whereas those by the minimal-responder model from Appendix A, Equation 6. The accuracies, in terms of proportion correct, were capped at 1.0. The values of K_i and K_m in Equations 4 and 6 were estimated by averaging K_{c_det}’s over array sizes 5 and 6 for each participant. In case that a participant’s estimated WM capacity was greater than or equal to the sample array size, s/he would presumably perform perfectly and thus had an accuracy of 1. The predicted accuracies were calculated by averaging all participants’ predicted proportion correct by each model, while the observed accuracies by first taking the mean proportion correct over the two recognition conditions and then averaging the individual mean proportion correct across all participants. A series of one-way (i.e., observed accuracy versus predicted accuracy) repeated-measures ANOVA were carried out at each array size to examine which model would have predicted accuracies significantly different from the observed values.

Echoing the divergence between K_{c_det}’s and K_i’s, the mean predicted accuracies by the ideal-responder model were significantly greater than the observed values at all array sizes (.0002 < p’s < .001). In a stark contrast, the mean predicted accuracies by the minimal-responder model were not statistically different from the observed values at all array sizes (.33 < p’s < .90), remarkably consistent with the convergence between K_{c_det}’s and K_m’s (see Figure 4).

Figure 4.

Mean proportion correct in Experiment 1 in the recognition conditions predicted by the ideal-responder model and by the minimal-responder model, along with the observed mean proportion correct over two recognition conditions as functions of array size.

Assessment of an alternative hypothesis

There could be an alternative explanation of our results to be in favor of the ideal-responder model. Theoretically, the recognition tasks might involve a more difficult retrieval process in WM than the change-detection task, so that accuracies cannot be modeled simply with Equation 4 that assumes a perfect retrieval likelihood for both the recognition and the detection tasks. As shown in Figure 4, the ideal-responder model is predicting accuracies too high. The reason for that may be that the model takes into account only the gain from full use of WM of non-critical items but not the loss from a low retrieval likelihood in the recognition task. In other words, if the perfect retrieval assumed by Equation 4 is adjusted to a level low enough to cancel out the performance gain from full use of WM of noncritical items, the predicted accuracies by the ideal-responder model (graphically, the dash line with open circle markers in Figure 4) would move downward to converge with the observed accuracies (graphically, the solid lines with black square markers in Figure 4). We show this mathematically in the last section of Appendix A, on the possible role of retrieval likelihood. With a new retrieval parameter added to the ideal-responder model and with just one specific value of this new parameter, this model becomes identical to the minimal-responder model.

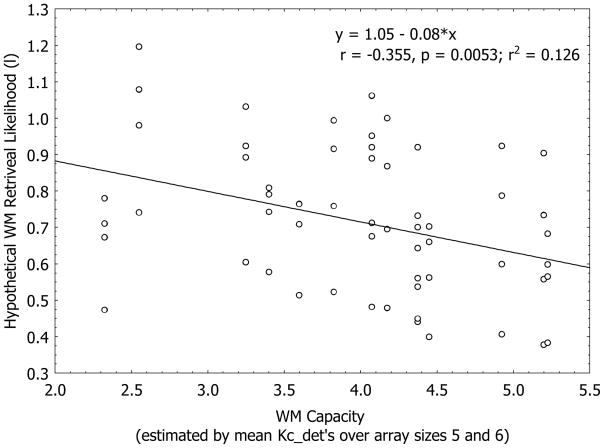
This alternative account, however, creates more problems than benefits. First of all, with an extra parameter l, the revised ideal-responder model is mathematically less parsimonious than the original minimal-responder model. It seems conceptually invalid in that it is determined solely by the array size but not individual WM capacity, and we can find nothing in the research literature suggesting that there is a psychological process corresponding to this extra parameter. More importantly, the empirical data shows that l correlates negatively (r = −.36, p < .01) with individual WM capacity, indicating a direct violation of the usual expectation that the WM retrieval likelihood l should be positively correlated with WM capacity (see Figure 5). Taking the above three problems into account, we believe that the revised ideal-responder model is not a viable alternative explanation for our findings.

Figure 5.

Correlation in Experiment 1 between the hypothetical retrieval likelihood l and WM capacity. According to Equation 9, $l=\frac{{Ac}_{il}\times N-1}{K_i}$, in which Ac_il takes the value of the mean accuracy over two recognition conditions and K_i the mean value of K_{c_det}’s over array sizes 5 and 6.

Discussion

The result of Experiment 1 precisely verifies Prediction 2, which is a necessary condition to rule out the ideal-responder model but to justify the minimal-responder model. Also, the assessment of capacity measures, including K_{c_det}, K_{m_iden} and K_{m_loc}, provides further assurance that the minimal-responder model meets theoretical and empirical requirements of a valid WM model.

It should be noted that for the smaller set sizes, N=3 and N=4, the ideal responder model cannot be fairly tested. According to Appendix A’s Equation 5, $K_i=N\times ({Ac}_i-\frac{1}{N})$. With this equation for N=3, perfect performance would result in a K_i=2; with N=4, perfect performance would result in K_i=3. These values of K_i with perfect performance are still considerably smaller than the obtained benchmark values (as shown in Figure 2, for N=3, mean K_{c_det}=2.9; for N=4, mean K_{c_det}=3.7). However, this methodological concern would not be an issue for array sizes 5 and 6, where K_i’s are not restricted by the observed accuracies to converge with K_{c_det}’s. For these set sizes, the recognition task accuracies that would be needed for the ideal-responder model to produce K estimates convergent with the change-detection model (.98 and .84, respectively) were possible, but the actual recognition task accuracies for these set sizes were considerably lower (.82 and .75).

Our much more impressive result is not just ruling out the ideal-responder model per se, but also showing the close correspondence of the benchmark and minimal-responder models (Figures 3 and 4). Note that the results at the larger set sizes strongly confirming the minimal-responder model and ruling out the ideal-responder model are in no way dependent on the presence of smaller set sizes in the procedure or results. Our results clearly show that the participants behaved as minimal responders who did not utilize memory of non-critical items when the critical item was unavailable in WM, although we cannot rule out the possibility that the non-critical items still exist in WM and would be used under some other circumstances.

Experiment 2

It is possible that participants’ response strategy in the recognition tasks might have been influenced by the change-detection task, in which keeping in mind the non-critical items was useless once the probe appeared. That is the case because in that task, any change in the identity of the probe was a change to a letter that was not in the array, and the identity of any array item at a different location was irrelevant. In order to rule out the possibility that this aspect of the change-detection task might have implicitly encouraged the minimal-responder strategy in the recognition tasks, we conducted Experiment 2, in which a changed probe always consisted of a letter presented at a location that had been occupied by a different letter in the array. This we term a probed feature-switch detection task. The purpose of using this task was to make the ideal-responder strategy, with its elimination of irrelevant options based on memory of noncritical items, beneficial to all three types of tasks. If this responder strategy still loses, participants’ failure to use it cannot be attributed to an inappropriate carryover in strategy from change detection to recognition trials.

We analyze the second experiment using the same models as in the first experiment (see Appendix A), but we refer to the probed feature-switch detection result as K_{c_fsdet}, instead of K_c. The rationale is that if the minimal-responder model is true in change detection, then the only relevant item in the feature-switch detection process is the critical item, i.e., the letter from the array in the location of the probe, just as in Experiment 1. If that is the case and if the identity and location recognition tasks are carried out in the same way as before, then K_{c_fsdet} and K_m should converge, just as K_c and K_m converged in Experiment 1. If, on the other hand, in this kind of change detection task participants also use information about the letter at another location when it is relevant in determining that there was a change of location (e.g., if the ideal-responder model applies to change detection), then K_{c_fsdet} and K_m will not converge as in Experiment 1. Although K_{c_fsdet} is not a proven benchmark model for the probed feature-switch task in Experiment 2 as K_c was for the change-detection task in Experiment 1 (e.g., Rouder et al., 2008; Todd & Marois, 2004), the design of Experiment 2 is theoretically effective in examining the strategy carryover effect that the change-detection task might have on the recognition tasks.

Method

Participants

16 undergraduates (15 females and 1 male, aged 17–20 years old) from introductory psychology courses at University of Toronto-Mississauga participated in the experiment in exchange for course credit. They were fluent speakers of English, with normal hearing and normal or corrected-to-normal vision.

Apparatus, Stimuli, and Procedure

Experiment 2 was identical to Experiment 1 in almost all aspects with only one exception that the probed item in a change trial was randomly chosen from the non-critical items in the sample array. Given that each item was unique in the sample array, remembering non-critical items might help to detect a location switch if a noncritical item in WM happened to emerge at the location of the critical item.

Results

The number of items loaded into WM in the probed feature-switch detection task, denoted as K_{c_fsdet}, was estimated with the K_c model. As in Experiment 1, we also calculated K_{i_iden} and K_{i_loc} according to the ideal-responder model and K_{m_iden} and K_{m_loc} according to the minimal-responder model. As Table 3 shows, values of K_{c_fsdet}, K_{i_iden} and K_{i_loc}, and K_{m_iden} and K_{m_loc} were all comparable to their counterparts in Experiment 1 (cf. Table 1).

Table 3.

Mean estimates of items in working memory in every experimental condition, Experiment 2

Task Type	Array Size
	3	4	5	6
Feature-switch Detection (Kc fsdet)	2.81(0.05)	3.53(0.08)	3.77(0.19)	4.01(0.18)
Ideal Responder, Identity Recognition (Ki iden)	1.89(0.03)	2.57(0.07)	3.13(0.11)	3.17(0.16)
Ideal Responder, Location Recognition (Ki loc)	1.91(0.03)	2.71(0.07)	3.13(0.12)	3.12(0.17)
Minimal Responder, Identity Recognition (Km iden)	2.83(0.04)	3.43(0.09)	3.91(0.14)	3.81(0.19)
Minimal Responder, Location Recognition (Km loc)	2.87(0.04)	3.62(0.09)	3.91(0.14)	3.74(0.21)

Note. In the subscript, c=Cowan (2001) model, i=ideal-responder model, m=minimalresponder model, fsdet=feature-switch detection task, iden=identity-recognition task, loc=location-recognition task. Standard errors of mean in parentheses.

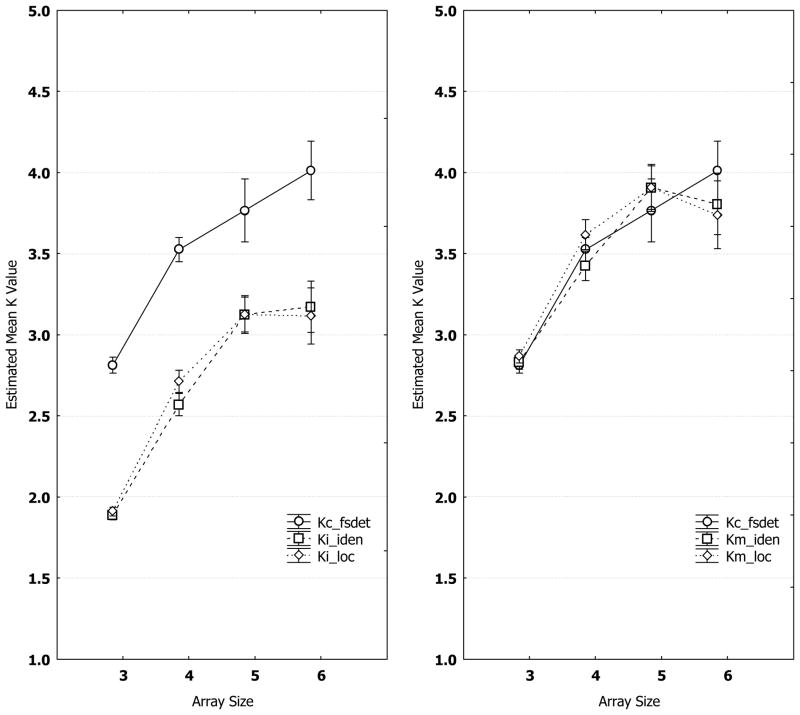
A two-way (3 task types × 4 array sizes) repeated-measure ANOVA was first carried out between K_{c_fsdet}, K_{i_iden} and K_{i_loc}. As shown in the left panel of Figure 6, there was a huge main effect of task type, F(2, 30)=123.65, p<.001, and η_p² = .89. A series of post hoc Newman-Keuls tests revealed K_{c_fsdet} as the source of the main effect (i.e., significantly greater than either K_{i_iden} or K_{i_loc}, p’s< .001). The other significant main effect was from array size, F(3, 45)=66.10, p<.001, and η_p² = .82, but the interaction between task type and array size was not significant. As for the two recognition tasks, a two-way (2 task types × 4 array sizes) repeated-measures ANOVA including only K_{i_iden} and K_{i_loc} found no significant main effect of task type and no significant interaction between array size and task type, except for a significant main effect of array size, F(3,45)= 60.40, p<.001, η_p² = .80. Therefore, the first half of Experiment 1 has been replicated, as the pattern, K_{c_fsdet}>K_{i_iden}=K_{i_loc}, was almost identical to that in Experiment 1. These results reassure us that the ideal-responder model could not be true, even though there was good reason to use the ideal-responder strategy in all conditions of Experiment 2.

Figure 6.

WM estimates in Experiment 2. Left panel: Mean WM estimates, K_{c_fsdet}, K_{i_iden}, and K_{i_loc} as a function of array size and task type. Right panel: Mean WM estimates, K_{c_fsdet}, K_{m_iden}, and K_{m_loc} as a function of array size and task type. In the subscript, c_fsdet stands for the Cowan model coupled with the feature-switch detection task, i_iden for the ideal-responder model with the identity-recognition task, i_loc for the ideal-responder model with the location-recognition task, m_iden for the minimal-responder model with the identity-recognition task, and m_loc for the minimal-responder model with the location-recognition task. The error bars indicate standard errors of the mean.

The second half of the replication was confirmed by another two-way (3 task types × 4 array sizes) repeated-measures ANOVA between K_{c_fsdet}, K_{m_iden}, and K_{m_loc}. As shown in the right panel of Figure 6, there were no significant main effect of task type, F(2, 30)=.22, p=.800, η_p² = .01, and no significant interaction between array size and task type either, F(6, 90)=1.32, p=.255, η_p² = .08, except for a significant main effect of array size, F(3, 45)=38.40, p <.001, η_p² = .72. In addition, a series of post hoc Newman-Keuls tests showed not a single significant difference among K_{c_fsdet}, K_{m_iden}, and K_{m_loc} at any array size, with .08 ≤ p’s ≤ 1. These results indicated, statistically, K_{c_fsdet}= K_{m_iden}= K_{m_loc}, replicating the major finding of Experiment 1 that the minimal-responder model converged with the benchmark model K_c in measuring WM items.

Discussion

Experiment 2 was designed to check whether the findings from Experiment 1 could be replicated when a potential confound in strategy use was eliminated. It arose from the change-detection task, which was likely to encourage the minimal-responder strategy. Experiment 2 replaced the change-detection task with the probed feature-switch detection task, which made all array items relevant to the response in order to encourage the ideal-responder strategy instead.

The result was a successful replication of the important finding of Experiment 1, with all K values being consistent with those in Experiment 1 (see Table 1 versus Table 3) and the K_c-K_m convergence and the K_c-K_i divergence being almost identical to those found in Experiment 1 (see Figure 2 and 3 versus Figure 6). The concern about a potential confound in Experiment 1 was ruled out, reassuring the conclusion that the participants were minimal-responders in the recognition tasks.

It is noteworthy that K_{c_fsdet} apparently displays an ascending trend, although it statistically converges at all array sizes with K_{m_iden} and K_{m_loc}, which actually level off over array sizes 5 and 6. The increases in the means of K_{c_fsdet} from array sizes 4 to 5 and from 5 to 6 did not reach statistical significance, but the ascending pattern in K_{c_fsdet} renders it a little bit different from K_{c_det} in Experiment 1. This slight discrepancy in K_c estimate should not have a bearing on the test of the minimal-responder model against the ideal-responder model for the recognition tasks, but would instead warrant further research in the future on the responder efficiency difference between the change-detection task and the probed feature-switch detection task.

General Discussion

To investigate the efficiency of WM processes, we designed WM tasks to test two competing responder models, the ideal-responder model and the minimal-responder model. The basic rationale for the test was to compare WM measures by the two models with that of a benchmark measure. The tasks were intermixed with no forewarning of what kind of information would be required when the post-array, post-retention-interval probe appeared, so estimates of items in WM should not differ for the three tasks when an appropriate model is used. Given that the visual stimuli are highly familiar and integrated items, the model of Cowan (2001) was chosen as the benchmark measure of the object-based visual WM. The results showed that WM measures based on the minimal-responder model converged beautifully with the benchmark model, whereas WM measures based on the ideal responder model were much lower than those based on the benchmark model. The results provide clear support for the minimal-responder model, suggesting that it is unlikely that people make full use of important but not immediately executable information in WM, such as information about the non-critical items that doesn’t directly lead to a successful response but is useful for increasing the chance of a successful response by allowing some options to be disqualified.

It is possible that the participants might be capable of using the non-critical items but might still tend to rely on an easier strategy that did not require holding non-critical items in WM until a response was finished. To address this concern, we tried to minimize the difficulty of tasks by using stimuli (i.e., English consonants) whose representations enjoyed supports from both semantic and lexical codes in long-term memory (Stuart & Hulme, 2000) and phonological codes in WM (Baddeley, 1986). We also provided strong feedback to motivate the participants to maximize their performance rather than to settle on an easy response strategy. Nevertheless, we cannot completely rule out the possibility that the participants might simply choose to be minimal responders because that is easier than being ideal responders.

It is a well-known consensus that WM is severely limited in capacity but highly accessible to various higher level cognitive activities (Baddeley, 1986; Conway, Kane, & Engle, 2003; Cowan, 2001; Cowan, 2005; Daneman & Carpenter, 1980; Miyake & Shah, 1999). One might expect that, given its scarcity and accessibility, task-related WM should be fully utilized by the mind. Ironically, the minimal-responder model verified by our data suggests that people might tend to unwisely ignore important but not immediately usable task-related information from WM. Perhaps this occurs because an ideal responder has to keep multiple items at once in WM so as to eliminate the non-critical items from the option set. Such processes might require switching attention from one item to another (Barrouillet, Portrat, & Camos, 2011; Oberauer, 2002), which can cause interference and make the task more challenging. Alternatively, items in WM may need to be continuously and concurrently refreshed by attention (e.g., Chen & Cowan, 2009). At the test array, the probe item attracts attention away from the non-critical items and, as a result, they might have faded away over time in the absence of attentional rehearsal before they could be mentally compared to the response choices. Future research is needed to investigate these possible alternative accounts of the cognitive mechanisms behind minimal responding.

The present findings have important implications for how an item’s identity is bound to its location. Change-detection procedures have shown that accuracy is sometimes higher in procedures in which a new item identity must be detected than in procedures in which the change that must be detected is a recombination of attributes, namely the identity of one former array object presented in the location of another (e.g., Cowan, Naveh-Benjamin, Kilb, & Saults, 2006; Morey, 2009; Wheeler & Treisman, 2002). The comparison leading to this result has typically been carried out, though, using an accuracy measure, whereas much is to be gained by using models that allow an estimation of the number of items in WM according to certain assumptions. To enable such models, we used a change-detection task with changes to letters not found in the studied array, in order to ensure that only the array item in the probed location could be of use; in contrast, though, we also used identity and location recognition tasks with recombination changes, to ensure that array items other than just the probed item could indeed be of use. We obtained near-perfect convergence of these tasks with the assumption of a minimal processing mode in which participants do not actually use their WM information about items other than the one probed. This convergence of the benchmark and minimal-responder models suggests that the minimal-responder assumption is apt. The additional implication we are pointing out here has to do with the nature of the WM representations. Given that the participant did not know what task was to be carried out on a trial until the probe was presented at the end of the trial, the representation of items in WM had to be the same in all tasks. The finding of a good match between the benchmark model and one model that required letter-location combination information suggests that the WM representations comprised bound identity-location pairs (cf. Morey, 2009; Treisman & Zhang, 2006).

Given the findings of our study, the ideal-responder model assumed by Alvarez & Thompson (2009) should have underestimated the number of visual objects stored in WM in their Experiment 1, exemplifying the need to consider responder efficiency in future modeling of the contents of WM. More importantly, the theoretical importance of our study is to open up a new perspective on WM research, and the notion of responder efficiency introduced in this paper should be particularly useful in quantitatively characterizing the WM system, such as assessing WM capacity and WM decay rate. In fact, no investigation of WM can be done without assumptions about how the WM that cannot be directly observed is channeled into a participant’s observable responses to a WM task. As we show in this study, some common assumptions are not always justifiable. On the road to understanding the WM system at the algorithmic level (Marr, 1982), many more assumptions about WM should be subjected to rigorous empirical examination in the near future.

Appendix A. Models of Working Memory Capacity

Benchmark Model

To develop the benchmark mathematical model, let N denote the number of items in a sample array and K the number of items loaded into WM. Given that the critical item is randomly chosen from the N items, the probability of its being held in WM would be $\frac{K}{N}$. In case of the critical item being held in WM, the conditional probability of a successful detection is 1. Otherwise, the probability of the condition that the critical item is not in WM is ( $1-\frac{K}{N}$) and the conditional probability of a correct response is the successful guessing rate. Overall, the probability of a correct response would be the probability of a successful detection plus the probability of a successful guessing. Let g denotes the probability of guessing a change, which is assumed constant throughout the test session. It follows that the successful guessing rate would be g for a change trial and 1-g for a no-change trial. Accordingly, the hit rate (hr) and the correct rejection rate (cr) can be expressed as a function of K, N and g in Equations 1 and 2, respectively.

$$hr=\frac{K}{N}+(1-\frac{K}{N})\times g$$ (1)

$$cr=\frac{K}{N}+(1-\frac{K}{N})\times (1-g)$$ (2)

The parameter g can be cancelled out by combining Equations 1 and 2, so that K can be expressed as a function of N, hr and cr as follows.

$$K=N\times (hr+cr-1)$$ (3)

Ideal-Responder and Minimal-Responder Models

These two models apply to situations in which alternative types of information can be used to solve the problem (i.e., the identity-recognition and location-recognition tasks illustrated in Figure 1). Specifically, although a feature of one item is queried by the probe, information about other items in the array can provide useful clues to the correct response. If an item’s location (or identity) is presented as a probe and the item is well-known in WM as a bound unit, then its identity (or location) can be retrieved as a response. If the probed item is not in WM, then the participant still might have some relevant information to infer a correct response because any other item in WM can be ruled out as a response choice, as the other items do not have the correct combination of identity and location. Participants use that other relevant information according to the ideal-responder model, but not according to the minimal-responder model. The latter is considered minimal in that it is based on a simplifying heuristic (e.g., Kahneman, 2003), which decreases the amount of calculation that must be performed to give a response.

Four WM measure formulae were used to calculate K_{i_iden}, K_{i_loc}, K_{m_iden} and K_{m_loc}. Although the identity-recognition and the location-recognition tasks appeared quite different in format, they share similar cognitive processes and thus are compatible with the same WM formulae. Therefore, both the identity-recognition and location-recognition tasks used one formula for an ideal responder and another one for a minimal responder.

For the ideal-responder model, let K_i denote the number of visual items loaded into WM by an ideal responder and N the number of visual items in the sample array. Given that the critical item is randomly selected from N visual stimuli, the probability of the critical item being held in WM is $\frac{K_i}{N}$. The probability of the critical item not in WM is $1-\frac{K_i}{N}$. In that case, the probability of selecting the correct option by chance would be $\frac{1}{N-K_i}$, as an ideal responder is presumably able to first eliminate from the N options K_i non-critical items held in visual WM and then make a random selection among the remaining (N-K_i) options. Given that a response would be correct either when the critical item is indeed recognized from WM or when the right option is guessed with no memory of the critical item, the probability of an accurate response (Ac) in a particular recognition task can be expressed as a function of K_i and N by Equation 4.

$$\begin{array}{ll}Ac=\frac{K_i}{N}+(1-\frac{K_i}{N})\times (\frac{1}{N-K_i})\hfill & \text{when}{K}_i<N\hfill \\ Ac=1\hfill & \text{when}{K}_i=N\hfill \end{array}$$ (4)

where Ac=Ac_iden for the identity-recognition task and Ac=Ac_loc for the location-recognition task. Rearranging terms, K_i can be expressed as a function of N and Ac as follows.

$$K_i=N\times (Ac-\frac{1}{N})$$ (5)

For the WM formula for a minimal responder who cannot benefit from the memory of non-critical items, let K_m denote the number of visual items loaded into WM and N the array size. The probability of a critical item being held in WM is $\frac{K_m}{N}$. In case of no critical item in visual WM, which happens at a probability of $1-\frac{K_m}{N}$, the probability of selecting the correct option by chance would be $\frac{1}{N}$, as a minimal responder can only make a random choice out of N options (rather than out of N-K_i options, as only an ideal responder is supposed to be able to do). Parallel to Equations 4, the minimal-responder model can be specified by Equation 6.

$$Ac=\frac{K_m}{N}+(1-\frac{K_m}{N})\times \frac{1}{N}$$ (6)

Rearranging terms, K_m can be expressed as a function of Ac and N as follows.

$$K_m=N\times (Ac-\frac{1}{N})\times \frac{N}{N-1}$$ (7)

In summary, all formulae for items in WM are as follows, with subscripts c for the model of Cowan (2001), i for the ideal-responder model, m for the minimal-responder model, iden for the identity-recognition task, and loc for the location-recognition task.

$$\begin{array}{l}{K}_{c\_det}=N\times (hr+cr-1)\\ K_{i\_\mathit{iden}}=N\times ({Ac}_{\mathit{iden}}-\frac{1}{N})\\ K_{i\_\mathit{loc}}=N\times ({Ac}_{\mathit{loc}}-\frac{1}{N})\\ K_{m\_\mathit{iden}}=N\times ({Ac}_{\mathit{iden}}-\frac{1}{N})\times \frac{N}{N-1}\\ K_{m\_\mathit{loc}}=N({Ac}_{\mathit{loc}}-\frac{1}{N})\times \frac{N}{N-1}\end{array}$$

The Possible Role of Imperfect Retrieval Likelihood

This explanation can be more precisely described with the following mathematical reasoning. Let l denote the WM retrieval likelihood (0≤ l ≤ 1) and Ac_il the accuracy of the recognition condition under the revised ideal-responder model with a retrieval likelihood parameter l. Conceptually, l is a function of an individual’s WM capacity, as the bigger an individual’s WM capacity, the higher his/her WM retrieval likelihood. Ac_il equals to the sum of probabilities of two events: 1) a correct response based on successful retrieval of K_i×l items, which include the critical item, from WM and 2) a correct response based on random guessing among N−K_i×l items from the option set in case the critical item is not among the retrieved items.

$${Ac}_{il}=\frac{K_i\times l}{N}+(1-\frac{K_i\times l}{N})\times \frac{1}{N-K_i\times l}$$ (8)

After some algebraic transformation, we have

$${Ac}_{il}=\frac{K_i\times l}{N}+\frac{1}{N}$$ (9)

In parallel, the performance accuracy of a minimal responder (Ac_m) is specified by Equation 6 as follows.

$${Ac}_m=\frac{K_m}{N}+(1-\frac{K_m}{N})\times \frac{1}{N}$$ (10)

In order to give Ac_il the same degree of fit as Ac_m has with the observed accuracies, we first rearrange Equation 10 to express Ac_m in the same form as Equation 9 for Ac_il.

$${Ac}_m=\frac{K_m\times \frac{N-1}{N}}{N}+\frac{1}{N}$$ (11)

As a comparison of Equations 9 and 11 reveals, Ac_m and Ac_il are mathematically indistinguishable when $l=\frac{N-1}{N}$. In other words, if we assign the value of $\frac{N-1}{N}$ to the retrieval likelihood parameter l, the revised ideal-responder model will fit the data as close as the minimal-responder model does.