Abstract
Improvement in performance following cognitive training is known to be further enhanced when coupled with brain stimulation. Here we ask whether training-induced changes can be maintained long term and, crucially, whether they can extend to other related but untrained skills. We trained overall 40 human participants on a simple and well established paradigm assessing the ability to discriminate numerosity–or the number of items in a set–which is thought to rely on an “approximate number sense” (ANS) associated with parietal lobes. We coupled training with parietal stimulation in the form of transcranial random noise stimulation (tRNS), a noninvasive technique that modulates neural activity. This yielded significantly better and longer lasting improvement (up to 16 weeks post-training) of the precision of the ANS compared with cognitive training in absence of stimulation, stimulation in absence of cognitive training, and cognitive training coupled to stimulation to a control site (motor areas). Critically, only ANS improvement induced by parietal tRNS + Training transferred to proficiency in other parietal lobe-based quantity judgment, i.e., time and space discrimination, but not to quantity-unrelated tasks measuring attention, executive functions, and visual pattern recognition. These results indicate that coupling intensive cognitive training with tRNS to critical brain regions resulted not only in the greatest and longer lasting improvement of numerosity discrimination, but importantly in this enhancement being transferable when trained and untrained abilities are carefully chosen to share common cognitive and neuronal components.
Introduction
“Brain training”, which aims at improving cognitive skills, has often proven successful (Draganski et al., 2004; Amitay et al., 2006; Jaeggi et al., 2008; Klingberg, 2010) although a key and highly controversial issue is whether training benefits can transfer to new, untrained skills. This is important not just because training programs are demanding on resources and hence require careful selection of the optimal training design, but also because in clinical and educational contexts it is essential to find the training protocol leading to the most robust and generalizable improvement. Generalization of training to new tasks or modalities has been previously shown (Green and Bevalier, 2003; Amitay et al., 2006; Jaeggi et al., 2008, 2011; Klingberg, 2010), although some of these findings have been questioned or not replicated (Sagi and Tanne, 1994; Ball et al., 2002; Sternberg, 2008; Hertzog, 2009; Owen et al., 2010; Boot et al., 2011; Slagter, 2012; Melby-Lervåg and Hulme, 2013; Redick et al., 2013), casting doubt on the utility of cognitive training. Unsuccessful transfer of trained abilities could be due to insufficient practice on the trained tasks, the use of inappropriate new tasks, or simply the fact that cognitive training is not strong enough to induce the necessary cortical changes that facilitate the generalization of learned skills (Lee et al., 2012).
One way to assist the cortical changes that support learning of a particular cognitive skill is by means of brain stimulation. Transcranial random noise stimulation (tRNS), a noninvasive brain stimulation technique that modulates neural activity (Terney et al., 2008; Fertonani et al., 2011; Mulquiney et al., 2011; Snowball et al., 2013), is of particular interest as it is known to potentiate the activity of the neuronal populations involved in a cognitive task and to facilitate brain plasticity, especially if combined with appropriate cognitive training (Cohen Kadosh et al., 2012). Critically, whether improvement following training and stimulation can transfer to other compatible skills has not yet been addressed.
Here we measured the following: (1) combined or independent effects (i.e., training only and stimulation only) of cognitive training and of brain stimulation to critical or control brain regions (parietal or motor), (2) any long-term effect of any cognitive improvement achieved, and critically (3) transfer to untrained tasks. We trained participants on a well known paradigm measuring “number acuity” (Halberda et al., 2008), i.e., the ability to discriminate the more numerous of two sets, an established measure of a parietal lobe-based foundational and universal ability to process number (Feigenson et al., 2004; Piazza et al., 2004; Cantlon et al., 2006; Izard et al., 2009). Since number is also thought to share parietal lobe-based quantity processing with continuous dimensions like time and space (Walsh, 2003; Cohen Kadosh et al., 2008; Cantlon et al., 2009; Cantlon, 2012), our reasoning was as follows: if brain stimulation and training operate on these common processes, then transfer to time and space processing may be observable following number training and parietal stimulation. Instead, if improvement in the trained numerosity task operates mainly on nonquantity processes like attention, executive functions, or visual recognition, then transfer may be also found on these processes rather than time and space only.
Materials and Methods
Participants
Forty right-handed, neurologically normal and stimulation-compatible (Wassermann, 1998) human participants (mean age: 25.8 range: 19–36, 18 males) with normal or corrected-to-normal vision gave written consent and were paid to participate in our double-blind study, which was approved by the local Ethics Committee.
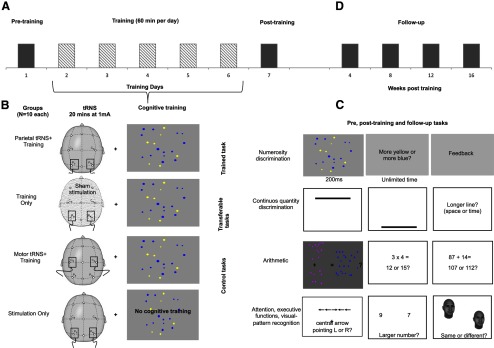
In the main condition, participants underwent training on the numerosity discrimination task for 5 consecutive days while they received tRNS to parietal regions (parietal tRNS + Training group, N = 10; Figure 1). Results from this condition were compared against three control groups. In one of the control groups, participants received no stimulation (sham) to the parietal regions during training (i.e., Training Only group, N = 10). This control condition served as a baseline to evaluate effects of tRNS on training. In a second control group, tRNS was delivered to the parietal regions without the training task (Stimulation Only group, N = 10). This condition allowed us to examine if parietal stimulation alone was sufficient to improve task performance. In a third control group, tRNS was delivered to the bilateral motor areas during training (Motor tRNS + Training, N = 10). This control condition allowed us to test whether any training-induced effect was area specific or occurred regardless of what brain area was stimulated. The bilateral motor areas were selected because they are not known to be involved in ANS. Data in participants of the Parietal tRNS + Training and of the Training Only groups were collected at the same time, whereas data in the other two control conditions were collected subsequently.
Figure 1.
The training paradigm and the tasks used. A, Participants in the parietal or motor tRNS + Training and in the Training Only groups were trained intensively (560 trials per day) on a numerosity discrimination task for 5 consecutive days, i.e., day 2–6 while (B) receiving real or sham stimulation to the parietal or motor areas. Participants on the Stimulation Only group received no training. Before the training (day 1, pretraining), all participants were tested with (C) the numerosity discrimination task in addition to other continuous quantity-based tasks (time and space discrimination), arithmetic and control tasks. The same cognitive tasks were repeated at the end of the training (day 7, post-training) to test for any training-induced change, and (D) in the parietal tRNS + Training and Training Only groups again at week 4, 8, 12, and 16 post-training to test for any long-term effect of the training.
Subjects were randomly assigned to the four groups overall matched for gender (χ2(1) = 0.4, p = 0.53), age (F(3,39) = 0.42, p = 0.74), general education (F(3,39) = 0.14, p = 0.9), and mathematical education (F(3,39) = 0.7, p = 0.55). Information on participants' education and mathematical education was collected to test the possible effects of these factors on learning.
Stimulation design
tRNS was delivered by a battery-driven electrical stimulator (Version DC-Stimulator-Plus; neuroConn) through two anode conductive rubber electrodes (size 7 × 5 cm), covered with conductive gel and saline solution and positioned over the subject's scalp, following a standard procedure (Terney et al., 2008). The electrodes were positioned on the target areas corresponding to parietal (P3 and P4) or motor regions (C3 and C4) following the standard 10–20 electroencephalogram procedure (Fig. 1). The parietal or motor tRNS + Training and the Stimulation Only groups were stimulated with a random noise mode for 20 min with a fade in/out period of 20 s, a current strength of 1000 μA, and a frequency of alternating current randomly selected from 0 to 250 Hz. This intensity has been shown to be safe in healthy volunteers (Ambrus et al., 2010; Fertonani et al., 2011). The same parameters were used for the Training Only (sham) group but the stimulation consisted only of the fade in/out period (i.e., 40 s in total), meaning that this group did not receive full stimulation during training; nevertheless, participants in this group maintained the same setting as the participants in the other groups as if they were receiving stimulation (Ambrus et al., 2010; Fertonani et al., 2011). During the whole time course of the study, participants were not told whether they received real or sham stimulation, similar to other reported studies (Terney et al., 2008; Fertonani et al., 2011; Mulquiney et al., 2011). When explicitly asked whether there was any discomfort or unusual sensation on their scalp, none of the participants reported any.
Experimental design
Participants in the parietal and motor tRNS + Training and in the Training Only groups were trained for 5 consecutive days (day 2–6) with the numerosity discrimination task (Training). In the tRNS + Training group, this cognitive training coincided with parietal or motor stimulation. The same parietal stimulation but no training was delivered to the Stimulation Only group. Participants in all groups were tested with a series of quantity-based, arithmetical, and control tasks before (Pretraining, Day 1) and after the training (Fig. 1, Post-training, Day 7).
To assess any long-term effect of the training (Follow-up), participants of the parietal tRNS + Training and of the Training Only groups were also retested with the same behavioral tasks at week 4, 8, 12, and 16 post-training (seven participants for each group were available for the follow-up tests). No follow-up tests were run on the Stimulation Only group, since they were not trained on the numerosity discrimination task. Likewise, no follow-up tests were performed on the Motor tRNS + Training group as no sufficient time had passed since the end of the training and the current report.
Stimulus presentation and data collection were controlled using the Cogent Graphics toolbox (http://www.vislab.ucl.ac.uk/Cogent) and MATLAB 7.11 software on a Sony PCG laptop computer with video mode of 640 × 480 pixels, and 60 Hz refresh rate. During all testing sessions participants sat in a quiet room under dimmed room lighting with their head on a chinrest facing the computer screen at a viewing distance of 57 cm from the monitor.
Training task: numerosity discrimination.
Participants received 1 h training for 5 consecutive days on a parametrically designed task requiring participants to discriminate the numerosity of two sets of stimuli, i.e., dots, an ability measured in terms of the Weber fraction (wf; Halberda et al., 2008, 2012). Sets of intermixed, computer-generated yellow and blue dots were each presented for 200 ms to participants who were instructed to make an unspeeded answer indicating which set contained more dots and were provided with feedback (Fig. 1). To become familiarized with the task, participants received at least 40 practice trials that were not included in the analysis. Each display contained 5–16 dots for each color such that the ratios between the larger and the smaller number of dots were as follows: 2:1, 4:3, 6:5, 8:7, 8:9, and 9:10. There were 40 trials for each of the easiest ratios (2:1 and 4:3), and 120 for each of the more difficult ratios (6:5, 8:7, 8:9, and 9:10) for a total of 560 trials presented in 10 blocks. We used a larger number of trials in the most difficult ratios to increase statistical power since we expected a low accuracy in these ratios. In each ratio, the “larger” set was equally assigned to the two colors. Following previous studies based on the same experimental paradigm (Halberda et al., 2008, 2012), we systematically controlled for the impact of continuous features that change with numerosity, and specifically we independently manipulated the size of the dots and the cumulative area covered by them. The diameter of a dot ranged approximately between 0.57 and 1.17 degrees of visual angle from a distance of 57 cm, and was varied approximately by up to ± 35% of the average display to discourage the use of individual dot size as a proxy for number, similar to previous studies (Halberda et al., 2008, 2012).
Pre-traing, post-training, and follow-up tasks.
We assessed whether training of numerosity discrimination may transfer to other types of quantity judgments, and specifically time and space processing following the theoretical suggestion that number, time, and space share common magnitude processes relying on parietal regions (Walsh, 2003; Cantlon et al., 2009; Cantlon, 2012).
Time and space processing were assessed with an established two-choice discrimination paradigm previously tested in healthy and neurological populations (Cappelletti et al., 2009, 2011). Participants performed two different tasks requiring them to compare visual stimuli along the dimension of time or the orthogonal dimension of length (Fig. 1). We used 1D stimuli to avoid possible visual confounds of density or area present in 2D stimuli (Dakin et al., 2011). Stimuli were two horizontal white lines (thickness 0.17 degrees) centered on the vertical meridian on a black background, and presented sequentially one line 5.07 degrees above the horizontal meridian and the other 5.07 degrees below in random order. The first line stimulus (the Reference) was fixed (length of 10.2 degrees and duration of 600 ms), while the second line (the Test) could vary according to the method of constant stimuli either in length or duration, depending on the dimension to be judged (the irrelevant dimension always matched the Reference). For each dimension the ratio between the smaller and the larger stimulus could vary unpredictably over five levels (steps of 0.257 degrees for length and 40 ms for time) with equal frequency: 1.06, 1.13, 1.2, 1.26, and 1.33 for time and 1.025, 1.05, 1.075, 1.10, and 1.25 for length, with optimal ranges established in our previous studies (Cappelletti et al., 2009, 2011). There were five blocks of 40 observations for each level of the test stimulus (total 200 observations for each task). Time and space tasks were run independently, with task order counterbalanced across participants and training sessions (pretraining and post-training) to avoid order effects.
Each trial began with a centrally displayed fixation point (diameter 0.17 degrees), which remained visible until a key press from the participant. The reference line was then immediately displayed centrally followed by the test line and an interstimulus interval of 100 ms. The screen then remained blank with a fixation cross in the middle until a response from the subject. The next trial immediately followed the response. In each task, participants made unspeeded responses by pressing either the “up” or “down” cursor-arrow keys of the computer keyboard if either the upper or the lower line appeared the longest, either in duration or in spatial extent. Correct answers were equally assigned to the up or down keys in each task. For each task, before the first experimental block participants had at least 20 practice trials that were not included in analysis.
We also tested symbolic (e.g., “87 + 14” = 104 or 109?) and nonsymbolic (e.g., ·· + ··· = ?) arithmetic skills following the proposal that they are linked to number acuity (Halberda et al., 2008). However, we predicted that benefit of training to these arithmetic tasks would be unlikely because they require additional memory and executive abilities that were not trained and are therefore improbable to result in improved arithmetic performance.
Participants were assessed on three arithmetical tasks required to verify the result of arithmetical problems based on nonsymbolic stimuli (i.e., addition and subtraction of dots, following a paradigm used by Barth et al., 2005) or symbolic stimuli (i.e., simple and complex arithmetic tested with single and multidigit operands). The simple symbolic arithmetical verification task consisted of 54 single-digit addition, subtraction, and multiplication problems presented in separate blocks; they were displayed with two one-digit or two-digit answers, one of which was correct while the other was one, two, or three units apart from the correct answer (“3 × 4” = 12 or 15?). The complex arithmetical verification task required choosing the results closer to the correct one of 192 multidigit problems presented in separate blocks (two-digit paired with two-digit for addition and subtraction; two-digit paired with one-digit for multiplication problems), with the two incorrect results being 3, 4, 7, or 8 units apart from the correct answer (for addition and subtraction problems, e.g., “87 + 14” = 104 or 109?), and 8, 9, 17, or 18 units for multiplication problems (e.g., “24 × 7” = 177 or 185?).
Finally, to test whether any change following training transferred to other nonquantity-based cognitive abilities, we tested participants' performance in three well established tasks tapping executive functions (Number Stroop task; Henik and Tzelgov, 1982), attention (Attention Network Test, ANT; Fan et al., 2002), and recognition of visual patterns (Face Sequential Matching task; Pitcher et al., 2009). We expected no change in these skills if the effect of stimulation and training were specific to quantity processing.
Stimuli in the two symbolic arithmetic tasks differed in the pretraining and post-training sessions to avoid effects simply derived from practice with the same trials. Stimuli were the same in parametrically designed tasks (e.g., time and space discrimination, visual pattern recognition) or when repeating the same stimuli was unlikely to affect performance (e.g., in the Number Stroop tasks). Tasks in the pretraining and post-training were administered in pseudorandom order to participants.
Data analyses
Following earlier studies, for each participant response distributions in the numerosity discrimination task were used to estimate the precision of the underlying numerical representation, expressed as a wf (Halberda et al., 2008). The calculation of the wf precisely followed previous studies (Halberda et al., 2008, 2012). It was based on a model assuming that the perceived numerosity of the two sets of dots (n1 and n2, respectively) is represented as two Gaussian random variables on a linear scale (that is with linearly increasing mean and linearly increasing SD) with means of n1 and n2, and with an SD of wf × n1 and wf × n2, respectively (Halberda et al., 2008). The wf determines the variation of the SD of the Gaussian random variables in each numerosity. The difference between the two Gaussian variables (i.e., the Gaussian of the set with the larger numerosity minus the Gaussian of the set with the smaller numerosity) returns a new Gaussian random variable (G(n2–n1)) with mean n2 − n1 and SD wf . The larger the SD of G(n2–n1), the larger is the overlap of the two Gaussian distributions representing the numerosity of the two sets and in turn the more difficult it is to discriminate between them. Therefore, a large wf indicates worse performance in the numerosity discrimination task. A similar procedure was used to calculate the wf for the time and space discrimination tasks.
For all the other tasks we used an index of accuracy (% correct) and/or speed (response times, RTs) of correct answers cleaned for 2 SD above and below the mean for each task and participant (removing between 0 and 3.4% of the data). For all data, the Shapiro–Wilk test confirmed the normality of the distribution. The data were analyzed using repeated-measures ANOVA, multiple regression and t test, with a p value < 0.05 considered significant for all statistical analyses. The data sphericity was tested using Mauchly's test where appropriate. When the sphericity test results were statistically significant, the data were corrected using Huynh–Feldt correction. For multiple comparisons, we used Sidak correction to test our specific a priori hypotheses, i.e., to compare the different training conditions.
Results
Effect of cognitive training and tRNS on number acuity
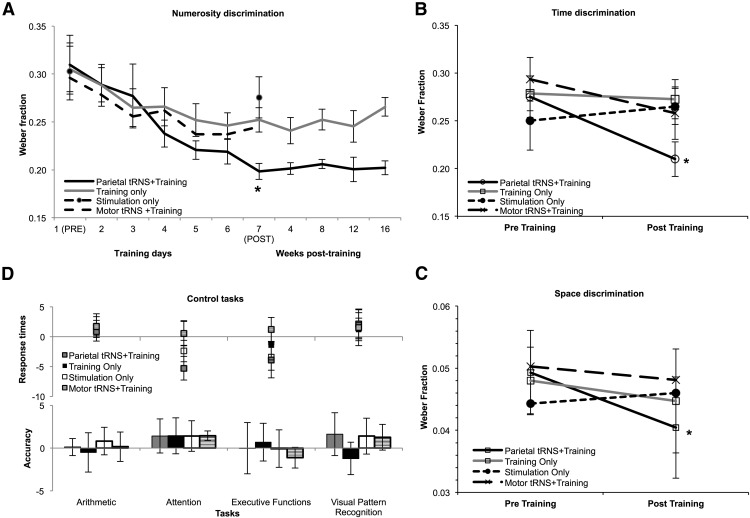
Participants' numerosity discrimination did not differ across groups at pretraining (F(3,39) = 0.02, p = 0.99). To test for any training-induced change in numerosity discrimination, a repeated-measures ANOVA was run with wf values of training (pre and post) as a within-subjects factor and group (Parietal tRNS + Training, Training Only, Stimulation Only, and Motor tRNS + Training) as a between-subjects factor. This indicated a significant improvement in number acuity following training (F(1,36) = 41.7, p < 0.001), as wf changed from 0.307 (SE = 0.014) to 0.246 (SE = 0.011) across groups corresponding to ∼18% enhancement. A further analysis based on the training days and group (Parietal tRNS + Training, Training Only, and Motor tRNS + Training), showed a significant linear trend (F(1,27) = 49.4, p < 0.001) that was specific for group (significant interaction: F(2,27) = 3.2, p = 0.05). Improvement in number acuity differed across groups as indicated by a significant interaction of training and group (F(3,36) = 3.4, p < 0.03), with no main effect of group (F(1,36) = 0.4, p = 0.7, ns). A significantly better performance was observed when training was coupled with parietal stimulation (wf from 0.309 to 0.198 corresponding to 33.6% improvement, SE = 0.04; t(9) = 4.8, p = 0.001), but also following training alone (wf from 0.305 to 0.252 corresponding to a 14.8% improvement, SE = 0.03; t(9) = 2.5, p = 0.03), and training coupled with motor tRNS (wf from 0.312 to 0.257 corresponding to 18.4% improvement, SE = 0.03; t(9) = 7.4, p < 0.001). In contrast, no significant enhancement was achieved with stimulation alone (wf from 0.303 to 0.276, corresponding to a 6.2% enhancement, SE = 0.03; t(9) = 1.7, p = 1.1, ns; Fig. 2A). Training coupled with parietal stimulation resulted in a significantly larger improvement compared with training alone (t(18) = 2.5, p < 0.02), and to training coupled with motor stimulation (t(18) = 2.8, p = 0.01). Improvement following Training alone or Training coupled with Motor Stimulation did not differ (t(18) = 0.6, p = 0.5).
Figure 2.
Results. Performance in the four groups expressed as Weber fraction in (A) the numerosity discrimination task at pretraining and at post-training, during each of the training days, and at week 4, 8, 12, and 16 after training; in the transfer tasks, i.e., time (B) and space (C) discrimination at pretraining and post-training; and (D) in tasks measuring arithmetic, attention, executive functions, and visual pattern recognition showing no training-induced changes in accuracy (correct answers) or RTs measured as percentage change from pretraining. Smaller wf indicate better performance.
We also tested whether improvement in number acuity could be accounted for by individual difference in gender, general education, or mathematical education but found that none of these factors were significant (gender: β = 0.12, SE = 0.05, t = 0.74, p = 0.46; general education: β = 0.26, SE = 0.05, t = 0.16, p = 0.1; mathematical education: β = 0.13, SE = 0.14, t = 0.8, p = 0.39). A specific analysis controlling for gender was run with wf values of training (pre and post) as a within-subjects factor, group (Parietal tRNS + Training, Training Only, Stimulation Only, and Motor tRNS + Training), and gender as a between-subjects factor. This confirmed the main effect of training (F(1,32) = 38.5, p < 0.001), which depended on the group (F(3,32) = 2.9, p = 0.04); none of the other effects reached significance.
To obtain a measure of training-induced changes in number acuity reflecting the day-by-day training (Fig. 1A, day 2–6), we also performed a multilevel mixed model, with wf values as dependent variable, group entered as factor, and the linear and quadratic trends for time (=consecutive training days) as covariates testing for the effect and the shape of learning. Fixed effects were included for group and the linear and quadratic trends of time, as well as the interaction of these latter trends with group. Subject-dependent random effects were intercepts and the linear and quadratic trends for time.
The random intercept was significant (Wald's Z = 7.7, p < 0.001), indicating that there were individual differences in performance. The linear trend for time was significant (F(1,314) = 9.5, p = 0.002), indicating a significant effect of training.
To obtain more reliable estimates of the true wf scores before and after training, the mixed-effect model was used to obtain new wf values (by saving the predicted values in the linear mixed model) at day 1 and 7, i.e., the pretraining and post-training days, such that they reflected the overall learning. These estimated scores were then used in a further repeated-measures ANOVA with training (pre and post) and group (Parietal tRNS + Training, Training Only, and Motor tRNS + Training groups) as factors. This new analysis confirmed the previous results showing a significant effect of training (F(1,27) = 160.82, p < 0.001), and a significant interaction with group (F(2,27) = 15.1, p < 0.001). Similar to the earlier analysis, there was a significantly stronger learning effect in the Parietal tRNS + Training group relative to Training Only group (t(18) = 4.2, p < 0.001) and the Motor tRNS + Training group (t(18) = 4.5, p < 0.001).
Overall these results showed that cognitive training alone lead to a significantly better improvement in number acuity relative to simply stimulating the brain with no training. However, as predicted, the largest improvement in number acuity was achieved by simultaneously combining cognitive training with parietal stimulation.
Transfer of trained skills to other cognitive skills
Continuous quantity processing (time and space discrimination)
Having found an improvement in number acuity when parietal stimulation was coupled with number training, we first tested whether enhanced number acuity transferred onto other tasks also requiring quantity processing, and specifically time and space. Such transfer may be suggestive of a link between numerosity and continuous quantity, as predicted by some theories (Walsh, 2003; Cantlon et al., 2009; Cantlon, 2012).
Participants' time and space discrimination did not differ across groups at pretraining (F(3,39) = 0.53, p < 0.6 and F(3,39) = 0.13, p < 0.9, respectively). To test for any training-induced changes, a repeated-measures ANOVA was run with the wf values of training (before and after) as a within-subjects factor and group (Parietal tRNS + Training, Training Only, Stimulation Only, and Motor tRNS + Training) as a between-subjects factor. This showed a general training-related improvement in time discrimination (F(1,36) = 4.3, p = 0.04), which depended on the group (significant training by group interaction, F(3,36) = 3.5, p = 0.05). Specifically, there was a significant enhancement from pretraining only when training and parietal stimulation were simultaneous (23% increase, t(9) = 5.2, p = 0.001; Fig. 2B). No significant improvement in time proficiency was observed in any of the other conditions (Training Only: 2.2% increase, t(9) = 0.3, p = 0.7, ns; Stimulation Only: 5% decrease, t(9) = 0.6, p = 0.5, ns; Motor tRNS + Training: 5.1% increase, t(9) = 2.0, p = 0.09, ns).
A similar ANOVA exploring performance in space discrimination showed a general improvement in performance following training (F(1,36) = 5.4, p < 0.03), which depended on the group (significant training by group interaction, F(3,36) = 3.1, p < 0.04). Critically, the effect of training on the numerosity task transferred to the ability to discriminate space only when training and parietal stimulation were simultaneous, with a significant enhancement from pretraining only in this training condition (18% increase, t(9) = 5.6, p < 0.001; Fig. 2C). No significant improvement in space proficiency was observed in any of the other conditions (Training Only: 6.8% increase, t(9) = 0.9, p = 0.3, ns; Stimulation Only: 3% decrease, t(9) = 0.3, p = 0.7, ns; Motor tRNS + Training: 4.4% increase, t(9) = 3.4, p = 0.74, ns).
RTs in the space and time discrimination tasks were unchanged after training, therefore excluding any RT-accuracy trade-off. Gender, general education, and mathematical education did not account for any of the improvement observed in time and space processing (all p > 0.2). Separate analyses specifically controlling for gender were run for time and space discrimination with wf values of training (pre and post) as a within-subjects factor, group (Parietal tRNS + Training, Training Only, Stimulation Only, and Motor tRNS + Training), and gender as a between-subjects factor. These analyses confirmed the main effect of training (time discrimination: F(1,32) = 4.2, p = 0.04; space discrimination: F(1,32) = 3.9, p = 0.05), which depended on the group (time discrimination: F(3,32) = 2.0, p = 0.05; space discrimination: F(3,32) = 3.6, p = 0.02); none of the other effects reached significance.
Arithmetical processing
Since there are suggestions of a link between number acuity and proficiency in arithmetical tasks (Halberda et al., 2008; but see Butterworth, 2010), we explored whether the observed improvement in numerosity discrimination transferred to arithmetical performance. Participants' arithmetic skills did not differ across groups at pretraining (all p > 0.2). Separate repeated-measure ANOVAs with training (pre and post) as a within-subjects factor and Group (Parietal tRNS + Training, Training Only, Stimulation Only, and Motor tRNS + Training) as a between-subjects factor were run on accuracy and RTs of correct responses only obtained in the three arithmetical tasks. These analyses indicated that performance in nonsymbolic arithmetical tasks (averaged across addition and subtraction problems) did not change in either accuracy or speed (no main effect of training, F(1,36) = 0.4, p = 0.5, ns and F(1,36) = 3.1, p = 0.09, ns, respectively) and regardless of whether participants received training associated with stimulation or stimulation and training alone (no significant interaction of Training and Group, accuracy: F(3,36) = 1.3, p = 0.3, ns and RTs: F(3,36) = 1.2, p = 0.3, ns). In the simple arithmetical tasks, both accuracy and RTs (averaged across the three types of arithmetical problems) remained unchanged following training (F(1,36) = 1.1, p = 0.3, ns; F(1,36) = 1.5, p = 0.2, respectively) and regardless of the group (no significant interaction of Training and Group: F(3,36) = 1.9, p = 0.13, ns; F(3,36) = 0.9, p = 0.44, respectively). Likewise, accuracy and RTs in the complex arithmetical tasks (averaged across the three types of arithmetical problems) did not change following training (F(3,36) = 0.1, p = 0.7, ns; F(1,36) = 1.8, p = 0.2, ns, respectively) and regardless of the group (F(3,36) = 0.5, p = 0.6, ns; F(3,36) = 0.07, p = 0.9, ns, respectively; Fig. 2D).
Attention, executive function, and visual pattern recognition
Our result showed that the improvement in numerosity discrimination transferred to other continuous quantity discrimination in the parietal tRNS + Training group relative to other groups. We tested whether this transfer was specific to quantity-related tasks or whether it also generalized to other nonquantity abilities, such as attention, executive functions, and recognition of visual patterns.
There was no group difference in performing any of the control tasks at pretraining (all p > 0.1). The effect of training on attention processes was examined in separate analyses of variance for each condition (alerting, orienting, and conflict; Fan et al., 2002) in the four groups (Parietal tRNS + Training, Training Only, Stimulation Only, and Motor tRNS + Training). A significant and group-unspecific (no significant interaction p = 0.7) effect of training was observed only in the executive control network (indexed by the difference between incongruent vs congruent trials, from 90.2 ms at pre-training to 67.5 ms at post-training, F(1,36) = 20.9, p < 0.001), which might be due to practice with the task. No significant changes were observed in alerting and orienting (all p > 0.1).
Executive functions were unchanged following training and regardless of the training group. Separate analyses of variance for the physical and the numerical Stroop tasks (Henik and Tzelgov, 1982) with training (pre and post) and condition (facilitation, i.e., congruent vs neutral trials; interference, i.e., incongruent vs neutral trials; and congruity, i.e., incongruent vs congruent trials) as within-subject factors and group (Parietal tRNS + Training, Training Only, Stimulation Only, and Motor tRNS + Training) as between-subject factors showed only a significant effect of condition (for Physical Stroop: F(2,72) = 88.8, p < 0.001; for Numerical Stroop: F(2,72) = 203.8, p < 0.001), due to the congruity effect being larger than facilitation and interference in both conditions (Physical Stroop, congruity vs facilitation: t(39) = 10.2, p < 0.001; congruity vs interference t(39) = 6.3, p < 0.001; Numerical Stroop, congruity vs facilitation: t(39) = 16.4, p < 0.001; congruity vs interference: t(39) = 9.6, p < 0.001). None of the other factors or their interaction reached significance (all p > 0.2).
Finally, performance in visual patterns recognition in the form of face processing (Pitcher et al., 2009) also did not change in accuracy or RTs following training (F(1,36) = 1.3, p = 0.27 and F(1,36) = 2.3, p < 0.1, respectively), and regardless of the group (no significant interaction of training and group in accuracy or RTs: (F(3,36) = 3.3, p = 0.8 and F(3,36) = 1.1, p = 0.3, respectively). These results therefore suggest that the improvement in numerosity discrimination and the transfer we observed in the continuous quantity discrimination tasks (Time and Space) were specific to these tasks rather than the result of a more generalized cognitive improvement (Fig. 2D).
Long-term effects of tRNS and cognitive training
To evaluate whether the improvement in number acuity was long lasting, participants' performance (indexed by wf) in the follow-up sessions was analyzed in separate repeated-measures ANOVAs for each group (Parietal tRNS + Training and Training Only) with follow-up (week 4, 8, 12, and 16) as a within-subjects factor.
In the Parietal tRNS + Training group performance in the numerosity discrimination task did not change significantly up to 16 week post-training (wf: 0.198 at post-training and 0.202 at 16 weeks post-training), as indicated by no significant effect of time post-training (F(3,18) = 0.11, p = 0.9, ns). In contrast, performance declined over time in the Training Only group (wf: 0.252 at post-training and 0.266 at 16 weeks post-training, F(3,18) = 4.7, p = 0.009). This suggests that the improvement in number acuity we observed following training was maintained long-term only when training was combined to parietal stimulation.
We also tested whether there was any long-term maintenance of the improvement observed in the time and space discrimination tasks. Separate repeated-measure ANOVAs for each group (Parietal tRNS + Training and Training Only) with follow-up (week 4, 8, 12, and 16) as within-subjects factor showed that in the Parietal tRNS + Training group performance declined after training in both space (F(3,18) = 3.6, p < 0.04) and time discrimination (F(3,18) = 2.9, p < 0.05). In the Training Only group performance in these tasks did not change after training (all p > 0.3), but rather than reflecting a stable improvement, this indicates that there was little or no change following training with no subsequent change.
Discussion
We observed a significant improvement (on average ∼18%) in performing a numerosity discrimination task following intensive and continuous repetition of the task. This improvement was significantly larger (about 33%) when training was accompanied by tRNS to brain areas that are critical for numerosity discrimination, i.e., the left and right parietal lobes. The improvement was much smaller when stimulation was not associated with cognitive training, when cognitive training was not associated with brain stimulation, or when training was coupled with stimulation to a control region (motor areas). The optimal training design consisting of cognitive training combined with parietal tRNS not only resulted in the greatest improvement of performance in the trained numerosity discrimination task, but in this improvement being retained up to 16 weeks after training. In contrast, training with no stimulation showed no such maintenance of learning.
Having established a robust improvement in number acuity following number training and parietal stimulation, we sought to test whether this improvement transferred to other untrained abilities. We specifically focused on skills that are thought to share cognitive and anatomical resources with the numerosity task, i.e., time and space discrimination (Walsh, 2003; Cantlon et al., 2009; Cantlon, 2012). Proficiency in these tasks increased significantly only when number training was associated with parietal tRNS but not in the other experimental conditions. This finding of transfer from numerosity proficiency to time and space reinforces the suggestion of a link between time, space, and number in terms of a parietal lobe-based shared magnitude system (Walsh, 2003; Cantlon et al., 2009; Cantlon, 2012). Transfer from numerosity to other quantity judgments also indicates that the improvement in the numerosity discrimination we observed is likely to reflect a change in the ability to process quantity rather than a spurious change in visual acuity or other peripheral skills that may support performance in numerosity discrimination. Further evidence that the improvement in numerosity discrimination did not reflect general cognitive enhancement is shown by lack of change in performing tasks measuring attention, executive functions, and visual pattern recognition.
Our results also showed no transfer from numerosity discrimination to arithmetical abilities, an effect predicted by theories suggesting a link between number acuity and proficiency in arithmetic (Halberda et al., 2008). This could be due to several reasons: arithmetic abilities may rely on parietal as well as frontal areas (Ischebeck et al., 2006), therefore stimulation to both these areas may be needed to enhance performance. Alternatively, numerosity discrimination may not be foundational to arithmetic (Butterworth, 2010), or it may be critical only in the developing brain, but these skills may not be so strongly linked in the adult brain (Price et al., 2012).
The issue of transfer of a trained skill to untrained ones is an exciting and much debated subject in recent training research (Boot et al., 2011). Being able to relocate trained skills is of great practical importance as it allows reducing training resources (i.e., people would not need to train on everything). Transfer is also critical in clinical and educational contexts where the overall aim is to learn or regain skills in the most generalizable possible way (Lee et al., 2012). However, previous training studies that specifically looked at the transferability of trained skills provided contradicting results as they either indicated a broad transfer from one task or modality to another (Amitay et al., 2006; Green and Bevalier, 2003; Jaeggi et al., 2008, 2011; Klingberg, 2010), or in contrast no transfer (Ball et al., 2002; Hertzog, 2009; Owen et al., 2010; Nitsche and Paulus, 2011; Lee et al., 2012). What factors may increase the chances to achieve transfer? Besides avoiding methodological pitfalls drawing to misleading conclusions (Boot et al., 2011), a number of aspects may determine successful transfer of trained skills to untrained ones, for instance, how close the trained and untrained skills are, how general are the transferable skills, and what is actually transferred, i.e., core cognitive components between trained and untrained skills or other more peripheral aspects such as the strategies that two tasks have in common or response-selection mechanisms (Boot et al., 2008, 2011; Taatgen, 2013).
Compared with previous training research, our study has several strengths that may explain why we found transfer from numerosity to other quantity discrimination tasks. First, we used only one well specified and established training task, numerosity discrimination, in association with other tasks that controlled for improvement of more generalized skills. Second, the trained tasks (numerosity discrimination) and those that benefited from the training (time and space discrimination) were carefully chosen for sharing some cognitive components in the form of quantity processing (Walsh, 2003; Cantlon et al., 2009; Cantlon, 2012), such that boosting this common processing can be expected to result in an advantage for all the tasks that are based on it (Taatgen, 2013). The third and main reason why we observed a successful transfer between numerosity and other quantity judgments is likely due to brain stimulation increasing the excitability of neurons that are shared by tasks requiring quantity judgments. tRNS alters cortex excitability by means of depolarizing the membrane resting potential rather than by directly stimulating neurons, most likely because changes in the sodium and calcium channels increase or decrease the firing rate of neurons (Terney et al., 2008; Fertonani et al., 2011), and lead to hemodynamic changes (Snowball et al., 2013). These effects have been explained in terms of the temporal summation of neural activity such that after depolarizing, the repolarization of sodium channels, which typically takes some time, can be shortened by repetitively applying random stimulation to these channels (Fertonani et al., 2011). It is conceivable that these changes in cellular excitability of number neurons (Nieder, 2005) coupled with cognitive training account for the large improvement in number acuity we observed. This would also explain why cognitive training alone (sham condition) or coupled with stimulation to brain areas not critical for number or quantity processing led to a more modest improvement. A similarly small improvement or even lack of it has been shown in other studies based on cognitive training only (Owen et al., 2010; Dewind and Brannon, 2012). It should also be emphasized that stimulation in absence of cognitive training was not sufficient to induce changes in performance similar to some previous studies (Antal et al., 2007; Galea and Celnik, 2009).
While cognitive improvements can be associated to stimulation-induced changes of the cell resting membrane potential, long-lasting effects of training are thought to be related to enduring transformation of synaptic strength of NMDA receptors, which are involved in neuroplastic changes (Liebetanz et al., 2002; Sparing and Mottaghy, 2008; Chaieb et al., 2011). We suggest that these cellular changes may support the long-term effects of tRNS that we observed in the numerosity discrimination performance, and explain why such changes were only present following parietal tRNS. Lack of cellular changes may also explain why there are no long-term effects following cognitive training in absence of stimulation (similar to our sham condition). Despite reliable long-term effects in the numerosity discrimination task, no long-term effects were shown in other quantity discrimination tasks (time and space).
In conclusion we have shown that by combining brain stimulation to critical areas with intense cognitive training, performance in a trained numerosity discrimination task can significantly improve and be maintained over time. This improvement, which might be specific for the stimulation parameters used, was considerably larger than using cognitive training or stimulation independently, or than coupling training with stimulation to brain areas not critical for quantity processing. By carefully choosing tasks sharing cognitive and neuronal components with numerosity discrimination, i.e., time and space discrimination, we also showed that tRNS and training led to significant transfer of improvement from the trained numerosity discrimination to time and space processing.
Footnotes
This work was supported by a Royal Society Dorothy Hodgkin Fellowship and Royal Society and British Academy grants. R.C.K. is supported by the Wellcome Trust (WT88378). We thank Maarten Speekenbrink for advice on statistical analysis.
R.C.K. filed a patent for an apparatus for improving and/or maintaining numerical ability. All the other authors declare no conflict of interest.
References
- Ambrus GG, Paulus W, Antal A. Cutaneous perception thresholds of electrical stimulation methods: comparison of tDCS and tRNS. Clin Neurophysiol. 2010;121:1908–1914. doi: 10.1016/j.clinph.2010.04.020. [DOI] [PubMed] [Google Scholar]
- Amitay S, Irwin A, Moore DR. Discrimination learning induced by training with identical stimuli. Nat Neurosci. 2006;9:1446–1448. doi: 10.1038/nn1787. [DOI] [PubMed] [Google Scholar]
- Antal A, Terney D, Poreisz C, Paulus W. Towards unravelling task-related modulations of neuroplastic changes induced in the human motor cortex. Eur J Neurosci. 2007;26:2687–2691. doi: 10.1111/j.1460-9568.2007.05896.x. [DOI] [PubMed] [Google Scholar]
- Ball K, Berch DB, Helmers KF, Jobe JB, Leveck MD, Marsiske M, Morris JN, Rebok GW, Smith DM, Tennstedt SL, Unverzagt FW, Willis SL. Effects of cognitive training interventions with older adults: a randomized controlled trial. JAMA. 2002;288:2271–2281. doi: 10.1001/jama.288.18.2271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barth H, La Mont K, Lipton J, Spelke ES. Abstract number and arithmetic in preschool children. Proc Natl Acad Sci U S A. 2005;102:14116–14121. doi: 10.1073/pnas.0505512102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boot WR, Kramer AF, Simons DJ, Fabiani M, Gratton G. The effects of videogame playing on attention, memory, and executive control. Acta Psychol. 2008;129:387–398. doi: 10.1016/j.actpsy.2008.09.005. [DOI] [PubMed] [Google Scholar]
- Boot WR, Blakely DP, Simons DJ. Do action videogames improve perception and cognition? Front Psychol. 2011;2:226. doi: 10.3389/fpsyg.2011.00226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butterworth B. Foundational numerical capacities and the origins of dyscalculia. Trends Cogn Sci. 2010;14:534–541. doi: 10.1016/j.tics.2010.09.007. [DOI] [PubMed] [Google Scholar]
- Cantlon JF. Math, monkeys, and the developing brain. Proc Natl Acad Sci U S A. 2012;(Suppl 1):10725–10732. doi: 10.1073/pnas.1201893109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM, Carter EJ, Pelphrey KA. Functional imaging of numerical processing in adults and 4-y-old children. PLoS Biol. 2006;4:e125. doi: 10.1371/journal.pbio.0040125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon JF, Platt ML, Brannon EM. Beyond the number domain. Trends Cogn Sci. 2009;13:83–91. doi: 10.1016/j.tics.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cappelletti M, Freeman ED, Cipolotti L. Interactions and dissociations between time, numerosity and space processing. Neuropsychologia. 2009;47:2732–2748. doi: 10.1016/j.neuropsychologia.2009.05.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cappelletti M, Freeman ED, Cipolotti L. Number and time doubly dissociate. Neuropsychologia. 2011;49:3078–3092. doi: 10.1016/j.neuropsychologia.2011.07.014. [DOI] [PubMed] [Google Scholar]
- Chaieb L, Paulus W, Antal A. Evaluating Aftereffects of short-duration transcranial random noise stimulation on cortical excitability. Neural Plast. 2011;2011:105927. doi: 10.1155/2011/105927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen Kadosh R, Lammertyn J, Izard V. Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Prog Neurobiol. 2008;84:132–147. doi: 10.1016/j.pneurobio.2007.11.001. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Levy N, O'Shea J, Shea N, Savulescu J. The neuroethics of non-invasive brain stimulation. Curr Biol. 2012;22:R108–R111. doi: 10.1016/j.cub.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dakin SC, Tibber MS, Greenwood JA, Kingdom FA, Morgan MJ. A common visual metric for approximate number and density. Proc Natl Acad Sci U S A. 2011;108:19552–19557. doi: 10.1073/pnas.1113195108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dewind NK, Brannon EM. Malleability of the approximate number system: effects of feedback and training. Front Hum Neurosci. 2012;6:68. doi: 10.3389/fnhum.2012.00068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Draganski B, Gaser C, Busch V, Schuierer G, Bogdahn U, May A. Neuroplasticity: changes in grey matter induced by training. Nature. 2004;427:311–312. doi: 10.1038/427311a. [DOI] [PubMed] [Google Scholar]
- Fan J, McCandliss BD, Sommer T, Raz A, Posner MI. Testing the efficiency and independence of attentional networks. J Cogn Neurosci. 2002;14:340–347. doi: 10.1162/089892902317361886. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke ES. Origins and endpoints of the core systems of number: reply to Fias and Verguts. Trends Cogn Sci. 2004;8:448–449. doi: 10.1016/j.tics.2004.08.010. [DOI] [PubMed] [Google Scholar]
- Fertonani A, Pirulli C, Miniussi C. Random noise stimulation improves neuroplasticity in perceptual learning. J Neurosci. 2011;31:15416–15423. doi: 10.1523/JNEUROSCI.2002-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galea JM, Celnik P. Brain polarization enhances the formation and retention of motor memories. J Neurophysiol. 2009;102:294–301. doi: 10.1152/jn.00184.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green CS, Bevalier D. Action video game modifies visual selective attention. Nature. 2003;423:534–537. doi: 10.1038/nature01647. [DOI] [PubMed] [Google Scholar]
- Halberda J, Mazzocco MM, Feigenson L. Individual differences in nonverbal number acuity predict maths achievement. Nature. 2008;455:665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Halberda J, Ly R, Wilmer JB, Naiman DQ, Germine L. Number sense across the lifespan as revealed by a massive Internet-based sample. Proc Natl Acad Sci U S A. 2012;109:11116–11120. doi: 10.1073/pnas.1200196109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henik A, Tzelgov J. Is three greater than five: the relation between physical and semantic size in comparison tasks. Mem Cognit. 1982;10:389–395. doi: 10.3758/BF03202431. [DOI] [PubMed] [Google Scholar]
- Hertzog C. Use it or lose it: an old hypothesis, new evidence, and an ongoing controversy. In: Bosworth H, Hertzog C, editors. Cognition and aging: research methodologies and empirical advances. Washington, DC: American Psychological Association; 2009. pp. 161–179. [Google Scholar]
- Ischebeck A, Zamarian L, Siedentopf C, Koppelstatter F, Benke T, Felber S, Delazer M. How specifically do we learn? Imaging the learning of multiplication and subtraction. Neuroimage. 2006;30:1365–1375. doi: 10.1016/j.neuroimage.2005.11.016. [DOI] [PubMed] [Google Scholar]
- Izard V, Sann C, Spelke ES, Streri A. Newborn infants perceive abstract numbers. Proc Natl Acad Sci U S A. 2009;106:10382–10385. doi: 10.1073/pnas.0812142106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaeggi SM, Buschkuehl M, Jonides J, Perrig WJ. Improving fluid intelligence with training on working memory. Proc Natl Acad Sci U S A. 2008;105:6829–6833. doi: 10.1073/pnas.0801268105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaeggi SM, Buschkuehl M, Jonides J, Shah P. Short- and long-term benefits of cognitive training. Proc Natl Acad Sci U S A. 2011;108:10081–10086. doi: 10.1073/pnas.1103228108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klingberg T. Training and plasticity of working memory. Trends Cogn Sci. 2010;14:317–324. doi: 10.1016/j.tics.2010.05.002. [DOI] [PubMed] [Google Scholar]
- Lee H, Boot WR, Basak C, Voss MW, Prakash RS, Neider M, Erickson KI, Simons DJ, Fabiani M, Gratton G, Low KA, Kramer AF. Performance gains from directed training do not transfer to untrained tasks. Acta Psychol. 2012;139:146–158. doi: 10.1016/j.actpsy.2011.11.003. [DOI] [PubMed] [Google Scholar]
- Liebetanz D, Nitsche MA, Tergau F, Paulus W. Pharmacological approach to synaptic and membrane mechanisms of DC-induced neuroplasticity in man. Brain. 2002;125:2238–2247. doi: 10.1093/brain/awf238. [DOI] [PubMed] [Google Scholar]
- Melby-Lervåg M, Hulme C. Is working memory training effective? A meta-analytic review. Dev Psychol. 2013;49:270–291. doi: 10.1037/a0028228. [DOI] [PubMed] [Google Scholar]
- Mulquiney PG, Hoy KE, Daskalakis ZJ, Fitzgerald PB. Improving working memory: exploring the effect of transcranial random noise stimulation and transcranial direct current stimulation on the dorsolateral prefrontal cortex. Clin Neurophysiol. 2011;122:2384–2389. doi: 10.1016/j.clinph.2011.05.009. [DOI] [PubMed] [Google Scholar]
- Nieder A. Counting on neurons: the neurobiology of numerical competence. Nat Rev Neurosci. 2005;6:177–190. doi: 10.1038/nrn1626. [DOI] [PubMed] [Google Scholar]
- Nitsche MA, Paulus W. Transcranial direct current stimulation–update 2011. Restor Neurol Neurosci. 2011;29:463–492. doi: 10.3233/RNN-2011-0618. [DOI] [PubMed] [Google Scholar]
- Owen AM, Hampshire A, Grahn JA, Stenton R, Dajani S, Burns AS, Howard RJ, Ballard CG. Putting brain training to the test. Nature. 2010;465:775–778. doi: 10.1038/nature09042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazza M, Izard V, Pinel P, Le Bihan D, Dehaene S. Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron. 2004;44:547–555. doi: 10.1016/j.neuron.2004.10.014. [DOI] [PubMed] [Google Scholar]
- Pitcher D, Charles L, Devlin JT, Walsh V, Duchaine B. Triple dissociation of faces, bodies, and objects in extrastriate cortex. Curr Biol. 2009;19:319–324. doi: 10.1016/j.cub.2009.01.007. [DOI] [PubMed] [Google Scholar]
- Price GR, Palmer D, Battista C, Ansari D. Nonsymbolic numerical magnitude comparison: reliability and validity of different task variants and outcome measures, and their relationship to arithmetic achievement in adults. Acta Psychol. 2012;140:50–57. doi: 10.1016/j.actpsy.2012.02.008. [DOI] [PubMed] [Google Scholar]
- Redick TS, Shipstead Z, Harrison TL, Hicks KL, Fried DE, Hambrick DZ, Kane MJ, Engle RW. No evidence of intelligence improvement after working memory training: a randomized, placebo-controlled study. J Exp Psychol Gen. 2013;142:359–379. doi: 10.1037/a0029082. [DOI] [PubMed] [Google Scholar]
- Sagi D, Tanne D. Perceptual learning: learning to see. Curr Opin Neurobiol. 1994;4:195–199. doi: 10.1016/0959-4388(94)90072-8. [DOI] [PubMed] [Google Scholar]
- Slagter HA. Conventional working memory training may not improve intelligence. Trends Cogn Sci. 2012;16:582–583. doi: 10.1016/j.tics.2012.10.001. [DOI] [PubMed] [Google Scholar]
- Snowball A, Tachtsidis I, Popescu T, Thompson J, Delazer M, Zamarian L, Zhu T, Cohen Kadosh R. Long-term enhancement of brain function and cognition using cognitive training and brain stimulation. Curr Biol. 2013;23:987–992. doi: 10.1016/j.cub.2013.04.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sparing R, Mottaghy FM. Noninvasive brain stimulation with transcranial magnetic or direct current stimulation—from insights into human memory to therapy of its dysfunction. Methods. 2008;44:329–337. doi: 10.1016/j.ymeth.2007.02.001. [DOI] [PubMed] [Google Scholar]
- Sternberg RJ. Increasing fluid intelligence is possible after all. Proc Natl Acad Sci U S A. 2008;105:6791–6792. doi: 10.1073/pnas.0803396105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taatgen NA. The nature and transfer of cognitive skills. Psychol Rev. 2013;120:439–471. doi: 10.1037/a0033138. [DOI] [PubMed] [Google Scholar]
- Terney D, Chaieb L, Moliadze V, Antal A, Paulus W. Increasing human brain excitability by transcranial high-frequency random noise stimulation. J Neurosci. 2008;28:14147–14155. doi: 10.1523/JNEUROSCI.4248-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh V. A theory of magnitude: common cortical metric of time, space and quantity. Trends Cogn Sci. 2003;7:483–488. doi: 10.1016/j.tics.2003.09.002. [DOI] [PubMed] [Google Scholar]
- Wassermann EM. Risk and safety of repetitive transcranial magnetic stimulation: report and recommendations from the International Workshop on the Safety of Repetitive Transcranial Magnetic Stimulation, June 5–7, 1996. Electroencephalogr Clin Neurophysiol. 1998;108:1–16. doi: 10.1016/S0168-5597(97)00096-8. [DOI] [PubMed] [Google Scholar]