Climate and Leishmaniasis in French Guiana

Abstract

To study the link between climatic variables and the incidence of leishmaniasis a study was conducted in Cayenne, French Guiana. Patients infected between January 1994 and December 2010. Meteorological data were studied in relation to the incidence of leishmaniasis using an ARIMA model. In the final model, the infections were negatively correlated with rainfall (with a 2-month lag) and with the number of days with rainfall > 50 mm (lags of 4 and 7 months). The variables that were positively correlated were temperature and the Multivariate El Niño Southern Oscillation Index with lags of 8 and 4 months, respectively. Significantly greater correlations were observed in March for rainfall and in November for the Multivariate El Niño/Southern Oscillation Index. Climate thus seems to be a non-negligible explanatory variable for the fluctuations of leishmaniasis. A decrease in rainfall is linked to increased cases 2 months later. This easily perceptible point could lead to an interesting prevention message.

Introduction

French Guiana benefits from an equatorial climate that is tempered by tradewinds. It lies in an area of East/West atmospheric circulation induced by two subtropical high pressure belts (the Azores to the North and St. Helen to the South) that clash at the intertropical convergence zone (ICZ). The ICZ sweeps over French Guiana twice a year and determines a seasonal cycle characterized by four seasons of uneven durations: a short rainy season from mid November to late January; a short dry season—the « little summer of March »—between early February and mid-March; a long rainy season from late March to late July; and a long dry season from late July to mid-November. The yearly rainfall is around 3 m on average along the seashore, and 2.5 m in the interior. Variations between years at a given site can be important. This interannual variability is in part linked to the El Nino global atmospheric circulation phenomenon, which arises in the southern Pacific. The Multivariate El Niño Southern Oscillation Index (ENSO) index allows monitoring the evolution of this phenomenon.

During El Niño periods, it is expected that the French Guianese climate will become hotter and drier, whereas during La Niña periods, it is expected that climate will be cooler and wetter.^1,2

Average temperatures are quasi constant throughout the year around 26°C (range 25.8–27.1). However, during the rainy season the temperatures are cooler and the diurnal variations lower than during the dry season. The relative humidity is always over 75% and may reach 100%. The territory's direct solar exposure, modulated by nebulosity, is on average 2,200 hours/year, and delivers a mean energy of 6 kWh/m²/day. Winds are weak to moderate throughout the year.

Leishmaniasis is a disease caused by protozoa. This parasite belongs to the Leishmania genus (Kinetoplastidae: Trypanosomatidae). Its transmission is performed by blood feeding sand flies, Phlebotomus (Diptera: Psychodidae).^3–5

Around 700 species of Phlebotomus can be found in the tropical and temperate zones around the world. The Phlebotomus genus can be found in the Old World and the Lutzomyia genus in the New World. The leishmania cycle requires the presence of an animal reservoir on which the female sand fly will infect itself during a blood meal. The transmission to a third host will take place during the blood meals following the development of the parasite in the digestive tract of the sand fly. In French Guiana, Humans are accidental hosts.^6,7 As for other vector-borne diseases, seasonal variations of the number of cases suggest a role for the climate in the transmission dynamics of leishmaniasis. In Venezuela and in Argentina, there was a correlation of vector densities and environmental variables^8,9 and a correlation between vector density and the number of cases of leishmaniasis.^8,10 The influence of interannual climatic variations linked to the El Nino phenomenon on the epidemic levels of visceral leishmaniasis have been described in Brazil.¹¹

In French Guiana, it has been reported that sunshine and ultraviolet radiation could influence the clinical presentation of leishmaniasis and the efficacy of pentamidine isethionate treatment.^12,13

Although in French Guiana it is known that there is a relationship between climate and leishmaniasis and the relationship between the two is not well characterized. The objective of this study was to investigate the correlation between climatic variations and the number of cases of leishmaniasis consulting at Cayenne General Hospital using time series.

Materials and methods

The study was observational, retrospective, ecological, and monocentric. The study population consisted of confirmed new cases of leishmaniasis diagnosed in the department of dermatology of Cayenne General Hospital for which the date of infection was between January 1, 1994 and December 31, 2010. A new case was defined by the absence of documented history of leishmaniasis in the 12 previous months before the date of consultation. The diagnosis was confirmed by the presence of Leishmania on the examination of May Grunwald Giemsa stained skin smears, or by a positive culture on RPMI medium, or by Leishmania DNA by polymerase chain reaction (PCR). The reported infection date corresponded to patients' reports of a short stay in the forest; in the absence of such information, the presumptive date of infection was estimated from the average incubation period that was 30 days before the appearance of clinical signs. The sample consisted of cases for which the infection place occurred at the geographical location defined hereafter.

The infection location was the location defined by the patient during the initial consultation. These locations where grouped by « Townships ». Military personnel, being treated by the military health system since 1998, were excluded from the sample.

The climatic variables used for the study were monthly data from Rochambeau Airport weather station between January 1993 and December 2010. The variables collected there were: Cumulated precipitation, average minimal temperature, average maximal temperature, average of average temperatures, average amplitude of temperatures, average relative humidity, number of days of rainfall > 30 mm, number of days of precipitation > 50 mm, number of days of rainfall > 100 mm.

For the study of the El Niño phenomenon, the indexes used were Multivariate El Niño/Southern Oscillation Index (MEI) and the Southern Oscillation Index (SOI) between January 1993 and December 2010 (source: National Oceanic and Atmospheric Administration [NOAA]). The MEI is a composite index calculated using six climatic variables: atmospheric pressure and air temperature at the sea level, cloud cover and zonal and southern components of winds. The positive values of the index are correlated to the El Niño episodes.

The climatic data from the Rochambeau weather station were considered to represent French Guiana. French Guiana being the size of Portugal, there could arguably have been significant weather variations between the more distant weather stations. The most distant weather stations were Maripasoula and Rochambeau. The correlation between monthly rainfall in these two stations over the 1994–2010 periods was 0.80 (P < 0.001). Therefore, we assumed it was reasonable to use the data from this weather station as a reflection of the weather in French Guiana.

The area that fit these criteria included all the townships of French Guiana.

The study sample, the geographical area and the climatic variables thus defined allowed two types of analyses:

Spearman test: univariate analysis of the link between local climatic variables and variations of the number of cases of leishmaniasis.

Study of the variation of the number of cases within a year: between 1994 and 2010, the cases of leishmaniasis were tallied for each of the 12 months within a year. The variation of these cumulated numbers was compared with the level of rainfall using Spearman's rank correlation. This analysis was done month per month and then with 1–6-month lags (lag 1 to 6). A similar procedure using averages was performed for minimal temperatures, maximal temperatures, average temperatures. The alpha risk was set at 1%.

Study of the interannual number of cases.

For each of the 17 years of the study, the cumulated number of cases was compared with the cumulated rainfall during the corresponding year and to the average of minimal/maximal, and mean temperatures. Spearman's rank correlation was used with an alpha risk set at 1%.

Time series: multivariate analysis of the link between local climatic variables and the El Niño phenomenon, and with the monthly variations of the number of cases of leishmaniasis.

An ARIMA model¹⁴ was used to evaluate the temporal relation between the El Niño phenomenon and the local climatic variables, and the monthly number of cases of leishmaniasis reported between 1994 and 2010. Before building the model, a log transformation of the case series was applied to stabilize variance.

Modeling with ARIMA involves the estimation of a series of parameters to account for the inherent dynamics in the time series, including the trends and autoregressive and moving average processes. The general model introduced by Box and Jenkins [19] includes autoregressive and moving average parameters, and explicitly includes differencing in the formulation of the model. An ARIMA (p, d, q) model comprises three types of parameters: the autoregressive parameters (p), number of differencing passes (d), and moving average parameters (q). The multiplicative seasonal ARIMA (p, d, q) (P, D, Q)'s model is an extension of the ARIMA method to time series in which a pattern repeats seasonally over time. Analogous to the simple ARIMA parameters, the seasonal parameters are seasonal autoregressive (P), seasonal differencing (D), and seasonal moving average parameters (Q). The length of the seasonal period is represented by s.

Various permutations of the order (p, d, q) (P, D, Q)s were computed, and the optimal combination of parameters using the « Akaike's information criterion (AIC) » was chosen. The smallest values of AIC were set as the standard to identify the best-fit model. Of all the models tested, the ARIMA (1,1,1) (0,1,1) model fit the data best according to the AIC. The best fitting model showed that a significant seasonal pattern explained the monthly cases of leishmaniasis.

The correlogram and partial correlogram graphs were also used to help in fixing the value of orders to include in the model. The likelihood ratio test was used to determine if inclusion of other covariates helped to improve the fit of the model.

Monthly series of climatic variables and of the El Niño phenomenon were then introduced in the ARIMA model with lags from 0 to 12 months to search for a potential link with the monthly number of cases of leishmaniasis. The studied explanatory variables were: MEI, SOI, cumulated rainfall, minimal temperatures, average temperatures, maximal temperatures, temperature amplitudes, relative humidity, and number of days of precipitation > 30 mm, 50 mm, and 100 mm. The series for which a significant association was observed during the univariate analysis (P < 0.02) were then integrated in a multivariate model. The use of a backward stepwise method was used to remove the non-significant variables from the final model (P < 0.05).

To ensure the validity of the final model, a Ljung-Box test was performed to verify that the residuals corresponded to white noise (random spread of residuals in time).

Finally, after removing the trend and the seasonal component of leishmaniasis cases and climatic variables, the average monthly correlation of residuals was tested to determine if there were periods of the year when the links described by the analysis were significantly preponderant.

Finally, to examine whether the association between weather and cutaneous leishmaniasis remains constant or whether it is particularly strong in certain months, the response and predictor time series were also modeled separately and the correlation between their residuals series at the appropriate lag were examined subsequently.

Data analysis was performed using R 2.11.1 software.

Results

Seasonality of infections: from January 1, 1994 to December 31, 2010, 1,302 cases of leishmaniasis were reported at the dermatology department of Cayenne General Hospital and were infected in the study area (excluding the military). During this period, the mean annual distribution was at the maximum 14.1 infections per month in December and at the minimum 1.5 infections per month in July.

Rainfall: The cumulated rainfall at the Rochambeau weather station between 1994 and 2010 were at a maximum in May (561 mm) and at a minimum in October (48 mm).

Temperatures: The temperatures at the Rochambeau weather station between 1994 and 2010 were at a maximum in October (32.5°C) and at a minimum in September and October (22.4°C).

Spearman's rank correlations.

Monthly average correlation between climate and infections.

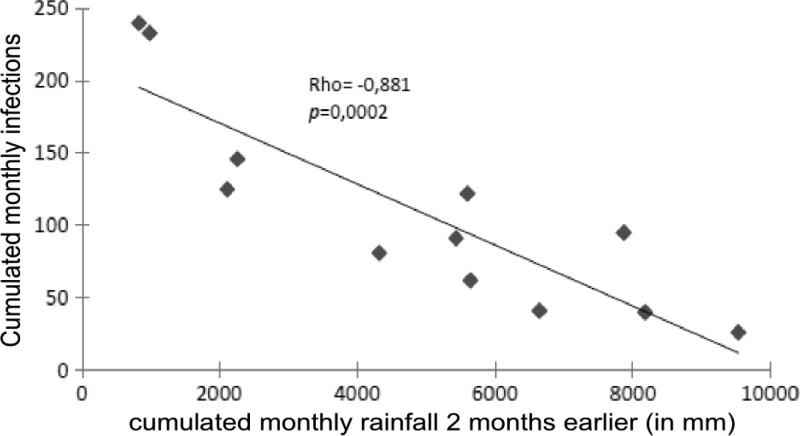
The number of infections was negatively correlated with rainfall with a 2- and 3-month lag (respective correlation coefficients −0.881 and −0.853; P < 0.001). There was also a negative correlation with the minimal temperature (2-, 3-, and 4-month lags) and a positive correlation with maximum temperature (3- and 4-month lags) (Table 1). No significant correlation was observed with the monthly average temperature (Table 1, Figure 1).

Table 1.

Monthly correlation matrix: cases of leishmaniasis/precipitation and cases of leishmanaisis/temperatures with lags from 0 to 6 months

Tested variable	Lag (months)	Correlation	P
Precipitation	Lag 0	−0.03497	0.9212
	Lag 1	−0.58042	0.0521
	Lag 2	−0.88112	0.0002*
	Lag 3	−0.85315	0.0008*
	Lag 4	−0.58741	0.0488
	Lag 5	−0.20979	0.5135
	Lag 6	0.16783	0.5960
Minimal temperature	Lag 0	0.14685	0.6431
	Lag 1	−0.36364	0.2463
	Lag 2	−0.79021	0.0036*
	Lag 3	−0.95804	< 0.0001*
	Lag 4	−0.86014	0.0006*
	Lag 5	−0.52448	0.0839
	Lag 6	−0.06993	0.8344
Maximum temperature	Lag 0	−0.19580	0.5429
	Lag 1	0.28671	0.3603
	Lag 2	0.64336	0.0269
	Lag 3	0.79021	0.0034*
	Lag 4	0.80420	0.0026*
	Lag 5	0.62937	0.0312
	Lag 6	0.31469	0.3139
Mean temperature	Lag 0	0.16783	0.5960
	Lag 1	0.53147	0.0771
	Lag 2	0.60839	0.0387
	Lag 3	0.46853	0.1244
	Lag 4	0.28671	0.3603
	Lag 5	0.13986	0.6591
	Lag 6	−0.03497	0.9212

Spearman's test, alpha = 1%.

^*Indicates significant values P < 0.01.

Figure 1.

Monthly correlations between leishmaniasis cases and rainfall 2 months earlier.

Average annual correlation between climate and number infections.

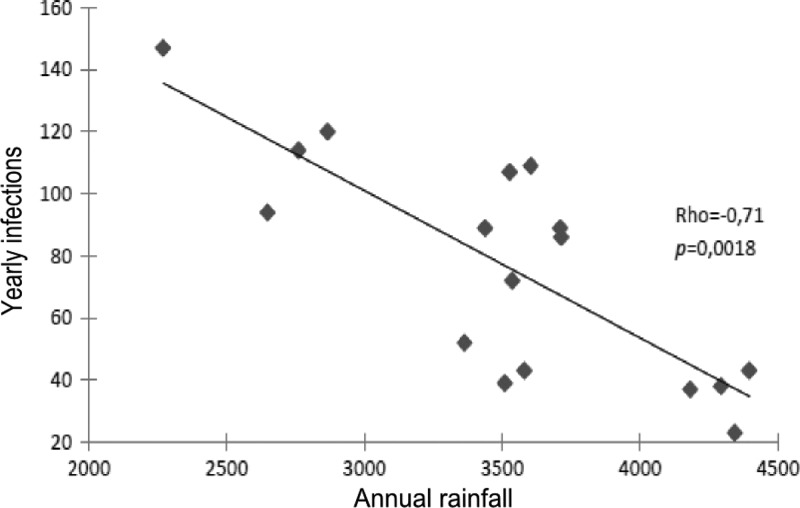
The number of annual infections were negatively correlated with rainfall, coefficient −0.71 (P = 0.0018) (Figure 2 ). No significant correlation was observed between temperature and the number of annual infections (Tables 1 and 2).

Figure 2.

Correlation between annual leishmaniasis cases and annual rainfall.

Table 2.

Correlations between annual leishmania infections, rainfall, and temperature (Spearman's rank correlation)^*

Tested variable	Correlation coefficient	P
Rainfall (annual sum)	−0.71	0.0018
Minimal temperature (annual mean)	0.45	0.0696
Maximal temperature (annual mean)	0.53	0.03
Average temperature (annual mean)	0.47	0.058

^*Spearman's rank correlation, alpha = 1%; P < 0.01.

Study of time series: multivariate analysis of the link between local climatic variables and the El Niño phenomenon with the monthly variations of the number of cases of leishmaniasis.

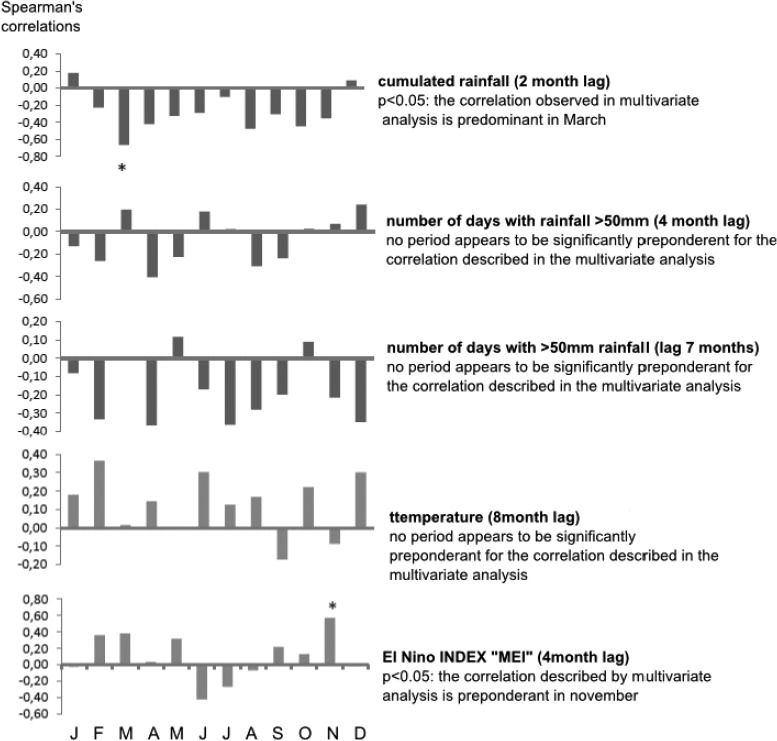
The study of time series with a monthly interval over the 1994–2010 periods shows a link between leishmaniasis and four of the climatic variables tested. In the final model, the infections were negatively correlated with rainfall (with a 2-month lag) and with the number of days with rainfall > 50 mm (lags of 4 and 7 months). The variables that were positively correlated were temperature and the MEI index with lags of 8 and 4 months, respectively. Significantly greater correlations were observed in March for rainfall and in November for the MEI (Figure 3 ). The model parameters are presented in Table 3.

Figure 3.

Monthly correlations of residuals: this analysis allowed determining whether correlations observed in the multivariate analysis were accentuated at certain periods of the year. Spearman's rank correlation, alpha = 5%.

Table 3.

Multivariate analysis of time series^*

Arima without climatic variables			(AIC = 397.4)
	Parameter	Standard deviation	P
Autoregressive term	0.76950	0.07500	0.00000
Moving average term	−0.27920	0.10730	0.00463
Seasonal moving average term	−1.00000	0.14380	0.00000
Arima with climatic variables			(AIC = 349.57)
Autoregressive term	0.57720	0.11430	< 0.00001
Moving average term	−0.11260	0.13670	0.20498
Seasonal moving average term	−0.99990	0.12030	0.00000
Cumulated rainfall (2 months lag)	−0.00100	0.00030	0.00012
Temperature (8 months lag)	0.22270	0.07820	0.00221
Number of days with > 50 mm of rain (4 months lag)	−0.06970	0.02800	0.00649
Number of days with > 50 mm of rain (7 months lag)	−0.10090	0.02840	0.00019
MEI “El Niño” index (4 months lag)	0.23910	0.08170	0.00172

^*Parameters of ARIMA models and climatic variables significantly correlated with leishmaniasis. Improvement of model by climatic variables (Akaike's information criterion [AIC] fraction): 1- (349.57/397.4) = 12% Ljung-Box white noise test: P = 0.9511.

Discussion

The study of the relation between climate and leishmaniasis showed a strong negative correlation between rainfall and the number of infections. This negative correlation persisted despite strict selection criteria (P < 0.01), which is not in itself an argument for a causal relationship but allows to posit rainfall as an indicator of risk periods at the monthly scale and the annual scale. On average, Leishmania infections increased 2 months after a relative decrease in rainfall and this correlation followed the same direction at the annual scale: dry years were years where infection numbers were greater. Cardenas and others¹⁵ showed that, in Columbia, during El Niño episodes leishmaniasis increased, whereas during La Niña periods it decreased; this is similar to the present observation. Chaves and others³ using time series analysis showed that it was possible to accurately predict leishmaniasis incidence dynamics up to 12 months before the incidence. The hypothesis of the influence of precipitation on the cycle of sand flies is supported by some entomologic observations. For instance, Galvez and others¹⁶ studied the density of Phlebotomus ariasi in the Madrid region and the density of that vector increased when rainfall decreased. Recent work by Quintana and Salomon in Argentina showed a strong negative correlation between rainfall and the abundance of sand flies.¹⁷

Unfortunately, most published studies only involve univariate analysis of climatic factors and thus take the risk of describing synchronous but possibly independent seasonal phenomenon. The advantage of ARIMA models, like the one used in this study, was to remove this seasonal component and to perform a multivariate analysis that confirms, with a similar 2-month lag, the negative correlation between rainfall and the number of infections. This is an additional argument in favor of an effect of rainfall on the cycle of sand flies. Rainfall variations seem to be an additional explanatory factor. It is possible to conjecture that important rainfall may lead to flush phlebotomine reproduction sites and temperature may condition reproduction cycles and the lifespan of sand flies.

Each geographical region has a specific climate, hosts, different vectors, and at times different Leishmania species. Thus, the extrapolation of studies conducted elsewhere to French Guiana should be cautious. However, targeted and repeated local entomological surveys at regular intervals could allow to better document the role of climate on the cycles of Lutzomyia and of Leishmania in French Guiana.

It is noteworthy that the precision of the multivariate model is only improved by 12% after the introduction of climatic variables, which implies the existence of other factors linked to the variations of the number of cases. The main hypothesis pertains to human activities in the ecotopes where the infection is acquired, but these activities (hunting, gold mining, agriculture, leisure, etc.) have fluctuations that are difficult to quantify and that are multifactoral; economic factors, climatic factors, military interventions against illegal gold mining are also relevant variables that complicate statistical modeling.

Reservoir animal species and their behaviors are also potential explanations. The Sloth, which is the main reservoir for Leishmania in French Guiana, is characterized by slow movements and frequent sleep (10 hours/day), thus the role of a migration of sloths on the number of cases seems unlikely. On the contrary, the small anteater is a nomad reservoir of Leishmania. In Brazil, it seems to be driving the geographical dispersion of L. guyanensis. Since 1990, a single study has looked at Leishmania reservoirs in French Guiana; Rotureau and others¹⁸ described the absence of Leishmania in 29 different bat species. Although these studies are costly, it seems important to update our knowledge on animal reservoirs of leishmaniasis.

To conclude, despite potential biases generated by the extrapolation of climatic data from the Rochambeau weather station and by the limitation of the sample to cases reported by the dermatology department, climate seems to be a non-negligible explanatory variable for the monthly and annual fluctuations of leishmaniasis in French Guiana. The use of ARIMA methods allowed getting more detail on the temporal relations between climate and leishmaniasis. Thus, a decrease in rainfall was linked to an increase in cases 2 months later. This easy perceptible point could lead to an interesting prevention message.