Specifications of a continual reassessment method design for phase I trials of combined drugs

Abstract

In studies of combinations of agents in phase I oncology trials, the dose–toxicity relationship may not be monotone for all combinations, in which case the toxicity probabilities follow a partial order. The continual reassessment method for partial orders (PO-CRM) is a design for phase I trials of combinations that leans upon identifying possible complete orders associated with the partial order. This article addresses some practical design considerations not previously undertaken when describing the PO-CRM. We describe an approach in choosing a proper subset of possible orderings, formulated according to the known toxicity relationships within a matrix of combination therapies. Other design issues, such as working model selection and stopping rules, are also discussed. We demonstrate the practical ability of PO-CRM as a phase I design for combinations through its use in a recent trial designed at the University of Virginia Cancer Center.

1. MOTIVATION

The primary objective of phase I trials in oncology is to find the maximum tolerated dose (MTD), defined as the highest dose that can be administered with an acceptable level of toxicity. The majority of methods for the design of these trials rely on the monotonicity assumption of the dose–toxicity curve. In this case, the curve is said to follow a ‘complete order’ because the ordering of probabilities of dose-limiting toxicity (DLT) for any pair of doses is known, and administration of greater doses of the agent can be expected to produce DLTs in increasing proportions of patients. In studies testing combinations of agents, the probabilities of DLT associated with the dose combinations often follow a ‘partial order’ in that there are pairs of dose combinations for which the ordering of the probabilities is not known. The method of Wages, Conaway, and O’Quigley (continual reassessment method for partial orders (PO-CRM)) [1] is a design for partially ordered phase I trials that combines features of the continual reassessment method (CRM) [2] and order restricted inference. This design was motivated by Conaway, Dunbar, and Peddada [3] in that it identifies possible complete orders for the toxicity probabilities that are consistent with the known orderings among the treatment combinations. Considering all possible orderings is reasonable in some studies, but generally, the number of orderings can be very large. One strategy for reducing the dimension of the problem is to, prior to the beginning of the trial, choose a small subset of orderings. Wages, Conaway, and O’Quigley [1] presented results demonstrating that choosing a subset of three orderings had good operating characteristics and was competitive with the drug combination methods of Yin and Yuan [4, 5]. In this article, we explain why choosing this subset of three orderings is insufficient for use in a broader range of scenarios than is presented in Wages et al. [1]. We outline a practical way to choose a proper subset of orderings that can be utilized regardless of the true ordering of DLT probabilities and the dimension of the drug combination space.

In addition to the issue of order selection, there are some practical design issues that were not addressed in Wages et al. [1]. For instance, PO-CRM was presented as a Bayesian method that began on the combination that investigators believed to be the closest to the target DLT rate. If the trial is investigating the safety of many combinations, it is possible to enroll the first patient cohort at a level that is too toxic. Wages, Conaway, and O’Quigley [6] presented a two-stage version of PO-CRM with an initial escalation stage beginning on the lowest combination, but that was intended for studies in which we could specify all possible complete orders associated with the partial order, which typically have a smaller number of dose levels (i.e., ≈ 6). Here, we describe a two-stage PO-CRM for a matrix of combination therapies. In this setting, we must choose a subset of possible orderings and are usually evaluating the safety of a large number of combinations (i.e., ≈ 12 – 16). The overall goal of this article is to highlight the practical ability of the PO-CRM to be used in dose–finding trials of combined drugs. To this end, we will focus on phase I design issues such as (1) two-stage designs; (2) choosing a proper subset of orderings; (3) choice of working model (skeleton) values; and (4) inclusion of stopping rules, none of which have been previously discussed in the context of using PO-CRM in a matrix of combinations. The simulation results demonstrate the ability of the PO-CRM to identify acceptable MTD combinations while significantly reducing the sample sizes that are typically needed in phase I trials of combined drugs.

2. SPECIFYING POSSIBLE DOSE–TOXICITY ORDERINGS

2.1. Strategy for a small number of orders

We begin the discussion of possible order selection with a drug combination example that appeared in Conaway, Dunbar, and Peddada [3]. This trial, discussed in Patnaik et al. [7], evaluated the safety and tolerability of Paclitaxel in combination with Carboplatin in patients with advanced solid tumors. Patients were treated with escalating doses of Paclitaxel ranging from 54 to 94.5 mg/m² and Carboplatin area under the plasma concentration versus time curve ranging from 6 to 9 mg·min/mL, every 21 days. The trial investigated the six drug combinations provided in Table I. As was discussed in [3], the toxicity ordering between some of the (Paclitaxel, Carboplatin) combinations is unknown and some are known, creating a partial order. For example, combination 2 (67.5, 6) has a larger dose of Paclitaxel and the same dose of Carboplatin as combination 1 (54, 6), so it can be assumed that combination 2 is as toxic or more toxic than combination 1, and the ordering is known between the treatments. The toxicity ordering for combinations 4 and 5 is unknown however as 4 (94.5, 6) has a larger dose of Paclitaxel and a smaller dose of Carboplatin than 5 (67.5, 7.5). Conaway, Dunbar, and Peddada [3], as well as Wages, Conaway, and O’Quigley [1, 6], discussed the idea of assessing the known and unknown orderings between the combinations and using this information to specify all possible orderings of the dose–toxicity relationship. The combinations in the trial of Patnaik et al. [7] yield six possible orderings: (1) 1–2–3–4–5–6; (2) 1–2–3–5–4–6; (3) 1–2–3–5–6–4; (4) 1–2–5–3–4–6; (5) 1–2–5–3–6–4; and (6) 1–2–5–6–3–4.

Table I.

Drug combinations used in phase I trial of Carboplatin and Paclitaxel.

Agent	Drug combination
	1	2	3	4	5	6
Paclitaxel	54	67.5	81	94.5	67.5	67.5
Carboplatin	6	6	6	6	7.5	9

One of our goals here is to present a more formal way of specifying these orderings, so that it may be practically performed regardless of the dimension of the drug combination space. To this end, consider the combinations discussed earlier displayed in a matrix, with each combination indexed by the dose level of each drug contained in the combination as in Table II. It is a reasonable assumption that the probability of toxicity for each drug increases monotonically when the other drug is being held fixed so that the DLT probabilities have a monotonic order across rows and up columns of the matrix of drug combinations. An easy way to begin formulating the possible orderings in a drug combination matrix is to order the treatments according to the rows and columns of the matrix. Denoting the probability of DLT at combination d_ij as π_ij, two complete orders of the DLT probabilities that are consistent with the partial order are the following:

Table II.

Combination labels of a phase I trial of Carboplatin and Paclitaxel.

Doses of Carboplatin	Doses of Paclitaxel
	54	67.5	81	94.5
9		d32
7.5		d22
6	d11	d12	d13	d14

• 1
  Across rows

  $${\pi }_{11}\le {\pi }_{12}\le {\pi }_{13}\le {\pi }_{14}\le {\pi }_{22}\le {\pi }_{32}$$
• 2
  Up columns

  $${\pi }_{11}\le {\pi }_{12}\le {\pi }_{22}\le {\pi }_{32}\le {\pi }_{13}\le {\pi }_{14}$$

These two orderings correspond to orderings (1) and (6), respectively, previously specified. It may be clear that we have monotonicity across rows and up columns, but we may not know the ordering between diagonal combinations in the matrix. For instance, because we increased the dosage of Carboplatin and decreased the level of Paclitaxel, the ordering between d₂₂ and d₁₃ is unknown. Therefore, another reasonable way to formulate orderings is according to the diagonals of the matrix and take account of the uncertainty of whether π₂₂ ≤ π₁₃ or π₁₃ ≤ π₂₂. We are going to consider the following four different orderings by the diagonals: (1) ordering down each diagonal; (2) ordering up each diagonal; (3) alternating up and down each diagonal beginning with down; and (4) alternating up and down each diagonal beginning with up.

• 3
  Up diagonals

  $${\pi }_{11}\le {\pi }_{12}\le {\pi }_{13}\le {\pi }_{22}\le {\pi }_{14}\le {\pi }_{32}$$
• 4
  Down diagonals

  $${\pi }_{11}\le {\pi }_{12}\le {\pi }_{22}\le {\pi }_{13}\le {\pi }_{32}\le {\pi }_{14}$$
• 5
  Alternating down-up diagonals

  $${\pi }_{11}\le {\pi }_{12}\le {\pi }_{22}\le {\pi }_{13}\le {\pi }_{14}\le {\pi }_{32}$$
• 6
  Alternating up-down diagonals

  $${\pi }_{11}\le {\pi }_{12}\le {\pi }_{13}\le {\pi }_{22}\le {\pi }_{32}\le {\pi }_{14}$$

These four orderings correspond to orderings (2), (5), (4), and (3), respectively, previously specified. These are the six possible complete orders associated with this partial ordering. This technique can be applied to the phase I combination trial of Berenson et al. [8] to formulate the five possible orderings (1 order is repeated) given in Wages, Conaway, and O’Quigley [1], as well as to the trial of Ranson et al. [9] to formulate the six possible orderings described in Wages, Conaway, and O’Quigley [10]. If there is a small number of combinations (≈6 – 8) and a small number of possible orderings (≤ 6), then this method of specifying orderings will generate all possible complete orders associated with the partial. Obviously, there can be trials that investigate a large number of combinations (i.e., ≈12–16) and have many possible orderings so that it will not be feasible to consider all of them.

2.2. Strategy for a large number of orders

We extend the strategy from the previous section into studies with a large number of orders. There are two motivating examples of this work, recently FDA approved, phase I combination trials were designed at the University of Virginia Cancer Center. We present one of those examples here. The trial design described in this article was implemented in these trials. The example is a phase I trial designed to determine the MTD of a combination of a toll-like receptor (TLR) agonists with or without a form of incomplete Freund’s adjuvant (IFA) for the treatment of melanoma. TLR, denoted 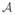, had four dose levels, and IFA had three subgroups: 0—IFA is not administered with any vaccine, V1—IFA is administered with just the first vaccine, and V6—IFA is administered in all vaccines. Therefore, there exist a total of 12 combinations, {d₁₁, d₁₂, d₁₃, d₂₁, …, d₄₂, d₄₃} under consideration, creating a 4×3 matrix order. The treatments are labeled in Table III.

Table III.

Combination labels for a toll-like receptor and incomplete Freund’s adjuvant forming a 4 × 3 matrix order.

Doses of	IFA
	0	V1	V6
4	d41	d42	d43
3	d31	d32	d33
2	d21	d22	d23
1	d11	d12	d13

IFA, incomplete Freund’s adjuvant.

We are going proceed by using movement across rows, up columns, and along diagonals, as outlined in the previous section, as a basis for choosing our subset of orderings. In an attempt to reduce the dimension of the problem, we need some practical way to arrange the combinations according to the diagonals of the matrix, no matter its dimension. We are going to rely on the technique described earlier and restrict our attention to only moving across rows, up columns, and up or down any diagonal.

In general, suppose there are M possible complete orders for the DLT probabilities associated with the combinations. It is only feasible for us to choose a subset of S possible orderings, indexed by s; s = 1, …, S. For any matrix of combinations, we recommend selecting the following subset of S = 6 orderings. Here, they are displayed in terms of the motivating example.

• s = 1: Across rows

  $${\pi }_{11}\le {\pi }_{12}\le {\pi }_{13}\le {\pi }_{21}\le {\pi }_{22}\le {\pi }_{23}\le {\pi }_{31}\le {\pi }_{32}\le {\pi }_{33}\le {\pi }_{41}\le {\pi }_{42}\le {\pi }_{43}$$
• s = 2: Up columns

  $${\pi }_{11}\le {\pi }_{21}\le {\pi }_{31}\le {\pi }_{41}\le {\pi }_{12}\le {\pi }_{22}\le {\pi }_{32}\le {\pi }_{42}\le {\pi }_{13}\le {\pi }_{23}\le {\pi }_{33}\le {\pi }_{43}$$
• s = 3: Up diagonals

  $${\pi }_{11}\le {\pi }_{12}\le {\pi }_{21}\le {\pi }_{13}\le {\pi }_{22}\le {\pi }_{31}\le {\pi }_{23}\le {\pi }_{32}\le {\pi }_{41}\le {\pi }_{33}\le {\pi }_{42}\le {\pi }_{43}$$
• s = 4: Down diagonals

  $${\pi }_{11}\le {\pi }_{21}\le {\pi }_{12}\le {\pi }_{31}\le {\pi }_{22}\le {\pi }_{13}\le {\pi }_{41}\le {\pi }_{32}\le {\pi }_{23}\le {\pi }_{42}\le {\pi }_{33}\le {\pi }_{43}$$
• s = 5: Alternating down-up diagonals

  $${\pi }_{11}\le {\pi }_{12}\le {\pi }_{21}\le {\pi }_{31}\le {\pi }_{22}\le {\pi }_{13}\le {\pi }_{23}\le {\pi }_{32}\le {\pi }_{41}\le {\pi }_{42}\le {\pi }_{33}\le {\pi }_{43}$$
• s = 6: Alternating up-down diagonals

  $${\pi }_{11}\le {\pi }_{21}\le {\pi }_{12}\le {\pi }_{13}\le {\pi }_{22}\le {\pi }_{31}\le {\pi }_{41}\le {\pi }_{32}\le {\pi }_{23}\le {\pi }_{33}\le {\pi }_{42}\le {\pi }_{43}$$

The design outlined in this paper can certainly accommodate other subset sizes consisting of alternative orderings, should we have some ordering information at our disposal. If, however, the only information we have is the assumption of a monotonicity across rows and up columns of the matrix, then we can use the methods outlined in the subsequent section based on this ’default’ subset of six orderings and have confidence in its performance (see simulation results). The dimension of the problem makes it difficult to practically consider much more information than what we have captured in these six orderings. We have provided a way of choosing a reasonable subset that is consistent with the partially known ordering information among combination, and that is independent of the dimension of the matrix. Plus, because we have demonstrated that this technique generates all possible complete orders in ’smaller’ combination trials, it is one that is generalizable to a wide range of drug combination studies.

In Wages, Conaway, and O’Quigley [1], the performance of PO-CRM was compared with that of both the latent contingency approach of Yin and Yuan [4] and the copula regression approach of Yin and Yuan [5]. Wages et al. [1] selected a subset of three orderings based on the diagonals of the combination matrix. For each scenario presented in [1, 4, 5], the true ordering of the toxicity probabilities was close to being ordered along the diagonals. In many of the scenarios, in and around the MTD combinations, at least one of the three orderings chosen for investigation matched the true ordering of toxicity probabilities. If the true DLT probabilities have this feature, the three orderings outlined in Wages et al. [1] could be used, and performance would likely be quite good. The set of the aforementioned six orderings has nearly identical performance in using the three orderings in Wages et al. [1] in these situations because it contains the subset of three ’diagonal’ orders. So, we do not lose anything by including the extra three orderings in our subset. However, if the true situation is an ordering along the rows or columns of the matrix, or some more unconventional ordering, performance diminishes when using only three ‘diagonal’ orders. On the other end of this spectrum is the idea of choosing more orderings to be in subset in the hopes of increasing the chances that the ‘correct’ one is included. To address these questions, we performed simulations comparing the choice of three versus six versus nine orderings in the subset. In most cases, the performance with the use of S = 6 was very close to that of S = 3; however, there were a few situations where S = 6 exhibited better performance. There were no scenarios in which S = 9 outperformed the other subset sizes, and we would expect performance to diminish as we continue to increase the value of S. There were no cases in which S = 6 performed worse than S = 3. In Appendix A (available online as Supporting Information), we have provided simulation results for several scenarios demonstrating a stronger performance using six orderings as opposed to three in a 4 × 4 matrix of combination therapies. These differences could be magnified as the dimension of the drug combination space grows. This subset of six orderings seems to strike the appropriate balance between choosing enough orderings so that we include one that is close to correct in the neighborhood of the MTD combination, without increasing the dimension of the problem so much so that we diminish the performance.

3. CHOICE OF SKELETON

As has been discussed within the context of CRM, it is necessary to take into account the impact that the choice of skeleton has on operating characteristics. Preferably, the skeleton values would be chosen in such a way that represents the clinician’s beliefs regarding the DLT probabilities at each dose level. Unfortunately, in practice, investigators have little or no information as to whether a selected skeleton is sensible because the true dose–toxicity curve is unknown. Further, the difficulty in specifying a skeleton is compounded by the fact that there is an absence of preceding information on a new drug being investigated, yielding a much uncertainty in providing a skeleton. It is difficult to have an investigator provide his or her best initial guess of the DLT probability at each dose, especially in the case where there are many drug combinations to consider.

O’Quigley and Zohar [11] indicate that ‘reasonable’ skeletons will have adequate spacing between values at adjacent levels. In this case, operating characteristics of CRM designs should be adequate. Specifying skeletons with adequate spacing on the interval (0,1) can be more challenging when there are many combinations. We can rely on the algorithm of Lee and Cheung [12] to generate adequate spacing between skeleton values at neighboring combinations, without having to rely on a clinician’s estimate at every combination. The algorithm of Lee and Cheung [12] requires four pieces of information in order to generate the skeleton; the prior MTD (ν), the target toxicity rate, θ, the number of combinations, d, and the value of the indifference interval half-width, δ. It is necessary to ensure that there is enough spacing both below and above the prior MTD (i.e., target value). Therefore, we recommend placing the prior MTD, ν, at a combination close to the middle dose levels, so that there is an approximately equal number of combinations below and above the prior MTD. Prior MTDs placed toward the boundary of the dose space will not produce skeletons with adequate spacing when there are many combinations being investigated. For instance, a prior MTD of ν = 6 was used to generate the skeleton implemented in the simulation results that investigated toxicity scenarios with 12 combinations. Using the required information, we can generate skeleton values using the getprior function in R package dfcrm. (i.e., getprior(δ, θ, ν, d)). We simply need to specify skeleton values at each combination that are adequately spaced, and adjust them to correspond to each of the possible orderings, in order for PO-CRM to have good performance in terms of identifying an MTD.

4. DOSE ESCALATION

4.1. Stage I

In Wages, Conaway and O’Quigley [1], the PO-CRM is presented in a Bayesian framework, where the trial begins at the combination believed by the investigator to be the closest to the target. Wages, Conaway, and O’Quigley [6] made the case for using an initial escalation stage in drug combination trials and discussed the need for a variant of the traditional escalation schemes because, in partially ordered trials, the most appropriate dose to which the trial should escalate could consist of more than one treatment combination. A specification for two-stage PO-CRM is how to rapidly escalate in the early part of the trial, which is based on how many patients to include in each cohort of the initial escalation scheme. This could be performed in groups of one, two, or three patients and we assess the impact of various cohort sizes in our simulation results.

In the first stage, we make use of ‘zoning’ the matrix of combinations according to the diagonals of the matrix in Table III. The trial could begin in zone Z₁ = {d₁₁}, and the first cohort of patients be enrolled on this ‘lowest’ combination. At the first observation of a toxicity in one of the patients, the first stage is closed, and the second stage, based on CRM modeling for partial orders (see later text), is opened. As long as no toxicities occur, cohorts of patients are examined at each dose within the currently occupied zone before escalating to the next highest zone. If d₁₁ was tried and deemed ‘safe’, the trial would escalate to zone Z₂ = {d₁₂, d₂₁}. If more than one dose is contained within a particular zone, we can sample without replacement from the doses available within the zone. Therefore, the next cohort is enrolled on a dose that is chosen randomly from d₁₂ and d₂₁. The trial is not allowed to advance to zone Z₃ = {d₁₃, d₂₂, d₃₁} in the first stage until a cohort of patients has been observed in all combinations in Z₂. This procedure continues until a toxicity is observed or all available zones have been exhausted. Subsequent to a DLT being observed, the second stage of the trial begins.

4.2. Stage II

Wages, Conaway, and O’Quigley [6] proposed a two-stage method for phase I trials involving partial orders, in which it was feasible to formulate all possible complete orders. Here, we extend this method into the setting of drug combination matrices, where we must consider a subset of possible complete orders. In general, suppose we choose a subset of S complete orders. Consider a trial investigating two agents, A and B. In general, suppose A has m dose levels, and B has p dose levels, so that there are m × p combinations, {d₁₁, …, d_mp} being studied. Let Y be a binary random variable, where 1 denotes the observation of a DLT. For a particular ordering, s, we model the true DLT probability, π_ij, at combination d_ij using a class of models ψ_s(d_ij, a), s = 1, …, S so that

$${\pi }_{ij}\approx {\psi }_s(d_{ij},a)={[{\alpha }_{ij}(s)]}^{a}i=1,\dots ,m;j=1,\dots ,p;s=1,\dots ,S$$ (1)

where {α₁₁(s), …, α_mp(s)} is the skeleton of the model under ordering s and 0 < a < ∞. We let the plausibility of each ordering be described by a set of prior probabilities p (s) = {p(1), …, p(S)}, where p (s) ≥ 0 and Σ_s p (s) = 1. The simplest case where we take p (s) = 1=S works well in practice and is suggested in the absence of information as to which order(s) may be more likely. The combination for the kth entered subject, X_k, is a random variable taking values x_k ∈{d₁₁, …, d_mp}; k = 1, …, n. After inclusion of the first k patients into the trial and observation of at least one DLT, if the data are to be analyzed under ordering s, then the log-likelihood can be written as

$${\mathcal{L}}_{sk}(a)=\sum _{\ell =1}^k{y}_{\ell }log{\psi }_s(x_{\ell },a)+\sum _{\ell =1}^k(1-y_{\ell })log(1-{\psi }_s(x_{\ell },a)),$$ (2)

which is maximized at â_sk. Having taken some value for s, the dose to be given to the (k + 1)th patient, x_k+1, is determined. Thus, we need some value for s so we weight each of the S candidate orderings as we make progress. A plausible choice for ordering weights is then given by

$${\omega }_k(s)=\frac{exp\{{\mathcal{L}}_{sk}({\widehat{a}}_{sk})\}p(s)}{{\displaystyle \sum _{s=1}^S}exp\{{\mathcal{L}}_{sk}({\widehat{a}}_{sk})\}p(s)}.$$

When a new patient is to be enrolled, we choose a single ordering, h, such that

$$h=arg\underset{s}{max}{\omega }_k(s),s=1,\dots ,S.$$

If there is a tie between the weight of two or more orderings, we randomly choose from among the tied orders. Given h, allocate the next patient to the dose combination x_k+1 = d_ij such that

$$x_{k+1}=arg\underset{d_{ij}}{min}\mid {\psi }_h(d_{ij},{\widehat{a}}_{hk})-\theta \mid ;i=1,\dots ,m;j=1,\dots ,p$$

for some target DLT rate θ. For trials subject to partial orders, there may be more than one combination with DLT probability closest to the target. If there is a ‘tie’ between two or more combinations, the patient will be randomized to one of the combinations with DLT probability closest to the target. The trial stops once enough information accumulates about the MTD.

4.3. Stopping the trial

There have been several publications over the last 20 years that explore stopping rules with CRM designs in phase I trials. The rule described by O’Quigley et al. [2] is based on confidence interval estimation, which indicates whether enough precision is present in order to stop the study early. This rule was theoretically validated by Shen and O’Quigley [13] and studied further by Heyd and Carlin [14]. A major shortcoming of a confidence interval-based rule is that a desired, conventional level of precision would necessitate many more patients than are typically available in phase I study. Consequently, it is unlikely that the trial would stop before a predetermined fixed sample size has been exhausted.

Another approach to stopping rules was suggested by O’Quigley and Reiner [15], which was based on binary outcome trees. This rule was based on the notion that continuing the trial would not lead to a change in the recommendation of the MTD with high probability. The drawback of this rule is that it requires computationally intensive combinatorial calculations and the use of computer algorithms. The idea underlying this approach arises from the convergence properties of the CRM. The method will converge to some level, and the rest of the available patients should be included at this level, which lead to a simple rule proposed by Korn et al. [16]. The rule is to stop when the dose recommended to the next patient has already been allocated a fixed number of times. For the sake of simplicity, this is the stopping rule we implement in this article.

In the first stage, the design will stop if escalation proceeds to the highest combination, and n_t patients are treated with no DLT on the highest combination d_mp. In this case, combination d_mp is declared the MTD. In the second stage, if the recommendation is to assign the next patient to a combination that already has n_t patients treated on the combination, the study is stopped and the recommended combination is declared the MTD. The simulations in the following section present results based on the stopping rule of n_t = 6 patients being already treated on a combination for the example discussed in Section 2.2. In Appendix B, we present simulation results run with n_t = 9. In general, making it so that the trial is ‘easier to stop’ will result in smaller sample sizes and fewer toxicities per trial on average but also in a smaller percentage of trials that recommended an ‘acceptable toxicity’. Our goal in the simulation results is not to recommend a stopping rule for combinations but rather to simply highlight the ability of the PO-CRM to recommend, as the MTD, combinations with acceptable toxicity based on a stopping rule such as the one chosen by the investigators of the example provided.

5. SIMULATION STUDIES

We examine the performance of the PO-CRM in six toxicity scenarios for the example outlined in Section 2.2 involving the 12 combinations, d₁₁, …, d₄₃, labeled in Table III. The true DLT rates for each of the scenarios (1–6) are provided in Table IV. The primary objective of the trial is to recommend a combination with a DLT rate closest to 0.20, keeping in mind that there may be more than one. However, selecting combinations with DLT rates that are within a certain range of target is still acceptable. To this end, Table IV highlights any combination with a DLT rate within 0.05 of the target rate, and we henceforth refer to these combinations as ‘acceptable’. The scenarios reflect a range of situations, with acceptable combinations beginning at the highest level of the drug combination matrix in Scenario 1 and moving down and left in the dose space as we go to Scenario 6. Scenarios 1 and 6 contain one acceptable combination, Scenarios 2 and 4 contain two acceptable combinations, and Scenarios 3 and 5 contain three acceptable combinations.

Table IV.

True dose-limiting toxicity probability scenarios 1–6 for the treatment combinations. Combinations with dose-limiting toxicity probabilities between 0.15 and 0.25 are in boldface.

Doses of	IFA
	0	V1	V6	0	V1	V6
	Scenario 1			Scenario 2
4	0.08	0.10	0.20	0.12	0.22	0.36
3	0.04	0.06	0.08	0.09	0.13	0.20
2	0.02	0.04	0.06	0.06	0.08	0.11
1	0.01	0.02	0.04	0.02	0.04	0.08
	Scenario 3			Scenario 4
4	0.30	0.36	0.42	0.33	0.44	0.55
3	0.16	0.23	0.28	0.29	0.35	0.42
2	0.08	0.14	0.20	0.12	0.20	0.33
1	0.03	0.06	0.12	0.04	0.10	0.18
	Scenario 5			Scenario 6
4	0.45	0.55	0.70	0.60	0.70	0.80
3	0.30	0.40	0.55	0.38	0.45	0.52
2	0.20	0.33	0.42	0.10	0.20	0.31
1	0.15	0.20	0.28	0.01	0.04	0.07

IFA, incomplete Freund’s adjuvant.

We implemented the subset of six complete orders described in Section 2 to model toxicity, and we incorporate a uniform prior distribution, p (s) = 1=6, s = 1, …, 6, on the orderings. The probability of dose-limiting toxic response is modeled via the power model (1) with the skeleton values generated according to the algorithm of Lee and Cheung [12] using a half-width value of δ = 0.04, a prior MTD of ν = 6 and a target of θ = 0.20. The location of these skeleton values were adjusted in order to correspond to the six orderings as in Table V using the getwm function in R package pocrm. We investigated the impact of using other skeletons on the operating characteristics of PO-CRM, and results indicating robustness to the choice of skeleton are provided in Appendix B.

Table V.

Skeleton values for six working models of toxicity probabilities. The values were generated using ‘getprior(0.04,0.20,6,12)’ in R package ’dfcrm’. The location of the values were adjusted to correspond to each of the possible orderings using the ‘getwm’ function in R package ‘pocrm’.

Order	Twelve treatment combinations
	d11	d12	d13	d21	d22	d23	d31	d32	d33	d41	d42	d43
s = 1	0.004	0.01	0.03	0.07	0.13	0.20	0.29	0.38	0.47	0.55	0.63	0.70
s = 2	0.004	0.13	0.47	0.01	0.20	0.55	0.03	0.29	0.63	0.07	0.38	0.70
s = 3	0.004	0.03	0.20	0.01	0.13	0.47	0.07	0.38	0.63	0.29	0.55	0.70
s = 4	0.004	0.01	0.07	0.03	0.13	0.29	0.20	0.38	0.55	0.47	0.63	0.70
s = 5	0.004	0.01	0.20	0.03	0.13	0.29	0.07	0.38	0.63	0.47	0.55	0.70
s = 6	0.004	0.03	0.07	0.01	0.13	0.47	0.20	0.38	0.55	0.29	0.63	0.70

We investigated three different sets of design specifications.

1. PO-CRM (A). The stopping rule defined in Section 4.3 was used with n_t = 6. The maximum sample size was n_max = 36 patients. Single-patient cohorts are used in Stages I and II.

2. PO-CRM (B). The stopping rule defined in Section 4.3 was used with n_t = 6. The maximum sample size was n_max = 36 patients. Two-patient cohorts are used in Stage I. Single-patient cohorts are used in Stage II.

3. PO-CRM (C). No stopping rule was used, and each trial exhausted the maximum sample size of n_max = 36 patients. Single-patient cohorts are used in Stages I and II.

We also generated results for a two-stage CRM for a fixed sample size of n_max = 36 patients, using single-patient cohorts. For the CRM, we assume that we completely know the ordering for all combinations under consideration, so it serves as a benchmark for how well the PO-CRM can perform. It is unreasonable to expect an approach for a partially known toxicity order to perform as well one that assumes a completely known order. Yet, our method reduces to the CRM when the toxicity order is completely known with respect to dose; hence, a direct comparison is useful in assessing how much information is lost as a result of not having a completely known ordering.

For each scenario, 2000 simulated trials were run, and the performance of the PO-CRM is summarized in Table VI. The table reports the proportion of trials in which the two-stage PO-CRM recommends a combination with a DLT rate within 0.05 of the target. This window indicates that a method is performing well in that for the sample sizes given in Table VI (≈20 – 36), we cannot expect a method to be able to distinguish between combinations with DLT rates within a few percentage points of one another. Our results include the proportion of patients allocated to combinations in this range of probabilities as well. The distribution of MTD combination selection and patient allocation across all combinations for PO-CRM (A) can be found in Appendix C. Table VI also gives the mean number of patients enrolled on each trial and the overall observed proportion of DLTs induced. Simulations were carried out using the functions of R package pocrm. The CRM simulations were generated using the dfcrm package in R with a skeleton of getprior(0.04, 0.20, 6, 12).

Table VI.

Summary statistics for the PO-CRM & CRM based on 2000 simulated trials of scenarios 1–6. For target θ = 0.20 and a maximum sample size of n_max = 36, the table reports (1) proportion of MTD selection for combinations within ± 0.05 of θ, (2) proportion of patients allocated to combinations within ± 0.05 of θ, (3) mean # of patients enrolled and (4) proportion of observed DLT’s.

	Scenario
	1	2	3	4	5	6
Design specifications	Proportion of MTD selection within ± 0.05 of θ
PO-CRM (A)	0.55	0.32	0.43	0.36	0.63	0.37
PO-CRM (B)	0.42	0.29	0.40	0.33	0.70	0.34
PO-CRM (C)	0.56	0.40	0.50	0.45	0.64	0.44
CRM	0.57	0.39	0.52	0.52	0.70	0.49
	Proportion of allocation within ± 0.05 of θ
PO-CRM (A)	0.18	0.21	0.33	0.28	0.52	0.20
PO-CRM (B)	0.10	0.13	0.29	0.27	0.61	0.18
PO-CRM (C)	0.35	0.26	0.38	0.34	0.60	0.29
CRM	0.36	0.24	0.38	0.39	0.68	0.31
	Mean number of patients enrolled
PO-CRM (A)	20.9	21.5	19.8	18.4	15.2	18.8
PO-CRM (B)	27.2	24.0	20.8	18.2	14.2	19.7
PO-CRM (C)	36.0	36.0	36.0	36.0	36.0	36.0
CRM	36.0	36.0	36.0	36.0	36.0	36.0
	Observed proportion of toxicity
PO-CRM (A)	0.08	0.13	0.18	0.22	0.26	0.22
PO-CRM (B)	0.07	0.11	0.15	0.18	0.24	0.18
PO-CRM (C)	0.11	0.15	0.18	0.21	0.24	0.21
CRM	0.11	0.14	0.17	0.20	0.22	0.20

PO-CRM, continual reassessment method for partial orders.

In general, it is clear from examining Table VI that the PO-CRM is performing well in terms of recommending acceptable combinations as well as treating patients at acceptable combinations. Scenarios 1 and 5 are those with the strongest performance for PO-CRM (A), yielding MTD recommendation for acceptable combinations in more than half of the simulated trials based on the data from between 15 and 21 patients, on average. The lowest MTD selection proportions for ‘acceptable’ combinations for PO-CRM (A) occur in Scenarios 2, 4, and 6, with probabilities of 0.32, 0.36, and 0.37, respectively. Although, they are lower than the other scenarios, these recommendation proportions were achieved with an average of between 18 and 22 patients, which are small trial sizes for drug combinations. These proportions increase with the inclusion of more patients in PO-CRM (C). In most scenarios and design specifications, the observed proportion of toxicity is close to the target DLT rate of 0.20. One exception occurs in Scenario 1 with an observed DLT rate of approximately 0.10, which is expected because all combinations are safe with true DLT rates at or below 0.20. Another exception occurs in Scenario 5 with observed proportion slightly higher than the target rate, which is also not unexpected because of the overly toxic nature of the true DLT rates in this scenario. Overall, the simulation results indicate that the PO-CRM is a practical design for dose-finding in a matrix of combination therapies.

The results for PO-CRM (A) and (B) highlight the trade-offs using a single-patient cohort versus two-patient cohort in Stage I. For some scenarios (2, 3, 4, and 6), the results are very similar. For others, the size of patient cohorts in Stage I has an impact on performance. For instance, in Scenario 1, PO-CRM (A) recommends an acceptable combination as the MTD in 55% of trials, whereas PO-CRM (B) does so in 42%. The MTD in Scenario 1 is the highest combination of the 12considered, making it possible to test many of the available combinations before we ever reach the MTD. Using single-patient cohorts, we will escalate more rapidly through lower combinations, allowing us to reach combinations around the MTD more quickly. By contrast, using two-patient cohort in this scenario will use up too many patients at suboptimal levels, which results in the diminished performance that is evident in the selection and allocation proportions of Scenario 1 in Table VI. On the other hand, in Scenario 5, the location of acceptable combinations is at the lower end of the drug combination matrix. In this case, PO-CRM (B) outperforms PO-CRM (A) in both selection and allocation proportions. Single-patient cohorts may escalate too quickly, so a more conservative two-patient cohort may be desirable in the presence of potentially toxic combinations. Overall, single-patient cohorts do at least slightly better in five of the six scenarios studied. Because drug combination trials are likely to have many levels to test, our recommendation would be to use single-patient cohorts in order to minimize the number of patients treated in the initial stage and maximize the number of patients used in the modeling stage. After all, the initial stage is simply a start-up phase until the first DLT, implemented because some investigators may be uncomfortable beginning at high dose without first testing low doses. However, if investigators feel it more appropriate to be conservative because of reservations about toxicity at lower levels, the use of two-patient cohort in the initial stage still has desirable operating characteristics across a broad range of scenarios.

The CRM, which assumes a completely known dose–toxicity ordering, provides a valuable assessment benchmark in evaluating how well a design for partial orders can possibly perform. It can be used as an upper bound for performance because we cannot expect a CRM design with a partially known ordering to outperform a CRM design with a fully known ordering, especially because the CRM has been shown to have excellent properties in terms of identifying the MTD in trials of a single agent [17]. In Scenario 2, PO-CRM (A) recommends an acceptable combination in only 32% of simulated trials, with an average trial size of 21.5 patients. However, the recommendation percentage of CRM is only 39% with a trial size of 36 patients, which provides a measure for what we can expect to be able to achieve. Even though PO-CRM only recommended acceptable combinations 32% of the time, the CRM benchmark tells us that it is possible to have only gained a few percentage points had we included approximately 15 more patients into the trial. In Scenario 1, PO-CRM (C) selects, as the MTD, an acceptable combination in 56% of simulated trials after a fixed sample size of 36 patients. The CRM based on a fully known ordering yields only a small gain recommending an acceptable combination in 57% of trials. In fact, in Scenarios 1–3, the MTD selection proportions are very close to that of the CRM. In Scenarios 4–6, there is a bit more separation between these respective proportions, but the largest difference is only 0.07 (Scenario 4). Consequently, for these scenarios, it can be argued that the potential for improvement of the POCRM is limited.

6. CONCLUDING REMARKS

In this article, we demonstrated the practical ability of PO-CRM to effectively estimate acceptable combinations in phase I clinical trials of two agents by addressing practical issues that have not been previously addressed when discussing PO-CRM as a viable phase I design for combinations. In these trials, the toxicity order of the combinations is usually not fully known, and PO-CRM requires the formulation of possible dose–toxicity orderings between the combinations. In general, there can be too many orderings to reasonably consider all of them in the method. We have provided a practical means of selecting a reasonable subset of orderings that can be implemented in a broad range of trials, regardless of the dimension of the drug combination space. The manuscript and appendices contain simulation results indicating that, in terms of identifying acceptable combinations, the CRM for partial orders performs well for 4 × 3 and 4 × 4 matrix orders. We also have results implementing our method with these six orderings on higher dimensions, such as 5 × 5 and 6 × 6, and we are happy to share these results with any interested reader.

A criticism of the PO-CRM has been that the investigator must provide some skeleton value for every combination, the number of which can typically be large. This article demonstrates that, after choosing the prior MTD to be somewhere close to the middle of the dose-combination space, we can rely on the algorithm of Lee and Cheung [12] to provide skeleton values with adequate spacing between adjacent levels. This is demonstrated by the skeleton robustness analysis of Appendix B. The creation of R package pocrm has simplified the process of skeleton specification for implementing PO-CRM. We only need to specify the subset of possible orderings and an increasing vector of skeleton values for the getwm function to generate a set of skeletons that corresponds to each of the possible orderings being considered (see Table V). Also, this paper addresses the issue of stopping rules. Although we make no recommendation on any one stopping rule, our simulation results demonstrate the ability of PO-CRM to recommend as the MTD and allocate patients to combinations with acceptable toxicity, using sample sizes smaller than have been typically reported in the previous literature on drug combination methods [1, 4, 5].

Most existing methods for combinations of agents address the need to reduce the dimension of the problem. As suggested by a reviewer, one approach of doing this is to restrict attention to a subset of combinations for which the ordering is known. For instance, we could choose an ordered subset by going up the first column and along the top row of the drug combination matrix. In Scenario 1, this would create a set of six ordered doses with true DLT probabilities {0.01, 0.02, 0.04, 0.08, 0.10, 0.20}, upon which we could run CRM and performance would likely be quite good. However, in Scenarios 4 and 6, this approach would produce a set with no doses having true DLT probability within ± 5% of the target 0.20, making it impossible to recommend an acceptable dose as the MTD. The problem with this strategy is that it limits the number of combinations being considered, which can run the risk of excluding all acceptable doses from being tested.

Finally, if for some reason, we happen to know the ordering of all combinations, our method reduces to the CRM, which is easily understood by clinicians and review boards. The selection of acceptable doses as the MTD, based on the CRM for a fully known true ordering, yields only a small gain relative to MTD prediction based on a partially known ordering. PO-CRM can be carried out via the use of an R package. We have tested our method in extensive simulation studies, of which only a small part is presented here. Overall, the strong showing of our method in extensive simulation studies make us feel confident in recommending it for practical use.