Application of a whole-body pharmacokinetic model for targeted radionuclide therapy to NM404 and FLT

Abstract

Introduction

We have previously developed a model that provides relative dosimetry estimates for targeted radionuclide therapy (TRT) agents. The whole body and tumor pharmacokinetic (PK) parameters of this model can be noninvasively measured with molecular imaging, providing a means of comparing potential TRT agents. Parameter sensitivities and noise will affect the accuracy and precision of the estimated PK values and hence dosimetry estimates. The aim of this work is to apply a PK model for TRT to two agents with different magnitudes of clearance rates, NM404 and FLT, explore parameter sensitivity with respect to time and investigate the effect of noise on parameter precision and accuracy.

Methods

Twenty-three tumor bearing mice were injected with a ‘slow-clearing’ agent, ¹²⁴I-NM404 (n=10), or a ‘fast-clearing agent, ¹⁸F-FLT (3′-deoxy-3′-fluorothymidine) (n=13), and imaged via microPET/CT pseudo-dynamically or dynamically, respectively. Regions-of-interest (ROI) were drawn within the heart and tumor to create time-concentration-curves (TCC) for blood pool and tumor. PK analysis was performed to estimate the mean and standard error of the central compartment efflux-to-influx ratio (k₁₂/k₂₁), central elimination rate constant (k_el), and tumor influx-to-efflux ratio (k₃₄/k₄₃), as well as the mean and standard deviation of the dosimetry estimates. NM404 and FLT parameter estimation results were used to analyze model accuracy and parameter sensitivity. The accuracy of the experimental sampling schedule was compared to that of an optimal sampling schedule found using Cramer-Rao Lower Bounds (CRLB) theory. Accuracy was assessed using correlation coefficient, bias, and standard error of the estimate normalized to the mean (SEE/mean).

Results

The PK parameter estimation of NM404 yielded a central clearance, k_el (0.009 ± 0.003 hr⁻¹), normal body retention, k₁₂/k₂₁ (0.69 ± 0.16), tumor retention, k₃₄/k₄₃ (1.44 ± 0.46) and predicted dosimetry, D_tumor (3.47 ± 1.24 Gy). The PK parameter estimation of FLT yielded a central elimination rate constant, k_el (0.050 ± 0.025 min⁻¹), normal body retention, k₁₂/k₂₁ (2.21 ± 0.62) and tumor retention, k₃₄/k₄₃ (0.65 ± 0.17), and predicted dosimetry, D_tumor (0.61 ± 0.20 Gy). Compared to experimental sampling, optimal sampling decreases the dosimetry bias and SEE/mean for NM404; however, it increases bias and decreases SEE/mean for FLT. For both NM404 and FLT, central compartment efflux rate constant, k₁₂, and central compartment influx rate constant, k₂₁, possess mirroring sensitivities at relatively early time points. The instantaneous concentration in the blood, C₀, was most sensitive at early time points; central elimination, k_el, and tumor efflux, k₄₃, are most sensitive at later time points.

Conclusions

A PK model for TRT was applied to both a slow-clearing, NM404, and fast-clearing, FLT, agent in a xenograft murine model. NM404 possesses more favorable PK values according to the PK TRT model. The precise and accurate measurement of k₁₂, k₂₁, k_el, k₃₄, and k₄₃ will translate into improved and precise dosimetry estimations. This work will guide the future use of this PK model for assessing the relative effectiveness of potential TRT agents.

INTRODUCTION

We have previously introduced a general pharmacokinetic (PK) model for targeted radionuclide therapy (TRT) that predicts the relative effectiveness of potential agents and provides a means of comparing them (Grudzinski et al., 2010). Molecular imaging is a powerful tool to noninvasively determine the PK parameters; however, it possesses innate sources of error that may make accurate and precise estimation of PK parameters difficult. In particular, noise and parameter sensitivity will affect the accuracy and precision of PK parameters and ultimately the predictive power of a model.

PK model analysis is required to determine how noise and parameter sensitivity will affect parameter estimation. For example, Muzi et al. demonstrated the impact of noise on the accuracy and precision of measured parameters in FLT studies and investigated the sensitivity of their kinetic model for FLT(Muzi et al., 2005a). The nature of our model will determine how noise and parameter sensitivity will affect the accuracy and precision of the estimated PK values necessary to predict TRT relative effectiveness.

Since PK parameters have been reported only for a few TRT agents, we aim to determine the PK parameters necessary for our TRT model of two agents of interest whose clearance rates differ by an order of magnitude. Moreover, we aim to investigate the effect of noise on parameter precision and accuracy and explore parameter sensitivity with respect to time. These analyses will assess how accurately and precisely one can predict the relative effectiveness of potential TRT agents using the presented PK model.

MATERIALS AND METHODS

Parameter estimation

NM404: A slow clearing TRT agent

Radioiodinated NM404 is a small molecular phospholipid ether analog that has displayed striking tumor uptake and prolonged tumor retention in over 45 spontaneous and xenograft tumor models (Pinchuk et al., 2006). Preclinical results strongly suggest that the agent is selectively taken up and retained in both primary and metastatic malignant tumors but not in benign or inflammatory lesions. This gives it great potential as an effective TRT agent when it is radiolabeled with ¹³¹I. NM404 can also be radiolabeled with ¹²⁴I (t_{1/2, phys} = 100.22 hours; t_{1/2, bio} ~ 100 hours) and imaged with ¹²⁴I -PET(Weichert et al., 2005). Thus, NM404 is an example of a diapeutic molecule that assumes either diagnostic or therapeutic functions depending on the iodine isotope with which it is radiolabeled. The diapeutic nature of the molecule makes it possible to noninvasively derive the necessary PK parameters using ¹²⁴I PET to predict the relative effectiveness of ¹³¹I-NM404 therapy. In this work, it will be used as an example of a TRT agent that is slowly taken up into a tumor and is slowly cleared from the blood.

Synthesis of 18-(p-iodophenyl)octadecyl phosphocholine (NM404) is accomplished via previously reported methodology (Pinchuk et al., 2006). Radioiodination with ¹²⁴I (IBA, Belgium) is routinely achieved in 70% isolated radiochemical yield by an isotope exchange reaction (Mangner et al., 1982). This procedure is currently approved in our existing physician-sponsored University of Wisconsin NM404 IND. Following purification (>99% pure) and accurate mass quantification by HPLC, the radiopharmaceutical is dissolved in absolute ethanol (50–500 ml) and Tween-20 (0.1 ml/mg of compound). The ethanol is removed under vacuum and the residue dissolved in sterile water to give a final solution containing no more than 0.4% Tween-20. Sterilization is achieved by filtration through a sterile 0.2 mm filter unit. Injection solutions are tested for pyrogens using the Limulus Amebocyte Lysate test kit. This is the same procedure employed for the preparation, purification and sterile formulation of ¹³¹I-labeled NM404 for past patient safety and PK studies.

FLT: A fast clearing TRT agent

3′-deoxy-3′-fluorothymidine (FLT) was originally a chemotherapy agent used to treat human immunodeficiency virus (HIV)(Sundseth et al., 1996). Because FLT correlates with thymidine kinase I expression, it is used as a means to measure cellular proliferation found within malignancies (Viertl et al., 2010; Brockenbrough et al., 2011). Clinically, it has been used extensively for diagnosis and grading (Dittmann et al., 2003; Choi et al., 2005). Furthermore, a kinetic model has been developed and validated for this agent in lung cancer patients that can be used for treatment response assessment (Muzi et al., 2005a; Muzi et al., 2005b). FLT was used in our work as an example of a tumor targeting agent that is taken up relatively quickly within a tumor and is cleared quickly from the blood.

¹⁸F- FLT was prepared as described by Martin et al.(Martin et al., 2002), modified for synthesis on a Scansys (Denmark) radiochemistry module. Firstly, 1.5 ml ¹⁸O H₂O was irradiated with 16.4 MeV protons to produce aqueous ¹⁸F (t_1/2 = 109.7 minutes; t_{1/2, bio} ~ 100 minutes) - on a PETtrace cyclotron (General Electric). Quaternary Ammonium (Waters, Massachusetts) cartridges trapped >95% of produced activity prior to elution with 500 uL 1 N K2CO3 and Kryptofix K2,2,2 in 80/20 MeCN/H2O. This mixture was azeotropically dried at 110 °C under argon flow to remove residual water and reacted with 10 mg of 3-N-Boc-1-[5-O-(4,40-dimethoxytrityl)-3-O-nosyl-2-deoxy-b-D-lyxofuranosyl]thymine (ABX, Germany) for 15 minutes at 140 °C in a closed vessel before a 2 minute deprotection with 0.5 mL 1N HCl at 110°C. After cooling, 1.0 mL of 2N sodium acetate neutralized the solution. The product was diluted in 50 mL water and loaded onto a C18 cartridge (Waters, Massachusetts) to remove unreacted fluoride and side-channel reaction impurities. ¹⁸F-FLT was then purified by reverse-phase HPLC (Alltech Econosil C18 10 × 250 mm, 6 ml/min 90/10 water/EtOH, RT = 700 +/− 15 sec.). After collection, product ¹⁸F-FLT was made isotonic with saline and sterilized by a 22 um filter. Average decay-corrected yields are 16% +/− 5% with specific activities of 4.1 +/− 1.1 Ci/umol.

Animal preparation

Twenty-three nude mice, purchased from Harlan (Madison, WI), were inoculated subcutaneously with 1 × 10⁶ human colon adenocarcinoma LS180 tumor cells suspended in PBS. The mice were housed under standard animal protocol conditions (temperature range, humidity range, 12-hr light-dark cycle) and the experiment was warranted and adhered by an animal use protocol created and approved by the University of Wisconsin - Madison animal use committee.

Ten mice were injected with ¹²⁴I- NM404 when their tumors reached volumes between 13 and 770 mm³ (7–14 days) and 13 mice were injected with ¹⁸F-FLT when their tumors reached volumes between 146 and 800 mm³ (4–14 days). To ensure a clean bolus injection, the tail vein was catheterized. Catheters were made using a 30 gauge needle, with the hub removed, attached to PE-1 tubing (Scientific Commodities, Lake Havasu, AZ). The line was filled with heparin whereby a small dose was given prior to injection. After injecting 80–230 μCi of ¹²⁴I- NM404 or 145–260 μCi of ¹⁸F-FLT, the catheter was flushed with 100–150 μL normal saline.

Data acquisition

All mice were imaged on the Inveon microPET/CT (Siemens, Knoxville, TN) and anesthetized with 2% Isoflurane during scanning. Mice injected with ¹²⁴I- NM404 were scanned 1, 6, 12, 24, 36, 48, 60, 72, 96, 120, 168 and 240 hours post injection. Each static PET acquisition was composed of 30–40 million counts. The resulting PET images were reconstructed from the 3-D acquisitions using ordered-subset expectation maximization (OSEM) 3D followed by maximum a posteriori (MAP) algorithm (Matrix size = [128,128,159], Pixel size = [0.861, 0.861, 0.796]mm, iterations = 18, subsets = 16, and beta smoothing factor = 0), which provides superior quantitative accuracy for ¹²⁴I acquisitions because of its noise suppression and increased recovery coefficient with respect to FBP and OSEM2D (Disselhorst et al., 2010).

Mice injected with ¹⁸F-FLT were first CT scanned and then continuously PET scanned for 60 minutes post injection. The data was temporally averaged into frames of 6×30, 7×60, 4×300, and 3×600 (frames, seconds). Each frame was reconstructed using the same algorithm that was used for ¹²⁴I so that a comparison between the agents can be made without introducing any bias. A transformation matrix was applied to both the NM404 and FLT data to ensure PET/CT co-registration and the CT data was used for both scatter and attenuation correction.

A pharmacokinetic model for targeted radionuclide therapy

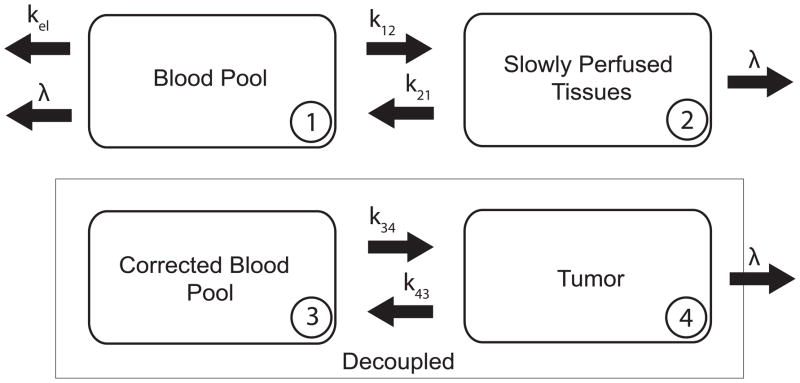
Fig. 1 is a schematic diagram of the proposed pharmacokinetic model for assessing the relative effectiveness of targeted radionuclide therapy agents(Grudzinski et al., 2010). The equations for the change in concentration of radioactivity for both normal body and tumor are:

$$\begin{array}{l}\frac{{dC}_1}{dt}=k_{21}{C}_2-\left(k_{12}+k_{el}+\lambda \right)C_1\\ \frac{{dC}_2}{dt}=k_{12}{C}_1-\left(k_{21}+\lambda \right)C_2\\ \frac{{dC}_4}{dt}=k_{34}{C}_1(t)=\left(k_{43}+\lambda \right)C_4\end{array}$$ (1)

Fig. 1.

Pharmacokinetic Model - A schematic representation of our pharmakokinetic model for TRT agents. The body is desrcibed by a two-compartment model that is decoupled from the tumor compartment. C₁ is the concentration in the blood pool (1), C₂ is the concentration in the slowly perfused tissues (2), and C₄ is the concentration in the tumor (4). The concentration in compartment 1 over time, C₁(t), becomes the forcing (input) function for the tumor. The units for the transfer constants, k₁₂, k₂₁, k₃₄, and k₄₃ are hr⁻¹.

C₁ is the concentration in the blood pool, C₂ is the concentration in the slowly perfused tissues (skin, fat, muscle, bone, and bone marrow), and C₄ is the concentration in the tumor. The units for the transfer rate constants, k₁₂, k₂₁, k₃₄, and k₄₃ are hr⁻¹. λ is the physical decay constant with units of hr⁻¹. The Corrected Blood Pool compartment, C₃, is the forcing function used for the tumor compartment which is the fit of the experimentally measured C₁ to the model.

To find the transfer rate constants in Eq. (1), PK analysis was performed. The PET data were decay corrected so that only biological clearance was considered. Regions-of-interest (ROIs) were drawn on the PET data within the heart and tumor using the CT data for reference to measure the time concentration-curves (TCCs) of C₁ and C₄. The nature of our model allows us to estimate all of the PK parameters using these two measurements (C₁ and C₄). To measure C₁, an ROI was drawn within the left ventricle as to only encompass blood and attempt to avoid spillover and partial volume effects from the heart wall. C₀ is the instantaneous concentration within the left ventricle after injection. As derived previously(Grudzinski et al., 2010), the TCC for C₁ can be described by

$$C_1(t)=C_0·\frac{\left(\alpha -k_{21}\right)}{(\alpha -\beta )}·exp(-\alpha ·t)+C_0·\frac{\left(k_{21}-\beta \right)}{(\alpha -\beta )}·exp(-\beta ·t)$$ (2)

The equation for C₁(t) was simplified into a bi-exponential function defined by

$$C_1(t)=A·exp(-\alpha ·t)+B·exp(-\beta ·t)$$ (3)

C₁ was fit to Eq. (3) using Levenberg-Marquardt nonlinear least-squares optimization (Levenberg, 1944; Marquardt, 1963; Gavin, 2010), implemented in Matlab. Eq. (4) was used to derive the micro-rate constants of C₁.

$$\begin{array}{l}{k}_{21}=\alpha -\frac{A(\alpha -\beta )}{C_0},\\ k_{21}=\frac{B(\alpha -\beta )}{C_0}+\beta ,\\ k_{el}=\alpha +\beta -k_{21}-k_{12}\end{array}$$ (4)

By fixing k₂₁, α, β, and C₀, C_tumor(t) was fit to Eq. (5) to determine the tumor specific micro-rate constants, k₃₄ and k₄₃. α and β are macro-rate constants between Compartment 1 and Compartment 2.

$$C_{\mathit{tumor}}(t)=C_0·k_{34}\left[\frac{(k_{21}-k_{43})}{(\alpha -k_{43})(\beta -k_{43})}exp(-k_{43}·t)+\frac{(k_{21}-\alpha )}{(\beta -\alpha )(k_{43}-\alpha )}exp(-\alpha ·t)+\frac{(k_{21}-\beta )}{(k_{43}-\beta )(\alpha -\beta )}exp(-\beta ·t)\right]$$ (5)

k₄₃ and k_34, the only free parameters in this optimization, are used in conjunction with k₁₂, k₂₁, and k_el to predict relative effectiveness of targeted radionuclide therapy agents on the basis of the tumor absorbed dose(Grudzinski et al., 2010). Eq. (6) describes the relationship between the PK parameters and absorbed dose to the tumor, D_tumor, predicted by the model.

$$D_{\mathit{tumor}}=D_{\mathit{thresh}}\left[\frac{k_{34}}{k_{43}}\left(\frac{1}{w_1+w_2\left(\frac{k_{12}}{k_{21}}\right)}\right)\right]$$ (6)

D_thresh is the total body dose threshold, and w₁ and w₂ are the proportion of the body encompassed by C₁ and C₂, respectively. This comparative model assumes that each potential agent is radiolabeled with the same long-lived beta emitting radionuclide and focuses solely on PK properties. The derivation of the model is shown in the Appendix. The effect of the long-lived radionuclide on the model is further explained.

Scope and Limitations

Early measurement of pharmacokinetic parameters of TRT agents may help predict relative effectiveness, which provides means to expedited agent development or rejection. Our relatively simple model could be used as an initial comparative evaluation of potential TRT agents. The comparative nature of our model requires a common dose limiting organ by which agents can be compared. Because whole body dose is often assumed to be a surrogate for bone marrow dose and bone marrow dose is often the dose limiting organ for TRT agents (Lassmann et al., 2005), our model uses the whole body to be dose-limiting. Some agents, like FLT, will of course be limited by doses to specific organs, particularly organs involved in clearance like the bladder and liver. While our model does not explicitly account for these dose-limiting organs, the limiting effect of clearance into these organs is in part accounted for in the k₁₂/k₂₁ term in Eq. (6). Promising TRT agents would require agent specific evaluation to determine organ and tumor doses. Once a potential TRT agent shows relative effectiveness via our model, three-dimensional dosimetric calculations can be done.

Another limitation of this model is that it assumes all tissue to be homogeneous media. Variations in atomic number within the body may influence the distribution of dose delivered by low-energy photons. For example, interfaces between soft tissues, air, and bone have the potential to create inhomogeneous dose distributions. Furthermore, by only considering self-dose within a compartment (radiation from beta particles) we have neglected cross-dose amongst compartments (radiation from gamma rays) which ultimately reduces the radiation dose absorbed by a compartment. Because of these limitations, the proposed model is not meant to provide absolute quantification of TRT radiation dosimetry. However, the model’s general nature could make it a valuable comparative tool.

Propagation of error

Levenberg-Marquardt optimization allows for the determination of both the asymptotic standard error of each parameter and the standard error of the fit(Gavin, 2010). Uncertainty in the data caused by variability in ROI definition, biological processes, and lack of counts within the ROI, translates into uncertainty in the dosimetry. The summation of these uncertainties were represented by a Gaussian probability density functions (PDF) at each data point and then propagated through the model by the fitting process. This leads to PDF’s for each PK parameter that ultimately create Gaussian PDF’s for D_tumor. Using Monte Carlo analysis, 1000 combinations of parameters were randomly sampled around a PDF with a width equal to the standard error and a center equal to the mean value of the PK parameters. Eq. (6) was used to compute D_tumor for each combination, respectively. The standard deviation of D_tumor was used to represent the uncertainty in dosimetry for each dataset.

Model analysis

The proposed PK model was evaluated to determine the extent to which the information obtained from a typical imaging study is sufficient to produce a unique solution with parameters that are both accurately and precisely measured. The model was characterized with respect to parameter sensitivity and susceptibility to noise to establish the most reliable approach for parameter estimation.

Sensitivity analysis

A sensitivity analysis was performed on the proposed PK model to measure the degree to which a change in an individual input parameter results in a change in the output of the model. Parameters with high sensitivity are more likely to be estimated accurately than those with lower sensitivity because noise will have a great affect. Parameters with similar sensitivity functions could be difficult to estimate independently. The sensitivity equation, shown in Eq. (7), represents the fractional change in the total time-concentration-curve (TCC) at a given time, t, after injection as a result of a small change in the parameter (δk_α) (Bassingthwaighte and Chaloupka, 1984).

$${\mathit{Sensitivity}}_{k_{\alpha }}(t)=\frac{\mathit{dTCC}(t)/\mathit{TCC}(t)}{{dk}_{\alpha }/k_{\alpha }}$$ (7)

Sensitivity analyses were performed according to the average parameter values for NM404 and FLT, which are shown in Table 1 and Table 2, respectively. The sensitivity of each parameter was derived by analytically differentiating the equation for each curve. The operating point, k_α, was set at the mean PK values for NM404 and FLT.

Table 1.

Parameter Values for NM404 within a LS180 Xenograft Model.

Parameter (units)	Mean Value	Range for optimization
C0 (%ID/ml)	15	11–21
k12 (hr−1)	0.13	0.05– 0.27
k21 (hr−1)	0.14	0.14 – 0.25
kel (hr−1)	0.02	0.007 – 0.044
k34 (hr−1)	0.03	0.023 – 0.061
k43 (hr−1)	0.02	0.007 – 0.027

Table 2.

Parameter Values for FLT Within a LS180 Xenograft Model.

Parameter (units)	Mean Value	Range for optimization
C0 (%ID/ml)	18	11–36
k12 (min−1)	0.39	0.17– 0.71
k21 (min−1)	0.21	0.073 – 0.29
kel (min−1)	0.02	0.011 – 0.071
k34 (min−1)	0.03	0.013 – 0.034
k43 (min−1)	0.02	0.027 – 0.070

Optimal Sampling

Because PK parameters are sensitive at different time points, temporal sampling has a great effect on the accuracy and precision of parameter estimation. Therefore, optimal sampling strategies could improve accuracy of parameter estimation, and several such strategies have been described in the literature (Li et al., 2001; Cercignani and Alexander, 2006; Xie et al., 2008). In addition, optimal sampling can reduce cost and patient discomfort associated with multiple imaging sessions if the model is expanded into human use.

The effects of temporal sampling on parameter estimates were evaluated using the theory of Cramer-Rao lower bounds (CRLB). CRLB finds the optimal sampling points that minimize the maximum prediction variance of the PK parameters while maximizing precision of parameter estimates⁷. CRLB was implemented in Matlab to derive the optimal sampling schedules for NM404 and FLT given the estimated PK parameter values obtained from the FLT and NM404 experiments. The latest time points considered in the optimization were 240 hours and 60 minutes post injection for NM404 and FLT, respectively. Objective functions were created based on CRLB to optimize sampling for multiple parameters simultaneously. The optimal sampling schedules for NM404 and FLT are shown in Fig. 2.

Fig. 2.

Optimal Sampling Schedules: (A) NM404 – 0, 3.86, 14.88, 71, and 179 hours. (B) FLT - 0, 2.44, 14.50, 37, and 58.50 minutes post injection.

Noise simulations

To investigate the model’s ability to accurately estimate the key PK parameters of NM404 and FLT across their expected preclinical range, it was necessary to use realistic standardized data. A set of 250 noisy simulated TCCs were generated for C₁ and C₄ according to both experimental and optimal sampling schedules and the values found in Table 1 and Table 2, respectively. Poisson noise was added to each simulated TCC, scaled to the total counts and the duration of each time frame according to Eq. (8):

$${\sigma }_{n,i}=c\sqrt{f_{n,i}{d}_i/t_i^{\mathit{dur}}}$$ (8)

where f_n,i is the activity concentration in the nth image ROI and at the ith scan after decay and scan-duration correction, d_i = exp(λt_i) is the isotope decay correction factor, with λ the decay constant and t_i the acquisition time at the ith scan, ${\text{t}}_{\text{i}}^{\text{dur}}$ is the scan duration at the ith scan, and c is a constant which scales the Gaussian noise with standard deviation close to the pre-clinical situation ²⁶. For the NM404 and FLT investigations, c was set to 2 and 7.5%, respectively, as to replicate the Gaussian noise seen in imaging studies, while the other variables of Eq. (8) were set to the NM404 and FLT experimental or optimal sampling parameters.

For both the experimental and optimal sampling schedules, the true (simulated input) and estimated parameter values were compared by examining the correlation coefficient for estimated versus true parameter, the percentage bias (the difference in the measurements for estimated vs. true parameter), and the precision (standard error of the estimate for the estimated vs. true parameter divided by the mean true parameter, SEE/mean).

RESULTS

Parameter estimation

Representative TCC and PET/CT data for NM404 and FLT are shown in Fig. 3. Notice how the differences in peak tumor uptake in (A) and (C) of Fig. 3 are reflected in the differences in tumor signal intensities within the PET/CT data of (B) and (D) of Fig. 3.

Fig. 3.

Representative Data from the Experiment – The concentration (%ID/ml) of NM404 and FLT in the tumor and blood over time are shown in (A) and (C), respectively. The dotted lines represent 95% confidence intervals for curve-fitting. Example PET/CT data sets are shown for NM404 and FLT in (B) and (D), respectively.

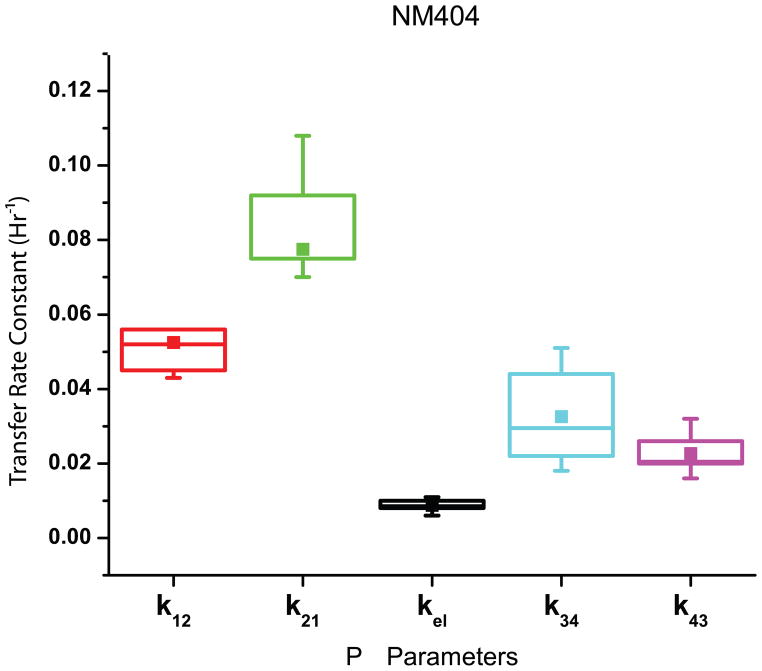
The estimates of the parameters for NM404 from the experimental data are found in Fig. 4. After estimating k₁₂ (0.054 ± 0.014 hr⁻¹), k₂₁ (0.079 ± 0.018 hr⁻¹), k_el (0.009 ± 0.003 hr⁻¹), k₃₄ (0.033 ± 0.012 hr⁻¹), and k₄₃ (0.023 ± 0.005 hr⁻¹), D_tumor (3.47 ± 1.24 Gy) was calculated by using Eq. (6). assuming that D_thresh = 2 Gy,w₁ = 0.2, and w₂ = 0.8.

Fig. 4.

A Graphical Representation of the Results for NM404 Parameter Estimation – The box plots indicate the range of the means for each for NM404 between 25 and 75% of the median. The mean is also indicated with a solid box.

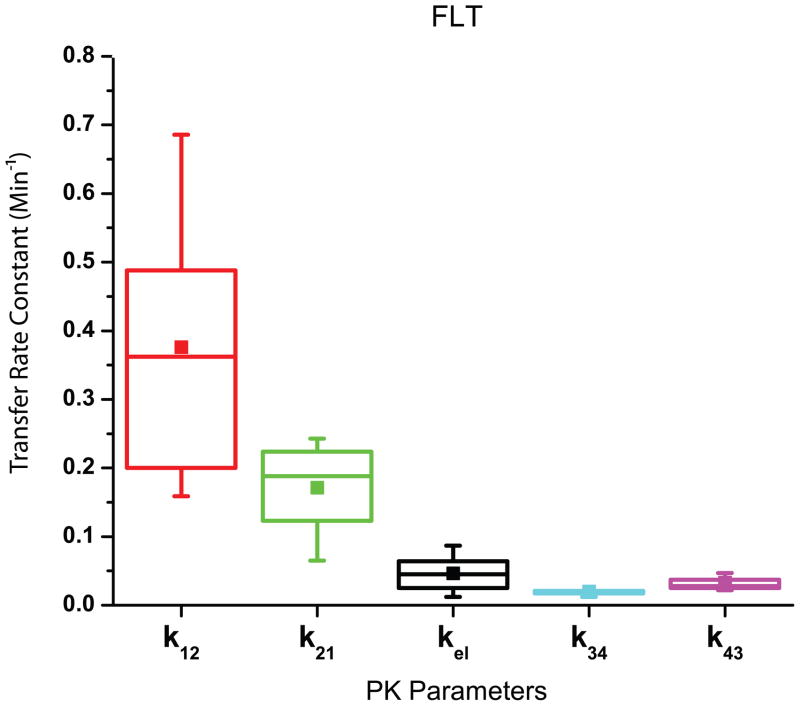
The results of the parameter estimation for FLT from the experimental data are found in Fig. 5. After deriving k₁₂ (0.408 ± 0.202 min⁻¹), k₂₁ (0.176 ± 0.061 min⁻¹), k_el (0.050 ± 0.025 min⁻¹), k₃₄ (0.020 ± 0.005 min⁻¹), and k₄₃ (0.033 ± 0.012 min⁻¹) D_tumor (0.61 ± 0.20 Gy) was calculated using Eq. (6) assuming D_thresh = 2 Gy, w₁ = 0.2, and w₂ = 0.8.

Fig. 5.

A Graphical Representation of the Results for FLT Parameter Estimation – The box plots indicate the range of the means for each PK parameter for FLT between 25 and 75% of the median. The mean is also indicated with a solid square.

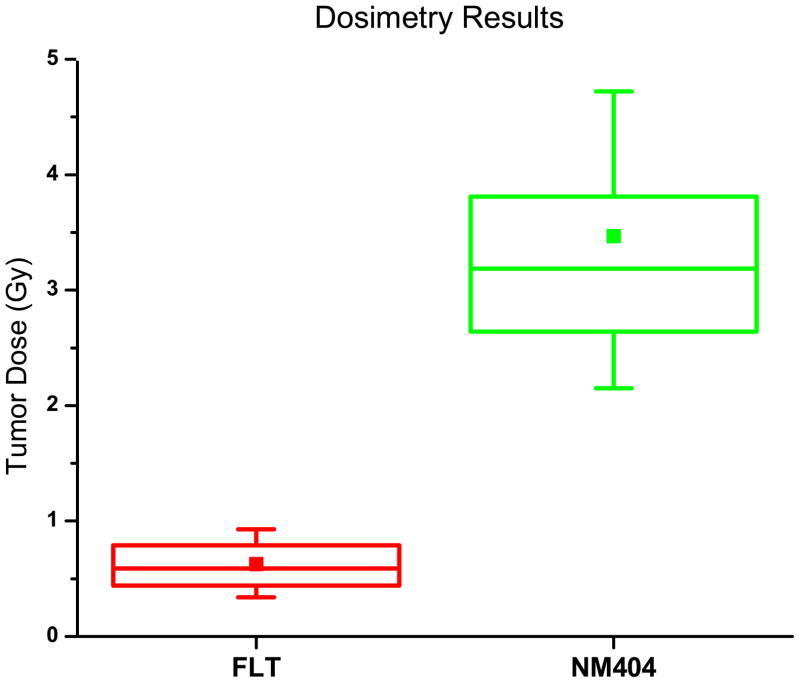
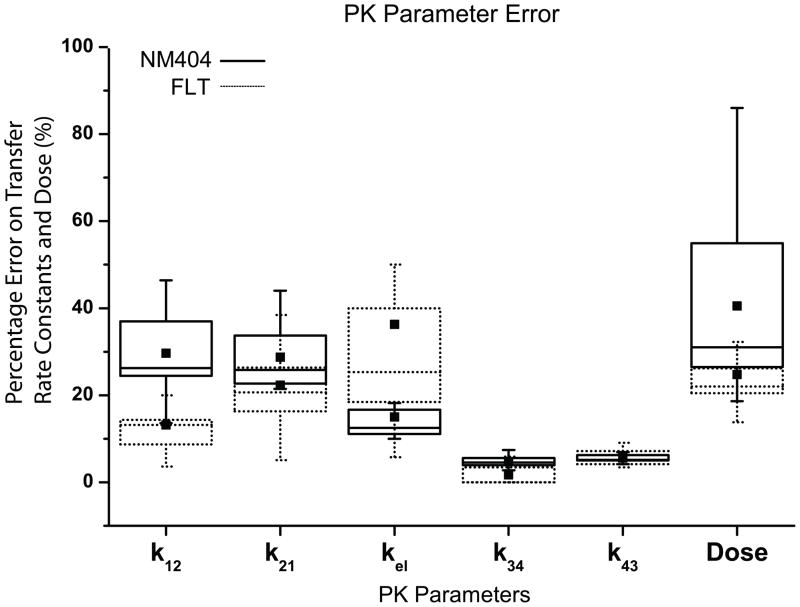
Fig. 6 shows the tumor dosimetry results from the experimental data for FLT and NM404. Notice that NM404 yields a greater D_tumor than FLT. Fig. 7 shows a graphical representation for percent error of the experimental data for NM404 and FLT. Notice that the percent error in dose is proportional to the percent error in k₁₂ and k₂₁.

Fig. 6.

Dosimetry Results – The box plots indicate the range of the results from the experiment between 25 and 75% of the median. The mean is also indicated with a solid square.

Fig. 7.

A Graphical Representation of the Parameter Percent Error for NM404 and FLT – The standard errors from the parameter estimation for NM404 were converted to percent error. The box plots indicate the range of the parameter error for each parameter between 25 and 75% of the median. The mean error is indicated with a solid square. The standard deviation of the Dose was taken as the standard deviation of the PDF generated from the Monte Carlo simulations outlined above.

Model analysis

Sensitivity analysis

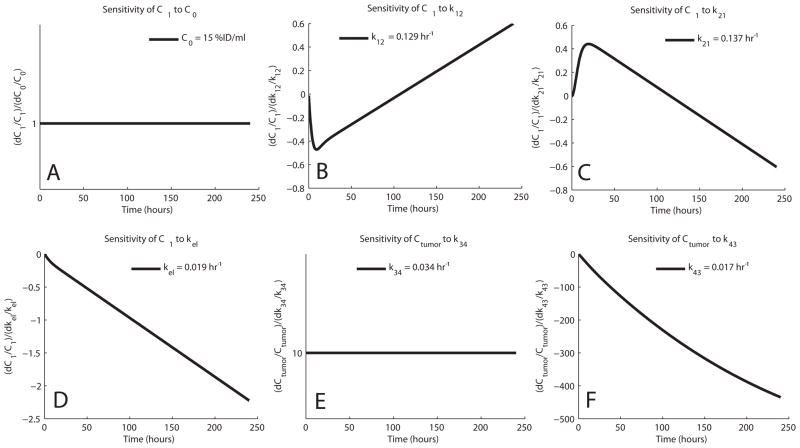
The relative sensitivities of C₁ and C₄ for NM404 and FLT are shown in Fig. 8 and Fig. 9, respectively. The curves show that the sensitivity of C₁ to k₂₁ mirrors that of k₁₂ indicating a high degree of overlapping sensitivity. This could cause difficulty in estimating these parameters independently and could be the reason why our data shows uncertainty in the parameter estimation for both NM404 and FLT.

Fig. 8.

Sensitivity Functions of NM404 – The sensitivity functions represent the time-dependent change in C₁ and C_tumor resulting from a change in the parameter value. Sensitivities are shown for C₀ (A), k₁₂ (B), k₂₁ (C), k_el (D), k₃₄ (E), and k₄₃ (F).

Fig. 9.

Sensitivity Functions of FLT- The sensitivity functions represent the time-dependent change in C₁ and C_tumor resulting from a change in the parameter value. Sensitivities are shown for C₀ (A), k₁₂ (B), k₂₁ (C), k_el (D), k₃₄ (E), and k₄₃ (F).

Noise simulations

Table 3 and Table 4 compare experimental sampling, optimal sampling, and optimal sampling with the last point removed for NM404 and FLT, respectively. The correlation coefficients for estimated versus true parameter values for all parameters are >92% and >90% for NM404 and FLT, respectively, which reflects robust estimates. The parameters with the highest bias and standard error in the estimates (SEE/mean) are k₁₂, k₂₁, and k_el for NM404, and k₁₂, k₂₁, and k₄₃ for FLT. The uncertainty in these estimations propagates into uncertainty in estimating absorbed dose (D_tumor). However, note that the body ratio, k₁₂/k₂₁, has less error than the individual parameters k₁₂ and k₂₁.

Table 3.

Model Accuracy for NM404 – The experimental simulations were performed with c = 2%

	Experiment Sampling			Optimal Sampling			Optimal Sampling - Last Point Removed
Parameter	r	Bias (%)	SEE/mean (%)	r	Bias (%)	SEE/mean (%)	r	Bias (%)	SEE/mean (%)
C0	0.98	4	5.1	1.0	0	1.4	1.0	0	1.4
k12	0.94	14	23	0.98	−1.3	9	0.98	−0.6	9.5
k21	0.93	9.3	17	0.93	−1.8	15	0.92	−1.3	16
k12/k21	0.99	5.7	8	1.0	0	5.6	0.99	0.1	7.5
kel	1.0	4.8	6.8	1.0	−0.2	3.4	0.99	−0.5	5.2
k34	1.0	−0.6	1.7	0.99	−0.2	2.8	0.99	0.5	3.4
k43	0.97	−1.1	3.3	0.93	−0.2	5.4	0.75	1.7	11.6
Dtumor	0.99	−5.0	8.3	0.99	−0.3	5.7	0.99	−1.6	8.6

Table 4.

Model Accuracy for FLT– The experimental simulations were performed with c = 7.5%

	Experiment Sampling			Optimal Sampling			Optimal Sampling - Last Point Removed
Parameter	r	Bias (%)	SEE/mean (%)	r	Bias (%)	SEE/mean (%)	r	Bias (%)	SEE/mean (%)
C0	0.98	0.4	6.0	1.0	1.9	3.4	1.00	2.1	3.4
k12	0.91	−0.7	14	0.97	3.8	9.7	0.97	0.8	8.7
k21	0.94	−1.0	13	0.97	2.7	8.5	0.88	15	24
k12/k21	0.99	0.4	5.5	1.0	1.1	5.2	0.98	−20	31
kel	0.93	0.9	16.5	0.99	4.5	8.0	0.36	66	84
k34	0.99	−0.6	3.5	0.97	−1.3	6.7	0.87	−1.5	14
k43	0.99	−0.8	5.1	0.94	−1.8	11.2	0.63	−2.2	38
Dtumor	1.0	−0.5	7.1	1.0	−0.9	6.0	0.07	−351	2746

With optimal sampling, the associated error (SEE/mean) for both k₁₂ and k₂₁ are decreased which decreases error in D_tumor. When the final data point is removed, the error of k₄₃ and k_el increases slightly for NM404 but drastically for FLT, which indicates that k₄₃ and k_el are most sensitive to later sampling points. The error associated with k₂₁ also increases drastically for FLT when the last point is removed. This indicates that the final time point is important for maintaining precision for k₂₁ as well.

DISCUSSION

The tumor dosimetry results in Fig. 6 demonstrate that NM404 shows more promise as a potential TRT agent than FLT. NM404 has both higher tumor influx-to-efflux ratios (k₃₄/k₄₃) and lower C₁ efflux-to-influx ratios (k₁₂/k₂₁) compared to FLT, which contributes to higher possible absorbed doses (D_tumor). It is advantageous to have a small k₁₂/k₂₁ ratio, like NM404 has, because the transfer from the central compartment into the peripheral compartment is slow. Referring to the derivation of the PK model(Grudzinski et al., 2010), there are two reasons why this is important. Firstly, the peripheral compartment is a majority of the whole-body. If the TRT agent remains in the peripheral compartment, including dose limiting organs, this will lead to lower achievable tumor doses because whole-body dose limits are reached earlier. Secondly, the central compartment TCC becomes the input into the tumor compartment which ultimately transfers the TRT agent into the tumor and increases the delivered dose.

Our propagation of error analysis dictates that noisy C₁ data translate into uncertain k₁₂ and k₂₁ values, which translate into uncertain dosimetry calculations and model predictions. Fig. 7 shows that there is more error in NM404 dose estimates compared to FLT because of larger errors in k₁₂ and k₂₁ estimates. Besides noise, ROI definition is another source of uncertainty that has the potential to cause error in the PK parameters. Automatic methods of ROI definition would most likely have smaller variances than manual methods due to their exact nature but might suffer from larger biases compared to manual methods.

The noise simulations showed that the parameters with the least precision and accuracy are k₁₂ and k₂₁, which can be attributed to overlapping sensitivity functions. However, the precision and accuracy of the ratio k₁₂/k₂₁ are relatively good (cf. Table 3 and Table 4). As estimates for D_tumor rely on this ratio, they are still very precise and accurate

Optimal sampling of a TCC takes into account the model sensitivity with respect to time, with the objective of reducing error propagation and improving the precision of parameter estimates. In our noise simulations, optimal sampling helps to make individual C₀, k₁₂, k₂₁, and k_el estimates more accurate and precise but k₃₄ and k₄₃ estimates less accurate and precise. This is due to the fact that the latest possible sampling point for the optimal sampling schedule was the latest sampling point in the experimental protocol. Despite the reduced precision in k₃₄ and k₄₃ estimates, optimal sampling helped improve the precision of estimates for D_tumor for both NM404 and FLT.

Optimal sampling can lead to more bias in the estimates. Interestingly, optimal sampling decreased the bias of NM404 but increased the bias for FLT compared to experimental sampling, indicating that the drastic reduction in sampling points for FLT introduces a bias to the estimates. This problem can be alleviated if additional sampling points are added at later time points for FLT.

Removing the last time point is detrimental to the accuracy and precision of the TRT model. If the last point of the optimal sampling schedule is removed, there is an increase in the errors associated with k₄₃ and k_el. The sensitivity functions in Figs. 8 and 9 indicate that these parameters are very sensitive to later sampling times, which reiterates the need for later samples to increase the precision of parameter estimation. Because of animal safety issues and decaying tracers, it is often difficult to adequately sample at very late time points and inaccuracy and imprecision are often unavoidable as a result.

CONCLUSIONS

We have developed a model that could allow researchers to assess the relative effectiveness of potential TRT agents at the early stages of development. Because the model involves comparison between agents, it relies on the measurement of PK parameters of TRT agents. In this work, we have for the first time determined the PK parameter values for two real agents, NM404 and FLT. The PK parameters were used to estimate D_tumor which is directly related to the relative effectiveness of the agent. The parameter estimation process showed that noisy data within C₁ led to uncertain k₁₂ and k₂₁ values. Sensitivity analysis showed that the sensitivity functions of k₁₂ and k₂₁ overlap which could describe their increased uncertainty. In addition, the sensitivity functions of k_el and k₄₃ showed that their measurement precision can be increased if the data is sampled at later time points. Model analysis showed that optimal sampling via CRLB can improve the accuracy and precision in measuring k₁₂ and k_21, whereas sampling at later time points can improve the accuracy of k_el and k₄₃. The precise and accurate measurement of k₁₂, k₂₁, k_el, k₃₄, and k₄₃ will translate into more accurate and precise D_tumor calculations.

Understanding our model can help reduce imaging time points without substantially decreasing parameter precision. Overall, we explored the relevant properties of the model that contribute to its optimal use. Our work demonstrates that relative effectiveness can be estimated accurately and precisely even though individual parameter might not be. We have introduced a PK modeling approach to compare potential TRT agents in relative terms, demonstrated such a comparison with NM404 and FLT, and explored the relevant properties of the model.

APPENDIX

The tumor compartment within the linear system is assumed not to perturb the two-compartment open model of the body because of its neglible volume compared to the other two body compartments. Therefore, the tumor compartment was decoupled from the normal body compartments. The equations for the change in concentration of radioactivity for both normal body and tumor are found in Eq. (1).

The units of the inter-compartmental rate constants, k₁₂, k₂₁, k₃₄, k₄₃, k_el, and physical decay constant, λ, are hr⁻¹. The solution to each equation, solved via Laplace transforms, represent the time-concentration-curve (TCC) of each compartment that are used to determine radiation dosimetry. The analytical solutions of radioactivity-concentration, C (t), are converted to time-activity, A (t), by incorporating the volume of each compartment and A₀, the initial activity within compartment 1. An analytical pharmacokinetic model was derived for each compartment:

$$\begin{array}{l}{A}_1(t)=V_1·\frac{A_0}{V_1}\left[\frac{(\zeta -\alpha )exp(-\alpha t)-(\zeta -\beta )exp(-\beta t)}{(\beta -\alpha )}\right]\\ A_2(t)=V_2·\frac{A_0·k_{12}}{V_1}\left[\frac{exp(-\alpha t)-exp(-\beta t)}{(\beta -\alpha )}\right]\\ A_4(t)=V_4·\frac{A_0·k_{34}}{V_1}\left[\frac{(\xi -\sigma )}{(\alpha -\sigma )(\beta -\sigma )}exp(-\sigma t)+\frac{(\xi -\alpha )}{(\beta -\alpha )(\sigma -\alpha )}exp(-\alpha t)+\frac{(\zeta -\beta )}{(\sigma -\beta )(\alpha -\beta )}exp(-\beta t)\right]\end{array}$$ (9)

where A₀ = injected activity, ζ = k₂₁ + λ, σ = k₄₃ +λ, γ = k₁₂ + k_el +λ

$$\alpha =\frac{1}{2}\left[(\gamma +\zeta )+\sqrt{{(\gamma +\zeta )}^2-4(\gamma \zeta -k_{21}{k}_{12})}\right],\beta =\frac{1}{2}\left[(\gamma +\zeta )-\sqrt{{(\gamma +\zeta )}^2-4(\gamma \zeta -k_{21}{k}_{12})}\right]$$ (10)

The analytical pharmacokinetic model was adapted into a targeted radionuclide therapy model by relating whole body dose threshold, D _thresh, to tumor dose, D_tumor, via specific pharmacokinetic parameters of each compartment. w₁ and w₂ are the proportion of the total body volume of each body compartment, respectively.

$$D_{\mathit{tumor}}=D_{\mathit{thresh}}\left[\frac{k_{34}}{k_{43}}\left(\frac{1}{w_1+w_2\left(\frac{k_{12}}{k_{21}}\right)}\right)+\lambda \frac{k_{34}}{k_{43}}\left((k_{43}-k_{21})(w_1{k}_{21}+w_2{k}_{12})-w_1{k}_{21}\right)\right]$$ (11)

The complete derivation of Eq. (11) is found in the Appendix of Grudzinski et al(Grudzinski et al., 2010). Our model assumes bone marrow to be the dose-limiting organ. Because whole body dose is a surrogate for bone marrow dose, the whole body dose threshold, D_thresh, is set according to a bone marrow limit of 2 Gy(Lassmann et al., 2005). Our model also assumes homogeneous uptake within each compartment, homogeneous dose deposition, and homogeneous tissue within each compartment. Lastly, each compartment only experiences self-dose, neighbouring dose deposition is neglected.

The targeting agent was assumed to be radio-labeled with a long-lived beta-emitting radionuclide such as ¹³¹I (λ=0.00361hr⁻¹) or ⁹⁰Y (λ= 0.0108hr⁻¹). This physical decay is reflected by λ in Eq. (1). Because the decay constant for most TRT radionuclides is very small, the second part of the Eq. (11) is negligible and the equation becomes:

$$D_{\mathit{tumor}}=D_{\mathit{thresh}}\left[\frac{k_{34}}{k_{43}}\left(\frac{1}{w_1+w_2\left(\frac{k_{12}}{k_{21}}\right)}\right)\right]$$ (12)