Evaluating Similarity Measures for Brain Image Registration

Abstract

Evaluation of similarity measures for image registration is a challenging problem due to its complex interaction with the underlying optimization, regularization, image type and modality. We propose a single performance metric, named robustness, as part of a new evaluation method which quantifies the effectiveness of similarity measures for brain image registration while eliminating the effects of the other parts of the registration process. We show empirically that similarity measures with higher robustness are more effective in registering degraded images and are also more successful in performing intermodal image registration. Further, we introduce a new similarity measure, called normalized spatial mutual information, for 3D brain image registration whose robustness is shown to be much higher than the existing ones. Consequently, it tolerates greater image degradation and provides more consistent outcomes for intermodal brain image registration.

1. INTRODUCTION

Image registration is extensively used in medical imaging for establishing correspondence between two images, and is a fundamental problem in this field. Registration computes a spatial transformation that aligns a source image to a target image. Registration methods previously have relied on matching corresponding features in the images [1–4], but more recently interest has been directed towards similarity measures (SMs) of a global correspondence nature obtained from image intensities. In this case, the performance of image registration directly depends on the effectiveness of the SM used in measuring image similarity. Brain image registration methods that rely on intensitybased SMs have been reviewed in a number of survey papers [5,6] and examined in a number of evaluation studies [7–11]. However, these studies do not evaluate SM as an independent and separate component of the image registration process. In [12], [13], a protocol was proposed to evaluate the effectiveness of SMs. In this protocol, a multidimensional parameter space was normalized and sampled so that similar changes in any parameter create similar averaged voxel shift in whole brain, then five different criteria were introduced for SM evaluation. Except for the capture range (the range of transformation parameters in which the SM value monotonically decreases), the other four criteria were defined based on the location of the local optima on each SM profile. However, our experiment shows that SM values outside the capture range are mostly random and not meaningful. We therefore define our criterion inside the capture range. Elastix [14] is a new toolkit that allows for components of a registration process to be replaced. Different SMs can be plugged into Elastix and for given registration components they can be evaluated. The same approach is used in [15] to evaluate SMs used for rigid and non-rigid (deformable) registration under the framework of Advanced Normalization Tools (ANTs), in which it is possible to evaluate a single component of the registration process while holding all other aspects constant. However, the complex interdependency of different registration components makes isolating the effects of the optimization component from the effects of the selected SM on the registration results a challenging task.

Here we tackle this issue by controlling the registration process. We create the source image by transforming the target image, which not only gives us control over the type of misregistration but also its severity. As a result, given the images to be registered, the outcome of the registration process only depends on the SM and the type of transformation used. We introduce robustness as our evaluation metric, which is formulated and quantified in this paper. Furthermore, we show that SMs with higher robustness are more tolerant to image degradation and are also more effective in intermodal brain image registration.

Before presenting the evaluation method, we provide a comprehensive review of SMs and categorize them based on their theoretical basis into: statistical measures, information theoretic measures, and spatial dependency measures. We also introduce a normalized version of a recently defined SM, named spatial mutual information (SMI) [16], and extend it to 3D for brain image volumes. Section 4 gives details of the dataset used for the evaluation, the widely used simulated magnetic resonance (MR) brain images of the BrainWeb database (www.bic.mni.mcgill.ca/brainweb/). In section 5, we evaluate the robustness of the reviewed SMs, study the relationship between robustness and image degradation, and show that robust SMs perform better in intermodal brain image registration.

2. Similarity Measures

This section presents an overview of the SMs used in brain image registration. In general, intensity-based similarity measures can be categorized into three groups: statistical measures, information theoretic measures, and measures in which the spatial dependency of neighboring pixels/voxels are taken into account. Hereafter, these measures are called spatial dependency measures. All SMs used in popular brain image registration software packages, such as AFNI, SPM, and FSL, are included in this study. However, the intention of the review here is not to include an exhaustive list of SMs.

3.1 Statistical Measures

There are different measures for reflecting the departure of two random variables (X,Y) from independence. The best known is Pearson Correlation Coefficient (PCC), which was first introduced by Galton and is defined as [17]

$$PCC=\frac{1}{N-1}\sum _{i=1}^N\left(\frac{x_i-{\mu }_x}{{\sigma }_x}\right)\left(\frac{y_i-{\mu }_y}{{\sigma }_y}\right)$$ (3)

where x_i and y_i denote realizations of random variables X and Y, N the number of the available sample pairs, µ_x the mean of X, µ_y the mean of Y, σ_x the standard deviation of X, and σ_y the standard deviation of Y. Spearman Correlation Coefficient (SCC) is another correlation measure that is defined as follows [18]:

$$SCC=1-6\sum _{i=1}^N\frac{d_i^2}{N(N^2-1)}$$ (4)

where d_i is the difference in statistical rank of corresponding variables and N is the same as in (3).

Mean Square Differences (MSD) is a measure that denotes the sum of squared differences between intensity pairs divided by the total number of sample pairs [19]:

$$MSD=\frac{1}{N}\sum _{i=1}^N{(x_i-y_i)}^2$$ (5)

where x_i, y_i, and N are the same as in (3). Often, the square root of MSD is considered, or MSD does not include the normalization factor N.

Hellinger Distance (HD) was originally introduced as a difference measure between two probability density functions (pdfs), and has been applied to image registration [20]. This measure is given by

$$HD=\frac{1}{N}{\left[\sum _{i=1}^N{(\sqrt[2]{x_i}-\sqrt[2]{y_i})}^2\right]}^{1/2}$$ (6)

where x_i, y_i, and N are the same as in (1). The list of similarity measures in this category is extensive, which we do not intend to cover them all here.

3.2 Information Theoretic Measures

These measures were first defined by Shannon in the field of communication, and later were considered for image registration by Viola [23] and Maes [24]. Under the spatial independency assumption, the statistical characteristics of image X are given by an individual random variable of this image, for instance X. Likewise, mutual information of two images X and Y is given by the mutual information of two random variables X, Y:

$$MI=I(X,Y)=\sum _{x\in \chi }\sum _{y\in \chi }{p}_{X,Y}(x,y)\mathit{\text{log}}\frac{p_{X,Y}(x,y)}{p_X(x)p_Y(y)}$$ (7)

where p_X (x) and p_Y (y) respectively denote the one-dimensional pdfs of the image X and Y represented by their normalized histograms and p_X,Y(x,y) is the two-dimensional joint pdf of the image pair (X,Y) represented by their normalized joint histogram all under the pixel/voxel independency assumption. χ is the finite discrete label set, which reflects the intensity values that exist in the image histogram bins.

There exist a number of other similarity measures that are similar to MI including Joint Entropy (JE) [25], and Normalized MI (NMI) [26]. NMI is a popular similarity measure in the literature for medical image registration, and also an effective one when performing multimodal medical image registration:

$$\begin{array}{l}NMI=\frac{H(X)+H(Y)}{H(X,Y)}\hfill \\ JE=H(X,Y)=-\sum _{x\in \chi }\sum _{y\in \chi }{p}_{X,Y}(x,y)\mathit{\text{log}}(p_{X,Y}(x,y))\hfill \\ H(X)=-\sum _{x\in \chi }{p}_X(x)\mathit{\text{log}}(p_X(x))\hfill \\ H(Y)=-\sum _{y\in \chi }{p}_Y(y)\mathit{\text{log}}(p_Y(y))\hfill \end{array}$$ (8)

where p_X(x), p_Y(x), p_X,Y(x,y), and χ are the same as in (7), H(X) and H(Y) are the entropies of random variables X and Y, respectively, and H(X,Y) or JE is the joint entropy of the corresponding pair (X, Y) under the pixel/voxel independency assumption.

Entropy Correlation Coefficient (ECC) is another measure defined in [25]:

$$ECC=\sqrt{\frac{2I(X,Y)}{H(X)+H(Y)}}$$ (9)

where I(X, Y) is given by (7) and H(X) and H(Y) are given by (8).

Kullback-Leibler Distance (KLD) is also a similarity measure defined in the information theory field and used for multimodal brain image registration in [27] and provides a statistical distance measure between two joint intensity distributions:

$$KLD=\sum _{x\in \chi }\sum _{y\in \chi }{p}_o(x,y)\mathit{\text{log}}\frac{p_o(x,y)}{p_e(x,y)}$$ (10)

where p_o(x,y), and p_s(x,y) are the observed and expected intensity distributions, respectively and χ is the same as in (7).

3.3 Spatial Dependency Measures

The inability of MI to capture image spatial information reduces its effectiveness as a SM. In 1996, a year after the introduction of MI by Viola and Maes et al., Studholme et al. [28] attempted to incorporate spatial information into the computation of MI. Furthermore, the second-order MI introduced by Rueckert et al. [29] to overcome this shortcoming as well.

Second Order Mutual Information (SOMI) involves the use of the co-occurrence matrix to estimate the four-dimensional joint pdf of an image pair. This measure is given by:

$$\mathit{\text{SOMI}}=\sum _{x,x\prime \in \chi }\sum _{y,y\prime \in \chi }{p}_{X,Y}(x,x\prime ,y,y\prime )\mathit{\text{log}}\frac{p_{X,Y}(x,x\prime ,y,y\prime )}{p_X(x,x\prime )P_Y(y,y\prime )}$$ (11)

where χ denotes a finite discrete label set, P_X(x,x′) the probability that x and x’ are adjacent in image X, p_Y(y,y′) the probability that y and y’ are adjacent in image Y, p_X,Y(x,x′,y,y′) the joint probability that (x, x′) are adjacent in image X and (y,y′) are adjacent in mage Y, and (x, y) denoting the corresponding pixels/voxels in the image pair. Unfortunately, the four-dimensional joint histogram for estimating p_X,Y(x,x′,y,y′) becomes sparse in practice since there are not sufficient data in a typical brain image to fill all of its histogram bins. In [29], Rueckert addressed this issue by reducing the size of the discrete label set to 16. However, this reduces the effectiveness of SOMI as a similarity measure; this drawback is thoroughly studied by Gao in [30] for the classical MI, and also in [31] for the SOMI.

Gradient Mutual Information (GMI) is a spatial similarity measure formed by combining MI and a gradient measure [32]. GMI is formulated as follows:

$$\begin{array}{l}GMI=G(X,Y)I(X,Y)\hfill \\ G(X,Y)=\sum _{(x,y)\in (\mathbf{X},\mathbf{Y})}w({\alpha }_{x,y}(\sigma ))\mathit{\text{min}}(|\nabla x(\sigma )|,|\nabla y(\sigma )|)\hfill \\ w(\alpha )=\frac{\text{cos}(2\alpha )+1}{2}\&{\alpha }_{x,y}(\sigma )=\mathit{\text{arccos}}\frac{\nabla x(\sigma ),\nabla x(\sigma )}{|\nabla x(\sigma )||\nabla y(\sigma )|}\hfill \end{array}$$ (12)

where G(X,Y) is the gradient part of the SM contributing to the spatial information, | ∇x(σ)| denotes the magnitude of the gradient vector of image X at point x with the scale of σ, and | ∇y(σ)| the magnitude of the gradient vector of image Y at point y with the scale of σ, and I(X,Y) is given by (5). Multimodal and rigid registrations have shown some improvement when using this similarity measure compared with MI [32].

The recently introduced Quadrilateral MRF model is used to compute Spatial Mutual Information (SMI) to overcome the dimensionality problem [16]:

$$SMI=I(\mathbf{X},\mathbf{Y})=mn\{H(Y,X_u)-H(Y,X)\}+\frac{mn}{2}\left\{\begin{array}{c}H(X_r,Y)+H(X_l,Y)\\ -H(Y_l,X_u)-H(Y_r,X_u)\end{array}\right\}$$ (13)

where mxn is the image size which is the same in both images, H(X,Y) is the joint entropy of the voxel X in image X with the corresponding voxel in image Y, H(Y,X_u) is the joint entropy of the voxel Y in image Y with the upper neighbor of its corresponding voxel in image X, H(Y_l,X_u) is the joint entropy of the left neighbor of voxel Y in image Y with the upper neighbor of the corresponding voxel X in image X, H(Y_r,X_u) is the joint entropy of the right neighbor of voxel Y in image Y with the upper neighbor of the corresponding voxel X in image X, H(X_r,Y) is the joint entropy of the voxel Y in image Y with the right neighbor of its corresponding voxel X in image X, and finally H(X_l,Y) is the joint entropy of the voxel Y in image Y with the left neighbor of its corresponding voxel X in image X. It is easy to show that Equation (13) is not symmetric in the sense that I(X, Y) ≠I(Y,X). Such a symmetric property is enforced in [16] by adding the symmetric counterpart of the joint entropy components of Equation (13), which results in the following equation for SMI:

$$SMI=\frac{mn}{2}\left\{\begin{array}{l}2H(Y,X_u)+2H(Y_u,X)-4H(X,Y)\hfill \\ +2H(X_r,Y)+2H(X,Y_r)-H(Y_l,X_u)\hfill \\ -H(X_l,Y_u)-H(Y_r,X_u)-H(X_r,Y_u)\hfill \end{array}\right\}$$ (14)

where mXn and, H(. , .) are the same as in (13), with their symmetric counterparts. It should be noted that H(X_l ,Y) and its symmetric counterpart H(X, Y_l) are omitted from Equation (14) since H(X_l ,Y) = H(X_r,Y) from a computational standpoint [33]. To prevent confusion we denote the original SMI defined by equation (13) as SMI_NS.

3.4 Normalization and 3D extension of SMI

In general, NMI is shown to be more effective than MI [26]. The same normalization is used here to define NSMI from the definition of SMI under the new constraint of QMRF. This can be simply formulated as follows:

$$NSMI=\frac{X(\mathbf{X})+H(\mathbf{Y})}{H(\mathbf{X},\mathbf{Y})}$$ (15)

where H(X), and H(Y) are given by [16]:

$$H(\mathbf{X})=mnH(X,X_u)+\frac{mn}{2}\left\{\begin{array}{c}H(X_r/X)+H(X_l/X)\\ -H(X_l,X_u)-H(X_r,X_u)\end{array}\right\}$$ (16)

and I(X,Y) is the SMI given by (13) or (14). NSMI can be obtained from either SMI or SMI_NS. We evaluate the two new similarity measures introduced here, NSMI and NSMI_NS, in section 5.

The interesting point here is that computing SMs over different set of brain image slices (sagittal, axial, coronal) results in the same values except for SMI and NSMI . This is evidence that voxel interdependency is discarded in all these SMs except for SMI and NSMI. Computation of the SMI, SMI_NS, NSMI, and NSMI_NS for 3D images, based on the method given in [16], requires having an extension of the Markovianity constraint to 3D volumes. Even though the definition of Markovianity can be simply extended to multidimensional spaces, a comprehensive and systematic formulation for 3D volumes currently does not exist. Therefore, we adopt an alternative approach to extend the applicability of these SMs to 3D brain images. The idea is to consider a 3D brain image as a composition of its 2D slices, noting that the slicing can be done in three different ways along three axes: transverse, sagittal and coronal. Hence, the product of the resulting three SMs can be used to serve as a 3D SM:

$$\begin{array}{l}SMI=SM{I}_{\mathit{\text{Tran}}}\times SM{I}_{\mathit{\text{Sag}}}\times SM{I}_{\mathit{\text{Cor}}}\hfill \\ NSMI=NSM{I}_{\mathit{\text{Tran}}}\times NSM{I}_{\mathit{\text{Sag}}}\times NSM{I}_{\mathit{\text{Cor}}}\hfill \end{array}$$ (17)

where SMI_Tran is the SM computed on the transverse slices, SM_sag the SM computed on the sagittal slices and SMI_Cor the SM computed on the coronal slices. It can easily be inferred from Equation (17) that the above 3D SMI and NSMI take into account all dependencies in the 3D neighboring voxels, even though they cannot mathematically be regarded as mutual information any more.

3. Evaluation Method

In this section, we introduce a method for systematically evaluating SMs for use in brain image registration. Brain image registration usually consists of five components: transformation model, regularization, cost function, optimization, and interpolation [5], [6], [14]. The cost function often contains a SM that measures image similarity. The objective of our evaluation method is to assess how effectively a SM can register two images while eliminating the effects of the other components of the registration process. We’ll start with a quick overview of the brain image registration process and then describe our evaluation method based on the established terminology.

In general, source and target images can be represented by X: ℜ³→ ℜ and Y: ℜ³ →ℜ, which associate scalar intensity values to points described by X = (x, y, z)^t in three-dimensional vector spaces ℜ³. The target image is fixed and the source image undergoes a spatial transformation of the form T(μ): ℜ3→ℜ3 with μ denoting a set of parameters³. The accuracy of such a mapping is defined based on correspondences between the two images, which can be quantified by a cost function of the form

$$C(T(\mathit{\mu }))=C(\mathbf{X}*T(\mathit{\mu }),\mathbf{Y})$$

where T(μ) denotes the admissible transformation functions with the parameter set μ, and C(.) is the cost function which uses a SM to measure the image correspondence. An optimization step is performed to maximize the cost function, that is

$$T_{\mathit{\text{opt}}}({\mathit{\mu }}_{\mathit{\text{opt}}})=\underset{T(\mu )\in \Im }{\text{arg max}}C(T(\mathit{\mu }))$$ (1)

where T_opt(µ_opt) denotes the solution to the registration problem, and ℑ is the set of all admissible transformations. Once T_opt(µ_opt) is obtained, the registration process is completed.

In many registration problems, especially in brain image registration, the type of misregistration/transformation T_opt (rigid-body, affine, non-rigid) is already known, so the problem is further simplified towards finding only the optimal parameter set µ_opt. As may be inferred from Equation (1), X and Y are fixed during the registration process and the cost function c(T(μ)):ℜ^d→ℜ maps the multidimensional parameters space μ to a single value (SM value). In the simplest case of one dimensional μ (i.e. T is translation along x axis), the plot of the cost function c(t(μ)) in terms of μ gives a one-dimensional curve which quantifies the relationship between the parameter μ and the SM value. We call this curve the profile of the SM for a given transformation type T. If the parameter μ is twodimensional (i.e. T is translation along x, y axes), then the profile of the SM is going to be a surface assigning a SM value for any combination of the parameters in μ.. Consequently, higher dimensions of μ will result in a higher dimensional profile, for example the dimensionality of μ for rigid body transformation is 6 (3 for translation along all the axes and 3 for rotation around all the axes) which results in a 6-dimensional profile. The high dimensionality of the parameter set μ, especially for a non-rigid transformation, makes the direct and mathematical analysis of this mapping quite challenging. Regardless of the dimensionality of the SM profile, for a given transformation T, the maximum of the profile curve denotes the global optimum T(µ_opt), and the second maximum points out the first local optimum T(µ_opt). We define the ratio of SM value at the global optimum to its value at the local optimum as robustness of the SM for a given transformation T,

$$R_T=20\text{log}\left(\frac{c(T({\mathit{\mu }}_{\mathit{\text{opt}}}))}{c(T({\mathit{\mu }}_{\mathit{\text{loc}}}))}\right)$$ (2)

Since the SM values at the local optimum are often very small numbers, we use a logarithmic scale decibel (db) to indicate the ratio of a physical quantity relative to its maximum possible value. It is clear that if R_T ≤ 0, then the profile curve is pointing to the local optimum as the registration solution and consequently the registration fails (assuming that the location of perfect registration is at the global optimum). Therefore, the most desirable SM is the one which has highly positive robustness (R_T > 0) in all the registration problems (e.g. rigid-body, affine, non-linear, intermodal, and etc.). Of course, there is no such SM in practice; however we demonstrate that the magnitude of the robustness R _T is an important criterion for evaluating SM effectiveness in brain image registration. Then, we lay out our method for evaluating SMs based on these findings.

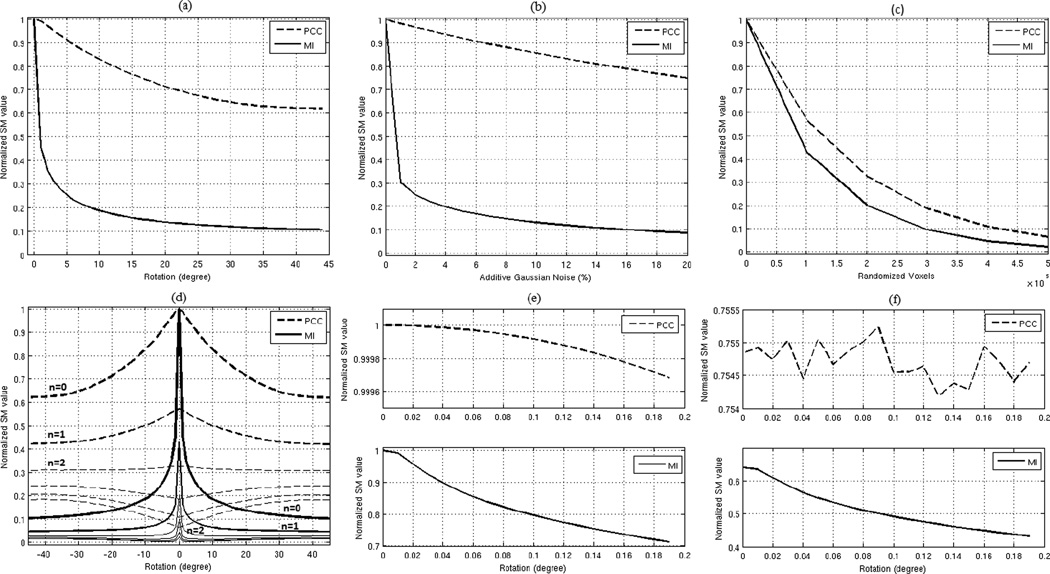
In practice, there are usually dis-similarities between the source and target images even when they are perfectly registered. Such dis-similarities are often referred to as initial or intrinsic differences. Intrinsic differences among brain images can be due to image noise, distortions, different scanners, different subjects, and different image modalities; even differences in acquisition time-sequences create differences between source and target images. Registration failures are often due to intrinsic differences between the source and target images. Intrinsic differences reduce the SM values in the same way that transformational dis-similarities do, for example Figs. 1a, 1b, and 1c show the effect of rotational transformation, different noise level, and randomizing voxel locations on the profiles of the two extensively used similarity measures of PCC and MI. In brain image registration, the source image always contains certain amount of intrinsic differences (due to one or combinations of the factors mentioned earlier) which reduces the SM value at the global optimum. Fig. 1d shows the MI and PCC profiles for rotational transform when different levels of intrinsic differences are imposed by randomizing the location of n × 10⁵ voxels (where n = (0,1,2,3,4,5)) in a typical human brain MR image (1 mm isometric voxel size). As seen in Fig. 1d, imposing these intrinsic differences creates two artifacts on the SM profiles; 1) it reduces the SM robustness R_T, and 2) it flattens the profile curve around the global optimal solution. The first artifact causes the registration to fail (when R_T becomes smaller than zero) and the second one introduces a slight inaccuracy into the results even when R_T > 0. As seen in Fig. 1d, by imposing 2 × 10⁵ voxels differences, the PCC rotational robustness becomes very close to zero, while the MI rotational robustness is still higher than zero (about 26 dB). This means that registering a rotationally misaligned source image by PCC is only possible if the intrinsic differences of the source and target images are less than that caused by randomizing 2 × 10⁵ voxels. If the rotational robustness of PCC, when there are no intrinsic differences, had been more than the one shown in Fig. 1a, then it would have tolerated more intrinsic differences, as it is in the case for MI. Since the rotational robustness of MI is higher than PCC, shown in Fig. 1a, it can tolerate intrinsic differences by randomizing up to 5 × 10⁵ voxels, as shown in Fig. 1d. It is clear that adding intrinsic differences beyond this point also causes the MI rotational robustness become less than zero and consequently fails registering images. However, the amount of intrinsic differences that each SM can tolerate is an important criterion and directly related to the robustness of the SM when there are no intrinsic differences between images for a given transformation type T.

Fig. 1.

a) Profile of PCC and MI for rotational transform in a typical brain image (1mm isometric voxel size), b) Profile of PCC and MI for different percentage of additive noise in the same image, c) Profile of PCC and MI for voxels randomization in the same image, d) The effect of different level of voxel randomization on the profile of the MI and PCC for rotational transform, e) Magnified version of PCC and MI profiles without randomized voxels in the range of [0 0.2] degrees, f) Magnified version of PCC and MI profiles with 10⁵ randomized voxels in the range of [0 0.2] degrees.

Robustness is also related to the accuracy of registration. Fig. 1e shows the magnified version of Fig. 1a in the range of [0 0.2] degrees. As seen in this figure, when there are no dis-similarities, both PCC and MI have a monotonically decreasing profile curve around the global optimum; however imposing only 10⁵ voxel dis-similarity changes the profile of the PCC as shown in Fig. 1f, which introduces a slight inaccuracy in the registration results. Whereas MI profile is still monotonically reduces in that range without having such an error. The profile of the MI will also have the same inaccuracy when we reach the intrinsic difference level of 4 × 10⁵. Therefore, by computing the robustness of each SM in the case of zero intrinsic differences, we have a systematic method of evaluating SM for each type of misregistration. Now let us describe our evaluation method.

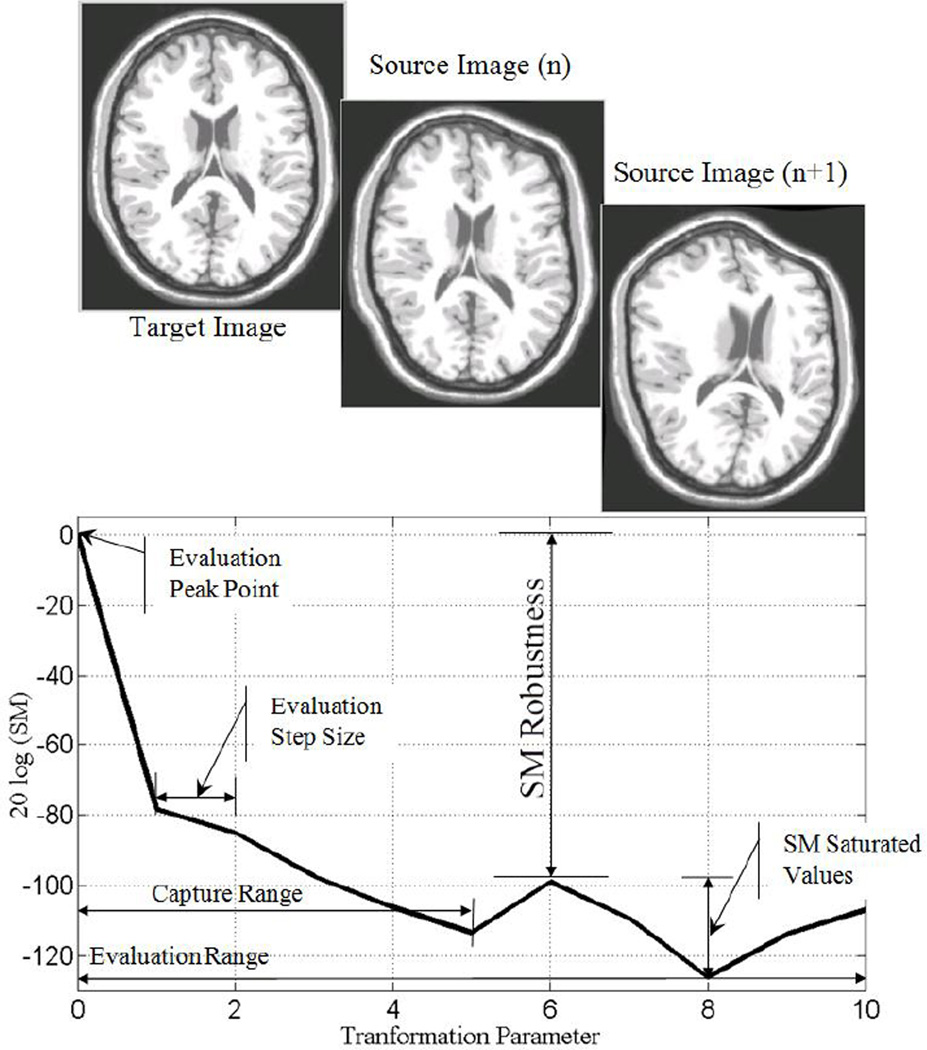
To have an unbiased evaluation, it is important to have a reference point which is fixed in all the experiments. We use the maximum value of the SM, when X and Y are intentionally chosen to be the same as the reference point in this evaluation. This is because for any transformation, regularization, cost function, optimization, and interpolation, if X and Y are intentionally chosen to be the same, then the computed SM for the image pair (X, Y) gives its maximum value. Thus, this maximum value is normalized to one and as described later in this section the range of SM variation will also be normalized to the range of [0 1] for each SM. The magnitudes of the transformation parameters μ are usually zero at the maximum point since there should be no change in the transformed source image. We refer to this point as the evaluation peak point (see Fig. 2) which is the same as the global optimum. Next, the severity of the misregistration is increased by increasing the magnitude of the transformation parameters μ by a small evaluation step size. The recomputed SM between the target image and the new transformed source image is less than its peak value. This process is continued iteratively by increasing the magnitudes of the transformation parameters μ by the evaluation step size, which results in a more severe misregistration in the source image, and a greater decrease in the recomputed SM for the new image pair. This iteration finally causes the recomputed SM to settle into its minimum value or range of values, which we refer to as saturated values, as shown in Fig. 2. The maximum of the SM saturated values is the local optimum. Therefore, the robustness of the SM for the given transformation can be computed by Equation (2). After obtaining the SM profile for the given transformation, then it needs to be normalized into the range of [0 1]. In despite of the computed values, each SM also has a theoretical maximum and minimum values, for instance magnitude of PCC is always in the range of [0 1] or mutual information is in the range of [0 q] where q ≤ min(H(X), H(Y)) and H(X), H(Y) are the entropy of images X, and Y, respectively. We used the theoretical maximum and minimum values to do this normalization; keeping in mind that in practice, as mentioned before, reaching to the maximum value for each SM is possible simply by choosing X = Y and T(μ) = I (identity matrix), whereas reaching the minimum value is not always possible. Once the normalization is done, for a given image and transformation type, the SM with higher robustness would be the one which is more effective in registering the same type of images for the given transformation T. In section 5, we empirically show that SMs with higher robustness tolerate more intrinsic differences and they are more effective in intermodal brain image registration.

Fig. 2.

Evaluation method: SM robustness as a function of transformation parameters that increasingly misregister a source image (transformed target image) from the original target image.

It is important to emphasize that robustness will be different for a different transformation or image type, for example, if the robustness of PCC is higher than MI for a rotational transformation, there is no guarantee that it will also be higher for a scaling transformation. Therefore, for each type of misregistration, the SM robustness needs to be computed separately. In the same way, rotational robustness for brain MR images may be different than satellite images or any other image type. However, as it will be shown in Table I, robustness of the same type of images (i.e., human brain T1 images) for a given transformation may have only slight differences. Therefore, we propose to compute each SM’s robustness for a few numbers of the same image types and report the average value as the final robustness. The focus of this paper is on human brain image registration, thus all the reported robustness are for brain images and may not be applicable to other types of images. In section 5, we compute the robustness of a selected set of SMs for a few transformation types; however the method is general-purpose in that it is applicable to any transformation, and any combination of the transformations. For example, if the combination of translational and scaling is the transformation of interest, then one might construct a two-dimensional profile surface for such a combination, i.e. the z axis will show the SM value and the x and y will be the parameters for scaling and translation. Please note that in the case of combined transformation there will be multiple capture ranges but only one robustness, which is the ration of the SM value at the global optimum and its value at the nearest local optimum.

Table I.

Robustness of various similarity measures corresponding to Fig. 4.

Category	SM	Min	Max	Mean	Median	STD
Spatial Dependency	NSMI	206.75	252.43	223.97	212.74	19.82
	SMI	189.74	235.47	206.99	195.76	19.85
	NSMINS	210.54	222.22	214.68	211.27	6.54
	SMINS	193.49	205.12	197.64	198.32	6.48
	GMI	33.84	37.77	35.78	35.74	1.96
	SOMI	15.93	16.63	16.26	16.22	0.35
Information Theoretic	NMI	26.43	29.38	28.11	28.51	1.51
	MI	20.87	23.66	22.46	22.87	1.44
	ECC	10.40	11.82	11.21	11.40	0.72
	JE	5.68	5.75	5.72	5.74	0.04
	KLD	0.99	1.07	1.03	1.02	0.04
Statistical	MSD	7.37	8.76	8.25	8.60	0.76
	HD	4.02	4.69	4.35	4.35	0.33
	PCC	2.79	5.30	3.99	3.88	1.26
	SCC	2.73	3.38	3.08	3.14	0.33

Robustness and capture range, as we defined in our evaluation method, are two different criteria for evaluating SMs. Robustness is an indicator of a SM’s capability to measure image similarity whereas capture range gives the range in which the SM actually measures such similarities; outside this range the SM values are random and should not be trusted to direct the optimization process. We have constructed this evaluation method only based on robustness because regularization, as a separate component of registration process, increases the capture range of a SM with the cost of losing robustness. Hence, considering capture range as another independent criterion introduces unnecessary complexity to the evaluation and also opens up a new discussion as how to decouple the effects of regularization method and SM in the final registration outcome. Thus, we leave the evaluation of capture range out of this study. However we should emphasize that without adequate capture range the most robust SMs might not be practically suitable for image registration, for instance if the SM profile become close to Dirac delta function (capture range=0), its robustness will be infinity but it will be practically unusable..

4. Human Brain Image Dataset

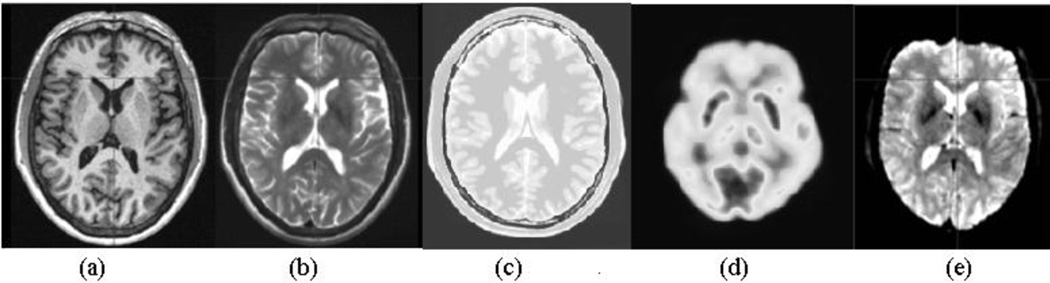
In order to evaluate and compare the performance of the listed SMs for 3D brain image registration, we used various modalities of 3D brain images. Digital brain phantom images of the BrainWeb database give three simulated structural MR images: T1-weighted (T1), T2-weighted (T2) and Proton Density (PD). For a thorough experimental evaluation, we wanted to include functional and physiological brain images as well, so we used the methods described in [34] and [35] to generate realistic Echo Planar Imaging (EPI) and Positron Emission Tomography (PET) images, respectively, from the BrainWeb images. The BrainWeb images have been used extensively to study the performance of anatomical brain mapping techniques such as nonlinear co-registration, cortical surface extraction, and tissue classification [36]. The main advantages of using this database are: (i) the answer is known prior to experimentation, and (ii) imaging parameters can be controlled independently. Since the source for simulation of the functional images is the same digital phantom, one has a systematic means of establishing a gold standard for registration and control over the level of image degradation for all the modalities. Fig. 3 shows samples of simulated brain images in our dataset.

Fig. 3.

Sample simulated brain images: (a) T1, (b) T2, (c) PD, (d) PET, (e) EPI functional.

We obtained T1, T2 and PD brain images with 1 mm isometric resolution, 8-bit quantization, and different levels of image degradation (noise and intensity non-uniformity) directly from the BrainWeb database. For the creation of the EPI functional brain images, we selected a typical EPI size of 64×64×36 (5.03×2.83×3.39 mm) and applied a local intensity fading to a small region in the anterior and inferior part of the prefrontal cortex and temporal lobes to partially simulate the effect of signal loss artifacts in each EPI before resampling to the corresponding high-resolution anatomical image using rigid registration [34].

We simulated PET brain images from the structural MR brain images as follows. First, we segmented the structural MR brain images into regions of different tissue types (gray matter, white matter, cerebral spinal fluid) and structures (skull, skin, and fat). Then we assigned 3D distributions of the tracer concentration and tissue attenuation coefficient throughout the segmented brain images, projected data through these distributions according to the PET acquisition geometry, and incorporated physical effects associated with data acquisition (i.e., photon attenuation, scatter, and random and statistical noise). Finally, we reconstructed a set of projections using the filtered back projection algorithm [35]. Every experiment in the next section was performed on all five modalities of the images stated in this section, and the average outcome is reported as the results.

5. Experimental Results

In this section, we apply the evaluation method described in section 2 to the dataset images in section 4 to examine the effectiveness of the listed SMs in section 3 under the performance metric of robustness. Then we show that the SMs with lower robustness are less tolerant to image degradation and more likely to fail in intermodal image registration. We use tri-linear interpolation throughout the paper.

5.1 Robustness

As mentioned earlier, SM robustness depends only on the transformation type and the image itself. We compute SM robustness separately for different types of spatial transformation (translation, rotation, scaling, non-linear). Although there are many non-linear (deformable) transformation types used in medical image registration, reviewed in [37], [38], here we only considered the B-spline model as a representative of non-rigid transformations.

5.1.1 Translation

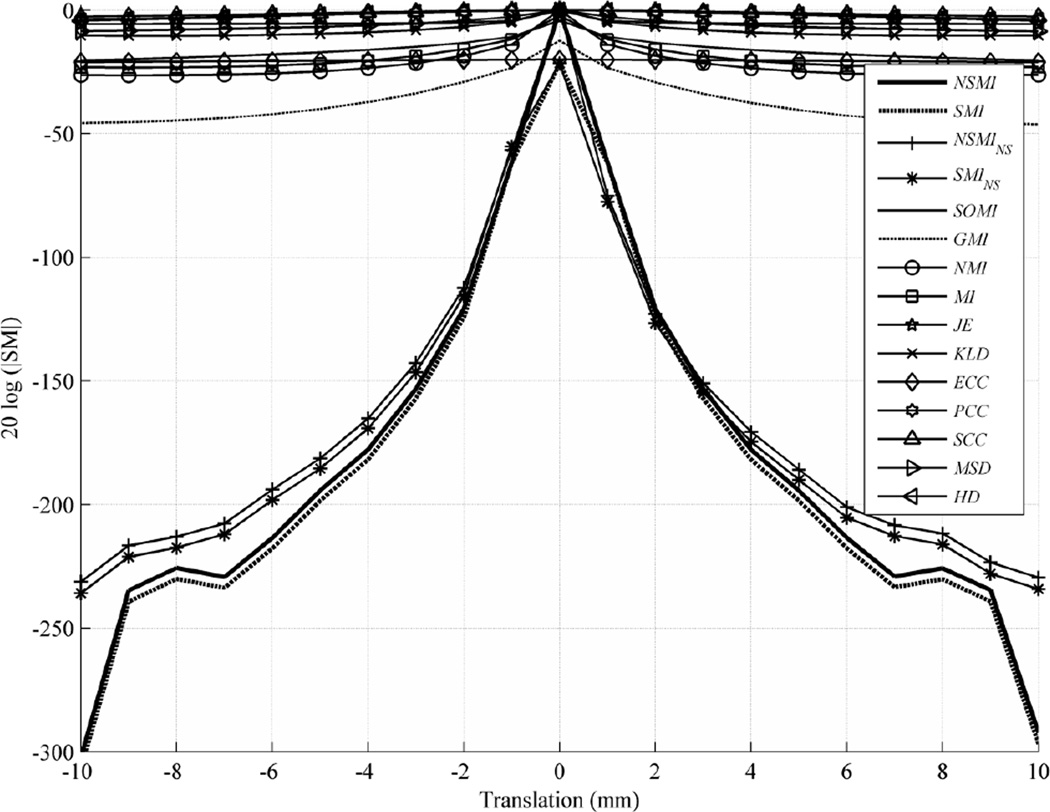
To study the behavior of the SMs under translational transformation, we applied a rigid-body shift along x axis to target image to create a source image. The evaluation range for this evaluation was [−10, 10] mm with an evaluation step size of 1 mm. Fig. 4 shows the outcome of this evaluation, depicting the average evaluation result over all image modalities in the dataset. To exhibit these results more clearly, the logarithmic scale (db=20log(|.|)) for the vertical axis is used, and all the SM values are normalized to the range [0, 1] in order to have a fair comparison. Details of each SM normalization are stated in Appendix A. Noting that drawing all 15 SMs in one figure makes its readability cumbersome, Table I lists the SMs in the order of their robustness from top to bottom in each category, and gives the standard deviation, median, and minimum/maximum values of the results.

Fig. 4.

Average evaluation outcome for 2D translations with step size of 1 mm and evaluation range of [−10, 10] mm.

Since all of the measures in each category behaved similarly, for the rest of the paper we selected and compared only the best performing SMs from each of the statistical (MSD) and information theoretic (NMI) categories and three SMs with spatial dependency (GMI, SOMI, and NSMI) for the sake of figure clarity. As can be seen from Table I, the robustness of NSMI was 224 db, outperforming NMI by 196 db, GMI by 188 db, SOMI by 208db, MSD by 216 db, and so on. Fig. 4 and Table 1 show the difference between symmetric SMI/NSMI and non-symmetric SMI_NS/NSMI_NS. One can see that SMI/NSMI performed slightly better and are more desirable for use in the optimization cost function. Subsequently, we selected only symmetric NSMI for comparison with the other selected SMs (MSD, NMI, SOMI, and GMI).

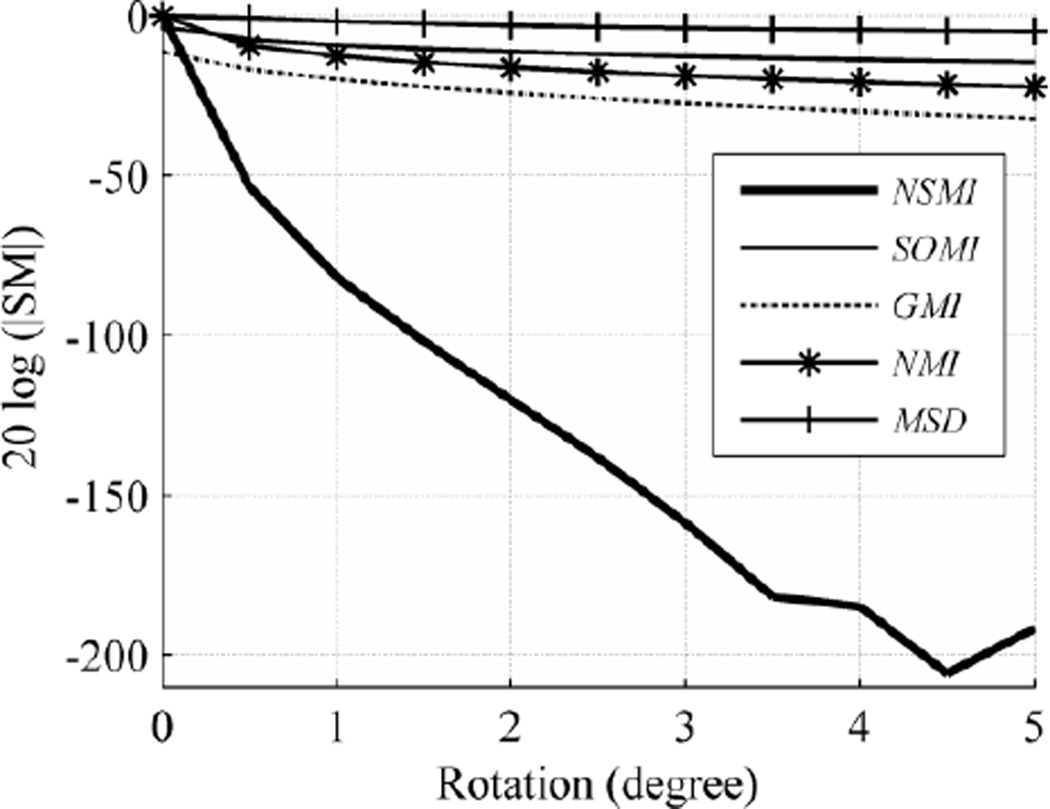
5.1.2 Rotation

For slice rotation, we considered a step size of 0.5 degree and an evaluation range of [0, +5] degrees. Since the selected SMs (MSD, NMI, SOMI, GMI, and NSMI) have almost symmetric behavior around the peak point, the same behavior is expected in the evaluation range of [−5, 0] degrees. It should be noted that we cropped both the target and source images to a smaller size to eliminate the rotational artifacts in the target image.

The final outcome shown in Fig. 5 is the average of all the results from different images in the database. As can be inferred from Fig. 5, the robustness of NSMI is higher than NMI by 170.9 db, GMI by 170.67 db, SOMI by 180.57 and MSD by 186.79 db. As listed in Table I, the deviation of each SM robustness is negligible with respect to the scale of each SM. Hence, only the average values in the figures are reported for clarity.

Fig. 5.

Average evaluation outcome for rotation with step size of 0.5 degree and evaluation range of [0 +5] degrees.

5.1.3 Scaling

We employed global scaling which takes place along all three axes at the same time. Up- and down-scaling (stretching and shrinking) have different effects on source images so we report their robustness separately. When a 3D image scales up (scale factor larger than 1), no loss of image information occurs, while scaling down (scale factor smaller than 1) leads to loss of image information. In either case, to be able to compute the SMs, it is required to have equal size source and target images.

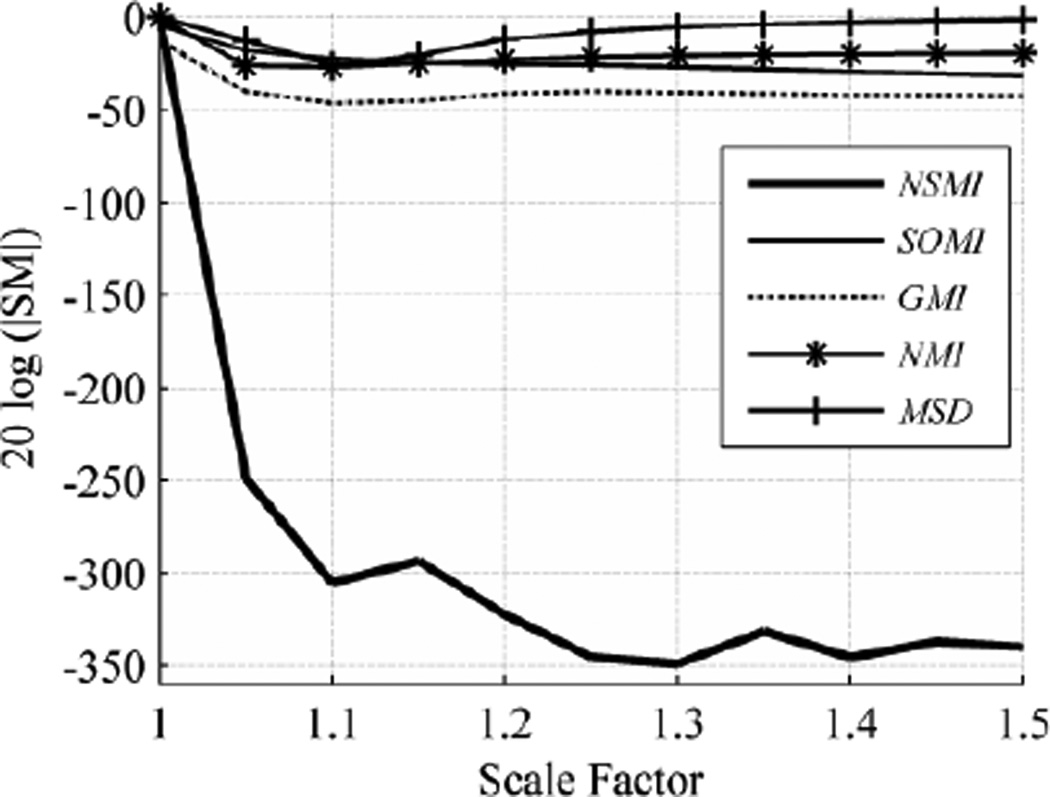
When the scale factor is larger than 1, the source image stretches. Resizing the target image to match the source image size causes no significant change in any of the SMs over the evaluation range. Therefore, we cropped the stretched image (source image) to match the target image size. Fig. 6 shows the evaluation outcome for scaling over the evaluation range [1, 1.5]. As shown in Fig. 6, the robustness of NSMI outperformed the robustness of GMI by 265.76 db, SOMI by 266.59 db, NMI by 274.99 db, and MSD by 292.24 db.

Fig. 6.

Average evaluation outcome for stretching with step size of 0.05 and evaluation range of [1, 1.5].

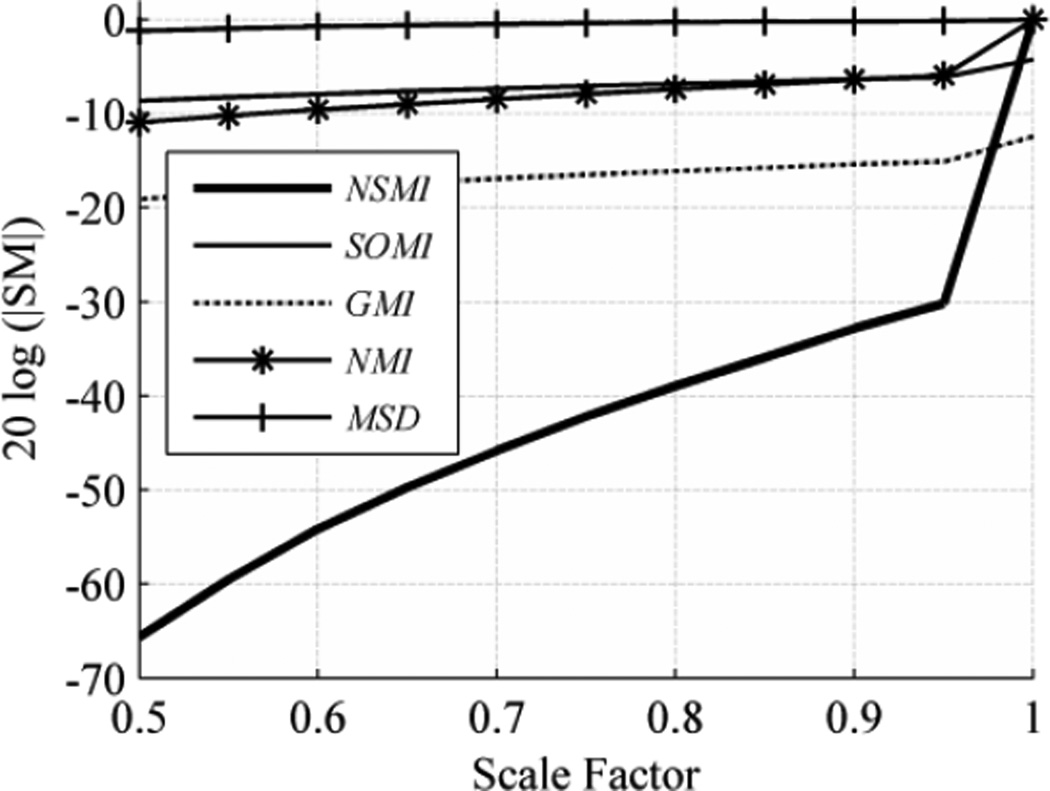
When the scale factor was smaller than 1, the resulting image shrank. To prevent any aliasing, antialiasing was applied and the smaller source image was resized to match the target image size. This situation is similar to the registration of a low-resolution image to a high-resolution one, for example when registering functional MR with anatomical MR images. Fig. 7 shows the evaluation outcome for shrinking over the evaluation range [0.5, 1] with step size of 0.05. As shown in Fig. 9, NSMI outperformed NMI by 54.69 db, GMI by 58.97 db, SOMI by 63.23 db and MSD by 64.23 db. It should be noted that no significant change in MSD occurred in this experiment. If one just wishes to see the effect of subsampling and smoothing on the SMs profiles then this is a good example, since in this experiment downscaling is done by subsampling and antialiasing via a Gaussian smoothing filter.

Fig. 7.

Average evaluation outcome for shrinking with step size of 0.05 and evaluation range of [0.5, 1].

5.1.4 Free Form Deformation

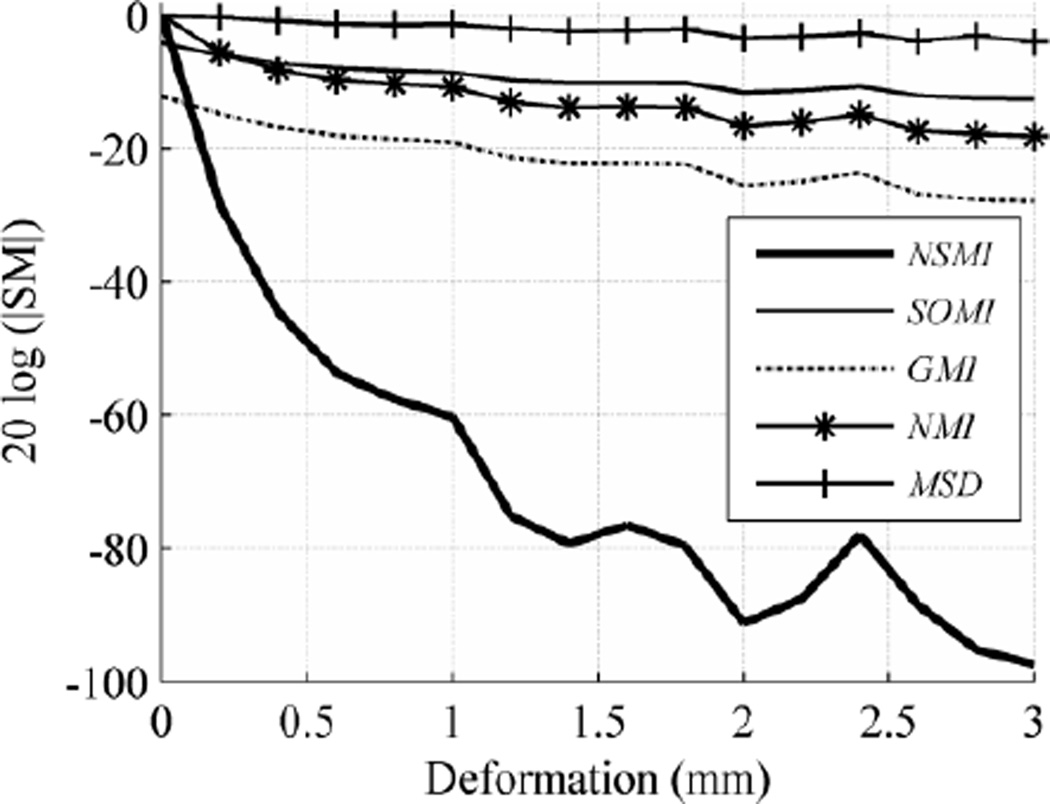
For non-rigid (deformable) transformations, the problem becomes more challenging. The issue is the number of degrees of freedom in the parameters of the non-rigid transformation which can be up to three times the image size. In addition to the large number of control parameters, there is also the choice associated with the transformation function. B-spline is the most widely used transformation function in non-rigid image registration [37], shown to be optimal as an approximation function [39], [40]. The theory and methods for object modeling using B-spline are well developed and discussed in [41].

We used a free-form deformation (FFD) model based on the cubic B-spline due to its use by many researchers in medical imaging, e.g. in [42] for heart modeling, in [43] for 3D object modeling, in [43] for registering SPECT cardiac images, and in [45] for registering dynamic contrast-enhanced MR breast images. The formulation of the FFD model based on the cubic B-spline is thoroughly covered in [38], [45]. In this experiment, we selected a uniformly spaced grid with a spacing size of δ=30 mm to serve as the FFD control points. The source images obtained from the BrainWeb phantom of size 217×181×181 were truncated to 210×180×180 for simplicity. This made the size of the control mesh 10×9×9 in which the number of degrees of freedom became 3×10×9×9=2,430. It is easy to see that examining the behavior of the SMs for deviations of all these control points is not practically feasible. Hence, a random number of control points (10 to 100) were randomly selected from the FFD mesh. These random points were made to deviate along all three directions. For evaluation purposes, it was necessary to control the severity of the deformation, but deviating all the control points along the same direction produces a uniform deformation throughout the image. Instead, the directions of the deviations in the selected control points were chosen randomly while their magnitudes were controlled by the evaluation procedure. Fig. 8 shows the evaluation outcome for the FFD transformation over the evaluation range [0, 3] mm with a step size of 0.2 mm. As seen in Fig. 8, NSMI outperformed GMI by 65.0 db, SOMI by 70 db, NMI by 51.61 db, and MSD by 75.2 db.

Fig. 8.

Averaged evaluation outcome for FFD transformation with step size of 0.2 and evaluation range of [0 3].

Of course, this small sample is not representative of the types of non-rigid misregistrations prevalent in brain image registration. In future work, it would be interesting to perform a statistical analysis to find the most representative types of non-rigid transformations and to apply these types of misregistrations.

5.2 Robustness to image degradation

So far in our evaluation protocol, target and simulated source images have not contained any kind of image degradation, so tests have resulted in the maximum possible robustness for each SM. Image degradation is one of the main causes of registration failure. In this experiment we not only evaluated SM tolerance to image degradation but also empirically demonstrated that SMs with higher robustness were more reliable in registering degraded images. Increasing the level of image degradation in source images eventually causes SMs to fail in registering images. However, the level of image degradation that causes each SM to fail is different.

There are a number of issues in validating the accuracy of a registration which are discussed in [46]. In the literature, it is common practice to report registration accuracy with respect to the parameter set of the spatial transformation μ. Even though this seems applicable for translational and rotational transformations (translational misregistration as the magnitude of the error and rotational misregistration as the phase of the error), it is not certain how to quantify accuracy for scaling and non-rigid transformation parameters. On the hand, as we mentioned earlier, the location of local optima are random and meaningless, thus cannot be used as the measure of accuracy. Therefore, we consider SM validation as a Boolean function here with a pass or fail outcome, computed separately for all the registration types and with a controlled level of image degradation. We define failure when the SM peak deviates from the gold standard for at least half of the evaluation step sizes. Fortunately, the BrainWeb database allows one to add a controlled level of simulated noise and Intensity Non-Uniformity (INU) to a source image. In this experiment, we added different levels of noise (5%, 10%, 20%, 40%) and INU (20%, 40%, 60%), and also different combinations of them to the (T1) target image to obtain the degraded source images. Then we evaluated all three registration types (rigid, affine, and non-rigid) with the most effective SMs (NSMI, NMI).

Based on the results reported in the previous subsection, NSMI was found to be the most effective SM. It outperformed NMI by 196 db in translation, by 170 db in rotation, by 274 db in scaling, and by 51 db in FFD misregistration. As can be seen in Table II, NMSI successfully registered all 11 degraded images for translation and scaling misregistration whereas NMI succeeded in only registering 3 of them. This is because NSMI robustness was higher than NMI by more than 200 db for these two types of misregistration. It failed in a couple of severe situations for rotation, whereas NMI failed in 8. This is because its robustness was less than that for translation and scaling (150 db higher than NMI). For FFD, NSMI only performed successful registration in three more situations than NMI, since its robustness differed by only 51 db. This clearly shows the relationship between the defined robustness and the stability of the SMs to image degradation. As shown in Table II, there were in total 44 experiments of which NSMI failed registering only 8 cases while NMI failed in 33 cases.

Table II.

Registration test results (pass/failed=X) for registering T1 target image to degraded and spatially transformed source image using NMI and NSMI

	NMI				NSMI
Degradation	Translation	Rotation	Scaling	Deformation	Translation	Rotation	Scaling	Deformation
5% Noise	pass	pass	pass	pass	pass	pass	pass	pass
20% INU	pass	pass	pass	pass	pass	pass	pass	pass
10% Noise	pass	pass	pass	X	pass	pass	pass	X
40% INU	X	X	X	X	pass	pass	pass	pass
20% Noise	X	X	X	X	pass	pass	pass	pass
60% INU	X	X	X	X	pass	pass	pass	X
40% Noise	X	X	X	X	pass	X	pass	X
5% noise & 40% INU	X	X	X	X	pass	pass	pass	pass
10% noise & 20% INU	X	X	X	X	pass	pass	pass	X
20% noise & 40% INU	X	X	X	X	pass	pass	pass	X
40% noise & 60% INU	X	X	X	X	pass	X	pass	X

5.3 Robustness to intermodal registration

In general, a consistent SM performs satisfactory registrations for all brain image modalities. So far we have shown the superiority of NSMI compared to other SMs by the robustness metric, and we have validated the results by performing registration between degraded images. In this section, we register between five different brain image modalities to demonstrate that more robust SMs are more successful in registering intermodal images. We obtained three structural (T1, T2, and PD) brain MR images directly from the BrainWeb database, and EPI and PET brain images through simulation as described in section 4. The availability of gold standards for these images made it possible to validate intermodal image registration. Any of the transformations discussed in this paper can be used for this evaluation; we selected spatial vector translation. Table III shows the result of this experiment; values in bold correspond to NSMI and values in italic font to NMI. The values along the diagonal of the table indicate the robustness of NSMI and NMI for registering an image to itself. As can be seen from this table, NSMI exhibited a superior performance to NMI for intermodal image registration. A simple way of evaluating SM consistency is to average the robustness of NSMI and NMI in all 25 experiments (robustness of a failed experiment is considered to be zero). In this way, the result for NSMI was 35 db and for NMI 12 db.

Table III.

Robustness (db) of NS, MI and NMI for intermodal image registration.

		Source Image
		T1	T2	PD	PET	EPI
Target Image	T1	83.97, 26.43	64.86, 12.61	59.94, 14.22	13.52, 6.67	11.22, failed
	T2	64.50, 13.79	86.86, 28.52	66.76, 18.97	57.23, 12.76	11.59, 0.92
	PD	61.08, 12.04	66.02, 17.93	92.07, 29.24	14.62, 12.49	10.90, 0.98
	PET	13.61, 3.13	51.57, 5.30	14.69, 5.89	78.99, 24.28	11.88, 1.02
	EPI	11.13, failed	12.25, 3.00	10.81, 3.25	34.50, 24.24	89.76, 18.63

6 Conclusion

In this work, we proposed a new method for evaluating the effectiveness of SMs in registering brain images, assuming that the image type and misregistration are given, which is the case in most brain image registration problems. This method uses a single performance metric, named robustness, obtained based on the misregistration type over a given image, which makes it possible to quantitatively compare different SMs. Even though this method is general-purpose in the sense that it is applicable to any image, our evaluation was focused on misregistered and degraded images of human brains. We computed robustness for selected SMs for five different modalities of brain images (T1, T2, PD, EPI, PET) and four different misregistration types (translation, rotation, scaling, and B-Spline), noting that the method can be easily extended to any combination of transformation as well. Furthermore, we have empirically shown that SMs with higher robustness are not only more tolerant to brain image degradation but are also more effective for intermodal brain image registration. We have defined the normalized SMI, NSMI, and empirically extended its definition to 3D brain images. Furthermore, we have reported that NSMI robustness was higher than the classical NMI by 196 db in translation, by 170 db in rotation, by 274 db in scaling, and by 51 db in FFD-type misregistration, which resulted in better accuracy and 200% improvement in intermodal image registration.

Our proposed evaluation method here was purely based on robustness; however capture rage also plays a significant role in the optimization of a registration problem. Evaluation of SM based on both robustness and capture range and their trade off through the regularization process seems a natural next step of this project.

Highlights.

1. Image registration is the most fundamental problem in neuroimaging

2. Functional imaging usefulness is directly depend on the underlying registration

3. Many similarity measures (SM) are used in brain image registration

4. Comparing the SM are made possible here by a single metric, Robustness

5. Shown that robust SM are more reliable in registering degraded and images

Appendix A. Normalization of Similarity Measures

This appendix covers the normalization or rescaling done on all the similarity measures so that they fall in the range [0, 1]. PCC SCC, and ECC are by default in the range [0, 1]. NMI and NSMI are both between the range [1, 2], therefore they are normalized simply by subtracting one from them. KLD is normalized simply by adding one. JE is downscaled by min(H(X),H(Y)) and its inverse is in the range [0, 1]. MI is always between 0 and 8, for 8-bit quantized images, thus it was downscaled by 8. The same rescaling was done for SOMI and GMI. MSD by default can be in the range of [0, 256²], however due to the [0 100] range observed in the experiments, it was downscaled by 100. Since the MSD peak point is a minimum, it is subtracted from one after downscaling. The experiments showed that HD is in the range [0 25], thus it was downscaled by 25 and subtracted from one. For SMI, the downscaling is more involved since the number of random variables in the image volume is the same as the image size. Hence, it is necessary to downscale SMI by the image size first and then by 8, for 8-bit quantized images, to map it to the range [0, 1].