On the possibility of quantitative refractive-index tomography of large biomedical samples with hard X-rays

Abstract

One of the most promising applications of the X-ray phase-contrast imaging is the three dimensional tomographic reconstruction of the index of refraction. However, results reported so far are limited to relatively small samples. We present here the tomographic reconstruction of the index of refraction distribution of a large biomedical sample (> 10 cm diameter). A quantitative study comparing the absorption and phase contrast (analyzer-based) tomography images shows that the distribution of the index of refraction obtained with the phase contrast method provides a more accurate depiction (3–10 times larger signal to noise ratio values) of the sample internal structure. Thanks to the higher sensitivity of this method, the improved precision was obtained using an incoming photon fluence on the sample several times smaller than in the case of absorption imaging.

1. Introduction

X-ray computed tomography (CT) proved to be a powerful method for the examination of the internal composition and structure of objects. CT can be combined with various imaging modalities allowing to accurately measure the physical properties of a sample. X-ray phase contrast imaging (PCI) can be used for measurements of the spatial derivatives of the phase shifts, i.e. refraction (deflection) angles, induced in the X-ray wave when propagating through an object. Combined with CT it allows the three dimensional (3D) reconstruction of the index of refraction distribution in a sample. It was shown that refraction based imaging can be much more sensitive to the sample composition than conventional absorption imaging, particularly in the hard X-ray regime [1]. Several methods have been developed over the last decade to reconstruct the index of refraction from CT data acquired using X-ray PCI techniques. These are, for instance, the diffraction enhanced imaging method [2] for analyzer-based imaging (ABI), the phase-stepping procedure [3] for grating interferometry and the recently developed approach for quantitative coded aperture imaging [4]. These methods have been applied to imaging of simple models or to few centimeters thick objects [4–6]. To the best of our knowledge, the validation of these quantitative procedures on large and complex objects is still missing in the literature. Demonstrating the possibility of an accurate reconstruction of the refractive index for thick and dense samples is therefore desirable, for instance, in the perspective of a clinical implementation of PCI-CT. In the present work we prove the potential of quantitative ABI by reconstructing the index of refraction in a whole human breast (embedded in an 11-cm diameter container) showing a high X-ray absorption (∼90%). We also report results of a quantitative comparison between refraction based CT (RCT) and absorption based tomography (ACT). The material density was used as a reference physical quantity for the comparison, since it can be derived from both CT imaging methods.

2. Mathematical description of the method

Propagation of hard X-rays through an object can be well described under the geometrical optics approximation using the notion of the complex index of refraction n = 1 − δ + iμλ/4π, where $i=\sqrt{-1}$, λ is the wavelength of the radiation, δ is the index of refraction decrement and μ is the linear attenuation coefficient. The distribution of δ inside the object can be written as:

$$\delta \left(\mathit{r}\right)=\overline{\delta }\left[1+\tilde{\delta }\left(\mathit{r}\right)\right]$$ (1)

where r = (x,y,z) are the coordinates in three dimensional (3-D) Euclidian space. If δ̃(r) ≠ 0, X-rays will experience refraction, and thus an angular deflection within the sample. The refractive index distribution expressed by Eq. (1) can be substituted into the beam propagation equation [7]. The mean value δ̄ is then removed since it is a common factor in both the left- and the right-hand sides of the equation. Therefore the angular deflection of an X-ray is proportional only to changes in the refractive index and does not depend on its mean value. In many practical cases the X-ray trajectory can be well approximated as a straight line. The total deflection angle α (Fig. 1(a)) of an X-ray propagating in a plane x = x ₀ through the object is:

$$\alpha \approx \int \frac{d\tilde{\delta }\left(y,z\right)}{dy}dz.$$ (2)

For a rotating sample, there exists a simple way to find the distribution of the δ̃(r) from measurements of the deflection angles by applying the filtered backprojection (FBP) algorithm to projections of the transversal gradient of δ̃(r) (gradient projections) [7]:

$$\tilde{\delta }\left(y,z\right)=\underset{0}{\overset{\pi }{\int }}{\left[\alpha \left(y^{\prime },\mathrm{\Theta }\right)*g\left(y^{\prime }\right)\right]}_{y^{\prime }=-z\mathit{sin}\mathrm{\Theta }+\mathit{ycos}\mathrm{\Theta }}d\mathrm{\Theta },$$ (3)

where Θ is the angle of rotation of the sample, * denotes the convolution operator, g(y′) is the filter function, which is the inverse Fourier transform of −isgn(Y′)/2π; sgn(Y′), and sgn(Y′) is the sign function in the reciprocal space, y′ is the y axis in the rotated tomographic coordinates.

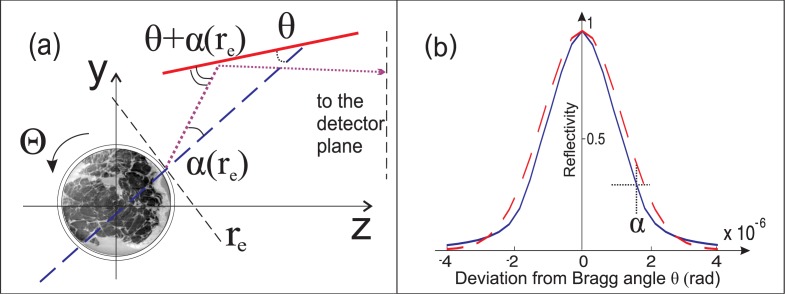
Fig. 1.

Sketch of the image formation process in a plane x = x ₀. (a) Dashed line indicates the propagation direction of the unperturbed X-ray that hits the AC surface (solid thick line) at the Bragg angle θ; the dotted line represents a ray at a point in the object exit plane r _e, which was deflected after propagation through the sample by an angle α. This ray impinges on the AC with an angle close to but not exactly equal to the Bragg angle, thus the intensity of the reflected ray decreases by a factor defined by the height of the RC at that angular point. (b) Normalized measured reflectivity (RC) of the AC (solid line) and its approximation by a Gaussian function (dashed line). The curves are drawn for φ = 0.

In order to measure experimentally the deflection angles the ABI technique was used. The basics of the method are described elsewhere [2, 8] and briefly represented in Fig. 1(a). The visualization of the phase effects is achieved by means of a perfect Bragg analyzer crystal (AC) positioned between the sample and the detector. The AC modulates X-rays emerging from the sample and acts as a very narrow angular slit, reflecting only those rays that make the correct angle (Bragg angle) with the atomic (Bragg) planes of the crystal. It can be shown that the resulting image intensity at the detector plane, z = z_d, can be expressed in a good approximation as [2]:

$$I_{z_d}\left(x,y\right)=I\left({\mathit{r}}_e\right)R\left[\phi -\alpha \left({\mathit{r}}_e\right)\right],$$ (4)

where I(r _e) is the intensity of the wave at the sample exit plane r _e = (x_e, y_e), R is the rocking curve (RC) [9] of the AC (Fig. 1(b)), and φ is the angular displacement of the AC from the Bragg angle for the used photon energy. Thus the image intensity I _zd (x, y) is defined by the intensity of the local (along the surface of crystal) reflection of the X-rays impinging on the AC at an angle equal to φ − α(r _e). The experimental R and, therefore, the image intensity are determined by the collimation of the beam formed by a block of monochromators and depend on the physical properties of the crystal. In order to derive α(r _e) from the image intensity function R can be approximated by a simpler function allowing analytical solution of this problem [2, 8, 10]. We calculated the deflection angle at the object exit plane by approximating the RC by a Gaussian function with a variance σ ² (dashed line in Fig. 1(b)). This yields the following expression for the PCI image intensity:

$$I_{z_d}\left(x,y\right)=I\left({\mathit{r}}_e\right)\mathit{exp}\left[-{\left(\phi -\alpha \left({\mathit{r}}_e\right)\right)}^2/{\sigma }^2\right].$$ (5)

This equation contains two unknown quantities: the deflection angle α(r _e) and the intensity of the X-ray beam I(r _e). A two equations system can be written if a pair of images is acquired at two different angular positions φ _1,2 of the AC; by solving this system α(r _e) can be calculated at every point in the object exit plane. A Gaussian function is a very good approximation for the slopes of the RC as discussed in [8, 10]. It allows to obtain an accurate estimation of the first derivative of the RC in the regions corresponding to the full width at half maximum. The remaining discrepancies can be neglected because there are other, more significant contributions to the experimental error (in particular, quantum noise and detector blurring). This was verified by a comparison of experimental images of simple plastic phantoms with the results of numerical simulation.

3. Experiment and results

The experiment was performed at the biomedical beamline (ID17) of the European Synchrotron Radiation Facility (ESRF, France). A double Si Laue crystal was used to select a quasi-monochromatic (ΔE/E ∼ 10⁻⁴) and quasi-parallel X-ray wave (divergence <1 mrad, horizontally, and <0.1 mrad, vertically) from the beam produced by a 21-pole wiggler. The photon energy was set to 50 keV. A 3 cm thick and symmetrically cut Si (333) crystal was used to analyze the X-ray beam after its propagation through the sample, while another identical crystal, placed right before the sample and set at the (333) reflection, was used as an additional monochromator. The full width at half maximum of the experimentally measured RC was equal to 1.9 μrad, which corresponds to σ ²=0.66 μrad². Two images at φ _1,2 ≈ ±0.9 μrad with respect to the Bragg angle were recorded for every angular view (projection) of the object. The two complete CT data sets (acquired as described below), consist each one of 500 projections uniformly sampling the range of Θ = [0..π) rad. A charge-coupled device detector (CCD) with a gadolinium-based fluorescent screen was used to register images with an effective pixel size of 96 × 96 μm². Estimated detection efficiency was rather low: only ∼3% of hard X-rays incident on the detector aperture contributed to images. The sample, a formalin fixed whole human breast provided by the Department of Pathology of the Ludwig Maximilians University (Munich, Germany), was embedded in a cylindrical container with an internal diameter of 10 cm and a wall thickness of 0.5 cm. The sample was installed in such a way that the rotation axis of the cylindrical container was parallel to the AC surface (see Fig. 1(a)). Since the height of the synchrotron beam was limited to 1.5 mm, per each angular position of the sample 80 vertical translations were necessary to image the entire object. Every five vertical steps reference images (taken with the sample out of the beam) were acquired in order to perform normalization, i.e. to correct for the beam inhomogeneities and fluctuations. The PCI CT scan of the entire sample was performed in about one hour and a half.

Deflection angles were calculated using Eq. (5) and RCT was performed according to Eq. (3). A reference ACT data set was obtained by removing the AC and placing the CCD camera directly downstream the object exit plane. The single Si (333) monochromator located just before the sample was removed to ensure that the X-ray beam impinges on the detector plane at the normal angle like in the RCT experiment. The ACT reconstruction was performed by using the FBP algorithm with the standard ramp filter; 2D maps of the distribution of the linear attenuation coefficient (Fig. 2(b)) were so obtained.

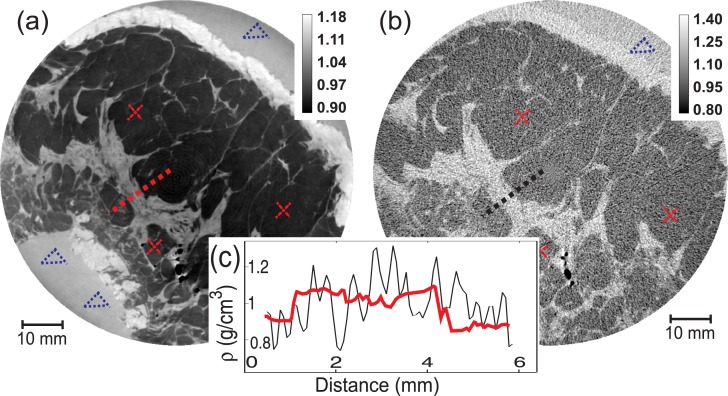
Fig. 2.

Distribution of the material density in a slice of the examined sample obtained using (a) refraction CT and (b) absorption CT. Darkest gray levels correspond to the fat tissue, brightest to the skin, intermediate gray values show other anatomical features. The group of black spots are air bubbles trapped inside the tissues. The unit of the colorbar values is g/cm³. To derive the density of the different materials several regions of an image were considered as it shown, for example, by triangles (formalin samples), and crosses (adipose tissue samples). In the inset (c), the 1D density profiles at the adipose-glandular-adipose tissue interfaces [indicated by dashed lines in (a) and (b)] for RCT and ACT correspondingly, are shown.

The density ρ of the different materials forming the sample can be calculated both from the real part of the index of refraction by using the asymptotic electrodynamics expression ρ ∼ κδ̃[11] and from the imaginary part as ρ ∼ τμ[12], where κ and τ are material-independent constants at a given photon energy. Figure 2 shows the distribution of the materials density within a slice of the human breast specimen obtained in the two cases (a: RCT; b: ACT). For every material, its density was estimated as the average value calculated from three 20×20 pixels regions taken in different zones across the image. These regions were chosen following the indications of the radiologist. The related standard deviations were used as the error Δρ of the density value. In the Table I values for the 10% formalin solution, the adipose tissue and other tissues forming the breast sample are compared with expected values taken from reference databases [13, 14]. Estimates derived from RCT and ACT measurements are both in agreement with the theoretical values within the calculated errors. The error bars of the RCT values are always smaller than those of the ACT case. Correspondingly, the signal to noise ratio (SNR, last two columns of the Table I), estimated as ρ̄/Δρ, is 3–10 times higher in the RCT images. The expected values are tabulated for a standard average unfixed breast. Small deviations of the effective calculated values from the tabulated ones are therefore easily justified. In Fig. 2(c) signal profiles drawn across the same region of the density images obtained with RCT and ACT are shown. These plots clearly demonstrate that the interfaces between different details and tissues are sharper in the RCT case than in ACT.

Table 1.

Estimation of the density of different materials derived from RCT and ACT reconstructions

Material (tissue)	Expected ρ̄, g/cm3	Measured RCT	ρ, g/cm3 ACT	SNR RCT	SNR ACT
Adipose	0.95	0.97±0.01	0.94±0.12	97	8
Skin	1.09	1.13±0.03	1.13±0.10	38	11
Glandular	1.04	1.05±0.02	1.13±0.13	52	9
Formaline 10%	1.08	1.10±0.02	1.10±0.10	55	11

The reduced amount of the high frequency noise in RCT image with respect to ACT image can be partially explained by the inherent properties of the filter function g(y) used for the reconstruction (see Eq. (3)). In order to make a straightforward comparison we used the most basic algorithms in both cases. That is why high frequency noise is amplified in ACT case, since the standard ramp filter without any additional window function was used. This noise is not that evident in RCT image, because the filter function for gradient projection is flat. The smaller SNR obtained for ACT are also related to the absence of the AC, which provided almost complete rejection of scattered (multiple incoherent scattering mechanism) photons during RCT scan.

The photon flux used to record the two CT data sets has been measured by means of a calibrated ionization chamber (PTW 31010, PTW, Freiburg, Germany). The measured photon fluxes incident on the sample, expressed in photons/mm²/sec, are (9.72 ± 0.04) × 10⁸ and (3.10 ± 0.02) × 10¹⁰ for RCT and ACT, respectively. By considering the total (for 500 projections) integration times, the respective fluences are (3.74 ± 0.01) × 10¹⁰ photons/mm² and (2.02±0.01)×10¹¹ photons/mm². The mean glandular dose was estimated by means of Monte Carlo simulation performed using the GATE code [15]. The values are ∼120 mGy and ∼340 mGy for RCT and ACT reconstructions correspondingly. This was the proof of principle study and we did not aim on optimizing performance of the setup. The rather high value of the dose deposited in the sample during RCT scan can be dramatically decreased by using a detector with a higher efficiency (up to one order of magnitude dose reduction) and by applying advanced reconstruction algorithms (an additional several times reduction; we are currently developing an efficient approach for the hard X-ray RCT). Results of this work indicate that RCT can provide a better depiction of the sample structure than ACT even at a reduced number of photons (∼6 times) and, therefore, absorbed radiation dose.

4. Conclusions

In summary we have reconstructed the 3D distribution of the index of refraction of a large and highly absorbing biological sample. PCI images were obtained by utilizing the analyzer based method and a non-linear extension for the diffraction enhanced imaging algorithm was used to calculate X-ray deflection angles. The RCT image reconstructed with FBP algorithm for gradient projections clearly depicts the internal structure of the sample. This result demonstrates that ABI-based index of refraction tomography in the hard X-ray domain can be very useful for a non-destructive characterization of large samples possessing low-contrast (e.g. soft tissues) internal features. RCT results were compared with ACT ones under the same experimental conditions. The density of the different materials was derived from both RCT and ACT images. It was shown that RCT significantly outperforms ACT in terms of image quality (higher SNR values and better delineation of the sample features for a given photon flux entering the sample). The more stringent requirements in terms of X-ray brilliance of PCI with respect to absorption imaging can be partially compensated by the higher sensitivity of the method used in our work. Thus we believe that the considered technique has a high potential in pre-clinical biomedical studies based on X-ray imaging of complex tissues, whole organs or small animals. In addition, the availability of compact high flux X-ray sources [1] may fundamentally change the practice of X-ray imaging and can largely extend the application of PCI techniques presently confined into synchrotron radiation facilities.