Compressive sensing with dispersion compensation on non-linear wavenumber sampled spectral domain optical coherence tomography

Abstract

We propose a novel compressive sensing (CS) method on spectral domain optical coherence tomography (SDOCT). By replacing the widely used uniform discrete Fourier transform (UDFT) matrix with a new sensing matrix which is a modification of the non-uniform discrete Fourier transform (NUDFT) matrix, it is shown that undersampled non-linear wavenumber spectral data can be used directly in the CS reconstruction. Thus k-space grid filling and k-linear mask calibration which were proposed to obtain linear wavenumber sampling from the non-linear wavenumber interferometric spectra in previous studies of CS in SDOCT (CS-SDOCT) are no longer needed. The NUDFT matrix is modified to promote the sparsity of reconstructed A-scans by making them symmetric while preserving the value of the desired half. In addition, we show that dispersion compensation can be implemented by multiplying the frequency-dependent correcting phase directly to the real spectra, eliminating the need for constructing complex component of the real spectra. This enables the incorporation of dispersion compensation into the CS reconstruction by adding the correcting term to the modified NUDFT matrix. With this new sensing matrix, A-scan with dispersion compensation can be reconstructed from undersampled non-linear wavenumber spectral data by CS reconstruction. Experimental results show that proposed method can achieve high quality imaging with dispersion compensation.

1. Introduction

Optical coherence tomography (OCT) is widely used as a routine medical diagnosis and screening tool in many clinical applications [1, 2]. Over the past decade, Fourier domain OCT (FDOCT) has shown superior sensitivity and imaging speed and has been replacing conventional time domain OCT (TDOCT) [3, 4].

Currently, FDOCT image generation algorithm requires the number of sampling points in spectral domain beyond the Nyquist rate which results in a high sampling rate for images requiring both large depth and high axial resolution. In spectral domain OCT (SDOCT), this requires a high-resolution spectrometer with a large linear array camera. While a laser source with high digitizer rate is necessary in swept source OCT (SSOCT). Such CCD/CMOS camera and laser source are usually expensive and significantly increases the acquisition time. In clinical applications of FDOCT where high-speed is desired, longer acquisition time makes the imaging susceptible to unavoidable motion artifact.

Recently, compressive sensing (CS) has been studied extensively since it requires only a portion of whole data for image reconstruction that satisfies image quality criteria [5, 6]. If the signal has a sparse representation and the sensing matrix satisfies restricted isometry property (RIP) [7], CS can obtain exact or accurate reconstruction from highly undersampled data. Applications of CS in FDOCT (CS-FDOCT) have been proposed [8–16] and high quality imaging has been achieved with a significantly reduced amount of data compared to Nyquist rate requirement.

Previous works on CS-FDOCT require linear wavenumber k-space undersampling because a uniform discrete Fourier transform (UDFT) matrix is used as the sensing matrix. This is inherited from conventional FDOCT image generation algorithms. However, in most FDOCT systems, the spectra are linear in wavelength and non-linear in wavenumber. Two methods have been proposed to obtain undersampled linear wavenumber data from the non-linear wavenum-ber spectra in SDOCT. In [9], k-space grid filling method is used to remapping the undersampled non-linear wavenumber data to linear wavenumber pixels according to a pre-calibrated functional dependency of wavenumber on pixel index. This method requires spectral calibration with numerical interpolation and is complicated and time-consuming itself. Another method uses a pre-calibrated k-linear random mask which enables obtaining a linear wavenumber subset by randomly undersampling directly from the non-linear wavenumber spectra [14]. The random mask is generated with the indices of the maximum and minimum points of the spectra by placing a single reflector in the sample arm. This method still needs pre-calibration. Also, even if only a slight change in the sampling rate is desired, the whole calibration process needs to be repeated. Besides, its sampling rate has an upper bound because of the nature of non-uniformity of the wavenumber.

Several approaches have been proposed to reconstruct OCT images from the nonlinear wavenumber whole spectra [17–23]. Non-uniform discrete or fast Fourier transform (NUDFT/NUFFT) is easy to implement and results in high quality images [20–23]. Applications of CS with the NUDFT/NUFFT matrix as the sensing matrix have also been studied, mainly for non-Cartesian sampling in magnetic resonance imaging (MRI) [24–27], which use the non-linear wavenumber spectral data directly. However, as will be shown in Section 3.1, CS with the undersampled NUDFT/NUFFT matrix as the sensing matrix cannot be applied directly to the non-linear wavenumber undersampling of FDOCT spectra because the reconstructed A-scan will have less sparsity in spatial domain which requires much more k-space sampling. Here the sparsity is defined as the number of coefficients to represent the signal is close to 0. In this paper, we modified the NUDFT matrix to promote the sparsity of A-scans by making them symmetric while preserving the intensity of the desired part of the A-scans. Therefore, the modified NUDFT matrix can be used as the sensing matrix in CS reconstruction on the non-linear wavenumber sampling of FDOCT signal.

Dispersion in FDOCT introduces a frequency-dependent phase to the Fourier components which degrades the axial resolution and reduces sensitivity [1]. Dispersion compensation methods have been successfully implemented in both hardware and software [28–31]. One widely used method is proposed in [28] by first resampling the non-linear wavenumber spectra with numerical interpolation; then constructing the complex representation of the real spectra with Hilbert transform; finally correcting the dispersion phase of the linear wavenumber complex signal. However, dispersion compensation has never been discussed in the context of CS reconstruction of FDOCT signal. In this paper, we show that dispersion compensation can be implemented by multiplying the dispersion correcting term directly to the non-linear wavenumber real spectra. This enables incorporation of dispersion compensation to CS reconstruction by adding dispersion correcting term to the modified NUDFT matrix. Dispersion compensation then becomes a by-product of CS reconstruction.

The main focus of this paper is to study of the novel sensing matrix (the MNUDFT matrix in Eq. (13)) with which dispersion compensated A-scan can be reconstructed from undersampled non-linear wavenumber sampling. The organization of this paper is as follows: Section 2 demonstrates the mathematical background of UDFT, NUDFT and CS in FDOCT; CS with the modified NUDFT matrix is proposed in Section 3; in Section 4, the dispersion compensation is incorporated to CS-FDOCT on the non-linear wavenumber undersampling; experimental results on SDOCT images are shown in Section 5, with discussion in Section 6, and conclusions in Section 7.

2. Mathematical background

2.1. Uniform discrete Fourier transform

In most FDOCT system, the spectra are non-linear in wavenumber which requires preprocessing procedures such as numerical interpolation to convert the dataset into linear in wavenumber if UDFT is to be applied. Denote y = [y ₀, y ₁,..., y_{N −1}]^T as the non-linear wavenumber k-space spectra (real value) and ŷ = [ŷ ₀, ŷ ₁,..., ŷ_{N −1}]^T as the linear wavenumber spectral data (real value) obtained from y. The uppercase T denotes the transpose. N is the whole signal length (no undersample). Denote x = [x ₀, x ₁,..., x_{N −1}]^T as the A-scan reconstructed from y and x̂ = [x̂ ₀, x̂ ₁,..., x̂_{N −1}]^T as the A-scan reconstructed from ŷ. k = [k ₀, k ₁,..., k_{N −1}]^T is the non-linear wavenumber corresponding to y while k̂ = [k̂ ₀, k̂ ₁,..., k̂_{N −1}]^T is the linear wavenumber corresponding to ŷ. Then x̂ can be obtained from ŷ through inverse UDFT:

$${\widehat{x}}_n=\frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}{\widehat{y}}_m\text{exp}\left(i\frac{2\pi }{\mathrm{\Delta }\widehat{k}}\left({\widehat{k}}_m-{\widehat{k}}_0\right)\times n\right)=\frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}{\widehat{y}}_m\text{exp}\left(i{\widehat{\omega }}_m\times n\right)$$ (1)

for n ∈ [0,...,N − 1]. i is the imaginary unit. Δk̂ = k̂_{N −1} − k̂ ₀ is the wavenumber range. ω̂_m = 2π/N × m. The derivation of the last part of Eq. (1) is because k̂ contains linear wavenumber: Δk̂ can be written as Δk̂ = N × δk̂ and k̂_m − k̂ ₀ = m ×δk̂.

2.2. Non-uniform discrete Fourier transform

It has been shown that the A-scan (x) can be reconstructed from the non-linear wavenumber spectra (y) through inverse NUDFT [20–23]. To avoid any numerical instability in computing the inverse NUDFT matrix, [23] uses the forward NUDFT matrix instead:

$$x_n=\frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}{y}_m\text{exp}\left(i\frac{2\pi }{\mathrm{\Delta }k}\left(k_m-k_0\right)\times n\right)=\frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}{y}_m\text{exp}\left(i{\omega }_m\times n\right)$$ (2)

for n ∈ [0,...,N − 1]. Δk = k_{N −1} − k ₀ is the wavenumber range (Δk = Δk̂). ω_m = 2π/Δk × (k_m − k ₀). In standard FDOCT where y and ŷ are real values, only the first halves of x and x̂ are displayed. In other words, n ∈ [0,...,N/2−1] in Eq. (1) and (2). Compared to the interpolation-UDFT method, inverse NUDFT method has several advantages: it is simple to implement and immune to the interpolation error which results in increased background noise and side-lobes, especially at larger image depth [23].

In the rest of this paper, if not specified, inverse NUDFT refers to transformation with the inverse NUDFT matrix which has the same form as the forward NUDFT matrix in Eq. (2). Constructing a new sensing matrix by starting from the forward NUDFT matrix, instead of the strict inverse NUDFT matrix, will be discussed in Section 6.

2.3. Compressive sensing in FDOCT

In CS-FDOCT, A-scan can be reconstructed from undersampled spectral data by solving the following optimization problem if it is sparse in some domain:

$$\underset{\mathbf{g}}{\text{minimize}}{\Vert \mathbf{W}\mathbf{g}\Vert }_1,\text{s}.\text{t}.{\Vert {\mathbf{F}}_u\mathbf{g}-{\mathbf{z}}_u\Vert }_2\le \epsilon$$ (3)

where g is the desired A-scan signal in spatial domain. W is the sparsifying operator which will transform g to a sparse representation, such as the wavelet transform matrix. If g is sparse in spatial domain, W shall be the identity matrix. F _u is the undersampled sensing matrix and z _u is the undersampled k-space data. ε controls the fidelity of the reconstruction to the sampled data or, equivalently, it reflects the noise level of z _u; ε ≈ 0 for noise-free data.

If F _u is the undersampled UDFT matrix, z _u has to be linear wavenumber sampling which is the case in traditional CS-FDOCT. However, as is mentioned in Section 1, acquisition of linear wavenumber sampling from the non-linear wavenumber spectra of FDOCT requires either k-space grid filling with spectral calibration or k-linear random mask calibration.

If undersampled NUDFT matrix is used as the sensing matrix, z _u is no longer required to be linear in wavenumber and the non-linear wavenumber spectra of FDOCT can be undersampled directly at an arbitrary sampling rate and used in CS reconstruction.

3. CS with the modified NUDFT matrix on the non-linear wavenumber sampling

3.1. A-scan sparsity of FDOCT using UDFT and NUDFT

CS reconstruction on the undersampled non-linear wavenumber spectral data with the NUDFT matrix as the sensing matrix has already been successfully implemented, mainly on non-Cartesian sampling of MRI [24–27]. Traditional CS-FDOCT on the UDFT matrix and the linear wavenumber sampling also shows that A-scans of FDOCT are sparse enough and can be reconstructed from highly undersampled data [8–16].

However, applying the NUDFT matrix and non-linear wavenumber sampling to CS-FDOCT would be a problem since the sparsity of the reconstructed A-scan is much less than that of the A-scan obtained from traditional CS-FDOCT with the UDFT matrix and linear wavenumber sampling. According to CS theory, the sampling rate for an accurate reconstruction depends highly on the A-scan’s sparsity. Decreased A-scan sparsity will require much more sampling.

The sparsities of the A-scans with both methods are compared using the whole k-space spectra. If UDFT is applied, the A-scan (x̂) can be obtained from the linear wavenumber spectra (ŷ) through Eq. (1). Because the elements of ŷ are real, x̂ is symmetric:

$${\widehat{x}}_{N-n}=\frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}{\widehat{y}}_m\text{exp}\left(i\frac{2\pi }{N}m\times \left(N-n\right)\right)=\frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}{\widehat{y}}_m\text{exp}\left(-i\frac{2\pi }{N}m\times n\right)={\left({\widehat{x}}_n\right)}^{*}$$ (4)

for n ∈ [1,...,N/2 − 1] because m is integer and exp(i2πm) = 1. (x̂_n)^* is the conjugate of x̂_n. This conjugate property implies that the intensity of x̂_{N − n} is the same as that of x̂_n for n ∈ [1,...,N/2 − 1]. Figure 1(a) shows the plot of an A-scan (belonging to a mouse paw scanning) obtained by applying inverse UDFT to ŷ which is obtained from the non-linear wavenumber spectra (y) using cubic interpolation.

Fig. 1.

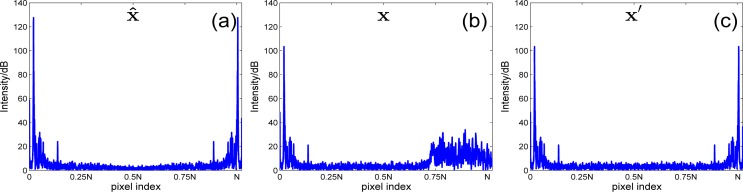
Sparsity comparison of A-scans by applying (a) inverse UDFT to the linear wavenumber whole spectra (ŷ), (b) inverse NUDFT to the non-linear wavenumber whole spectra (y), (c) modified inverse NUDFT to the non-linear wavenumber whole spectra (y)

If NUDFT is applied, the A-scan (x) can be obtained from the non-linear wavenumber spectra (y) through Eq. (2). Because y is non-linear in wavenumber, x is no longer symmetric:

$$x_{N-n}=\frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}{y}_m\text{exp}\left(i{\omega }_m\times \left(N-n\right)\right)=\frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}{y}_m\text{exp}\left(-i{\omega }_m\times n\right)\times \text{exp}\left(i{\omega }_{m}N\right)\ne {\left(x_n\right)}^{*}$$ (5)

for n ∈ [1,...,N/2 − 1] because usually exp(iω_mN) ≠ ±1. Figure 1(b) shows the plot of A-scan obtained by applying inverse NUDFT to y.

As can be seen in Fig. 1(a) and 1(b), the first halves of x̂ and x, i.e., [x̂ ₀,..., x̂_{N / 2−1}] and [x ₀,..., x_{N / 2−1}] have similar sparsity. But the sparsity of the second half of x is much less than that of x̂. The decrease of sparsity implies that more sampling is required to reconstruct x than x̂ using CS.

Although a specific example from a mouse paw scanning is displayed in Fig. 1, according to experimental results with different samples, it is quite universal that x has less sparsity than x̂. The influence of the decreased sparsity usually cannot be eliminated by using larger ε in CS reconstruction: In Fig. 1(b), [x _{0.75 N},..., x_{N −1}] has higher intensity than most of [x ₀,..., x_{N / 2−1}], which implies that most of [x ₀,..., x_{N / 2−1}] will receive a bigger penalty than [x _{0.75 N},..., x_{N −1}] during the reconstruction and is more likely to be zero with larger ε. Although the second halves of both x and x̂ will not be displayed for the standard FDOCT system, their sparsity will greatly influence the reconstruction of the FDOCT signal with CS since Eq. (3) tries to find the solution that minimizes the l1-norm of the whole A-scan.

3.2. The modified NUDFT matrix

The sparsity of the second half of x has a greater influence on the CS reconstruction of the whole x. In standard FDOCT, however, we do not care about the intensity of this undisplayed half of x as long as its sparsity is high enough. It would be perfect if the second half of x is always 0. However, that’s not typically true for arbitrary y.

It has already been shown in previous work of CS-SDOCT that x̂ can be accurately reconstructed with a relatively small sample size [9, 14, 16]. So our motivation is: since the first halves of x and x̂ have similar sparsity and x̂ can be reconstructed by CS, if the second half of x is symmetric to its first half, x and x̂ will have similar sparsity. Then x can be accurately reconstructed with almost the same amount of sampling required to reconstruct x̂ by CS. We find that this idea can be realized by modifying the NUDFT matrix.

The inverse NUDFT transformation in Eq. (2) can be written in matrix form as follows:

$$\left[\begin{array}{c}{x}_0\\ x_1\\ ⋮\\ x_N\end{array}\right]=\left[\begin{array}{cccc}h\left(0,0\right)& h\left(1,0\right)& \dots & h\left(N-1,0\right)\\ ⋮& ⋮& \ddots & ⋮\\ h\left(0,N/2\right)& h\left(1,N/2\right)& \dots & h\left(N-1,N/2\right)\\ ⋮& ⋮& \ddots & ⋮\\ h\left(0,N-1\right)& h\left(1,N-1\right)& \dots & h\left(N-1,N-1\right)\end{array}\right]\left[\begin{array}{c}{y}_0\\ y_1\\ ⋮\\ y_{N-1}\end{array}\right]$$ (6)

where h(p, q) = exp(iω_p * q).

It is easy to see that values of the bottom half of x ([x_{N / 2},..., x_{N −1}]) are only relevant to the bottom half of the inverse NUDFT matrix and y. Therefore, obtaining symmetric reconstructed A-scan (x′) can be realized by modifying the bottom half of the inverse NUDFT matrix:

$$\left[\begin{array}{c}{x}_0^{\prime }\\ x_1^{\prime }\\ ⋮\\ x_{N-1}^{\prime }\end{array}\right]=\left[\begin{array}{cccc}h\left(0,0\right)& h\left(1,0\right)& \dots & h\left(N-1,0\right)\\ h\left(0,1\right)& h\left(1,1\right)& \dots & h\left(N-1,1\right)\\ ⋮& ⋮& \ddots & ⋮\\ h\left(0,N/2-1\right)& h\left(1,N/2-1\right)& \dots & h\left(N-1,N/2-1\right)\\ h\left(0,N/2\right)& h\left(1,N/2\right)& \dots & h\left(N-1,N/2\right)\\ \mathbf{h}{\left(\mathbf{0},\mathbf{N}/\mathbf{2}-\mathbf{1}\right)}^{*}& \mathbf{h}{\left(\mathbf{1},\mathbf{N}/\mathbf{2}-\mathbf{1}\right)}^{*}& \dots & \mathbf{h}{\left(\mathbf{N}-\mathbf{1},\mathbf{N}/\mathbf{2}-\mathbf{1}\right)}^{*}\\ ⋮& ⋮& \ddots & ⋮\\ \mathbf{h}{\left(\mathbf{0},\mathbf{1}\right)}^{*}& \mathbf{h}{\left(\mathbf{1},\mathbf{1}\right)}^{*}& \dots & \mathbf{h}{\left(\mathbf{N}-\mathbf{1},\mathbf{1}\right)}^{*}\end{array}\right]\left[\begin{array}{c}{y}_0\\ y_1\\ ⋮\\ y_{N-1}\end{array}\right]$$ (7)

where h(p, q)^* = exp(−iω_p × q) is the conjugate of h(p, q). Elements from the second row to the last row of the bottom half of the transformation matrix (rows in bold) are conjugate to those of the symmetric rows in the top half, e.g., elements of the row corresponding to x′ _{( N / 2+1)} are conjugate to the elements of the row corresponding to x′ _{( N / 2−1)}. It can be proved that x′ is symmetric:

$$x_{N-n}^{\prime }=\frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}{y}_{m}h{\left(m,n\right)}^{*}={\left(\frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}{y}_{m}h\left(m,n\right)\right)}^{*}={\left(x_n^{\prime }\right)}^{*}$$ (8)

which implies that x′_{N − n} and x′_n have the same intensity for n ∈ [1,...,N/2 − 1]. Thus x′ is symmetric. It is also easy to see that [x′ ₀, x′ ₁,..., x′_{N / 2−1}] is the same as [x ₀, x ₁,..., x_{N / 2−1}]. Thus, proposed modification preserves the intensity of the desired part of the A-scan. The first and (N/2 + 1)th row of the modified inverse NUDFT matrix are unchanged, which makes x′ and x̂ to have the same symmetric structure. Figure 1(c) shows the plot of x′ whose sparsity is similar to x̂ and much higher than x. Proposed method shows good performance at promoting the sparsity of A-scan.

The modified inverse NUDFT matrix in Eq. (7), however, cannot be used directly as the sensing matrix in CS-FDOCT because the sensing matrix should transform data from spatial domain to k-space according to Eq. (3). Thus, its inverse matrix, i.e. the modified NUDFT matrix is needed. Based on the fact that the inverse NUDFT matrix in Eq. (6) is indeed the forward NUDFT matrix instead of the strict inverse NUDFT matrix, the modified NUDFT matrix can be easily obtained by taking conjugate transpose of the transformation matrix in Eq. (7).

Using the undersampled modified NUDFT matrix as the sensing matrix, A-scan can be reconstructed with high accuracy by CS from undersampled non-linear wavenumber spectral data.

4. CS with dispersion compensation

4.1. Dispersion compensation with NUDFT on non-linear wavenumber real spectra

Dispersion degrades FDOCT image quality by introducing a frequency-dependent phase term to the Fourier components of the signal. One widely used method to compensate the dispersion is proposed in [28] which first resamples the non-linear wavenumber spectra with numerical interpolation; generates the imaginary part of the signal with Hilbert transform; then corrects the phase of the linear wavenumber complex signal to compensate dispersion; finally applies UDFT to the corrected spectrum to obtain the A-scan. However, this method cannot be applied to undersampled spectral data because both interpolation and Hilbert transform require whole spectra which makes it very difficult to obtain undersampled dispersion compensated linear wavenumber spectral data. Also, this method cannot be applied as post processing to the reconstructed A-scan with dispersion because it corrects the dispersion in k-space, not in spatial domain. Thus it is difficult to incorporate this widely used dispersion compensation method into CS-FDOCT directly.

Therefore, we propose and validate a dispersion compensation method by first multiplying the correcting phase directly to the non-linear wavenumber real spectra; then applying NUDFT to the corrected spectrum to reconstruct the A-scan. This method eliminates the need for interpolation and Hilbert transform which are used to transform the spectra to be first linear in wavenumber then complex. It will be shown in Section 4.3 that after transformation, proposed dispersion compensation method has the form similar to that of the inverse NUDFT-based FDOCT image generation algorithm in Eq. (6). Then the transformation matrix is modified in the same way mentioned in Section 3.2 to promote the A-scan’s sparsity and its undersampled matrix can be used in CS reconstruction on the non-linear wavenumber real sampling to obtain dispersion compensated A-scan.

Multiplying the correcting phase directly to the non-linear wavenumber real spectra can be written as:

$$\begin{array}{lll}{I}_{\mathit{comp}}\left({\omega }_m\right)\hfill & =\hfill & \mathit{Re}\left\{2\times {\mathrm{\Sigma }}_n\sqrt{S_n\left({\omega }_m\right)S_r\left({\omega }_m\right)}\text{exp}\left(-i\left[{\omega }_m{\tau }_n+\mathrm{\Phi }\left({\omega }_m\right)\right]\right)\right\}\times \text{exp}\left(i\mathrm{\Phi }\left({\omega }_m\right)\right)\hfill \\ \hfill & =\hfill & \left({\mathrm{\Sigma }}_n{A}_n\left({\omega }_m\right)(\text{exp}\left(-i\left[{\omega }_m{\tau }_n+\mathrm{\Phi }\left({\omega }_m\right)\right]+\text{exp}\left(i\left[{\omega }_m{\tau }_n+\mathrm{\Phi }\left({\omega }_m\right)\right]\right)\right)\right)\text{exp}\left(i\mathrm{\Phi }\left({\omega }_m\right)\right)\hfill \\ \hfill & =\hfill & \underset{A_1}{\underbrace{{\sum }_n{A}_n\left({\omega }_m\right)\text{exp}\left(-i\left[{\omega }_m{\tau }_n\right]\right)}}+\underset{A_2}{\underbrace{{\sum }_n{A}_n\left({\omega }_m\right)\text{exp}\left(i\left[{\omega }_m{\tau }_n+2\mathrm{\Phi }\left({\omega }_m\right)\right]\right)}}\hfill \end{array}$$ (9)

for m ∈ [0,...,N − 1]. I _comp(ω) is the corrected spectrum. S_n(ω) is the intensity of light reflected from the n-th layer in the sample; S_r(ω) is the intensity of light reflected from the reference arm; τ_n is the optical group delay of the n-th reflection to the reference light path. Φ(ω) is the dispersion term. A_n(ω_m) substitutes $\sqrt{S_n\left({\omega }_m\right)S_r\left({\omega }_m\right)}$ from the second row. The first term after the first equal mark is the interferometric signal with some degree of dispersion (i.e. y in previous sections) while the second term is the dispersion compensation term. Compensating second and third order dispersion is usually sufficient where Φ(ω) = −a ₂(ω − ω ^*)² −a ₃(ω − ω ^*)³. ω ^* is the central angular frequency; a ₂ and a ₃ are constant. In the last row, the term A ₁ is the desired dispersion compensated spectra. However, proposed method will also introduce an undesired term in I _comp(ω): A ₂.

Then inverse NUDFT is applied to the corrected spectrum I _comp(ω). Denote the results of applying the inverse NUDFT to A ₁ and A ₂ as T ₁ and T ₂ respectively. The resulting A-scan is the sum of T ₁ and T ₂. In standard FDOCT system, only the first half of the A-scan will be shown. The first half of T ₁ is the desired dispersion compensated A-scan with better resolution while the first half of T ₂ degrades the A-scan’s resolution. However, as will be shown below, the intensity of first half of T ₂ is relatively small compared to that of the first half of T ₁. In other words, T ₁ dominates the displayed half of the A-scan and the resolution degradation caused by T ₂ has little effect.

4.2. Experimental validation

To illustrate this domination effect, the simulation with only one reflector (n = 1) is shown in Fig. 2 which plots the intensity ratio value of (|T ₁(τ ₁)|/|T ₂(τ ₁)|) with different reflector position τ ₁ (from 1 to N/2−1). The simulation is done with different level of dispersion (a ₂ ∈ {−500, −250, −100, 0, 100, 250, 500} fs ²; a ₃ = 0) to demonstrate that intensity of T ₁ is much higher than that of T ₂ regardless of the level of dispersion. ω is obtained from the SDOCT system used in the study. S_n and S_r are set as 1 since their values do not influence the plot.

Fig. 2.

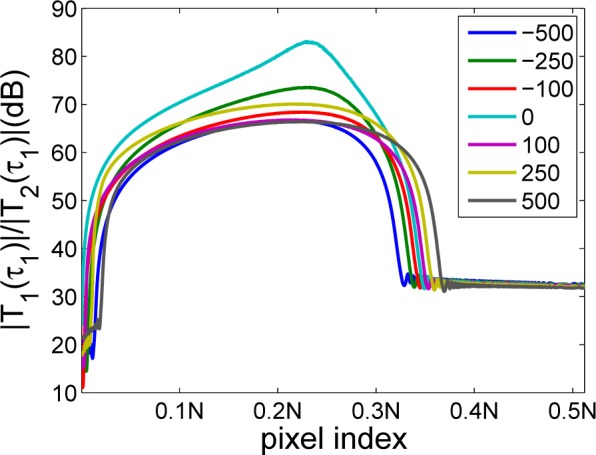
Plot of |T ₁(τ ₁)|/|T ₂(τ ₁)| versus different reflector position τ ₁. Simulation is done with different level of dispersion (a ₂ ∈ {−500, −250, −100, 0, 100, 250, 500} fs ²; a ₃ = 0).

As can be seen in Fig. 2, most of (|T ₁(τ ₁)|/|T ₂(τ ₁)|) is above 30dB when the reflector is in the displayed half of the A-scan. T ₁ dominates T ₂ under various dispersion condition. The curve without dispersion shows higher ratio as expected.

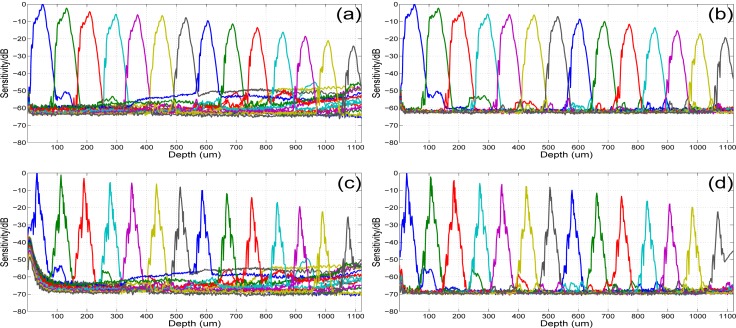
Sensitivity roll-off of the proposed dispersion compensation method on the non-linear wavenumber real spectra (y) is compared with those by applying (1) inverse UDFT to the linear wavenumber real spectra (ŷ) without dispersion compensation; (2) inverse NUDFT to y without dispersion compensation; (3) dispersion compensation method in [28]. Here 124 A-scans with 2048-pixel each were averaged for each position. A 2cm water cell was inserted to the reference arm of the interferometer to introduce large dispersion mismatch (both y and ŷ contains dispersion). The dispersion coefficients were empirically set as a ₂ = 460 fs ² and a ₃ = 134 fs ³. The results are shown in Fig. 3 (intensity of each A-scan is normalized). Figure 3(b) shows flatter sensitivity roll-off with smaller background noise and side-lobes at larger image depth than Fig. 3(a), which is consistent with the observation in [20, 23]. Peaks in Fig. 3(c) and 3(d) are much sharper than those in Fig. 3(a) and 3(b), indicating the FWHM of 4μm against 22μm. Figure 3(d) also shows better sensitivity than Fig. 3(c) as well as less background noise and side-lobes. Thus, proposed method shows good potential at compensating dispersion and outperforms the dispersion compensation method in [28].

Fig. 3.

Sensitivity roll-off of systems applying (a) inverse UDFT to the linear wavenumber real spectra without dispersion compensation, (b) inverse NUDFT to the non-linear wavenumber real spectra without dispersion compensation, (c) dispersion compensation method in [28], (d) proposed dispersion compensation method on the non-linear wavenumber real spectra. A 2cm water cell is inserted to introduce large dispersion mismatch.

The above two calculations show that the influence of undesired term T ₂ is relatively small compared with T ₁ on the displayed half of reconstructed A-scan and that multiplying the correcting term directly to the non-linear wavenumber real spectra could achieve a satisfying dispersion compensation effect.

4.3. Incorporation of dispersion compensation to CS-FDOCT

Dispersion compensation method proposed in Section 4.2 can be written in matrix form as:

$$\left[\begin{array}{c}{x}_0^c\\ x_1^c\\ ⋮\\ x_{N-1}^c\end{array}\right]=\left[\begin{array}{cccc}h\left(0,0\right)& h\left(1,0\right)& \dots & h\left(N-1,0\right)\\ ⋮& ⋮& \ddots & ⋮\\ h\left(0,N/2\right)& h\left(1,N/2\right)& \dots & h\left(N-1,N/2\right)\\ ⋮& ⋮& \ddots & ⋮\\ h\left(0,N-1\right)& h\left(1,N-1\right)& \dots & h\left(N-1,N-1\right)\end{array}\right]\left(\left[\begin{array}{c}{y}_0\\ y_1\\ ⋮\\ y_{N-1}\end{array}\right].*\left[\begin{array}{c}{e}^{i\mathrm{\Phi }\left({\omega }_0\right)}\\ e^{i\mathrm{\Phi }\left({\omega }_1\right)}\\ ⋮\\ e^{i\mathrm{\Phi }\left({\omega }_{N-1}\right)}\end{array}\right]\right)$$ (10)

where ${\mathbf{x}}^{\mathbf{c}}={\left[x_0^c,x_1^c,\dots ,x_{N-1}^c\right]}^T$ is the dispersion-compensated A-scan; “.*” stands for the component-wise multiplication. The transformation matrix is the inverse NUDFT matrix.

Denote exp(iΦ(ω_n)) as Φ_n for n ∈ [0, 1,...,N − 1], then Eq. (10) can be rewritten by incorporating the dispersion compensation term into the inverse NUDFT matrix:

$$\left[\begin{array}{c}{x}_0^c\\ x_1^c\\ ⋮\\ x_{N-1}^c\end{array}\right]=\left[\begin{array}{cccc}h\left(0,0\right){\mathrm{\Phi }}_0& h\left(1,0\right){\mathrm{\Phi }}_1& \dots & h\left(N-1,0\right){\mathrm{\Phi }}_{N-1}\\ ⋮& ⋮& \ddots & ⋮\\ h\left(0,N/2\right){\mathrm{\Phi }}_0& h\left(1,N/2\right){\mathrm{\Phi }}_1& \dots & h\left(N-1,N/2\right){\mathrm{\Phi }}_{N-1}\\ ⋮& ⋮& \ddots & ⋮\\ h\left(0,N-1\right){\mathrm{\Phi }}_0& h\left(1,N-1\right){\mathrm{\Phi }}_1& \dots & h\left(N-1,N-1\right){\mathrm{\Phi }}_{N-1}\end{array}\right]\left[\begin{array}{c}{y}_0\\ y_1\\ ⋮\\ y_{N-1}\end{array}\right]$$ (11)

where h(p, q)Φ_n = exp(iω_p × q) × exp(iΦ(ω_n)). Although the transformation matrix in Eq. (11) does not have the same form as the inverse NUDFT matrix in Eq. (2), it could still be considered an inverse NUDFT matrix because the phases in each row are non-linear in wavenumber.

Eq. (11) gives a transformation between the dispersion-compensated A-scan and the non-linear wavenumber real spectra, building the foundation of CS reconstruction. However, it cannot be used directly in CS-FDOCT because of decreased A-scan sparsity problem mentioned in Section 3.1. Thus the transformation matrix in Eq. (11) also needs modification to make x ^c symmetric for higher sparsity:

$$\left[\begin{array}{c}{x}_0^{\prime c}\\ x_1^c\\ ⋮\\ x_{N-1}^{\prime c}\end{array}\right]=\left[\begin{array}{cccc}h\left(0,0\right){\mathrm{\Phi }}_0& h\left(1,0\right){\mathrm{\Phi }}_1& \dots & h\left(N-1,0\right){\mathrm{\Phi }}_{N-1}\\ h\left(0,1\right){\mathrm{\Phi }}_0& h\left(1,1\right){\mathrm{\Phi }}_1& \dots & h\left(N-1,1\right){\mathrm{\Phi }}_{N-1}\\ ⋮& ⋮& \ddots & ⋮\\ h\left(0,N/2-1\right){\mathrm{\Phi }}_0& h\left(1,N/2-1\right){\mathrm{\Phi }}_1& \dots & h\left(N-1,N/2-1\right){\mathrm{\Phi }}_{N-1}\\ h\left(0,N/2\right){\mathrm{\Phi }}_0& h\left(1,N/2\right){\mathrm{\Phi }}_1& \dots & h\left(N-1,N/2\right){\mathrm{\Phi }}_{N-1}\\ {\left(h\left(0,N/2-1\right){\mathrm{\Phi }}_0\right)}^{*}& {\left(h\left(1,N/2-1\right){\mathrm{\Phi }}_1\right)}^{*}& \dots & {\left(h\left(N-1,N/2-1\right){\mathrm{\Phi }}_{N-1}\right)}^{*}\\ ⋮& ⋮& \ddots & ⋮\\ {\left(h\left(0,1\right){\mathrm{\Phi }}_0\right)}^{*}& {\left(h\left(1,1\right){\mathrm{\Phi }}_1\right)}^{*}& \dots & {\left(h\left(N-1,1\right){\mathrm{\Phi }}_{N-1}\right)}^{*}\end{array}\right]\left[\begin{array}{c}{y}_0\\ y_1\\ ⋮\\ y_{N-1}\end{array}\right]$$ (12)

The modification also preserves the value of desired half of the A-scan: ${\left[x_0^c,x_1^c,\dots ,x_{N/2-1}^c\right]}^T={\left[x_0^{\prime c},x_1^{\prime c},\dots ,x_{N/2-1}^{\prime c}\right]}^T$.

The sensing matrix required for CS reconstruction can be obtained in the same way as in Section 3.2: take the conjugate transpose of the transformation matrix in Eq. (12):

$$\left[\begin{array}{ccccccc}{\left(h\left(0,0\right){\mathrm{\Phi }}_0\right)}^{*}& \dots & {\left(h\left(0,N/2-1\right){\mathrm{\Phi }}_0\right)}^{*}& \dots & h\left(0,N/2-1\right){\mathrm{\Phi }}_0& \dots & h\left(0,1\right){\mathrm{\Phi }}_0\\ ⋮& \ddots & ⋮& \ddots & ⋮& \ddots & ⋮\\ {\left(h\left(N-1,0\right){\mathrm{\Phi }}_{N-1}\right)}^{*}& \dots & {\left(h\left(N-1,N/2-1\right){\mathrm{\Phi }}_{N-1}\right)}^{*}& \dots & h\left(N-1,N/2-1\right){\mathrm{\Phi }}_{N-1}& \dots & h\left(N-1,1\right){\mathrm{\Phi }}_{N-1}\end{array}\right]$$ (13)

With the undersampled matrix of Eq. (13), dispersion compensated A-scan can be reconstructed from undersampled non-linear wavenumber spectral data. It is noteworthy to mention that with proposed sensing matrix, dispersion compensation becomes a by-product of CS reconstruction and no additional dispersion compensation procedure is needed.

5. Experimental results

To evaluate the effect of proposed method, k-space data from a SDOCT system are used. The system uses a spectrometer having a 12-bit CMOS line scan camera (EM4, e2v, USA) with 2048 pixels at 70 kHz line rate. A superluminescent laser diode (SLED) is used as the light source which provides an output power of 10 mW and an effective bandwidth of 105nm centered at 845nm. The experimental axial resolution of the system is 4.0μm in air while the transversal resolution is approximately 12μm. All animal studies were conducted in accordance with the Johns Hopkins University Animal Care and Use Committee Guidelines. Spectral data were post-processed with MATLAB^® R2012b on a desktop with Intel^® Core^TM 2 Duo CPU (E8400, 3.0GHz), 4GB RAM, Windows^® 7 64-bit operation system. The CS reconstruction algorithm is SPGL1 with default parameters [32, 33].

Proposed sensing matrix in Eq. (13) (denoted as the MNUDFT matrix) is applied to CS reconstruction on the undersampled non-linear wavenumber real spectra. For comparison purpose, the following results are also evaluated: 1) original image obtained by applying NUDFT to 100% of the non-linear wavenumber real spectra; 2) image reconstructed using CS on the undersampled non-linear wavenumber real spectra with the NUDFT matrix as the sensing matrix.

The undersampled non-linear wavenumber spectral data is obtained by applying a pseudo-random mask to the original spectra. Variable density random sampling [12] is used to generate this mask. This evaluation method is widely used in the studies of CS-SDOCT [9, 14, 16]. A CCD camera with randomly addressable pixels [9,34–36] can be used to practically implement random undersampling of spectral data in an SDOCT system.

The same undersampled data, reconstruction domain and ε are used in the CS reconstructions of the same object. According to experimental results, OCT signal is sparse in spatial domain in most cases. However, it is usually sparser in wavelet domain than spatial domain. The reconstruction domain is chosen to optimize the reconstruction result. Besides, the sampling rate is chosen to balance the size of spectral data and the image quality while ε is selected to balance the loss of useful information and the reduction of noise. The dispersion compensation parameters a ₂ and a ₃ are set empirically.

To carry out a quantitative assessment of reconstruction results of different methods, the local contrast and signal to noise ratio (SNR) are computed. Their definitions are as follows:

$$\text{local}\hspace{0.17em}\text{contrast}=\frac{{\mu }_o}{{\mu }_b}$$ (14)

$$\text{SNR}=20\times {\text{log}}_{10}\left(\frac{\sqrt{\frac{1}{N_o}{\sum }_{\left(i,j\right)\in \text{object}}I{\left(i,j\right)}^2}}{\sqrt{\frac{1}{N_b}{\sum }_{\left(i,j\right)\in \text{background}}I{\left(i,j\right)}^2}}\right)$$ (15)

where N_o and N_b are the number of pixels in the selected object region and background region respectively. As is shown in Fig. 4, 5, and 6, area in the red rectangles are selected object region while the green rectangle area is selected background region. They have the same size. I(i, j) is the intensity. μ_o and μ_b are mean of intensity of the object region and background region respectively.

Fig. 4.

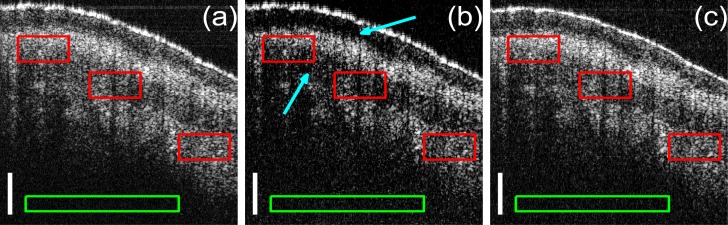
B-scans of a mouse paw. (a) original image obtained by applying NUDFT to 100% of the acquired non-linear wavenumber spectra; (b) CS reconstruction result with the NUDFT matrix from 40% of the acquired non-linear wavenumber spectra; (c) CS reconstruction result with the MNUDFT matrix from 40% of the acquired non-linear wavenumber spectra; The scale bars represent 100μm. Image size in pixel is 450 × 1000

Fig. 5.

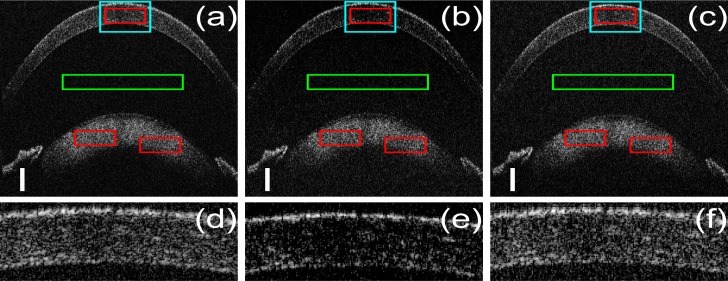
B-scans of a mouse cornea; (a) original image obtained by applying NUDFT to 100% of the acquired non-linear wavenumber spectra; (b) CS reconstruction result with the NUDFT matrix from 37.5% of the acquired non-linear wavenumber spectra; (c) CS reconstruction result with the MNUDFT matrix from 37.5% of the acquired non-linear wavenumber spectra; (d), (e) and (f) are zoom in of the cyan rectangle areas in (a), (b) and (c) respectively. The scale bars represent 100μm. Image size in pixel is 700 × 1000.

Fig. 6.

B-scans of a polymer-layered phantom with 2.4cm water induced dispersion; (a) original image obtained by applying NUDFT to 100% of the acquired non-linear wavenumber spectra; (b) CS reconstruction result with the NUDFT matrix from 50% of the acquired non-linear wavenumber spectra; (c) CS reconstruction result with the MNUDFT matrix from 50% of the acquired non-linear wavenumber spectra; (d) image obtained by applying the forward MNUDFT matrix to 100% of the acquired non-linear wavenumber spectra. The scale bars represent 100μm. Image size in pixel is 450 × 1000.

The comparison is first implemented on the mouse paw scanning which contains several layers. The CS reconstructions use 40% spectral data; W is the four-level daubechies4 wavelet transform matrix. Compensation parameters are set as a ₂ = 157 fs ² and a ₃ = 170 fs ³. All images are shown in the same dynamic range. Figure 4(b) exhibits bad quality because of the decreased A-scan sparsity problem. It achieves accurate reconstruction for pixels with high intensity but loses information for the pixels with relative low intensity. The layer beneath the surface is difficult to see due to the CS reconstruction error, as is pointed out by the arrows. Figure 4(c) has much better quality, which is very close to 4(a) which uses 100% sampling rate. Besides, Fig. 4(c) shows obvious dispersion compensation effect with clear and thin tissue boundary compared to 4(a) and 4(b). The overall contrast of 4(c) is better than that of 4(a) with 100% sampling rate because CS is well known to be good at reducing noise [15, 37]. The local contrast and SNR of Fig. 4(a), 4(b) and 4(c) are listed in Table 1 which shows that CS reconstruction with the MNUDFT matrix obtains better image quality.

Table 1.

Local contrast and SNR of the B-scans of mouse paw in Fig. 4

	original	CS+NUDFT	CS+MNUDFT
Local contrast(dB)	4.63	3.50	5.42
SNR(dB)	14.06	11.44	16.07

The mouse cornea images are shown in Fig. 5. CS reconstructions used 37.5% sampling rate. W is the identity matrix. a ₂ = 120 fs ² and a ₃ = 100 fs ³. Figure 5(c) is very close to 5(a) while Fig. 5(b) shows obvious artifact and information loss. Regions of interest (ROI) are extracted from the reconstructed images (cyan rectangles in Fig. 5(a), 5(b) and 5(c)). Figure 5(f) shows that CS with the MNUDFT matrix preserves almost all the structures in the original image which uses 100% sampling rate while Fig. 5(e) are void of fine details. Table 2 lists the local contrast and SNR of Fig. 5(a), 5(b) and 5(c).

Table 2.

Local contrast and SNR of the B-scans of mouse cornea in Fig. 5

	original	CS+NUDFT	CS+MNUDFT
Local contrast(dB)	2.68	2.12	3.50
SNR(dB)	8.81	8.04	9.67

To give an in-depth assessment of the dispersion compensation effect of CS with the MNUDFT matrix, a 2.4cm water cell was placed in the reference arm when imaging a polymer-layered phantom to intentionally introduce a large dispersion mismatch between the two arms. CS reconstructions use 50% sampling rate. W is the four-level daubechies4 wavelet transform matrix. a ₂ = 575 fs ² and a ₃ = 295 fs ³. The B-scan obtained by applying the forward MNUDFT matrix to 100% of the acquired spectra (Eq. (12)) is added in Fig. 6(d) to show that MNUDFT can also achieve obvious dispersion compensation when used in the traditional imaging generation. Figure 6(a) shows much bigger dispersion than the previous cases. Figure 6(b) is void of fine details and there are obvious artifacts in the area outside the phantom. Dispersion compensated images, Fig. 6(c) and 6(d), are highly clear compared to Fig. 6(a), especially near the upper surface. Both of them show obvious dispersion reduction which validates the proposed method while CS uses only 50% of the acquired spectra and achieves better image quality, as is shown in Table 3.

Table 3.

Local contrast and SNR of the B-scans of polymer-layered phantom in Fig. 6

	original	CS+NUDFT	CS+MNUDFT	MNUDFT
Local contrast(dB)	4.43	2.12	7.71	6.13
SNR(dB)	15.99	9.79	27.23	23.82

6. Discussion

The MNUDFT matrix is created by “mirroring” its first half: setting columns of the right half to be conjugate to the corresponding columns at the left half. This modification itself is not unique. Looking at the MNUDFT matrix in Eq. (13), one can easily create another sensing matrix by changing the order of the columns of its right half. Although the resulting A-scan will not be symmetric any more, this does not change the performance of the method since its l1-norm is unchanged and the displayed half of the A-scan is preserved.

Although, according to Eq. (7) and (12), setting the entire bottom half of the transformation matrix to zero will maximize the sparsity of the undisplayed half of the A-scan, one cannot simply drop the information in this way since it will make all the right half of the MNUDFT matrix zero. Denote the proposed MNUDFT matrix as H. It implies y = H * x̃ where y is the acquired spectra with non-linear wavenumber and x̃ is the A-scan. If the right half of H are all zero, no matter what value the bottom half of x̃ is (including the desired zero value), y = H * x̃ does not hold any more if the first half of x̃ is unchanged. Thus the basic principle is violated. In addition, the new sensing matrix should not have any two columns/rows the same, as is required by the standard CS theory [5, 6].

The proposition of the MNUDFT matrix starts from the forward NUDFT matrix instead of the strict inverse NUDFT matrix. This substitution does not change the effect of proposed method because the forward NUDFT matrix is only used to demonstrate what the A-scan would be after the modification. The usage of the forward NUDFT matrix to compute the A-scan has already been validated by the experiments in [20, 23]. Then the MNUDFT matrix can be easily obtained because the modification is done on its conjugate transpose matrix. After all, the matrix that will be used in CS reconstruction as the sensing matrix is the MNUDFT matrix. Selected CS reconstruction algorithm relies on the sensing matrix and its conjugate transpose, not its inverse. Starting from the forward NUDFT matrix instead of the strict inverse NUDFT matrix is because it helps to demonstrate the motivation of proposed method.

Dispersion compensation coefficients a ₂ and a ₃ used in this paper were obtained empirically from the system in the study. However, these two parameters can be obtained automatically using an iterative procedure which optimizes the sharpness of the reconstructed image, as in [28].

Another interesting subject is incorporating dispersion compensation directly to UDFT-based CS-FDOCT on undersampled linear wavenumber spectral data. No interpolation is needed in this case. The Hilbert transform cannot be applied to undersampled data. This can be overcome by multiplying the dispersion compensation term directly to the real spectra. But the remaining processing actually becomes CS reconstruction with the NUDFT matrix: the transformation equation on 100% spectral data (ŷ) in this case is very similar to Equation (11) except that the non-linear angular frequency ω is replaced by the linear angular frequency ω̂. Denote the transformation matrix as D. Because Φ(ω̂) is non-equispaced, the phase of arbitrary row in D is no longer equispaced. Thus D is a NUDFT matrix, which may introduce low sparsity to the resulting A-scan. Thus, modification on D is still needed to improve the sparsity of the resulting A-scan, especially when the dispersion is big.

We have shown that CS reconstruction with the proposed MNUDFT matrix on undersampled nonlinear wavenumber data represents a simpler approach compared to traditional CS-FDOCT based on the UDFT matrix and undersampled linear wavenumber data. The time for CS reconstructions in both cases are almost the same. However, many properties such as the difference in sampling rate and robustness to noise of UDFT and MNUDFT based CS-FDOCT still need more study.

There is some difference when choosing the CS reconstruction algorithm because the MNUDFT matrix is not unitary. Several CS reconstruction algorithms-such as NESTA [38] and CSALSA [39]-cannot or are difficult to use to solve the CS optimization problem defined in Eq. (3), because they require either ${\mathbf{F}}_{\mathbf{u}}^{\mathbf{T}}{\mathbf{F}}_{\mathbf{u}}=\mathbf{I}$ or explicit ${\left(\mathbf{I}-{\mathbf{F}}_{\mathbf{u}}^{\mathbf{T}}{\mathbf{F}}_{\mathbf{u}}\right)}^{-1}$ ( ${\mathbf{F}}_{\mathbf{u}}^{\mathbf{T}}$ is the conjugate transpose of F_u). SPGL1 is chosen as the reconstruction algorithm, in part because it does not require unitary sensing matrix.

7. Conclusion

In this paper, we propose a novel CS-FDOCT method based on the MNUDFT matrix which can be applied to the non-linear wavenumber spectral sampling instead of the linear wavenumber sampling in traditional CS-FDOCT with the UDFT matrix. In addition, dispersion compensation by multiplying the correcting term directly to the non-linear wavenumber real spectra is proposed and incorporated into the sensing matrix of CS. Experimental results show that proposed method achieves high quality images with good dispersion reduction.