Static and dynamic crystalline lens accommodation evaluated using quantitative 3-D OCT

Abstract

Custom high-resolution high-speed anterior segment spectral domain Optical Coherence Tomography (OCT) provided with automatic quantification and distortion correction algorithms was used to characterize three-dimensionally (3-D) the human crystalline lens in vivo in four subjects, for accommodative demands between 0 to 6 D in 1 D steps. Anterior and posterior lens radii of curvature decreased with accommodative demand at rates of 0.73 and 0.20 mm/D, resulting in an increase of the estimated optical power of the eye of 0.62 D per diopter of accommodative demand. Dynamic fluctuations in crystalline lens radii of curvature, anterior chamber depth and lens thickness were also estimated from dynamic 2-D OCT images (14 Hz), acquired during 5-s of steady fixation, for different accommodative demands. Estimates of the eye power from dynamical geometrical measurements revealed an increase of the fluctuations of the accommodative response from 0.07 D to 0.47 D between 0 and 6 D (0.044 D per D of accommodative demand). A sensitivity analysis showed that the fluctuations of accommodation were driven by dynamic changes in the lens surfaces, particularly in the posterior lens surface.

1. Introduction

Focusing of objects at different distances by the young human eye is enabled by modification of the shape of the crystalline lens by action of the ciliary muscle, which changes the tension applied on the zonulae attached to the capsular bag surrounding the lens in response to an accommodation stimulus. In a relaxed state of accommodation (far focus) the zonulae pull the lens, which becomes flatter. In the accommodated state (near focus) the zonulae lose tension and the capsular bag molds the lens into an un-accommodated state. This focusing capability (accommodation) is lost with age, reaching a point in which near tasks are adversely affected (a condition known as presbyopia). Accurate measurement of lens geometry is crucial for the understanding of crystalline lens optical properties and of the physical changes of the lens with accommodation and aging, for the design and evaluation of accommodation-restoration solutions for presbyopia, and to increase the predictability of intraocular lens implantation procedures. Until recently, most knowledge of the optical properties of the lens in vivo came from indirect measurements (i.e. the optical aberrations of the lens being typically computed as the difference of corneal and ocular wave aberrations). Also, the accommodative response of the lens is typically measured by monitoring refractive changes of the eye, using techniques such as dynamic retinoscopy [1], open-field autorefractometry [2], and aberrometry [3–7].

In particular, those technologies have been used to assess the dynamics of the accommodative response when subjects focus a stationary target, providing insights into the mechanism of accommodation [8]. Fluctuations of accommodation have been suggested as an active method to maintain the accommodative response using directional cues [9,10], or alternatively, a passive consequence of zonular tension reduction with increased accommodation [11]. Refractometric measurements of the fluctuations in spherical error are potentially affected by multiple factors (including corneal or retinal changes related to pulsation). However, dynamic imaging of the accommodating crystalline lens will allow direct assessment of the dynamic shape changes, directly on the organ responsible for accommodation.

The geometry of the crystalline lens has been reported in vivo using different techniques. A Purkinje-imaging based method has been used to estimate the radii of curvature, tilt and decentration of the lens [12,13]. However, this technique does not provide an image of the anterior chamber of the eye, as opposed to direct imaging methods that do allow visualization of the crystalline lens, such as Scheimpflug imaging [14,15]. Scheimpflug imaging provides cross-sectional images of the crystalline lens, although due to the particular geometrical configuration of the system (and to the fact that the lens surfaces are visualized through refractive surfaces), images need to be corrected from geometrical and optical distortions to obtain accurate estimates of lens surface radii of curvature and asphericities [16–18]. However, the slit-lamp configuration of Scheimpflug imaging-based systems frequently limits the view of the posterior lens. Commercial instruments provide quantitative information for the cornea but not for the lens, since they do not correct for optical distortion in the lens region. The anterior chamber of the eye has also been imaged by means of Magnetic Resonance Imaging (MRI) [16,19], and ultrasound biometry [20]. Among other disadvantages, these techniques require long acquisition times, with significantly lower resolution than optical techniques, which impose major problems (including motion artifacts or low sampling density), preventing quantification of the crystalline lens geometry with high accuracy.

Optical Coherence Tomography (OCT) is a promising tool to image the anterior segment of the eye, due to its high-resolution, high-speed and non-contact nature [21–25]. Provided with automatic quantification algorithms and with fan and optical distortion correction [26,27], OCT has allowed 3-D quantification of the cornea [28,29], and lens [30], as well as 3-D optical biometry [31]. The high speed acquisition of Fourier OCT techniques opens the possibility for tracking the crystalline lens dynamical changes, as the reported characteristic frequency of the fluctuations of accommodation falls within the bandwidth of state-of-the art OCT technology.

However, OCT imaging of the crystalline lens imposes some challenges, including a limited axial range, compromised by the resolution of the spectrometer (in spectrometer based OCT systems) or a limited instantaneous linewidth of tunable light source (in swept source OCT systems [32],), which may be insufficient to image the entire anterior segment of the eye. Several strategies have been proposed to overcome these limitations: doubling of the axial range by complex conjugate images removal [33], dual channel OCT systems that combine two sOCT systems focused at different planes [34–36], merging of images obtained focusing at different planes [28], optical switch to focus at different planes [37], ultralong scan depth OCT [38], and increased coherence length of swept sources [39,40]. Some of these techniques have been successfully used to quantify the 3-D geometry of the anterior segment of the eye [30,39]. Ortiz et al. reported the first 3-D in vivo topography of the human crystalline lens [30]. Quantitative analysis (in most cases limited to axial biometry) has also been reported from 2-D cross-sections of the anterior segment of the accommodating human eye in vivo [19,36–38].

In the current study we characterized the geometry of the crystalline lens (anterior and posterior lens radii of curvature) for different accommodative demands (0 to 6 D) from 3-D quantitative sOCT anterior segment. We also estimated the dynamic fluctuations of crystalline lens geometry under steady fixation for different accommodative stimuli, to isolate the crystalline lens contributions to the dynamics of accommodation.

2. Methods

2.1 OCT system

A custom-developed spectral OCT system developed in collaboration with Optical Biomedical Imaging Group at Nicolaus Copernicus University (Torun, Poland) was used to collect the images [33]. The setup is based on a fiber-optics Michelson interferometer configuration with a superluminescent diode (SLD) (λ₀ = 840 nm, Δλ = 50 nm) as a light source, and a spectrometer (volume diffraction grating, and a 12-bit 4096-pixel linescan CMOS camera) as a detector. The distance between the centers of the scanning mirrors is 13.8 mm and the focal length of the collimating lens before the eye is 75 mm.

The effective acquisition speed is 25000 AScans/s, which optimized balance between speed and SNR. The axial range of the instrument is 7 mm in air (around 5.2 mm in tissue), resulting in a theoretical axial pixel resolution of 3.4 μm. The axial resolution predicted by the bandwidth of the SLD laser source is 6.9 μm.

The axial measurement range can be doubled by using a piezotranslator mounted in the reference mirror that allows implementation of a technique of complex conjugate images removal based on a joint Spectral and Time domain OCT [33].

An additional beam splitter was placed in the sample arm in order to incorporate an accommodating channel to the sOCT system. In this channel, a Badal system mounted on a motorized stage (VXM-1, Velmex) was used both for compensating spherical refractive errors and for inducing accommodative demands. A 12 mm x 9 mm SVGA OLED minidisplay (LE400, LiteEye Systems) was used to present the fixation stimulus. The fixation stimulus consisted of a black and white Maltese cross with eight arms (see Fig. 1 in Gambra et al. [7]). The target subtended 5.14 deg and had a luminance of 50 cd/m².

Fig. 1.

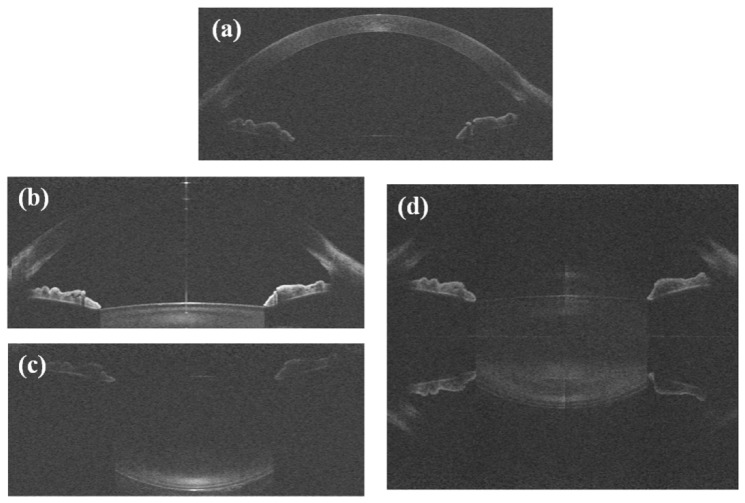
Typical raw sOCT images: (a) cornea; (b) anterior crystalline lens surface; (c) posterior crystalline lens surface, imaged separately in the 3-D protocol; (d) entire crystalline lens, imaged simultaneously using the complex conjugate images removal technique, in the dynamic 2-D image acquisition. After the unfolding procedure, a mirror image of some elements of the eye can still be seen.

2.2 Subjects

Images were collected on the left eyes of 4 young subjects (mean age: 26.5 ± 2.5). Their refractions ranged between 0 to −6 D sphere and 0 to 1 D cylinder, and were optically corrected during the experiment. Spherical error was corrected by means of the Badal optometer, and cylinder by cylindrical trial lenses placed in a pupil conjugate plane in the accommodation channel. All subjects were trained subjects capable of accommodating, as assessed with IR dynamic retinoscopy (PowerRef II, Plusoptix) prior to the experiment.

Subjects signed a consent form approved by the Institutional Review Boards after they had been informed on the nature and possible consequences of the study, in accordance to the tenets of the Declaration of Helsinki.

2.3 Imaging protocols

All measurements were performed under natural viewing conditions and undilated pupils. The subjects were stabilized using a bite bar and front rest. Alignment of the subject was performed with respect to the anterior corneal specular reflection, while the subject fixated a reference Maltese cross target projected on the minidisplay.

The SLD power exposure was fixed at 800 μW. The position of the reference mirror was changed manually between two fixed positions (one for imaging the cornea and the other, for the lens) during the experimental session in order to achieve optimal imaging of the different structures. This is needed because, although axial range would be sufficient to image the entire anterior segment at once, the sensitivity drop of the sOCT prevents from obtaining good image quality along the entire axial range. Typical raw sOCT images of the ocular surfaces are shown in Fig. 1.

2.3.1 3-D imaging of the anterior segment

The anterior segment of the eye was imaged while stimulating accommodation from 0 to 6 D in 1-D steps. A total of 15 sets of 3-D data were collected in each subject’s left eye for each condition of static accommodation: 5 images of the cornea, 5 images of the anterior part of the lens and 5 images of the posterior part of the lens. In order to minimize the impact of motion artifacts, every set of 3-D images was collected in less than 1 s.

Measurements were collected on a 6 mm (horizontal) x 15 mm (vertical) zone, using 40 B-Scans composed of a collection of 600 A-Scans, providing a lateral resolution of 0.025 mm for the horizontal meridian and 0.15 mm for the vertical meridian. Note that this “lateral resolution” refers to the scanning density, not to the resolution of the system (which is determined by the size of the scanning ray).

2.3.2 Dynamics of the central B-scan

B-scans of the central horizontal meridian were acquired dynamically at a frequency of 14 Hz. The axial measurement range was doubled by using the piezotranslator function, in order to image the anterior and posterior surfaces of the lens simultaneously. Images of the lens were obtained in one subject while stimulating accommodation from 0 to 6 D in 1-D steps. For each accommodative condition, one 3-D image of the cornea (from which the apex image was selected) and 5 sets of 70 images of the central section (15 mm lateral range) of the entire crystalline lens were acquired during 5 seconds. Every lens cross-sectional image (and every corneal B-scan) was composed by a collection of 1668 A-Scans, providing a lateral resolution of 0.009 mm.

3.1 Image processing

The 3-D image processing tools developed to obtain quantitative information of the anterior chamber structures have been described in prior publications [26,27,30,41]. Automatic image processing analysis includes denoising, multilayer segmentation, and merging of 3-D volumes. Fan and optical distortion correction algorithms were applied to the segmented surfaces of cornea and crystalline lens, using ray-tracing analysis [26,27]. The corneal refractive index was taken as 1.376, the aqueous humor refractive index as 1.336, and the crystalline lens refractive index was obtained from the age-dependent average refractive index expression derived by Uhlhorn et al. (1.4104-1.4113 for the subjects of our study) [42]. A constant refractive index was used for all the accommodative demands since the equivalent refractive index does not change significantly during accommodation [43,44]. Optical distortion correction by the corneal surfaces (for the anterior lens) and corneal and anterior lens surfaces (for the posterior surface) were corrected using 3-D ray tracing routines, as described by Ortiz et al. [30]. For the current study, the technique was also adapted to the correction of cross-sectional images of the lens. The B-scan of the cornea 3-D measurements in which the apex reflection was observed was selected and used for optical distortion correction of the 2-D lens images. Corneal cross-sections were merged with the lens cross-sectional images, using the pupil inner edges as a landmark. A ray-tracing analysis (here in 2-D) similar to that used in the corrections of 3-D data sets was implemented and applied to correct the anterior and posterior lens surface from the corneal and anterior lens refraction.

3.2. Data analysis

3.2.1 Lens phakometry

The surfaces of the lens were fitted by quadrics, both in 3-D and in 2-D, in a 5-mm diameter optical zone centered at their apexes. In 3-D, the lens radii of curvature were obtained by fitting to a sphere of radius of curvature R. Dynamic 2-D lens horizontal sections were fitted by circumferences (defined by the radius of curvature R).

3.2.2 Pupillometry, anterior chamber depth and lens thickness

Pupil center and diameter were estimated in the 3-D images using previously presented image analysis tools [30]. The anterior chamber depth (ACD) was estimated as the distance between the intersections of the vector defined by the centers of curvature of the posterior cornea and anterior lens with the corresponding surfaces. The lens thickness (LT) was estimated as the distance between the intersection of the vector that joins the centers of curvature of anterior and posterior lens with the corresponding surfaces. These definitions were applied for both the 3-D and 2-D sets of data.

3.2.3 Accommodative response

The accommodative response of the eye was estimated considering the variation of lens geometry (and position) with increasing accommodative demand, and computed for each data set obtained during the dynamic acquisition. A schematic eye model was used in order to estimate the change in refraction of the entire eye. Eye refraction was estimated under the paraxial approximation (see equations below), using the measured data of corneal radius of curvature, lens radii of curvature, ACD and LT. The accommodative response of the eye was obtained from the change in its total refraction with increasing accommodative demand, and compared with the isolated contribution of the crystalline lens (Eq. (2)).

$$P=P_C+P_L-\frac{ACD\cdot P_C\cdot P_L}{n_h}+\frac{\left(n_l-n_h\right)\cdot LT\cdot P_C}{n_h{}^2{R}_p}$$ (1)

$$\begin{array}{l}{P}_C=\frac{n_h-1}{n_h{R}_C}\\ P_L=\frac{n_l-n_h}{n_h}\left(\frac{1}{R_a}-\frac{1}{R_p}\right)+\frac{{\left(n_l-n_h\right)}^{2}LT}{n_l{n}_h{R}_a{R}_p}\end{array}$$ (2)

where P is the power of the eye and P_C and P_L the power of the equivalent cornea and of the crystalline lens, respectively; n_l is the equivalent refractive index of the lens according to Dubbelman and Van der Heijde [45], and n_h is the refractive index of aqueous and vitreous humors; R_c, R_a and R_p are the radii of curvature of the equivalent cornea and of the anterior and posterior lens surfaces, respectively; ACD is the anterior chamber depth; and LT is lens thickness.

Images providing insufficient quality to allow correct surface segmentation (usually due to insufficient signal in the posterior lens surface) were removed. When performing a Fourier analysis in the 2-D data, these removed data were replaced by a linear interpolation between the calculated values for their closest neighbors. The rate of total number of data and removed data sets was less than 5.5%.

3.2.4 Fluctuations of accommodation

The fluctuations of the accommodative response during sustained accommodation were calculated as the standard deviation of the estimated accommodative response. These were computed for each accommodative demand (5-second periods). The contribution of the noise inherent to the OCT system and image processing was estimated (from a series of images obtained under paralyzed accommodation with Tropicamide 1%) and taken into account (using error propagation) in the determination of the fluctuations associated solely to the accommodative response.

Alternatively, we obtained the frequency spectra of the accommodative responses for each of the 5-second sequences (for the different accommodative demands), using Fourier analysis. The area under the frequency spectra was numerically calculated for low (0–0.6 Hz) and high (0.9–2.5 Hz) frequency regions. The area under these curves, particularly in the low frequency range, has been related to the magnitude of the fluctuations of accommodation [46].

The fluctuations of other biometric and phakometric magnitudes (ACD, LT) and of the radii of curvature of the lens were also estimated and compared with the fluctuations of the optical power. A sensitivity analysis was performed to assess the impact of each of these magnitudes on the fluctuations of the optical power of the lens, by recalculating these fluctuations while keeping constant (and equal to their mean value) the rest of the magnitudes.

Furthermore, the coefficient of correlation (r) between the dynamic ACD and LT was calculated for every accommodative state in order to assess whether the changes in ACD were either due to changes in lens thickness or to translational lens movements. If r = −1 the decrease in the ACD would be related to the increase in LT, while if r = 0 the decrease in ACD would be related to a forward shift of the lens. Finally, correlations between the changes in LT and radii of curvature were performed to assess whether the fluctuations in LT were primarily due to fluctuations in lens radii of curvature.

4. Results

4.1 3-D imaging of the segment

4.1.1 OCT images

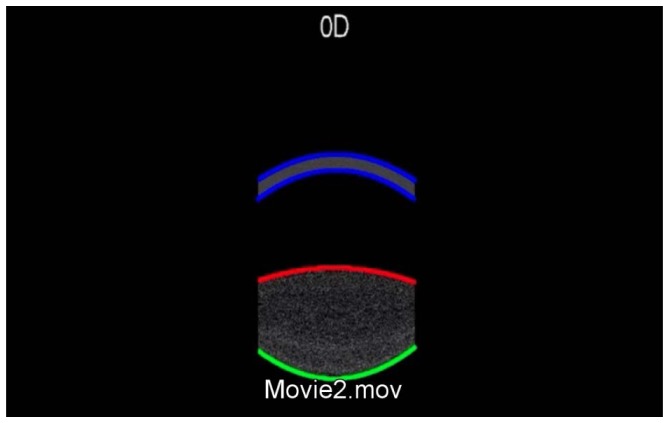
Figure 2 (Media 1 ^{(7.1MB, MOV)} ) shows a lateral view of the 3-D rendering of the crystalline lens (following image processing, including 3-D merging and distortion correction) for subject #4 and for accommodative demands ranging from 0 to 6 D.

Fig. 2.

(Media 1 ^{(7.1MB, MOV)} ): Distortion-corrected lateral view of the 3-D rendering of the crystalline lens, from data images acquired at accommodative demands ranging from 0 to 6 D in 1-D steps.

4.1.2 Radii of curvature

Figure 3 shows the change of radii of curvature of the anterior and posterior surfaces with accommodative demand. Data are for the four individual subjects, and the average across subjects. As previously reported, the lens (particularly the lens anterior surface) becomes steeper with the accommodative demand.

Fig. 3.

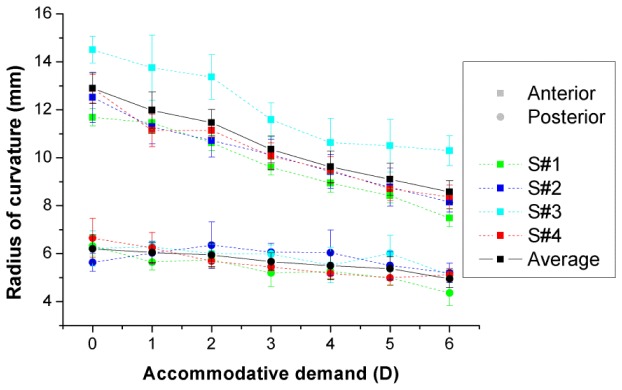
Radii of curvature of the anterior (squares) and posterior (circles) surfaces of the lens for the individual subjects (color symbols with dashed lines) and the average across subjects (black symbols with solid lines). Data for each subject are average of 5 repeated measurements. Error bars stand for standard deviation of repeated measurements. The radius of curvature of the posterior surface of the lens is negative, but has been depicted positive for illustration purposes.

4.1.3 Accommodative response

The optical power of the lens was estimated for all subjects, using Eq. (2). The optical power of the lens ranged from 16.1 to 18.8 D across subjects in the unaccommodated condition, and from 20.39 to 22.14 D in the condition of highest accommodative demand. The average lens optical power change rate was 0.82 D/D (of accommodative demand). Figure 4 shows the change in the total eye optical power estimated from biometric and geometrical data for all subjects, using Eq. (1). The maximum amplitude of the accommodative response was on average 3.83 D, for an accommodative demand of 6 D. The average total optical power change rate was 0.62 D/D.

Fig. 4.

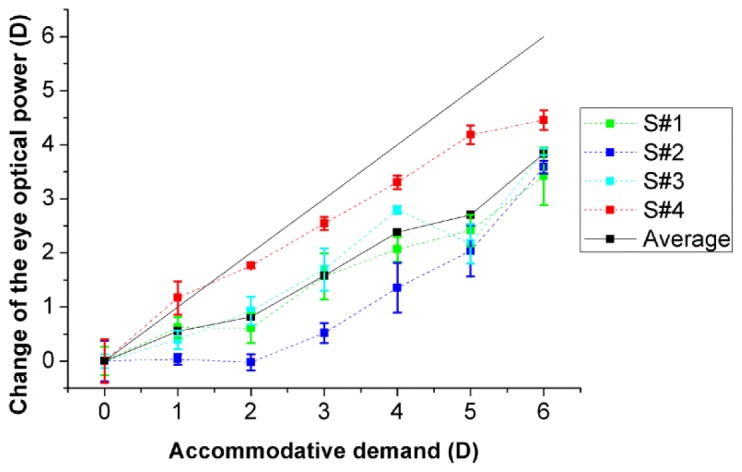
Change in the optical power of the eye with accommodative demand, with respect to the value obtained for the unaccommodated condition (0D). Data are average of 5 repeated measurements for each subject. Solid line corresponds to the ideal response. Error bars stand for half of the standard deviation of repeated measurements (for clarity).

4.2 Biometry and phakometry with dynamic central B-scan cross-sections

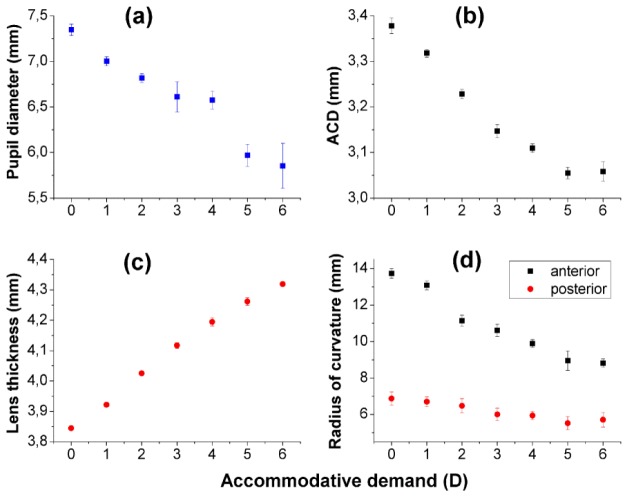
Figure 5 shows pupil diameter (a), anterior chamber depth (b), lens thickness (c), and lens radii of curvature (d) as a function of accommodative demand, estimated from cross-sectional OCT images, for subject #4. Each data point is the average of 58-70 measurements during sustained accommodation (recorded during 5 s at each accommodative level).

Fig. 5.

Anterior segment geometry as a function of accommodative demand: (a) Pupil diameter, (b) anterior chamber depth, (c) lens thickness, and (d) lens radii of curvature. Error bars stand for the standard deviation of data from 58 to 70 images acquired during 5 seconds of sustained accommodation (at each accommodative demand).

Pupil diameter decreased from 0 to 6 D of accommodative demand by 1.49 mm on average (Fig. 5(a)), ACD by 0.320 mm on average (Fig. 5(b)) and lens thickness increased by 0.473 mm on average (Fig. 5(c)). These results are consistent with a forward shift of the lens with accommodation (by around 0.083 mm from 0 to 6 D of accommodative demand).

The lens radii of curvature obtained from horizontal cross-sectional images (Fig. 5(d)) are similar to the radii of curvature obtained in a different set of 3-D sets of data on the same eye: the anterior and posterior radius of curvature were, respectively, 4.5 and 8.1% higher than the average radii of curvature from 3-D data (with this difference remaining similar across accommodative demands). The difference between the 3-D and 2-D comes from the fact that in 3-D radii of curvature from all meridians are added whereas in the 2-D they correspond to horizontal section only. This is consistent with a previous report in an un-accommodated eye [30], in which horizontal radii of curvature was higher than the vertical one for this particular subject.

Similarly as done with the 3-D data, the optical power of the lens was estimated from the 2-D phakometric data for the different accommodative demands. The change in the eye optical power with accommodation was 10% lower when obtained from 2-D cross-sections (0.67 D/D) than from 3-D data sets (0.75 D/D, for S#4), consistent with the slightly higher horizontal lens radii of curvature.

4.3 Dynamics of the central B-scan

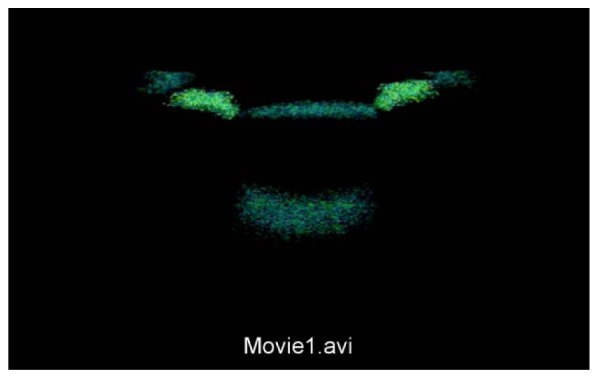
Figure 6 (Media 2 ^{(919.6KB, AVI)} ) shows a real-time video sequence of the dynamics of anterior segment horizontal cross-sections during 35 seconds (sustained accommodation for 5-seconds, for accommodative demands ranging from 0 to 6 D). The superimposed lines represent the corresponding edge fittings for the anterior and posterior corneal and lens surfaces, after distortion correction. The fluctuations of accommodations, as well as the change in lens shape and pupil diameter with increased accommodation can be observed in this video.

Fig. 6.

(Media 2 ^{(919.6KB, AVI)} ): Dynamic fluctuations of the horizontal section of the anterior segment (5-second sequences for each accommodative stimulus, ranging from 0 to 6 D). Data are following image processing, including merging and distortion corrections. The superimposed lines are circumference section fittings to the anterior and posterior cornea and lens.

Figure 7 shows the temporal variation of the eye optical power during the 5-second of sustained accommodation, for each accommodative demand, estimated from Eq. (1) using the radii of curvature and biometric data obtained for each image of the sequence.

Fig. 7.

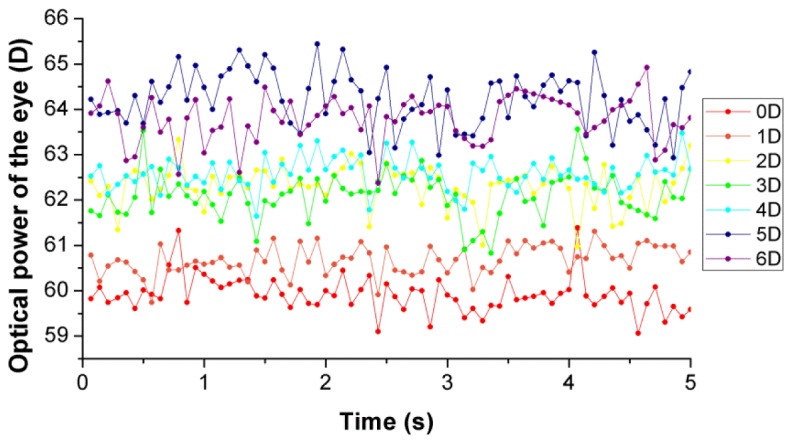
Optical power of the eye during 5 seconds of sustained accommodation, for different accommodative demands.

Figure 8(a) shows the fluctuations of the lens optical power (blue symbols) and eye optical power (green symbols), defined as the standard deviation of the estimated power, for each accommodative demand. The lens power fluctuations arise from variations in the lens radii of curvature and lens thickness. The entire eye power fluctuations also incorporate the variations in ACD (but not potential changes in corneal power or eye axial length), as well as the fluctuations of the optical power of the lens. The fluctuations of the eye optical power are on average 0.16 D lower than the fluctuations of the lens optical power. The fluctuations of accommodation increase significantly with accommodative demand, at a rate of 0.044 D/D of accommodative demand.

Fig. 8.

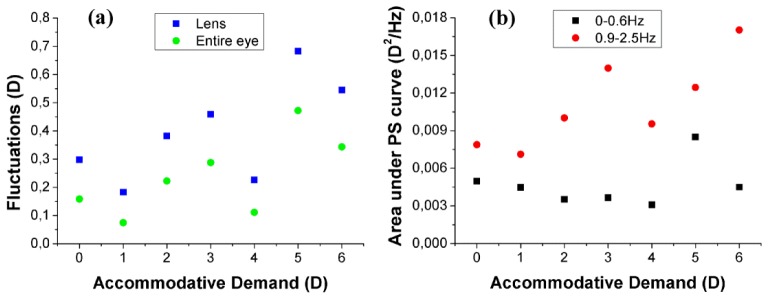
(a) Fluctuations of the optical power of the lens and of the entire eye calculated as the standard deviation of the power estimates during 5-seconds of sustained accommodation, as a function of the accommodative demand. (b) Area under the power spectrum density curve of the optical power of the eye in two different frequency bands (0-0.6 Hz and 0.9-2.5 Hz), as a function of accommodative demand.

Figure 8(b) shows the area under the power spectrum density curve of the optical power of the eye, numerically calculated for low (0–0.6 Hz) and high (0.9–2.5 Hz) frequency bands. The correlation between the standard deviation of the optical power and the area under the power spectrum density was higher for the high frequency range (r = 0.74, p = 0.056) than for the low frequency range (r = 0.69, p = 0.084).

Fluctuations of the optical power of the lens due only to ACD, LT and anterior and posterior radii of curvature (calculated from the experimental data, by allowing one magnitude to vary while keeping constant the other three) were estimated. The results of this sensitivity analysis are shown in Fig. 9 , where the contribution of the different parameters is shown for the different accommodative demands. Fluctuations in optical power are primarily dominated by changes in the radii of curvature of the lens, especially the posterior surface. The contribution of the fluctuations of the anterior radius of curvature to the overall fluctuations tends to increase with accommodative demand, while the contributions of ACD and LT are always very small and do not show a trend with accommodation.

Fig. 9.

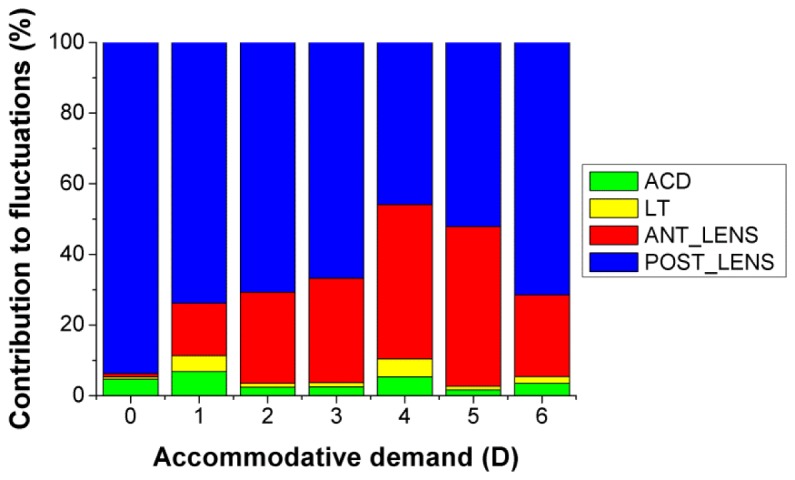
Relative contribution of the anterior chamber depth (ACD), lens thickness (LT) and anterior and posterior lens radii to the fluctuations of the optical power of the eye.

Fluctuations in ACD, lens thickness, radii of curvature of the lens surfaces were also estimated and Pearson’s correlation coefficient (r) between some of these magnitudes was calculated for every accommodative demand. No significant correlation was found between the ACD and LT, except for 3 D of accommodative demand (r = −0.37, p = 0.002). Besides, LT correlated significantly with anterior lens radius for 1 D (r = −0.35, p = 0.003), 2 D (r = −0.3, p = 0.002) and 3D (r = −0.32, p = 0.010), and with posterior lens radius only for 0 D (r = −0.26, p = 0.038).

On the other hand, mean values of ACD, lens thickness, and radii of curvature of the lens surfaces correlate across accommodation with the mean value of the optical power of the eye (r modulus ranging from 0.92 to 0.99), as expected from the results already shown in Fig. 5.

5. Discussion

Ortiz et al. [30] used quantitative sOCT to obtain the first 3-D topography of the crystalline lens in vivo. In this study, we have extended that methodology to assess changes in the shape of the crystalline lens with accommodation, and provided, for the first time to our knowledge, phakometric measurements with accommodation derived from 3-D data. In addition, we have also shown the capability of the OCT technology, making use of its high acquisition rates, to assess the dynamics of accommodation.

Despite the relatively long axial range, the sensitivity drop in the sOCT system prevents from imaging simultaneously the entire anterior segment of the eye. We have overcome the problem by imaging separately the different surfaces and using the limbus and the iris as landmarks for registration of different images at different planes of focus. Swept source OCT imaging can be alternatively used to image the cornea and the lens simultaneously [39,40].

The measured lens radii of curvature, obtained from 3-D OCT images, are comparable to values in the literature. In the un-accommodated condition, we found average radii of 12.90 ± 0.64 mm for the anterior lens and 6.20 ± 0.59 mm for the posterior lens. In a previous report using similar methodology, Ortiz et al. reported 11.90 ± 1.34 mm for anterior lens radius of curvature and 6.86 ± 0.63 mm for the posterior lens, in 3 subjects [30]. Dubbelman et al. reported an age-dependent expression for the anterior and posterior lens radius of human lenses in vivo based on corrected Scheimpflug measurements, which predicts 11.25-11.59 mm and 5.85-5.92 mm for the anterior and posterior lens radii respectively for the age range of the subjects of our study [45]. Rosales et al. measured the crystalline lens radii of curvature using both Purkinje and Scheimpflug imaging, and reported average values of 10.8 mm and 11.1 mm, and 6.7 mm and 6.1 mm from each technique, for anterior and posterior lens radius of curvature, respectively [13]. Koretz et al. used both Scheimpflug and MRI in a comparative study, and obtained values of 11.90 mm and 5.58 mm for the anterior and posterior lens radii of curvature, respectively, with Scheimpflug photography, and 11.20 mm and 6.15 mm, respectively with MRI [16]. Finally, in recent study using 2-D OCT, Shao et al. reported values of 11.87 mm and 5.68 mm for the anterior and posterior lens radii of curvature, respectively, in a single 26-year-old subject [36]. The lens radii of curvature ranges of our study (11.7-14.5 mm and 5.6-6.6 mm, for anterior and posterior lens surfaces) match well those reported by Dubbelman et al. (9-14 mm and 4.7-7 mm, respectively) [45].

In addition, we have measured the lens shape in 3-D, for increasing accommodative demand (0 to 6 D, 1-D steps). We found a decrease of 0.73 mm/D accommodative demand for the anterior lens radius of curvature, and 0.20 mm/D for the posterior lens (see Fig. 3). These rates can be compared with those obtained in the literature using Scheimpflug or Purkinje imaging. Differences may arise from differences in the accommodative demand range used for testing and the actual accommodative response. Dubbelman et al. using 2-D Scheimpflug photography for accommodative demands up to 8 D reported rates of 0.61 ± 0.15 mm/D and 0.13 ± 0.06 mm/D for the anterior and posterior lens radius, respectively [17]. Rosales et al. reported 0.64 mm/D (Scheimpflug) and 0.57 mm/D, (Purkinje) for the anterior lens, and 0.23 mm/D (Scheimpflug) and 0.29 mm/D (Purkinje) for the posterior lens, for an 8-D accommodative demand range [13]. Garner and Yap using Purkinje imaging reported rates of 0.62 mm/D and 0.17 mm/D for the anterior and posterior lens, respectively, for a 8-D accommodative range [12]. Shao et al. using 2-D sOCT reported rates of 1.06 mm/D and 0.29 mm/D for the anterior and posterior lens, respectively for a 4-D accommodative demand range [36].

Assuming an equivalent refraction index for the crystalline lens (according to that reported by Dubbelman et al. in subjects of the same age range [45]) we estimated the change of the optical power of the eye from physical changes in the lens and anterior segment biometry. We found that the change in the optical power of the eye with accommodation (0.62 D/D) is smaller than the change in the optical power of the crystalline lens (0.82 D/D). This difference can be explained considering Eq. (1), which shows that the lens power has contributions of opposite sign to the eye optical power. Assuming that the accommodative response is equal to the estimated change of the optical power of the eye, we found an accommodative response amplitude of 3.83 D, which is similar to the accommodative response of 3.78 D reported in Gambra et al. in 5 young subjects [7], the 3.5 D reported by He et al. [3], and the 4 D reported by Plainis et al. [5], all of them using a Hartmann-Shack–based measurements of refraction, and for a similar accommodative-demand range of 6 D range. Besides, McClelland and Saunders measured the accommodative response to a 6 D stimulus in 40 subjects, and reported average values of 4.57 ± 0.69 and 4.43 ± 0.73 using dynamic retinoscopy and a Shin-Nippon autorefractor, respectively [47]. The effective accommodation amplitude, discounting the effect of the accommodative lead at 0 D (between 0.5 and 1 D in most studies [3,5,7]) is very similar to that obtained on anatomical bases in our study.

Besides phakometric changes, we also report biometric changes with accommodation, obtained from sOCT. The change in ACD and LT with accommodative demand (−0.057 mm/D and 0.081 mm/D of accommodative demand, see Fig. 5(b) and 5(c)) are within the ranges reported in the literature: −0.037 mm/D (ACD) and 0.045 mm/D (LT), for a 27 year old subject, for an accommodative demand range of 8 D, using Scheimpflug imaging [17]; −0.062 mm/D (ACD) and 0.066 mm/D (LT), in 15 subjects, with an accommodative demand of 5 D, using MRI [19]; −0.033 mm/D (ACD) and 0.034 mm/D (LT) in one 37-old subject, for an accommodative demand range of 5.5 D using 2-D OCT [19]; −0.025 mm/D (ACD) and 0.06 mm/D (LT) in a 26-old subject for an accommodative demand range of 4 D using 2-D OCT [36]; and −0.019 mm/D (ACD) and 0.058 mm/D (LT) for an accommodative demand range of 4 D, using 2-D OCT [37]. Due to the limited the axial range of the sOCT, we are not able to provide data of the changes in the axial length of the eye with accommodation, that have been provided by partial coherence interferometry [48], combination of two OCT systems focused in different planes [35] or rapid switch between planes [37].

Finally, several studies have evaluated the fluctuations of refractive error upon accommodation to steady targets, as a function of the accommodative demand. Potential noise in the system has been discounted. Also, from previous studies in vitro, the effects of error propagation throughout the different optical surfaces is small [26,27]. As OCT allows imaging the different optical surfaces of the eye, this study has extended previous reports on microfluctuations using ultrasonography that could only measure axial distances [49]. Some studies report a systematic increase of these fluctuations for increased accommodation [7,50], and other studies report a maximum value for intermediate levels of accommodation [5,11]. Our study has extended this work by assessing the isolated contributions of lens shape changes, and biometrical changes to the dynamics of accommodation. Estimations of the eye power from geometrical measurements reveal an increase of the fluctuations with accommodation, ranging from 0.07 D to 0.47 D between 0 and 6 D (0.044 D per D of accommodative demand). These fluctuations and its changes with accommodation are comparable to those reported by Gambra et al. [7], from dynamic Hartmann-Shack–based measurements of refraction (from 0.09 D to 0.31 D for 0-6 D accommodative demand range, with a slope of 0.049 D/D) and Kotulak and Schor, who found a slope of 0.047 D/D using an infrared optometer [50]. A sensitivity analysis revealed that the fluctuations of accommodation were driven by dynamic changes in the lens surfaces, particularly in the posterior lens surface.