Real-time optical pH measurement in a standard microfluidic cell culture system

Abstract

The rapid growth of microfluidic cell culturing in biological and biomedical research and industry calls for fast, non-invasive and reliable methods of evaluating conditions such as pH inside a microfluidic system. We show that by careful calibration it is possible to measure pH within microfluidic chambers with high accuracy and precision, using a direct single-pass measurement of light absorption in a commercially available phenol-red-containing cell culture medium. The measurement is carried out using a standard laboratory microscope and, contrary to previously reported methods, requires no modification of the microfluidic device design. We demonstrate the validity of this method by measuring absorption of light transmitted through 30-micrometer thick microfluidic chambers, using an inverted microscope fitted with a scientific-grade digital camera and two bandpass filters. In the pH range of 7–8, our measurements have a standard deviation and absolute error below 0.05 for a measurement volume smaller than 4 nL.

1. Introduction

Microfluidic devices are promising for a wide range of bioapplications [1]. Microfluidic devices specifically designed for cell culture first appeared about a decade ago [2] and since then a growing number of miniature scale bioreactors for cell culture have been reported, primarily with the aim of bringing experimental resolution closer to the single-cell level. Such microfluidic cell culture systems can, for example, provide a platform for high throughput screening and validation of drug candidates [3]. Microfluidic devices offer precise control of experimental conditions via automation, parallelization and direct coupling to miniaturized downstream analysis platforms. By dramatically reducing the scale of the culture platform, these devices allow researchers to capture perturbations in a small subset of cells or even individual cells [4]. To achieve this goal, cells must be cultured in very small medium volumes, ranging from tens of nanoliters to a few microliters.

Cell culture in microfluidic systems, however, does not come without challenges. In most cases, the cells are closed off from the outside world within the microfluidic chip and their microenvironment cannot be probed directly with standard tools. Even when the sample medium has been extracted from the chip, its volume is often far too small to allow simple measurements using conventional laboratory equipment, such as benchtop pH meters. Consequently, many on-chip analysis methods have been developed in order to take full advantage of the integrated setup and to overcome the necessity of interfacing macro-scale equipment with micro-scale experiments. Fluorescent on-chip labeling has been widely used to track cellular proliferation and migration as well as intracellular protein localization [5]. Antibody-based binding assays have also been adapted to the microfluidic platform to produce fast and precise on-chip protein immunoassays [6] or In-Cell Western blots [7], and integrated PCR systems have enabled researchers to perform nucleic acid analysis [8]. However, simple methods to analyze the properties the cellular microenvironment are still in short supply.

A critical parameter in the cellular environment is the pH of the culture medium. The optimal pH for most cultured cells lies in a narrow range around 7.4 [9]. This may deviate slightly from one cell line to another, but most commercially available media are designed to keep pH close to 7.4, typically using either a sodium bicarbonate buffer or HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid). Cellular respiration produces carbon dioxide and lactate that can acidify the culture medium over time, which may significantly affect the microenvironment of the cells due to the small volume of growth medium. In order to properly monitor the cellular environment, it is therefore important to have a general, rapid, accurate, and non-invasive method of evaluating pH in the culture medium in real time. Most commercially available cell culture media contain phenol red, a commonly used pH indicator. The phenol red molecule has an acid and a base form, with absorption peaks at 430 nm and 560 nm, respectively, thus changing the color of the culture medium depending on pH. This allows for a quick but approximate visual evaluation of the pH of the culture medium. More accurate pH measurements in conventional cell culture (mL volumes), however, are generally carried out with a pH meter using a standard ion-selective glass electrode.

In a microfluidic environment, the small volume of the culture medium makes a direct measurement of pH more difficult. Several approaches to address this problem have been presented in the literature. One approach involves incorporating microelectrodes into the culture device that can be connected to off-chip analysis hardware [10]. When properly calibrated, this approach can offer fast and precise measurements over a wide range of pH values. An obvious disadvantage, however, is that electrodes embedded into a disposable chip increase fabrication complexity and call for a specifically designed culture platform. Furthermore, this system requires about half a microliter of fluid for the measurement [10], which is an order of magnitude larger than in some reported bioreactors [11]. Methods relying on adding pH-sensitive fluorescent dyes to the culture medium [12] or incorporating them into hydrogel analysis platforms [13] have also been reported. However, addition of fluorescent compounds to the culture medium may not be feasible due to possible effects on the cultured cells, and hydrogel analysis platforms require specific microfluidic system designs.

As discussed above, colorimetric methods based on light absorption of phenol red can be used to determine pH in microfluidic cell culture. The main difficulty in implementing absorption measurements in microfluidic systems, however, is related to the short light path through the absorbing medium. Several approaches have been suggested to increase the light path to improve detection accuracy, through modification of the microfluidic chip design such as the integration of optical fibers, complex mirror designs, and/or integrated optical cavities [14], again adding significantly to fabrication complexity and potentially interfering with the design flexibility of the microfluidic system.

In the present paper, however, we demonstrate that an accurate evaluation of pH in a conventional microfluidic system is possible using only a single-pass absorption measurement and standard imaging equipment. The only prerequisites are that the imaging area should include a non-absorbing part (e.g. an area immediately beside the microfluidic chamber) and that intensity calibration can be performed beforehand with a non-absorbing liquid. Our approach offers a simple and accurate method to measure pH of commercially available culture media in microfluidic chambers (based, e.g., on PDMS or any other optically transparent material), using only nL of culture medium as the actual measurement volume. The pH measurement can be carried out using transmitted-light microscope equipped with a fluorescence-grade (low-noise) digital camera and two bandpass filters. More generally, our results show how proper image analysis and calibration allows such imaging equipment (available in most biomedical research labs) to be used directly for the measurement of variables that can be linked to spectral modifications of optical absorption, in liquids or thin solid sections, even when the level of absorption is very small (<1%).

2. Theory

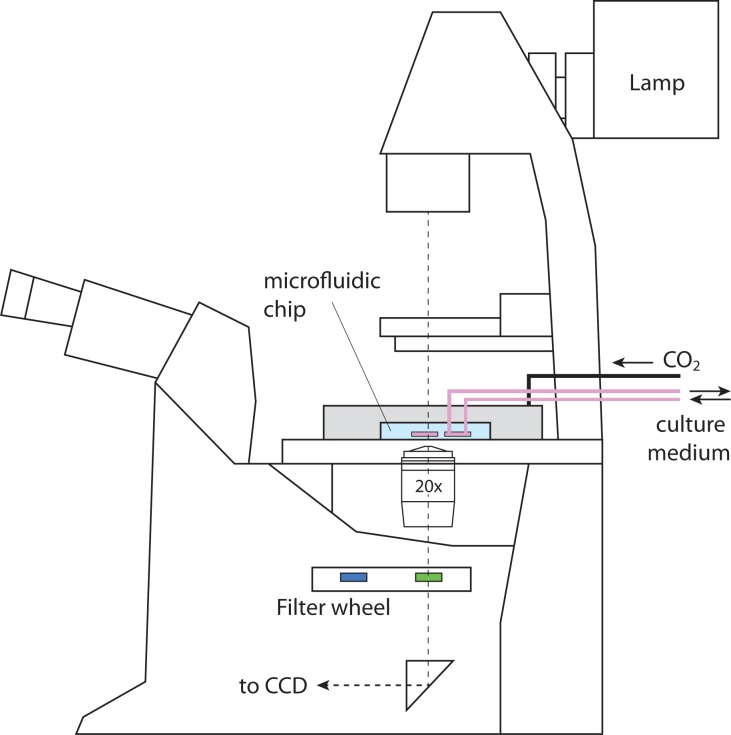
We consider the absorption of light transmitted through a microfluidic chamber, as schematically shown in Fig. 1. The transmitted light is collected by the microscope objective, passed through selected bandpass filters, and the resulting image is projected onto a charge-coupled device (CCD) camera. The light intensity from the lamp in the plane of the microfluidic chamber is assumed to have the form

$$I=I_{\mathit{lamp}}(t)\cdot f(x,y,\lambda )$$ (1)

where I is the intensity, I_lamp(t) is the base intensity of the lamp, which can fluctuate with time, and f(x, y, λ) describes the spatial variation at wavelength λ due to non-uniformity of the light source, dust particles, or other static effects.

Fig. 1.

Schematic layout of a live-cell microfluidic measurement system. Incubator box for temperature control not shown.

Now consider that an absorbing layer is introduced, consisting of a solution of phenol red. Absorption by phenol red can be described in terms of it being a simple weak acid. The chemical formula is C₁₉H₁₄O₅S ≡ HX, where we collect all atoms except for one hydrogen atom as X. The compound then partly dissociates into its conjugate base X ⁻ and a proton H ⁺. The ratio between the concentrations of the acid and base versions is related to the pH value according to

$$\text{pH}=\text{p}{K}_a+\text{log}\hspace{0.17em}\left(\frac{\left[X^{-}\right]}{\left[HX\right]}\right),$$ (2)

where K_a is the acid dissociation constant of phenol red, pK_a = −10log(K_a), and [·] denotes concentration.

Following a ratiometric approach, transmitted intensity can be measured at two given wavelengths, corresponding to the absorption peaks of the acid and base forms of phenol red, respectively:

$$I_i=I_{\mathit{lamp}}(t)\cdot f(x,y,{\lambda }_i)\cdot e^{-{\alpha }_i\rho d},$$ (3)

for i = 1, 2. The measured values can then be used to determine the ratio between the absorption coefficients α ₁, α ₂. Here, ρ is the concentration of phenol red and d the thickness of the microfluidic chamber. When absorption in very small, however, a couple of important issues must be considered. First, since we wish to use imaging through color filters to record the intensity at different wavelengths, the total power can change between measurements, made at different times t ₁ and t ₂. Second, the thickness d of the chambers is not strictly known, and can vary slightly between chambers. We need to cancel out I_lamp(t) · f(x, y, λ) to be able to determine α ₁/α ₂. In order to accomplish this, a calibration picture is taken at the two different wavelengths before the experiment (at time t ₀), filling the chamber with phenol-free buffer. When an actual measurement (made at time t ₁) is normalized by these calibration images, we get

$$I_i(x,y,{\lambda }_i,t_1)/I(x,y,{\lambda }_i,t_0)=\frac{I_{\mathit{lamp}}(t_1)}{I_{\mathit{lamp}}(t_0)}\cdot e^{-{\alpha }_{{\lambda }_i}\rho d}$$ (4)

for i = 1, 2. In order to eliminate the time variance, we make sure to have in the frame not only the microfluidic chamber itself, but also an area outside the chamber, where the light passes only through the chip and substrate materials (PDMS and glass in our case), which should not show any absorbance compared to the calibration image. The relative intensity in that area gives the value I_lamp(t ₁)/I_lamp(t ₀), yielding the relative transmission T _λ1 = e ^−α_λ1ρd. We do the same for λ ₂, and calculate:

$$\text{ln}(T_{{\lambda }_1})/\text{ln}(T_{{\lambda }_2})={\alpha }_{{\lambda }_1}/{\alpha }_{{\lambda }_2}.$$ (5)

The ratio α _λ1/α _λ2 thus determined can be compared to separately measured or published (see e.g. Ref. [15]) absorption spectra of phenol red at different pH values. It should be pointed out that although the spatial intensity variations f(x, y, λ) have been cancelled out, the ratio α _λ1/α _λ2 can still vary spatially due to lateral pH gradients, enabling also imaging of spatial variations in pH within the microfluidic system.

The absorbance of a solution of phenol red can be written as

$$A_{\lambda }={\alpha }_{\lambda }\rho d={\alpha }_{HX}^{\lambda }\left[HX\right]d+{\alpha }_{X^{-}}^{\lambda }\left[X^{-}\right]d$$ (6)

and the absorbance ratio at the peak absorption wavelengths of the acid and base forms becomes

$$A_{{\lambda }_1}/A_{{\lambda }_2}=\frac{{\alpha }_{HX}^{{\lambda }_1}\left[HX\right]+{\alpha }_{X^{-}}^{{\lambda }_1}\left[X^{-}\right]}{{\alpha }_{HX}^{{\lambda }_2}\left[HX\right]+{\alpha }_{X^{-}}^{{\lambda }_2}\left[X^{-}\right]}=\frac{{\alpha }_{HX}^{{\lambda }_1}+{\alpha }_{X^{-}}^{{\lambda }_1}\left[X^{-}\right]/\left[HX\right]}{{\alpha }_{HX}^{{\lambda }_2}+{\alpha }_{X^{-}}^{{\lambda }_2}\left[X^{-}\right]/\left[HX\right]}.$$ (7)

If the relative strength of absorption coefficients ${\alpha }_{HX}^{\lambda }$ and ${\alpha }_{X^{-}}^{\lambda }$ at the respective wavelengths is known from a separate measurement or from tabulated values, the ratio [X ⁻]/[HX] can be determined and therefore the pH value using Eq. (2), provided that the value of pK_a is also known. Prior knowledge of the values of the absorption coefficients and the dissociation constant is, however, not strictly necessary, as the absorbance ratio can be pre-calibrated using several solutions of known pH, as discussed in the following section.

It is important to note, that as the dissociation constant K_a in Eq. (2) depends on parameters such as temperature and ionic strength, a measurement of absorption spectra should correspond to the particular temperature (37°C in the case of mammalian cell culture) and the particular cell culture medium being used.

3. Implementation

We performed pH measurements using a fully motorized Leica DMI6000 inverted microscope with an incubation chamber, fitted with a QImaging ExiBlue CCD camera. We used microfluidic PDMS chips fabricated at the Stanford Microfluidics Foundry, based on a design by Gomez-Sjoberg et al. [11] For imaging at different wavelengths, we used 10-nm-wide bandpass filters (Thorlabs, 430 nm and 560 nm center wavelengths) selected to match the absorption peaks of the phenol red acid and base forms. The system is operated with Matlab software developed by Gomez-Sjoberg et al. [11]

As described in the previous section, the first step is to take calibration images through the two different bandpass filters, filling the chambers with water or phenol-free PBS buffer. A typical frame used in our measurements can be seen in Fig. 2. The larger image shows an entire chamber, with connecting channels, valves, etc. As shown in the inset, the actual measurement frame covers part of the culture chamber as well as a part of the surrounding PDMS to allow correcting for overall intensity fluctuations. We note that in our system, the time-dependent intensity fluctuation of the microscope lamp was significant for our measurement, on the order of 1% on a timescale of 1 second.

Fig. 2.

Close-up of a microfluidic chamber, design by Gomez-Sjoberg et al. [11]. The inset shows the typical image frame and the areas used for reference measurement (top) and the different rectangle sizes used pH measurements (bottom).

To reduce noise in the measurement, image intensity must be integrated over a number of camera pixels. We averaged the intensity over areas of varying size and position, as shown by the red squares in the inset of Fig. 2. For each measurement, 20 image acquisitions were made to determine a mean intensity and its standard deviation. For our specific setup, this resulted in a total measurement time of about 10 seconds per chamber, including the time required to mechanically switch between filters. However, the measurement time will, in general, depend on the setup and desired measurement accuracy.

All measurements were performed at 37°C (standard temperature for mammalian cell culture). Before pH measurements were performed, the microfluidic chambers were rinsed with PBS and loaded with sample fluid (PBS solutions or DMEM/F12 medium). To assert the accuracy and precision of our method, five PBS solutions containing phenol-red, ranging from pH 6.4 to pH 8.4, as measured with a benchtop pH meter (Fisher Scientific Accumet XL25), were prepared and consecutively measured in the microfluidic chip. The concentration of phenol red was 15 mg/L, a value that has been cell culture tested by Sigma-Aldrich. Twelve chambers were used, in order to determine variations between chambers. Furthermore, pH measurements were repeated 9 times, with a time interval of several minutes. Images were recorded and intensity measurements derived, based on different sizes of the measurement area, as shown above. In our measurements, the level of optical absorption by phenol red was typically of the order of 0.1–1%.

4. Results

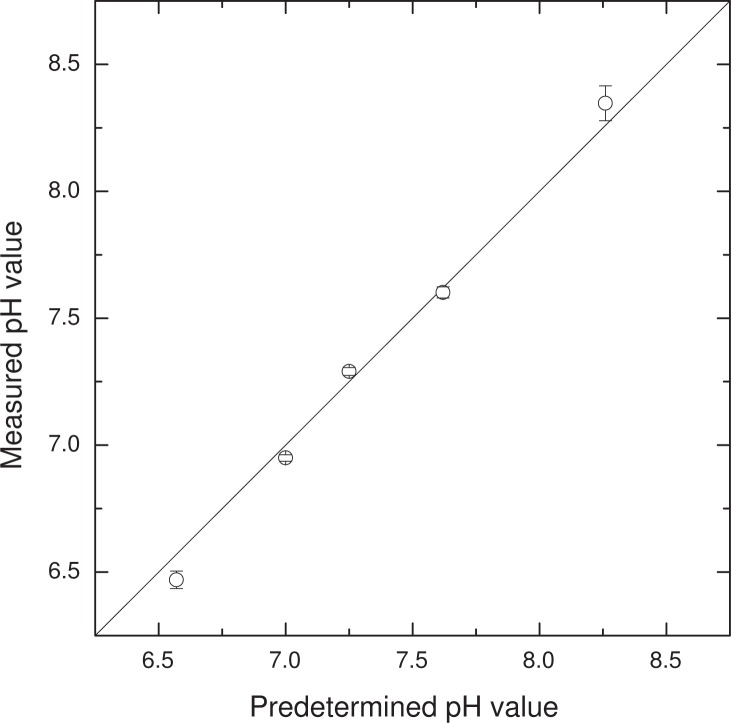
Figure 3 demonstrates the validity of the approach, showing the mean pH and standard deviation of all measurements made with the largest measurement area shown in Fig. 2. The standard deviation is mainly related to chambers-to-chamber variation, a part of which may be due to actual pH variations caused by incomplete flushing, chemical traces, etc. As mentioned in the previous section, determining the pH requires a knowledge of the relative value of absorption coefficients and pK_a. Using tabulated transmission spectra (courtesy of Dr. Jack Goldsmith at USCA), we calculated pH values based on Eq. (2), using a fitted value of pK_a giving the lowest standard error of the measured values compared to predetermined pH. This yields a pK_a value of 7.7, which is slightly lower than the commonly reported value of 7.9 at 37°C. The reason for this deviation is that the apparent pK_a differs from the actual one and depends on various environmental factors, such as ionic concentrations [16]. Nevertheless, calibration measurements carried out using samples of cell culture medium with different known pH values will yield an absorbance ratio A _λ1/A _λ2 which allows subsequent pH measurements to be carried out in the same medium without any knowledge of absorption coefficients or pK_a values.

Fig. 3.

pH values determined with optical absorption measurements, against pre-calibrated values. Error bars represent the standard deviation of 108 individual measurements (12 chambers, 9 individual measurements taken at time intervals of several minutes). The standard deviation and absolute error are also shown in Fig. 4.

The standard deviation and absolute error for different sizes of the measurement areas is shown in Fig. 4. In order to convert the size of the measurement area to a more general result, we have multiplied it by the average chamber thickness to determine the actual liquid volume used for the absorption measurement. The standard deviation decreases with increasing measurement volume, as expected, but increases substantially above pH 8 and below pH 7. For pH< 7 and pH> 8, the optical absorption at 560 nm and 430 nm, respectively, decreases rapidly, reducing the signal-to-noise ratio. The maximum sensitivity of the measurement is shifted slightly away from pK_a by the fact that the optical absorption strength of X⁻ and HX is not equal. Naturally, the precision of the measurement also depends on the phenol red concentration and the chamber thickness. The absolute error in our measurements is below 0.05 for pH 7–8, as shown in the bottom panel of Fig. 4.

Fig. 4.

Standard deviation of the pH value determined with absorption measurements (symbols, top panel) and deviation from predetermined pH value (symbols, bottom panel). Different liquid volumes correspond to the measurement areas shown in the inset of Fig. 2. Solid lines are guides to the eye. The increased uncertainty at low and high pH values is related to low absorption by the acid and base forms of phenol red. The minimum uncertainty is shifted from pK_a due to a difference in absorption strength of the acid and base forms.

An important issue in the absorption measurement relates to the uptake of phenol molecules into the PDMS matrix. Uptake of small molecules is of general concern in PDMS-based microfluidics, disturbing, e.g., measurements involving fluorescent labels [17]. In the case of phenol red, molecules accumulate in the PDMS in the conformation corresponding to the pH value at the time of uptake. This will cause increasing background absorption, introducing a time-dependent bias in the pH measurement. This long-term effect can be corrected for by recalibration; filling the chambers with a clear buffer and recording a new reference image. The period of time until a recalibration is needed depends on the time scale of the measurement, the pH range, the phenol concentration and the accuracy requirements of the experiment. Alternative methods to prevent unwanted uptake of molecules have also been explored in the literature, including coating the inside of the PDMS chambers [18] or using different materials for casting the microfluidic circuits [19].

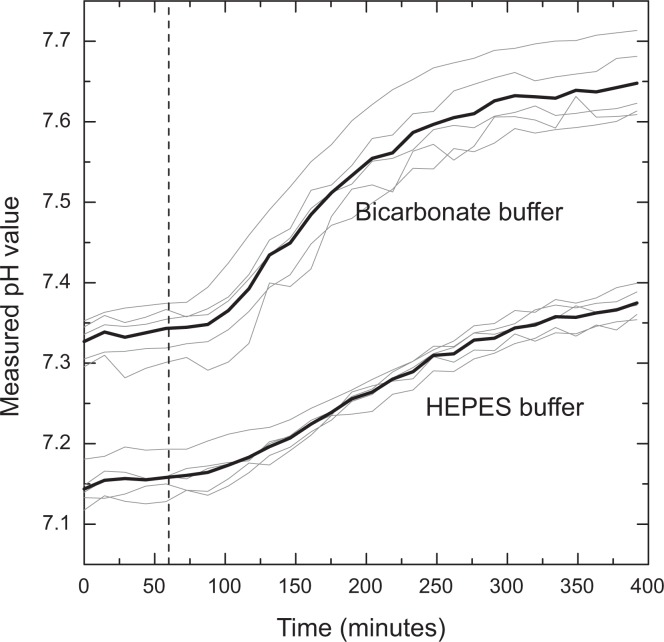
In order to demonstrate an application of our measurement approach, the pH value of Dulbecco’s modified Eagle’s medium with F12 nutrient supplements (DMEM/F12, Invitrogen) containing phenol red (8.1 mg/L) was monitored over time as the CO₂ concentration was changed in the environment surrounding the culture chip (abruptly reduced from 10% to 0.04%). PDMS is porous enough for CO₂ to diffuse through, thus affecting the pH of the medium within. Five chambers were filled with DMEM/F12 medium containing a HEPES buffer (3.5 g/L) and five chambers were filled with DMEM/F12 medium containing a sodium bicarbonate buffer (2.4 g/L). As shown in Fig. 5, there was a substantial shift of pH in all chambers over a period of 3–4 hours. As expected, the HEPES-containing medium showed less sensitivity to the external CO₂ concentration than the bicarbonate-containing medium, although the pH level of both media is observed to change significantly. The equilibration time will depend on the thickness of the PDMS chip, which in our case was about 5 mm.

Fig. 5.

Evolution of pH with changing CO₂ concentration in the environment surrounding a PDMS microfluidic chip containing DMEM/F12 medium with phenol red and either a bicarbonate buffer or a HEPES buffer. The figure shows measurements from five separate microfluidic chambers (solid gray lines) as well as their average (solid black lines). Atmospheric CO₂ levels were equilibrated at 10% at the beginning of measurements. After 60 minutes (dashed line), the CO₂ levels surrounding the chip were reduced to 0.04%. CO₂ reduction results in increasing pH in all chambers. The increase is more pronounced in the chambers containing DMEM/F12 with a bicarbonate buffer.

5. Conclusions

In this work we have investigated pH estimation in microfluidic systems, using ratiometric absorption imaging, with phenol red as the absorbant. Using absorption volumes of the order of 1 nL, we measured pH accurately with standard deviation below 0.04 and mean absolute error below 0.05 in the most relevant interval of pH ≃7–8. This level of accuracy and precision is certainly sufficient for most applications in cell culture research. The method was used to monitor pH after an abrupt change in CO₂ concentration outside the PDMS chip, establishing the time it takes for the system to reach chemical equilibrium and the effect of using differently buffered media.

The presented method is fully compatible with conventional microfluidic circuits and requires only standard life-science laboratory equipment (transmitted-light microscope, low-noise camera, image analysis software) in addition to a couple of low-cost bandpass filters. Our method therefore represents a general microfluidics measurement protocol of pH or other variables that can be ratiometrically quantified by spectral absorption signatures within the typical wavelength range of standard imaging equipment.