Internal Models Engaged by Brain-computer Interface Control

Abstract

Internal models have been proposed to explain the brain’s ability to compensate for sensory feedback delays by predicting the sensory consequences of movement commands. Single-neuron studies in the oculomotor and vestibulo-ocular systems have provided evidence of internal models, as have behavioral studies in the skeletomotor system. Here, we present evidence of internal models from simultaneously recorded population activity underlying closed-loop brain-computer interface (BCI) control. We studied cursor-based BCI control by a nonhuman primate implanted with a multi-electrode array in motor cortex. Using a novel BCI task, we measured the visual feedback processing delay to be about 130 milliseconds. By examining the task-based appropriateness of the population activity at different time lags, we found evidence that the subject compensates for the feedback delay by predicting upcoming cursor positions, suggesting the use of an internal forward model. Lastly, we examined the time course of internal model adaptation after altering the mapping between population activity and cursor movements. This study suggests that closed-loop BCI experiments combined with novel statistical analyses can provide insight into the neural substrates of feedback motor control and motor learning.

I. Introduction

How does the motor system compensate for sensory feedback processing delays? Internal models could enable the brain to predict the result of a motor command before sensory feedback reflects movement execution [1]. Single-neuron studies have implicated internal models in the oculomotor [2] and vestibulo-ocular [3] systems. Behavioral studies of arm reaching also provide evidence of internal models (for review, see [4]), but neural correlates thereof have been limited due to the complexities of the skeletomotor control system. In particular, arm movements involve large numbers of neurons across multiple brain areas that drive a nonlinear effector. Multiple modalities of sensory feedback contribute to control, where each modality has its own associated delays and coordinate frames.

In this work we consider a cursor-based brain-computer interface (BCI), which can be viewed as a simplified motor control system. In BCI, the activity of all neurons that drive the cursor is fully observed, the relationship between neural activity and cursor movements (i.e., the BCI decoder) is known and determined by the experimenter, and only visual feedback is presented to the subject. Although we are also interested in the assistive benefits of BCI, here we leverage BCI infrastructure for basic scientific studies of feedback motor control.

In this study, we asked the following three questions: (i) What is the subject’s visual feedback delay during BCI control? (ii) Is there evidence that the subject uses an internal model to compensate for the feedback delay? (iii)What is the time course of internal model adaptation during BCI learning? Section II describes the closed-loop BCI experiments, and Section III investigates the three questions above.

II. Methods

Experimental details were previously described in Chase et al. [5]. Briefly, a 96-electrode Utah array was implanted in proximal arm area of motor cortex (M1) in a Rhesus monkey (Macaca mulatta). Across 89 experimental sessions, single- and multi-unit spikes were sorted, and spike counts from 15–40 units were recorded in Δt ≈ 33 millisecond non-overlapping bins. Two-dimensional cursor velocity was linearly decoded from recorded spike counts according to

$${\mathbf{v}}_t={\mathbf{B}}_1({\mathbf{u}}_t-{\mathbf{b}}_0)$$ (1)

where v_t ∈ ℝ² is the decoded cursor velocity at timestep t, u_t ∈ ℝ^q is the spike count vector across q simultaneously recorded units at timestep t, and {B₁ ∈ ℝ^2×q, b₀ ∈ ℝ^q} are decoding parameters determined by the population vector algorithm (PVA) [6]. The BCI cursor position, p_t, was determined by integrating time-averaged decoded velocities

$${\mathbf{p}}_t={\mathbf{p}}_{t-1}+\left(\frac{1}{5}\sum _{k=0}^4{\mathbf{v}}_{t-k}\right)\mathrm{\Delta }t$$ (2)

We analyzed two types of 16-target center-out BCI cursor control experiments: (i) invisible zone (IZ) experiments enabled us to characterize strategies for feedback delay compensation; and (ii) rotation perturbation (RP) experiments enabled us to test predictions about the subject’s internal model. In IZ trials, the cursor began at the workspace center, but was not presented to the subject until its decoded position exited a workspace-centered circular invisible zone. We analyzed 10,320 successful IZ trials recorded over 69 sessions. We also analyzed 20 RP experiments. In RP trials, the cursor was always visible to the subject, but following a control session (typically 160 trials) came a perturbation session (typically 240 trials), in which decoding parameter B₁ was switched to B₂ such that 50% of the recorded units’ preferred directions were rotated by 60° in the decoder (equivalent to rotating the corresponding columns of B₁ by 60°). In both IZ and RP experiments, a trial was deemed successful and terminated as soon as the cursor visibly overlapped with the target.

III. Results

A. Visual Feedback Delay

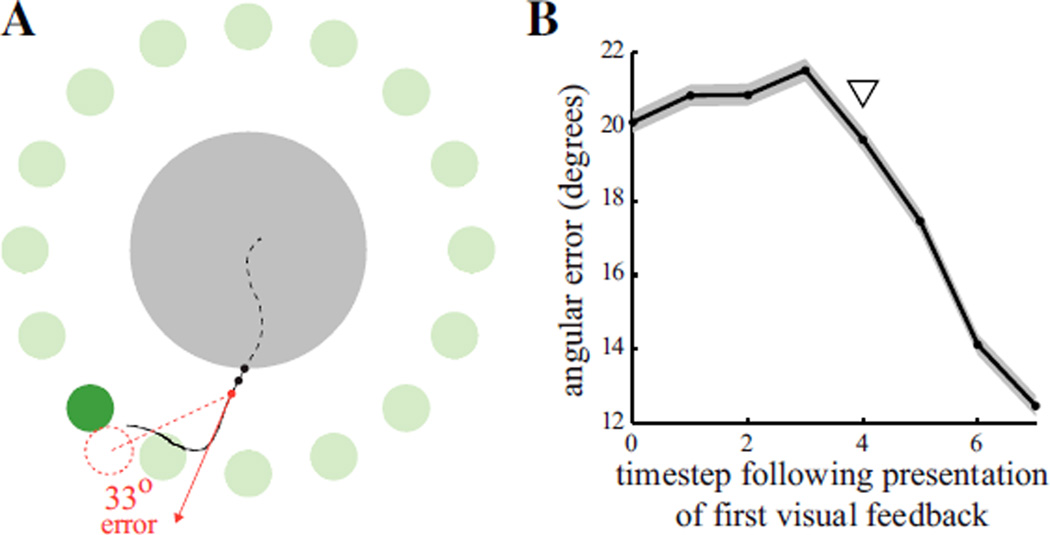
We used IZ experiments to characterize the visual feedback delay experienced by a subject operating our BCI system. During the initial portion of each trial, the subject directs the cursor toward the target, but with some initial error due to the absence of visual feedback before the cursor emerges from the invisible zone (Fig. 1A). Once the cursor exits the invisible zone, visual and motor processing delay the generation of corrective neural commands in M1. We quantified this visual feedback delay by estimating the time at which recorded neural activity first began to correct the initial error. For each IZ trial, we computed an error trajectory, defined as the timestep-by-timestep angles between decoded velocity (from equation 1) and the cursor-to-target direction. We aligned each trial’s error trajectory according to the timestep of the first cursor presentation (i.e., upon exiting the invisible zone), and averaged across trials. The first reduction in mean angular error occurred four timesteps after the cursor exited the invisible zone (triangle in Fig. 1B), indicating that the subject’s visual feedback delay was roughly four timesteps, or about 130 milliseconds. This result is consistent with previous reports of single-cell latencies in M1 [7].

Fig. 1.

Estimating visual feedback delay. (A) Cursor trajectory (black line) to a target (green circle) during an IZ trial. Angular aiming error is shown for the third timestep after the cursor exited the invisible zone (gray circle). Solid red line shows the direction of the decoded velocity (from equation 1). Dashed red line shows the smallest angular correction that would bring the cursor (dashed red circle) to the target and achieve task success. (B) Trial-averaged angular errors for IZ trials, indicating error correction (triangle) four timesteps following cursor visibility. Shaded region indicates +/− SEM (n = 10, 320).

B. Strategies for Feedback Delay Compensation

What aiming strategy does the brain employ to compensate for the visual feedback delay? We asked whether the subject aims from an outdated visual feedback of cursor position (Strategy 1) or from an internal prediction of the current cursor position (Strategy 2). The following analyses are based on the four-timestep visual feedback delay determined in Section III-A. At a particular timestep, we asked whether decoded velocity from the current neural command was more appropriate for aiming from the four-timestep-old visual feedback of cursor position (Strategy 1) or from the current cursor position (Strategy 2).

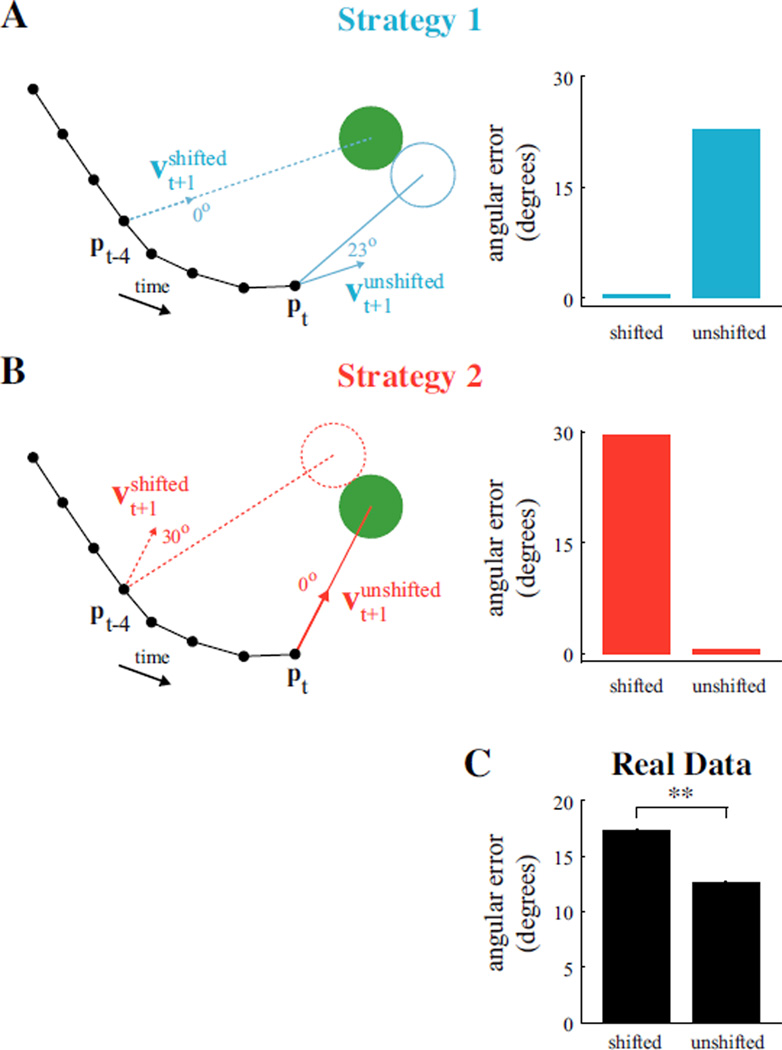
If the subject aims from the most recent feedback (Strategy 1), the decoded velocity applied at the current cursor position will not push the cursor straight toward the target, as illustrated by the solid blue arrow in Fig. 2A. However, if the subject can predict the current cursor position and aim from this prediction to the target (Strategy 2), the decoded velocity will push the cursor straight toward the target, as shown by the solid red arrow in Fig. 2B. Strategy 2 posits that internal estimates are consistent with actual cursor positions. We asked whether the recorded neural activity was more consistent with Strategy 1 or Strategy 2.

Fig. 2.

Comparison of aiming strategies. (A) Strategy 1—aim from the most recently perceived visual feedback, which is four timesteps old. (Left) Hypothetical trial under Strategy 1. When applied to the current cursor position (unshifted), the aim-from-feedback velocity command (solid blue arrow) would result in the cursor (blue circle) missing the target (green circle) by 23°. (Right) Hypothetical results from assessing angular errors of shifted and unshifted neural commands generated according to Strategy 1. (B) Strategy 2—aim from current cursor position. (Left) Hypothetical trial under Strategy 2. (Right) Hypothetical results from assessing angular errors of neural commands generated according to Strategy 2. (C) Averaged angular error across 9,750 IZ trials. Decoded velocities had smaller angular errors when assessed from unshifted cursor positions than when shifted to originate from cursor positions occurring four timesteps earlier (p < 0.001). Neural activity was more consistent with Strategy 2 than Strategy 1. Error bars (barely visible) indicate +/− SEM (n = 9, 750).

To discriminate between these two aiming strategies upon observing a neural aiming command at timestep t, we computed (i) angular aiming error when the decoded velocity vector is shifted to begin at the four timestep-old cursor position, p_t−4 and (ii) aiming error when the velocity vector is unshifted (i.e., when the vector originates from the current cursor position, p_t). If the subject aims from the feedback, the shifted velocity decode will have zero error, while the unshifted decoded velocity will have nonzero error (Fig. 2A-right). If the subject aims from the current cursor position, the shifted decode will yield nonzero error, while the unshifted decode will yield zero error (Fig. 2B-right).

We assessed the four-timestep-shifted and unshifted velocity decodes across the first seven timesteps of each IZ trial such that all shifted positions were visible to the subject. Of the 10,320 IZ trials in our dataset, we analyzed the 9,750 trials for which target acquisition required four or more timesteps beyond the invisible zone exit time. We found Strategy 2 to be more consistent with the neural data. As shown in Fig. 2C, decoded velocity vectors had smaller angular errors when assessed as originating from the current cursor position, rather than from the four-timestep-old cursor position.

Taken in combination with our characterization of the visual feedback delay, these results indicate that despite only having access to the true cursor position four timesteps ago, the subject’s current neural command reflects knowledge of the current cursor position. This neurophysiological evidence suggests that the subject uses an internal forward model to predict the current cursor position.

C. Timescale of Internal Forward Model Adaptation During Closed-loop BCI Control

Next, we examined the timescale of internal model adaptation. In general, the subject’s internal model cannot be directly measured, but with the appropriate experimental setup, we can reasonably approximate the subject’s internal model. In RP experiments, we assumed that after 160 consecutive trials of proficient BCI cursor movements under the control session decoder (B₁ from equation 1), the subject developed an internal forward model that was consistent with B₁. We asked to what extent recorded neural commands remained appropriate under B₁, when the decoder was switched to a perturbation session decoder (B₂, as described in Section II).

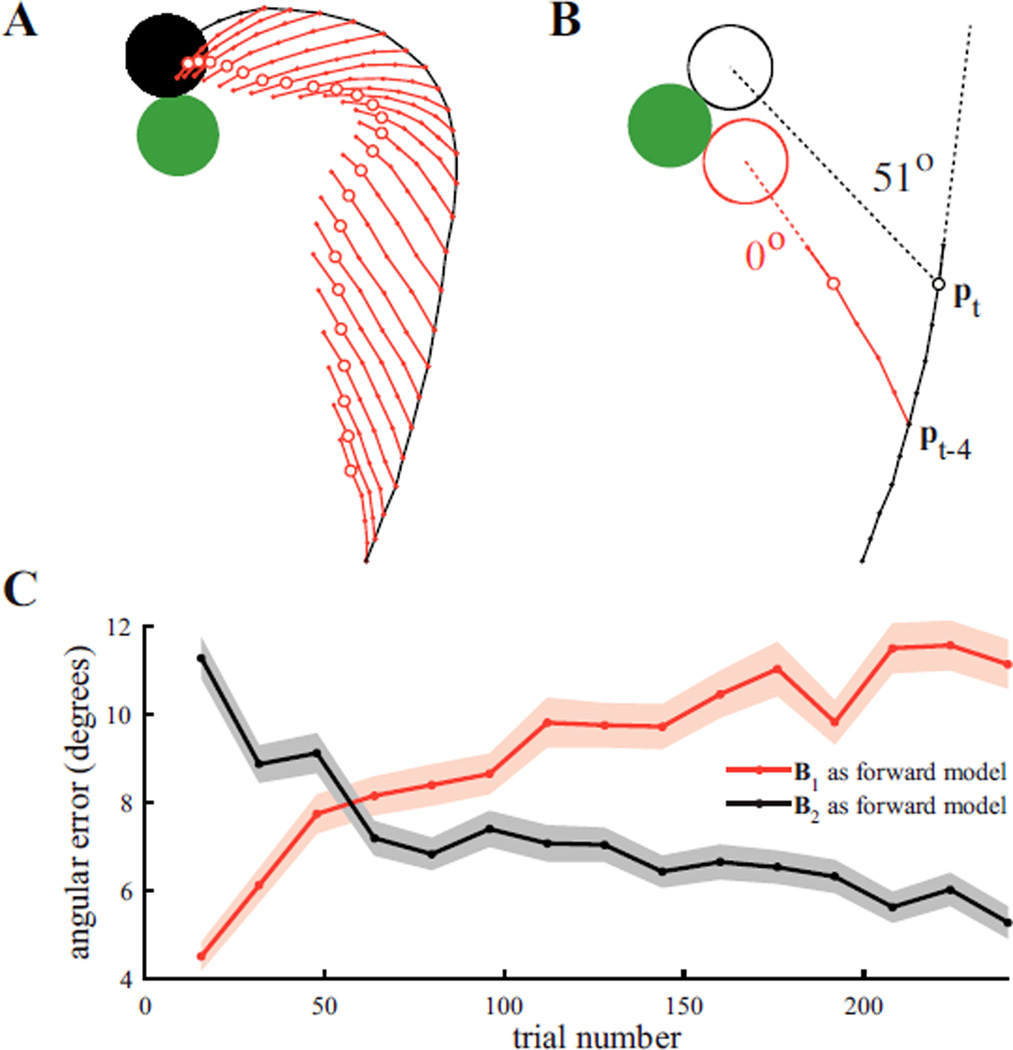
The B₂-decoded cursor trajectory during the first trial of a perturbation session is shown in Figure 3A, along with a set of “whiskers” illustrating how the same recorded neural activity would have driven the cursor under B₁. Interestingly, these whiskers all point toward the target, even when the actual cursor velocity does not. A particular whisker can be interpreted as the unfolding of internal cursor position estimates through forward model B₁. For example (Fig. 3B), suppose that at timestep t the cursor is at position p_t. Given the four-timestep feedback delay, p_t−4 is the most recent cursor position perceived by the subject. By internally propagating previously issued neural commands through B₁, the subject can aim from an internal estimate of the timestep t cursor position (small open red circles in Figs. 3A and 3B). The whisker segment beyond the open circle represents the subject’s intended aiming command to push the cursor to its timestep t + 1 position. In this analysis, cursor positions, whisker positions and velocity commands were filtered according to equation 2. For the timestep highlighted by Fig. 3B, the cursor would have hit the target had it continued straight along the issued aiming command, and thus the aiming command incurs zero error under forward model B₁. If the subject was operating under an internal model B₂, the subject’s timestep t estimate of cursor position would be the actual position, p_t, and the resulting neural command would have missed the target by 51°.

Fig. 3.

Internal model adaptation. (A) The first perturbation trial from an RP experiment. The B₂-decoded cursor trajectory (black line) was displayed to the subject online. B₁-decoded “whiskers” (red lines) were not displayed to the subject. (B) Aiming errors assessed at a single timestep from the trial in (A). Using B₁ as the forward model, the red whisker achieves zero error. Using B₂ as the forward model, the cursor would have missed the target by 51°. (C) Average angular aiming errors under B₁ and B₂. Angular errors for B₁ and B₂ were computed using the last segment of each whisker, as in (B). Angular errors were averaged within a trial, then averaged in non-overlapping blocks of 16 trials and across 20 RP experiments. Trial numbers correspond to the last trial included when averaging across trials. Shaded regions indicate +/− SEM (n = 320).

Consider the scenario in which the subject’s internal model completely adapts from B₁ to B₂. In this case, the subject’s internal estimate of the current cursor position would always exactly match the true current cursor position, despite the fact that the visual feedback delay prevents the subject from directly observing the current cursor position. Additionally, the subject’s next aiming command would match the actual BCI cursor velocity. By comparing perturbation session angular errors associated with the B₁-decoded whiskers to angular errors in the actual, online cursor velocities, we can determine the extent to which the subject’s neural activity reflected internal model B₁ or B₂.

Averaging across the perturbation sessions of twenty RP experiments, we found that angular aiming errors corresponding to B₁ predictions remained significantly lower than those corresponding to B₂ for the first 48 trials (p < 0.05), and 80 trials following the decoder switch, this trend reversed such that errors corresponding to B₁ predictions were significantly higher than those corresponding to B₂ (p < 0.05). This trend continued without reaching a plateau in corresponding error angles throughout the 240 trials we analyzed across all experiments. Thus we found that the subject’s internal model adapts to become increasingly consistent with B₂, while becoming inconsistent with B₁.

IV. Discussion

Despite the rather substantial visual feedback delay we identified (130 milliseconds), we show that the subject’s neural activity reflects the most recently displayed cursor position, implicating an internal model for BCI cursor control. We show that when cursor dynamics are perturbed, neural activity is initially consistent with an internal model of the original cursor dynamics, and adapts through experience to reflect an internal model consistent with the perturbed cursor dynamics.

Neural activity during IZ trials was more consistent with aiming from current cursor positions than from previous positions. This result specifically informs BCI decoder calibration procedures, which require paired examples of movement intention and neural activity. When calibrating a decoder based on examples of cursor control, the experimenter typically chooses from the following two assumptions: (i) intended movement direction points from the current cursor position to the target [8]; or (ii) intended movement direction points from a previous cursor position to the target (due to feedback delay). Our results from Section III-B suggest that assumption (i) is better than (ii), despite the substantial visual feedback delay. The same reasoning applies to tuning curve estimation from closed-loop BCI data [9], [10].

To aim from the current cursor position, Strategy 2 of Section III-B posits that the subject can perfectly predict the current cursor position. While we believe this to be a reasonable assumption, we know it cannot be entirely true, even when the subject demonstrates proficient control. Perfect predictions are implausible because (i) it is unlikely that the subject knows exactly which neurons contribute to cursor movement, (ii) spike generation involves stochastic processes, and (iii) there is likely a mismatch between the subject’s internal model and the decoder. These effects explain nonzero aiming errors in Fig. 2C and trial-to-trial variability in cursor trajectories. Because aiming errors are significant, the subject depends critically on visual feedback, and it is this dependence that enables us to differentiate between the aiming strategies presented in Section III-B.

Given the visual feedback delay, how could the subject predict the current cursor position without knowing the exact spike counts driving cursor movement? In this work, we take the view that the activity of recorded M1 neurons reflects a low-dimensional aiming command. In addition to generating activity in M1, this aiming command is likely sent in parallel (i.e., as efference copy or corollary discharge [2], [3]) to an internal model, possibly in the cerebellum [11]. If this internal model is appropriately tuned, its predictions can reasonably approximate the output of the BCI decoder.

Scenarios in which the internal model and effector are mismatched may offer the greatest insight into the neural underpinnings of motor control. For example, our analysis in Section III-C was enabled by inducing a mismatch between the subject’s internal model and the decoder. In early perturbation trials, cursor movements were poorly controlled, despite our finding that neural activity was consistent with aiming straight to the target under an alternative internal model.

In this work, experiment design afforded us a reasonable guess of the subject’s internal model. If instead we were able to estimate the subject’s internal model directly, we might be able to better explain neural activity and, in theory, track the subject’s internal model during adaptation. Statistical techniques designed to extract internal models from neural activity will enable more precise investigation of closed-loop motor control and motor learning.