Risk of radiogenic second cancers following volumetric modulated arc therapy and proton arc therapy for prostate cancer

Abstract

Prostate cancer patients who undergo radiotherapy are at an increased risk to develop a radiogenic second cancer. Proton therapy has been shown to reduce the predicted risk of second cancer when compared to intensity modulated radiotherapy. However, it is unknown if this is also true for the rotational therapies proton arc therapy and volumetric modulated arc therapy (VMAT). The objective of this study was to compare the predicted risk of cancer following proton arc therapy and VMAT for prostate cancer. Proton arc therapy and VMAT plans were created for 3 patients. Various risk models were combined with the dosimetric data (therapeutic and stray dose) to predict the excess relative risk (ERR) of cancer in the bladder and rectum. Ratios of ERR values (RRR) from proton arc therapy and VMAT were calculated. RRR values ranged from 0.74 to 0.99, and all RRR values were shown to be statistically less than 1, except for the value calculated with the linear-non-threshold risk model. We conclude that the predicted risk of cancer in the bladder or rectum following proton arc therapy for prostate cancer is either less than or approximately equal to the risk following VMAT, depending on which risk model is applied.

1. Introduction

The increased risk of a radiogenic second cancer following radiotherapy for prostate cancer (Brenner et al 2000, Baxter et al 2005, Moon et al 2006, Kendal et al 2007, Newhauser and Durante 2011) is a concern because of the large population of survivors and decreasing age of diagnosis (SEER 2007, Jemal et al 2010, Newhauser and Durante 2011). For example, Brenner et al (2000) reported an absolute risk of second cancer of 1.4% for patients that survived at least 10 years following prostate radiotherapy. With approximately 480,890 new prostate cancer cases diagnosed every year (Siegel et al 2011), an average age at diagnosis of 67 years (SEER 2007), a relative 10 year survival of 98% (ACS 2012), a cumulative probability of death from other causes at that age over 10 years of 30% (SSA 2012), and nearly two thirds of cancer patients receiving radiotherapy as part of their treatment (Smart 2009) we would expect on the order of 3,000 new cases of cancer caused by radiotherapy of the prostate each year. Therefore, any reduction in risk of second cancer from prostate radiotherapy could have a significant public health impact.

While it has been observed in patient studies that prostate radiotherapy carries an absolute risk of second cancer, these types of studies do not provide enough detail to differentiate between different radiotherapy techniques. To differentiate between techniques, incredibly detailed follow-up data would be required for each technique, which might take longer to collect than the clinical lifetime of the technique. An alternative method for differentiating between specific types of radiotherapy techniques is to apply a risk model to the dosimetric information for a specific treatment to predict the risk of second cancer.

Second cancer risks following intensity modulated photon radiotherapy (IMRT) (Kry et al 2005, Schneider et al 2006, Schneider et al 2007, Fontenot et al 2009, Bednarz et al 2010) and proton therapy (Schneider et al 2006, Schneider et al 2007, Taddei et al 2008, Fontenot et al 2009) of the prostate were predicted in previous studies, all of which revealed an advantage for proton therapy. Fontenot et al (2009) found that the partially in-field organs—the bladder and rectum—carried the greatest predicted risk of a second cancer.

While the lower predicted risk following proton therapy compared to IMRT for prostate cancer has been estabilished in prior studies, there are nascent and proposed rotational variations of IMRT and proton therapy, volumetric modulated arc therapy (VMAT) (Yu 1995, Otto 2008, Bzdusek et al 2009) and proton arc therapy (Isacsson et al 1997, Sandison et al 1997, Deasy et al 1997, Oelfke and Bortfeld 2000, Flynn et al 2007, Caporaso et al 2008), for which the second cancer risks are unknown. The use of VMAT has grown in the recent years and become a common choice for treatment of prostate cancer; treatment planning studies have shown comparable or decreased dose to organs at risk and reduced treatment time when compared to IMRT (Teoh et al 2011). On the other hand, proton arc therapy has not yet been implemented, but it has been proposed, and could become a treatment option for prostate cancer in the future. Because rotational radiotherapy distributes lower dose over a larger volume of normal tissue than static-beam radiotherapy (Kjaer-Kristoffersen et al 2009, Zhang et al 2009), it cannot be assumed that the predicted risks of second cancer incidence after rotational radiotherapy are equivalent to those after static-beam delivery. Therefore, to characterize the risk of developing a second cancer following these new techniques, a detailed study that is specific to rotational delivery is required.

The objective of this study was to compare the predicted risk of second cancer incidence in the bladder and rectum following proton arc therapy and VMAT for prostate cancer, taking into account both therapeutic and stray radiation. Specifically, we predicted the excess relative risk (ERR) values of the two modalities for those organs and then calculated the ratios of the ERR values (RRRs). To make these predictions, we first had to determine therapeutic doses, which we calculated using a commercial treatment planning system (TPS), and stray doses, which were from Monte Carlo simulations or previously published estimates. Then, for each of the modalities, we applied various risk models to the dosimetric data for the bladder and rectum, the organs at greatest predicted risk of a second cancer.

2. Materials and methods

2.1 Patient selection and organs at risk

This study was carried out under an institutional review board-approved protocol for retrospective treatment planning studies. Dosimetric assessments and risk calculations were based on data from 3 patients with prostate cancer who had been treated at our institution. All 3 patients underwent passively-scattered proton therapy for intermediate-stage prostate adenocarcinoma at ages of 46, 56, and 60 years at the time of treatment. All patients had undergone simulation computed tomography (CT) and treatment with water-filled balloons inserted into the rectum to improve rectal sparing. The clinical target volume (CTV) included the prostate and proximal seminal vesicles, and the planning target volume (PTV) was created by applying a margin to the CTV of 5 mm posteriorly and 7 mm in all other anatomical directions.

The 3 patients selected for this work were previously studied by Fontenot et al (2009, 2010), who compared the risks of second cancer between passively scattered proton therapy and IMRT. The patient selection criteria were described in that work in detail; briefly, the investigators conducted a retrospective chart review to determine the average proton beam range required for prostate cancer patients treated at our institution between January and July 2007. Then, 1 small, 1 medium, and 1 large patient with proton beam ranges equal to the mean and plus or minus two standard deviations (SD) were selected for retrospective treatment planning and second cancer risk assessment in the bladder and rectum (Fontenot et al 2009).

In the present study, we considered the predicted risk of incidence of second cancers in the bladder and rectum. However, because the contents of the bladder and rectum are not part of the organs themselves, we used the bladder wall and rectal wall volumes for the dosimetric assessments and risk calculations rather than the volumes of the entire bladder and rectum. The use of bladder wall and rectal wall volumes for risk assessment was consistent with the recommendations in Publication 110 from the International Commission on Radiological Protection (ICRP 2009). The thicknesses of the bladder wall and rectal wall were defined as 5 mm (Manieri et al 1998) and 3 mm (Huh et al 2003), respectively, which was consistent with the radiographically visible anatomy.

2.2 Treatment planning

A commercial TPS (Eclipse, Varian Medical Systems, Palo Alto, CA; version 8.6.15 for VMAT and version 8.9.08 for proton therapy) with heterogeneity corrections and a 2.5 mm calculation grid was used for treatment planning. All treatment plans were prescribed to a mean dose of 76 Gy to the PTV for photons and 76 Gy (RBE) to the PTV for protons, where 1 Gy (photons) = 1.1 Gy (RBE) (protons) to account for the assumed higher relative biological effectiveness (RBE) of protons, as described by the International Commission on Radiation Units and Measurements (ICRU 2007). Treatment plans were normalized so that at least 99% of the PTV received the prescribed dose. All treatment plans were reviewed and approved by a board-certified radiation oncologist.

The VMAT treatment plan was consistent with the prevailing clinical practice at our institution. Two 6-MV overlapping partial arcs were utilized, each subtending angles of 110-250 degrees, with the collimator rotated to 30 degrees for one arc and to 330 degrees for the other. This technique was developed to minimize entrance dose to the rectum and smear out interleaf leakage.

Proton arc therapy was approximated in the TPS with 16 equally spaced static passively scattered proton beams. This approach was similar to that of Flynn et al (2007), who approximated spot-scanned proton arc therapy with 9 equally spaced static beams. The beam energy varied with the patient habitus and beam angle and ranged from 160 MeV to 250 MeV. Uniform beam weighting was used for the entire 360 degrees. The lateral, proximal, and distal margins were calculated with clinically used equations using the methods of Moyers et al (2001, 2003).

Multiple constraints were applied during the treatment planning process to ensure clinical feasibility for proton arc treatments. For patient comfort and throughput efficiency, we limited the treatment time to 5 minutes. We constrained gantry rotation speed to between 0.1 rpm and 1 rpm, and imposed a maximum (theoretical) proton multileaf collimator (MLC) (Bues et al 2005) leaf speed of 3 cm/s that we estimated from the literature (Wijesooriya et al 2005). Finally, the dose rate was constrained to the clinically available interval at our institution of 0.2 Gy/min to 2 Gy/min.

Although we maintained clinical feasibility for many aspects of proton arc therapy, a few aspects of delivery with passively scattered protons remain to be solved. For example, the treatment plans included beam-specific range compensator devices and range modulation widths; it would be impractical to deliver these plans using currently-available passively-scattered treatment delivery systems. It is possible that a solution will be found for passively-scattered beams, and an alternative is magnetically-scanned proton beam therapy, where range modulator wheels and compensators are not necessary. However, we chose to plan with passively scattered proton beams since the endpoint in our study is the predicted risk of second cancer, and the larger production of neutrons from a passively scattered beam yields a conservative estimate of risk following scanned-beam proton therapy (Brenner and Hall 2008), including proton arc therapy.

2.3 Therapeutic and stray dose determination

The therapeutic dose was obtained from the TPS by exporting the differential dose-volume histograms (DVHs) for each organ. Because a differential DVH reports the differential volume of the organ receiving each level of dose, we could perform a more a comprehensive analysis than we could have using the mean organ dose alone.

Stray dose for VMAT was estimated with a method based on the work of Howell et al (2010a, 2010b). They carried out detailed measurements of out-of-field dose with thermoluminescent dosimeters (TLDs) and found that the TPS used in this study underestimated the dose in the regions outside the 5% isodose region by an average of 40%. In our study, portions of both the bladder and rectum were outside the 5% isodose region. Thus, we applied a 40% correction factor to the dose bins representing less than 5% of the prescribed dose.

Stray neutron dose for the medium-sized patient's proton arc treatment was calculated with Monte Carlo simulations using a previously-benchmarked model of the proton nozzle used at our institution. We used an in-house code (Newhauser et al 2007) that automated the Monte Carlo simulations through a series of pre- and post-processing data-handling modules that (1) converted patient computed tomography and treatment plan data from the Digital Imaging and Communications in Medicine (DICOM) format used by the commercial TPS into the Monte Carlo input format, (2) ran Monte Carlo simulations (MCNPX version 2.7c, Los Alamos, NM) on a cluster, and (3) converted the MCNPX output into DICOM files. Then, those files were imported into the TPS, and the stray neutron doses were evaluated using the dosimetric tools within the TPS.

The stray neutron doses for the small and large patients' proton arc treatments were approximated on the basis of neutron doses reported by Fontenot et al (2009) for parallel-opposed passively scattered proton beams for the same patients for the same proton beam line. Even though the distribution of neutrons throughout the patient anatomy might have differed slightly because of the different beam arrangement, this approximation provided a conservative estimate of the total neutron production for proton arc therapy, due to the larger number of neutrons created by the higher beam energy and the larger amount of tissue traversed for parallel-opposed beam proton therapy (Zheng et al 2008, Sengbusch et al 2009).

2.4 Equivalent dose determination

We applied organ-specific neutron radiation weighting factors values (w̅_R) that were previously determined for the same 3 patients by Fontenot et al (2009), who computed the fluence-weighted average values using neutron spectra from Monte Carlo simulations and conversion coefficients from ICRP Publication 92 (2003). The stray equivalent dose, H₂ (in Sv), was calculated using the formalism in ICRP Publication 60 (1991):

$$H_2={\overline{w}}_{\text{R}}\times D_2,$$ (1)

where w̅_R is the fluence-weighted average radiation weighting factor for neutrons and D₂ is the stray absorbed dose (in Gy) in a specified tissue.

The total equivalent dose for a given tissue, H_T (in Sv), was calculated using the following equation:

$$H_{\text{T}}=H_1+H_2,$$ (2)

where H₁ is the therapeutic dose and H₂ the stray equivalent dose, both in Sv. For photons, 1 Gy is equivalent to 1 Sv because of a mean radiation weighting factor of 1 (ICRP 1991). For protons, Gy (RBE) denotes the photon RBE-equivalent dose; thus, 1 Gy (RBE) was assumed to be radiobiologically equivalent to 1 Sv.

2.5 Risk prediction

We used the ERR to quantify the predicted risk of second cancer incidence, that is, the rate of cancer in an exposed population relative to the rate of cancer in an unexposed population minus 1. The linear-non-threshold (LNT) risk model was used to calculate the baseline predicted ERR values in this study. The risk coefficients for the LNT risk model were derived from the Biological Effects of Ionizing Radiation-VII report (NRC 2006), which accounts for sex, organ type, age at exposure (60 years for our study), and attained age (70 years for our study). Because the report provides a coefficient for the whole colon, we applied a fractional mass term (ICRP 2002) to predict risk for the rectum only. For this work, the risk coefficients were 0.51 ERR/Sv for the colon and 0.40 ERR/Sv for the bladder (Fontenot et al 2009). Therefore, the ERR for each tissue (T) was given by

$${\mathit{\text{ERR}}}_{\text{T}}=\frac{m_{\text{subregion}}}{m_{\text{T}}}\times R_{\text{T}}\times H_{\text{T}},$$ (3)

where $\frac{m_{\text{subregion}}}{m_{\text{T}}}$ is the fractional mass of the subregion compared to the total mass of the organ tissue (0.2 for the rectum as a fraction of the colon, and 1 for the bladder because the whole organ was considered), R_T is the organ-specific risk coefficient, and H_T is the total equivalent dose.

Because the LNT risk model is only recommended for doses up to approximately 2.5 Sv, alternative risk models were also investigated. The true dose-response relationship may be tissue-specific, but the linear-plateau and linear-exponential risk models are plausible alternatives to the LNT risk model (Lindsay et al 2001, Hall and Wuu 2003, Hall 2004, Dasu and Toma-Dasu 2005, Schneider et al 2005, Sigurdson et al 2005, Ronckers et al 2006, Ruben et al 2008). Therefore, linear-exponential and linear-plateau risk models with inflection points of 10 Sv and 40 Sv (expressed as linear-exponential-x and linear-plateau-x, where x denotes the numeric dose value of the inflection point) were investigated because they spanned the most plausible dose-response relationships observed in studies of patient follow-up data (Schneider and Kaser-Hotz 2005, Sigurdson et al 2005, Travis et al 2005, Ruben et al 2008, Fontenot et al 2009, Fontenot et al 2010). Figure 1 illustrates examples of the risk models used in this work.

Figure 1.

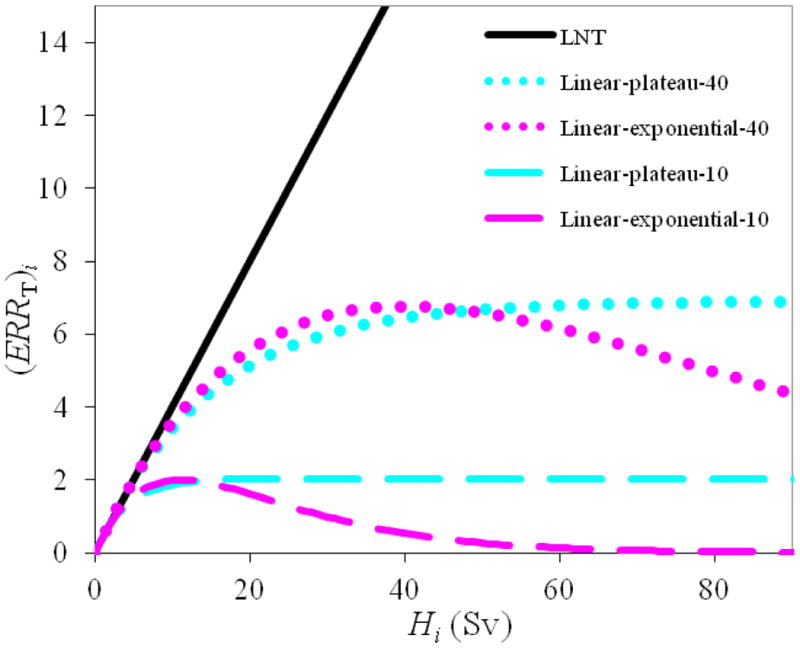
Examples of the linear-non-threshold (LNT), linear-exponential-10 and -40, and linear-plateau-10 and -40 risk models used to predict ERR for a given tissue (T) and dose-bin (i), corresponding to equations (3), (4), and (5), respectively (Fontenot et al 2009). Volume-weighting for the fractional volume of a specific dose bin, $\frac{V_i}{V_T}$, was set to 1 for this figure.

For these non-linear alternative risk models, the inhomogeneous distribution of dose affected the predicted risk. Therefore, the ERR was calculated for each dose bin of the differential DVH instead of using the mean organ dose. The ERR for each dose bin was calculated by

$${({\mathit{\text{ERR}}}_{\text{T}})}_{\text{i}}=\frac{m_{\text{subregion}}}{m_{\text{T}}}\times \frac{V_i}{V_{\text{T}}}\times {\left(\frac{\mathit{\text{ERR}}}{H}\right)}_{\text{T}}^0\times H_i\times e^{-{\alpha }_{\text{T}}{H}_i}$$ (4)

for the linear-exponential risk model and

$${({\mathit{\text{ERR}}}_{\text{T}})}_{\text{i}}=\frac{m_{\text{subregion}}}{m_{\text{T}}}\times \frac{V_i}{V_{\text{T}}}\times \frac{{\left(\frac{\mathit{\text{ERR}}}{H}\right)}_{\text{T}}^0}{{\alpha }_{\text{T}}}\times (1-e^{-{\alpha }_{\text{T}}{H}_i})$$ (5)

for the linear-plateau risk model. $\frac{m_{\text{subregion}}}{m_{\text{T}}}$ is the fractional mass of the subregion compared to the total mass of the organ tissue (0.2 for the rectum as a fraction of the colon, and 1 for the bladder), $\frac{V_i}{V_{\text{T}}}$ is the fractional volume of the dose bin compared to the total volume of the organ tissue, ${\left(\frac{\mathit{\text{ERR}}}{H}\right)}_{\text{T}}^0$ is the organ-specific term for which the risk model reduces to the LNT risk model at low doses, H_i is the equivalent dose for the dose bin, and α_T is the tissue-specific parameter that accounts for cell sterilization (Fontenot et al 2009, Fontenot et al 2010). The risk for the tissue is therefore given by

$${\mathit{\text{ERR}}}_{\text{T}}=\sum _{i=1}^n{\mathit{\text{ERR}}}_i$$ (6)

where ERR_T is the sum over all n dose bins from the differential DVH for the tissue, and ERR_i is the ERR of the dose bin given by the linear-exponential (eq. 4) or linear-plateau (eq. 5) risk model (Fontenot et al 2010).

The total ERR for a modality (x) is the sum of the tissue-specific ERRs. In this case, the sum is over two organs (the bladder and the rectum):

$${\mathit{\text{ERR}}}_{\text{x}}=\sum _{\text{T}=1}^2{\mathit{\text{ERR}}}_{\text{T}}.$$ (7)

Finally, the RRR was calculated to compare the two modalities, defined in this study as

$$\mathit{\text{RRR}}=\frac{{\mathit{\text{ERR}}}_{\text{PAT}}}{{\mathit{\text{ERR}}}_{\text{VMAT}}}.$$ (8)

According to this definition, an RRR greater than 1 would indicate a higher risk of a second cancer following proton arc therapy (PAT), and an RRR less than 1 would indicate a higher risk after VMAT.

2.6 Statistical analysis

The Student's t-test and exact sign test were used to test for significance in the differences in predicted risk after proton versus photon arc therapy. We chose to complete both tests to take advantage of the properties of each: the Student's t-test takes the magnitude of differences into consideration (but is susceptible to outliers), and the exact sign test is insensitive to outliers and appropriate for small sample sizes (but neglects the magnitude of differences). Specifically, the null hypothesis was that the RRR was equal to or greater than 1, and the alternative hypothesis was that the RRR was less than 1 (indicating an advantage for proton arc therapy); a p-value of less than 0.05 was considered significant in both tests. We used one-sided tests because we expected that the risk would be lower for proton arc therapy than for VMAT. The statistical software package StatXact, version 7.0 (Cytel Studio, Cambridge, MA), was used for this analysis.

2.7 Uncertainty analysis

Uncertainty in RRR was estimated for each patient by propagating the uncertainties associated with the dose determination, neutron w̅_R , and risk models. The methodology for uncertainty analysis was extended and based on the work of Fontenot et al (2010). This estimation of the asymmetric relative uncertainties in RRR (based on 1σ, or a 68% confidence interval), $\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)$, is given by

$$+{\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)}^2={\left(\frac{\text{∑}_{\text{T}=1}^2{\mathit{\text{ERR}}}_{\text{T}}^2{\left(\frac{{\sigma }_D}{D}\right)}^2}{{\left(\text{∑}_{\text{T}=1}^2{\mathit{\text{ERR}}}_{\text{T}}\right)}^2}\right)}_V+{\left(\frac{\text{∑}_{\text{T}=1}^2({\mathit{\text{ERR}}}_1^2{\left(\frac{{\sigma }_{D_1}}{D_1}\right)}^2+{\mathit{\text{ERR}}}_2^2{\left(\frac{{\sigma }_{D_2}}{D_2}\right)}^2)}{{\left(\text{∑}_{\text{T}=1}^2{\mathit{\text{ERR}}}_{\text{T}}\right)}^2}\right)}_P+{\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)}_{\overline{w_{\text{R}}}}^2$$ (9)

$$-{\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)}^2={\left(\frac{\text{∑}_{\text{T}=1}^2{\mathit{\text{ERR}}}_{\text{T}}^2{\left(\frac{{\sigma }_D}{D}\right)}^2}{{\left(\text{∑}_{\text{T}=1}^2{\mathit{\text{ERR}}}_{\text{T}}\right)}^2}\right)}_V+{\left(\frac{\text{∑}_{\text{T}=1}^2\left({\mathit{\text{ERR}}}_1^2{\left(\frac{{\sigma }_{D_1}}{D_1}\right)}^2+{\mathit{\text{ERR}}}_2^2{\left(\frac{{\sigma }_{D_2}}{D_2}\right)}^2\right)}{{\left(\text{∑}_{\text{T}=1}^2{\mathit{\text{ERR}}}_{\text{T}}\right)}^2}\right)}_P+{\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)}_{\overline{w_{\text{R}}}}^2+{\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)}_{RM}^2,$$ (10)

where the plus and minus signs on ${\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)}^2$ indicate the positive and negative uncertainty in the RRR values, respectively. The subscript V indicates VMAT, and the subscript P indicates proton arc therapy. The summations are over 2 tissues (T) the bladder and the rectum. For VMAT, $\left(\frac{{\sigma }_D}{D}\right)$ is the relative uncertainty in the therapeutic dose and the correction method for estimating the stray dose. For proton arc therapy, the subscript 1 denotes therapeutic dose, and 2 denotes stray dose. Therefore, $\left(\frac{{\sigma }_{D_1}}{D_1}\right)$ is the relative uncertainty in the therapeutic dose, and $(\frac{{\sigma }_{D_2}}{D_2})$ is the relative uncertainty in the stray neutron dose. ${\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)}_{\overline{w_{\text{R}}}}$ and ${\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)}_{RM}$ are the relative uncertainties in the w̅_R value and the risk model, respectively.

$\left(\frac{{\sigma }_D}{D}\right)$ was determined by taking the quadratic sum of the assumed uncertainty in the VMAT therapeutic dose and the calculated uncertainty in the VMAT stray dose. The uncertainty in the therapeutic dose was conservatively estimated at 2%. The uncertainty in the VMAT stray dose was calculated with an uncertainty analysis. Howell et al (2010a, 2010b) found that the stray dose was underestimated by a mean ± SD of 40% ± 20%. Therefore, following the method of Howell et al, the mean dose was found with the lower- and upper-bound corrections (20% and 60%), and the interval in mean dose values was used to estimate the uncertainty in the dose. For proton arc therapy, $\left(\frac{{\sigma }_{D_1}}{D_1}\right)$ was taken as 5% (Giebeler 2009) and $\left(\frac{{\sigma }_{D_2}}{D_2}\right)$ was found to be 1% according to the quadratic sum of the statistical uncertainty from the Monte Carlo simulations for each beam's contribution to the stray dose. ${\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)}_{\overline{w_{\text{R}}}}$ was estimated at 4.7% by calculating the interval of RRR values resulting from the likely interval of w̅_R values (from 0.5 to 5). Then, half of the interval in RRR values was assumed to be 2σ of the distribution. Similarly, ${\left(\frac{{\sigma }_{\mathit{\text{RRR}}}}{\mathit{\text{RRR}}}\right)}_{RM}$ was estimated to be 26.2% by calculating the range of RRR values resulting from the likely range of risk models. Because the LNT risk model was our baseline risk model, all of the alternative values of RRR were smaller than the baseline. This interval was assumed to be 1σ of the distribution and was only applicable to the negative side of the uncertainty. Therefore, the resulting uncertainty is asymmetric with contributions from uncertainty in dose and neutron weighting factor in the positive direction and contributions from uncertainty in dose, neutron weighting factor, and risk model in the negative direction.

3. Results

All treatment plans provided clinically acceptable coverage of the target, that is, at least 99% of the PTV received at least 76 Gy or Gy (RBE). Dose distributions for the VMAT and proton arc treatment plans for the medium-sized patient are shown in figures 2(a) and (b), respectively. Similar dose distributions were observed for the small and large patients. Figure 2 shows that proton arc therapy distributed the low dose over a smaller volume of normal tissue than VMAT. On average, proton arc therapy reduced the volume of normal tissue exposed to doses between 10 and 30 Gy or Gy (RBE) by 73% compared to VMAT. All plans met the clinical DVH constraints of the prevailing standard-of-care at our institution.

Figure 2.

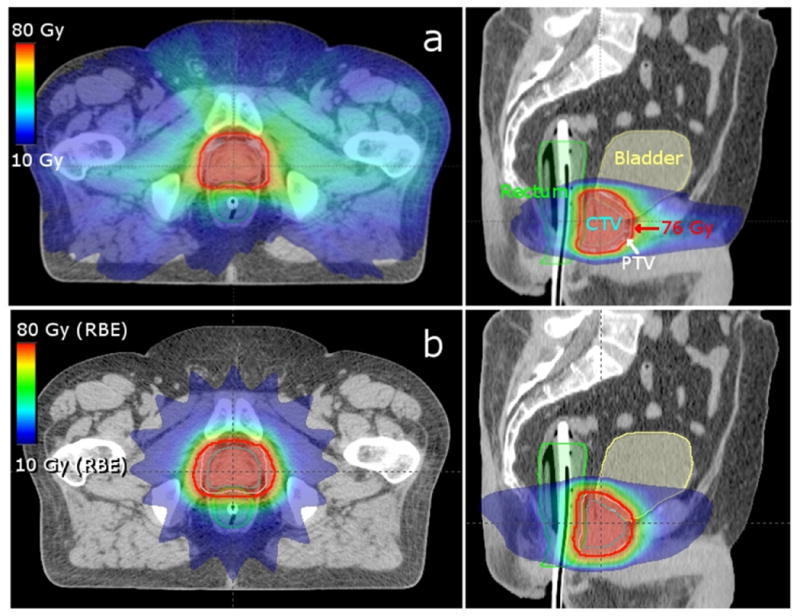
Axial (left) and sagittal (right) images of the medium-sized patient's VMAT (a) and proton arc therapy (b) treatment plans. The prescription isodose line (76 Gy or Gy (RBE)) is outlined in red, the CTV in cyan, the PTV in white, the bladder in yellow, and the rectum in green.

Cumulative DVHs of dose in the bladder wall and rectal wall for the VMAT and proton arc treatment plans for the medium-sized patient are shown in figure 3 (not including stray dose). Similar DVHs were observed for the small and large patients. There were only small differences in DVHs observed between the modalities for the bladder wall. For the rectal wall, the volume receiving medium to high doses was consistently slightly larger for proton arc therapy.

Figure 3.

Cumulative DVHs (cumulative volume as a function of dose) for the bladder wall (top) and rectal wall (bottom) for the medium patient. The VMAT dose is reported in Gy, and the proton arc therapy dose is reported in Gy (RBE).

The mean equivalent doses from stray radiation are listed in table 1. For all 3 patients, the stray doses were higher for proton arc therapy than for VMAT. The Monte Carlo-calculated proton arc therapy stray doses for the medium-sized patient agreed well with the estimations from the literature (table 1). However, the Monte Carlo simulations yielded slightly higher stray dose to the rectum than the calculation from the literature, which likely reflects the parallel-opposed beam geometry of the calculated value from the literature. As discussed above, the parallel-opposed geometry, while yielding a conservative estimate of the total neutron production for proton arc therapy, will likely underestimate neutrons in the rectum due to the lack of a posterior beam.

Table 1.

Mean values of equivalent dose from stray radiation (H_Stray) to the bladder wall and rectal wall of the small, medium, and large patients for the entire VMAT or proton arc therapy treatment. For proton arc therapy (PAT), the stray doses were calculated from the literature for the small and large patients and calculated with Monte Carlo simulations for the medium-sized patient. Values from the literature (Fontenot et al 2009) for the medium-sized patient are presented in parentheses for comparison.

	HT (Sv)
	VMAT		PAT
Patient Habitus	Bladder Wall	Rectal Wall	Bladder Wall	Rectal Wall
Small	0.28	0.28	0.82	0.61
Medium	0.43	0.27	0.96 (0.97)	1.13 (0.76)
Large	0.30	0.08	1.06	0.88

An example of a representative differential DVH and how each dose bin contributed to the ERR from the linear-exponential-10 risk model for the medium-sized patient is shown in figure 4, where it can be seen that the contribution diminished as the equivalent dose increased. The predicted ERR values are listed in table 2, and the RRR values are plotted in figure 5. The mean RRR varied between 0.74 and 0.99, depending on the risk model used, and the distribution of RRR values was statistically less than 1 (for both statistical tests), except for the LNT risk model. The uncertainties in the dose determination, neutron w̅_R , and risk models were applied to the baseline LNT RRR values to provide a 68% confidence interval (figure 6).

Figure 4.

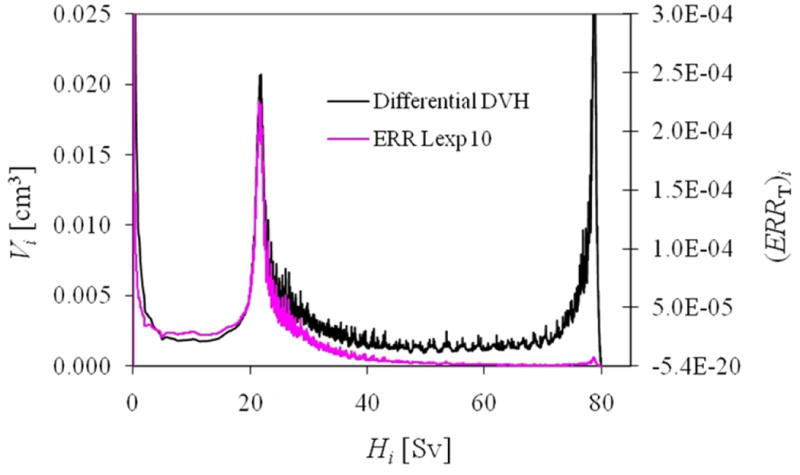
Calculated differential volume (left scale) and ERR from the linear-exponential risk model with an inflection point at 10 Sv (ERR Lexp 10, right scale) as a function of equivalent dose for the rectal wall for the medium-sized patient.

Table 2.

Predicted ERR values of second cancer in the bladder and rectum for VMAT and proton arc therapy (PAT) for various risk models. Lexp 10: linear-exponential-10, Lexp 40: linear-exponential-40, Lplat 10: linear-plateau-10, Lplat 40: linear-plateau-40.

		ERR
Patient Habitus	Modality	LNT	Lexp 10	Lexp 40	Lplat 10	Lplat 40
Small	VMAT	11.40	1.40	4.63	2.07	4.74
	PAT	11.59	1.02	3.68	1.74	4.31
Medium	VMAT	9.18	1.32	3.74	1.82	3.86
	PAT	9.71	0.88	3.35	1.49	3.55
Large	VMAT	13.95	1.34	5.18	2.21	5.37
	PAT	12.61	1.09	4.60	1.93	4.89
Mean	VMAT	11.51	1.35	4.51	2.03	4.66
	PAT	11.31	1.00	3.88	1.72	4.25

Figure 5.

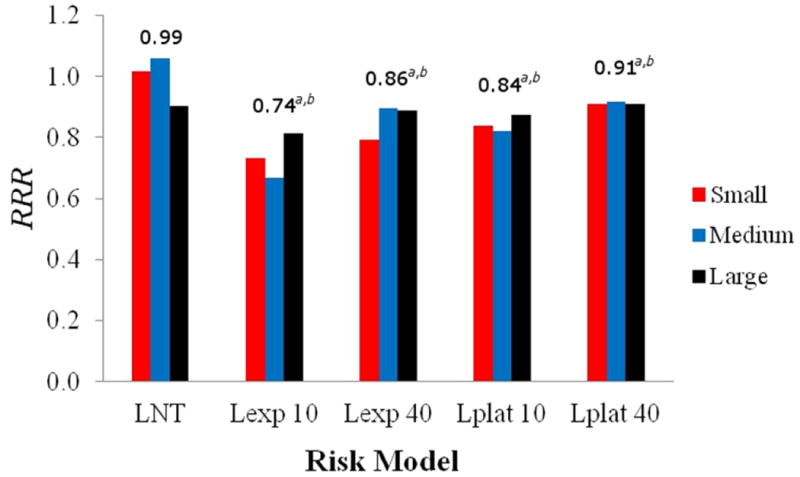
Predicted RRR of second cancer in the bladder and rectum following prostate radiotherapy for VMAT and proton arc therapy for the small, medium, and large patients for the linear-non-threshold (LNT), linear-exponential-10 (Lexp 10), linear-exponential-40 (Lexp 40), linear-plateau-10 (Lplat 10), and linear-plateau-40 (Lplat 40) risk models. The mean RRR is listed above each group, where a and b represent a statistically significant advantage for proton arc therapy (p-value < 0.05) with respect to risk calculated with the Student's t-test and exact sign test, respectively.

Figure 6.

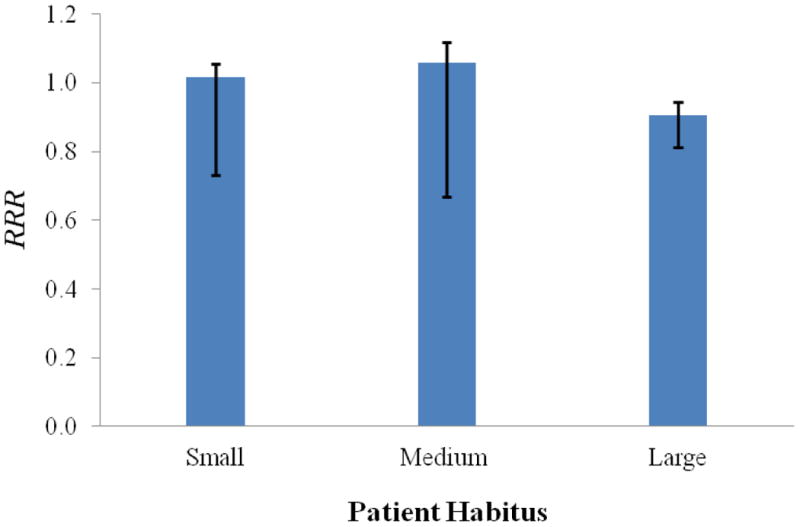
Predicted RRR values for the small, medium, and large patients. The LNT risk model was used to calculated baseline RRR values, and uncertainties in the dose determination, neutron w̅_R , and risk models were applied to the baseline LNT RRR values to provide a 68% confidence interval. It can be seen that the uncertainties are asymmetric, which resulted from the asymmetric uncertainties in the risk models (eqs. 9 and 10).

4. Discussion

The findings of this study revealed that proton arc therapy significantly reduces the predicted risk of radiogenic second cancer in the bladder and rectum following prostate radiotherapy compared with that following VMAT. However, this was only true when we predicted risk with the linear-exponential and linear-plateau risk models. No significant difference was seen between the modalities when the risk was predicted with the LNT risk model. While there is evidence in the literature that suggests the linear-exponential and linear-plateau models might be more appropriate than the linear-non-threshold model for these types of high-dose risk projections (Hall and Wuu 2003, Schneider et al 2005), there remains uncertainty regarding which risk model should be applied to patients receiving cancer radiotherapy. Regardless of the risk model selected, our findings revealed that proton arc therapy did not increase the predicted risk when compared to VMAT.

The results of this study are significant because they underscore the potential for reducing the incidence of second cancers by careful selection of radiotherapy technique. Although the absolute risk for an individual patient is most likely on the order of a percent or two (Brenner et al 2000), the impact on public health could be large because of the large population of prostate cancer survivors in developed countries.

A major strength of this study is its novelty; to our knowledge, this was the first study to predict the risk of second cancer incidence following VMAT and proton arc therapy for prostate cancer. We compared our results with studies that evaluated the risk of second cancer following proton and photon static beam radiotherapies for prostate cancer. Given the differences in the treatment modalities and other methods, our results are in good agreement with the existing literature. In one study, Schneider et al (2007) reported the relative risks of second cancer following spot-scanned proton therapy (vs 6-MV IMRT) were 0.49, 0.50, and 0.51 for the LNT, linear-exponential, and linear-plateau risk models, respectively. In another study, Fontenot et al (2009) found the mean RRR for second cancer following passively scattered proton therapy for the same 3 patients studied in this work to be 0.68 for the LNT risk model. They also found the RRR for the medium-sized patient to be 0.66, 0.69, 0.69, 0.60, and 0.62 for the LNT, linear-exponential-10 and -40, and linear-plateau-10 and -40 risk models, respectively. In order to compare our data with those from the literature, we completed risk calculations from therapeutic dose to the entire bladder and rectum volumes (i.e., wall plus contents). We found the risk (from therapeutic radiation) following VMAT to be less than the risk following IMRT and, similarly, the risk following parallel-opposed beam proton therapy to be less than the risk following uniformly weighted proton arc therapy (table 3) (Fontenot et al 2009). Additionally, because of the distribution of dose, we found that the predicted risks for all treatment modalities were an average of 32% higher for the bladder and 11% higher for the rectum when predicted with the wall contours rather than the whole-organ contours (table 3).

Table 3.

Predicted ERR values of second cancer incidence in the bladder, bladder wall, rectum, and rectal wall predicted with the LNT risk model from therapeutic radiation from IMRT (Fontenot et al 2009), VMAT (this work), lateral-opposed beam proton therapy (Proton (lat-opposed)) (Fontenot et al 2009), and uniformly weighted proton arc therapy (PAT (uniform)) (this work).

Organ	ERR
	IMRT	VMAT	Proton (lat-opposed)	PAT (uniform)
Bladder	8.88	5.25	3.68	4.86
Bladder Wall	10.44	6.55	5.26	6.24
Rectum	3.32	2.09	2.01	2.74
Rectal Wall	3.43	2.43	2.19	2.97

Other important strengths of this study included utilization of detailed, patient-specific dose calculations for both therapeutic and stray exposures. By calculating dose on the patient CT geometry, we were able to perform risk calculations based on the three-dimensional distribution of dose in the organ of interest, not just the mean dose to that organ. Those predicted risk calculations were further strengthened by the application of uncertainty analysis, which provide prospective for the large amount of uncertainty involved with this type of calculation (figure 6). In addition, limitations and constraints were applied during the treatment planning process for proton arc therapy to maintain clinical realism and feasibility of this theoretical treatment technique.

A limitation of this study is that the beam weighting differed between the therapies, which produced differences in dose distribution. Non-uniform beam weighting was used for VMAT to avoid photon entrance dose to the rectum and because the inverse planning algorithm automatically modulated the dose. This produced a dose distribution that was more anterior for VMAT (figure 2). Uniform beam weighting was chosen for proton arc therapy as a simple first approach for the treatment technique, but the present findings suggest that it would be interesting to study non-uniform beam weighting for proton arc therapy. Future enhancements to treatment planning methods for proton arc therapy, e.g., the capaibilty to optimize proton fluence weights versus gantry angle, would likely open avenues to reduce second cancer risks below what was predicted in this study. The effect of non-uniform beam weighting on RRR is currently under investigation in our laboratory. In addition, this work could be further strengthened by a detailed study of the effects of PTV margin size on the uncertainty in the RRR. Such an investigation was beyond the scope of the present study but is part of our ongoing work in the area of uncertainty analysis.

In summary, this study demonstrated that a simple form of proton arc therapy can provide comparable target coverage to VMAT while also providing lower bladder and rectal doses. Moreover, these lower normal tissue doses decreased predicted risk second cancer incidence. Because prostate cancer is the most common cancer in men, a small decrease in second cancers could have a substantial impact on public health. Also, the potential benefits of proton arc therapy may be further enhanced by the application of non-uniform beam weighting. While our work focused on prostate cancer, the methods of this proof-of-principle study can be applied to other cancer sites.