Muscle oxygenation measurement in humans by noninvasive optical spectroscopy and Locally Weighted Regression

Abstract

We have developed a method to make real-time, continuous, noninvasive measurements of muscle oxygenation (Mox) from the surface of the skin. A key development was measurement in both the visible and near infrared (NIR) regions. Measurement of both oxygenated and deoxygenated myoglobin and hemoglobin resulted in a more accurate measurement of Mox than could be achieved with measurement of only the deoxygenated components, as in traditional near-infrared spectroscopy (NIRS). Using the second derivative with respect to wavelength reduced the effects of scattering on the spectra and also made oxygenated and deoxygenated forms more distinguishable from each other. Selecting spectral bands where oxygenated and deoxygenated forms absorb filtered out noise and spectral features unrelated to Mox. NIR and visible bands were scaled relative to each other in order to correct for errors introduced by normalization. Multivariate Curve Resolution (MCR) was used to estimate Mox from spectra within each data set collected from healthy subjects. A Locally Weighted Regression (LWR) model was built from calibration set spectra and associated Mox values from 20 subjects using 2562 spectra. LWR and Partial Least Squares (PLS) allow accurate measurement of Mox despite variations in skin pigment or fat layer thickness in different subjects. The method estimated Mox in five healthy subjects with an RMSE of 5.4%.

1. Introduction

Optical spectroscopy is increasingly being used in the clinical setting to noninvasively monitor patients. The nonionizing radiation used and the potential for inexpensive, portable devices make optical spectroscopy attractive for continuous monitoring in challenging clinical settings like ambulances, emergency departments, intensive care units, and operating rooms.

Hemoglobin is one of the most commonly measured biological chromophores. It is a protein in blood that has four oxygen binding sites. Pulse oximetry is the standard of care in hospitals and uses two wavelengths, one in the visible region and one in the infrared, to measure the oxygen saturation of hemoglobin in arterial blood. While pulse oximetry is valuable in the assessment of oxygen availability in the arterial blood, it does not yield information about whether enough oxygen is actually getting into tissues to meet metabolic demands.

Because oxygen is essential for life, an enormous amount of medical treatment centers around normalizing or stabilizing oxygen levels in the body. Despite significant advances in medical monitoring, there currently is no device that continuously and quantitatively measures oxygen levels at the cellular level, where oxygen is metabolized. Recently, there has been interest in optical monitoring of tissue oxygenation in brain [1,2] and muscle [2,3]. Near-infrared spectroscopy (NIRS) devices typically measure 2–6 wavelengths in the NIR region. Measurement of only a few wavelengths limits the ability to sensitively measure tissue hemoglobin saturation. In a study of trauma patients, a commercially available NIRS device that measures six wavelengths could identify severe hemorrhagic shock, but could not distinguish mild and moderate shock from healthy controls [4]. Another NIRS device that measures two NIR wavelengths has found increasing popularity as a trend monitor in operating rooms and intensive care units, but its clinical value has been questioned [5,6].

Our laboratory has measured myoglobin saturation [7–10] and hemoglobin saturation [11,12] in vivo using Partial Least Squares (PLS) calibrated with spectra of solutions acquired in vitro. Myoglobin is a protein found within muscle cells, and has one oxygen binding site. It functions as an intracellular store and carrier for oxygen [13]. Our approach using PLS with full spectra in the visible and NIR regions allowed accurate and separate measurements of myoglobin and hemoglobin saturation despite the fact that the two proteins have very similar and highly overlapping absorbance spectra. PLS calibration on in vitro spectra is not practical for clinical monitoring because PLS estimates are typically only valid for subject spectra containing physiological interferences very similar to those in the calibration set [14]. It is impractical and perhaps impossible to make appropriate in vitro calibration sets when attempting to make single, instantaneous muscle oxygenation (Mox) estimates on subjects randomly selected from a heterogeneous population.

The goal of the present study was to develop a spectral analysis method to yield accurate, real-time measurements of Mox that could potentially be used in a clinical monitor. Mox is a measure of the percentage of oxygenated myoglobin and hemoglobin out of the total myoglobin and hemoglobin in the optical path. Individual saturations of myoglobin and hemoglobin were not determined. Mox has contributions from venous, capillary, and arterial blood and myoglobin.

Full spectra were acquired between 540 nm and 800 nm, allowing measurement of both oxygenated and deoxygenated forms of myoglobin and hemoglobin. This is in contrast to NIRS devices that measure only deoxygenated hemoglobin in the NIR. Preprocessing included second derivatives, variable selection, scaling between visible and NIR regions to balance information content between the two regions, and total signal normalization. Multivariate Curve Resolution (MCR) was used to estimate Mox in 20 healthy subjects. Those Mox estimates were then used in the Locally Weighted Regression (LWR) training set. LWR provides a means to utilize the stability and simplicity of a linear regression model in the presence of nonlinear, difficult-to-model interferences [15]. In the case of transcutaneous Mox estimation, the various physiological variations from subject to subject (e.g., variations in skin tone and intervening fat layer thickness) are the nonlinear effects to be minimized. For each measurement from a subject for which Mox is to be estimated, LWR automatically selects the most similar subset of the training set and builds a “local” PLS model to estimate Mox. This provides a PLS model that is more valid than one based on in vitro spectra because it is built from human subjects with similar physical characteristics, notably skin tone and body mass index. The method was validated on five additional healthy subjects.

2. Materials and methods

2.1. Experimental

2.1.1. Optical spectroscopy

The optical system is composed of an imaging spectrometer (JY Horiba iHR320), a thermoelectrically-cooled CCD camera (JY Horiba Synapse, 256×1024 format), a custom-designed LED light source (Innovations in Optics Inc.), and a custom-designed fiber optic probe (Fiberoptic Systems Inc.). The 300-groove grating in the spectrometer was centered at 670 nm and the wavelength resolution was approximately 0.25 nm pixel⁻¹.

The fiber optic probe is bifurcated, with one branch connected to the light source and the other branch coupled to the spectrometer entrance slit. The common end of the probe was placed on the back of the subject’s hand over the thenar muscle group and was held in place with an elastic bandage. Three probes were used, each with a constant separation between source and detection fibers of 13 mm, 14 mm, or 15 mm. The largest probe that yielded spectra with adequate signal-to-noise ratios was used in each individual subject. Hand spectra were referenced to a spectrum collected from 1% intralipid to calculate an approximate absorbance response.

2.1.2. Human subject protocol

With approval from the University of Washington Institutional Review Board, healthy controls between the ages of 18 and 80 were recruited. After consent was obtained, subjects were interviewed to determine whether they had cardiovascular or pulmonary disease, diabetes, or a history of deep vein thrombosis. Subjects were excluded from the study if they had one or more of these conditions. Baseline blood pressures and pulse rates were recorded, in addition to height and weight. Twenty-five subjects were studied, with body mass indices of 24.2 ± 3.0.

Spectra (540–800 nm) were acquired at a rate of either 0.33 Hz or 0.5 Hz during a 3-min period of rest while each subject breathed room air. An oxygen mask was then placed over the face for 3 min, and the subject breathed 100% O₂. A blood pressure cuff was inflated on the upper arm to a pressure that was 60 mm Hg above the subject’s systolic blood pressure or to 200 mm Hg, whichever was less. The cuff was inflated for 15 min, and the oxygen mask was removed approximately 2 min into the period of arm ischemia. A recovery period of 5 min followed to ensure normalization of blood perfusion to the arm. Spectral acquisition was continuous throughout the entire protocol.

Consecutive spectra were averaged to improve signal-to-noise ratios. When the acquisition rate was 0.33 Hz, three spectra were averaged together, producing a new rate of 0.11 Hz. When the acquisition rate was 0.5 Hz, five spectra were averaged together for a new rate of 0.1 Hz.

Spectra collected from the hand at rest while breathing 100% O₂ represented the most oxygenated condition that we could practically produce in the subjects (Fig. 1). We assumed that these spectra represented Mox values of 100% but we have not verified with an independent measure that myoglobin and hemoglobin in the hand were fully saturated with oxygen. Spectra collected at the end of the 15-min period of arm ischemia were assumed to represent Mox values of 0% (Fig. 1). In healthy subjects, it has been observed that 15 min of arm ischemia is sufficient to achieve complete deoxygenation of skeletal muscle and blood in the hand because myoglobin and hemoglobin saturations plateau to a minimum value [12]. Spectra acquired during the period of arm ischemia represent intermediate Mox values between 0% and 100%.

Fig. 1.

Spectra acquired from a healthy human subject at extremes of muscle oxygenation. The solid spectrum was acquired after 3 min of 100% O₂ breathing. The dashed spectrum was acquired after 15 min of arm ischemia. Oxymyoglobin and oxyhemoglobin absorb near 580 nm in the visible region; deoxymyoglobin and deoxyhemoglobin absorb near 760 nm in the near infrared region. The visible and NIR bands that were used to estimate Mox are indicated by the sets of vertical dashed lines. In the wavelength region between 610 nm and 730 nm, the detector was saturated. These spectral values do not represent measurements of tissue absorbance and were not used in the spectral analysis.

2.2. Analysis

All analyses were performed using PLS Toolbox Version 6.2 (Eigenvector Research Inc.) running in Matlab R2009b (Mathworks Inc.).

To help remove baseline and background signals due to scattering phenomena, second derivatives with respect to wavelength were taken using the Savitzky–Golay algorithm with a 65-point window and a second order polynomial [16]. The visible wavelength region was restricted to 562.2–601.7 nm and the NIR region was restricted to 744.7–802.2 nm. These wavelength regions were selected because they encompass the absorbances of the oxygenated and deoxygenated species, respectively. The two regions were scaled relative to each other to correct for differences in absorptivity of the species in the visible and NIR regions of the spectra. The magnitude of this adjustment was determined using the method described in Section 2.2.2. The two discontinuous wavelength regions were then concatenated. Finally, to correct for changes in illumination and path length, as well as other total-signal influences, each spectrum was normalized to its total summed absorbance.

2.2.1. Estimation of Mox reference values by MCR

As no accurate primary method exists to determine the actual Mox in human subjects at any given point in time, MCR [17,18] was used to estimate Mox during ischemia. Separate two-factor MCR models were calculated for each subject to recover estimates of the oxygenated and deoxygenated component spectra and corresponding contributions of each species at each point in time.

Each model used a closure constraint to assure that the summation of the two recovered contribution profiles would always be 100%. Assuming that the spectra collected just prior to cuff inflation during breathing of pure oxygen are close to 100% Mox, the five spectra at this point in every run were constrained to give a 100%:0% ratio of oxygenated to deoxygenated species. Likewise, the last five spectra in each run prior to cuff release were constrained to give a 0%:100% ratio. The average spectra from each of these time periods were used as the initial guesses for the pure-component spectra in the MCR. Because the closure constraint requires that the two contribution profiles sum to 100%, the recovered oxygenated species contribution profile is equivalent to the estimated Mox for the subject. An example Mox profile is shown in Fig. 2.

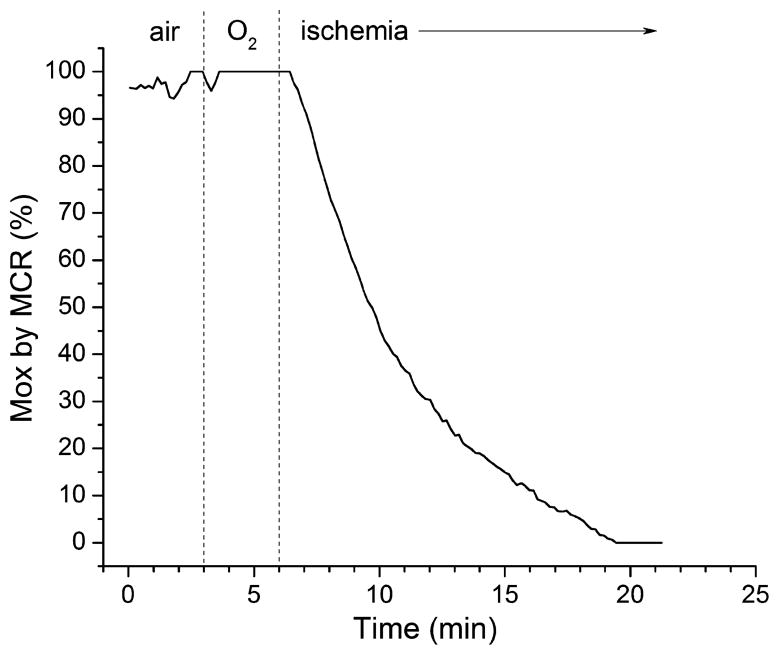
Fig. 2.

Muscle oxygenation (Mox) in a healthy human subject estimated by MCR. The subject breathed air for 3 min, then 100% O₂ for 3 min, and then underwent a 15-min period of arm ischemia.

It is important to note that this procedure to recover the Mox profiles is only an approximation of the actual Mox, which may be influenced by optical variations (such as skin-probe boundary changes). However, it is also assumed that when all the subjects’ results are combined during the LWR modeling later, these effects will be diminished by an averaging of the pool of all subjects.

2.2.2. Correction of absorptivity effects

Because there is always an ambiguity in the total volume of muscle interrogated, the total observed absorbance is also ambiguous. For example, an increase in the absorbance observed for the deoxygenated species could be due to either a decrease in Mox or an increase in total interrogated volume. To correct for these effects, each spectrum was normalized to the total absolute value of the observed signal (the sum of the absolute value) after taking the second derivative and before MCR. This had two side effects: First, it means relative absorbances of the oxygenated and deoxygenated species could be used to calculate Mox. Second, it introduced an unintended nonlinearity between calculated Mox and true Mox due to the difference in absorptivity between the oxygenated and deoxygenated species, as described below. Note that this effect was not a nonlinearity between observed absorbances at different wavelengths (which would lead to a higher multivariate rank of the set of spectra), but one simply between the calculated and true Mox.

The total absorbance summed across all wavelengths, A_obs, can be written as a summation of the absorbances of the oxygenated and deoxygenated species:

$$A_{\text{obs}}=E_{\text{o}}{BC}_{\text{o}}+E_{\text{d}}{BC}_{\text{d}}$$ (1)

where B is the effective path length, E_o and E_d are the total absorptivities summed across all wavelengths of the oxygenated and deoxygenated species, respectively, and C_o and C_d are the concentrations of oxygenated and deoxygenated species, respectively. If the two absorptivity profiles had the same integrated areas, A_obs would only be influenced by changes in path length or total myoglobin + hemoglobin concentration (C_o + C_d) and dividing each spectrum by A_obs would correct for changes in those properties. However, because E_o and E_d are not equal, the total summed absorbance, A_obs, will vary with Mox even in the absence of changes in path length or C_o + C_d.

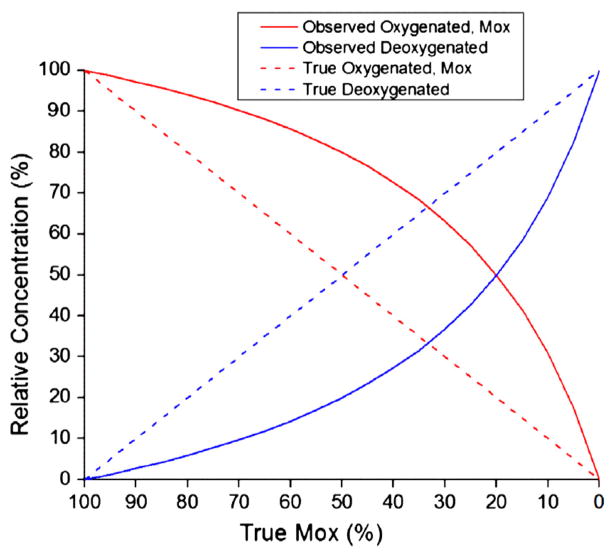
Fig. 3 illustrates the problem that would occur with normalization if there were a 4:1 ratio between E_o and E_d. The dotted lines represent “true” oxygenated and deoxygenated species concentrations (in relative %) as Mox decreases linearly from left to right. The solid lines show the concentrations that would be calculated from normalized spectra. At 50% true Mox, the observed Mox would be 80%, reflecting the 4:1 contributions to A_obs from E_o and E_d when C_o = C_d. At 100% Mox, the summed absorbance is dominated by the oxygenated species absorbance (A_obs = E_oBC), while at 0% Mox, the summed absorbance is dominated by the deoxygenated species (A_obs = E_dBC). A_obs at 100% Mox would be four times greater than A_obs at 0% Mox. Thus, as Mox varies, A_obs is not a constant but is changing as a proportion of the absorptivity of the oxygenated or deoxygenated species. The effect of the non-constant A_obs is that observed Mox would be consistently overestimated in this example.

Fig. 3.

Normalization bias effect. Since the integrated areas of absorptivity profiles of oxygenated and deoxygenated species are not equal, normalization introduces an unintended nonlinearity to recovered relative oxygenated and deoxygenated concentrations. Dotted lines represent true relative concentrations and by definition, true Mox is equal to “True Oxygenated”. True Mox decreases from left to right, as during ischemia. If the ratio of the integrated areas of oxygenated to deoxygenated absorptivity profiles were 4:1, the observed relative concentrations would be those shown by the solid lines. The observed Mox, equal to “Observed Oxygenated”, would be consistently overestimated.

One approach to correct for this effect is to scale the visible region of the spectrum (dominated by the oxygenated species) relative to the NIR region (dominated by the deoxygenated species) by a factor corresponding to the ratio between E_o and E_d. Estimating an appropriate scaling factor was achieved by taking advantage of the fact that when there are no major path length effects (such as in the highly-controlled ischemia trials), normalization has little effect except to introduce the nonlinearity. Once the scaling factor is correct, normalization should have almost no effect on Mox values recovered using MCR. By adjusting the NIR:Vis scaling factor and then examining Mox profiles recovered with and without normalization, we identified a factor at which the profiles were not significantly changed by normalization. This was considered the “optimal scaling factor” for the given subject. The 50% Mox point was used as a reference to indicate how similar the profiles were with and without normalization.

Fig. 4A and B show an example of the change in Mox profile resulting from normalization before a scaling factor was applied. In Fig. 4C and D, the 50% Mox points of unnormalized and normalized data sets were identical when a scaling factor of 5.3 was used.

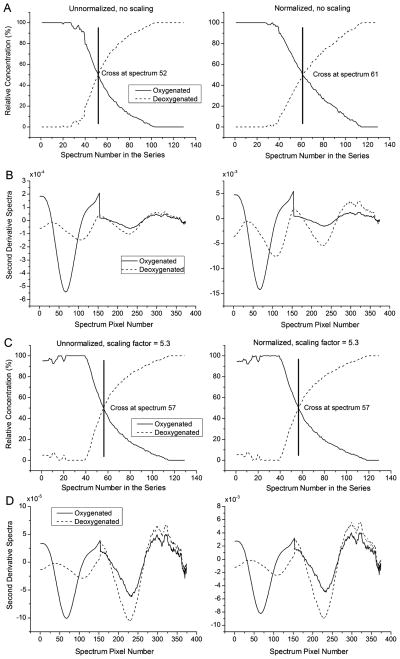
Fig. 4.

Scaling correction for absorptivity effects. (A) MCR results without (left) and with (right) normalization show that the 50% Mox point is affected by normalization. (B) Concatenated second-derivative spectra. The visible region comprises 562–601 nm and the NIR region comprises 744–802 nm. (C) Up-weighting the NIR region where deoxygenated species have predominant intensity corrects for the normalization effect. This example shows results when the NIR region was up-scaled by a factor of 5.3. The optimal scaling factor was determined by adjusting the scaling until the 50% Mox points for unnormalized (left) and normalized (right) cases were equal and (D) concatenated second-derivative spectra with the scaling, without and with normalization.

This process was repeated for all 20 training subjects and the median optimal scaling factor of 4.7 was selected for all subsequent spectral adjustments. Each training subject’s spectra were corrected by the median optimal scaling factor and the Mox profiles were estimated using the MCR procedure described earlier. Finding a single factor to use for all subjects provides for the most general correction of absorptivity and possible optical effects without over-correcting for a single subject. It also provides a means to analyze subjects for which the normalized and non-normalized results were too severely different (probably due to actual path length or optical effects) and enables use of the models for application to future clinical subjects for which we will have only a single point, and not an entire ischemic profile.

2.2.3. Locally Weighted Regression modeling

Given the estimated Mox values and the individual spectra for all subjects as a whole, an LWR model was created that used a two principal component PCA model to select training spectra. For any given Mox estimate to be made, 200 training spectra were selected and a one latent variable PLS model was calculated and used for predictions. An attractive feature of such an empirical, inverse least squares PLS model is that having relatively few constraints allows flexibility in correcting for interferences. In contrast, a classical least squares method like MCR would have a greater number of constraints that would likely degrade prediction accuracy.

The training spectra provided to the LWR model were preprocessed similarly to that described for the MCR estimation procedure (2nd derivative, 4.7 NIR:Vis scaling, area normalization) but the spectra and estimated Mox values were also mean-centered to allow for an intercept in the linear regression. The number of principal components, number of training spectra selected, and number of PLS latent variables to be used were all selected using cross-validation in which the entire set of spectra from a given subject were left out of the training set, and the remaining 19 subjects were used to estimate the left-out subject’s Mox. The error in these Mox estimations was summarized in the root mean squared error of cross-validation (RMSECV) which is the square root of the average error of prediction for all samples when they were left out of the training set [14]. This was repeated for various settings of the LWR algorithm with general agreement that the selected LWR parameters gave stable and reliable results.

2.2.4. Partial Least Squares modeling

For comparison to the LWR models, an identical modeling effort was made using standard (non-locally-weighted) PLS modeling. For these models, the identical calibration data were analyzed with a standard PLS algorithm using cross-validation to determine the number of PLS latent variables. The smallest cross-validation error was observed at 2 latent variables.

2.2.5. Quality of spectral fit parameters

In both the PLS and LWR models, it is important to assess how well the model fits a given spectrum when making a Mox prediction for that spectrum. For factor-based models such as PLS and LWR, this can be done using the Hotelling’s T² and Q residuals [14]. Generically, these models decompose a data matrix, X (in which rows are spectra), into scores T, loadings P, and spectral residuals R, according to the equation:

$$\mathbf{X}={\mathbf{TP}}^T+\mathbf{R}$$ (2)

Hotelling’s T² is calculated as a weighted sum of the scores and describes whether the features described by the loadings of the model are present in similar scale to what was observed in the calibration data. The Q residuals are calculated as the sum of the squared residuals in each row of the R matrix [14]. When making a prediction for a new sample, a new Hotelling’s T² value and Q residual value are calculated and compared to the values obtained for the calibration data. If a new value is substantially different from the calibration data, it is inferred that the new spectrum contains some feature(s) which were not observed in the calibration data and, thus, the predictions for Mox should not be used.

3. Results and discussion

3.1. Cross-validation

While building the models, cross-validation was used as described earlier. For the LWR model, cross-validation indicated very little change as a function of either the number of principal components (PCs) in the model or the number of samples selected for each local model. Models were examined with 1–6 PCs, 100, 150, or 200 selected samples, and 1–3 latent variables in the local PLS model. The RMSECV ranged from 6.5% at 2 PCs and 200 samples selected for each local model up to 8.1% at 6 PCs and 100 samples selected. In comparison, the best standard PLS model (not LWR-based model) provided an RMSECV of 9.3% obtained with 1 latent variable. All LWR and PLS models with more than 1 latent variable gave RMSECVs above 9.3%. In all cases, the subjects in the calibration set displayed Hotelling’s T² and Q residuals that indicated there were no unusual subjects or samples in the calibration set.

3.2. Validation subject results

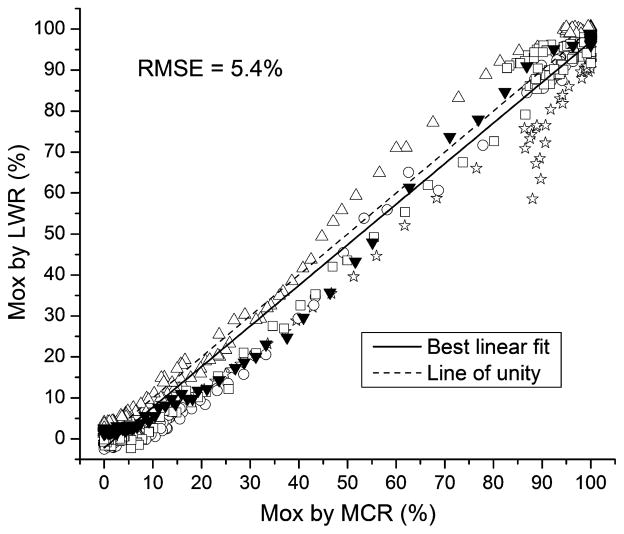
In order to validate the model, Mox measurements were made from five healthy subjects that were not included in the model. These subjects underwent the same protocol as the 20 subjects included in the model. Fig. 5 shows that the LWR model produced accurate Mox measurements compared to MCR estimates of Mox obtained from each subject’s data set. The best-fit line had a slope of 0.99 and a y-intercept of −2.2, very similar to the line of unity. The root mean square error (RMSE) for all 654 spectra was 5.4%.

Fig. 5.

Accuracy of muscle oxygenation (Mox) measurements by LWR in five healthy human subjects. Mox was measured accurately across its range from 0% to 100%.

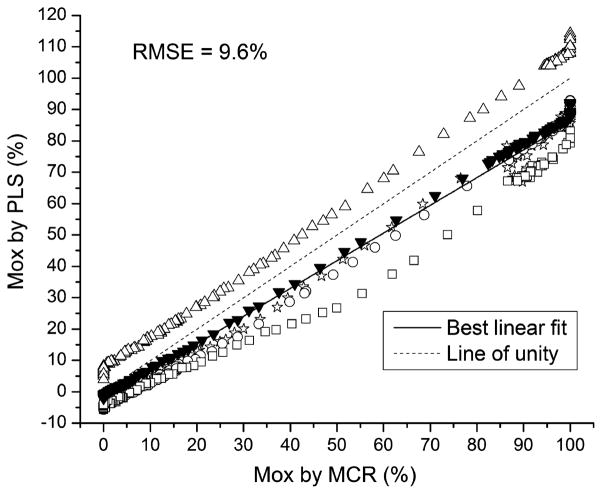
For comparison, the results for the standard PLS model applied to the same five test subjects are shown in Fig. 6. Because the PLS model is required to take into account all subjects equally, the model must be a “consensus”, resulting in a per-subject bias. All of the subjects showed notable systematic offsets from the MCR estimates. The RMSE for the test subjects using the PLS model was 9.6%.

Fig. 6.

Accuracy of muscle oxygenation (Mox) measurements by PLS in five healthy human subjects. All subjects showed a systematic bias at all Mox levels.

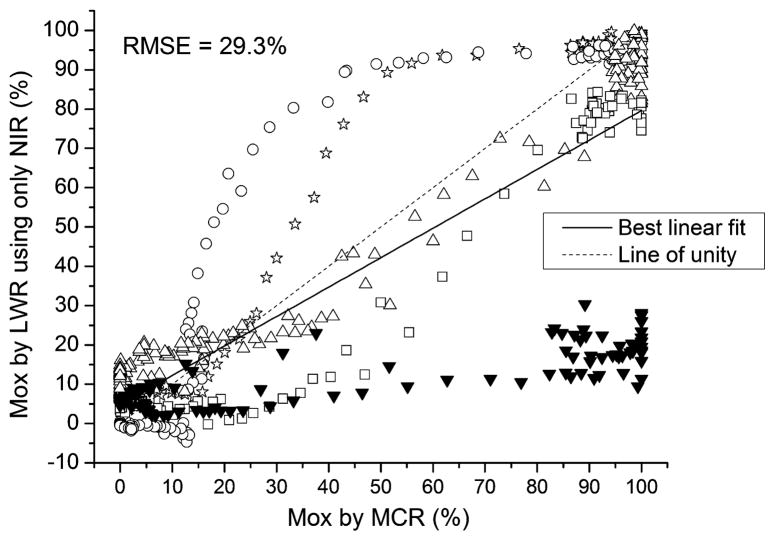
Finally, an additional LWR model was built with the wavelength range limited to only the NIR portion of the spectrum (744.7–802.2 nm). In this model, the predictions showed little to no trend with Mox and produced an RMSE of 29.3% (Fig. 7). Such a poor result is expected considering that removing the visible portion of the spectrum leaves no ability to correct for path length and absorbance effects. It demonstrates the need for obtaining both the visible and NIR portions together for the Mox evaluation. Interestingly, these poor results are probably overly optimistic considering that reference Mox values were obtained from MCR using the full wavelength range. If the MCR step was similarly limited in wavelength window, no sensible reference values could even be obtained for the calibration samples.

Fig. 7.

Muscle oxygenation (Mox) measurements by LWR in five healthy human subjects when only the NIR portion of the spectra was used. Accuracy was very poor. The advantage of including the visible region in the analysis is apparent when these results are compared to those in Fig. 5.

3.3. Application to trauma patients

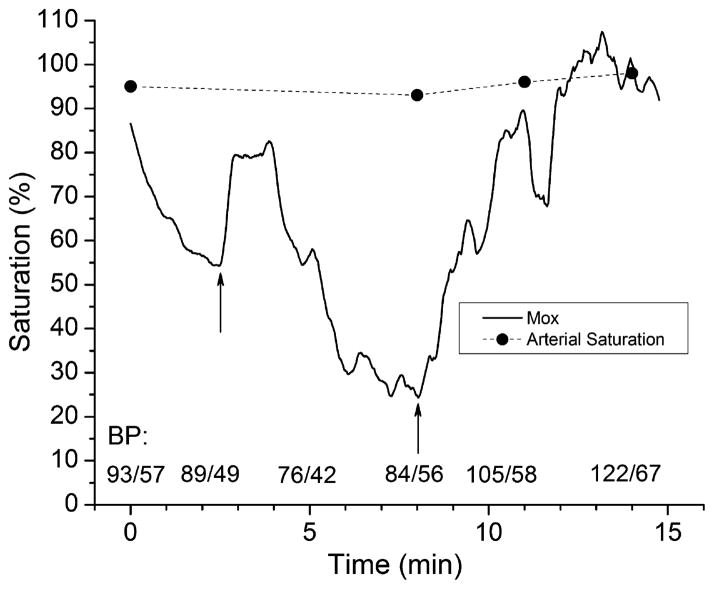
Mox was measured in a preliminary study of trauma patients admitted to Harborview Medical Center in Seattle, WA. Spectra were acquired for 15 min as soon as possible upon admission to the emergency department. The LWR model was applied to the spectra from each patient. Fig. 8 shows the Mox time course in one patient. Mox has a good correlation with blood pressure; it provides a continuous and real-time indication of tissue perfusion. The sharp increases in Mox at approximately t = 2 min and 8 min correlated with intravenous saline infusions given for low blood pressure that temporarily improved tissue perfusion. In contrast, arterial blood saturation measured by pulse oximetry was not sensitive to changes in tissue perfusion.

Fig. 8.

Muscle oxygenation (Mox) is indicative of tissue perfusion. Mox was measured in a trauma patient who received saline infusions at t = 2 and 8 min (indicated by arrows), causing increases in blood pressure (BP) and corresponding increases in Mox. Arterial saturation measured by pulse oximetry was not sensitive to changes in tissue perfusion.

4. Conclusions

The results for both the validation subjects and a trauma patient indicate that the use of joined visible and NIR spectra can provide Mox estimates better than what has been previously reported for single- or double-wavelength NIR methods. In addition, these results show that the LWR models are capable of making reasonable estimates of Mox, even when presented with the limited range of physiological variability provided in this small calibration set. The accuracy of these predictions should only improve when additional calibration subjects, representing a wider variety of skin tones and body mass indices, are added to the calibration set.

Further improvements in model performance would also be expected by using a modified method for training sample selection. In this work, the sample-to-sample distance in the PCA score space was used. This PCA model captured the variance associated with both the subject-to-subject variability (which is most critical to correct) and the varying Mox caused by ischemia in individual subjects. Thus, samples were selected both on the similarity of the subject as well as the similarity of the extent of ischemia to test spectra. The predictions made from the ordinary PLS model show that the calibration and test subjects were generally in error by a constant slope and/or offset across all Mox values. From this, we would anticipate that a modified sample selection method which focuses more on subject-to-subject variability (for example, discarding all spectra for individuals which are dissimilar and keeping all spectra for individuals which are similar) would tend to create models that capture the specific slope and offset scaling relevant for the tested individual. Such models may provide better predictions than our current model.

This work also demonstrates that the use of MCR with simple equality and closure constraints provides a reasonable inference of Mox in the absence of any true primary reference. This use of a carefully controlled experimental protocol and inferential estimates of Mox can be used to easily produce additional calibration data for the models.

Highlights.

• We propose a new method for measuring muscle oxygenation (Mox) from optical spectra.

• Optical reflectance spectra were measured from the hand in the visible-NIR region (540–800 nm).

• Locally Weighted Regression (LWR) with Partial Least Squares (PLS) was implemented.

• Muscle oxygenation using LWR–PLS was more accurate than standard PLS.

• Multivariate Curve Resolution can estimate Mox under controlled experimental conditions.

Abbreviations

Mox

muscle oxygenation

NIR

near infrared

NIRS

near-infrared spectroscopy

LWR

Locally Weighted Regression

MCR

Multivariate Curve Resolution

PLS

Partial Least Squares

A_obs

total absorbance summed across all wavelengths

B

effective path length

E_o and E_d

total absorptivities summed across all wavelengths of the oxygenated and deoxygenated species, respectively

C_o and C_d

concentrations of oxygenated and deoxygenated species, respectively

RMSECV

root mean squared error of cross-validation

PCs

principal components

RMSE

root mean square error