Active Decorrelation in the Basal Ganglia

Abstract

The cytoarchitecturally-homogeneous appearance of the globus pallidus, subthalamic nucleus and substantia nigra has long been said to imply a high degree of afferent convergence and sharing of inputs by nearby neurons. Moreover, axon collaterals of neurons in the external segment of the globus pallidus and the substantia nigra pars reticulata arborize locally and make inhibitory synapses on other cells of the same type. These features suggest that the connectivity of the basal ganglia may impose spike-time correlations among the cells, and it has been puzzling that experimental studies have failed to demonstrate such correlations. One possible solution arises from studies of firing patterns in basal ganglia cells, which reveal that they are nearly all pacemaker cells. Their high rate of firing does not depend on synaptic excitation, but they fire irregularly because a dense barrage of synaptic inputs normally perturbs the timing of their autonomous activity. Theoretical and computational studies show that the responses of repetitively firing neurons to shared input or mutual synaptic coupling often defy classical intuitions about temporal synaptic integration. The patterns of spike timing among such neurons depend on the ionic mechanism of pacemaking, the level of background uncorrelated cellular and synaptic noise, and the firing rates of the neurons, as well as the properties of their synaptic connections. Application of these concepts to the basal ganglia circuitry suggests that the connectivity and physiology of these nuclei may be configured to prevent the establishment of permanent spike-timing relationships between neurons. The development of highly synchronous oscillatory patterns of activity in Parkinson’s disease may result from the loss of pacemaking by some basal ganglia neurons, and accompanying breakdown of the mechanisms responsible for active decorrelation.

In the basal ganglia, as in many other brain structures, neurons receive enormously many synaptic inputs distributed on dendritic fields that traverse hundreds of micrometers of synaptically-dense neuropil. The dendritic field of each cell occupies a volume shared with the dendrites and axons of thousands of others. This provides substantial opportunity for nearby neurons to share common input from individual afferent axons, interconnect directly, and to be connected indirectly by way of shared pools of intermediary neurons. Input sharing and interconnection may impose an irreducible structural correlation in the timing of action potentials in nearby neurons (Moore et al. 1970). This spike-time correlation is irreducible in that it reflects the structure of the network and will be present whenever the network is active, even if the activity of all inputs were completely uncorrelated. Dynamic spike-timing correlations among inputs, imposed by transient structured patterns of input, may produce an an additional degree of correlation. Dynamic correlations of this sort might be considered signals – assemblies of cells momentarily firing together as a representation of a stimulus, movement, or internal state. To maximize the information content of this kind of signal correlation, the irreducible background texture of correlation among neurons imposed by network structure should be minimized (Rieke et al. 1997). Of course in some cases the structural correlations among neurons in a network are an important part of its computation. For example, network structure may impose negative correlations in firing between neighboring neurons in a sensory map to enhance local contrast. Sometimes the patterns of local connectivity arise from a learning rule and anticipate stable statistical features of the input that have been learned by the network. In these cases, the reduction in the information content of spike times in the network is computationally beneficial; that reduction in information may in fact be the computation.

Neurons in the non-striatal portions of the basal ganglia, the internal and external segments of the globus pallidus (GPi and GPe), the subthalamic nucleus (STN) and the substantia nigra pars reticulata (SNr), all have extended and highly overlapping dendritic fields. The interconnections among these structures and the projections of their afferents are organized topographically, so that nearby axonal arborizations are functionally related (e.g. Bevan et al. 1994; Shink et al. 1996; Wilson and Phelan, 1982), but the dendritic trees of the recipient neurons often reach across large portions of the topographical maps (e.g. Kita and Kitai, 1994; Kita et al. 1983; Koshimizu et al. 2013; Grofova et al. 1982; Parent et al. 2001; Sadek et al. 2007). In some of these structures, especially the GPe and SNr, the neurons have axon collaterals that form arborizations in the vicinity of their dendritic trees and contact other neurons of the same type (e.g. Deniau, et al. 1982; Sadek et al. 2007). Two of the structures, the GPe and STN, are reciprocally connected (Shink et al. 1996). The STN exerts a powerful excitatory influence on the GPe, which then inhibits the STN neurons. All of these synaptic arrangements, which are characteristic of non-striatal basal ganglia structures, seem likely to generate a large degree of convergence and input sharing among neurons, and in some cases, direct and indirect interconnections.

It is therefore surprising that cells in GPe and GPi exhibit practically no spike-timing correlations among themselves, either in the internal and external segment (Bar-Gad et al. 2003; Nini et al. 1995; Raz et al. 2000). The same is true for cells in the SNr (Wilson et al. 1977). It is true in animals that are awake but immobilized (Wilson et al. 1977), in anesthetized animals (at least for some anesthetics, Deister et al. 2013; Magill et al. 2000; Magill et al. 2001), and in ones that are actively performing motor tasks (Nini et al. 1995). It is true for cells located so closely that they are recorded from the same electrode, and for cells located far away from each other (Mitelman et al. 2011). It is apparently less true for neurons in the STN in anesthetized animals (Ryan et al. 1992) although the spike-timing correlations there disappear during EEG activation and so probably result from slow synchronous activity in the cortex and not necessarily from structural input sharing (Magill et al 2000). The absence of structural spike-timing correlations is even more surprising considering that in experimental models of Parkinson’s disease, neurons in both segments of the globus pallidus become highly correlated so that nearly any pair of cells recorded is likely to show a significant cross-correlation. These presumably pathological correlations are associated with a rhythmic modulation of firing rate between 7 and 15 Hz. Considering these observations, Bar-Gad et al. (2003) suggested that there must be a mechanism that actively decorrelates the activity of pallidal neurons, and that the decorrelation mechanism fails in Parkinson’s disease.

How Much Input Sharing is There Really?

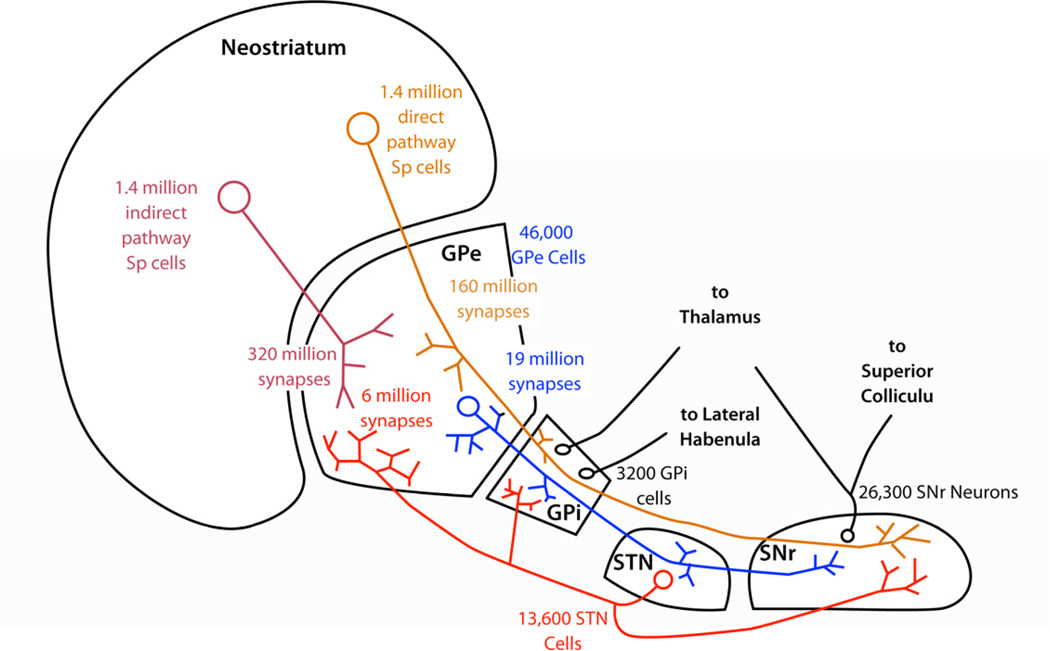
The basal ganglia are often depicted as a feedforward network consisting of 3 layers, with dramatic reduction in cell numbers at each stage from the cortical inputs to the final output neurons in GPi and SNr (Nauta, 1979). In the basal ganglia of the rat, for example, there are about 17 million corticostriatal neurons innervating the striatum on each side (Zheng and Wilson, 2002). The axons of 2.8 million striatal neurons make inhibitory synapses on 46,000 neurons of the ipsilateral external pallidal segment (GPe), and the axons of half of these cells form the direct pathway that innervates 3,200 cells in the GPi and 26,300 cells in the SNr (Oorschot, 1996). In humans, striatal neurons number about 100 million, there are about 500,000 cells in GPe, and about 160,000 cells in GPi (Thôrmer et al. 1975; Schröder et al, 1975).

In the striatum, spiny neurons each receive about 10,000 synaptic contacts from excitatory axons. About half of these or more are from the cerebral cortex, and cortical axons are arranged in a topographical organization, but with a high degree of overlap among functionally interconnected cortical areas (see review in Gerfen and Wilson, 1996). Each cortical axon makes very few synaptic contacts on each spiny cell (Kincaid et al. 1998). Nearby spiny neurons are also directly interconnected by inhibitory synapses formed by their local collateral axonal arborizations (e.g. Wilson and Groves, 1980). Because spiny neurons have highly overlapping dendritic trees and cortical axons have large axonal arborizations, it might be expected that there would be a large degree of input sharing among those cells. This, combined with their mutual inhibition, might create strong structural spike-timing correlations between them. In fact, nearby spiny neurons do not show such spike-timing correlations, even during the Up state in the anesthetized animal, when cortico-striatal axons are highly active and comprise a powerful excitatory synaptic barrage (Stern et al. 1997). The weak effects of shared synaptic inputs can be revealed in the cross-correlation of their membrane potentials, but it is not expressed in short-term correlations of spike timing (Stern et al. 1998). Under these conditions, which seem ideal for revealing structural spike-timing correlations, the cross-correlations of striatal spiny neurons are dominated by slow components representing the dynamic correlations among cortical neurons which underly the slow wave oscillations in the cortex. The reason spiny cells lack spike-timing correlations caused by shared input is that despite appearances, there is very little sharing of cortical input among spiny neurons, even those with almost total overlap of dendritic fields (Zheng and Wilson 2002). Although striatal spiny cells receive a very large number (> 5000) of cortical synapses, they each receive contacts from a tiny proportion of the cortical axons arborizing in their vicinity (~380,000). Each spiny neuron samples the cortical innervation extremely sparsely, and so there is only a tiny chance that another cell will sample a substantially similar set of inputs (Kincaid et al. 1998; Zheng and Wilson 2002). Likewise, whereas each striatal spiny neuron receives inhibition from as many as 500 other spiny neurons in its vicinity, these inputs are located on distal dendrites, are weak and asynchronous (Koos et al. 2004) and unless experimentally made to fire synchronously do not produce spike-timing correlations that can be detected using the usual methods.

Perhaps the absence of spike timing correlations among GPe, GPi, or SNr cells is likewise because they do not share a large proportion of their striatal innervation. About half (1.4 million in the rat) of the striatal neurons are indirect pathway neurons, and each makes about 226 synapses in a specific restricted part of the GPe also targeted by nearby striatal cells. (Kawaguchi et al., 1990). GPe cells’ den-drites extend nearly a millimeter in length and so may receive synaptic inputs from axons contained in a large subregion of the nucleus (e.g. Kita 2007). Because there are so many striatal neurons and so few pallidal neurons, it is unlikely that the up to ~226 (of the 46,000) rat GPe cells sharing input from one striatal neuron also share input from many or even any of the others, and so the overall degree of structural correlation imposed by sharing of striatal inputs may be extremely small. Likewise for the projections of the ~1.4 million direct pathway striatal spiny neurons that make synapses on 3,200 GPi (entopeduncular nucleus) or 26,300 SNr cells in the rat.

This argument has also been applied to the GPe to STN projection in an elegant combined anatomical and physiological study by Baufreton et al. (2009). They showed that each STN-projecting GPe neuron makes ~273 synapses distributed on a somewhat smaller number of the 13,600 STN neurons on each side. They calculate that each STN neuron receives input from less than 2% of GPe-STN afferents. On this basis, they conclude that the proportion of inhibitory pallidal inputs shared by STN neurons likewise averages less than 2%.

The subthalamic nucleus receives excitatory inputs from the thalamus and cortex. The number of thalamo-subthalamic neurons is not known, but a recent paper by Kita and Kita (2013) indicated that an enormous number (as many as 5–10%) of cortical layer V output neurons in frontal regions of cortex may each contribute a small number (<100) of boutons to the dense corticosubthalamic innervation. Like the other projections from large neuron populations to smaller cell groups in the basal ganglia, the corticosubthalamic projection may also fail to produce a large degree of input sharing among neurons.

This argument may even apply to the STN-GPe projection, despite the fact that the cell number ratio is reversed. The reason is the apparently small number of STN-derived synapses formed on each GPe cell. The rat subthalamic nucleus contains about 13,600 neurons, about 80% of which project to the Gpe (Koshimizu et al. 2013) to form a major excitatory innervation of the GPe (Kita 2007). Using the estimates of Kawaguchi et al. (1998) for the striato-pallidal projection, there are about 480 million striatal-GPe synapses (320 million from the indirect pathway and 160 million from the direct pathway). These are estimated to be about 80% of all synapses in the GPe, whereas asymmetric (excitatory) inputs represent 10% (Kita, 2007). By this accounting, there are about 60 million excitatory synapses in the rat GPe. The STN is usually considered to be the largest contributor to this innervation, but the most recent results suggest that it may not be. In a study by Koshimizu et al. (2013), 8 of 10 STN neurons studied contributed projections to the GPe, and each of these made between 245 and 1450 presynaptic boutons (average of 558 for the 8 cells with GPe projections). Assuming this sample is representative, STN neurons make only about 6 million synapses in the GPe, only about 1/10 of all the excitatory synaptic contacts in that structure. If the STN made synapses randomly in their targets, each GPe neuron would receive input from only about 1.2% of the STN cells, and any two GPe neurons would share on average only 1.6 STN afferents. If this estimate of the size of the STN input is accurate, other excitatory inputs to the GPe (such as cortex and thalamus) may be more significant than previously thought.

One caveat to all of these calculations is the unlikely assumption that axons make synapses at random among neurons in their target structures. We assume random connectivity because we don’t know the rules that govern the formation of the axonal arborizations, but there is good evidence that they aren’t random. For one thing, the distributions of bouton number per axon in all the studies cited above are far too broad. For example, in the Koshimizu et al. (2013) sample, each STN axon made between 245 and 1450 synaptic boutons in the GPe. If subthalamic axons were all the same, randomly making synapses in the GPe with some constant probability p and a total number of potential postsynaptic sites N, the distribution of boutons across a sample of axons like this would be binomial, with N = 6,000,000 and p = 558/6,000,000. That binomial distribution is very narrow, predicting that nearly all axons will form between 500 and 600 boutons. Only one axon in the entire Koshmizu et al. sample lies within that range. Some other kind of process is responsible for the distribution of bouton numbers; one in which axons do not all have an equal chance at innervating the GPe. It is possible that the majority of STN-GPe synapses are made by a much smaller number of axons, not yet sampled in experiments, and the total STN-GPe innervation is much larger than estimated. In this case input sharing would be much larger than expected. This would help to explain the small proportion of the total excitatory innervation apparently represented by the STN based on their sample. A similar bouton number distribution issue arises in the Baufreton et al. (2009) observations, in which the range of bouton numbers ran from 46 to 455, and the Kita and Kita (2013) sample, in which cortical axons formed 4–94 boutons in the STN. In all of these studies, the variation in bouton numbers observed across axons is much wider than expected by chance.

Another issue arises from the topographical organization of the projections, and this concern also applies to all the calculations. If we posit that subsets of axons are systematically restricted to making synapses on a subset of the target neurons, the proportion of shared synaptic input expected will increase proportionately. This does not affect the estimates of the average connectivity (e.g. the 2% value for average proportion of GPe cells innervating each STN cell by Baufreton et al.), but it severely impacts the calculation of input sharing (e.g. the conclusion that therefore STN cells share only 2% of their GPe innervation). For example, it is well known that the STN and GPe projections are organized topographically to some degree (Shink et al. 1996). The Baufreton et al. (2009) and the Koshimizu et al. (2013) papers emphasize that the boutons formed by single STN-GPe and GPe-STN axons were clustered and restricted to a subset of the nucleus. Baufreton et al. (2009) measured the volume occupied by individual GPe-STN axons, which averaged only 3.8% of the STN volume. If instead of assuming random connectivity, one assumes that the topographic organization of reciprocal GPe and STN connections were tightly arranged so that 3.8% of GPe cells make all their contacts with 3.8% of STN cells and visa versa, the estimates of input sharing go up dramatically. Under these rules GPe cells would be expected to share 42 (32%) of their STN-derived afferents and STN cells would share 463 (52%) of afferents from the STN. A similar adjustment would be necessary for the striatal inputs to the GPe and the cortical input to the STN, depending on the granularity of their topographic maps.

Thus the original intuitive expectation of shared input among neurons based on their extended dendritic trees is probably a misconception. On the contrary, if there were no topographic specificity and each neuron sampled the afferent inputs equally, the amount of sharing of inputs would be much lower than it probably is, given the topographic organization that is known to exist. However, our knowledge of the topographical arrangement of afferent axons is not quantitative, so the estimates of sharing cannot be corrected at the necessary level of precision to make the appropriate adjustment. The estimates of input sharing given above for all the non-striatal pathways are based on average connectivity and should be considered only a lower limit.

In addition to shared input, firing of GPe and SNr cells might become correlated with others of the same type by local inhibition. GPe neurons inhibit each other via local collaterals, which are organized into two sets, one remaining near the neuron of origin and one projecting to other regions of the GPe (Sadek et al. 2007). Shink and Smith (1995) calculated that these axons account for 10% of axo-somatic and 5% of axo-dendritic synapses in the GPe. In the single axon study by Sadek et al. (2007) local axon collaterals made between 135 and 649 axonal boutons, averaging 413 across their sample as a whole. They reported that each bouton made only one synapse, so the 46,000 GPe neurons make about 19 million total synapses in the GPe. At least some of the variance in the number of boutons formed per cell was accounted for by the difference between two different kinds of GPe cells, one located near the boundary with the striatum, and one located more centrally. Taking that difference into account, the distribution of GPe collateral arborizations is more consistent with a constant probability model than that of the STN-GPe projection. Even so, it is apparent that synaptic contacts by those axons are not made at random. The local part of the collateral field follows the shape of the dendritic field, rather than forming a cloud of synapses around the neuron, and axons tend to make multiple synapses on single target cells. These synaptic contacts are relatively strong and proximal, compared to synapses of striatal origin (e.g. Kita 2007; Sims et al. 2008). It is impossible from existing data to even begin to estimate the number of different GPe cells contributing to the collateral innervation of any other cell.

Synaptic Integration in Repetitively-Firing Neurons

The assumption that shared inputs and mutual coupling produce structural spike-time correlations among neurons is based on a particular view of synaptic integration. That view was derived from the study of neurons possessing a stable resting potential and subjected to an irregular background synaptic excitation that occasionally drives them across the action potential threshold. For such cells, the synaptic potential produced by a synaptic input is short-lived, decaying away in time as the charge deposited on the membrane dissipates through the membrane conductance. Brief subthreshold excitatory synaptic inputs act to increase the probability of an action potential for a period of time determined by the rate of charge dissipation. Shared synaptic inputs create correlations in firing of neurons by raising or lowering their probabilities of firing at about the same time. For such neurons, shared inputs (excitatory or inhibitory) will always produce positive correlations in the time of firing, and synaptic unidirectional coupling will produce transient asymmetric positive or negative correlations, depending on the sign of the synaptic effect (Bryant et al. 1973), and with a delay corresponding to the conduction time.

The intuitions built for understanding these neurons’ interactions do not all apply to neuron that fire repetitively, either because they are autonomous oscillators (as in GPe, GPi, STN and SNr) or because they have an average synaptic drive that depolarizes them above threshold. These neurons fire tonically, even in the absence of any transient synaptic events, and the occurrence of an action potential does not signal the recent occurrence of any particular synaptic event or combination of them. Instead of either immediately triggering an action potential or dissipating away, subthreshold synaptic inputs may act to alter the time of the next spontaneous action potential (e.g. Gutkin, et al. 2005). Inputs applied at any time during the interspike interval may exert some influence on the timing of the next spike. They do this by altering the multidimensional trajectory followed by the neuron from one spike to the other (e.g. Oprisan, 2012). This greatly increases the effective integration time for synapses, from the order of one membrane time constant to the order of the interspike interval. The peculiar rules for temporal integration in repetitively firing neurons also alter the interpretation of synaptic sign. Usually, an excitatory input will advance and an inhibitory one will delay the time of the next action potential as one might expect, but there are instances in which an excitatory input applied at the right time during the interspike interval can delay the next action potential instead, and an inhibitory one can advance it (e.g. Rinzel and Ermentrout, 1989). This distinction does not depend on any special features of the synapse, but is determined by the intrinsic properties of the postsynaptic cell. Synaptic inputs arriving at different times in the interspike interval will always have quantitatively different effects on the time of the next spike, even if there is not a sign change. Two neurons firing repetitively but independently and receiving the same input at the same time will encounter the input at different phases in their interspike interval and will experience different changes in phase. They may emerge from the encounter with no change in relative phase, closer in phase to each other, or farther away.

These differences in temporal synaptic integration introduce some new ways that a synapse may affect spike timing of a repetitively firing postsynaptic neuron, and alters the interpretation of spike timing correlations (and their absence).

Intrinsic Pacema in the Basal Ganglia

It has long been perplexing that GPe, GPi and SNr cells fire so rapidly and consistently, given that most synapses in those structures are inhibitory. The puzzle was solved by the discovery that these cells are intrinsic pacemakers, whose firing rate is not very dependent on the average synaptic input. For example, Kita et al. (2004) blocked both glutamate and GABA receptors in the GPe in vivo by injection of antagonists in the vicinity of a recorded neuron. Injection of either GABA or glutamate antagonists alone produced moderate firing rate changes. After blocking nearly all fast synaptic transmission the firing returned to near-baseline levels, but the pattern of firing was changed dramatically. Although they fired irregularly before synaptic input was blocked, the cells fired rhythmically afterwards, like GPe neurons recorded in slices (e.g. Mercer et al. 2007). This relative insensitivity of GPe cells’ firing rates to the net tonic level of synaptic input is also evident in reports of their firing patterns in anesthetized animals. In normal rats, GPe cells show weak or sometimes no modulation of firing rates correlated with the ~1Hz rhythm in the cortex (Magill et al. 2000; 2001), despite the fact that both striatal and STN inputs to the GPe are both powerfully and globally sculpted by this rhythm. (Stern, et al. 1998; Magill et al. 2000). These results all suggest that under normal circumstances, the main effect of synaptic inputs to GPe neurons is a spike-by-spike perturbation of intrinsic rhythmic firing that alters spike timing, rather than a continuous modulation of firing rate.

The mechanism of pacemaking in SNr, STN and GPe neurons has been determined by intracellular recording studies in slices after blockade of synaptic input (e.g. Atherton and Bevan, 2005; Bevan and Wilson, 1999; Mercer et al. 2007). In all these cells, a persistent sodium current generates a net inward current over nearly the entire period of the interspike interval. During the afterhyperpolarization that immediately follows an action potential, when the sodium current is at its weakest, GPe and SNr cells are depolarized back into the range of the sodium current by the hyperpolarization-activated cation current (HCN). In many mouse GPe cells, pacemaking is apparently dependent on the HCN current, being absent in mutants lacking critical HCN subunits (Chan et al. 2004). GPi cells also apparently are intrinsic pacemakers with similar activity (Nakanishi et al. 1990), but the mechanism of their oscillation has not yet been described in detail.

This mechanism of oscillation, held in common by neurons in all the non-striatal basal ganglia structures, results in an extremely small slope conductance during much of the interspike interval. This occurs because the negative slope conductance caused by the persistent sodium current balances the positive conductances generated by potassium channels and synaptic conductances (Farries and Wilson, 2012). Slope conductance determines the rate of decay of the effects synapses exert on spike timing. When the slope conductance is low, synaptic changes in membrane potential are retained, and appear as alterations in the subsequent trajectory of membrane potential and advances or delays in spike timing, rather than as transient changes in firing probability.

These results suggest that the expectation of spike-timing correlations in the basal ganglia may be based on an erroneous view of temporal synaptic integration in those structures. Instead of viewing them as elaborate arcs of connected neurons that propagate changes in action potential probability along cells in a chain, they may be better viewed as systems of coupled oscillators that interact through phase changes. Could that explain the absence of spike timing correlations between pallidal and subthalamic cells? How should neurons in systems of coupled oscillators respond to sharing of inputs, or to direct or indirect synaptic coupling?

Synchronization by Shared Inputs

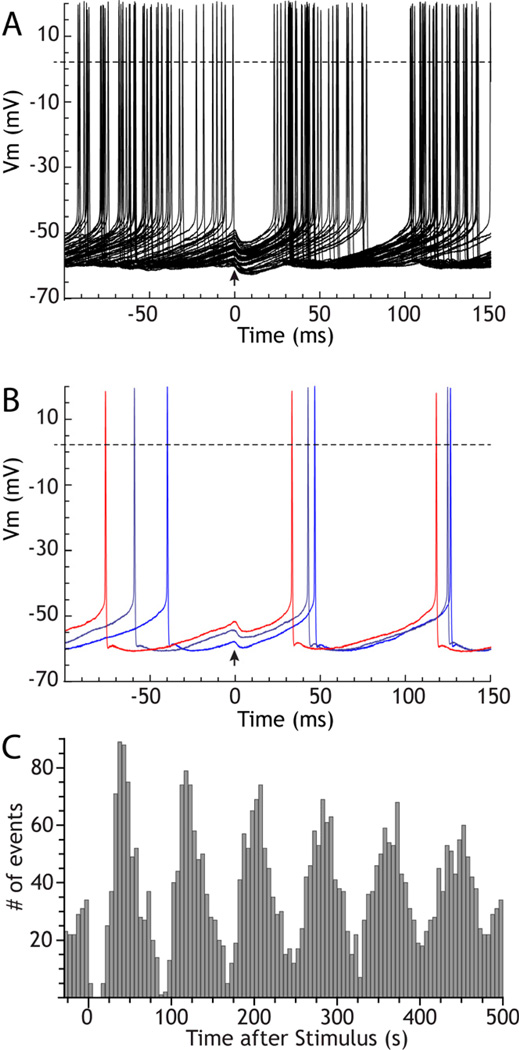
Studies of the synaptic responses of repetitively firing basal ganglia neurons have repeatedly demonstrated that inhibitory inputs can reset their rhythmic activity. In these experiments, synaptic currents (or brief injected currents) are presented repeatedly but at low frequency compared to the firing rate of the cell, and the responses are superimposed (Bevan et al. 2002; Baufreton et al. 2009; Chan et al. 2004; Kita 2001; Stanford 2003). An example for a GPe cell is shown in Figure 2A–C. Because the spacing between stimuli is long compared to the cell’s oscillation, stimulus arrival is effectively asynchronous with the cell’s firing and occurs at a different, effectively random, phase of the interspike interval on each trial. The resetting effect of the stimulus is indicated by a narrow variance of the times of occurrence of the first post-stimulus action potential. A post-stimulus time histogram constructed from those results shows a slowly decaying rhythmic response (as in Figure 2C). The oscillatory reset by strong inhibition occurs because the hyperpolarizing stimulus returns the voltage and voltage-sensitive ion channels to a state similar to that immediately after an action potential. Upon removal of inhibition, the sequence of voltage sensitive currents that normally follows an action potential (absent the spike afterhyperpolarization current) will play out in a similar way and lead to a next action potential at a predictable time (e.g. Farries and Wilson, 2012b). It may also be obvious that if the stimulus were excitatory and suprathreshold, it would cause the cell to fire immediately, which would also then evoke a spike afterhyperpolarization and reset the rhythm even more effectively (e.g. Farries et al. 2010). But it is less obvious why a weak excitatory input that does not trigger an immediate action potential, or an inhibitory input that only partly hyperpolarizes the membrane would also act to reset the cell’s rhythm and cause a weak but unmistakable rhythmic change in post-stimulus firing pattern seen in the poststimulus histogram. The solution to this can be obtained from a study of the phase resetting curve.

Figure 2. Inhibitory resetting of the autonomous firing of a rat GPe cell.

The cell was recorded using the perforated patch method in a GPe slice. The stimulus (at arrow) was an artificial GABA_A synaptic conductance with a 0.25 ms rise time constant, a 6 ms decay time constant, peak amplitude of 3 nS, and reversal potential of −65 mV. A. 50 superimposed trials aligned to the stimulus. The stimulus was presented so that it arrived at randomized phases in the ongoing activity. B. 3 trials selected from A to show that the stimulus changes spike timing differently depending on the phase of its arrival, and this is responsible for the reduction in variance of spike times. C. Post-stimulus histogram of spike times constructed for 620 stimulus presentations.

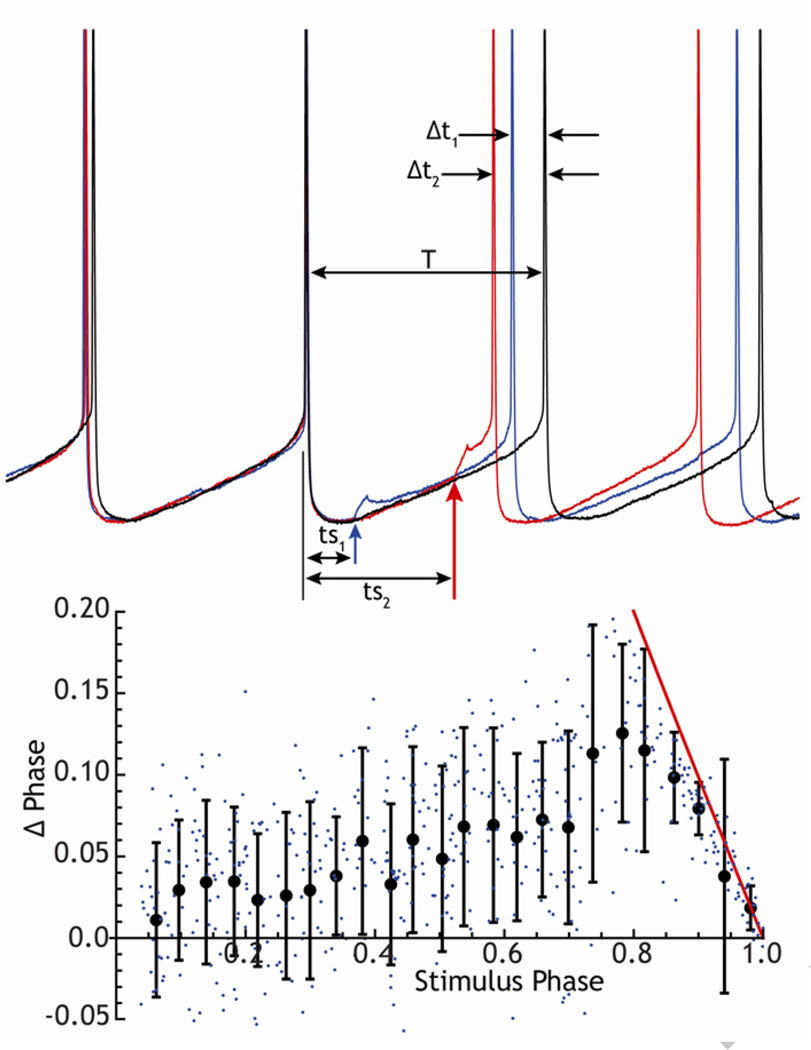
In a repetitively firing neuron, the change in spike timing caused by a subthreshold stimulus is determined by the time of arrival of the stimulus within the cell’s interspike interval. The graph describing the change in spike timing versus the timing of the stimulus is called the phase resetting curve (e.g. Gutkin et al. 2005). It can be experimentally determined by applying a stimulus (e.g. a brief current pulse or small synaptic input) at various times after a spontaneous action potential, and measuring its effect on the timing of the next action potential, as shown for a GPe neuron in Figure 3. The change in spike timing (usually normalized to phase by the average interspike interval) is plotted against the timing of the stimulus within the interspike interval (likewise normalized). For many repetitively firing neurons, including those in the GPe, STN, GPi and SNr, the phase resetting curve resembles the one shown in Figure 3. Stimuli presented at all phases alter spike timing without necessarily directly triggering a spike. In contrast to the behavior of cells driven to fire from a rest state, the most effective stimuli are not those that immediately precede an action potential, but rather ones that occur at intermediate times during the interspike interval (about 80% of the way through the ISI for the example in Fig. 3, about 60% in Fig. 4). For inhibitory synaptic inputs, the sign of the phase change is reversed; inhibitory stimuli produce phase delays and corresponding delays in the time of the next spike. These delays are responsible for the phase resetting seen experimentally in basal ganglia neurons after hyperperpolarizing current pulses or stimulation of inhibitory afferent fibers.

Figure 3. Construction of the phase-resetting curve for a GPe neuron.

Top: example traces showing interspike membrane potential trajectories in the absence of stimulation, and with brief (5 ms) subthreshold current pulses (40 pA) applied at two different times (ts₁, ts₂) in the interspike interval. These produce correspondingly different changes in spike timing t₁ and t₂. Bottom: phase resetting curve constructed from 500 trials like the ones at top. Individual points are single trials, the solid line is the resetting curve for suprathreshold stimuli.

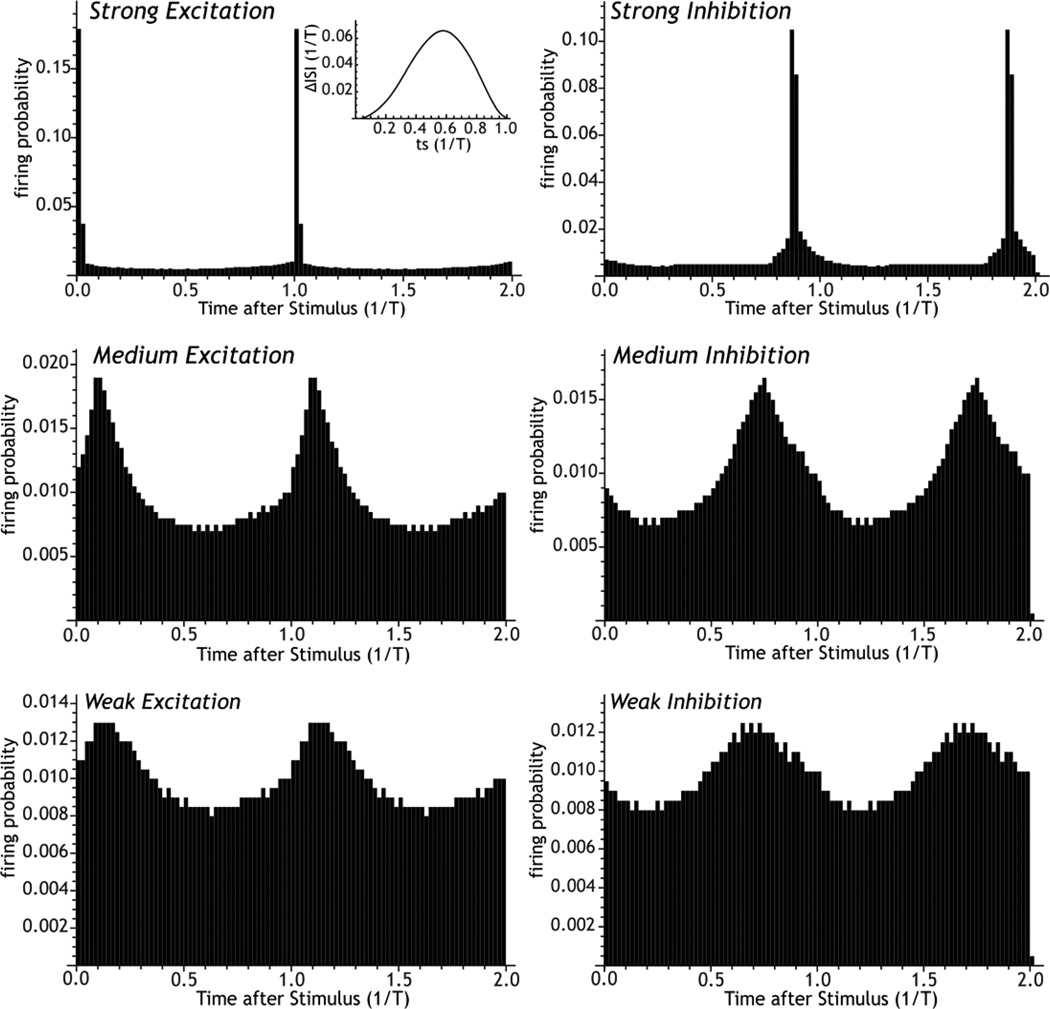
Figure 4. Construction of post-stimulus histograms.

Post stimulus histograms calculated for excitatory and inhibitory phase resetting using an idealized GP-like phase-resetting curve (inset). The strength and the phase of resetting produced by stimulation depends on stimulus intensity. For weak stimuli, excitatory and inhibitory stimuli reset to diametrically opposite phases, but at high stimulus levels, they approach the same phase. There is no threshold for the phase resetting effect of synaptic input.

The post-stimulus histograms for excitatory and inhibitory current pulses may be predicted from the phase resetting curve (e.g. Gutkin et al. 2004; Wilson et al. 2011) as shown in Figure 4. For that figure, post-stimulus histograms were constructed by densely and uniformly sampling all stimulus phases, and spike timing advances and delays were obtained from the curve to generate a large number of simulated stimulus trials. Stimulus intensity was altered by scaling the phase resetting curve. The degree of resetting, seen as a non-uniform distribution of spike times following the stimulus, is determined by the shape of the phase-resetting curve and the strength of the stimulus. The phase resetting effect of a stimulus is not restricted to large stimuli that directly fire action potentials and completely reset the membrane, but occurs in a graded way for stimuli of all sizes. For phase resetting curves of the kinds seen in basal ganglia neurons all asynchronously-presented stimuli, large and small, excitatory and inhibitory, reset the single cell rhythm to some degree. For small stimuli, excitatory and inhibitory stimuli reset the phase of the oscillation to diametrically opposite phases on average, but the difference between excitatory and inhibitory phase resetting decreases as the stimulus intensity increases.

Of course, if there are more than one stimulus presented in the interspike interval, each stimulus will exert some influence on the timing of the next spike. For subthreshold stimuli, excitatory and inhibitory stimuli have opposite effects, but their effects are not commutative. The order of stimulation matters because the phase change caused by the first stimulus alters the phase (but not the time) at which the second stimulus arrives. In an intact network there may be many stimuli, both excitatory and inhibitory, that occur during the interspike interval. Each will cause some change in spike timing, and the effect of an experimentally-applied stimulus may account for only a small proportion of the variance in spike timing. In that case, construction of the phase resetting curve may require averaging of many trials. Even when background synaptic events are suppressed, as in brain slices, intrinsic membrane noise produces irregularity in spike timing (White et al. 1998b), which produces variance in the phase-resetting curve (Ermentrout et al. 2011, also see Figure 3). The phase resetting curves of basal ganglia neurons are readily measured in the low-variance situation in slices (e.g. Farries and Wilson 2012a), or from conductance-based models of the neurons (Schultheiss et al. 2010), and can account for the phase resetting effects seen experimentally.

Does Phase Resetting Imply Synchronization?

Although the data are derived from a single neuron, the conclusion usually drawn from phase-resetting in studies of basal ganglia neurons is that shared excitatory or inhibitory inputs will produce synchrony among cells, and so these stimuli are described as synchronizing (Baufreton et al. 2009; Chan et al. 2004; Kita 2001; Stanford 2003). To understand why, imagine that the traces in Figure 2A are from a sample of simultaneously recorded identical neurons, rather than a set of stimulus presentations in the same cell. Identical neurons receiving common input of any size or sign will have their rhythmic firing reset to some degree by the stimulus, and they will emerge on average closer in phase than they were before. On any one stimulus presentation, the phase difference between any pair of cells may be unchanged, reduced or increased, depending on the difference between their phases at the time of stimulus occurrence. But averaging over all possible initial phase differences, the effect of a single stimulus is a net reduction in the phase differences between identical neurons, just as it reduces the differences in spike timing for a single cell. Identical neurons (i.e. with identical phase resetting curves and identical firing rates) would thus become synchronized by shared randomly patterned excitatory or inhibitory input. The situation is slightly more complicated if the random shared stimulus occurs more often, so that more than one shared stimulus arrives during the interspike interval. But in this case as well, shared inputs will correlate identical pacemakers (e.g. Galán et al. 2006). From this, one would expect that autonomously firing neurons, like those in the GPe, GPi, STN and SNr, would be even more susceptible to becoming correlated by shared inputs than neurons that are excited to fire from a rest state. But this conclusion is based on idealized, identical neurons, not on neurons subject to background noise or heterogeneous rates or phase resetting curves.

It is important to note that this conclusion holds only for random stimulus patterns. Thus the synchronization of identical independent pacemakers by shared noise is usually called stochastic synchrony. Unless it is presented very infrequently, a periodically repeating stimulus will not sample the phase response curve randomly and uniformly, and so can produce a variety of complex responses that include both correlated and uncorrelated patterns, even in identical neurons. This may be significant in interpretation of the response to periodic components of the synaptic input, such as the oscillations that accompany Parkinson’s disease. It has also been used in a model of the therapeutic effect of deep brain stimulation (Wilson et al., 2011).

Independent Inputs and Intrinsic Noise

Unlike shared synaptic input, stimuli presented independently to each cell, both unshared synaptic inputs and intrinsic noise, produce independent phase changes whose accumulation causes cells to gradually become less correlated. Because there is always some intrinsic cellular noise, oscillatory auto- and cross-correlations will decay with increasing time lags, even for oscillating cells in slices. In the extreme case of a dense barrage of independent inputs combined with a smaller proportion of shared inputs, the cross correlation imposed by shared input to identical oscillators may lose its rhythmicity almost entirely, and be reduced to a symmetric peak surrounded by weak troughs. This extreme form of irregularity by dense independent input does not imply that the cells have stopped their repetitive firing. Each action potential may still reset the process that will ultimately lead to the next, but the timing of action potentials may be densely perturbed, producing the characteristic highly skewed interspike distribution seen during irregular firing.

Firing Rate Heterogeneity and Shared Input

The synchronizing effect of phase resetting by subthreshold shared input depends critically on the similarity in phase resetting curves and firing rates of the postsynaptic neurons (Burton et al. 2012). For the result described above, in which a shared input synchronizes a pair of repetitively-firing neurons, the two cells must not only have the same phase resetting curve, but also the same firing rate. The temporal scale of the poststimulus time histogram for repetitively-firing neurons is determined by the period of firing. Two cells with identical phase resetting curves, but different firing rates will have poststimulus time histograms that peak at different times after the stimulus, and the difference in peaks at larger lags will be greater still. If the cells sharing a common input do not have commensurate rates (forming an integer ratio), they may show no cross-correlation at all, even when the shared stimulus is strong enough to produce large responses in the individual neurons. For a population of neurons with a continuous distribution of firing rates, even strong shared inputs (that produce clear responses in all the neurons individually) may not produce a consistent degree of synchrony across the group of postsynaptic cells. Heterogeneity in phase resetting curves caused by variations in ion channel composition within cell types, and by regenerative currents in dendrites (Edgerton and Jaeger 2011; Günay et al. 2008) may likewise disrupt synchronization caused by shared inputs.

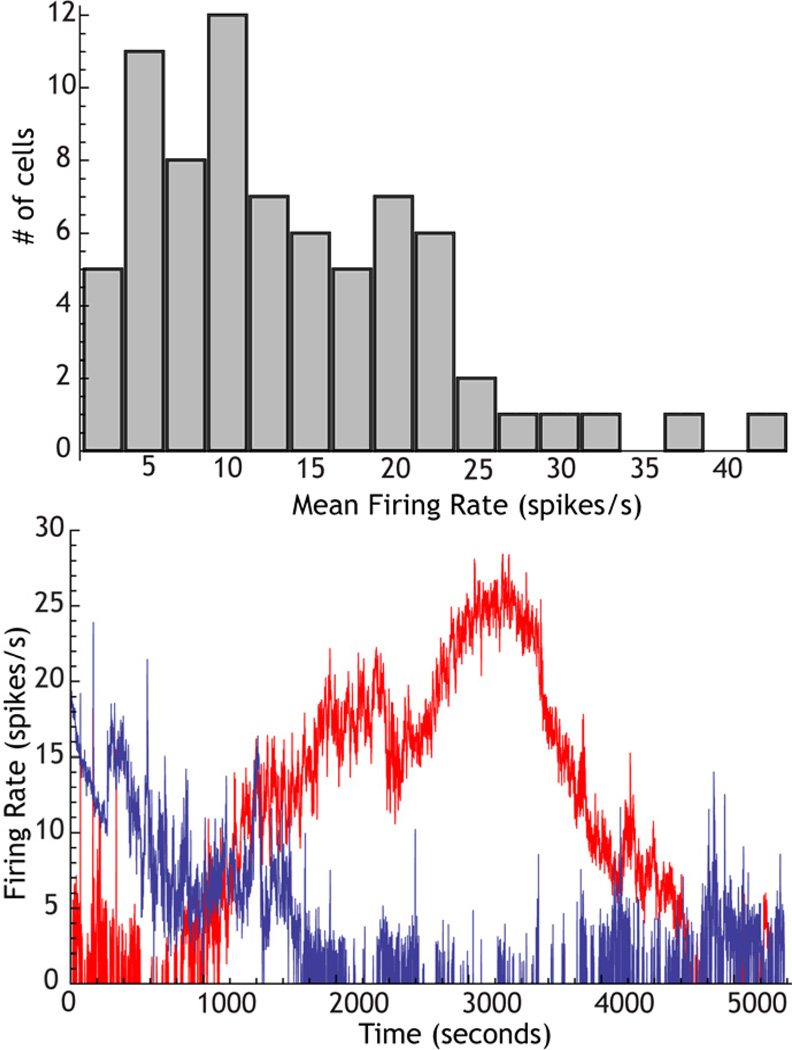
Studies of firing rate generally report means and standard deviations for a group of cells, and only means are interpreted, discussed, and compared across groups. But the importance of rate heterogeneity in synchronization by shared inputs suggests that a broad distribution of rates may be more than a ob-stacle to achieving statistical significance for differences between means. In the GPe, the range of firing rate samples are especially large, varying from less than 1 spike/s to greater than 40 spikes/s (Deister et al. 2012). Rate heterogeneity in the globus pallidus is not dependent on synaptic input. Firing rate heterogeneity as seen for autonomous activity in slices is shown in Figure 5 (data from Deister et al. 2012). The broad range of firing rates is seen even after blockade of fast synaptic transmission, and covers nearly the same range seen in vivo. This confirms the conclusions of studies cited earlier, which indicate that the spontaneous firing of globus pallidus cells, both in slices and in vivo, is intrinsic in nature. Some of the variation in firing rate is no doubt accounted for by the presence of several subtypes of globus pallidus neurons that on average differ in firing rate (Mallet et al. 2012). But long duration observation of GPe cells in slices and in vivo show that individual neurons wander in rates over nearly the entire range seen for the population (Deister et al. 2012, also see Figure 5). This ensures that at any one moment, there is a wide range of firing rates within the population. The mechanism responsible for wandering in rate is apparently variation in the strength of a nonspecific cation current with a reversal potential near −40 mV, and so is likely to be mediated by the HCN channel. Mouse knockouts of HCN show reduced inci-dence of pacemaking in the GPe (Chan et al. 2011). These results suggest that rate heterogeneity is not an incidental feature of globus pallidus cell physiology, but is an active process that insures a wide range of firing rates in the nucleus at all times. This wide range of firing rates is a powerful foe of synchronization by shared input in that structure. It should be noted that expression of HCN and the HCN current are also downregulated after dopamine-depleting lesions with 6-OHDA, and this may contribute to the neuro-pathology seen after those lesions and in Parkinson’s disease (Chan et al. 2011, also see below).

Figure 5. The origin of rate heterogeneity in the GPe.

Top: Distribution of firing rates for 3 min samples of activity in GPe neurons recorded in rat slices. Note the broad range of firing rates. Bottom: A pair of GPe neurons recorded simultaneously, showing independent spontaneous wander of firing rates over nearly the entire range seen in the histogram.

Synaptic Coupling

Subthalamic neurons, and neurons in the GPi have been reported to have sparse or no local axonal collaterals (Kita et al. 1983; Koshimizu et al. 2013; Sato et al. 2000), and so the repetitively-firing neurons in those structures may not be synaptically coupled. In the GPe and in the SNr, local collateral arborizations have been clearly demonstrated anatomically (Bevan et al. 1998; Grofova et al. 1982; Kita and Kitai, 1994; Sadek et al. 2007) and the inhibitory effect of the synapses has been demonstrated physiologically (Deniau et al. 1982; Sims et al. 2008).

The influence of synaptic coupling in synchronizing networks of repetitively active neurons is even more counterintuitive than that for shared input. One normally begins to think about synaptic coupling by imagining a pair of identical oscillating neurons mutually connected by identical (in this case inhibitory) synapses (e.g. Van Vreeswijk et al. 1995). Ideally, if the two cells are firing rhythmically at exactly the same rate, in the absence of any noise or independent synaptic input, they will be correlated whether they are connected or not. Because their firing rates are constant and identical (they are idealized neurons), they maintain whatever phase relationship they had when they began. If they are synaptically coupled, they will perturb each other whenever they fire, and even (especially) if their effects on each other are extremely weak, they will gradually shift into a specific preferred phase relationship that would be apparent in the cross-correlation. Either the cells will come to fire simultaneously (synchronously) or they will phase-lock at some non-zero phase relationship, which is usually called asynchronous firing. There is a well-developed theory that may be applied to synaptically coupled ideal oscillatory neurons, and that predicts the conditions under which they may become synchronized and those that forbid synchronization (Ermentrout 1996; Hansel et al. 1995; Izhikevich, 2007; Schwemmer and Lewis, 2012). The most basic results are that pairs of neurons may spontaneously synchronize when coupled with either excitation or inhibition, but in either case it depends on the specific properties of the synaptic connections and the details of the mechanism responsible for their repetitive firing. The cross-correlation for the case of synchronous firing consists of a peak at zero, flanked by troughs, and then peaks and troughs repeating with period equal to the period of the cells’ oscillation. When mutual inhibition produces asynchronous firing, there is a trough at zero that may be symmetrical (for antiphase phase-locking) or asymmetrical around zero (for all other values of the angle of phase-lock), but also with peaks repeating at the common inter-spike interval. For pairs of identical simple oscillators, all coupling arrangements lead to highly correlated (but not necessary synchronous) firing, and therefore oscillatory neurons are said to be more sensitive to becoming correlated by synaptic coupling than cells firing irregularly. This arises from the same reason that they are often more easily correlated by shared inputs. The periodic nature of their firing allows for accumulation of small increments in mutual influence over many cycles of the oscillation. If, on every cycle, the phase difference between cell A and B on average approaches the stable phase-locked solution, even by a small amount, the nature of periodic firing causes these small changes to be retained and the cells will approach a steady state spike-timing relationship over time.

Network Synchrony and Asynchrony

It might seem unimportant for the question of basal ganglia spike timing correlation whether the collateral inhibition among GPe cells causes them to tend to phase-lock at zero phase difference, and be synchronous, or to phase-lock at some non-zero phase. For a simple pair of noise-free identical neurons, both conditions will produce a strong correlation in spike timing that could readily be detected in their cross-correlation. But the distinction is critical in a mutually connected network with more than two neurons. If the neurons tend to synchronize with each other, they will cooperate to synchronize the activity of a third neuron added to the network. As more neurons are added, the synchronizing effect of mutual coupling will increase. In a large interconnected network, the combined effect of all the cells in the network is the input to all of the cells (Hansel et al. 1995). If synchronous, it is a powerful input shared by all cells, and the cross-correlation between any pair of cells in the network will reflect the synchrony of the entire network. In contrast, if a pair of cells tend to phase-lock at some non-zero angle, addition of a third neuron will tend to disrupt their correlation. The third neuron cannot phase-lock to both of them at the preferred angle. As more neurons are added to the mutually-connected network, correlations must become much more complex (e.g. cells firing in a particular sequence), or be disrupted completely. It is not simply that the cells fail to become synchronized. The interactions between cells actively destabilize synchrony, and perhaps any stationary pattern at all.

In the GPe, the interconnections among neurons are fewer than those arising from the striatum, but are proximally located on the cells and generate individually larger synaptic currents. They may not be as powerful in vivo as they appear in highly controlled experiments, however. The GPe synapse on STN neurons undergoes a profound depression at rates comparable to those of spontaneous activity in GPe (Atherton et al. 2013). If the local collaterals of these cells undergo a similar depression, they may actually be much weaker than they appear when measured in the usual way (in which background firing is suppressed). Even if the local collaterals are weak, coupling between the cells could act either to synchronize them (correlate them at zero phase lag) or to desynchronize them (correlate them at non-zero phase lag), so long as they have a periodic component to their firing. For GPe cells, the collateral interconnections produce asychronous firing. This can be seen in Figure 6, which shows two simultaneously recorded GPe cells in a rat slice preparation artificially connected by GABA_A-like synapses generated using conductance clamp. When each cell fired, a synaptic conductance was applied in the other adjusted to recreate the synaptic conductances of the collateral interconnections among GPe cells. (Sims et al. 2008). The artificial synaptic conductances had a 0.1 ms delay, a rise time of 0.25 ms, a reversal potential of −65 mV, and a decay time constant of 6 ms. The cells’ average firing rates were set to be similar by injecting constant current. GPe cells tested in this way fire in approximate antiphase with each other. The mutual connections between GPe cells, at least, appear to actively oppose synchronous activity in their network.

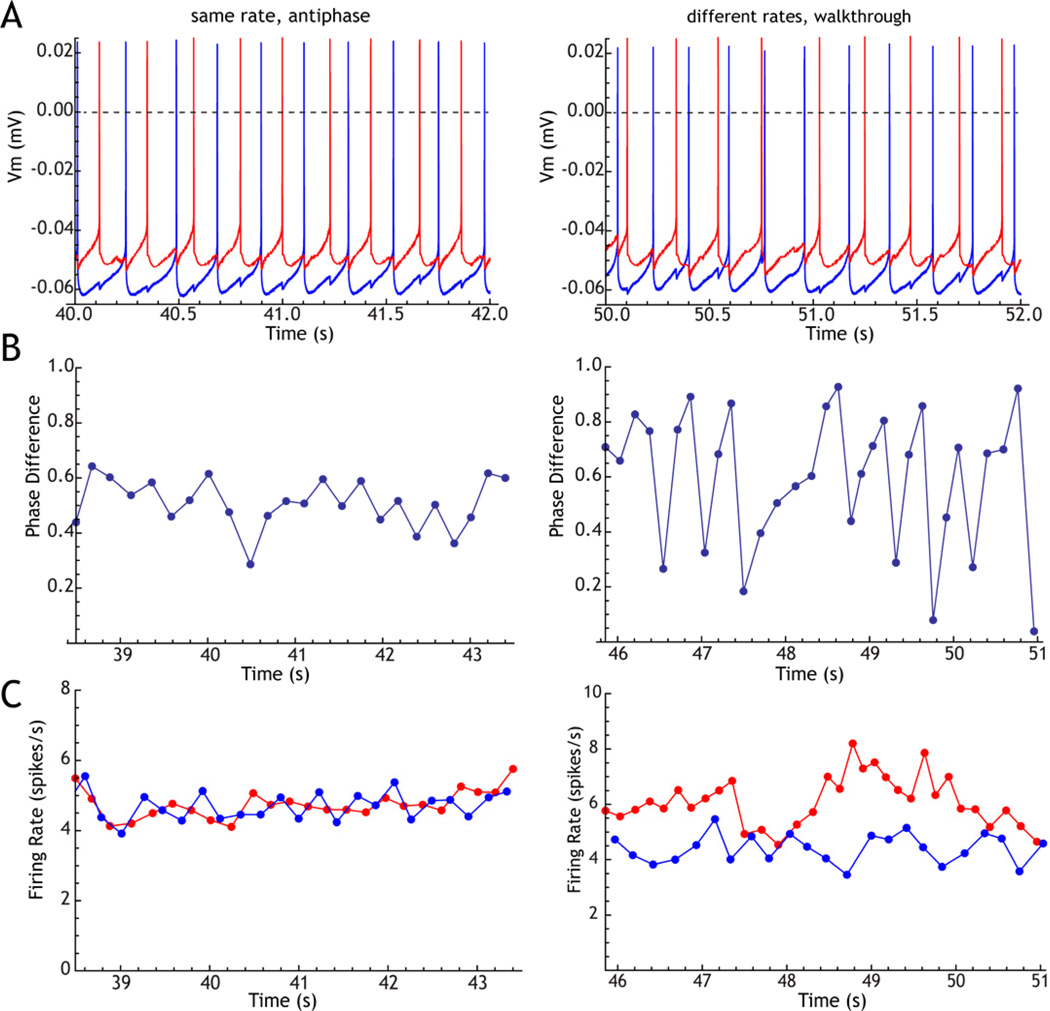
Figure 6. Effect of rate difference on phase-locking of GPe neurons.

A pair of neurons recorded simultaneously in a slice was coupled by reciprocal GABA_A-like synaptic connections. The rates were controlled by passing constant current, to be approximately equal (left column) or to differ by about 30% (right column). A. Example traces showing stable antiphase firing with equal rates, and phase-walkthrough when rates differ (the faster cell advances phase relative to the slower one). B. Evolution of phase difference between the two cells. C. Instantaneous firing rates for the two cells.

Firing Rate Heterogeneity and Synaptic Coupling

Most of the theoretical results assume that synaptic coupling is asymptotically weak and the neurons are noiseless and identical. Many of their conclusions can be generalized to synaptic inputs of realistic size, and to cells with noise due to independent random input or intrinsic membrane noise, and even to cells with a small amount of rate heterogeneity (e.g. Chow et al. 1998; Neltner et al. 2000; White et al. 1998a). Anything more than a tiny rate heterogeneity, however, can be very destructive to correlations among mutually connected neurons. The effect of rate heterogeneity on antiphase firing for two mutually inhibitory GPe neurons is shown in Figure 6. Even a small change in the firing rate of one of the neurons in the pair destabilizes the constant phase relationship that was established when the cells’ firing rates were similar. It also destabilizes the firing rates themselves. The cells shift gradually in phase past each other. If they were uncoupled, this shift would occur at a constant rate, with an equal phase change between cells on each cycle. When coupled by mutual inhibition each alters the rate of the other, spike-by-spike, in a way that depends on their relative phases. Because they do not settle into a single phase relationship, the effect of each on the other’s rate is also unsettled, and the rates of both cells fluctuate (Fig. 6C). In a large network of mutually inhibitory neurons, the stability of any phase-locked state relies on the entrainment of each cell’s own oscillation to the oscillatory net input from the population. Any cells that are not entrained to the population will tend to disrupt phase locking in the rest. For GPe cells, whose firing rates are constantly changing, population entrainment by mutual coupling would be challenged by the disruptive effect of rate heterogeneity.

Irregularity

The irregular firing of neurons caused by intrinsic noise and by uncorrelated synaptic background activity limits the degree to which small effects of synaptic coupling can accumulate, just as it does for the correlating effect of shared input. Between action potentials, the uncorrelated synaptic barrage to each cell causes them to alter their spike timing independently and those differences also accumulate over time. This has a diffusive effect, so that the cells’ relative phases will be gradually randomized between action potentials and limit the accumulation of effects of coupling. The synaptic effect of coupling must be large enough to overcome the phase-randomizing effect of the background synaptic barrage and intrinsic membrane noise (Neltler, 2000; White et al. 1998a). Neither of these can be considered constant. Even the intrinsic irregularity of neurons is determined by the interactions of ion channels responsible for their repetitive firing. For example, in GPe neurons, both HCN channels and SK channels have been shown to regularize firing, by acting in opposition to noise generated by stochastic opening of ion channels (Chan et al. 2004; Deister et al. 2009).

Enemies of Synchrony

Oscillatory neurons are naturally sensitive to synchronization by both shared inputs and by mutual connections, but the same properties also make them sensitive to several kinds of synchrony-disrupting effects present in most neuronal populations. Intrinsic and independent synaptic background noise generate a passive kind of decorrelation mechanism. They both act in a diffusive manner, causing the synchronizing effect of shared stimuli to be forgotten over time. Firing rate heterogeneity produces a more active disruptive effect on the correlating effect of shared input, and especially on synchronization by shared periodic inputs or mutual synaptic coupling. In the GPe, and perhaps elsewhere, there is an active cellular mechanism that enforces rate heterogeneity by causing all the cells to wander in rate independently of each other. Finally, the synaptic connections among GPe neurons act in a synchrony-disrupting, rather than a synchrony-enhancing fashion to oppose correlation among cells in that structure. Because the GPe is a major source of input to the neurons of the STN, GPi and SNr, the absence of correlations in the GPe may be key in preventing the formation of strong correlations in the other structures as well.

Synchrony in Parkinson’s Disease

The fact that neurons in the GPe, GPi and SNr have fewer spike-timing correlations than expected from a casual examination of their synaptic connections would not have seemed so meaningful, if it had just been nothing more than that. It is the pervasive increase in such correlations in Parkinson’s disease that makes their absence in the healthy basal ganglia seem important. What could be changing in these structures in Parkinson’s disease that would produce such dramatic changes?

As already described, the firing rates of GPe neurons in rats are normally resistant to modulations of their rate despite the massive highly coherent changes in the overall volume of synaptic barrage from the striatum and the STN that accompany the slow delta-range oscillations seen during sleep and urethane anesthesia. In animals given dopamine-depleting 6-OHDA lesions, the GPe neurons acquire dramatic rate modulations in response to those same oscillations in the firing rate of their cortical and STN inputs (Magill et al. 2001). The modulation of cortical and striatal cells rates by Up and Down states may be altered by dopamine denervation, but they are already highly coherent in normal animals (Stern et al. 1997; 1998). The change seen in the GPe is not merely an increase in modulation, it is the emergence of a strong modulation where there previously was nearly nothing (Magill et al. 2001). This change in sensitivity to coherent changes in firing rate of inputs is not restricted to slow frequencies during sleep and anesthesia, but is also seen for beta-frequency oscillations elicited by cortical activation (Mallet et al 2008). The entrainment of the cells by oscillations in the 20 Hz range is accompanied by strong spike-timing correlations. These resemble those seen in GPe neurons in primates with experimental parkinsonism and in human Parkinson’s disease patients. This qualitative change in the entrainment of GPe neurons by afferent inputs may thus have a direct relationship to the neuropathology of Parkinson’s disease.

What could cause the breakdown in the mechanisms that resist spike-timing correlation? One possibility is a change in the connectivity of the network. Most of the estimates of input sharing and mutual interconnections have been made in healthy animals. In at least one pathway, the GPe-STN connection, new synapses are apparently formed after dopamine-depleting lesions (Fan et al. 2012). These new synapses did not change the divergence or convergence of the pathway, but were additional synapses made between neurons that were already synaptically connected. They were therefore connection strengthening rather than network remodeling changes. ¶There may be similar changes in synaptic connectivity throughout the rest of the network, that have not yet been discovered.

All of the active decorrelation mechanisms described here depend on the repetitive firing of neurons in non-striatal basal ganglia networks. The most simple explanation for a failure of these mechanisms is the loss of autonomous activity. The continuous repetitive firing of basal ganglia neurons is generated by intrinsic pacemaker mechanisms. Chan et al. (2011) report that pacemaking by GPe neurons is weakened after dopamine-depleting lesions to the point that a large proportion of neurons can no longer support autonomous firing in slices, or continue firing in the absence of excitatory input in vivo. This was associated with a reduced expression of HCN channels, one of the ion channels supporting autonomous firing in those neurons. Animals with reduced HCN expression were also shown to also have reduced autonomous activity. The loss of repetitive firing in the GPe is consistent with the reduction in firing rate seen in that nucleus in experimental Parkinson’s disease in primates (although that change is usually attributed to increased striatal inhibition). The firing seen in the nucleus after the loss of autonomous activity would be much more sensitive to shared inputs and local interconnections, for the reasons described above. The desynchronizing effect of local collaterals, for example, might be reversed to have a correlating effect. Chan et al. reported that restoring autonomous activity in the GPe by increasing the expression of HCN did not reverse the behavioral symptoms of dopamine-depleting lesions. Perhaps the GPe is not the only basal ganglia structure in which autonomous firing is lost after dopamine depleting lesions.

If loss of desynchronizing mechanisms in the nonstriatal basal ganglia were responsible for some of the pathophysiology of Parkinson’s disease, then stimuli that acted to desynchronize that system might be beneficial as a treatment. There is reason to think that deep brain stimulation in the clinically effective range of frequencies might act to desynchronize the output of the basal ganglia, and that this could contribute to the effectiveness of this treatment (Wilson et al. 2011).

Spike-timing ane the Basal Ganglia Output Signal

The relationship between behavior and neuronal firing rate of basal ganglia neurons has been studied in behaving animals in a variety of ways, starting with the original papers by DeLong (e.g. 1972). The design of many experiments and the style of their interpretation usually makes a (sometimes implicit) assumption that slow (~ 100 ms) changes in firing rate in single neurons are the signals that the basal ganglia sends to its target structures in the thalamus, superior colliculus and lateral habenular nucleus. Originally, this conclusion was aligned with the then-contemporary view that the basal ganglia are associated with relatively slow sensory-guided or ramp-like, as opposed to pre-programmed ballistic, components of behavior (Kornhuber, 1971). Today, the notion of discrete decision-making in the basal ganglia is similarly based on the view that the basal ganglia output signal contains a very low information content. For example, the idea that the STN neurons are part of a Stop pathway for behavior (e.g. Aron et al. 2007), condenses the activity in 13,500 neurons on each side of the rat brain (much more in humans) to a one-bit signal issued on a time scale of 10–100 ms. In the strong form of this view, the information content in each neuron need be only about one 1000th of a bit per second. It could be several fold higher if different parts of the STN are executing Stop decisions for several different ongoing behaviors at the same time. On the other hand, studies of the entropy of firing patterns of GPe neurons indicates that these cells could in principle individually carry much higher information rates (e.g. Cruz et al. 2009). Because the neurons normally fire without any background spike-timing correlations, the entropy of the population of GPe neurons is much larger still.

If the timing of action potentials in non-striatal basal ganglia neurons, and not just their mean rates, carry essential signals to the targets of these neurons, then the statistical independence of the firing times of each neuron may be essential to maximize the information content in the channel. Increases in the number of neurons in these structures across phylogeny would be accompanied by corresponding increases in information-carrying capacity. The generation of spurious spike-timing correlations among the cells in Parkinson’s disease would represent a massive reduction in the information content of the basal ganglia output that could be its principal pathophysiological basis.

Figure 1. The connectivity of the basal ganglia in the rat.

Cell numbers decrease dramatically from the neostriatum to the output cells of the GPi (entopeduncular nucleus in the rat) and SNr. However, the most critical numbers for input sharing are the number of synapses made per neuron in target structures. These numbers are mostly available for the GPe, but not for the other non-striatal nuclei.

Highlights.

• Input sharing by basal ganglia neuron may not be as high as once thought.

• Temporal integration in pacemaker neurons defies our common intuition.

• Pacemaking may underly active decorrelation in basal ganglia.

• Weakened pacemaking in Parkinson’s disease, may underlie synchronization.