A visual-search model observer for multislice-multiview SPECT images

Abstract

Purpose: Mathematical model observers are intended for efficient assessment of diagnostic image quality, but model-observer studies often are not representative of clinical realities. Model observers based on a visual-search (VS) paradigm may allow for greater clinical relevance. The author has compared the performances of several VS model observers with those of human observers and an existing scanning model observer for a study involving nodule detection and localization in simulated Tc-99m single-photon emission computed tomography (SPECT) lung volumes.

Methods: A localization receiver operating characteristic (LROC) study compared two iterative SPECT reconstruction strategies: an all-corrections (AllC) strategy with compensations for attenuation, scatter, and distance-dependent camera resolution and an “RC” strategy with resolution compensation only. Nodules in the simulation phantom were of three different relative contrasts. Observers in the study had access to the coronal, sagittal, and transverse displays of the reconstructed volumes. Three human observers each read 50 training volumes and 100 test volumes per reconstruction strategy. The same images were analyzed by a channelized nonprewhitening (CNPW) scanning observer and two VS observers. The VS observers implemented holistic search processes that identified focal points of Tc-99m uptake for subsequent analysis by the CNPW scanning model. The level of prior knowledge about the background structure in the images was a study variable for the model observers. Performance was scored by area under the LROC curve.

Results: The average human-observer performances were respectively 0.67 ± 0.04 and 0.61 ± 0.03 for the RC and AllC strategies. Given approximate knowledge about the background structure, both VS models scored 0.69 ± 0.08 (RC) and 0.66 ± 0.08 (AllC). The scanning observer reversed the strategy ranking in scoring 0.73 ± 0.08 with the AllC strategy and 0.64 ± 0.08 with the RC strategy. The VS observers exhibited less sensitivity to variations in background knowledge compared to the scanning observer.

Conclusions: The VS framework has the potential to increase the clinical similitude of model-observer studies and to enhance the ability of existing model observers to quantitatively predict human-observer performance.

INTRODUCTION

Human-observer performance in lesion-detection studies has become an accepted figure of merit for assessing image quality for many applications in medical imaging research. Because of the complications and expense involved with these studies, observers are usually asked to perform the detection task with solitary 2D images. This single-slice display format often presents insufficient context for separating anatomical noise from likely lesion sites, sometimes leading to bias in the study results.¹ Volumetric studies, on the other hand, mirror the clinical reality in which the physician has access to an entire image volume presented as multiple slices in multiple views (typically the coronal, sagittal, and transverse views).

The difficulties associated with human-observer studies have spurred research into mathematical models (or model observers) which can serve as surrogates for human observers. The increased demands of reading image volumes as opposed to single slices calls for 3D model observers which are not only efficient to apply but which also provide reliable predictions of human performance. Several model observers have been proposed for volumetric studies (e.g., Refs. ^{2, 3, 4, 5}), but many of these are signal-known-exactly (SKE) models which detect lesions at a prespecified location.^{2, 3, 5}

At issue with model observers which perform relatively simple tasks is how to interpret the study results. Beyond the expectation that the results will predict human performance at the same task is the further expectation that the study will have some relevance for tasks which better describe clinical practice. But establishing the degree of relevance can be challenging when the model task deviates too much from the clinical tasks of interest.⁶ We are investigating whether this challenge may be overcome by consideration of appropriately complex tasks for model observers in the first place.

Addressing such tasks can require model observers which perform both localization and detection. Scanning models for this purpose, derived as fundamental extensions of the models used in SKE tasks,⁷ perform what may be classified as “signal-known-statistically, background-known-exactly” (SKS-BKE) tasks. They accomplish the task by examining every possible lesion location in an image. Model observers for BKE tasks can be appropriate when quantum noise is a significant factor in task performance, as was the case in a prior study of single-photon emission computed tomography (SPECT) mediastinal lesion detection by scanning observers.⁴ These observers operated on stacks of transverse SPECT image slices. However, a more recent study involving solitary pulmonary nodule (SPN) detection in SPECT lung images⁸ calls into question the robustness of the scanning model when performance is limited more by anatomical noise or lesion conspicuity than by quantum noise.

The deficiencies of BKE studies for image quality assessment are well known from past work by Wagner and Brown⁹ and Barrett et al.¹⁰ When the lesion location is known, observer models with so-called “background-known-statistically” (BKS) tasks may provide a greater degree of clinical realism. The BKS paradigm is not desirable in the context of detection-localization tasks for reasons of concordance with humans (see Sec. 2D2), but similar effects might be attained from model observers which implement the two-phase visual-search (VS) paradigm presented by Kundel et al.¹¹ for how radiologists read images. Besides allowing for greater clinical realism in model-observer studies, VS also improves on the scanning process as a description of human search. The result could be more accurate predictions of human performance.

For this paper, we tested this supposition for the task of SPN detection and localization in simulated SPECT lung volumes. We have been investigating a VS framework for model observers¹² that allows for an initial holistic search controlled by salient image features such as local intensity, contrast, and edge structure. (The relative importance of these various features depends on the imaging modality and the application.) This search phase identifies candidate locations in the image for a subsequent analysis and decision-making phase with a statistical discriminant. The performances of two VS observers, a scanning channelized nonprewhitening (CNPW) observer,⁴ and a group of human observers were measured in a localization receiver operating characteristic (LROC) study that utilized a multiview-multislice display format for the image volumes. The two VS observers used slightly different holistic search processes. The level of prior knowledge about the background structure in the volumes was a study variable for the model observers. While the LROC data for the human observers were acquired as part of an earlier study,¹³ the associated data analysis was extended for the present work.

METHODS

Data simulation

The imaging protocol that we simulated was based on Tc-99m-labeled NeoTect,¹⁴ a polypeptide that binds to somatostatin receptors. Although the use of FDG PET has largely supplanted SPECT for lung cancer detection, NeoTect remains a viable alternative for imaging centers which do not offer PET.¹⁵ The NeoTect protocol also has proven valuable for our evaluations of localizing model observers in nuclear medicine applications.

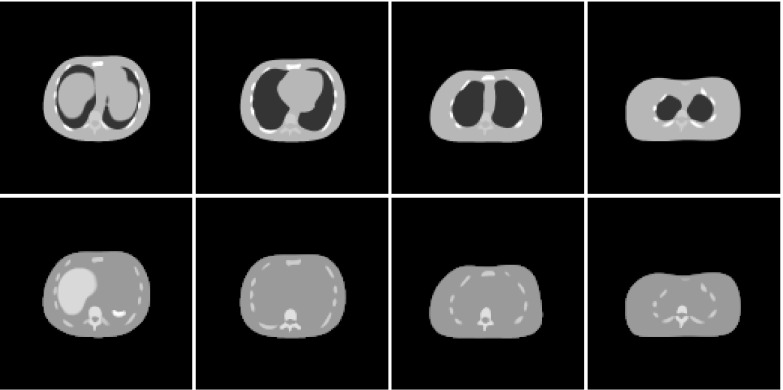
The simulation made use of the NURBS-based mathematical cardiac torso phantom (NCAT) phantom.¹⁶ NURBS stands for “nonuniform rational B-splines.” A single body geometry of this phantom was generated with 256³ cubic voxels (voxel width = 0.208 cm). The physical densities of some of the organs are given in Table 1. The NeoTect distribution assigned to the various tissues and organs of the NCAT phantom was based on pharmacokinetic data supplied by the manufacturer. Table 2 lists these assigned activities. The distribution of Neotect within the lesion-free (or normal) lungs was uniform. Figure 1 shows the tracer distribution and the physical densities in several transverse slices from the normal phantom. Lesions could appear within the lungs, which appear as the dark areas within the density slices.

Table 1.

Physical densities in the NCAT phantom.

Organ	Density (g/cm3)
Lung	0.30
Fat	0.92
Muscle	1.02
Dry spine bone	1.22
Dry rib bone	1.79

Table 2.

Relative activities assigned to the NCAT phantom. “Other” refers to the heart, lungs, stomach, and remaining organs.

Organ	Activity
Kidney	450
Spleen	180
Spine	73
Liver	60
Rib	43
Other	10

Figure 1.

Physical density (top) and NeoTect distribution (bottom) in four transverse slices from the NCAT phantom. Differences in NeoTect uptake have been compressed to enhance visibility. The slice at left includes portions of the liver, spleen, stomach, and heart. The other slices are progressively higher in the torso. The lungs are the dark regions within the torso in the density images.

The lesions were modeled as spherical, soft-tissue masses having a diameter of one cm and a density approximating that of water. Lesion placement within the lungs was automated by first identifying the set of voxel indices (denoted as Ω) where a lesion could be centered. To ensure that lesions were fully contained within the lungs, a two-voxel margin was established around the outer lung boundaries. All voxels inside of this margin were represented in Ω. We then sampled from a uniform probability distribution defined on Ω. As indicated by Fig. 1, the points in Ω were largely contiguous. Sampling redundancy was controlled by establishing a spherical region with a radius of nine voxels about each sampled point. Voxels within this region were excluded from Ω for subsequent sampling. We note that the voxels in Ω also represent the model observer search regions (see Secs. 2C, 2D).

A high-count (or quasi-noise-free) set of 120 256 × 256 projection images for the normal phantom was created with a Monte-Carlo projector¹⁷ that accurately modeled photon attenuation, in-body scatter and the response of a low-energy, ultra-high-resolution collimator. The projections simulated a step-and-shoot acquisition at 3° intervals over a 360° rotation. Two energy windows—a 21-keV photopeak window centered at 140 keV and a 3-keV scatter window centered at 123 keV—were set. High-count projections of the tracer-avid lung lesions were generated separately and then combined with the normal projections to synthesize projection sets for lesion-present (or abnormal) cases. The lesion projections were scaled to produce lesion-to-lung activity ratios of 10:1, 12:1, and 14:1. Lesions with these ratios are respectively designated as having “low,” “mid,” and “high” contrast. With 75 lesion locations, there was an equal number of low, mid, and high-contrast cases. Each abnormal case in our study contained a single lung lesion.

A two-step process was applied to these projection sets to create noisy data for reconstruction. The noise-free projection images were first rebinned to 128 × 128 (pixel width = 0.416 cm) to match the dimensions of clinical acquisitions. Independent Poisson noise consistent with a photopeak acquisition of 23.2 million counts was then added to each set of projections. This count level was determined as an upper limit from a set of nine clinical NeoTect scans acquired with a 24-min imaging protocol on a dual-headed SPECT camera.

Image reconstruction

This study comparing human and model observers grew out of an investigation of the desirability of attenuation correction (AC) for SPECT lung reconstructions. The human-observer study reported herein was originally aimed at determining whether the benefits of AC would compensate for the concurrent loss of the lung outlines for SPN detection. The image volumes were reconstructed with two strategies based on the rescaled block iterative (RBI) reconstruction algorithm.¹⁸ The all-corrections (denoted as AllC) strategy applied AC, scatter correction (SC), and distance-dependent resolution compensation (RC). The second strategy used RC only. All the corrections were applied as part of the iterative cycle. The SC was implemented through a dual-energy-window scatter estimate¹⁹ while an idealized attenuation map for lesion-absent data was devised by converting the physical density values of the NCAT phantom to linear attenuation coefficients for 140-keV photons (linear attenuation coefficient for water = 0.153 cm⁻¹). For the lesion-present data, this map was augmented by the addition of the soft-tissue lesion at the appropriate lung location. The lung and lesion attenuation coefficients were 0.043 cm⁻¹ and 0.153 cm⁻¹, respectively.

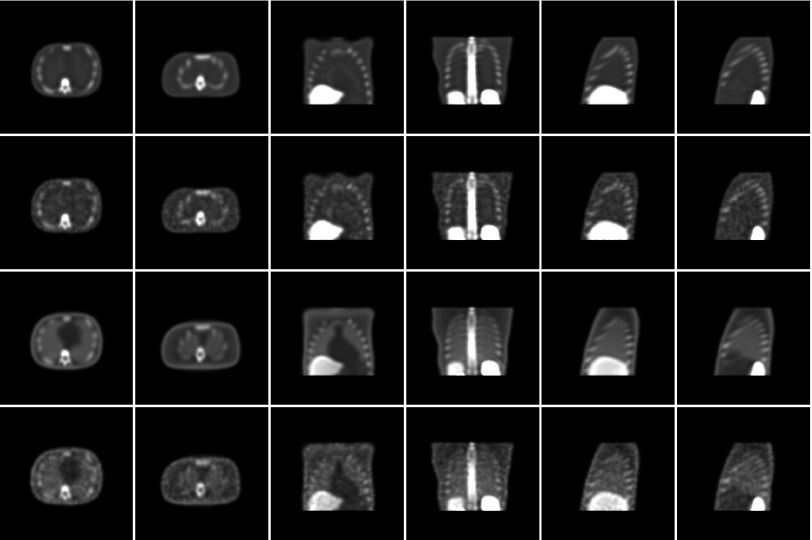
Both reconstruction strategies used 5 RBI iterations based on 30 ordered subsets of four projections each. A 3D Gaussian postfilter with a full-width at half-max of two pixels (0.834 cm) was also applied. These parameter values were based on previous single-slice study results with human observers.²⁰ In all, 150 noisy image volumes per strategy were reconstructed, with an abnormal/normal volume pair for each of the 75 lesion locations. As final postprocessing, the volumes underwent a strategy-specific upper-thresholding (see Ref. 1 for details). The voxel values were then quantized to eight bits and a display volume consisting of 70 128 × 128 transverse slices was extracted. Lesions could appear in a central 49 transverse slices of this volume. The remaining slices contained too little lung area to fully insert a 1-cm lesion. Sample slices taken from both the noise-free and noisy reconstructions of the NCAT background for the two strategies are shown in Fig. 2.

Figure 2.

Comparison of transverse, coronal, and sagittal images extracted from normal reconstructions. Each column pertains to a fixed slice from the NCAT phantom. From top to bottom, the rows represent: (1) noise-free AllC reconstructions; (2) noisy AllC reconstructions; (3) noise-free RC reconstructions; and (4) noisy RC reconstructions.

Detection-localization tasks

Let vector f represent a reconstructed image (either a 2D slice or a stack of 2D slices) having N voxels. The image stack may be referred to as a volume. We consider the general detection-localization task for which test image f is either lesion-absent or has a lesion centered on one of the J voxels indicated by Ω. An observer chooses from one of the J + 1 hypotheses:

$$\begin{array}{ccc}\hfill H_0& :& \mathbf{f}\equiv \mathbf{b}+\mathbf{n},\hfill \end{array}$$ (1)

$$\begin{array}{ccc}\hfill H_j& :& \mathbf{f}\equiv \mathbf{b}+{\mathbf{s}}_j+\mathbf{n}(j=1,...,J),\hfill \end{array}$$ (2)

where b is the mean background corresponding to f, n is zero-mean stochastic noise, and s_j is the reconstructed lesion at the jth location. Each hypothesis is framed as an equivalence (symbol “≡”); strict equality between the two sides in Eqs. 1, 2 does not hold when nonlinear reconstruction or postprocessing methods are applied. In terms of our present simulation, b and n are respectively the reconstructed normal phantom sans noise and the reconstructed Poisson noise.

LROC methodology may be used to assess observer performance for this task if we have the observer assign each test image a localization r and a scalar confidence rating λ. An image is classified as abnormal at threshold λ_c if λ > λ_c. The LROC curve relates the probability of a true-positive response conditioned on correct localization to the probability of a false-positive response as λ_c varies. Area under the curve (denoted as A_L) can be used as the performance figure of merit.

As a practical matter, the number of distinct hypotheses that an observer chooses from for a given f can be much less than J when the possible lesion locations are contiguous. In our SPN study, observers do not have to precisely determine the center of the lesion but instead get credit for finding the lesion when r is within a specified distance of the center. We refer to this distance as the radius of correct localization r_CL. Details on how this empirical quantity is set are given in Sec. 2E. Lesion size and system resolution both have an effect on r_CL.

What an observer knows about the various image components in Eqs. 1, 2 can greatly affect task performance. For human observers, this knowledge generally evolves through training. Researchers mimic this training with model observers by using the task paradigms referred to in the Introduction. The assumptions for one SPN task carried out by the scanning observer match those from the multislice lymphoma study described in Ref. 4. The background b is considered known while the profile of the reconstructed lesion is taken to be invariant with location and also known to the observer. This invariant profile is represented in our studies by the mean reconstructed lesion. Under these conditions, were J = 1, then this would be an SKE-BKE task. With J > 1, we have an SKS-BKE task.

Model observers

CNPW scanning observer

The scanning CNPW observer operates on f by first making a scalar perception measurement z_j at each location in Ω. As in Sec. 2C, f may be a slice or a volume. The LROC data are then

$$\begin{array}{ccc}\hfill \mathbf{r}& =& \arg \underset{j\in \Omega }{\max }{z}_j,\hfill \end{array}$$ (3)

$$\begin{array}{ccc}\hfill \lambda & =& \underset{j\in \Omega }{\max }{z}_j.\hfill \end{array}$$ (4)

Measurement z_j at the jth pixel is computed according to the scalar product

$$z_j={\mathbf{w}}_j^t[\mathbf{f}-\mathbf{b}],$$ (5)

where w_j is the jth CNPW template and the superscript “t” denotes the transpose. The templates for our studies are estimated from training images.

When f is 2D, the template for the CNPW observer is derived by projecting the mean 2D reconstructed lesion profile onto a set of C spatial frequency channels, as indicated by the equation

$${\mathbf{w}}_j={\mathbf{U}}_j{\left[{\mathbf{U}}_j\right]}^t{\overline{\mathbf{s}}}_j.$$ (6)

Here, the C columns of the N × C matrix U_j contain the discretized spatial responses of the channels centered on the jth location. Vector ${\overline{\mathbf{s}}}_j$ in Eq. 6 is the mean lesion profile shifted to the jth location. A 2D CNPW template based on square-profile channels²¹ is shown in Fig. 3a. With the shift-invariance of both U_j and ${\overline{\mathbf{s}}}_j$, the calculation of a perception vector Z containing all the z_j is efficiently produced from the 2D cross-correlation

$$\mathbf{Z}=\mathbf{w}★★[\mathbf{f}-\mathbf{b}]$$ (7)

between the observer template and the background-subtracted test image.

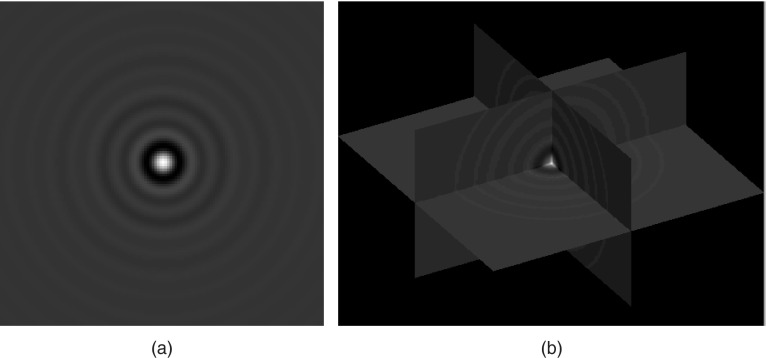
Figure 3.

(a) A 2D CNPW-observer template derived from a set of three square-profile channels. (b) A 3D CNPW-observer template derived from the same channel set for coronal, sagittal, and transverse views. As shown, the horizontal plane applies to the transverse slice. The two vertical planes apply to the coronal and sagittal slices.

The obvious extension of Eq. 7 to image volumes would implement a 3D cross-correlation. However, there are any number of possible definitions of a 3D template for this purpose (see, for instance, Ref. 3). The examples we tested, based on a perception model presented in Ref. 4, assume that the human observer assesses a given lesion position by summing the perception measurements obtained at that position in the coronal, sagittal, and transverse 2D slices. The 3D model-observer template for this is constructed by forming the 2D templates for each of those three slices, and then combining those templates in the same manner as the axial planes x = 0, y = 0, and z = 0 intersect in a 3D Cartesian coordinate system. All other template voxels are zero. Figure 3b shows an example 3D template constructed from the same channels used in Fig. 3a. Square channels were chosen for the examples of Fig. 3 to lend structure to the template images, but for this study, we used the sparse set of three difference-of-Gaussian (DOG) channels described in Ref. 22. The spatial responses for these channels are displayed in Fig. 4.

Figure 4.

Spatial responses for the three difference-of-Gaussian (DOG) channels used in this study.

The 3D template of Fig. 3b accounts for the multiple views of the volume, but is not multislice. A human observer would be likely to also examine neighboring image slices when assessing whether a lesion is present at a given location. We model this by adding additional planes to the template. For example, with two new planes added to each side of the axial planes, the observer integrates information from five slices for each of the three orthogonal views when assessing a given location. The geometric extent of the lesion is accounted for since each of these new template planes is constructed using the corresponding slice through the mean lesion.

BKS and quasi-BKE tasks

The scanning observer used in this work is an extension of the Hotelling-type models commonly applied for location-known detection tasks. Here, “Hotelling-type” refers to linear observers whose templates are determined by the first- and/or second-order statistics of the image classes that the test images are drawn from. For location-known tasks, these models are popular both for their ability to predict human performance (particularly when outfitted with channel models akin to the human visual system²¹) and for computational tractability. In particular, Hotelling models are relatively easy to devise for SKE-BKS tasks compared to the Bayesian ideal observer.

In the case of the scanning CNPW observer for BKE tasks, the relevant statistical template components in Eqs. 5, 6 are the mean reconstructed lesion profile ${\overline{\mathbf{s}}}_j$ and the mean background b. Modifying this observer to create a BKS task simply requires replacing b with the average $\overline{\mathbf{b}}$ formed from the mean backgrounds in a study. But not only would this require ad hoc approximations for our study, since all the test cases were generated from the same mean background, but the idea of using $\overline{\mathbf{b}}$ as a reference image is not an apt description for how humans approach detection tasks.

We instead applied an alternative, heuristic approach to imparting uncertainty in background knowledge with the scanning observer. As written with b, Eq. 5 reflects an ideal prior knowledge about the anatomical background. We also tested the scanning observer without the background subtraction, thereby simulating an inaccurate assumption of an homogeneous background, as well as with degraded knowledge in the form of an approximate mean $\widehat{\mathbf{b}}$ created by smoothing b with a 6×6×6 boxcar filter. In our discussions, we shall refer to these two variations on the BKE task as the “background-assumed-homogeneous” (BAH) and “background-known-approximately” (BKA) tasks. With the latter task, high-frequency anatomical noise is preserved as a factor in the lesion detection. The perception vector for the BKA task is the sum of the BKE perception vector in Eq. 7 and the deterministic cross-correlation vector $\mathbf{w}★★(\mathbf{b}-\widehat{\mathbf{b}})$.

The VS observer

The VS model observer implements a two-stage approach to image interpretation described by Kundel et al.¹¹ The first stage involves a brief holistic search of the image for identifying suspicious candidate regions while the second stage combines more-deliberate candidate analysis and decision making. Two VS observers were tested in our study. With both of these, the holistic search process was guided by characteristics of the test image at hand. Given that lesion detection in emission tomography is fundamentally a hot-spot search, a natural first step is to identify prospective regions of high activity, or “blobs.” Suspicious blobs are characterized by local intensity maxima and attraction regions (defined below). Each intensity maximum represents a blob focal point and relevant blobs for a given image have focal points within the specified Ω. To be useful, it must be possible for this blob search to miss the actual lesion in a test image.

In this work, focal points were located using an iterative, 3D gradient-ascent algorithm (with line search) applied to the voxel grayscale values. Beginning the iteration with the center of a given voxel in Ω as the coordinates x₀ of an initial guess, one follows the intensity gradient to subsequent iterative guesses x_k (iteration k > 0) to determine a corresponding convergence point $\tilde{\mathbf{x}}$ that lies in the 3D space bounded by the reconstruction volume. In our nomenclature, the focal point is the voxel containing $\tilde{\mathbf{x}}$ and the starting voxel is in the region of attraction for this focal point. The attraction region—the set of voxels which converge to the focal point—makes up the blob. Repeating the iterative process for all the lung voxels as initial guesses leads to a mapping of the focal points and their corresponding regions of attraction.

A blob whose region of attraction includes the focal point is considered “complete.” Incomplete blobs—for which the region of attraction does not include the focal point—may result from the quantization involved in determining a focal point from $\tilde{\mathbf{x}}$. This type of blob evolves when the gradient-ascent method identifies a boundary between adjacent blobs that passes between $\tilde{\mathbf{x}}$ and the voxel center. Incomplete blobs were excluded from the holistic search as being of generally lower intensity than the adjacent blobs.

The gradient at any point in the image was determined using trilinear interpolation with the gradient values calculated at the nearest eight voxel centers. Convergence was evaluated on the basis of Euclidean distance, with the requirement that ‖x_k − x_{k − 1}‖ < ε for a suitably small value of ε. (This study used ε = 10⁻⁷.) One version of the VS observer (the base model) analyzed the complete blobs from the clustering process. However, the gradient-ascent method can be expected to oversegment the relatively noisy SPECT volumes. A second VS observer model (the extended model) counteracted this oversegmentation with a blob merging process that used focal-point separation as the criterion. Through this process, pairs of blobs whose focal points were within a distance r_merge were combined, with the focal point for the aggregate blob being the focal point of the larger of the constituent blobs. The value of r_merge was taken to be the estimated radius of the mean lesion $\overline{\mathbf{s}}$.

The final outcome of the extended holistic search was then decided with a local-contrast constraint. A simple definition of blob contrast considered the maximum and minimum grayscale values in the attraction region. This contrast constraint excludes “singleton” blobs consisting of just one voxel. The blob contrasts were calculated and only those blobs whose contrast was within some fraction ν of the maximum were retained as suspicious candidates. For this study, ν was arbitrarily set to 0.5.

The subsequent analysis and decision making for these VS observers was conducted by applying the CNPW observer only at the focal points for the suspicious blobs. The BKE, BKA, and BAH task variations that were tested with the scanning observer (see Sec. 2D2) were also considered for the VS observers.

The LROC study

Three nonradiologists participated in the study. As imaging scientists, they each had extensive experience with similar detection-localization tasks involving simulated images. No attempt was made to correct each observer's vision to 20/20.

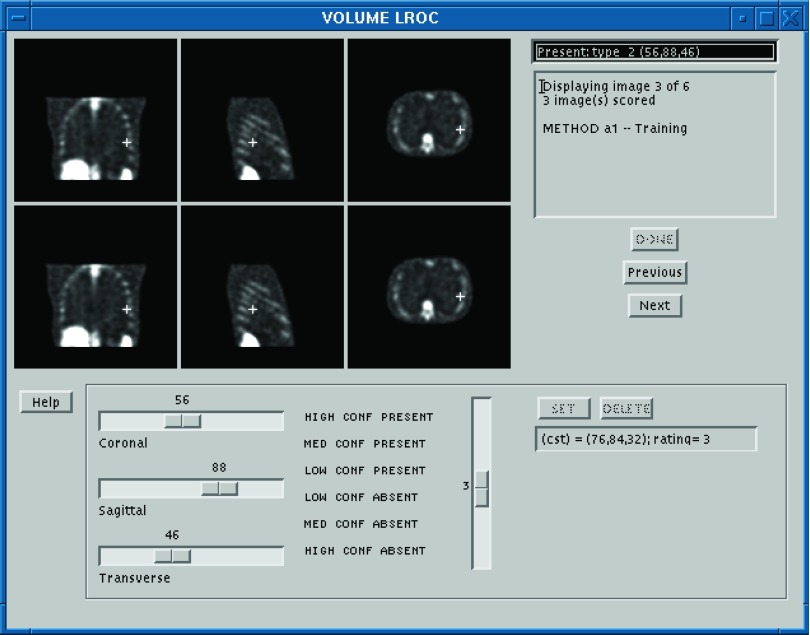
The observers used a graphical interface for viewing and scoring the images (see screenshot in Fig. 5) that was constructed with the IDL programming language (Exelis Visual Information Solutions, Boulder, CO, USA). The interface allowed the observers to selectively scroll through the transverse, coronal, and sagittal views. The mapping between the grayscale values and the luminosity for the display monitor was not calibrated. The observers were not allowed to adjust the display but were permitted to vary both the room lighting and their viewing distance.

Figure 5.

Computer interface for the human-observer LROC study. An observer uses the horizontal sliders to control the displays in the bottom set of windows. A localization is set by clicking somewhere in one of these windows with the mouse cursor. Confidence ratings are input using the vertical slider. During a training session (shown here), feedback in the form of the noise-free image is provided in the upper set of windows.

Rating data in the human study were collected on a six-point ordinal scale. The 150 volumes per strategy were divided into a set of 50 training volumes and a set of 100 test volumes. Both sets contained equal proportions of normal and abnormal cases. As preliminary training, each observer read a set of 20 volumes per strategy. This was followed by five separate sessions of six retraining volumes and 20 test volumes per strategy. Each of these reading sets could contain uneven numbers of normal and abnormal cases. The reading order of the test sets and of the volumes within a given set varied with observer.

An observer's raw data from the five test sets for a given strategy were pooled to form a single dataset for analysis. As mentioned in Sec. 2C, a localization was considered correct if it lay within a sphere of radius r_CL centered on the true location. This radius of correct localization was determined empirically from the human observer data and this single value was applied for all observers (i.e., human and mathematical). The radius is set by examining how the fraction of lesions found for each reconstruction strategy increases with the sphere radius. The objective is to pick a radius within an interval where the fraction is relatively constant across the different strategies. More details on the choice of r_CL are presented in Sec. 3.

An LROC curve and accompanying estimate of A_L were obtained from each observer's data using the Swensson software.²³ The overall performance for a given strategy was calculated as the average A_L over the three observers. We denote this overall mean as ${\overline{A}}_L$. A three-way ANOVA with reconstruction strategy, observer, and lesion contrast as fixed factors was used to test the statistical significance of the results. Recall that our simulation featured only a single NCAT phantom. With this lack of anatomical variation, lesion contrast was deemed the most effective summary of case effect.

For the model observers, confidence ratings and localizations were determined according to Eqs. 3, 4. Correct localizations were assessed with the same r_CL as in the human-observer study. As the Swensson code does not support continuous rating data, Wilcoxon estimates of A_L were used as figures of merit for the model observers. Standard errors for these estimates were calculated using the formula given by Tang and Balakrishnan.²⁴

RESULTS

Radius of correct localization

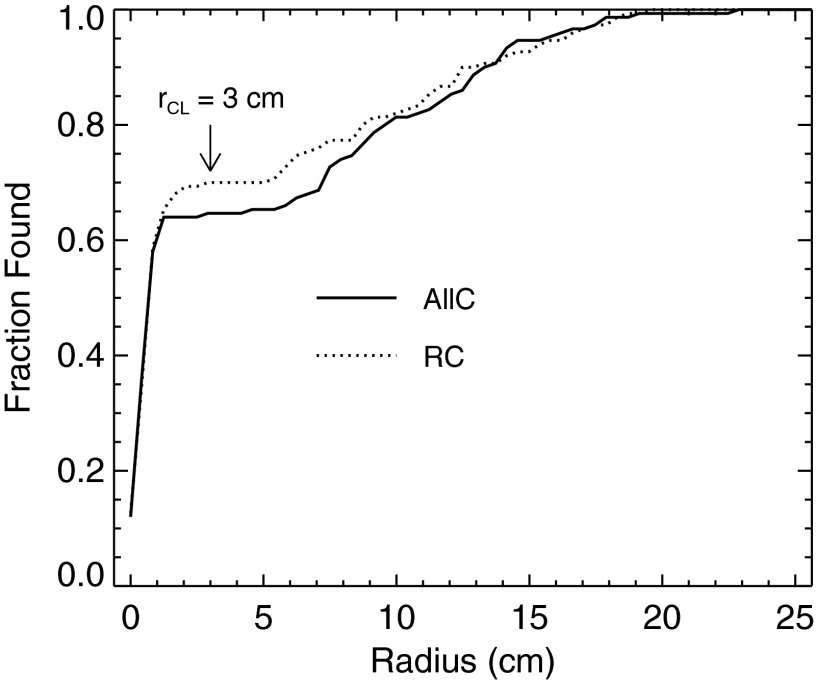
Reliable quantification of the differences in observer performance in our study hinges on the determination of r_CL. Figure 6 plots the fraction of lesions found by the human observers as a function of r_CL. Each line in the graph represents one of the reconstruction strategies. The localization data from the three observers were combined in calculating the fractions. Both strategies show a first plateau in the range of 2–5 cm. On this basis, r_CL was set to 3.0 cm (approximately 7.2 voxels) for analysis of the LROC data.

Figure 6.

Establishing the radius of correct localization r_CL from the human-observer data. The fraction of lesions found for a given strategy is plotted as a function of the proposed radius. The localization data from the three observers were pooled for this analysis, yielding 150 localizations (3 × 50 abnormal volumes) per strategy. The selected value of r_CL is indicated by the arrow.

Human-observer study

The individual and average human-observer LROC performances computed with this localization radius are summarized in Table 3. The uncertainties in ${\overline{A}}_L$ represent the standard deviations in the individual-observer performances. Also included in the table is a subanalysis of performance as a function of the three relative lesion contrasts. This subanalysis allows a qualitative comparison of case effects for the human and model observers, but quantitative assessments with the contrast-specific values of A_L are difficult because of the relatively low number of cases per contrast.

Table 3.

Human-observer performances in the SPN detection-localization study. The uncertainties in A_L for the individual observers are as reported by the Swensson LROC fitting software. Uncertainties for the contrast-specific values of A_L are on the order of 0.12. The uncertainties in ${\overline{A}}_L$ represent the standard deviation in the performances of the individual observers.

	AllC				RC
	Contrast				Contrast
Observer	Low	Mid	High	Overall	Low	Mid	High	Overall
Human 1	0.46	0.57	0.87	0.63 ± 0.07	0.56	0.73	0.89	0.72 ± 0.06
Human 2	0.38	0.66	0.84	0.63 ± 0.07	0.44	0.67	0.86	0.66 ± 0.06
Human 3	0.35	0.62	0.74	0.57 ± 0.07	0.39	0.67	0.88	0.64 ± 0.07
Average	0.40	0.62	0.82	0.61 ± 0.03	0.46	0.69	0.88	0.67 ± 0.04

Nominally, all the observers performed best with the RC reconstruction strategy and the overall RC performance was ${\overline{A}}_L$ = 0.67 compared to 0.61 for the AllC strategy. The variations in performance seen with increased lesion contrast were largely the same for the two strategies. For example, the mean AllC scores with the low and mid-contrast lesions were 0.40 and 0.62, respectively, compared to the RC values of 0.46 and 0.69. However, average performance at a given lesion contrast was in each instance higher with the RC strategy than with the AllC strategy.

The outcome from the multireader-multicase analysis of the human scores is presented in Table 4. The effects of lesion contrast (p = 0.0003) and reconstruction strategy (p = 0.045) were both significant at the α = 0.05 level, while no significant differences were found among the observers or with any of the two-way interactions.

Table 4.

Results from the three-way ANOVA conducted with the human-observer scores. The analysis tested reconstruction strategy, observer, and lesion contrast as factors. The contrast and strategy effects were both significant at the α = 0.05 level.

Factor	df	ss	F	Pr(>F)
Strategy	1	0.019	8.23	0.045
Observer	2	0.015	3.21	0.15
Contrast	2	0.53	113.68	0.0003
Strategy:Observer	2	0.0027	0.58	0.60
Strategy:Contrast	2	0.00017	0.036	0.96
Observer:Contrast	4	0.012	1.24	0.42
Residuals	4	0.0093

Holistic-search statistics

In contrast to the exhaustive search of the scanning observer, a VS observer analyzes only the blob focal points determined by the holistic search. We tested a base search and an extended search with the VS models in this work. Figure 7 illustrates the extent to which the base search reduces the locations of interest in the lungs. With the AllC strategy, there was an average of 498.7 focal points per volume and a standard deviation among the volumes of 28.6 focal points. With the RC strategy, the average was 722.8 points per volume (standard deviation = 36.1 focal points). These statistics exclude incomplete and singleton blobs as defined in Sec. 2D3. It is reasonable that the RC strategy should exhibit the higher number of blobs since the reconstruction process was inconsistent with how the projection data were created.

Figure 7.

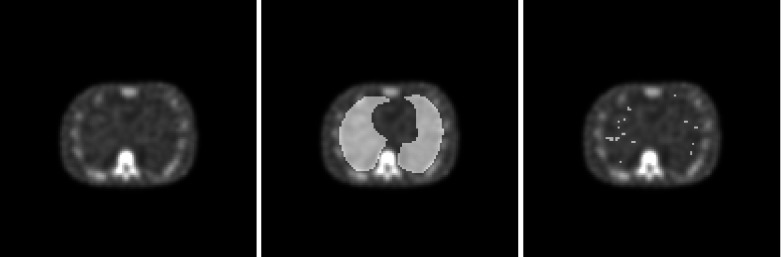
Search regions for the model observers. At left is a sample transverse slices from an AllC-reconstructed volume. The middle image shows the lung regions (Ω for the scanning observer) as an overlay. The right-hand image indicates the lung focal points determined by the base search.

For the extended holistic search, the subsequent blob processing combined blob pairs on the basis of focal-point separation. Singleton blobs were included in this process. The separation threshold r_merge was 3.85 pixels for the AllC volumes and 3.65 pixels for the RC volumes. After the merging operation, the respective AllC and RC averages dropped to 110.0 and 167.7 focal points per volume. The standard deviations after the merge (5.2 focal points for AllC and 6.6 focal points for RC) were also proportionally lower.

The last step in the extended holistic search was enforcement of a lower limit on blob contrast for suspicious candidates. This brought another substantial reduction in the focal-point statistics, with averages of 37.4 and 42.4 focal points, respectively, for the AllC and RC strategies. The standard deviations after this contrast thresholding (25.3 focal points for AllC and 23.3 focal points for RC) are high compared to those of the postmerge statistics, reflecting the situation where volumes with relatively obvious lesions had very few candidate locations (oftentimes only one) while normal cases and more-difficult abnormal cases had upwards of 50 or 60 candidates to analyze.

The performances of the base and extended VS observers are discussed next.

Model-observer studies

The scanning and VS observers were applied for the BKE, BKA, and BAH tasks, which presented different levels of prior knowledge about the anatomical background in the test images. Table 5 gives the overall and contrast-specific performances from these studies. The listed uncertainties are largely comparable with those in Table 3 for the individual human observers, which is to be expected since every observer in this work read the same cases. The results in Table 5 were obtained with the multiview CNPW template described in Sec. 2D1; performances were essentially unchanged with the multiview-multislice template. The variation in holistic search (base versus extended) for the VS observer also produced minimal performance differences. Henceforth, our discussion of the VS observer will reference the extended version alone.

Table 5.

Model-observer performances for the BKE, BKA, and BAH tasks. The data references both the base (b) and the extended (e) VS observers.

		AllC				RC
		Contrast				Contrast
Task	Observer	Low	Mid	High	Overall	Low	Mid	High	Overall
BKE	Scanning	0.92	1.0	1.0	0.97 ± 0.03	0.86	1.0	1.0	0.95 ± 0.04
	VS (b)	0.64	0.68	0.81	0.71 ± 0.08	0.81	0.88	0.88	0.86 ± 0.07
	VS (e)	0.64	0.64	0.81	0.70 ± 0.08	0.81	0.88	0.88	0.86 ± 0.07
BKA	Scanning	0.41	0.92	0.87	0.73 ± 0.08	0.44	0.64	0.86	0.64 ± 0.08
	VS (b)	0.54	0.65	0.81	0.66 ± 0.08	0.54	0.74	0.81	0.69 ± 0.08
	VS (e)	0.54	0.65	0.81	0.66 ± 0.08	0.53	0.74	0.81	0.69 ± 0.08
BAH	Scanning	0.00	0.00	0.06	0.02 ± 0.01	0.00	0.00	0.06	0.02 ± 0.01
	VS (b)	0.41	0.64	0.81	0.62 ± 0.08	0.32	0.54	0.72	0.52 ± 0.08
	VS (e)	0.41	0.64	0.81	0.62 ± 0.08	0.33	0.55	0.66	0.51 ± 0.08

With either model observer, reductions in the accuracy of the background knowledge led to degraded performances with both strategies while tending to have a greater impact on the RC performances. From Table 5, the BKE scores for the VS observer were 0.86 (RC) and 0.70 (AllC), while the corresponding BKA scores were 0.69 and 0.66. The strategy ranking was reversed for the BAH task (0.62 for the AllC strategy versus 0.51 for the RC strategy).

In favoring the RC strategy for the BKE and BKA tasks, the VS observer demonstrated considerably less sensitivity to reductions in background knowledge compared to the scanning observer. With the latter observer, the BKE and BKA scores for the AllC strategy were 0.97 and 0.73, respectively. With the RC strategy, the scores were 0.95 (BKE) and 0.64 (BKA). The assumption of an homogeneous background essentially incapacitated the scanning observer.

The results in Table 5 also indicate that the model observers had generally realistic responses to changes in lesion contrast, in that detection of the lower-contrast lesions was most affected by deviations from the BKE task. The results from the VS observer for the AllC strategy are particularly interesting in this regard, as the downward trend in overall performance (0.70 for BKE, 0.66 for BKA, and 0.62 for BAH) is attributable solely to reduced detection of the low-contrast set of lesions. This was not the case with the RC strategy or for either strategy with the scanning observer, for which the BKA and BAH tasks caused decreased detectability for all three lesion-contrast groups.

DISCUSSION

Our general interest is in developing model observers that can accurately predict human performance in clinically realistic tasks. Besides serving to define image quality for these tasks, such models could be used to collect data in preparation for human-observer studies. One limitation of the current VS models is the need for prior knowledge about the image backgrounds, which constrains studies to the use of image simulations.

The first-time use of a human-model observer for some imaging application generally calls for validation studies (such as the present work) to ensure that human performance is being tracked. How much validation is required is often an open question. One of our motivations for investigating the VS framework is the idea that more faithful rendering of the human search-and-detection process could lead to more reliable model observers with less need for validation. If this is borne out, then the VS models might eventually serve as stand-ins for human observers in the validation of simpler model-observer tasks (such as SKE studies) that one may wish to use in the initial stages of system development.

Task-based characteristics of the model observers

As a strict indicator of model validation, one might consider the case-by-case concurrence in the raw data from the model and human observers. For the present, however, we consider just the quantitative agreement between observer scores. On this basis, the model-observer results from Table 5 indicate that the BKA task came closest to mimicking the detection task faced by the human observers. However, this task was implemented using an arbitrary definition of $\widehat{\mathbf{b}}$, and so provides only a snapshot of the capabilities of the VS and scanning observers. Although less predictive of the human study, the BKE and BAH tasks are important for more fully characterizing the model observers.

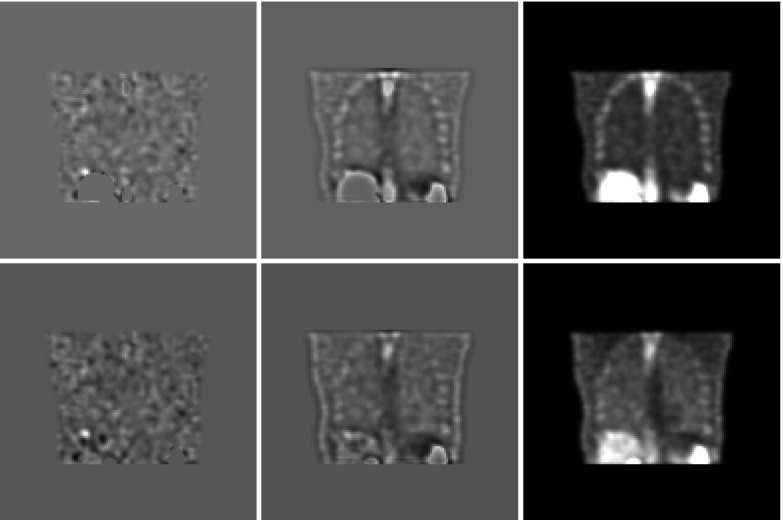
With the BKE task, the scanning observer achieved the highest scores of any observers in our study. As the lung backgrounds have relatively low levels of quantum noise, the mean background subtraction in Eq. 5 rendered most of the lesions easily detectable (see Fig. 8) given that the scanning observer looked everywhere in the lungs. Thus, one of the important strengths of LROC methodology—the ability to use realistic lesion contrasts, was negated with this combination of task and observer. In general, one expects the scanning observer to prefer the less-noisy AllC volumes, but the strategies were essentially indistinguishable for this trivial detection task.

Figure 8.

Comparison of the image processing performed by the model observers for the BKE, BKA, and BAH tasks. Results of the background subtraction carried out for a single test case are shown for the AllC strategy (top row) and the RC strategy (bottom row). At left, subtraction of b reveals a lesion in close proximity to the liver. Lesion detection is less certain with subtraction of the approximate reference image $\widehat{\mathbf{b}}$ (middle column). For the BAH task, there is no background subtraction (right-hand column).

The exhaustive search by the scanning observer also led to the catastrophic BAH results. The moderate postsmoothing that was part of both reconstruction strategies caused activity to blur into the lungs from the surrounding organs. In most cases, human observers can compensate for this, but the spill-in created chronic false positive locations that were identified by the scanning observer in multiple test images. The VS observer is less susceptible to spill-in effects because it rejects blobs whose focal points are outside the lungs.

In the BAH task, the VS observer performed better with the AllC strategy than with the RC strategy, but more accurate background knowledge reverses the ranking. In fact, the greatest difference in A_L between the two strategies was obtained by the VS observer in the BKE setting. Two main factors influenced this result. Recall that a lesion could only be detected if it was first identified as a focal point by the holistic search. The higher average lesion contrast in the RC volumes (48.8 ± 15.9 versus 45.3 ± 12.7 for AllC, expressed in grayscale levels) aided in this identification. The other factor was the lack of an effective penalty for over-identification of nonlesion focal points. As Fig. 8 makes clear, any lesion identified as a focal point in the BKE task had a high likelihood of being detected in the subsequent analysis stage of the VS observer.

Assessing observer agreement

The reader may refer back to Tables 3, 5 to compare the human-observer results with those from the scanning and VS observers for the BKA task. With this task, the effects of background variation on the model observers were instilled by moderately corrupting the prior knowledge of b to produce an approximation $\widehat{\mathbf{b}}$. The VS observer augments these effects with posterior information gleaned from the test image under consideration, resulting in performances that are comparable with those of the individual human observers. Recall that the strategy effect was significant for the human-observer data only by virtue of the MRMC analysis; as applied, each model observer can offer no better statistical power than that from an individual human observer (Additional power may be gained by reversing the roles of the training and study images, which is not recommended for human observers.)

Putting aside the question of statistical power, the difference between the AllC and RC BKA performances given in Table 5 for each model observer can be understood in reference to our discussion of the BKE results from Sec. 4A. Relative to the BKE task, the BKA task offered ample complexity for revealing the scanning-model preference for the less-noisy AllC images while also penalizing more effectively the tendency of the VS observer to over-identify nonlesion candidates in the RC volumes. From this standpoint, the predictive abilities of the two model observers are more distinct than suggested by the uncertainties in Table 5.

Observer uncertainty

Treating the BKA paradigm as a middle ground between the BKE and BAH task extremes helps to elucidate model-observer behavior, but the arbitrary definition of $\widehat{\mathbf{b}}$ constrains any quantitative comparison of the predictive abilities of our models. The comparative stability of the VS model under different levels of background knowledge is an important finding of this work, but there is the possibility that another definition of $\widehat{\mathbf{b}}$ could improve the concordance between the scanning and human observers.

The BKA and BAH tasks present different levels of observer uncertainty. As described in Sec. 2D2, this uncertainty takes the form of a deterministic quantity added to the perception vector for the BKE task. One may be tempted to include a random term as a form of observer internal noise (such as the mechanisms applied in Refs. ⁴ or ²⁵) in order to improve the agreement between the human and scanning observers. With simple BKE tasks, it can be difficult to devise a stable internal noise model for the scanning observer that will affect both the confidence rating and localization data.⁴ More generally, however, the BKE assumption represents modeling error in our studies that may not be reliably compensated for by internal noise.

Interpreting the human-observer results

The model-observer studies with the different tasks also lend insight into the cognitive abilities of our human observers and the generalizability of their study results. It may seem counterintuitive that adding AC and SC to the image reconstruction process should degrade detection performance compared to having RC alone. The RC images offer relatively higher lesion contrast (Sec. 4A), but this will be advantageous only if an observer can adequately gauge the normal levels of Tc-99m uptake in the areas of f around the suspicious lesion locations. It is evident from our results that the humans consistently extracted useful background information from the test images, although not to the optimal extent represented by the BKE task.

The humans’ abilities in this regard may have been unduly enhanced by having only one phantom in our studies. A greater variety of phantoms, perhaps with inhomogeneous uptake in the different organs, may be necessary to impose realistic case uncertainties in the studies. As demonstrated with the VS observer, RC performance is more sensitive than AllC performance to changes in the quality of the observer's background knowledge.

Study limitations and future work

Our study has demonstrated the potential of the VS framework for modeling human observers with SPECT images, but there are several limitations to consider. One limitation with the study design was that the model observers knew the exact extent of the lung regions while the human observers did not. The model-observer scores thus represent estimates of the performance that would be achieved with adjunct anatomical information. This was primarily an issue for the AllC strategy, as the appearance of the lung outlines in the RC volumes (see Fig. 2) helped establish appropriate search regions. With each strategy, there were 150 localizations involving lesion-present images (three human observers × 50 abnormal test images per strategy). For the AllC cases, 16.7% of these localizations were outside of the lungs compared to 2% with the RC cases. However, these mislocalizations correlated with case difficulty to some degree, making it difficult to isolate the search-region bias in the AllC performances.

The minimal variability in the imaging simulation is a more significant study limitation, not only for comparing the reconstruction strategies, but also for assessing the observer models. SPECT projections were acquired from a single phantom at one noise level and the reconstructed volumes were generated with a preoptimized set of parameters. A more thorough assessment of our observer models will require observer studies that present wider variations in both patient cases and technical image quality. Key to these studies will be understanding how various parts of our models (such as the definition of $\widehat{\mathbf{b}}$ and the holistic-search process) must adapt to these variations.

Considering alternative methods of identifying blob candidates for the VS observers is also important, both with an eye toward characterizing the essential ingredients of a holistic-search model and for improving computational efficiency. With the gradient-ascent clustering method, the VS observers took approximately 60 min to read 100 test images. The scanning observer required 7 min.

One must expect the accuracy of the VS model to vary depending on the details of the clustering method, but this is likely not a severe restriction of the VS framework. Some analysis of the robustness of the gradient-ascent method was included in this study. The basic VS model applied a relatively bare-bones search process that largely ignored blob size and contrast in tallying high numbers of blob candidates. The extended model greatly reduced the candidate totals through merging and contrast selection, but this had virtually no impact on observer performance. We are in the process of testing the validity of other clustering algorithms.

CONCLUSIONS

Differences between the scanning and VS observers are attributable to the latter's ability to gather focal-point information in images. As demonstrated by the results of this LROC study with image volumes, the VS framework has the potential to improve the clinical realism of model-observer studies while at the same time enhancing the ability of existing model observers to predict human-observer performance.