Variable selection in monotone single-index models via the adaptive LASSO

Abstract

We consider the problem of variable selection for monotone single-index models. A single-index model assumes that the expectation of the outcome is an unknown function of a linear combination of covariates. Assuming monotonicity of the unknown function is often reasonable, and allows for more straightforward inference. We present an adaptive LASSO penalized least squares approach to estimating the index parameter and the unknown function in these models for continuous outcome. Monotone function estimates are achieved using the pooled adjacent violators algorithm, followed by kernel regression. In the iterative estimation process, a linear approximation to the unknown function is used, therefore reducing the situation to that of linear regression, and allowing for the use of standard LASSO algorithms, such as coordinate descent. Results of a simulation study indicate that the proposed methods perform well under a variety of circumstances, and that an assumption of monotonicity, when appropriate, noticeably improves performance. The proposed methods are applied to data from a randomized clinical trial for the treatment of a critical illness in the intensive care unit.

1. Introduction

Linear regression is a simple and commonly-used technique for assessing relationships of the form y = β^T x + ε between an outcome of interest, y, and a set of covariates, x₁, …, x_p; however, in many cases, a more general model may be desirable. As noted by [1], one particularly useful and more general variation of the linear regression formulation is the single-index model

$$y_i=\eta ({\mathit{\beta }}^T{\mathit{x}}_i)+{\epsilon }_i,$$ (1)

where x_i’s are subject-specific covariate vectors, β = (β₁, …, β_p)^T, y_i ∈ ℝ, η is an unknown function, ε₁, …, ε_n are iid errors with mean zero and variance σ², and ε_i’s and x_i’s are independent. To ensure identifiability, no intercept is included, and β₁ is assumed to be equal to 1. These models are able to capture important features in high-dimensional data, while avoiding the difficulties associated with high-dimensionality, as dimensionality is reduced from many covariates to a univariate index [2]. Single-index models have applications to a number of fields, including discrete choice analysis in econometrics and dose-response models in biometrics [1].

There is a rich literature on estimation of β and η, including [1], [2], [3], [4], [5], [6], among many others. Additionally, variable selection for single-index models was considered by [7], who proposed the separated cross-validation method, and [8], who applied the smoothly clipped absolute deviation (SCAD) approach to partially linear single-index models. However, little consideration has been given to such problems for monotone single-index models, where η is required to be non-decreasing (or non-increasing). In the case of linear models, a great many authors, including [9], [10], [11] and [12] have considered variable selection via penalized least squares, which allows for simultaneous selection of variables and estimation of regression parameters. Several penalty functions, including the SCAD [10], the adaptive LASSO [11] and the adaptive elastic-net [12], have been shown to possess favorable theoretical properties, including the oracle properties; that is, consistency of selection and asymptotic normality, with the asymptotic covariance matrix being the same as that which would be obtained if the true underlying model were known. Hence, for large samples, oracle procedures perform as well as if the true underlying model were known in advance. Furthermore, [8] established the oracle properties for the SCAD for partially linear single-index models. Given the desirable properties of the SCAD, adaptive LASSO and adaptive elastic-net approaches, it is natural to consider the extension of these methods to monotone single-index models. Unlike the adaptive LASSO and adaptive elastic-net, which present a convex optimization problem, the SCAD optimization problem is non-convex, and thus more computationally demanding [13]. In addition, the adaptive elastic-net and SCAD methods require the selection of two tuning parameters, whereas the adaptive LASSO requires the selection of a single tuning parameter. Therefore, for convenience, computational efficiency, and because covariates in our example data are not highly correlated (a condition under which the adaptive elastic-net is especially good), we consider adaptive LASSO penalized least squares estimation of β in monotone single-index models.

The assumption of monotonicity and the desire to select a subset of the covariates are motivated in part by the randomized clinical trial data considered in [14]. A monotonicity assumption is often reasonable, and such an assumption may improve prediction and reduction in model complexity, while also allowing for more straightforward inference. Foster et al. [14] consider methods for subgroup identification in randomized clinical trial data. In such cases, should a subgroup be identified, it is desirable that this subgroup be easily described, and depend on only a small number of covariates. Application of the methods proposed in this paper result in estimates η̂ and β̂, such that ŷ_i = η̂(β̂^T x_i), where η̂ is monotone and β̂ generally includes a number of zero values. Using this model, one can classify individuals with ŷ’s beyond some predefined threshold, c, as being in the subgroup. Then, because of the monotonicity of η̂, the predefined threshold can be converted into an equivalent threshold, c′, on β̂^T x, and the impact of the chosen covariates on subgroup membership can be easily described. Without the assumption of monotonicity, the subgroup may be a collection of several disjoint subregions of the covariate space, making each covariate’s impact on subgroup membership more difficult to ascertain.

The remaining sections of this article are as follows. In Section 2, we consider penalized least-squares estimation for monotone single-index models, briefly discuss asymptotics, and discuss a method to obtain standard error estimates for β. In Section 3, we present the results of a simulation study implemented to assess the performance of the adaptive LASSO penalized single-index models. In Section 4, we briefly discuss the application of this method to the randomized clinical trial data, and in Section 5, we give concluding remarks.

2. Estimation for monotone single index models

Our estimation procedure iterates between estimation of β and η until convergence. Given some η, the penalized least-squares estimator of β can be found by minimizing

$$Q(\mathit{\beta })=\sum _{i=1}^n{\left(y_i-\eta ({\mathit{\beta }}^T{\mathit{x}}_i)\right)}^2+{\lambda }_n\sum _{j=2}^p{w}_j\mid {\beta }_j\mid ,$$ (2)

where w_j, j = 2, …, p are known weights and covariates x_i are standardized to have mean zero and variance 1. Due to the identifiability constraint specified in model (1), β₁ is not penalized. Following [11], we choose w_j = |β̂_init;j|^−γ for γ > 0, where β̂_init is a n^α-consistent estimator of β, where $0<\alpha <\frac{1}{2}$. We use linear ordinary least squares (OLS) estimates for β̂_init, as under the assumptions of Theorem 2.1 in [15], these are shown to be $\sqrt{n}$-consistent up to a multiplicative scalar. Once obtained, β̂_init is rescaled by β̂_1,init. Alternatively, weights could be defined using the unpenalized single-index model estimates of β.

For a given β, without considering the monotonicity constraint, η can be estimated at some point t using the Nadaraya-Watson kernel-weighted average:

$$\widehat{\eta }(t;\mathit{\beta },\mathit{y},\mathit{X},h)=\frac{{\sum }_j{y}_{j}K\left(\frac{t-{\mathit{\beta }}^T{\mathit{x}}_j}{h}\right)}{{\sum }_{j}K\left(\frac{t-{\mathit{\beta }}^T{\mathit{x}}_j}{h}\right)},$$ (3)

where X is the covariate matrix, K is a fixed kernel function and h is a bandwidth. Note that, when β is known, η̂ is determined by h, so a value of h must be chosen. We consider kernel functions which are symmetric probability densities. For numerical stability, we hold (3) fixed for all t outside the range of the β^T x’s. That is, η̂(t) = η̂(min_i(β^T x_i)) if t < min_i(β^T x_i) and η̂(max_i(β^T x_i)) if t > max_i(β^T x_i).

Combining (2) and (3), the adaptive LASSO estimator for β is obtained by minimizing

$$\widehat{Q}(\mathit{\beta },h)=\sum _i\text{'}{\left(y_i-\widehat{\eta }({\mathit{\beta }}^T{\mathit{x}}_i;\mathit{\beta },\mathit{y},\mathit{X},h)\right)}^2+{\lambda }_n\sum _{j=2}^p{w}_j\mid {\beta }_j\mid$$ (4)

with respect to β, where ${\sum }_i^{\prime }$ denotes summation over i such that the denominator in the kernel estimator is not too close to zero. Details can be found in [1]. With the inclusion of the penalty term in (4), β̂ becomes a function of λ_n, so in addition to h, a value of λ_n must be chosen if β̂ is to be obtained. Throughout this paper, we refer to the method of estimating β and η without a monotonicity constraint, using objective function (4), as the unconstrained approach.

2.1. A smooth monotone function estimate for η with fixed β

There are a variety of ways to obtain smooth monotone regression function estimates, including quadratic B-splines [16], I-splines [17], empirical distribution tilting [18], the scatterplot smoothing approach of [19], and the kernel-based approach of [20] and [21]. We consider the kernel-based method of the latter two papers, which we briefly describe below.

Assume β is known. The proposed monotone estimator η̂_m requires two steps:

Isotonization

This step involves the application of the pooled adjacent violator algorithm (PAVA) [22]. Using (β^T x_i, y_i) ordered by increasing β^T x_i as data, PAVA produces monotone estimates m̂₁, …, m̂_n, which are averages of y_j’s near i (unless y’s are already monotone, in which case m̂_i = y_i), and which are not necessarily smooth [19].

Smoothing

Apply the kernel estimator (3) with y_i replaced by m̂_i for all i to estimate η. That is, η̂_m(t) = η̂(t; β, m̂, X, h).

Since m̂₁, …, m̂_n are monotone, the resulting function estimate is monotone in t. It is worth noting that this may not necessarily be the case for other smoothing methods, such as local linear regression.

As previously mentioned, a bandwidth is needed to estimate η, and can be found using cross-validation; however, our algorithm requires estimation of both η and its derivative η′, so care must be taken. In particular, to ensure good algorithmic convergence, it is crucial that η̂′ be smooth, but to obtain a smooth estimate of η′, it is often necessary to oversmooth η. Thus, we restrict the range of potential bandwidths in our cross-validation. Specifically, h is restricted to be between 0.1^*sd(Xβ) and sd(Xβ), as values in this range were found to perform well in our simulations.

2.2. Estimation for β with fixed η

The shooting algorithm proposed by [23] has been shown to perform well in solving LASSO penalized least-squares problems for linear models [24]. Therefore, we consider the application of this algorithm to LASSO problems for the single-index model. One way to achieve this is to employ a linear approximation via Taylor series expansion of η(β^T x_i) about ${\mathit{\beta }}_0^T{\mathit{x}}_i$, where β₀ is known. We define the linear approximation as follows:

$$\eta \left({\mathit{\beta }}^T{\mathit{x}}_i\right)\approx \eta \left({\mathit{\beta }}_0^T{\mathit{x}}_i\right)+{\eta }^{\prime }\left({\mathit{\beta }}_0^T{\mathit{x}}_i\right)\left[{\mathit{\beta }}^T{\mathit{x}}_i-{\mathit{\beta }}_0^T{\mathit{x}}_i\right].$$ (5)

Let

$$y_i^{\ast }=y_i-\eta \left({\mathit{\beta }}_0^T{\mathit{x}}_i\right)+{\eta }^{\prime }\left({\mathit{\beta }}_0^T{\mathit{x}}_i\right){\mathit{\beta }}_0^T{\mathit{x}}_i$$

and

$${\mathit{x}}_i^{\ast }={\eta }^{\prime }\left({\mathit{\beta }}_0^T{\mathit{x}}_i\right){\mathit{x}}_i.$$

Then we have

$$y_i-\eta \left({\mathit{\beta }}^T{\mathit{x}}_i\right)\approx y_i-\eta \left({\mathit{\beta }}_0^T{\mathit{x}}_i\right)-{\eta }^{\prime }\left({\mathit{\beta }}_0^T{\mathit{x}}_i\right)\left[{\mathit{\beta }}^T{\mathit{x}}_i-{\mathit{\beta }}_0^T{\mathit{x}}_i\right]=y_i^{\ast }-{\mathit{\beta }}^T{\mathit{x}}_i^{\ast },$$

and (4) can be approximated by

$${\widehat{Q}}_{\mathit{lin}}(\beta )=\sum _i\text{'}{\left(y_i^{\ast }-{\mathit{\beta }}^T{\mathit{x}}_i^{\ast }\right)}^2+{\lambda }_n\sum _{j=2}^p{w}_j\mid {\beta }_j\mid ,$$ (6)

which is a LASSO penalized least-squares problem for the linear model, and can thus be solved using the shooting algorithm.

Note that (5) involves an estimate of η′. This estimate is obtained as follows. Sort the observations by increasing ${\mathit{\beta }}_0^T{\mathit{x}}_i$, and define new data {(x̃_i, ỹ_i) :, i = 1, …, n − 1} where ${\stackrel{\sim }{y}}_i=\frac{\eta ({\mathit{\beta }}_0^T{\mathit{x}}_{i+1})-\eta ({\mathit{\beta }}_0^T{\mathit{x}}_i)}{{\mathit{\beta }}_0^T{\mathit{x}}_{i+1}-{\mathit{\beta }}_0^T{\mathit{x}}_i}$, and ${\stackrel{\sim }{\mathit{x}}}_i={\mathit{x}}_i+\frac{{\mathit{x}}_{i+1}-{\mathit{x}}_i}{2}$. This new data should “look like” data coming from the model ỹ_i = η′(β^T x_i) + ε̃_i, so η′(t) can be estimated using (3), but with {(x_i, y_i) : i = 1, …, n} replaced by {(x̃_i, ỹ_i) : i = 1, …, n − 1}, i.e. η̂′(t) = η̂(t; β, ỹ, X̃, h̃), where h̃ is a new bandwidth for the derivative estimate. To select h̃, cross-validation can again be used.

2.3. Algorithm

The algorithm to obtain final estimates of η and β iterates between the steps in Sections 2.1 and 2.2 until convergence. After k iterations, let β̂^(k), ${\widehat{\eta }}_m^{(k)}$ and ${\widehat{m}}_1^{(k)},\dots ,{\widehat{m}}_n^{(k)}$ denote the current estimates of β and η and the current PAVA estimates respectively. For a given λ_n, the “final” estimates of β and η are obtained as follows:

1. Using data {(β̂^(k)T x_i, y_i) : i = 1, …, n}, apply PAVA to obtain new monotone data $\left\{({\widehat{\mathit{\beta }}}^{(k)T}{\mathit{x}}_i,{\widehat{m}}_i^{(k+1)}):i=1,\dots ,n\right\}$, and define the monotone function estimate ${\widehat{\eta }}_m^{(k+1)}(t)$ using (3). Select h via a grid search on values {0.1^*sd(Xβ̂^(k)), 0.2^*sd(Xβ̂^(k)), …, sd(Xβ̂^(k))} using leave-one-out cross-validation. For computational convenience, fix h after a small number, say a, of iterations (i.e. when k = a).

2. Using data $\left\{({\widehat{\mathit{\beta }}}^{(k)T}{\mathit{x}}_i,{\widehat{m}}_i^{(k+1)}):i=1,\dots ,n\right\}$, obtain the derivative data $\left\{({\widehat{\mathit{\beta }}}^{(k)T}{\stackrel{\sim }{\mathit{x}}}_i,{\stackrel{\sim }{y}}_i^{(k+1)}):i=1,\dots ,n-1\right\}$, and define the derivative η̂^(k+1)′(t) using (3). Select h̃ from the grid {0.1^*sd(Xβ̂^(k)), 0.2^*sd(Xβ̂^(k)), …, sd(Xβ̂^(k))} using leave-one-out cross-validation. As with h, h̃ is fixed after a iterations.

3. Let the general notation z^(kl) indicate the l^th update to z^(k). Using approximation (5), obtain data $\left\{({\mathit{x}}_i^{\ast (k^1)},y_i^{\ast (k^1)}):i=1,\dots ,n\right\}$, and minimize ${\widehat{Q}}_{\mathit{lin}}^{(k^1)}(\mathit{\beta })$ from (6), giving β̂^(k1). Repeat this step m − 1 more times, for a total of m iterations, each time updating the linear approximation (5), so that β̂^(km) ≡ β̂^(k+1) comes from data $\left\{({\mathit{x}}_i^{\ast (k^m)},y_i^{\ast (k^m)}):i=1,\dots n\right\}\equiv \left\{({\mathit{x}}_i^{\ast (k+1)},y_i^{\ast (k+1)}):i=1,\dots ,n\right\}$.

4. Cycle through steps 1–3 until ||β̂^(k+1) − β̂^(k)|| becomes smaller than a prespecified precision level. The final estimate of η is then obtained by implementing step 1 once more using the converged β estimate.

The identifiability constraint is imposed by rescaling β̂^(k) by ${\widehat{\beta }}_1^{(k)}$ each time Step 3 is completed, so it is desirable that β₁ be nonzero to avoid potential numerical problems. To help ensure this in practice, one could first fit a linear model, and choose the largest (or most significant) β_j estimate to be that which is subsequently unpenalized and forced to be 1. If in the final model another coefficient is larger, then one could re-run the analysis with that coefficient being the one which is upenalized and forced to be 1. As suggested by one of the reviewers, one could also consider a sensitivity analysis in which multiple models were fit, each time forcing a different coefficient to be 1.

A value of λ_n must be chosen before β can be estimated. Suppose that β̂(λ_n) and η̂_m(t; λ_n) are the estimates of β and η(t), given tuning parameter λ_n. To choose a value of λ_n, we use the Bayes information criterion (BIC) measure of [8]. Specifically, we choose the value of λ_n that minimizes:

$$\mathit{BIC}({\lambda }_n)=log\left\{\frac{1}{n}\underset{i}{{\sum }^{\prime }}{\left(y_i-{\widehat{\eta }}_m(\widehat{\mathit{\beta }}{({\lambda }_n)}^T{\mathit{x}}_i;{\lambda }_n)\right)}^2\right\}+\frac{log(n)}{n}{DF}_{{\lambda }_n},$$

where DF_λn is one less than the number of non-zero values in β̂(λ_n), since β̂₁ is forced to be nonzero. To find the optimal λ_n, a grid search is employed.

In the remaining sections, the monotone-constrained method described above is referred to as the constrained approach.

2.4. Asymptotics

Using the results of [1] and arguments similar to [11], it is possible to establish the oracle properties for the unconstrained approach. We provide an outline of such an argument here.

Suppose the regularity conditions of [1] hold. Then, by their main theorem, we can rewrite the sum of squares portion of (4) as a sum of three terms, S̃, T, and R, where S̃ and T depend only on β and h respectively, and the remainder term R is negligible. Thus, as S̃ is the only term which depends on β, (4) can be reduced to $\stackrel{\sim }{S}(\mathit{\beta })+{\lambda }_n{\sum }_{j=2}^p{w}_j\mid {\beta }_j\mid =n{\left\{{\mathit{W}}_0^{1/2}(\mathit{\beta }-{\mathit{\beta }}_0)-\frac{\sigma }{\sqrt{n}}\mathit{Z}\right\}}^T\left\{{\mathit{W}}_0^{1/2}(\mathit{\beta }-{\mathit{\beta }}_0)-\frac{\sigma }{\sqrt{n}}\mathit{Z}\right\}+{\lambda }_n{\sum }_{j=2}^p{w}_j\mid {\beta }_j\mid$, where W₀ is a p × p matrix, β₀ is the true index parameter, and Z is an asymptotically normal N(0, I) p-vector. Now suppose that $\frac{{\lambda }_n}{\sqrt{n}}\to 0$, and λ_nn^{(γ − 1)/2} → ∞, where $\gamma \in (0,\frac{3}{5}]$, and let $\mathit{\beta }={\mathit{\beta }}_0+\frac{\mathit{u}}{\sqrt{n}}$, where ||u|| ≤ C. From here, following arguments very similar to [11], the oracle properties can be established.

It seems that the oracle properties will also hold for β estimates from the constrained approach under certain conditions. Specifically, under the conditions of Theorem 2 in [21], we have η̂_m(t) = η̂(t) + O_p(n^−8/15), for all t, where η̂_m is our monotone estimator of η and η̂ is the Nadaraya-Watson kernel-weighted average. Thus, it is possible to reduce the penalized sum of squares for the constrained approach to (4) plus a negligible remainder term. The oracle properties for the constrained approach would hold by the same reasoning used for the unconstrained approach.

In practice it is difficult to verify that the conditions needed for the theory hold. Because a data-driven method (BIC) is used to select the tuning parameter, λ_n, we cannot guarantee the required rate of convergence. Thus, the assumptions $\frac{{\lambda }_n}{\sqrt{n}}\to 0$ and λ_nn^{(γ − 1)/2} → ∞ may not hold.

2.5. Bootstrap standard errors

Standard errors for our β estimates can be obtained via the bootstrap. In particular, for a given data set, we employ the adaptive LASSO-based residual bootstrap (ARB) approach discussed by [25] to obtain many, say M, bootstrap data sets. A penalized single-index model is then fit on each of these bootstrap data sets, giving M sets of estimates. The estimated standard errors are then obtained by taking the standard deviations of the M estimates for each β_j.

For a given data set, we obtain a residual bootstrap data set as follows. Suppose β̂ and η̂ are final estimates of β and η for a particular data set. Let e_i = y_i − η̂(β̂^T x_i), i = 1, …, n be the residuals for this data set. A residual bootstrap data set is then obtained by replacing y_i with $\widehat{\eta }({\widehat{\mathit{\beta }}}^T{\mathit{x}}_{\mathit{i}})+e_i^{\ast }$, i = 1, …, n, where { $e_1^{\ast },\dots ,e_n^{\ast }$} is a random sample (drawn with replacement) from the centered residuals, $e_i-\frac{1}{n}{\sum }_{i=1}^n{e}_i$, i = 1, …, n. The covariate matrix remains the same across the bootstrap data sets.

Based on additional simulations (results not given), creating residual bootstrap data sets using permuted (sampled without replacement) residuals gives nearly identical results to those shown in Table 2. As noted by one reviewer, in practice, the interpretation for the standard errors can be awkward, particulary in cases where a number of covariates are highly correlated. In such cases, one might expect the distribution of these estimates to be a mixture of a continuous distribution and a point mass at zero. Thus, the estimates are a product of both selection and estimation, which can make interpretation difficult. This may be due to the known shortcomings of the adaptive LASSO for highly correlated predictors. If one believes that a number of covariates may be highly correlated, an alternative approach, such as the adaptive elastic-net, may perform better, and may lead to bootstrap standard error estimates based on a smaller number of zeros.

Table 2.

Performance of standard error estimates

Method	β̂2		β̂7
	SD	SE (SEsd)	SD	SE (SEsd)
Cons.:	0.25	0.20 (0.08)	0.20	0.18 (0.06)
Uncons.:	0.28	0.34 (0.41)	0.28	0.27 (0.26)

Note: required 102 simulated data sets due to numerical problems.

We generally suggest that one reselect λ_n with each bootstrap data set; however, our simulations (results not shown) suggest that holding λ_n fixed across bootstrap data sets gives standard error estimates which are nearly identical to those found by reselecting λ_n for each bootstrap data set. Thus, it may be reasonable to consider fixed-λ_n bootstrap standard errors if reselecting λ_n for each bootstrap data set is too computationally burdensome.

3. Simulations

A simulation study was performed using R software to evaluate the performance of the proposed methods. To comply with the conditions in Section 2.4, a value of $\frac{3}{5}$ was chosen for γ for adaptive LASSO. Additionally, for each example, a large test set (n = 10, 000) was generated, and final β estimates from each of the simulated data sets were used to calculate the mean squared error (MSE) for this large test set. To evaluate the performance of all methods considered, we recorded the number of correct and incorrect zero values in β̂, as well as the total proportion of β̂_j’s correctly estimated as zero or non-zero for each data set. The average of these proportions across all simulated data sets is referred to in Table 1 as the relative frequency correct. We also computed the false discovery rate (FDR), which is the percentage of non-zero β̂ values which should have been zero. For each data set, the optimal tuning parameter value λ_n was chosen from the grid {0, 0.01, …, 0.25} using BIC.

Table 1.

Simulation results: variable selection performance

Method	Rel. Freq Correct	Avg. No. β̂ = 0*		FDR	Mean Test MSE (×100)
		Correct	Incorrect
Case (i)1
Cons.:	0.92	6.22	0.00	0.21	4.93
Uncons.:	0.85	5.47	0.01	0.34	5.63
Cons. oracle:	1.00	7.00	0.00	0.00	4.74
Uncons. oracle:	1.00	7.00	0.00	0.00	4.96
Case (ii)2**
Cons.:	0.89	6.09	0.17	0.24	10.87
Uncons.:	0.75	4.68	0.16	0.45	12.84
Cons. oracle:	1.00	7.00	0.00	0.00	10.07
Uncons. oracle:	1.00	7.00	0.00	0.00	10.56
Case (iii)3
Cons.:	0.86	6.25	0.65	0.24	4.64
Uncons.:	0.73	4.83	0.56	0.47	5.51
Cons. oracle:	1.00	7.00	0.00	0.00	4.45
Uncons. oracle:	1.00	7.00	0.00	0.00	4.65
Case (iv)4
Cons.:	0.88	6.15	0.32	0.24	4.79
Uncons.:	0.82	5.45	0.27	0.36	5.38
Cons. oracle:	1.00	7.00	0.00	0.00	4.51
Uncons. oracle:	1.00	7.00	0.00	0.00	4.78
Case (v)5
Cons.:	0.94	53.70	0.10	0.53	5.64
Uncons.:	0.87	49.36	0.13	0.74	7.16
Cons. oracle:	1.00	57.00	0.00	0.00	4.74
Uncons. oracle:	1.00	57.00	0.00	0.00	4.96

Note: “oracle” indicates true zero β values known. η is estimated in all methods.

^*Average number of variables dropped in final model.

¹β = (1, 0.8, 0, 0, 0, 0, −0.7, 0, 0, 0)^T, Corr(x_ij, x_ik) = 0, j ≠ k, σ = 0.20.

²Same as Case (i), but σ = 0.3.

³Same as Case (i), but β₇ = −0.2.

⁴Same as Case (i), but Corr(x_ij, x_ik) = 0.5, j ≠ k.

⁵Same as Case (i), but β = (1, 0.8, 0, 0, 0, 0, −0.7, 0, 0, 0, 0_1×50)^T.

^**Required 101 simulated data sets due to numerical problems.

3.1. Examples

For all simulations, 100 data sets of size 100 were generated from the model

$$y_i={({\mathit{\beta }}^T{\mathit{x}}_i)}^3+{\epsilon }_i,$$

where x_i’s were $\mathit{Unif}[-\frac{1}{2},\frac{1}{2}]$, and error terms were normal with mean zero and variance σ². We considered five different cases:

1. β = (1, 0.8, 0, 0, 0, 0, −0.7, 0, 0, 0)^T, x_i’s independent, and ε’s independent with σ = 0.20;

2. Same as case (i), but with σ = 0.30;

3. Same as case (i), but with β changed to (1, 0.8, 0, 0, 0, 0, −0.2, 0, 0, 0)^T;

4. Same as case (i), but with Corr(x_ij, x_ik) = 0.5, j ≠ k;

5. Same as case (i), but with an additional 50 noise covariates, so that β = (1, 0.8, 0, 0, 0, 0, −0.7, 0, 0, 0, 0_1×50)^T.

From Table 1, we can see that, in all cases, the constrained approach shows noticeably better reduction in model complexity and smaller FDR than the unconstrained approach. Additionally, the constrained approach has mean test MSEs which are smaller, and closer to the corresponding oracle test MSEs than the unconstrained approach. Reduction in model complexity for the constrained approach appears to be reasonably insensitive to the changes in simulation settings considered above; however, the unconstrained approach appears to suffer in this regard, especially when true parameter values are decreased or error standard deviation is increased.

Additional simulations were implemented to evaluate the performance of the proposed methods under alternative monotonic functions, η (results not shown). In particular, we considered a linear function, and two spline functions; one resembling the cubic function from the above examples, but with two knots chosen to create a wider “flat” section around the origin, and one which is constant to the left of the origin and quadratic to the right. As expected, both methods performed well in the linear case. In the cubic spline case, reduction in model complexity was good, but mean test MSE became noticeably larger, and in the case of the constant spline with the quadratic knot, mean test MSE was good, but reduction in model complexity was noticeably worse. Thus, as one might expect, the proposed methods are less useful in cases where η contains large sections which are nearly flat, or exactly constant.

To evaluate the performance of our standard error estimates, residual bootstrap standard errors (based on 100 bootstrap data sets) were calculated for case (i) above. Let SD denote the standard deviation of the 100 β_j estimates, j = 1, …, p. Additionally, let SE and SE_sd denote the mean and the standard deviation of the 100 estimated SE’s respectively. Looking at Table 2, we can see that the standard error estimates appear to perform reasonably well, though they sometimes slightly underestimate or overestimate the true values.

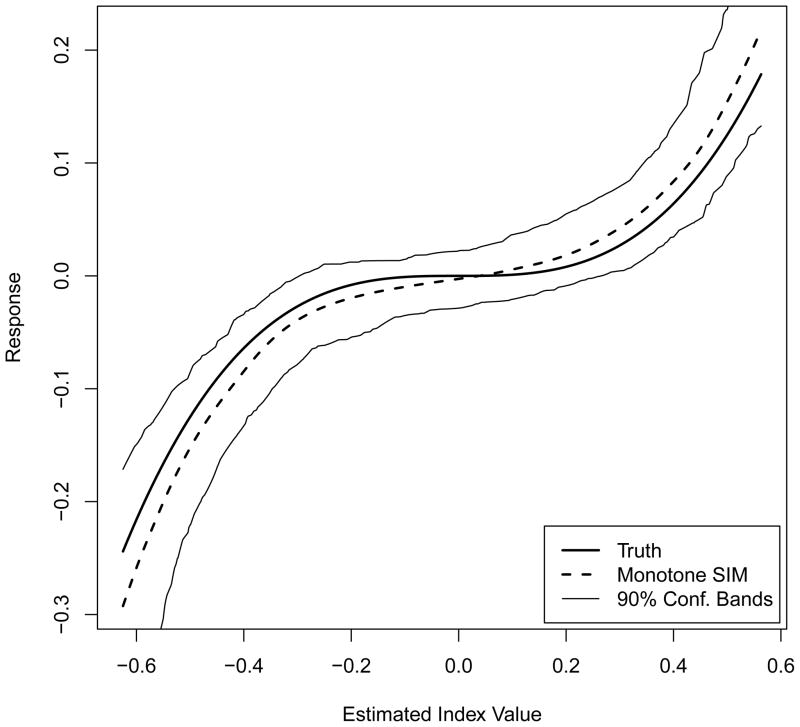
To demonstrate the ability of penalized monotone single-index models to capture non linear relationships, we computed η̂_m values across a fine grid of input values and averaged these η̂_m’s across the 100 data sets in case (i). These average values can be found in Figure 1, along with the true function η and 90% empirical pointwise confidence bands for η̂_m. As we can see, the monotone function estimate η̂_m appears to closely follow the true function.

Figure 1.

Average η̂_m values from 100 simulations

Because we are interested in using the proposed methods to identify subgroups, we also compared “enhancement” classification between the two methods for case (i). For this comparison, we consider a subject to be enhanced if η(x^T β) > 0. On average, 88% of subjects identified as enhanced by the constrained approach were truly enhanced, whereas for the unconstrained approach, only 73% were correctly identified on average. Thus, the constrained approach may be advantageous for applications to subgroup identification.

The two methods methods require approximately the same amount of time to complete a single iteration of our algorithm for a given value of λ. However, for some data sets, the constrained approach requires more iterations to achieve the same degree of convergence as the unconstrained approach. For example, for case (i) of our simulations, the median run time for a data set for the constrained approach was approximately 64% longer than that for the unconstrained approach.

4. Example data

In this example, we apply the proposed methods to the Eli Lilly data in [14], which come from a randomized, double-blinded clinical trial in patients with a critical illness in the ICU conducted over a decade ago. We consider 1019 individuals, of whom 512 received the experimental treatment in addition to the standard of care. The remaining patients received placebo with the standard of care. The intervention is a drug that is intended to improve survival in patients with a critical illness, and the endpoint was survival at 28 days post-randomization to treatment/placebo. We consider 58 covariates analyzed by [14], which include demographic, laboratory, medical history and questionnaire data. Of these, 9 are binary, 22 are regarded as continuous, and 27 are dummy variables coming from subdivision of 12 categorical variables.

In [14], a random forest was used to obtain two predicted probabilities, P̂_1i and P̂_0i, for each individual, where P_1i is the probability of survival at 28 days post-randomization for subject i if that individual had received treatment and P_0i is that if subject i had received placebo. The estimation of these probabilities was motivated by the fact that the methods of [14] were designed to identify subgroups of enhanced treatment effect in randomized clinical trial data. Therefore, a new outcome representing the treatment effect for person i, Z_i = P̂_1i − P̂_0i, i = 1, … n, was subsequently defined, since individuals in such a subgroup should ideally have values of P_1i which are much larger than P_0i. Then, a single regression tree was fit using Z as the outcome and the covariates as predictors. This tree identified subgroups of enhanced treatment effect which depended on age at admission, baseline creatinine clearance, baseline interleukin 6 and hypertension (yes, no or unknown). This method was referred to by [14] as “Virtual Twins.”

Using Z as the outcome and the 58 covariates as predictors, we fit penalized single-index models with and without monotonicity constraints. All covariates were standardized in this analysis due to large differences in scale, and age at admission was chosen to be the first column of X, as its corresponding initial estimate was the largest and most significant value of β̂_init It should be noted that this analysis was also performed with baseline creatinine clearance as the first column (results now shown), and the same six additional covariates were chosen, along with one other. The relative magnitude of the coefficients in this analysis were similar for most variables. Results from these models (with age at admission as first column of X) can be found in Table 3. Estimates for the constrained and unconstrained approaches were fairly similar, though an additional covariate, baseline index of independence in activities of daily living (ADL) [26], was included by the constrained approach.

Table 3.

Estimates for Eli Lilly data

Variable	Unconstrained Estimate	SE	Constrained Estimate	SE
Age	1.00	-	1.00	-
ADL1	-	-	−0.13	0.04
Platelet Count	−0.12	0.03	−0.19	0.08
Creat. Clear.	−0.70	0.17	−0.81	0.21
Interleukin 6	0.60	0.11	0.70	0.13
# Organ Fail.	0.14	0.06	0.23	0.11
APACHE II2	0.24	0.09	0.33	0.14

¹Baseline index of independence in activities of daily living.

²Pre-infusion acute physiology and chronic health evaluation II score.

In addition to β estimates, we computed bootstrap standard errors using 300 bootstrap samples. Because less important covariates will tend to be removed from the model in most bootstrap samples, resulting in many zero bootstrap estimates, we expect such covariates to have very small bootstrap standard errors.

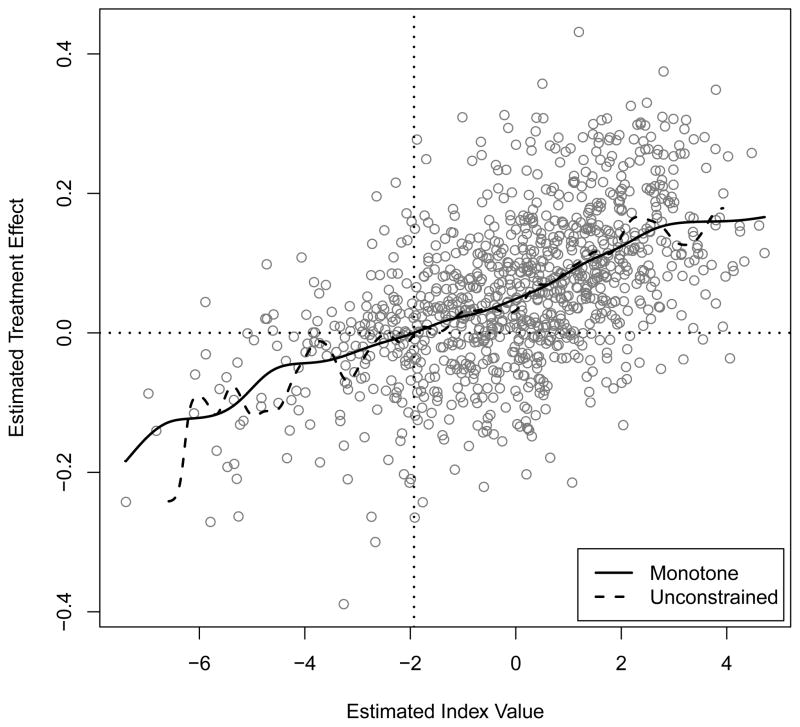
The six covariates selected by both methods were age at admission, baseline central lab platelet count, baseline creatinine clearance, baseline interleukin 6 (log scale), number of baseline organ failures, and pre-infusion acute physiology and chronic health evaluation II (APACHE II) score, of which age at admission, creatinine clearance and interleukin 6 were also selected by the Virtual Twins method. Plots of the data (from the constrained approach) and the final η estimates can be found in Figure 2. We can see that both estimates of η are reasonably close, with the constrained estimate being noticeably more smooth. From Figure 2, we can see that the predicted region of enhanced treatment effect consists of β̂^T x values which are larger than approximately −2, with the degree of enhancement increasing as β̂^T x becomes larger. The constrained and unconstrained approaches identified 847 and 864 subjects as being enhanced, respectively, and of the 864 identified by the unconstrained approach, 845 were also identified by the constrained approach. Furthermore, for the constrained model, older individuals and those with higher baseline IL-6 respond very well to treatment, and patients with lower baseline creatinine clearance show a greater treatment differential. The findings from this analysis are reasonably consistent with the original conclusions from this trial, which suggested that patients who had higher risk factors for mortality responded better to the treatment.

Figure 2.

Estimates of function η̂(·) from Eli Lilly data. Index values in the plotted data are β̂^T x, where β̂ comes from the constrained approach, and treatment effect estimates are the Z values from Virtual Twins procedure. Those points to the right of the vertical dotted line would be considered “enhanced” based on this analysis.

As both fits suggest a relationship which is close to linear, an adaptive LASSO penalized linear model was also fit (results not shown), once using the default tuning parameter selection settings (10-fold cross-validation using squared error loss) in the R glmnet package, and once using BIC to select the tuning parameter. The model resulting from the default tuning parameter selection settings contained 24 covariates, while the model selected using BIC contained 7 covariates. Although BIC is known to give smaller models than cross-validation, this dramatic difference in model complexity was mildly surprising to us. Based on the results of the linear model (using BIC), it appears that the single-index models may not have added much compared to a linear model in this case.

5. Discussion

We proposed the use of adaptive LASSO variable selection for monotone single-index models, and showed that it performs well in a variety of situations. The constrained approach noticeably outperformed the unconstrained, and has the advantage of more straightforward interpretation. A linear approximation to η via Taylor series was also proposed, thus allowing for the use of standard LASSO algorithms, such as coordinate descent, which have been shown to perform well. In addition, we suggested the use of residual bootstrap standard errors for β estimates, and showed that they perform reasonably well in simulations.

We argue that the unconstrained adaptive LASSO penalized single-index model estimates possess the oracle properties when η is estimated using the Nadaraya-Watson formula. Additionally, we briefly argue that, following the results of [21], the oracle properties may also hold for the constrained approach, and it would be interesting to investigate this more formally. Furthermore, the proof outlined in Section 2.4 assumes that β is in a $\sqrt{n}$-neighborhood of the true value, which is likely true given that the initial estimator of β is in a $\sqrt{n}$-neighborhood of β₀.

Our method of obtaining a monotone function estimate is very similar to that of [19]. They suggested that it may be possible to improve the estimation of the monotone penalized single-index model if one considers “one-step” monotone function estimates, such as those suggested by [16] and [17]. This is worthy of further investigation.

The adaptive LASSO penalty was chosen for convenience; however, one may wish to consider other penalty functions. For instance, as noted by a reviewer, the adaptive elastic-net can often outperform the adaptive LASSO approach, particularly when covariates are highly correlated. Note that the linear approximation to the function η does not involve the penalty function. Thus, the proposed method and algorithm could easily be modified if one wished to use a different penalty function, such as the SCAD or adaptive elastic-net.