Abstract
Recently, researchers have used a potential-outcome framework to estimate causally interpretable direct and indirect effects of an intervention or exposure on an outcome. One approach to causal-mediation analysis uses the so-called mediation formula to estimate the natural direct and indirect effects. This approach generalizes classical mediation estimators and allows for arbitrary distributions for the outcome variable and mediator. A limitation of the standard (parametric) mediation formula approach is that it requires a specified mediator regression model and distribution; such a model may be difficult to construct and may not be of primary interest. To address this limitation, we propose a new method for causal-mediation analysis that uses the empirical distribution function, thereby avoiding parametric distribution assumptions for the mediator. In order to adjust for confounders of the exposure-mediator and exposure-outcome relationships, inverse-probability weighting is incorporated based on a supplementary model of the probability of exposure. This method, which yields estimates of the natural direct and indirect effects for a specified reference group, is applied to data from a cohort study of dental caries in very-low-birth-weight adolescents to investigate the oral-hygiene index as a possible mediator. Simulation studies show low bias in the estimation of direct and indirect effects in a variety of distribution scenarios, whereas the standard mediation formula approach can be considerably biased when the distribution of the mediator is incorrectly specified.
Researchers conduct mediation analyses to determine the extent to which a treatment or exposure effect on a final outcome is explained by a causal intermediate variable, or mediator. Mediation analysis typically involves the decomposition of the exposure effects into an indirect effect (mediated by the intermediate variable) and a direct effect (not mediated by this variable, though possibly by unobserved intermediate variables). A causal-model approach to mediation analysis, based on potential-outcomes, has been taken by a number of methodologists.1–7 The causal-model / potential-outcomes framework provides a principled approach, with clearly stated assumptions, that views mediation in terms of conceived manipulations.
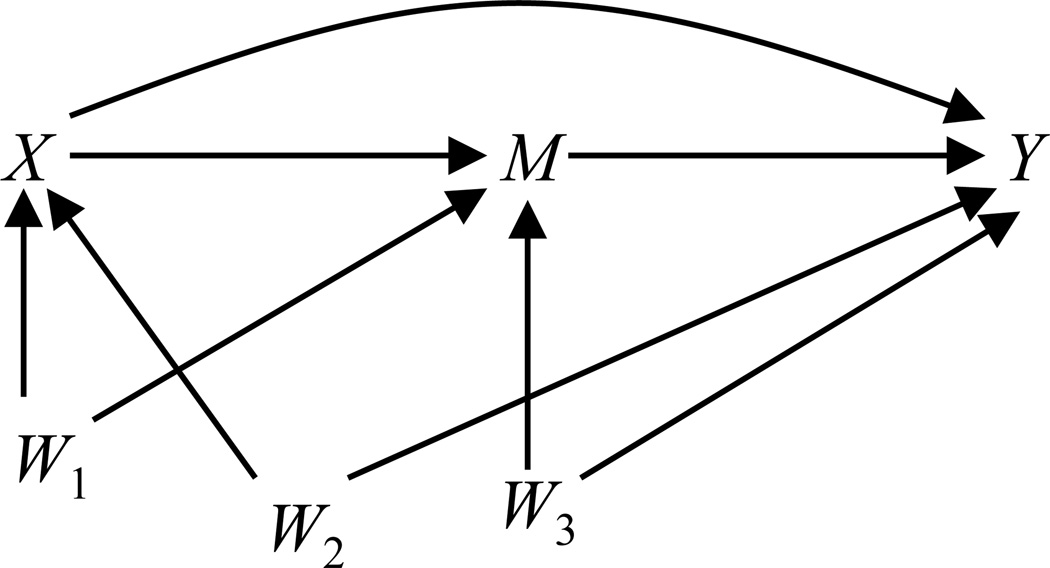
Using the potential-outcomes framework, we can define the estimands of interest using nested potential-outcomes.4 We assume a causal model, technically a directed acyclic graph (DAG) as illustrated in Figure 1, in which an exposure variable (X) causes a final response variable (Y), directly or through a mediator variable (M). In addition, some baseline variables (W) may confound the relationships among these three model variables. We let W1, W2, and W3 denote the confounders of the X-M, X-Y, and M-Y relationships, respectively. For brevity, we let Wj,j´ denote the vector containing the union of covariates given by Wj and Wj´, and let W represent the vector including all of the covariates. The subscript i will be used to denote an observed value for individual i. Thus, we let Xi denote the exposure observed for individual i (Xi=1 if exposed, Xi=0 otherwise). Further, we let Mi(x) denote the potential-outcome for M were individual i given exposure level x, and let Yi(x, M(x´)) denote the potential-outcome for Y, were individual i given exposure level x, but with the mediator, M, set to the level the individual would have if given exposure level x´. We will drop the subscript i for individual where this will not cause confusion. Focusing on population effects, we define the (natural) direct effect (at reference exposure level x) as
and the (natural) indirect effect as
Figure 1.
Mediation model with confounders (W’s); X=exposure, M=mediator, Y=final response
Then the total effect, T = E{Y(1, M(1))} − E{Y(0, M(0))} can be written as T = D(0) + I(1) or T = D(1) + I(0). Although either decomposition may be of interest depending on the context, we will focus on the latter; our methodology, however, can be applied to either. Note that D(x) and I(x), as defined above, represent the “natural” direct and indirect effects whereby M is set to a (random) potential-outcome for each individual, as opposed to “controlled” direct and indirect effects in which M is fixed at a particular common value. These estimands will be our focus throughout the paper. For a binary response, the above expressions represent effects on the risk difference scale. Alternative definitions of natural and controlled direct and indirect effects for a binary outcome are based on an odds-ratio scale8,9 and a risk-ratio scale.10
An important implied assumption of our causal model (Figure 1) is that the confounding variables – in particular, W3, representing confounders of the M-Y relationship – are not affected by X. If such a link is expected, the present model and method would not be applicable; rather, one should consider a method for the more complex causal model in which the causal link is drawn between X and W3.11,7
To identify the natural direct and indirect effects, we need to make further assumptions. We will use the following sequential ignorability assumption as given by Imai et al.,6
Assumption 1 (Sequential ignorability).
| (1) |
| (2) |
for all x, x'=0,1, and all w in the support of the distribution of W.
Imai et al.6 showed that under Assumption 1 the direct and indirect effects are nonparametrically identifiable. Under additional assumptions implied by the model represented in Figure 1 (or Model 4 below), the expected potential-outcome for Y can be written as follows:
| (3) |
where FW (w) and FM|X,W1,3 (m) represent, respectively, the distribution function of W and the conditional distribution function of M given X and W1,3.
The above formula, a version of what is referred to by Pearl12 as the “mediation formula,” provides estimable expressions for the natural direct and indirect effects defined above. Estimation typically proceeds by fitting specified regression models for Y and M to the data. For example, Albert and Nelson7 assumed the following set of generalized linear models (which will also be used in the present paper):
| (4a) |
| (4b) |
where h1, h2 are invertible link functions, and the β’s and γ’s are unknown regression parameters (possibly vectors). Plugging in estimates for model parameters in (4) (along with any other parameter values needed for the distribution of M) into the mediation formula (3) provides estimates for the expected potential-outcomes of Y and consequently the natural direct and indirect effects.
When E(Y | M, X, W2,3) can be appropriately modeled using a function that is linear in M, then only the conditional mean (rather than the distribution) of M is needed, and (3) can be evaluated simply by plugging in E(M | X=x´,W1,3) for M in the regression model for Y. Earlier approaches13 took advantage of this situation to provide simple expressions for the direct and indirect effects. However, when the assumption of a linear model cannot sensibly be made (for example, when Y is binary or a count variable), then expression (3) does not reduce, and the complete distribution function for M is needed. Huang et al.8 addressed the nonlinear case (specifically, a logistic regression model for a binary response variable) in the context of a binary M. This case – similarly, that of any bounded discrete distribution for M – is relatively straightforward, as the integration over M in the mediation formula can be written as a summation.7 In an alternative approach, approximate formulae for the natural direct and indirect effects for a binary response on an odds-ratio scale have been provided under the assumptions of a normally distributed mediator and a rare outcome.9
The use of the mediation formula for nonlinear models is more challenging when the mediator is continuous as integration is required. Possible approaches include numerical integration and Monte Carlo integration.6 An alternative approach, proposed for either controlled or natural direct and indirect effects, uses marginal-structural models in conjunction with inversely proportional weighting.5 A limitation of this approach is that it requires that the structural model for Y be linear in the mediator. A double-robust estimator for the natural direct effect has been developed,14 while a recent semiparametric approach15,16 offers multiply robust inference (that is, consistent estimators when any subset of models for the outcome, mediator, and exposure are correctly specified) for natural direct and indirect effects. All of these approaches require the specification of a regression model for M (albeit considered as a “working” model by some). However, often we may wish to avoiding making distributional assumptions about, or developing a regression model for, M.
In the present paper, we address the above situation by taking a distribution-free approach with regard to the mediator (M). Specifically, we use the empirical distribution function rather than an assumed parametric distribution for M in the mediation formula. It should be noted that the parametric approach to mediation formula (3) uses a regression model for M to allow conditioning on W. A challenge is that the analogous use of (3) with a (conditional) empirical distribution function for M would incur the “curse of dimensionality”.17,15 We therefore consider an alternative approach using the joint empirical distribution of M and W, along with inverse-probability weighting where needed for covariate alignment, to allow inference to a selected reference group. We next derive the proposed “empirical” mediation approach for the case of “no X confounding” before considering the “general confounding” case for which we will present an approach using inverse-probability weighting.
METHODS
We seek to develop an estimator for E{Y(x, M(x´))} utilizing formula (3) (thus assuming sequential ignorability and the graph in Figure 1) but without a distributional assumption for M. We assume a generalized linear model of the form (4a) for Y, and, adding a distributional assumption for Y, use maximum likelihood estimation to estimate the β’s. We use the hat-notation to indicate estimates; for example, β̂1 denotes the estimate of β1. Below, we derive estimators for the two cases corresponding to “no X confounding” (that is, where there are no confounders of the X-M or X-Y relationships) and “general confounding” (as in Figure 1).
No X Confounding
In this case, both W1 and W2 are the empty set, so that expression (3) is obtained with W3 in place of W2,3, W1,3, and W. The regression of Y on M, X, and W3 may be estimated as described above. Our remaining task is to estimate the product of distributions used in the integration in (3), namely, FM|X =x',W3 FW3. Because W3 and X are independent, it follows that FM|X =x',W3 FW3 = FM,W3|X =x', the joint distribution of M and W3 given X=x´. This term, therefore, can be estimated using the empirical distribution function for (M,W3) given X=x´ which we denote as, F̂M,W3|X = x'. An advantage of using the joint distribution is that we are no longer subject to the “curse of dimensionality” that would accrue by conditioning on covariates. Our estimator is, then,
| (5) |
where g = h2−1 and Πx' is the subset (of size Nx') of subjects observed at exposure level x´.
Using this expression, we can estimate the natural direct and indirect effects as follows:
| (6a) |
| (6b) |
In addition, the estimated total effect is T̂ = D̂(1) + Î(0). Note that under the current assumptions inference here is to the whole sample. Similar expressions may be obtained for the other direct and indirect effects, D(0) and I(1). Pearl12 provides further discussion on the choice among these alternative estimands.
General Confounding
We now consider the general situation represented in Figure 1, which includes confounders between each pair of the model variables. In this case, we no longer have equality between FM|X =x',W1,3 FW (as used in (3)) and the joint distribution FM,W|X =x'. As a first step in overcoming this difficulty, we consider the estimand E{Y (x,M(x')) | X = x'} ; that is, we use the subsample Πx' as a reference group. Later, we will consider an arbitrary reference group (not necessarily X=x´) written as X = r. To maintain a single notation we will write r = Ω to indicate the whole sample (which is equivalent to no conditioning). Thus, X=Ω is a shorthand for (X=0) ∪ (X=1). The above conditional expected value estimand can be written in the form of (3) but where the outer integration is over the conditional distribution FW|X =x'. This provides the product distribution FM|X =x',W FW|X =x', which is equal to the joint distribution FM,W|X =x'. Thus, in the general confounding case, we have expression (5), with w2,3 in place of w3 and the interpretation of β̂3 modified accordingly, as a consistent estimator of E{Y (x,M(x')) | X = x'}, a result derived in detail in the Appendix.
From this result, we see that under general confounding, the previous estimator ((6a), again, with w2,3 in place of w3) is consistent for the direct effect for the exposed subgroup. That is, letting Dr(x) ≡ E{Y(1,M(x)) | X=r} − E{Y(0,M(x)) | X=r} denote the (natural) direct effect for reference group Πr, we have a consistent estimator for D1(1) as
| (7) |
Note that this estimator, representing a contrast involving the same exposure group, does not require weighting or even W1 to be observed.
On the other hand, the estimated indirect effect (as in (6b)) represents a contrast between the exposed and non-exposed groups; thus, the latter is not interpretable as a causal effect for any given subpopulation. In order to obtain an indirect effect estimator that is valid for a selected reference group (including the whole sample if desired), we propose an approach based on inversely proportional weighting. The idea is to re-weight individuals in a given exposure group(s) so that the resulting distribution for the relevant confounders (W1,2 in the present case), and thus the estimated conditional expected value of Y, corresponds to the selected reference group. As noted previously,18 the standard inverse-probability-weighting approach implicitly uses the overall population (as represented in the sample) as the reference group; however, one may alternatively use a particular exposure group as the reference group. We will focus on the exposed subsample as the reference group, a designation applicable to our data example below.
To obtain weights we specify a supplementary model for the probability of exposure as a function of covariates (also known as the propensity score). The most common modeling approach uses a logistic regression model. We will utilize this approach and assume the model,
| (8) |
We denote estimates for α0, α1 (for example, using maximum likelihood estimation) as α̂0, α̂1. Note that model (8) includes all predictors of X (in the context of the model implied by Figure 1). We consider this choice of covariates to be appropriate as the causal model implies that both W1 and W2, though not W3, would be included in the data generating model for X, and therefore, P(X=1 | W) = P(X=1 | W1,2). Alternative propensity-score models and variable selection strategies have been proposed in the literature.19,20
For the conditional expected potential-outcome for reference group Πr, our proposed inverse-probability-weighting estimator is
| (9) |
where S = ∑i∈Πx' P̂(X = r | W1,2 = w1,2i)/P̂(X = x' | W1,2 = w1,2i) is the sum of the weights. Note that when r=x´ this formula reduces to provide an unweighted estimator. When r ≠ x´ then the weight for individual i is either (1−ei)/ei (for r=0) or ei/(1−ei) (for r=1), where ei ≡ P̂(X = 1|W1,2 = w1,2i) is the propensity score. Also, for the whole sample (r= Ω), P̂(X = r |W1,2 = w1,2i) = P̂(X = r) = 1.
We can now construct the estimator for the (natural) indirect effect for reference group Πr denoted as Ir(x) ≡ E{Y(x,M(1)) | X=r} − E{Y(x,M(0)) | X=r}. Using the above weighting approach, we obtain the estimator for the indirect effect I1(0) as
| (10) |
where S = ∑i∈Π0 {ei/(1 − ei)} and ei = 1/[1 + exp{−(α̂0 + α̂1 w1,2i)}] under model (8). Thus, designating exposed persons as the reference group, we use weights equal to 1 for people in the exposed group and equal to ei / (1 − ei) for the ith individual in the non-exposed group. To estimate standard errors for the above estimators and to obtain confidence intervals, we consider several alternative bootstrap resampling strategies, including the percentile method (using the α/2 and (1 − α/2) percentiles of the bootstrap distribution for a 1 − α percent confidence interval), a bias-corrected (BC) version of the percentile interval known as the BC method,21 and the “standard interval,” which uses the standard normal percentiles with the bootstrap-estimated standard error.
EXAMPLE
We provide an illustrative example using data from a dental caries study.22 The study involved a cohort of very low birth weight (VLBW, less than 1500g at birth) and normal birth weight (“term”, at least 2500g at birth) children, the latter obtained by matching according to race and socioeconomic status, who were followed from birth through adolescence.23 A dental clinical exam at around age 14 years provided the number of decayed, missing, and filled teeth (thus, the analysis variable, DMFT – also referenced to below as “affected teeth”) and the oral-hygiene-index score, an indicator of effective oral health behavior. Contrary to expectation, the primary analysis22 found that average number of affected teeth was lower in the VLBW compared with the term group. A follow-up question was whether any of the measured intermediate variables mediated this observed relationship between birth weight and affected teeth. For the present analysis, we considered the oral-hygiene index as a possible mediator, with DMFT as the final outcome, and birth status (VLBW versus term) as the exposure variable. We wanted to allow for the possibility that race (African American versus others), sex, and socioeconomic status (low versus high) would each affect all three model variables, and therefore we used them as a common set of confounders for the three model relationships. We sought to assess, for the VLBW (“exposed”) group, the direct effect of birth status on the number of decayed, missing, and filled teeth and its indirect effect though the oral hygiene index.
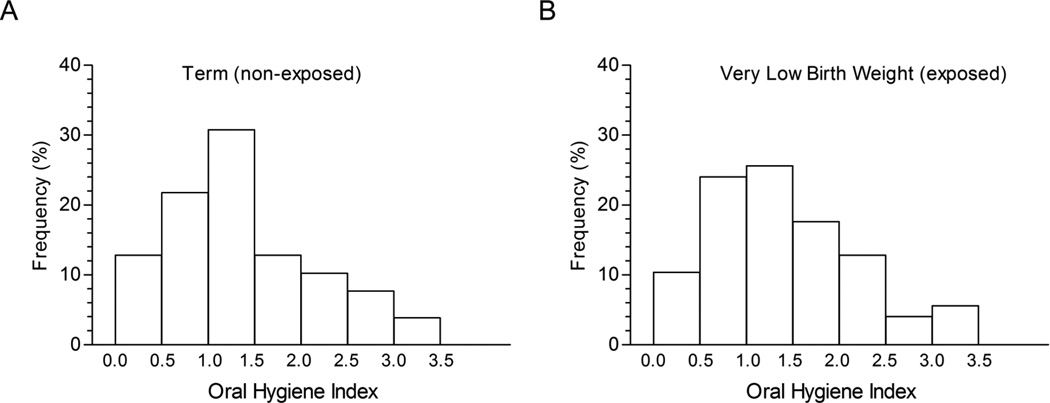
The number of decayed, missing, and filled teeth is a count outcome, and so we assumed that it follows a negative binomial distribution and modeled its conditional expected value using a loglinear model. As this model is nonlinear, we applied the mediation formula in conjunction with the assumptions and models given in the preceding section. The empirical mediation method was indicated here due to the apparent non-normality of the oral-hygiene index, the putative mediator. Figure 2 provides histograms for the oral-hygiene index for the two birth-status groups, showing right skewness and low kurtosis in the oral-hygiene index distribution. The analysis (complete case) sample involved 125 VLBW and 78 term subjects. The mean number of decayed, missing and filled teeth was 1.67 (standard error = 2.74) for the VLBW group, and 2.42 (2.97) for the term group; for the oral-hygiene index, the mean (standard error) was 1.17 (0.78) for the VLBW group and 1.15 (0.79) for the term group. The empirical mediation method used the above empirical estimators, (7) and (10), for the natural direct (D1(1)) and natural indirect (I1(0)) effects of birth status, with VLBW (the “exposed” group) as the reference group with regard to the covariate distribution. This choice is appropriate for the present data set as the study design involved the selection of term (“non-exposed”) infants via matching to the VLBW infants.
Figure 2.
Histograms for the oral hygiene index score for each exposure group
The empirical method estimate for the direct effect is −0.71 (95% bootstrap standard confidence interval [CI]= −1.53 to 0.11) and for the indirect effect, −0.001 (−0.16 to 0.15). Thus, we estimated that the mean number of affected teeth for VLBW individuals would increase by 0.71 if birth status were changed to term but the oral hygiene index kept the same. Similarly, we estimated that the mean number of decayed, missing and filled teeth would decrease by 0.001 (that is, hardly at all) if the oral hygiene index were changed from the value that would be observed if the person had been term to the value that would be observed if the person had been VLBW, without otherwise changing the birth status. The integration approach6 (assuming the oral-hygiene index to be normally distributed, with VLBW as the reference group) provided substantially the same results as the empirical approach – virtually the same estimate and 95% confidence interval bounds for the direct effect, and an estimated indirect effect of 0.04 (95% CI= −0.20 to 0.29). In sum, we find that there is no evidence for a mediation effect of birth status (VLBW versus term) on the number of decayed, missing, and filled teeth through the oral-hygiene index, and the estimated direct effect represents nearly the entire total estimated effect of birth status.
SIMULATIONS
We conducted a simulation study to further examine the properties of our proposed estimators and to compare them with estimators based on the fully parametric (“integration”) approach to the mediation formula. We considered six cases corresponding to the choice of one of two distributions (and regression link functions) for Y and one of three for M as follows,
Y: 1) negative binomial (log); 2) bernoulli (logit);
M: 1) normal (identity); 2) chi-squared (log); 3) beta (logit).
The assumed model corresponds to the causal diagram in Figure 1. For simplicity, we considered a single standard normally distributed covariate, W, that confounds each of the three model relationships; thus, W is equal to W1, W2, and W3 in the more general model. Further, Y is assumed to follow a generalized linear model (as in (4a) with X, M, and W as covariates), and M, a generalized linear model (as in (4b) with X and W as covariates). We also assumed that X is generated as a function of W according to a logistic regression model (as in (8)). However, to study robustness of the proposed method to this assumption, we also generated X according to a corresponding probit model. For each set of distributions for Y and M, we examined three situations in regard to the proportions of direct and indirect effects: a) all direct; b) all indirect; and c) approximately equal direct and indirect effects. The regression coefficient values (including intercepts) used for the scenarios are given in Table 1. In addition, to examine the potential for instability of weights, we considered these same scenarios but with the coefficient of W in the exposure (propensity score) model approximately tripled (namely, 0.3 changed to 1.0, 0.5 to 1.5, and 0.7 to 2.0). Focusing on the case of equal direct and indirect effects, we label this “low-overlap” case as scenario d. These scenarios were used for both the logistic regression and the probit X-models. For each scenario we considered total sample sizes (N) of 200 and 2000.
Table 1.
Regression coefficient values used in simulation study
| Distributions | Scenario | Outcome (Y) | Mediator (M) | Exposure (X) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Y | Ma | Int | X | M | W | Int | X | W | Int | W | |
| NegBin | N | 1a | −0.2 | 1.0 | 0 | 0.4 | 1.0 | 0.8 | 0.5 | −0.1 | 0.7 |
| 1b | −0.2 | 0 | 0.5 | 0.3 | 1.4 | 1.0 | 0.5 | −0.1 | 0.7 | ||
| 1c | −0.2 | 0.4 | 0.6 | 0.4 | 1.0 | 1.2 | 0.5 | −0.1 | 0.7 | ||
| C | 2a | −0.3 | 0.8 | 0 | 0.3 | 0.6 | 0.3 | 0.3 | −0.1 | 0.5 | |
| 2b | −0.4 | 0 | 0.3 | 0.3 | 0.6 | 0.3 | 0.3 | −0.1 | 0.5 | ||
| 2c | −0.4 | 0.3 | 0.3 | 0.3 | 0.6 | 0.3 | 0.3 | −0.1 | 0.5 | ||
| B | 3a | −0.3 | 1.2 | 0 | 0.5 | 0.6 | 1.0 | 0.5 | −0.1 | 0.5 | |
| 3b | −0.3 | 0 | 1.8 | 0.5 | 0.6 | 1.6 | 0.5 | −0.1 | 0.5 | ||
| 3c | −0.5 | 0.2 | 1.4 | 0.3 | 0.6 | 1.4 | 0.5 | −0.1 | 0.5 | ||
| Bernoulli | N | 4a | −0.2 | 0.6 | 0 | 0.3 | 0.6 | 0.5 | 0.4 | −0.1 | 0.3 |
| 4b | −0.2 | 0 | 0.7 | 0.3 | 0.6 | 1.0 | 0.6 | −0.1 | 0.3 | ||
| 4c | −0.2 | 0.9 | 0.7 | 0.3 | 0.6 | 1.0 | 0.6 | −0.1 | 0.3 | ||
| C | 5a | −0.2 | 0.6 | 0 | 0.3 | 0.6 | 0.5 | 0.4 | −0.1 | 0.3 | |
| 5b | −0.2 | 0 | 0.2 | 0.3 | 0.6 | 0.6 | 0.5 | −0.1 | 0.3 | ||
| 5c | −0.2 | 0.6 | 0.2 | 0.3 | 0.6 | 0.8 | 0.6 | −0.1 | 0.3 | ||
| B | 6a | −0.2 | 0.5 | 0 | 0.3 | 0.6 | 1.0 | 0.6 | −0.1 | 0.3 | |
| 6b | −0.2 | 0 | 1.8 | 0.3 | 0.6 | 1.4 | 0.6 | −0.1 | 0.3 | ||
| 6c | −0.2 | 0.3 | 1.15 | 0.3 | 0.6 | 1.4 | 0.6 | −0.1 | 0.3 | ||
Mediator distribution: N = normal; C = chi-square; B = beta
For each selected scenario (and sample size), simulated data sets were generated as follows. The values of W, X, M, and Y corresponding to a given subject were generated sequentially according to the above models; the set of variables were then generated independently between subjects. For each dataset, we estimated D1(1) and I1(0), the natural direct and indirect effects for the exposed group, using estimators (7) and (10). For comparison, we estimated the same estimands using the mediation formula (3) in which we assumed a normal distribution for M and used a numerical integration algorithm to evaluate the integral over M. As values for the covariate W were considered as fixed, we averaged over the observed W’s in the reference group (namely, X=1, “exposed”) in lieu of integration in (3). We performed 1000 replications for each scenario and sample size.
For each scenario, method (“integration” versus “empirical” mediation approaches), and mediation effect (direct or indirect), we computed the following statistics over the replicated data sets: the average bias (estimate minus true value), the relative bias (bias divided by the true value, for non-null effects), the simulation standard error of the bias, and the coverage percentage for bootstrap confidence intervals. The true values for the estimands for a given dataset were obtained by applying the mediation formula (3) using the true model and parameter values for the conditional expected value of Y, integrating over the true distribution for M, and averaging over the W’s corresponding to exposed subjects in the dataset. The overall “true” value, as provided in Tables 2 and 3, was obtained as the average of these true values over the multiple replications. All simulations, as well as the preceding data analysis, were conducted in SAS Version 9.2 using SAS/IML and the GENMOD and REG procedures.
Table 2.
Simulation results for the direct and indirect effects - negative binomial Y, logistic regression X-model (correctly fit), (n = 200)
| Mediator | Scenario | Effect | True | Integration Approach | Empirical Approach | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | Relative Bias (%) |
SE of Bias |
CP1 (%) |
CP2 (%) |
Bias | Relative Bias (%) |
SE of Bias |
CP1 (%) |
CP2 (%) |
||||
| N | 1a | D | 1.73 | 0.014 | 0.81 | 0.010 | 94.7 | 94.8 | 0.014 | 0.80 | 0.010 | 94.7 | 94.9 |
| I | 0.00 | 0.003 | - | 0.002 | 93.9 | 97.5 | 0.003 | - | 0.003 | 31.2 | 96.9 | ||
| 1b | D | 0.00 | −0.011 | - | 0.022 | 95.3 | 95.6 | −0.011 | - | 0.022 | 95.3 | 95.6 | |
| I | 1.67 | 0.020 | 1.30 | 0.015 | 94.2 | 93.7 | 0.012 | 0.72 | 0.020 | 70.2 | 91.2 | ||
| 1c | D | 2.83 | −0.078 | −2.79 | 0.033 | 95.0 | 95.6 | −0.088 | −3.13 | 0.033 | 94.3 | 95.2 | |
| I | 2.95 | 0.052 | 1.70 | 0.027 | 93.0 | 93.0 | 0.083 | 2.59 | 0.033 | 76.2 | 89.4 | ||
| 1d | D | 3.28 | −0.069 | −2.13 | 0.045 | 94.0 | 95.5 | −0.078 | −2.41 | 0.045 | 93.4 | 94.6 | |
| I | 3.42 | 0.093 | 2.76 | 0.033 | 95.4 | 93.8 | 0.382 | 10.9 | 0.055 | 67.3 | 93.6 | ||
| C | 2a | D | 1.02 | −0.005 | −0.49 | 0.007 | 93.9 | 94.4 | −0.004 | −0.43 | 0.007 | 94.0 | 94.5 |
| I | 0.00 | −0.002 | - | 0.001 | 97.8 | 100 | −0.000 | - | 0.001 | 31.5 | 98.3 | ||
| 2b | D | 0.00 | −0.014 | - | 0.012 | 95.5 | 96.9 | −0.020 | - | 0.026 | 95.5 | 97.2 | |
| I | 1.09 | −0.69 | −62.6 | 0.008 | 26.9 | 20.7 | −0.004 | −3.00 | 0.087 | 59.3 | 61.8 | ||
| 2c | D | 1.15 | −0.36 | −30.6 | 0.014 | 85.9 | 86.4 | −0.026 | −2.42 | 0.035 | 90.7 | 92.5 | |
| I | 1.09 | −0.67 | −61.4 | 0.008 | 28.2 | 22.5 | −0.075 | −8.43 | 0.11 | 60.0 | 64.3 | ||
| 2d | D | 1.35 | −0.46 | −34.0 | 0.018 | 83.1 | 86.2 | 0.083 | 6.40 | 0.14 | 87.7 | 92.0 | |
| I | 1.33 | −0.87 | −64.5 | 0.010 | 27.5 | 22.3 | 0.39 | 28.3 | 0.27 | 72.9 | 80.9 | ||
| B | 3a | D | 2.19 | −0.007 | −0.29 | 0.010 | 94.2 | 94.7 | −0.010 | −0.43 | 0.010 | 94.5 | 95.0 |
| I | 0.00 | 0.003 | - | 0.002 | 94.7 | 98.3 | 0.001 | - | 0.003 | 30.5 | 94.9 | ||
| 3b | D | 0.00 | −0.10 | - | 0.028 | 93.5 | 94.7 | −0.079 | - | 0.025 | 93.4 | 94.2 | |
| I | 1.40 | 0.76 | 54.2 | 0.021 | 75.3 | 92.4 | 0.015 | 1.00 | 0.017 | 45.5 | 92.3 | ||
| 3c | D | 0.53 | 0.040 | 7.27 | 0.014 | 93.1 | 93.6 | 0.014 | 2.45 | 0.014 | 93.1 | 93.5 | |
| I | 0.55 | 0.19 | 35.4 | 0.009 | 89.1 | 96.6 | −0.002 | −0.35 | 0.007 | 63.8 | 94.0 | ||
| 3d | D | 0.59 | −0.013 | −2.28 | 0.018 | 94.0 | 95.1 | −0.037 | −6.30 | 0.017 | 93.7 | 95.1 | |
| I | 0.57 | 0.24 | 42.0 | 0.010 | 88.2 | 97.5 | 0.018 | 3.14 | 0.014 | 38.5 | 97.4 | ||
Mediator: N = normal; C = chi-square; B = beta
Effect: D = (Natural) direct effect for exposed, D1(1); I = (Natural) indirect effect for exposed, I1(0)
CP1: bootstrap percentile CI coverage probability
CP2: standard CI coverage probability
Table 3.
Simulation results for the direct and indirect effects - negative binomial Y, logistic regression X-model (incorrectly fit), (n = 200)
| Mediator | Scenario | Effect | True | Integration Approach | Empirical Approach | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | Relative Bias (%) |
SE of Bias |
CP1 (%) |
CP2 (%) |
Bias | Relative Bias (%) |
SE of Bias |
CP1 (%) |
CP2 (%) |
||||
| N | 1a | D | 1.82 | −0.010 | −0.53 | 0.010 | 94.4 | 94.6 | −0.011 | −0.54 | 0.010 | 94.4 | 94.7 |
| I | 0.00 | 0.003 | - | 0.002 | 94.4 | 97.8 | 0.020 | - | 0.004 | 17.5 | 98.5 | ||
| 1b | D | 0.00 | −0.029 | - | 0.026 | 94.8 | 95.7 | −0.028 | - | 0.026 | 94.8 | 95.4 | |
| I | 1.78 | 0.048 | 2.74 | 0.018 | 93.8 | 93.7 | 0.13 | 7.17 | 0.025 | 61.3 | 93.8 | ||
| 1c | D | 3.09 | −0.043 | −1.37 | 0.039 | 94.5 | 95.8 | −0.054 | −1.70 | 0.040 | 93.7 | 95.5 | |
| I | 3.23 | 0.093 | 2.86 | 0.031 | 92.8 | 92.8 | 0.22 | 6.61 | 0.041 | 71.1 | 91.3 | ||
| 1d | D | 3.44 | −0.12 | −3.39 | 0.053 | 92.6 | 96.3 | −0.13 | −3.72 | 0.053 | 92.5 | 95.7 | |
| I | 3.59 | 0.097 | 2.57 | 0.041 | 92.7 | 92.0 | 1.04 | 28.5 | 0.056 | 67.1 | 95.8 | ||
| C | 2a | D | 1.06 | −0.014 | −1.28 | 0.008 | 93.6 | 94.1 | −0.013 | −1.21 | 0.008 | 93.4 | 94.0 |
| I | 0.00 | <0.001 | - | 0.001 | 97.5 | 99.9 | 0.004 | - | 0.002 | 21.0 | 99.4 | ||
| 2b | D | 0.00 | −0.004 | - | 0.014 | 94.2 | 95.2 | −0.013 | - | 0.022 | 94.2 | 95.0 | |
| I | 1.21 | −0.75 | −61.7 | 0.009 | 31.3 | 24.6 | −0.10 | −10.5 | 0.24 | 63.8 | 70.5 | ||
| 2c | D | 1.25 | −0.38 | −30.2 | 0.015 | 84.9 | 86.2 | −0.049 | −4.13 | 0.030 | 89.9 | 92.8 | |
| I | 1.21 | −0.76 | −62.6 | 0.009 | 28.7 | 22.6 | −0.51 | −42.5 | 0.40 | 66.8 | 70.5 | ||
| 2d | D | 1.43 | −0.49 | −33.7 | 0.021 | 85.8 | 91.3 | −0.068 | −4.76 | 0.041 | 91.1 | 94.8 | |
| I | 1.42 | −0.93 | −65.3 | 0.012 | 33.8 | 28.1 | 0.035 | 7.68 | 0.45 | 72.0 | 87.9 | ||
| B | 3a | D | 2.32 | 0.024 | 1.05 | 0.011 | 94.3 | 94.5 | 0.021 | 0.91 | 0.011 | 94.1 | 94.5 |
| I | 0.00 | 0.002 | - | 0.002 | 94.1 | 98.4 | 0.014 | - | 0.003 | 11.7 | 98.3 | ||
| 3b | D | 0.00 | −0.009 | - | 0.030 | 93.9 | 94.6 | 0.003 | - | 0.027 | 93.9 | 94.5 | |
| I | 1.47 | 0.78 | 53.1 | 0.022 | 78.0 | 93.7 | −0.050 | −3.45 | 0.025 | 28.8 | 92.1 | ||
| 3c | D | 0.56 | 0.029 | 5.36 | 0.016 | 93.4 | 93.9 | 0.003 | 0.54 | 0.015 | 93.9 | 94.4 | |
| I | 0.56 | 0.21 | 37.3 | 0.009 | 89.4 | 97.2 | <0.001 | 0.05 | 0.007 | 46.1 | 97.7 | ||
| 3d | D | 0.61 | −0.003 | −0.47 | 0.020 | 95.0 | 94.6 | −0.028 | −4.57 | 0.019 | 95.7 | 95.1 | |
| I | 0.58 | 0.26 | 45.5 | 0.011 | 88.8 | 97.4 | 0.22 | 38.0 | 0.013 | 38.4 | 99.0 | ||
Mediator: N = normal; C = chi-square; B = beta
Effect: D = (Natural) direct effect for exposed, D1(1); I = (Natural) indirect effect for exposed, I1(0)
CP1: bootstrap percentile CI coverage probability
CP2: standard CI coverage probability
“<0.001” implies less than 0.001 in absolute value
The simulation results for negative binomial Y and N=200 are shown in Table 2 (logistic regression [correctly fit] X-model) and Table 3 (probit [incorrectly fit] X-Model). We see from Table 2 that the biases for the empirical approach are fairly small for scenarios with a correctly fit X-model and moderate overlap (scenarios a–c). Specifically, the relative bias is less than 4% for all scenarios except one, Scenario 2c, where the (absolute value of the) relative bias for the indirect effect is around 8%. For the integration approach the biases are low (though comparable to the empirical approach) when the mediator is normally distributed. However, for scenarios where the mediator is non-normally (chi-square or beta) distributed, the relative bias (absolute value) for the integration approach is as high as 62 percent. In the case of low overlap (the d scenarios), both approaches show substantial biases. Though the relative bias for the empirical approach here is as high as 28%, it still does considerably better than the integration approach except in the normal case. In the case of the larger number of subjects of 2000, (absolute values of) relative biases for the empirical estimators are reduced to less than 5% for all scenarios with the correctly fit X-model, while biases for the integration approach remain as high as 64% (results not shown). We note that the case of moderate overlap provided stable weights, with an average minimum and average maximum over the generated data sets for Scenario 1c (as a representative example) equal to 0.15 and 4.4, respectively. Understandably, instability of weights increased in the case of low overlap, with the average minimum and maximum for Scenario 1d equal to 0.006 and 18.1.
Table 3 shows that biases for the empirical approach may be substantial with an incorrectly fit X-model. However, for the moderate overlap scenarios (a–c) relative biases were still within 11%, except for Scenario 2c where it was 42%. In the high-overlap scenarios (d), the relative biases generally increased. However, the biases were still lower for the empirical than the integration approach (whose results are similar for both X models) except in the normal case.
The tables show low coverage of bootstrap percentile intervals in many scenarios for the empirical estimators, which is not improved by bias correction (results not shown). The standard intervals perform more satisfactorily, though are often conservative. The results for Bernoulli-distributed Y are similar to those described above, though with generally smaller biases and standard errors throughout (results not shown).
DISCUSSION
We have presented an approach to the estimation of natural direct and indirect effects that avoids a distributional assumption, as well as the specification of a regression model, for the mediator (M). The main idea of this approach is to use the mediation formula with the empirical distribution function for M in conjunction with inverse-probability weighting. This “empirical” mediation analysis offers a computationally simple and robust alternative to fully parametric6 and semiparametric approaches.15,16 Sample SAS code, used to compute the empirical and integration estimates for the dental data, is provided in an eAppendix (http://links.lww.com).
Our simulation study showed that the empirical approach performs well under various distributions for M, while the parametric mediation formula approach may be sensitive to the assumption of a normally distributed mediator. Our focus was on a negative binomial response variable following a loglinear model. The relatively low bias found in the case of a binary response variable may reflect the fact that our causal effects estimands were defined based on a difference in means scale.
On the other hand, the empirical approach relies on a correct specification of the propensity score model. The empirical approach will therefore tend to be of interest in situations where modeling the mediator may be relatively difficult and where it is relatively easy to model the probability of exposure.
A number of refinements of the proposed method, as implemented in this paper, may be of interest. In the present version, we make distributional assumptions about Y, allowing maximum likelihood estimation of the regression coefficients. However, this aspect of the method is not essential (for example, quasi-likelihood could be used) and a more completely distribution-free approach is possible if desired. In addition, propensity-score weighting may lead to unstable estimates, particularly with inadequate overlap of the covariate distribution for the exposure groups.24 A reasonable solution in this situation may be to truncate the weights (that is, discard observations with estimated propensity score outside a specified range, such as 0.1 to 0.9), which may be viewed as conducting inference on a modified target population for which there is sufficient overlap in the covariate distribution between treatment groups.25
Supplementary Material
Acknowledgements
We thank the editor and reviewers for their insightful comments that helped improve the paper. Thanks also go to Wei Wang for assistance in conducting the simulation studies and in preparation of the paper, Suchitra Nelson for helpful discussion and for providing data from her study of dental outcomes in very low birth weight and normal birth weight children [NIDCR/NIH research grant number R21-DE16469] and Dr. Lynn Singer for data from her cohort study of these children [grant numbers MC-390592, MC-00127, MC-00334 from the Maternal and Child Health Program, Health Resources and Services Administration, Department of Health and Human Services].
Supported by the National Institute of Dental and Craniofacial Research / NIH (grant numbers R03DE018391 and R01DE022674).
APPENDIX
Consistency of Estimators
First, we show in the general confounding case, that the unweighted estimator (given as a special case of (9), or (5) with w2,3 in place of w3) is a consistent estimator of E{Y(x,M(x´)) | X=x´}. We assume sequential ignorability (3), consistency (Yi(X=Xi) = Yi), and model (4a), along with the causal model implied by Figure 1. First we note that
| (A1) |
Note that the equality in the second line above uses the assumption M∐W2|W1,3, X which is implied from the graph shown in Figure 1. Consistency of the estimator (1/Nx') ∑i∈Πx' g (β̂0 + β̂1x + β̂2mi + β̂3w2,3i) follows by noting that it is obtained from (A1) by replacing the integration (over the conditional joint distribution of (M,W) given X=x´) by summation over the empirical distribution of (M,W) given X=x´, and the regression coefficients (β’s) by their corresponding maximum likelihood estimates (denoted with hats). More generally, (1/Nx') ∑i∈Πx'ĝ*(x, mi,wi) provides a consistent estimator for E{Y(x,M(x´)) | X=x´} so long as ĝ*(x,m,w) for some function g* is a consistent estimator for E(Y | X=x, M=m, W=w).
Next we show consistency of the inverse-probability-weighting estimator (9) for E{Y(x,M(x´)) | X=r}, the expected potential-outcome for a reference group with exposure status X=r (possibly not equal to x´). In addition to the previous assumptions we require a correct specification of the exposure model (assumed to follow a logistic regression model (8) in our application). For brevity, let Hx,m,w ≡ E(Y | X=x, M=m, W=w), the conditional expected value of Y. Assuming the model used in the paper (4a), this would correspond to g(β0+ β1x + β2m + β3w2,3). We also write Hi(x) ≡ E(Yi(x,Mi(Xi)=mi) | Mi=mi, Wi=wi) as the predicted potential-outcome when X is set to x but M set to its observed value for individual i; note that, under Assumption 1, this equals E(Y | X=x, M=mi, W=wi) which equals g(β0+ β1x + β2mi + β3w2,3i) under Model 4a. We write Ĥi(x) to denote the maximum likelihood estimate of Hi(x). We consider the estimator
| (A2) |
where C is a normalizing constant (that is, the reciprocal of the sum of the weights in (A2)). Note that the term P̂(X = x') / P̂(X = r) cancels out in (A2) making this expression equal to (9); however, the term is left in here for the demonstration below. We see (by substitution of the empirical joint distribution function for FM,W|X=x´ and maximum likelihood estimates of the α’s and β’s) that the above estimator (A2) is consistent for
which can be re-expressed as
| (A3) |
| (A4) |
Expression (A3) follows from the main identifiability result of Imai et al.,6 while (A4) follows from sequential ignorability (Assumption 1). Consistency of (9) implies consistency of the natural direct and indirect estimators (in particular, (7) and (10)).
REFERENCES
- 1.Robins JM, Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology. 1992;3:143–155. doi: 10.1097/00001648-199203000-00013. 1992. [DOI] [PubMed] [Google Scholar]
- 2.Rubin DB. Direct and indirect causal effects via potential outcomes. Scan J Stat. 2004;31:161–170. [Google Scholar]
- 3.Ten Have TR, Joffe MM, Lynch KG, Brown GK, Maisto SA, Beck AT. Causal mediation analyses with rank preserving models. Biometrics. 2007;63:926–934. doi: 10.1111/j.1541-0420.2007.00766.x. [DOI] [PubMed] [Google Scholar]
- 4.Albert JM. Mediation analysis via potential outcomes models. Stat Med. 2008;27:1282–1304. doi: 10.1002/sim.3016. [DOI] [PubMed] [Google Scholar]
- 5.VanderWeele TJ. Marginal structural models for the estimation of direct and indirect effects. Epidemiology. 2009;20:18–26. doi: 10.1097/EDE.0b013e31818f69ce. [DOI] [PubMed] [Google Scholar]
- 6.Imai K, Keele L, Yamamoto T. Identification, inference and sensitivity analysis for causal mediation effects. Stat Sci. 2010;25:51–71. [Google Scholar]
- 7.Albert JM, Nelson S. Generalized causal mediation analysis. Biometrics. 2011;67:1028–1038. doi: 10.1111/j.1541-0420.2010.01547.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Huang B, Sivaganesan S, Succop P, Goodman E. Statistical assessment of mediational effects for logistic mediational models. Stat Med. 2004;23:2713–2728. doi: 10.1002/sim.1847. [DOI] [PubMed] [Google Scholar]
- 9.VanderWeele TJ, Vansteelandt S. Odds ratios for mediation analysis for a dichotomous outcome. American Journal of Epidemiology. 2010;172:1339–1348. doi: 10.1093/aje/kwq332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vansteelandt S. Estimating direct effects in cohort and case–control studies. Epidemiology. 2009;20:851–860. doi: 10.1097/EDE.0b013e3181b6f4c9. [DOI] [PubMed] [Google Scholar]
- 11.Avin C, Shpitser I, Pearl J. Identifiability of path-specific effects. International Joint Conference on Artificial Intelligence. 2005;19:357–363. [Google Scholar]
- 12.Pearl J. The causal mediation formula – a guide to the assessment of the pathways and mechanisms. Prevent Sci. 2011 doi: 10.1007/s11121-011-0270-1. In press. [DOI] [PubMed] [Google Scholar]
- 13.MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychol Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.van der Laan MJ, Petersen ML. Direct effect models. The International Journal of Biostatistics. 2001;4(1) doi: 10.2202/1557-4679.1064. Article 23. [DOI] [PubMed] [Google Scholar]
- 15.Tchetgen Tchetgen EJ, Shpitser I. Semiparametric estimation of models for natural direct and indirect effects. Harvard University Biostatistics Working Paper Series. 2011 Working Paper 129. [Google Scholar]
- 16.Tchetgen Tchetgen EJ, Shpitser I. Semiparametric theory for causal mediation analysis: efficiency bounds, multiple robustness, and sensitivity analysis. Harvard University Biostatistics Working Paper Series. 2011 doi: 10.1214/12-AOS990. Working Paper 130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Robins JM, Ritov Y. Toward a curse of dimensionality appropriate (CODA) asymptotic theory for semi-parametric models. Stat Med. 1997;16:285–319. doi: 10.1002/(sici)1097-0258(19970215)16:3<285::aid-sim535>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- 18.Sato T, Matsuyama Y. Marginal structural models as a tool for standardization. Epidemiology. 2003;14:680–686. doi: 10.1097/01.EDE.0000081989.82616.7d. [DOI] [PubMed] [Google Scholar]
- 19.Austin PC, Grootendorst P, Anderson GM. A comparison of the ability of different propensity score models to balance measured variables between treated and untreated subjects: a Monte Carlo study. Stat Med. 2007;26:734–753. doi: 10.1002/sim.2580. [DOI] [PubMed] [Google Scholar]
- 20.McCaffrey DF, Ridgeway G, Morral AR. Propensity score estimation with booted regression for evaluating causal effects in observational studies. Psychol Methods. 2004;9:403–425. doi: 10.1037/1082-989X.9.4.403. [DOI] [PubMed] [Google Scholar]
- 21.DiCiccio TJ, Efron B. Bootstrap confidence intervals. Stat Sci. 1996;11:189–212. [Google Scholar]
- 22.Nelson S, Albert JM, Lombardi G, Wishnek S, Asaad G, Kirchner HL, Singer LT. Dental caries and enamel defects in very low birth weight adolescents. Caries Res. 2010;44:509–518. doi: 10.1159/000320160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Singer LT, Yamashita TS, Lilien L, Collin M, Baley J. A longitudinal study of infants with bronchopulmonary dysplasia and very low birthweight. Pediatrics. 1997;100:987–993. doi: 10.1542/peds.100.6.987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Petersen ML, Porter KE, Gruber S, Wang Y, van der Laan MJ. Diagnosing and responding to violations in the positivity assumption. Stat Methods Med Res. 2012;21:31–54. doi: 10.1177/0962280210386207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Crump RK, Hotz VJ, Imbens GW, Mitnik OA. Dealing with limited overlap in estimation of average treatment effects. Biometrika. 2009;96:187–199. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.