Skip to main content
PMC home page
Cognitive Neurodynamics logoLink to Cognitive Neurodynamics
. 2013 Feb 1;7(5):441–447. doi: 10.1007/s11571-013-9246-0

Responses of cutaneous mechanoreceptors within fingerpad to stimulus information for tactile softness sensation of materials

Jiyong Hu 1,2,✉, Qun Zhao 1, Ruitao Jiang 1, Rubin Wang 3, Xin Ding 1,2
PMCID: PMC3773325  PMID: 24427218

Abstract

Softness sensation is one of primitive tactile textures. While the psychophysical characteristics of softness sensation have been thoroughly studied, it is lack of a deep understanding of the underlying neuromechanical principles. On the stimulus–response processes of human fingerpad touching fabrics and the physiological properties of slowly adapting type I (SAIs) cutaneous mechanoreceptors within fingerpad, a fabric-skin-receptor coupling model was built and validated. By the fabric-skin-receptor model a series of numerical experiments was conducted, and how the evoked neural responses of cutaneous mechanoreceptors change with the composite compliance of both fingerpad skin and the materials in contact was investigated. The results indicated that the evoked neural responses of populations of cutaneous mechanoreceptors by the physical stimulus from fabrics were nearly proportional to the perceived softness magnitude, and nonlinearly increased and then decreased with the effective elastic modulus of fabrics or the relative elastic modulus of fabrics to soft tissues within fingerpad, where the nonlinear inflection point depended on the touching force level. Therefore, it concluded that the tactile judgment of the physical information for softness sensation of objects was an encoding of neural responses of populations of SAIs cutaneous mechanoreceptors, and the physical information depended on the mechanical interaction of fingerpad and objects in contact.

Keywords: Mechanoreceptors, Tactile, Softness, Elastic modulus, Neuromechanics

Introduction

Followed Webber’s study on the relationship from physical stimulus to sensory responses, some researchers concerned on the effect of texture property of objects on the evoked responses of human tactile nervous system. Unfortunately, little progress has been made in the relationship between neurophysiological and psychophysical responses and the material properties other than surface roughness (Bergmann Tiest 2010).

Specifically, Srinivasan and LaMotte (1995, 1996) tested the evoked responses of cutaneous mechanoreceptors within fingertip by a given intensity of physical stimulus such as the elastic compliance and the spring stiffness. Their experimental results showed that the differences in the sufficiency of tactile information for the discrimination of object compliances could be explained by the mechanics of contact of the fingerpad and the object, and that the slowly adapting type I (SAIs) of cutaneous mechanoreceptors was mainly responsible for the discrimination of compliance of object surface. Lately, our lumped theoretical modeling and simulating results (Hu et al. 2009) and the observation from some tactile discrimination experiments (Bicchi et al. 2000; Liu and Song 2008) further clarified the first results suggested by Srinivasan. The present study will use the bulky thin-sheet materials as the tactile discrimination subject, and tests the role of SAIs in encoding tactile softness of fabrics.

It is well known that the SAI cutaneous mechanoreceptors are a type of mechanical transducers. The mechanical signals exerted on the SAIs sheet are transduced into the neural signals utilized by central nervous system. These cutaneous mechanical signals excited by external stimulus on skin, e.g. elastic stress or strain components, stimulate and change the dynamically balanced electrical potential of cell membrane of cutaneous mechanoreceptors, and then are transmitted and modulated into the neural information for tactile cognition behavior by the voltage gate-controlled theory (Lumpkin and Caterina 2007). To identify the relationship between the neural response and the compliance intensity of objects in contact with human skin, the best method is to record the real-time responses of all of evoked cutaneous mechanoreceptors, while the present electrophysiological experimental techniques are limited in devices and other experimental conditions. Therefore, a fabric-skin-receptor coupling model is needed to simulate the sensing processes of cutaneous mechanoreceptors to external stimulus. However, the prior equivalent biomechanical model (Hu et al. 2009) didn’t consider the neurodynamical behavior of cutaneous mechanoreceptors, and the fiber-skin-receptor model (Hu et al. 2011) couldn’t express the contact mechanics between fingerpad and a sheet of fabric.

For the existing art of study on the neural response of cutaneous mechanoreceptors to the stimulus of objects with different elastic modulus, this work focused on the case of thin-sheet fabrics as the subject of tactile discrimination by fingertip touching method, and on the basis of the typical physiological properties of SAIs mechanoreceptors developed a fabric-skin-receptor coupling model to discuss the tactile discrimination of fabric softness.

Modeling and methods

From the last section, the sensing processes of material properties by cutaneous mechanoreceptors could be abstracted into three sub-processes, namely contact interaction, transduction, and modulation. The transduction transformed stresses of soft tissues in the vicinity of individual SAIs cutaneous mechanoreceptors into biological current entering the afferent fibers through its membrane, a quantity known as the receptor current. In the model, inputs were filtered separately, then summed and converted into current to form the input into neural dynamical modulation model. Additionally, a statistical empirical model was used to describe the distribution of SAIs cutaneous mechanoreceptors within fingertip.

Contact mechanics

When human fingertip touches fabric surfaces, the contact interaction deforms the soft tissues within fingerpad and the fabric,and the individual deformation magnitude depends on their intrinsic mechanical behavior. To describe the contact mechanics, it was assumed that

  1. The mechanical behavior of each of contact bodies is elastic;

  2. the contact region between fingertip and fabric is circular;

The first assumption was based on the results that the evoked neural responses of SAIs cutaneous mechanoreceptors mainly depended on the quasi-static deformation of skin. Usually, the shape of contact region between fingerpad and object was oval or spherical, and the influence of the second assumption would be indirectly discussed by the change of contact center. The detail effect of distribution anisotropy of mechanoreceptor on tactile discrimination of softness was not the interest of the present work.

In combination with the assumptions and the classic contact mechanics theory (Johnson 1985), the contact pressure of fingertip touching fabric was written as (Hu et al. 2010)

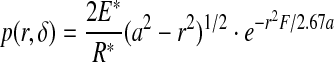graphic file with name M1.gif 1

in which

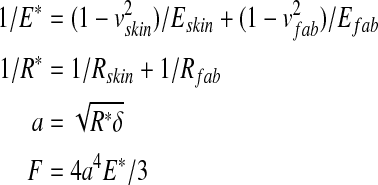graphic file with name M2.gif

where δ—the rigid body approach of bones of fingers to fabric, E—the Young modulus, v—the Poisson ratio, a—the maximum contact radius, r—distance from the contact center, F—the total touching force. For the mechanical behavior of fingerpad skin, the bulky modulus under compression was given by:

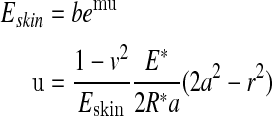graphic file with name M3.gif

in which the constants m and b was obtained by the equation fitting to the experimental curve, and u was the compression deflection of fingerpad skin.

And then, the stress components of soft tissues within fingerpad were derived as (Johnson 1985)

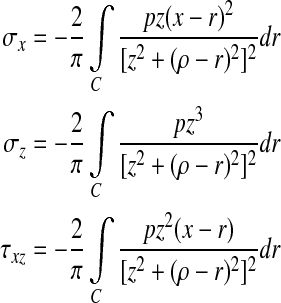graphic file with name M4.gif 2

where C is the contact domain. In the Cartesian three-axis rectangular coordinate system (x, y, z), 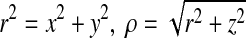Inline graphic. Here, the size of z represents the distance from mechanoreceptors to fingerpad surface.

On the other hand, when fingerpad touches thin-sheet materials, the perceived softness sensation mainly depended on their apparent thickness change and the bending deformation (Bergmann Tiest 2010). However, the thickness change of fabric was much less than its bending deformation. Thus, the effective elastic modulus of fabric was derived from the pure bending theory of thin plate, and was written as:

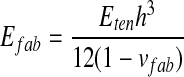graphic file with name M6.gif

in which h is the thickness of fabrics, Eten the tensile Young modulus of fabric, and v the Poisson ratio.

Transduction and modulation

While all types of in vivo observations match mechanical stimuli in the skin with the generated spikes at SAIs’ cell—the gross input–output relationship, other intermediate transformations were not currently observable. For example, we could neither measure the specific forces local to SAIs’ cell nor observe the transformation of those local forces to the timing of elicited spikes. It was reported that the maximum compressive or tensile component of stresses dominated the responses of SAI’s cutaneous mechanoreceptors. While the relationship between stresses and receptor current was unknown, mechanical sensory cells such as hair cells and pain receptors exhibited sigmoidal stimulus-current curves (Holt and Corey 2000; Siemens et al. 2006), and the same trend of tension-Voltage for muscles existed (Karagueuzian and Katzung 1982). For this reason, the transduction of SAI mechanoreceptors in this work was described as a sigmoidal function by

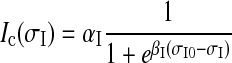graphic file with name M7.gif 3

where αI and βI specify the shape of the transduction function, and σI is the compressive stresses that give rises to the receptor current Ic and was derived from Eq. (2). During simulation, the model parameters αI, βI, and σI0 were firstly modified, so that this equation was capable of capturing the typical physiological properties of SAIs’ cutaneous mechanoreceptors.

Although the functional model of biological neural networks has been developed (Lo 2010), the current after transduction in the present simulation was input into the modulation model, namely the classical Hodgkin–Huxley equation systems (HH), which has been used to express human sensory responses (Du et al. 2012). Additionally, two revisions were made. Firstly, the temperature coefficient CTx (x = Na, K, L, K+) depended on the difference of the actual temperature T of human fingertip in present work (T = 32 °C) and the laboratory temperature T0 for squid membranes in Hodgkin’s experiments (Hodgkin and Huxley 1952). Secondly, the presence of transient K+ channels in higher organisms have been shown to regulate the discharge patterns of neurons, and the transient K+ channels (Connor and Stevens 1971; Connor et al. 1977; Wellnitz 2010) were then added to the original HH model. Thus, the modulation model from the HH equation systems (Hodgkin and Huxley 1952) was written as

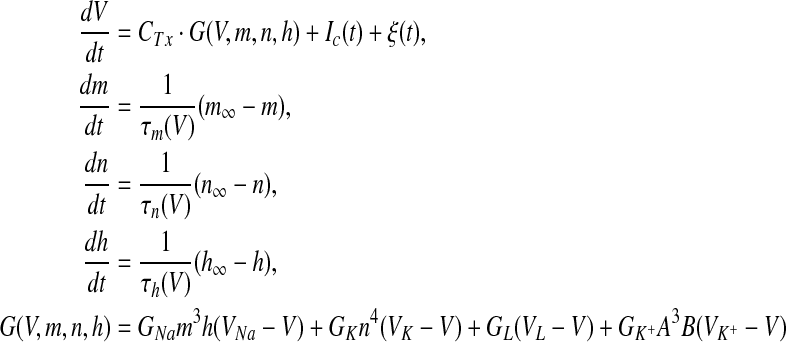graphic file with name M8.gif 4

in which the specific values for the constants of original HH equation systems and K+ channels were referred to Hodgkin and Huxley (1952) and Connor et al. (1977), and ε(t) the normal Gaussian noises. The drive current Ic was the sensing current by external stimulus (μA/cm2), which was calculated by Eq. (3). By a preliminary experiment, the optimized values for parameters in Eqs. (3) and (4) other than the original HH equation systems were αI = 20.3, βI = 0.6, CTNa = 1.05, CTK = 1.16, CTL = 1, C+TK=1.5, respectively.

Anatomical mapping of SAIs

In literatures there was not a clear description of spatial distribution pattern of SAIs cutaneous mechanoreceptors, and the Gaussian distribution pattern has been proposed to describe the change in spatial innervation density of low-threshold mechanoreceptors and free nerve endings in the extremities (Burgess and Perl 1973; Güçlü and Bolanowski 2002; Johansson and Vallbo 1979). In this context, all of SAIs cutaneous mechanoreceptors were assumed to distribute in a plane parallel with fingerpad, and the y-coordinates to be uniformly distributed along the medio-lateral line across human fingerpad. And also, the density of x-coordinates decreases proximally from the maximum at fingertip to the minimum at the first finger knuckle by obeying a half-Gaussian peak function. In terms of an independent x- and y-coordinate anatomical distribution, the joint probability density of SAIs cutaneous mechanoreceptors mapping into anatomical organization was

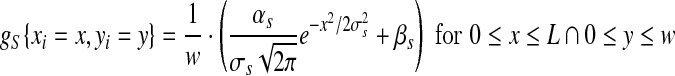graphic file with name M9.gif 5

and

graphic file with name M10.gif

where L, w—the length and width of the skin domain of human fingertip in study (L = 30 mm, w = 20 mm); αs, βs, σs—constants dependent on density dmax, dmin and dmean. The maximum and minimum SAIs’ density (dmax = 70.225 units/cm2 and dmin = 7.95 units/cm2) were respectively the upper and low quartile and estimated from the average innervation density (dmean = 41.605 units/cm2) on human fingertip (Johansson and Vallbo 1979). Parameters αS and βS were determined by the integral of the density function being unity (Güçlü and Bolanowski 2002), and was αS = 12.1534, βS = 19.9993, respectively.

Simulation and results

Simulation

After a preliminary simulation and validation of the established coupling model, the present work performed two series of numerical experiments to simulate the process of fingertip touching fabric, and represented the neural responses of SAIs cutaneous mechanoreceptors to the main material quality for tactile softness.

The first series of experiments simulated the case that each of subjects evaluates a set of fabrics with different effective elastic modulus. In this experiment, the distance of the bone center of fingertip approaching to fabric kept constant (1.0 mm), and the contact force was 1.0 N or so, which was comparable to the exerted mean force for tactile evaluation on material properties by fingertip (Bergmann Tiest 2010). By a comparison of the perceived softness magnitude with the evoked neural responses experiment, the model parameters were further modified. The results would uncover the relationship between neural responses and the effective elastic modulus of fabric.

The second series of experiments simulated the case of different subjects touching fabrics by a shift of contact center or depth of receptor underlying fingerpad skin and a change of fingerpad touching force when the other constraints kept constant. The experimental results would show the effect of the contact incline angle between fingertip and object surfaces or the distribution density of SAIs’ in the fingertip on tactile judgment of fabric softness.

The spiking rates and the inter-spike time were used to characterize the evoked neural responses of SAIs cutaneous mechanoreceptors, and for each of numerical experiments they were counted and their mean values as well the standard deviation were calculated.

Results and discussion

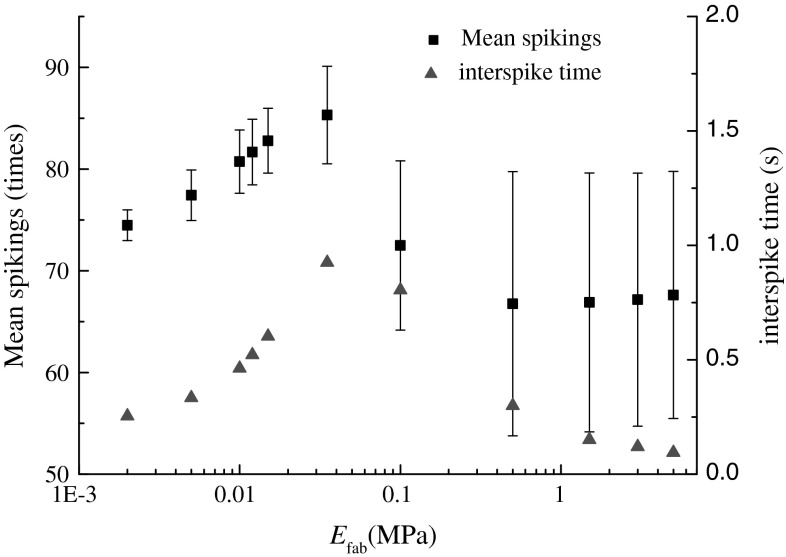
Figure 1 showed a significantly nonlinear change of the evoked neural responses of SAIs cutaneous mechanoreceptors with the effective elastic modulus of fabrics (t = 34.90, p ≈ 0), and the neural responses was significantly correlated negatively with the effective elastic modulus (Pearson_mean_spikings = −0.64, p < 0.03, Pearson_interspike = −0.63, p < 0.036). When the effective elastic modulus of fabrics was low, its increase apparently evoked stronger neural responses. Up to a limit of the effective elastic modulus of fabrics, the neural responses rapidly decreased and then leveled off. This phenomenon showed that the stimulus to cutaneous mechanoreceptors, namely the elastic deformation transferred from the dominate contribution of fabric to that of soft tissues within fingerpad (Hu et al. 2009), and for very high elastic modulus of fabric the domination of skin soft tissues in total elastic deformation leaded to the saturation of activation of cutaneous mechanoreceptor. Considering the conclusion that the evoked neural responses of populations of cutaneous mechanoreceptors were linearly related to the perceived intensity (Bensmaia 2008; Johnson et al. 2002), and the present results represented the trend of perceived softness changing with the effective elastic modulus of a set of fabric samples.

Fig. 1.

Fig. 1

Open in a new tab

Relationship between the effective elastic modulus of fabrics and the evoked neural responses

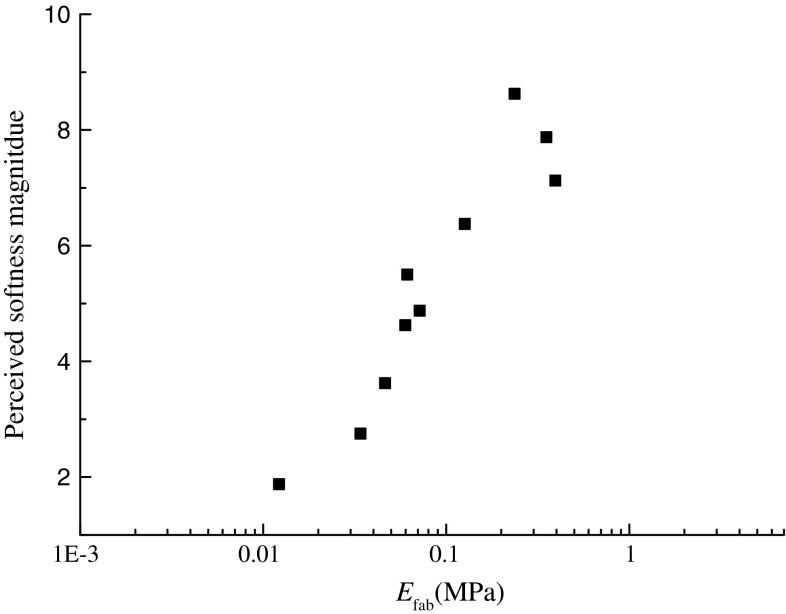
To validate the presumption that the perceived softness nonlinearly changed with the effective elastic modulus of fabrics, by a magnitude estimation experiments, thirty students evaluated the softness of a set of cotton fabric samples, the mean magnitude of perceived softness was calculated. The results from the sensory evaluation experiments were showed in Fig. 2. The similar change trend to that in Fig. 1 was observed, and the perceived softness magnitude increased with the effective elastic modulus of these fabric samples and up to a limit decreased. Compared to the results in Fig. 1, the perceived softness magnitude was significantly linear correlation with the evoked neural responses at a significant level of 0.05 (linear slope = 0.76). Indeed, investigations across the human cutaneous somatosensory system have shown that the evoked responses of cutaneous mechanoreceptors to physical stimulus were consistent with the psychophysical responses (Johnson et al. 2002), and then the present result indicated that the built fabric-skin-receptors model predicted the typical neural behavior of SAIs cutaneous mechanoreceptors and the typical tactile responses. Here, the comparison between sensory responses and neural responses neglected the perceptual learning (Stemme et al. 2011).

Fig. 2.

Fig. 2

Open in a new tab

Dependence of perceived softness magnitude on the effective elastic modulus of fabrics. The perceived softness magnitude was obtained by the standardized magnitude estimation experiments of 12 pieces of daily clothing fabrics with a size of 20 by 20 cm

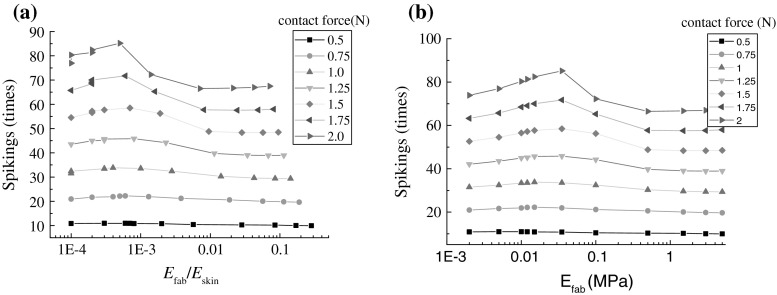
On the other hand, the nonlinear change in Fig. 1 was consistent with the previous conclusion, namely that the tactile discrimination of fabric softness depended on the ratio of bulk deformation of fingertip to the effective elastic modulus of fabrics (Hu et al. 2009). To clearly show the dependence of the evoked neural response on the ratio of elastic modulus of two contact bodies, Fig. 3 plotted their dependence under different contact loadings. In Fig. 3a, the spiking times changed with the elastic modulus ratio, which depended on the contact loading intensity. Only when the contact loading intensity went beyond the mean touching force for softness discrimination, the nonlinear change phenomenon could be significantly observed. And also, Fig. 3a showed a location difference of the inflection point from that Fig. 3b, and this further suggested that the tactile judgment of fabric softness depended on both the effective elastic modulus of fabrics and the bulky modulus of fingerpad under compression.

Fig. 3.

Fig. 3

Open in a new tab

Dependence of neural responses on the material elastic modulus under different contact loading level: a the ratio of effective elastic modulus of fabric to the bulky modulus of fingerpad; b effective elastic modulus of fabric

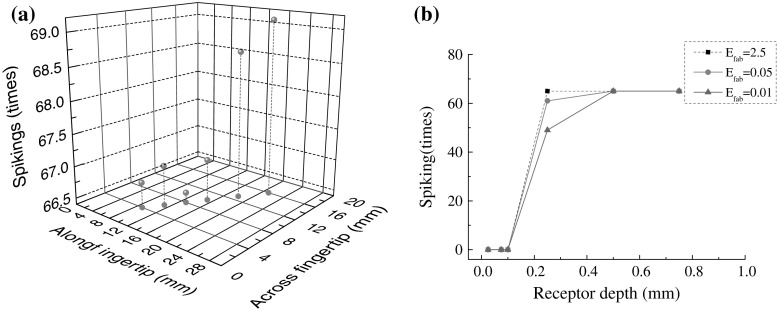
After a discussion about the dependence of neural responses of SAIs cutaneous mechanoreceptors on the material elastic modulus of both fabrics and fingerpad skin, the influences of the contact center and the mean depth of SAIs cutaneous mechanoreceptors underlying fingerpad skin were investigated. Figure 4a showed an increase of the total evoked spiking times with the contact center from the distal to proximal along fingertip. This phenomenon was consistent with the distribution of mechanoreceptors, and the evoked discharge of multiple Merkel cells assigned with a single SAI afferent joined. It indicated that the spatial summation of stimulus information could facilitate the tactile judgment of fabric softness. In this sense, the incline angle of finger would change the perceived softness magnitude in terms of the asymmetrical distribution of SAIs cutaneous mechanoreceptors within human fingertip. Although the SAIs cutaneous mechanoreceptors distributed along 0.5–0.9 mm depth (Wellnitz 2010), this difference of distribution depth has nearly no effect on the evoked spiking times, and even an large change of the effective compliance of fabrics occurred, as showed in Fig. 4b.

Fig. 4.

Fig. 4

Open in a new tab

dependence of neural responses of SAIs cutaneous mechanoreceptor on the spatial location: a the contact center, b the depth of SAIs underlying fingerpad skin

Conclusions

From Srinivasan’s suggestion that the neural responses of SAIs of cutaneous mechanoreceptors were highly related to the change of object compliance, this work built a fabric-skin-receptor coupling model to uncover the neural encoding of tactile softness sensation of fabrics, this model was validated by the fact that the neural responses of SAIs cutaneous mechanoreceptors predicted by the built fabric-skin-receptor coupling model was consistent with the subjective evaluation on tactile softness of fabric samples. From the results of two series of numerical experiments by the built model, the following conclusions were drawn.

The present results validated that the tactile judgment of fabric softness was an encoding of neural responses of populations of SAIs cutaneous mechanoreceptors, and that the exploratory manner of fingertip touching fabrics had an observable influence on the neural responses and then perceived softness magnitude.

The relationship between tactile response and material compliance was further specified. The tactile judgment of thin-sheet material elastic modulus, specifically the discriminability, was not only dependent on the effective elastic modulus of these materials, but mainly on the ratio of their modulus to the bulky modulus of fingerpad skin under compression, while the inflection point was related to the level of the touching force.

Altogether the evoked neural responses of populations of cutaneous mechanoreceptors encoded the composite compliance of both fingerpad skin and the object under compression, and the neural encoding of material properties of objects could be identified by an object-skin-receptor coupling model. However, the underlying cell or ionic channel mechanism for the observed stimulus–response relationship needs to study further.

Acknowledgments

This work was supported by the National Natural Science Foundation through project (No. 51175076, No. 11232005), the Natural Science Foundation of Shanghai through project (No. 12ZR1400500) and the Fundamental Research Funds for the Central Universities.

References

  1. Bensmaia SJ. Tactile intensity and population codes. Behav Brain Res. 2008;190(2):165–173. doi: 10.1016/j.bbr.2008.02.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bergmann Tiest WM. Tactual perception of material properties. Vision Res. 2010;50(24):2775–2782. doi: 10.1016/j.visres.2010.10.005. [DOI] [PubMed] [Google Scholar]
  3. Bicchi A, Scilingo EP, DeRossi D. Haptic discrimination of softness in teleoperation: the role of the contact area spread rate. IEEE Trans Robot Autom. 2000;16(5):496–504. doi: 10.1109/70.880800. [DOI] [Google Scholar]
  4. Burgess PR, Perl ER. Cutaneous mechanoreceptors and nociceptors. In: Iggo A, editor. Handbook of sensory physiology, somatosensory system. New York: Springer; 1973. [Google Scholar]
  5. Connor JA, Stevens CF. Voltage clamp studies of a transient outward membrane current in gastropod neural somato. J Physiol. 1971;213(1):21–30. doi: 10.1113/jphysiol.1971.sp009365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Connor JA, Walter D, McKown R. Neural repetitive firing: modifications of the Hodgkin–Huxley axon suggested by experimental results from crustacean axons. Biophys J. 1977;18(1):81–102. doi: 10.1016/S0006-3495(77)85598-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Du Y, Wang R, Han F, et al. Firing pattern and synchronization property analysis in a network model of the olfactory bulb. Cogn Neurodyn. 2012;6(2):203–209. doi: 10.1007/s11571-011-9189-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Güçlü B, Bolanowski SJ. Modeling population responses of rapidly-adapting mechanoreceptive fibers. J Comput Neurosci. 2002;12(3):201–218. doi: 10.1023/A:1016535413000. [DOI] [PubMed] [Google Scholar]
  9. Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Holt JR, Corey DP. Two mechanisms for transducer adaptation in vertebrate hair cells. PANS. 2000;97(22):11730–11735. doi: 10.1073/pnas.97.22.11730. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hu J, Ding X, Wang R, et al. Mechanistic principles of sensory analysis on object softness by touch means Chinese. J Theor Appl Mech. 2009;41(5):761–768. [Google Scholar]
  12. Hu J, Ding X, Wang R (2010) Effect of fingerpad mechanics and anatomical structures on tactile detection of compliant object. Paper presented at IEEE: the 6th international conference on natural computation (ICNC’10), Yantai, China August 2010, pp 2097–2101
  13. Hu J, Li Y, Ding X, et al. Neuromechanical representation of fabric-evoked prickliness: a fiber-skin-neuron model. Cogn Neurodyn. 2011;5(2):161–170. doi: 10.1007/s11571-010-9144-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Johansson RS, Vallbo AB. Tactile sensibility in the human hand: relative and absolute densities of four types of mechanoreceptive units in glabrous skin. J Physiol. 1979;286(1):283–300. doi: 10.1113/jphysiol.1979.sp012619. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Johnson KL. Contact mechanics. London: The Press Syndicate of the University of Cambridge; 1985. [Google Scholar]
  16. Johnson KO, Hsiao SS, Yashioka T. Neural coding and the basic law of psychophysics. Neuroscientist. 2002;8(2):111–121. doi: 10.1177/107385840200800207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Karagueuzian HS, Katzung BG. Voltage-clamp studies of transient inward current and mechanical oscillations induced by ouabain in ferret papillary muscle. J Physiol. 1982;327(1):255–271. doi: 10.1113/jphysiol.1982.sp014230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Liu J, Song AG. Discrimination and memory experiments on haptic perception of softness. Percept Mot Skills. 2008;106(1):295–306. doi: 10.2466/pms.106.1.295-306. [DOI] [PubMed] [Google Scholar]
  19. Lo JT. Functional model of biological neural networks. Cogn Neurodyn. 2010;4(4):295–313. doi: 10.1007/s11571-010-9110-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lumpkin EA, Caterina MJ. Mechanisms of sensory transduction in the skin. Nature. 2007;445(7130):858–865. doi: 10.1038/nature05662. [DOI] [PubMed] [Google Scholar]
  21. Siemens J, Zhou S, Piskorowski R, et al. Spider toxins activate the capsaicin receptor to produce inflammatory pain. Nature. 2006;444(7116):208–212. doi: 10.1038/nature05285. [DOI] [PubMed] [Google Scholar]
  22. Srinivasan MA, LaMotte RH. Tactual discrimination of softness. J Neurophysiol. 1995;73(1):88–101. doi: 10.1152/jn.1995.73.1.88. [DOI] [PubMed] [Google Scholar]
  23. Srinivasan MA, Lamotte RH. Tactual discrimination of softness: abilities and mechanisms. In: Franzen O, Johansson R, Terenius L, editors. Somesthesis and the neurobiology of the somatosensory cortex. Basel: Birkhauser Verlag; 1996. [Google Scholar]
  24. Stemme A, Deco G, Lang W. Perceptual learning with perceptions. Cogn Neurodyn. 2011;5(1):31–43. doi: 10.1007/s11571-010-9134-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Wellnitz SA (2010) Merkel cells in the structure and function of SAI touch receptors. Dissertation, Baylor College of Medicine

Articles from Cognitive Neurodynamics are provided here courtesy of Springer Science+Business Media B.V.

RESOURCES