Directional data analysis under the general projected normal distribution

Abstract

The projected normal distribution is an under-utilized model for explaining directional data. In particular, the general version provides flexibility, e.g., asymmetry and possible bimodality along with convenient regression specification. Here, we clarify the properties of this general class. We also develop fully Bayesian hierarchical models for analyzing circular data using this class. We show how they can be fit using MCMC methods with suitable latent variables. We show how posterior inference for distributional features such as the angular mean direction and concentration can be implemented as well as how prediction within the regression setting can be handled. With regard to model comparison, we argue for an out-of-sample approach using both a predictive likelihood scoring loss criterion and a cumulative rank probability score criterion.

1. Introduction

Directional data arise naturally in many scientific fields where observations are recorded as directions or angles relative to a system with a fixed orientation. Examples of circular data include wind directions, wave directions or directions of animal movement. A different type of circular data arises from converting periodic time data to angular measurements, for example, time data measured on a 24 h clock can be converted with 0:00 corresponding to 0 and 24:00 to 2π. The circular nature of such data creates difficulties in applying ordinary statistical methods used for inline data. For example, with angular observations 1°, 0° and 359°, it is inappropriate to use the arithmetic mean, which is 120°. (Of course, the variance and other linear features suffer from similar problems.) A more sensible measurement is the angular mean direction (formally defined in Section 2) which is 0°. Over the last fifty years, substantial techniques and methods have been developed paralleling those for linear data [12, 14, 7, 1]. Lee [11] gives a recent review of statistical methods for analyzing circular data.

Corresponding to the usual parametric distributions for linear variables, there are several parametric distributions for circular variables. The most commonly used circular distribution is the von Mises distribution (also known as circular normal distribution). The von Mises distribution is the maximum entropy distribution on the circle for a fixed mean direction and dispersion and can be considered as an analogue of the normal distribution on the real line. The von Mises distribution M (μ, κ) has two parameters: the mean direction μ and the concentration parameter κ. It is unimodal and symmetric about its mode which is the same as the mean direction μ. The mean resultant length has the expression I₁(κ)/I₀(κ), where I_v is the modified Bessel function of the first kind of order v.

Circular distributions can also be obtained by radial projection of bivariate distributions on the plane. For any random vector Y ∈ ℜ² with Pr(Y = 0) = 0, U = Y/‖Y‖ is a random point on the unit circle. The angle between the unit vector to this point and, say the x-axis becomes a random angle. An important distribution within this family is the projected normal distribution, where Y follows a bivariate normal distribution N₂(μ, Σ). The projected normal distribution, denoted as PN₂(μ, Σ), is also referred to as an offset normal distribution [12, 7] or an angular Gaussian distribution [22]. The projected normal distribution with identity covariance matrix, also known as the displaced normal[10], has attracted some work in the literature; see references below. However, like the von Mises, it suffers the limitation of symmetry and unimodality. For general Σ, the projected normal distribution will be asymmetric and can be bimodal, and is thus a more flexible family compared to the von Mises distribution. However, due to the unwieldy expression for the density function (see (1) below), the general version has received little attention in the literature.

The contribution of this paper is to demonstrate how to handle circular data using the general projected normal distribution PN₂(μ, Σ). We show how to implement flexible circular regression modeling with linear covariates under the assumption of a general projected normal distribution. We work in a fully Bayesian framework and provide full inference including mean direction, concentration, regression coefficients, and predictive distributions with highest posterior density (HPD) arcs to produce credible sets. We also argue for the use of out-of-sample model comparison, employing a log likelihood scoring rule, a continuous rank probability score rule, and the mean length of HPD intervals of the predictive distribution.

The regression model with circular response and linear covariates is referred to as Linear-Circular regression [7]. Previously proposed circular regression models are mostly based on the assumption of the von Mises distribution [4, 8, 2]. Gould [4] sets ${\mu }_i={\mu }_0+{\text{x}\prime }_i\beta$ and κ_i = κ for i = 1, …, n, allowing the mean of von Mises distribution to vary by levels of covariates. Johnson and Wehrly [8] consider only one covariate and propose the location model and concentration model, where a link function is used to convert the covariate to a value between 0 and 1. The location model takes μ_i = μ₀ + 2π F(x_i) and κ_i = κ, where F is chosen to be a known cumulative distribution function. Fisher and Lee [2] further generalize the Johnson-Wehrly models by a monotone link function g(·) mapping the linear predictor ${\text{x}\prime }_i\beta$ to (−π, π), with g(0) = 0. (A common choice for g(·) is the arctan function.) Their location model takes ${\mu }_i={\mu }_0+g({\text{x}\prime }_i\beta )$ and κ_i = κ. However, computational difficulty arises when fitting a Fisher-Lee model with more than one covariate due to the multimodality of the likelihood.

Returning to the projected normal model with identity covariance matrix, Presnell et al. [17] introduce the spherically projected multivariate linear model based on the assumption of a projected normal distribution. Their paper demonstrates that the projected normal distribution has convenient regression specification and obtains the maximum likelihood estimates for the circular regression model using the EM algorithm. Extending Presnell et al. [17], Nuñez-Antonio and Gutiérrez-Peña [15] and Nuñez-Antonio et al. [16] show how to fit the projected normal distribution in a Bayesian framework using a Gibbs sampler, without and with covariates, respectively. Hernandez-Stumpfhauser et al. [6] build a mixed effect model based on the projected normal distribution by including the factors into the mean vector μ. Again, the above papers set the covariance matrix of the projected normal Σ to be I, arguing that this avoids an identifiability issue, that it is a rich enough model, and that it provides computational convenience. Again, our goal is to demonstrate the benefits of working with the more general Σ.

The format of the paper is as follows. Section 2 illustrates the general projected normal distribution and its properties. Section 3 demonstrates how to implement model fitting, inference and prediction and proposes the criteria for model comparison. Section 4 provides simulation examples and real data examples on directions of animal movements. Section 5 offers a summary and future directions.

2. The general projected normal model

In the sequel, we shall use ϕ_r and Φ_r to denote the pdf and cdf of a r-dimensional standard normal distribution. Assume a random vector Y = (Y₁, …, Y_r)′ follows an r ≥ 2-dimensional multivariate normal distribution, with mean μ and covariance matrix Σ. The corresponding random unit vector U = Y/‖Y‖ is said to follow a projected normal distribution [18, 14] with the same parameters, denoted as PN_r(μ, Σ). Here, we confine ourselves to the circular projected normal distribution, the special case when r = 2. Let ϕ₂(y₁, y₂; μ, Σ) be the density function of the bivariate normal distribution with mean vector μ = (μ₁, μ₂)′ and covariance matrix Σ. Let ${\sigma }_1^2$ and ${\sigma }_2^2$ be the variances of Y₁ and Y₂ and ρ denote the correlation between the two variables. The corresponding covariance matrix has the expression,

$$\sum =\left(\begin{array}{cc}{\sigma }_1^2& \rho {\sigma }_1{\sigma }_2\\ \rho {\sigma }_1{\sigma }_2& {\sigma }_2^2\end{array}\right).$$

In this case, we convert Y, equivalently U to a random angular variable Θ through U₁ = cos Θ and U₂ = sin Θ whence tan Θ = Y₂/Y₁ = U₂/U₁ which exists with probability 1. Inversion for Θ requires care since the period for the tan function is only π. The usual choice is the arctan^* function¹. The resulting density function, f(θ; μ₁, μ₂, σ₁, σ₂, ρ), is [12, pp. 52],

$$\begin{array}{c}f(\theta |\mu ,\sum )=\frac{{\varphi }_2({\mu }_1,{\mu }_2;0,\sum )}{C(\theta )}\\ +\frac{aD(\theta ){\Phi }_1\{D(\theta ){\varphi }_1\}[a{\{C(\theta )\}}^{-\frac{1}{2}}({\mu }_1\sin \theta -{\mu }_2\cos \theta )]}{C(\theta )},\end{array}$$ (1)

where ϕ and Φ are defined at the beginning of this section, and

$$\begin{array}{c}a={\{{\sigma }_1{\sigma }_2\sqrt{1-{\rho }^2}\}}^{-1},\\ C(\theta )=a^2({\sigma }_2^2{\cos }^2\theta -\rho {\sigma }_1{\sigma }_2\sin 2\theta +{\sigma }_1^2{\sin }^2\theta ),\\ D(\theta )=a^2{\{C(\theta )\}}^{-\frac{1}{2}}\{{\mu }_1{\sigma }_2({\sigma }_2\cos \theta -\rho {\sigma }_1\sin \theta )+{\mu }_2{\sigma }_1({\sigma }_1\sin \theta -\rho {\sigma }_2\cos \theta )\}.\end{array}$$

Because of the complicated form of this density function, the general version of the projected normal has only been considered theoretically. Data analysis and inference in the literature has been confined to the case of the projected normal PN₂(μ, I) [17, 15, 6, 16]. In this case, a = 1, C(θ) = 1 and D(θ) = μ₁ cos θ + μ₂ sin θ.

With the identity covariance matrix, the corresponding density function is symmetric and unimodal. Thus PN₂(μ, I) and the von Mises distribution M(μ, κ) each have two parameters and they can be aligned by matching the mean direction and the mean resultant length. When μ₁ = μ₂ = 0, the distribution reduces to the uniform distribution on the circle.

The mean direction for the projected normal is the unit vector, E(U)/‖E(U)‖ and the associated mean resultant length, γ = ‖E(U)‖ ≤ 1, provides a concentration. The angular mean direction, ω, arises from E(U) = (E cos Θ, E sin Θ)′. That is, cos ω = E cos Θ/γ, sin ω = E sin Θ/γ and tan ω = E sin Θ/E cos Θ = E(U₂)/E(U₁). Thus, since Y₁ = ‖Y‖ cos Θ and Y₂ = ‖Y‖ sin Θ, we can see that, in general,

$$\tan \omega =\frac{\text{E}(Y_2/\Vert \text{Y}\Vert )}{\text{E}(Y_1/\Vert \text{Y}\Vert )}.$$

In Appendix A we show that when Σ = I, tan ω = μ₂/μ₁ but that this is not true for general Σ. For instance, with Σ = I, for μ₁ = 0 and μ₂ ≠ 0, the angular mean direction is π/2 if μ₂ is positive and is 3π/2 if μ₂ is negative. When μ₁ ≠ 0 and μ₂ = 0, the angular mean direction is 0 if μ₁ is positive and is π if μ₁ is negative. To our knowledge, a closed form expression for the angular mean direction in the general case μ₁ ≠ 0 and μ₂ ≠ 0 is not available. When Σ = I, Kendall [10] provides a formula for the mean resultant length (or concentration), γ = ‖μ‖, i.e., γ = (πζ/2)^1/2exp(−ζ)(I₀(ζ) + I₁(ζ)) where ζ = γ²/4, and I_v is the modified Bessel function of the first kind of order v. Again, a closed form expression in the general case is not available. However, both mean direction and mean resultant length can be computed using numerical integration or Monte Carlo methods. Below, we obtain these in a regression context using Monte Carlo methods.

Special cases of PN₂(μ, I) with varying parameter μ₁ are shown in Figure 1. In general, with increasing γ, the density becomes increasingly peaked.

Figure 1.

Density of PN₂ with μ₂ = 0, Σ = I for different values of μ₁

Another special case of a general projected normal distribution is the angular central Gaussian distribution PN₂(0, Σ). The angular central Gaussian is symmetric and antipodal, with two equal modes in exactly opposite directions. When σ₁ = σ₂ = σ, the density reduces to

$$f(\theta |0,0,\sigma ,\rho )=\frac{\sqrt{1-{\rho }^2}}{2\pi (1-\rho sin2\theta )},$$

revealing symmetry relative to the increasing 45°-line when ρ > 0, relative to the decreasing 45°-line when ρ < 0. Equivalently, f(θ|0, 0, σ, −ρ) = f(θ + π/2|0, 0, σ, ρ).

Let Σ = VΛV′ be an eigen-decomposition of Σ with V the matrix of unit eigenvectors and Λ the diagonal matrix of eigenvalues. Thus the bivariate random vector Y ~ V Λ^½ N(0, I), where V is the rotation matrix. For any ρ > 0 and σ₁ = σ₂, the rotation matrix is $V=\left(\begin{array}{cc}1/\sqrt{2}& -1/\sqrt{2}\\ 1/\sqrt{2}& 1/\sqrt{2}\end{array}\right)$ and the modes occur at π/4 and 5π/4; for any ρ < 0 and σ₁ = σ₂, the rotation matrix is $V=\left(\begin{array}{cc}-1/\sqrt{2}& -1/\sqrt{2}\\ 1/\sqrt{2}& -1/\sqrt{2}\end{array}\right)$ and the modes occur at 3π/4 and 7π/4. In the case of σ₁ = σ₂, the parameter ρ changes the concentration of the circular density, but not the modal axis (see Figure 2(a)). When σ₁ ≠ σ₂, no simple rotations are available (see Figure 2(b)). The angular central Gaussian distribution always produces a symmetric and antipodal density, except in the uniform case where σ₁ = σ₂ and ρ = 0.

Figure 2.

Density of PN₂ with μ₁ = μ₂ = 0, (a) σ₁ = σ₂, (b) σ₁ = 2σ₂ for different values of ρ

In general, the shape of the PN₂(μ, Σ) density with μ ≠ 0 and Σ ≠ I can be asymmetric or possibly bimodal (antipodality with different amplitudes or more general bimodality but no more than two modes) (see Figure 3). The five parameters μ₁, μ₂, σ₁, σ₂ and ρ together determine the shape of the density. However, unlike in the previous special cases, it is not clear how changing a single parameter affects the shape of the density. This suggests that, in the general case, interpretation of the parameters can be difficult. However, if the goal is flexibility and prediction, this specification can be attractive.

Figure 3.

Shapes for the general projected normal distribution

Since the distribution of U, hence, Θ does not change if the random vector Y is scaled by any a > 0, a further constraint on the parameters is needed for identifiability. To fix the scale of Σ, without loss of generality, we set σ₂ = 1, so that the covariance matrix Σ becomes $\sum =\left(\begin{array}{cc}{\tau }^2& \rho \tau \\ \rho \tau & 1\end{array}\right)$, and thus, we have a four parameter (μ₁, μ₂, τ and ρ) distribution.

In many applications, one encounters asymmetric circular data so that fitting them with a unimodal and symmetric model may result in misleading conclusions. In Section 4 below, we revisit the classical turtle movement dataset [14]; this dataset, shown in Figure 6, provides an example of circular data where an assumption of symmetry and unimodality does not seem appropriate. Asymmetry and bimodality can also be obtained by mixing two von Mises distributions, with directly interpretable parameters. However, such mixtures need to be identified and parameter estimation can be difficult if the component modes are not well-separated; see Jones and James [9] and Spurr and Koutbeiy [19] for parameter estimation based on numerical optimization. Moreover, if the goal is to capture asymmetry, it is not clear that a two-component mixture model is an appropriate specification. The general projected normal distribution provides an alternative which is straightforward to fit (within a Bayesian framework) and allows assessment of departure from symmetry and unimodality through departure of Σ from I.

Figure 6.

Turtle data example

The regression specification under the general projected model is ${\Theta }_i\stackrel{\text{ind}}{~}P{N}_2(B^T{\text{X}}_i,\sum )$, with regression coefficient matrix $B_{2\times p}^T=({\beta }_1,\dots ,{\beta }_p)$ and covariates X_i = (1, X_i,1, …, X_i,p−1)′. In this model, changing the levels of the covariates is equivalent to changing the mean vector μ_i. With a fixed covariance matrix, different levels of the covariates can result in very different predictive distributions. However, smoothness of X in μ₁(X) and μ₂(X) induces smoothness in PN₂(B^TX, Σ) over X and thus smoothness in the mean directions and concentrations, as we illustrate in Section 4.3 below.

3. Bayesian inference for the general PN

With conditionally independent observations, fitting a general projected normal model in the Bayesian framework is straightforward; we illustrate both without and with covariates.

3.1. Model fitting

As discussed in the previous section, the covariance matrix is set to be $\sum =\left(\begin{array}{cc}{\tau }^2& \rho \tau \\ \rho \tau & 1\end{array}\right)$, so that, with no covariates, we have four parameters to estimate: μ₁, μ₂, τ and ρ. For data θ = (θ₁, θ₂, …, θ_n), the likelihood is ${{\displaystyle \prod }}_{i=1}^{n}f({\theta }_i)$, where f(θ_i) has the expression shown in (1). A prior is added for μ₁, μ₂, τ and ρ. In implementing MCMC to fit the model, it is easiest to introduce a latent realization r_i associated with θ_i, whence a vector r = (r₁, r₂, …, r_n). The joint density of (Θ, R) can be obtained by changing variables from Y = (Y₁, Y₂)′ to (R, Θ)′. The likelihood under this data augmentation is:

$$\begin{array}{c}{\displaystyle \prod }_{i=1}^{n}f(r_i,{\theta }_i|\mu ,\sum )={(2\pi )}^{-n}|\sum {|}^{-\frac{n}{2}}\\ \exp (-\frac{{{\displaystyle \sum }}_{i=1}^n[(r_i{\text{u}}_i-\mu )\prime {\sum }^{-1}(r_i{\text{u}}_i-\mu )]}{2}){\displaystyle \prod }_{i=1}^n{r}_i\end{array}$$ (2)

where u_i = (cos θ_i, sin θ_i)′. Conjugacy for μ arises under a bivariate normal prior, e.g., μ ~ N(0, λ₀ I). However, there is still no closed form for the full conditional posteriors of τ², ρ and the augmented parameter r. For τ², we choose the prior as an inverse Gamma IG(a_τ, b_τ) with mean b_τ/(a_τ − 1) = 1; for ρ, a uniform distribution between −1 and 1. For the MCMC implementation, the full conditional distributions are given in Appendix B.

For the PN regression model with p − 1 covariates, the parameters to infer about are the regression coefficients $B_{2\times p}^T=({\beta }_1,\dots {\beta }_p)$, along with τ² and ρ. The likelihood under the data augmentation becomes:

$$\begin{array}{c}{\displaystyle \prod _{i=0}^{n}f(r_i,{\theta }_i|B,\sum )}={(2\text{π})}^{-n}|\sum {|}^{-\frac{n}{2}}{\displaystyle \prod _{i=1}^n{r}_i}\\ \exp (-\frac{{\displaystyle {\sum }_{i=1}^n[(r_i{\text{u}}_i-B^T{\text{x}}_i)\prime {\sum }^{-1}(r_i{\text{u}}_i-B^T{\text{x}}_i)]}}{2})\end{array}$$ (3)

where x_i = (1, x_i,1, …, x_{i, p−1})′. For convenience, we partition the coefficient matrix $B_{2\times p}^T$ as B^T = (β₁, …, β_p), with β_j ∈ ℜ², j = 1, …, p. Again, a Gaussian prior is chosen for β_j, e.g., β_j ~ N(0, λ₀I). The full conditionals are again provided in Appendix B.

3.2. Inference

Using MCMC model fitting, we obtain posterior samples for the parameters μ and Σ, or B and Σ for the density estimation or regression model, respectively.

In the “no covariates” case, the posterior density estimate is f(θ|data) = ∫f(θ|Ψ)f(Ψ|data) dΨ, where Ψ = {μ, Σ}. As a mixture of general PN densities, its form is very flexible. Posterior samples of the parameters provide the usual Rao-Blackwellized estimator. That is, given a posterior sample of the parameters ${\mu }_1^{(g)}$, ${\mu }_2^{(g)}$, ${({\tau }^2)}^{(g)}$, and ρ^(g), g = 1, …, G, we evaluate f(θ|μ^(g), Σ^(g)) (expression (1)) on a uniform grid of points on [0, 2π). Then, averaging over g yields an estimate of the posterior at the resolution of the grid points.

As previously indicated, closed form expressions for the mean direction and the mean resultant length of the projected normal distribution are only available for the special case PN₂(μ, I). MCMC Bayesian model fitting enables inference for the mean direction and mean resultant length without requiring analytical forms; in fact, we obtain posterior samples. According to the definition, the mean direction is $\omega ={arctan}^{\ast }\left(\frac{\beta }{\alpha }\right)$ and the resultant length is $\text{γ}=\sqrt{({\alpha }^2+{\beta }^2)}$, where α = E cos Θ and β = E sin Θ. Thus, for each posterior draw, ${\mu }_1^{(g)}$, ${\mu }_2^{(g)}$, ${({\tau }^2)}^{(g)}$ and ρ^(g), we obtain α^(g) and β^(g) by Monte Carlo integration. Therefore, we obtain the posterior samples ω^(g) and γ^(g) as arctan*(β^(g)/α^(g)) and $\sqrt{{({\alpha }^{(g)})}^2+{({\beta }^{(g)})}^2}$, respectively. Illustrative posterior distributions are provided below.

It is worth noting that ω and γ are parametric functional associated with f(θ|μ, Σ) and we are obtaining the posterior distribution associated with these functionals. If we wanted ω and γ associated with f(θ|data), we are seeking constants and it would be easiest to obtain sample estimates by taking draws from this distribution. This would be done by drawing θ^(g) from f(θ|μ^(g), Σ^(g)) created as above. In fact, we would draw Y^(g) from N(μ^(g), Σ^(g)) and convert to θ^(g). We recall the usual method-of-moments estimates, i.e., for each θ^(g), obtain (cos θ^(g), sin θ^(g)). Compute $\overline{C}={\sum }_{g}cos{\theta }^{(g)}/G$ and $\overline{S}={\sum }_{g}sin{\theta }^{(g)}/G$. Then, $\widehat{\omega }={arctan}^{\ast }\frac{\overline{S}}{\overline{C}}$ and $\widehat{\gamma }=\sqrt{{\overline{C}}^2+{\overline{S}}^2}$.

For the PN regression model, besides estimation of the regression coefficients, we are also interested in prediction at new levels of the covariates say, x^*. However, given the posterior sample of parameters and the covariates, the values of the density function f(θ|x^*, B^(g), Σ^(g)) are calculated on a uniform grid over [0, 2π). By taking the average of the density values on each grid over the samples, we obtain the predictive distribution given the covariates x^*. Again, as a mixture of general PN densities, its shape is very flexible. In particular, equal tail credible intervals may be inappropriate; HPD credible intervals are more sensible. In general, the HPD arc is not trivial to calculate but it can be obtained numerically.

3.3. Model comparison using proper scoring rules

For the PN regression model, we focus on the the performance of out-of-sample prediction. We fit models using the training data θ = (θ₁, …, θ_n)′, and evaluate models using a holdout set ${\theta }^{\ast }=({\theta }_1^{\ast },\dots ,{\theta }_m^{\ast })\prime$. As previously discussed, given the covariate levels, x^*, we can calculate the length of the HPD credible interval and also see whether the holdout value θ^* falls in this HPD region.

However, if predictive distributions are a goal, then model performance should be judged with regard to the entire predictive distribution. We need to compare the predictive distribution at x^* with the held out θ^*. Two proper scoring rules for doing this are the predictive log scoring loss (PLSL) [3] and the continuous ranked probability score (CRPS) as in [5]. Using posterior samples under (3), for the former, we calculate the quantity

$$\text{PLSL}=-\frac{2}{G}{\displaystyle \sum }_{g=1}^G{\displaystyle \sum }_{j=1}^m\text{log}f({\theta }_j^{\ast }|x_j^{\ast },B^{(g)},{\sum }^{(g)}).$$

As a model comparison criterion, the model with smaller PLSL is favored.

For the latter, Grimit et al. [5] developed the continuous ranked probability score (CRPS) for circular variables,

$${\text{CRPS}}_{\text{circ}}(F,{\theta }^{\ast })=\text{E}\{\alpha (\Theta ,{\theta }^{\ast })\}-\frac{1}{2}\text{E}\{\alpha (\Theta ,\Theta \prime )\},$$

where F is the circular predictive distribution, θ^* is the holdout value, α is the angular distance ² and Θ and Θ′ are independent copies of a circular random variable with distribution F. Although we do not have an explicit expression for the predictive distribution, F, the CRPS is readily approximated in the Bayesian framework. With posterior samples ${\theta }_i^{(g)}$ from $P{N}_2({(B^{(g)})}^T{\text{x}}_j^{\ast },{\sum }^{(g)})$, the CRPS associated with the i-th holdout value can be approximated by

$${\text{GRPS}}_i=\frac{1}{G}{\displaystyle \sum }_{g=1}^G\alpha ({\theta }_i^{(g)},{\theta }_i^{\ast })-\frac{1}{2G^2}{\displaystyle \sum }_{g=1}^G{\displaystyle \sum }_{k=1}^G\alpha ({\theta }_i^{(g)},{\theta }_i^{(k)}).$$

Finally, we compare the models by taking average CRPS over holdout samples. Again, the model with the smaller CRPS is favored. Both criteria are utilized in Section 4.

4. Examples

Having shown how to fit a general PN model in the Bayesian framework using MCMC, we now present several illustrations. In Section 4.1 we consider simulated examples while in Sections 4.2 and 4.3 we consider two real datasets. The first is the classic turtle movement dataset (mentioned in Section 2), which we use to illustrate density estimation; the second dataset concerns butterfly orientations [21, 17], which we use to illustrate circular regression with linear covariates.

4.1. Simulation: Density estimation and PN regression

First, we illustrate the density estimation using samples generated from a skewed PN distribution. The parameter values used in this example are μ₁ = −0.19, μ₂ = 1.25, σ₁ = 1.58, σ₂ = 1.4 and ρ = −0.84; the distribution is shown as the solid line in Figure 4. Four different sample sizes were used, n = 200, 500, 1000 and 2000. We fit the general projected normal and displaced normal (Σ = I) as described in Section 3 and display the posterior estimates, using a set of grid points, in Figure 4 (only shown for n = 200 and 2000). In addition, we fit a two component mixture of von Mises by utilizing the movMF function in the R package “movMF”. The result is also shown in Figure 4. We see that the projected normal recovers the true distribution quite well, even for the smaller sample size. The displaced normal and the von Mises mixture are not adequate. Posterior samples of the mean direction and mean resultant length for all four sample sizes are obtained, following Section 3.2, and the resultant posterior density plots are shown in Figure 5.

Figure 4.

Simulation results of density estimation

Figure 5.

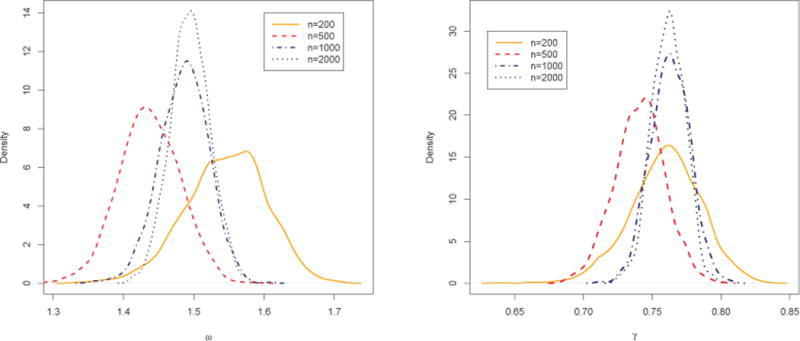
Posterior distributions of mean direction ω and mean resultant length γ

Next, we turn to the regression problem, employing simulation examples with focus on prediction and model comparison. We simulate θ_i, i = 1, …, n + m, from a general projected normal distribution PN₂(B^T x_i, Σ), where x_i = (1, x_i,1, …, x_{i, p−1})′. From many simulation examples we have run, to illustrate here, we choose two τ² values, 1 and 2.56, keeping ρ = .4 with n = 60 and 200. We take p = 3 where the covariates x_i,1 and x_i,2 are generated uniformly on (−1, 1) and the regression coefficients are set to be β₁ = (2, −2)′, β₂ = (1, −1)′ and β₃ = (1, 1)′. From Section 3, the prior for τ² is IG(5, 4) and for the β’s, λ₀ = 0.5. The performance of prediction is evaluated on a validation set of size m = 100. We run Metropolis-Hastings within the Gibbs sampler for 25000 iterations with a burn-in of 5000, thinning the remainder by collecting every 5th sample.

For each of the four cases, both the general projected normal regression PN(B^T x_i, Σ) and the displaced normal regression PN(B^T x_i, I) are fitted for comparison. The posterior summaries for the parameters are shown in Table 1. As we would expect, the general PN outperforms the displaced PN. The latter gives point estimates that are less well-centered with credible intervals that are too tight. It performs relatively worse for the larger τ² and for the larger training sample size. We see the benefit of using Σ ≠ I when this is the case.

Table 1.

Simulation Results of PN regression (n, τ², ρ): posterior mean, lower and upper bounds of 95% credible interval for parameters τ², ρ and β_j = (β_j1, β_j2)′ (j = 1, 2, 3)

		n = 60, τ2 = 1, ρ = 0.4						n = 200, τ2 = 1, ρ = 0.4
		Σ ≠ I			Σ = I			Σ ≠ I			Σ = I
par.	true	mean	2.5%	97.5%	mean	2.5%	97.5%	mean	2.5%	97.5%	mean	2.5%	97.5%
β11	2	1.66	1.27	2.22	1.81	1.41	2.23	1.69	1.51	1.95	1.50	1.32	1.70
β21	1	1.14	0.36	1.86	1.32	0.64	2.09	0.58	0.28	0.86	0.34	0.05	0.61
β31	1	0.88	0.27	1.56	0.85	0.22	1.42	1.21	0.91	1.49	0.84	0.56	1.14
β12	−2	−1.78	−2.28	−1.39	−1.90	−2.31	−1.49	−1.78	−2.01	−1.54	−1.58	−1.76	−1.40
β22	−1	−0.55	−1.26	0.19	−0.70	−1.45	−0.05	−0.61	−0.92	−0.31	−0.38	−0.65	−0.10
β32	1	0.89	0.26	1.58	0.96	0.38	1.56	0.59	0.28	0.90	0.58	0.29	0.84
τ2	1	0.91	0.49	1.55	–	–	–	0.76	0.56	1.04	–	–	–
ρ	0.4	0.23	−0.15	0.62	–	–	–	0.42	0.12	0.68	–	–	–

		n = 60, τ2 = 2.56, ρ = 0.4						n = 200, τ2 = 2.56, ρ = 0.4
		Σ ≠ I			Σ = I			Σ ≠ I			Σ = I
par.	true	mean	2.5%	97.5%	mean	2.5%	97.5%	mean	2.5%	97.5%	mean	2.5%	97.5%
β11	2	1.41	0.96	1.98	1.18	0.86	1.49	1.61	1.27	1.91	1.22	1.03	1.40
β21	1	0.58	−0.37	1.46	0.41	−0.20	1.00	0.81	0.43	1.20	0.41	0.12	0.71
β31	1	1.03	0.25	1.90	0.74	0.15	1.36	0.65	0.26	1.07	0.49	0.22	0.76
β12	−2	−1.79	−2.27	−1.06	−1.52	−1.22	−0.65	−1.67	−1.88	−1.43	−1.25	−1.43	−1.08
β22	−1	−0.44	−1.20	0.56	−0.39	−1.00	0.21	−0.64	−0.94	−0.27	−0.28	−0.54	−0.02
β32	1	0.93	0.26	1.65	0.66	0.04	1.30	0.60	0.29	0.91	0.35	0.12	0.60
τ2	2.56	2.03	1.10	3.29	–	–	–	1.83	1.15	2.53	–	–	–
ρ	0.4	0.58	0.15	0.83	–	–	–	0.62	0.47	0.75	–	–	–

To compare predictive performance, we look at the average length of predictive 95% credible intervals over all holdout samples and also the percentage of holdout values falling into their corresponding 95% credible intervals. We also compute the predictive log scoring loss (PLSL) and the average predictive CRPS. The results are summarized in Table 2. For the smaller training set, the results are a bit mixed, perhaps not surprising. However, for the larger sample size, PLSL and average CRPS (which is known to be conservative) favor the general version; so does the average length of the predictive interval. We also see that the PLSL and average CRPS decrease with sample size and increase as the concentration decreases.

Table 2.

Model comparison of PN regression under each combination of (n, τ², ρ): general PN Σ ≠ I (left column) and displaced normal Σ = I (right column)

(n, τ2, ρ)	(60, 1, 0.4)		(60, 2.56, 0.4)
PLSL	121.89	122.70	183.65	171.45
average CRPS	0.2511	0.2531	0.3124	0.3129
average length of predictive CI	1.88	1.92	2.20	3.74
percentage (%)	98	94	95	98

(n, τ2, ρ)	(200, 1, 0.4)		(200, 2.56, 0.4)
PLSL	106.64	117.09	148.35	164.50
average CRPS	0.2421	0.2444	0.2997	0.3072
average length of predictive CI	1.68	2.15	2.08	2.94
percentage (%)	98	100	96	100

4.2. Turtle Movement

We consider a turtle dataset due to Dr. E. Gould of the Johns Hopkins School of Hygiene. The data are the directions of turtle movements after a certain treatment and can be found in Stephens [20, pp. 27] or Mardia and Jupp [14, pp. 9]. The circular plot of the raw data is given in Figure 6. We can see that, while most of the turtles moved in one main direction, a small portion of them moved in another, almost opposite direction. We fit the general PN and displaced normal and report the posterior mean of the density in Figure 6(a). The prior used here follows Section 3.1: IG(5, 4) for τ² and N(0, 0.5I) for μ. We also fit a single von Mises using the mle.vonmises function of R package “circular”, which is also shown in Figure 6(a). It is clear that the data can not be adequately described by a single symmetric and unimodal distribution.

Stephens [20] fit a special case of a two component von Mises, with the same concentration and modes π radians apart. Mardia [13] later fit a general two component mixture with different concentrations and modes. In Figure 6(b), we plot the posterior mean density estimate from our PN model together with the density based on the parameter estimates of Mardia [13]. The general PN distribution provides density estimation comparable with the mixture of two von Mises distributions. The latter does have five parameters, compared with four for the general PN, and also introduces potential identifiability problems. As noted in Section 2, interpretation of the parameters in the general projected normal is difficult, hence, less clear than in the case of the mixture of two von Mises distributions. But again, with the goal of capturing departure from symmetry, it is not apparent that a two-component mixture model is an appropriate specification.

4.3. Butterfly Migration

Finally, we illustrate the PN regression model using data from a study by T. J. Walker and J. J. Whitesell of migratory butterflies entering northern Florida. More detail regarding the biological background and data collection methods can be found in Walker and Littell [21]. For illustration, we only use the data for the species cloudless sulphur. One purpose of this study is to examine the effect of distance from the coast on the direction of butterfly migration. Therefore, we include the standardized distance to the coast (in kilometers) as a covariate in the regression model. We also include the standardized temperature. So, for the i-th observation, x_i = (1, distcoast_i, temp_i)′. The total number of observations is 233 and we hold out 40, chosen at random, as a validation set. Again, we fit the general PN and the displaced PN, adding to the priors of the previous subsection for τ² and ρ a normal prior with λ₀ = 0.5 for the β’s. The posterior estimates and uncertainties are reported in Table 3. The percentage of hold out values falling into the 95% HPD predictive intervals is 100% for both; the average lengths of the predictive intervals for the holdout set are 2.09 and 2.56, respectively. The average CRPS for the general version is 0.1987; for the identity version it is 0.2044. The mean PLSLs are 34.55 and 40.10, respectively. All these criteria suggest that the general PN regression is a preferable model for this dataset. Also, we provide predictive density plots for two illustrative holdout observations in Figure 7. We see shorter HPD credible intervals for the general PN, revealed by highlighting the lengths at the bottom.

Table 3.

Butterfly data example: posterior summaries of parameters

	Σ ≠ I			Σ = I
par.	mean	2.5%	97.5%	mean	2.5%	97.5%
β10	−1.95	−2.10	−1.80	−1.81	−1.97	−1.63
β11	0.10	−0.08	0.27	−0.04	−0.20	0.11
β12	0.22	0.01	0.40	0.11	−0.11	0.30
β20	0.53	0.38	0.68	0.43	0.24	0.59
β21	0.22	0.05	0.40	0.33	0.17	0.48
β22	−0.94	−1.11	−0.76	−0.82	−0.98	−0.66
τ2	0.82	0.66	1.02	–	–	–
ρ	−0.21	−0.37	−0.04	–	–	–

Figure 7.

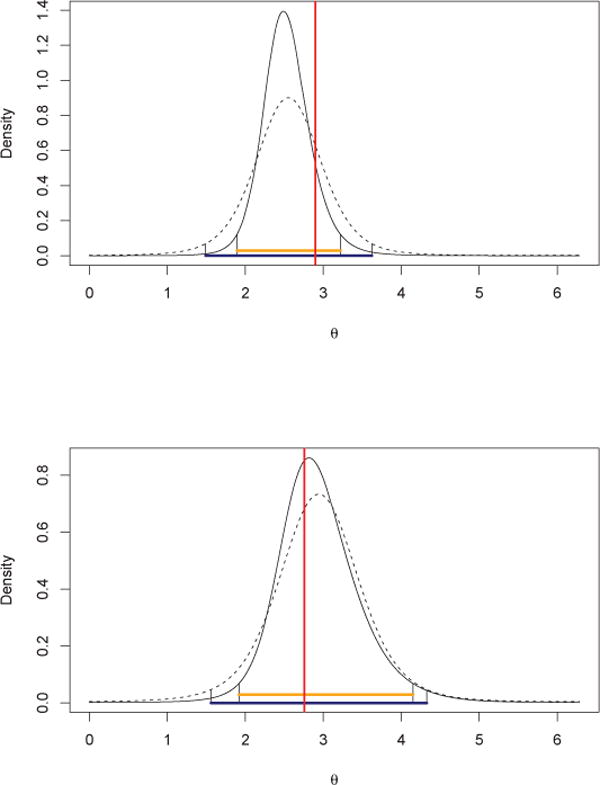
Predictive density and its 95% HPD credible intervals for two hold out observations: the solid line is the predictive density for the general PN regression and the dotted line is for the identity version. The vertical line shows the true hold out value θ^*.

Finally, in order to see how the mean direction ω and the concentration γ respond to changes in the X’s, we present Figure 8. Here, we show the change in mean direction and mean resultant length with respect to change in the temperature, while fixing the value of the standardized distance to the coast (distcoast_i = 1). We allow the standardized temperature X₂ to range from −2 to 2 and obtain posterior estimates of ω(X₂) and γ(X₂) associated with f(θ|data) by Monte Carlo methods. In Figure 8, we can observe that change in temperature leads to smooth change in the mean direction of the butterfly migration, while also resulting in smooth change in the mean resultant length. As the temperature increases, the butterfly migration direction shifts and is relatively less concentrated in the mean direction.

Figure 8.

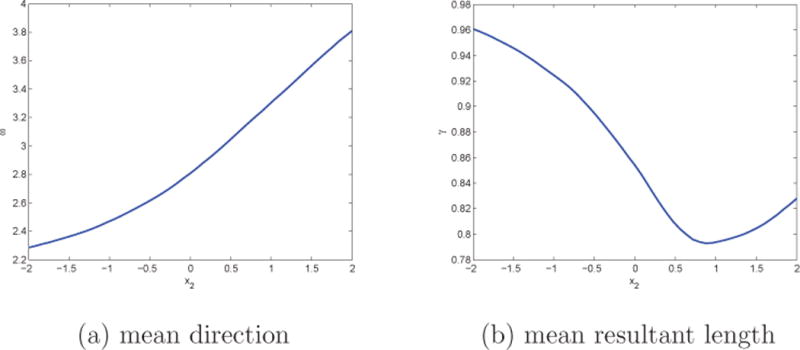
Change in mean direction ω and mean resultant length γ with changing temperature x₂ under the general PN regression for the butterfly data

5. Summary and future work

We have argued that the flexibility of the general PN model as well as the convenient regression linkage to linear explanatory variables makes it an attractive model for angular data. In particular, we have shown how to straightforwardly fit these models within a Bayesian framework, obtaining full posterior inference. Using both PLSL and CRPS, we have demonstrated that the general PN outperforms the displaced PN (Σ = I) using simulated data when the former is true and with two real datasets. Finally, in the Bayesian context, we have shown how we can see the response of the mean direction and concentration to change in covariate level.

As in the turtle data example, it may be asserted that, for independent observations on a sphere, mixtures of von Mises distributions can achieve comparable flexibility to the general PN. In this regard, we note that we are currently investigating mixing with PN’s, both discrete and continuous mixtures. The former leads to a dense class theorem, the latter leads to projected t-distributions. PN’s also offer convenient multivariate extension to dependent observations, each on a circle or, more generally, on a sphere, through suitable multivariate normal distributions; the von Mises does not easily extend beyond two or three dimensions in this case. Of particular interest for space and space-time directional data is a spatial and spatiotemporal projected Gaussian process which we will report on in a forthcoming manuscript.

Appendix A. Mean direction calculation for PN₂(μ, I) from Section 2

Assume X₁ and X₂ are two independent variables, X₁ ~ N(μ₁, 1) and X₂ ~ N(μ₂, 1). The joint density of X₁ and X₂ is

$$f(x_1,x_2)=\frac{1}{2\text{π}}exp(-\frac{1}{2}[{(x_1-{\mu }_1)}^2+{(x_2-{\mu }_2)}^2]).$$

Change variables (X₁, X₂) to (R, Θ), i.e., X₁ = R cos Θ, X₂ = R sin Θ and |J| = R. Let ${\mu }_0^2={\mu }_1^2+{\mu }_2^2$, where μ₁ = μ₀ cos α and μ₂ = μ₀ sin α, ∀α.

$$\begin{array}{c}f(\theta ,r)=\frac{1}{2\text{π}}rexp(-\frac{1}{2}(r^2-2r({\mu }_{1}cos\theta +{\mu }_{2}sin\theta )+{\mu }_1^2+{\mu }_2^2))\\ =\frac{1}{2\text{π}}rexp(-\frac{1}{2}(r^2-2r{\mu }_0(cos\alpha cos\theta +sin\alpha sin\theta )+{\mu }_0^2))\\ =\frac{1}{2\text{π}}rexp(-\frac{1}{2}{[r^2-{\mu }_{0}cos(\theta -\alpha )]}^2)exp(-\frac{1}{2}{\mu }_0^2{sin}^2(\theta -\alpha ))\end{array}$$

$$\begin{array}{c}f(\theta )={{\displaystyle \int }}_0^{\infty }f(\theta ,r)\text{dr}\\ =\frac{1}{\sqrt{2\text{π}}}exp(-\frac{1}{2}{\mu }_0^2{sin}^2(\theta -\alpha ))\frac{1}{\sqrt{2\text{π}}}{{\displaystyle \int }}_0^{\infty }rexp(-\frac{1}{2}{[r-{\mu }_{0}cos(\theta -\alpha )]}^2)\text{dr}\end{array}$$

Use the result,

$$\frac{1}{\sqrt{2\text{π}}}{{\displaystyle \int }}_0^{\infty }rexp\left(-\frac{1}{2}{(r-a)}^2\right)\text{dr}={\varphi }_1(a)+a{\Phi }_1(a)$$

where ϕ₁(·) and Φ₁(·) are the standard univariate normal pdf and cdf, respectively. Let g(x) = ϕ₁(x) + xΦ₁(x), then

$$\frac{1}{\sqrt{2\text{π}}}{{\displaystyle \int }}_0^{\infty }rexp(-\frac{1}{2}{[r-{\mu }_{0}cos(\theta -\alpha )]}^2)\text{dr}=g({\mu }_{0}cos(\theta -\alpha )).$$

Under careful calculation,

$$\begin{array}{c}\text{E}sin(\theta -\alpha )={{\displaystyle \int }}_0^{2\text{π}}sin(\theta -\alpha )f(\theta )d\theta \\ ={{\displaystyle \int }}_0^{2\text{π}}sin(\theta -\alpha )\frac{1}{\sqrt{2\text{π}}}exp(-\frac{1}{2}{\mu }_0^2{sin}^2(\theta -\alpha ))g({\mu }_{0}cos(\theta -\alpha ))d\theta \\ =0\end{array}$$

$$\text{E}(sin\theta cos\alpha -sin\alpha cos\theta )=0\Rightarrow \frac{{\mu }_1}{{\mu }_0}\text{E}sin\theta =\frac{{\mu }_2}{{\mu }_0}\text{E}cos\theta \Rightarrow {\mu }_1\text{E}sin\theta ={\mu }_2\text{E}cos\theta$$

According to the definition of mean direction, $arctan\left(\frac{\text{E}sin\theta }{\text{E}cos\theta }\right)=arctan\left(\frac{{\mu }_2}{{\mu }_1}\right)$ when μ₁ ≠ 0.

Appendix B. Posterior Computation

The full conditionals for the parameters of the projected normal model without covariates are:

• f(μ|θ, r, τ², ρ) ~ N(μ̃, Σ̃), where $\stackrel{\sim }{\mu }=\sum ^{\sim }{\sum }^{-1}{{\displaystyle \sum }}_{i=1}^n{r}_i{\text{u}}_i$ and Σ̃ = (nΣ⁻¹ + I/λ₀)⁻¹.

• $f(r_i|{\theta }_i,\mu ,{\tau }^2,\rho )\propto r_{i}exp(-\frac{{\text{u}}_i^T{\sum }^{-1}{\text{u}}_i{r}_i^2-2{\text{u}}_i^T{\sum }^{-1}\mu r_i}{2})I_{(0,\infty )}(r_i)$.

• $f({\tau }^2,\rho |\text{r},\theta ,\mu ,\rho )\propto {{\displaystyle \prod }}_{i=1}^{n}f({\theta }_i,r_i|\mu ,\sum ){({\tau }^2)}^{-a_{\tau }-1}{e}^{-\frac{b_{\tau }}{{\tau }^2}}$. Use the truncated normal kernel (τ²)^* ~ N₊(τ², c₂) and ρ^* ~ T N(ρ, c₃, −1, 1).

The full conditionals for the parameters of the PN regression model are:

• β_j ~ B N(μ̃_j, Σ̃_j), where ${\stackrel{\sim }{\mu }}_j={\sum ^{\sim }}_j{\sum }^{-1}(-{{\displaystyle \sum }}_{i=1}^n{x}_{i,j-1}{{\displaystyle \sum }}_{k\ne j}{x}_{i,k-1}{\beta }_k+{{\displaystyle \sum }}_{i=1}^n{x}_{i,j-1}{r}_i{\text{u}}_i)$ and $\sum ^{\sim }={({{\displaystyle \sum }}_{i=1}^n{x}_{ij-1}^2{\sum }^{-1}+{\lambda }_0^{-1}\text{I})}^{-1}$.

• $f(r_i|{\theta }_i,\mu ,{\tau }^2,\rho )\propto r_{i}exp(-\frac{{\text{u}}_i^T{\sum }^{-1}{\text{u}}_i{r}_i^2-2{\text{u}}_i^T{\sum }^{-1}{\mu }_i{r}_i}{2})I_{(0,\infty )}(r_i)$, where ${\mu }_i=B_{2\times p}^T{\text{x}}_i$.

• $f({\tau }^2,\rho |\text{r},\theta ,\mu ,\rho )\propto {{\displaystyle \prod }}_{i=1}^{n}f({\theta }_i,r_i|B,\sum ){({\tau }^2)}^{-a_{\tau }-1}{e}^{-\frac{b_{\tau }}{{\tau }^2}}$. Use the truncated normal kernel (τ²)^* ~ N₊(τ², c₂) and ρ^* ~ T N(ρ, c₃, −1, 1).