Computational prediction of cleavage using proteasomal in vitro digestion and MHC I ligand data

Abstract

Proteasomes are responsible for the production of the majority of cytotoxic T lymphocyte (CTL) epitopes. Hence, it is important to identify correctly which peptides will be generated by proteasomes from an unknown protein. However, the pool of proteasome cleavage data used in the prediction algorithms, whether from major histocompatibility complex (MHC) I ligand or in vitro digestion data, is not identical to in vivo proteasomal digestion products. Therefore, the accuracy and reliability of these models still need to be improved. In this paper, three types of proteasomal cleavage data, constitutive proteasome (cCP), immunoproteasome (iCP) in vitro cleavage, and MHC I ligand data, were used for training cleave-site predictive methods based on the kernel-function stabilized matrix method (KSMM). The predictive accuracies of the KSMM+pair coefficients were 75.0%, 72.3%, and 83.1% for cCP, iCP, and MHC I ligand data, respectively, which were comparable to the results from support vector machine (SVM). The three proteasomal cleavage methods were combined in turn with MHC I-peptide binding predictions to model MHC I-peptide processing and the presentation pathway. These integrations markedly improved MHC I peptide identification, increasing area under the receiver operator characteristics (ROC) curve (AUC) values from 0.82 to 0.91. The results suggested that both MHC I ligand and proteasomal in vitro degradation data can give an exact simulation of in vivo processed digestion. The information extracted from cCP and iCP in vitro cleavage data demonstrated that both cCP and iCP are selective in their usage of peptide bonds for cleavage.

1. Introduction

The proteasome plays an important role in the preservation of protein homeostasis as its proteolytic activity can efficiently clear unneeded foreign viral proteins or damaged intracellular self-proteins. The proteasome has also been associated with the supply of the majority of cytotoxic T lymphocyte (CTL) epitopes for antigen presentation. There are three classes of vertebrate proteasomes: constitutive proteasomes (cCPs), immunoproteasomes (iCPs), and thymoproteasomes (tCPs). cCPs are expressed in most tissues (e.g., hematopoietic cells, lymphocytes, and monocytes). iCPs are developed from cCPs: with the stimulation of interferon (IFN)-γ, the three catalytic subunits β ₁, β ₂, and β ₅ of cCPs are replaced by their homologous counterparts β _1i, β _2i, and β _5i to form iCPs. tCPs are found in thymic epithelial cells and participate in T cell positive selection (Huber et al., 2012). Relative to cCPs, iCPs exhibit altered cleavage preferences, resulting in increased peptide supply for epitope presentation.

Several methods for computational recognition of proteasomal cleavage sites have been presented, e.g., PAProC (Nussbaum et al., 2001), support vector machines (SVMs) (Bhasin and Raghava, 2005), kinetic models (Holzhütter and Kloetzel, 2000), and artificial neural networks (Keşmir et al., 2002). There is also a method for predicting the production probability of an entire peptide using a linear score function (Ginodi et al., 2008). All of these methods are based on experimental proteasomal cleavage sites and statistical analysis of the flanking regions of such sites. Kernel-function stabilized matrix method (KSMM) used in this paper is a modified version of the stabilized matrix method (SMM) (Peters et al., 2003). SMM is a linear method which has been successfully applied to the prediction of MHC-peptide binding affinities, antigenic peptides presented by transporters associated with antigen processing (TAPs) and proteasomal cleavage sites (Peters et al., 2003; Peters and Sette, 2005; Nielsen et al., 2007). Its online software can be found at http://70.167.3.42/smm/. However, some studies found that the contributions of amino acids (AAs) to the predictive values (like binding affinities) are not linearly related (Jacob and Vert, 2008). This led to a lower prediction accuracy of SMM (Nielsen et al., 2007). Thus, it is reasonable to develop a nonlinear method KSMM by integrating kernel functions into SMM. In addition, the kernel functions are incorporated into pair-coefficients estimation between AAs in different peptide positions. The benchmark for cleavage data shows that KSMM is consistently better than SMM and that KSMM+pair coefficients are comparable to SVMs.

There are usually two types of data used in these models, proteasomal in vitro degradation data and MHC I ligand data. However, these two types of proteasomal digestion data do not necessarily bear enough resemblance to natural proteasomal cleavage. The proteasomal in vitro degradation data are generated by activated 20S proteasomes, but the bulk of cellular proteins (80%–90%) are degraded by 26S proteasomes (Sorokin et al., 2009). The 20S proteasome forms the catalytic core of the 26S proteasome, and generates a different pool of products from 26S proteasomes (Emmerich et al., 2000). As the C-termini of MHC I ligands are mostly cleaved by proteasomes (Heinemeyer et al., 2004), MHC I ligands are also used for studying the specificity of the proteasome. However, MHC I ligands represent only a subset of in vivo degradation products: in view of the length distribution of degradation products, possible CTL epitopes must be 8–15 AAs long, accounting for 15% of the cleavage products (Keşmir et al., 2003). As 1%–2% of them are MHC I epitopes (Kosmrlj et al., 2010), MHC I ligands account for at most 0.3% of the cleavage products. Therefore, the accuracy and reliability of these models still need to be improved (Diez-Rivero et al., 2010). In this study, the two types of data, from experimentally identified cCP and iCP digestion products and naturally processed MHC I ligands, both of which are mainly from viruses, were used for training and evaluating KSMM. These three cleavage models, singly or combined with peptide binding prediction, were tested for CTL epitope identification. cCP and iCP cleavage specificities were predicted computationally through reduction of the noise from the experimental data, and the profiles of the cCP and iCP interacting with their substrate were analyzed from our research results. This approach might lead to a better understanding of the processing of MHC I antigens and to the design of peptide vaccines with longer half-life.

2. Materials and methods

2.1. Data

2.1.1. cCP and iCP in vitro cleavage training data

Firstly, we trained the cCP predictive model. For the purpose of extracting comprehensive experimental information and reducing the risk of over-training the model with a limited sample size, proteasomal digestion products of both whole proteins and short peptides were included in the cCP and iCP training sets. We made the assumption that there was no difference in the proteasomal proteolysis degradation of whole proteins and peptides. We collected four fully quantified cCP in vitro digests of whole proteins (Emmerich et al., 2000; Toes et al., 2001; Lucchiari-Hartz et al., 2003; Tenzer et al., 2004): yeast enolase, bovine casein, prion protein, and Nef protein, as well as cCP in vitro digests of 32 peptides 10–56 AAs in length for training our cCP predictive model. Twenty-five of the 32 peptide digest datasets were extracted from cCP in vitro studies (Rivett, 1985; Dick L.R. et al., 1994; Leibovitz et al., 1994; Niedermann et al., 1995; 1996; 1997; Ossendorp et al., 1996; Shimbara et al., 1997; Dick T.P. et al., 1998; Alvarez et al., 2001; Cascio et al., 2001; Peters et al., 2002; Sun et al., 2002; Vigneron et al., 2004; Warren et al., 2006; Chapiro et al., 2006; Goldobin and Zaikin, 2009; Ma et al., 2011). The 7 remaining samples were downloaded from Tenzer-Suppl-Table1.xls at http://70.167.3.42/supplement/ (Jan. 11, 2006). The final cCP training set comprised 650 cleavage sites and 1 184 internal non-cleavage sites. Secondly, we trained iCP predictive models. The iCP degradation training data consisted of results of three whole proteins (Toes et al., 2001; Lucchiari-Hartz et al., 2003; Tenzer et al., 2004): yeast enolase, prion protein and Nef protein, and iCP in vitro digests of 27 peptides 18–56 AAs in length, including 21 peptide products from iCP in vitro digestion studies (Ehring et al., 1996; Beekman et al., 2000; Morel et al., 2000; Alvarez et al., 2001; Mommaas et al., 2002; Peters et al., 2002; Schultz et al., 2002; Sun et al., 2002; Chapiro et al., 2006; Ma et al., 2011) and 6 peptide products from Tenzer-Suppl-Table1.xls at http://70.167.3.42/supplement/ (Jan. 11, 2006). This gave a total of 537 internal cleavage sites and 961 internal non-cleavage sites.

2.1.2. CTL epitope data

The third method was trained with CTL epitope data. Proteasomes generate most MHC I peptides, but other proteases have also been found to generate some MHC I peptides (Cascio et al., 2001). The use of MHC I peptides for training proteasomal cleavage models is based on the hypothesis that MHC I peptides are all generated by proteasomes. A total of 6 277 naturally processed MHC I epitopes were extracted from the Antigen database (Blythe et al., 2002). Because the C-terminus of ligands presented by human leukocyte antigen (HLA)-A^*03 is very unlikely to be generated by the proteasome (Tenzer et al., 2005), HLA-A3 restricted epitopes were excluded from the training set. The C-termini of these epitopes were assigned as cleavage samples, and the internal positions within epitopes were assigned as non-cleavage samples. Non-cleavage samples that showed strong cleavage characteristics (e.g., those duplicated as cleavage samples) were discarded. The final CTL epitope training data contained 6 872 non-cleavage and 1 362 cleavage sites. The training set was referred to as ‘Antigen-human’. In these cleavage training sets, peptides duplicated or included in the test set of Saxová et al. (2003) were discarded.

2.1.3. MHC I binding affinity data

Datasets for binding affinity predictive models consisted of a training set and a test set extracted from the MHCBN database (Bhasin et al., 2003). Three hundred and sixteen peptides with measured half maximal inhibitory concentration (IC₅₀) constituted the training set, which is termed ‘MHCBN-train’. Binding affinity in practical calculation is defined as −lg 50 000 (IC₅₀ in nmol/L) (Nielsen et al., 2007). Nine hundred and seventy-five peptides that had interacted with HLA-A^*0201 constituted the test set. Every peptide could be mapped back to either a human protein or a protein from a human pathogen in the SwissProt database (Bairoch and Apweiler, 2000). Peptides that did not have an exact matched source protein or a duplicate in the proteasomal in vitro digestion data and the Antigen-human dataset were discarded. The resulting test set contained 754 peptides, including 621 binders and 133 non-binders. The test set was referred to as ‘MHCBN-test’.

2.2. Sequence encoding

A cleavage within the peptide was mapped back to its source protein to flank the cleavage site region (PL … P2 P1 | P1′ … P2′ PL′). The cleavage site is signified by ‘|’ and the N-terminus is on the left. Following the suggestions of Keşmir et al. (2003) and Tenzer et al. (2005), a window size of 8 was used for training the three cleavage models. Through the AA descriptors, peptides can be represented by numerical vectors. For the MHC I binding affinity models, we used 5z-scale descriptors (Sandberg et al., 1998); and for the cleavage prediction models, we used sparse binary descriptors (Nussbaum et al., 2001). Every peptide corresponds to an attribute value. An MHC I epitope has a binding affinity of [0, 1], and in vitro cleavage samples and CTL epitope cleavage samples have a cleavage value which is either 1 (positive sample) or −1 (negative sample). So every training set and test set can be denoted by 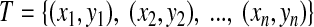, where 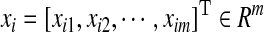is the peptide-sequence encoding vector, and y_i is its attribute value.

2.3. Kernel-function stabilized matrix method

The key idea of SMM is to seek a vector w, which can reflect the corresponding relationship of vector x_i and value y_i. Given an input x, the model can predict the reasonable output 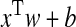, which best approximates the unknown y. The corresponding minimized energy function is

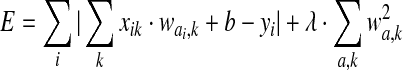, (1)

where b is a constant offset, and λ is the penalty parameter controlling the trade-off between the margin maximization and the degree of misclassification. If the pair coefficient 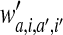quantifies the effect of interactions between an AA a at position i and an AA a′ at position i′ on the binding or cleavage, then the minimized energy function for the combined SMM+pair coefficient algorithm (Peters et al., 2003) is

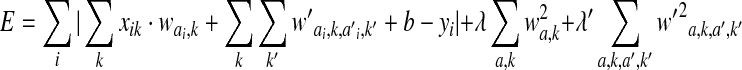. (2)

We then set out to introduce KSMM by incorporation of kernel functions into SMM. For different problems, the most suitable kernel functions are different. We compared three kernel functions: linear, polynomial, and radial-based (Eqs. (3)–(5)). KSMM with a linear kernel is the same as SMM.

Linear kernel function:

. (3)

Polynomial kernel function:

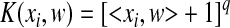. (4)

Radial-based kernel function:

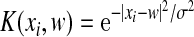. (5)

Thus, the minimized energy function (Eq. (1)) is rewritten as

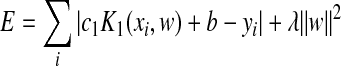, (6)

where c ₁ is a constant that scales the predictive attribute range [−1, 1]. The optimal value for λ is determined by minimizing the distance defined by the first term in Eq. (6).

It is impossible to estimate all pairs of AAs in the samples with limited data. For 8-mer peptides, the number of different pair coefficients reaches 20×20×28=11 200. We follow the proposal of Peters et al. (2003) that defines N _min as the minimum number of peptides in the training set that we can determine reliably, and discard the pair coefficients which have less than N _min peptides. N _min was set at 40, 12, and 12 for the Antigen-human, cCP, and iCP training data respectively, and pair coefficients 682, 340, and 212, respectively needed to be identified. The presence or absence of a chosen pair of AAs in the samples was represented by 1/0 in a sparse binary encoding vector 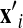. Using the optimal value for the vector w determined from Eq. (6), we drew the coefficient vector w′ of peptide position pairs from the systematic difference between the predicted values y _pred and the measured values y _meas. The optimal value for the pair coefficients vector w′ was searched by minimizing the energy function equation:

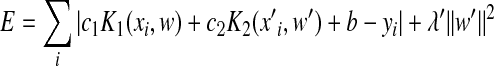, (7)

where c ₂ is a scale parameter. The optimal value for λ′ was determined by minimizing the distance defined by the first term in Eq. (7). The same kernel function was used for K ₁ and K ₂ in Eq. (7). Table 1 lists the ranges and best values (BVs) of different parameters in KSMM.

Table 1.

Ranges and best values (BVs) of different parameters in KSMM

Function type	Kernel function parameter			Scale parameter		Penalty parameter
	Range	BV of K 1	BV of K 2	c 1	c 2	Range	BV of λ	BV of λ′
Polynomial	2–6	4.00	4.00	2.00	1.00	10−2−106	10.00	100.00
Radial-based	10−4–104	2.00	2.00	4.00	0.80	10−2–106	10.00	10.00
Linear				1.00	1.00	10−2–106	1.00	5.00

Monte Carlo (MC) method (Metropolis and Ulam, 1949) was implemented for optimizing components of vectors w and w′. Our algorithm has two stages: firstly, to effectively escape from local minima, the MC calculations are repeated 200 times with different initial configurations. For each run, 20 000 MC moves are carried out and the final energy and weight matrix are recorded. In each move, the components of the vector are assigned random values. Secondly, the average of the top 10 records in stage 1 is treated as the initial weight of the vector. In each MC move, two components of the vector are selected at random, and the weights on these two components are updated, keeping the sum of the weights unchanged.

The probability of accepting a move in our algorithm is

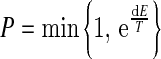, (8)

where dE is the difference in energy between the end and start weights, and T is a scalar. Eq. (8) shows that moves that decrease E will always be accepted, since P=1 (dE>0). On the other hand, moves that increase E will be accepted with P=exp(dE/T) (dE<0). T is lowered during the calculation in order to reduce the probability of accepting unfavorable moves. Finally, the classification function of the prediction is

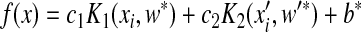, (9)

where w ^* and 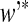are the weight vectors of the optimal plane in feature space, and b ^* is the threshold value of classification.

2.4. Performance evaluation measures

When using in vitro digestion data and MHC binding data, it is easy to make a clear assignment of positive and negative samples. However, for Antigen-human, definite negative samples do not exist. Goldberg et al. (2002) demonstrated that internal positions within the epitopes are also cleaved. To obtain the most cleavage characteristics, we adopted Saxová’s schema which assumes that positions within an epitope are less likely to be cleaved than C-terminus. Under this requirement, classification using Antigen-human is as follows:

TP (true positive): PC>Td,

FN (false negative): PC<Td,

TN (true negative): for every internal position i within the epitope, Pi<PC or Pi<Td,

FP (false positive): at least one internal position i within the epitope, Pi>PC and Pi>Td,

where PC is the predictive cleavage score at the C-terminus, Pi is the predictive cleavage score at the position i, and Td is the threshold value for sorting predictive cleavage scores into cleavage and non-cleavage sites. The following measures are introduced, namely sensitivity (SE), specificity (SP), accuracy (AC), and Matthews correlation coefficient (MCC) (Saxová et al., 2003):

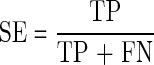, (10)

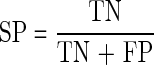, (11)

, (12)

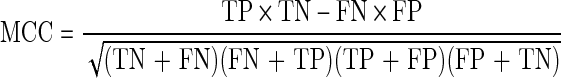. (13)

The receiver operator characteristics (ROC) curve is a 2D curve in which the true positive rate is plotted on the Y axis and the false positive rate is plotted on the X axis over a continuous range of cut-off values from high to low. The area under the ROC curve (AUC) reflects the ability of a model to distinguish a randomly chosen positive instance from a randomly chosen negative one (Swets, 1988). A random model has an AUC of about 0.5, but reasonable models should have AUC values higher than 0.7. In this study, ROC analysis was used to measure the ability of different models to identify the CTL epitopes. For a robust comparison of different methods, we generated 10 sets by randomly drawing n samples from the test set with a constant ratio of positives to negatives, where n is the size of MHCBN-test. We then performed ROC analyses 10 times. A method is considered significantly better than another if the distribution of its AUC values in a paired two-tailed t-test is significantly higher (P≤0.05).

3. Results

3.1. Comparison of KSMM and SVM in proteasomal cleavage benchmarking

We have developed a kernel-based prediction method called KSMM. A 5-fold cross-validation technique using three types of proteasome data was used to evaluate the performance of classifiers with different kernels. The results are summarized in Table 2. To identify the quality of KSMM, the SVM method was also implemented using the freely downloadable software LIBSVM (Chang and Lin, 2011). SVM is a popular machine learning tool. Due to its superiority in bioinformatics classification problems, SVM has been used in a wide range of protein-peptide interaction computational predictions (Bhasin and Raghava, 2005; Liu et al., 2009). Polynomial KSMM performed the best when cCP in vitro data were used (Table 2), achieving an accuracy of 75% and an MCC of 0.482. Using iCP digested data, radial-based SVM had the highest accuracy (72.4%) and MCC (0.461). For the MHC I ligand data, radial-based KSMM was able to recognize the cleavage sites and non-cleavage sites with >83% accuracy. Taken together, KSMM is a bioinformatics tool that is comparable to the SVM method. The incorporation of kernels into SMM method gave a significant improvement: the accuracy of KSMM with nonlinear kernels was 3% higher than that of SMM (linear kernel).

Table 2.

Performance of different classifiers using iCP and cCP in vitro digestion and MHC I ligand data

Classifier	cCP in vitro data				iCP in vitro data				MHC I ligand data
	SE	SP	AC	MCC	SE	SP	AC	MCC	SE	SP	AC	MCC
KSMM
Linear	68.5	68.2	68.3	0.385	67.8	70.3	69.4	0.370	80.0	79.8	79.9	0.603
Radial-based	74.5	74.3	74.3	0.471	72.9	72.0	72.3	0.436	82.9	83.2	83.1	0.661
Polynomial	74.8	75.1	75.0	0.482	71.1	72.0	71.7	0.419	81.6	82.5	82.1	0.640
SVM
Radial-based	82.1	69.7	74.0	0.476	79.5	68.3	72.4	0.461	83.2	81.7	82.5	0.649
Polynomial	80.3	70.1	73.6	0.457	77.0	67.4	70.9	0.428	81.5	81.4	81.5	0.630

SE: sensitivity; SP: specificity; AC: accuracy; MCC: Matthews correlation coefficient

Using the MHC I ligand test set and the cCP in vitro test set of Saxová et al. (2003), we tested the quality of three proteasomal classifiers: polynomial KSMM trained with cCP in vitro data (KSMM-c), radial-based KSMM trained with iCP in vitro data (KSMM-i), and radial-based KSMM trained with MHC I ligands (KSMM-ld). The comparison shows that our classifiers gave the most satisfying performance using both in vitro and MHC I data (Table 3). The results of PRProC (Nussbaum et al., 2001), FragPredict (Holzhütter and Kloetzel, 2000), and NetChop (Keşmir et al., 2002) were given by Saxová et al. (2003). An unexpected result is that KSMM-i outperforms KSMM-c using the cCP digestion data.

Table 3.

Performance of the KSMM-based classifiers on evaluation data

Method	cCP in vitro			MHC I ligand
	SE	SP	MCC	SE	SP	MCC
PAProC	45.6	30.0	−0.25	46.4	64.7	0.11
FragPredict	83.5	16.5	0.00	72.1	41.4	0.12
NetChop 1.0	39.8	16.3	−0.14	34.4	91.4	0.31
NetChop 2.0	73.6	42.4	0.16	57.4	76.4	0.32
KSMM-c	73.8	77.7	0.46	61.5	56.3	0.18
KSMM-i	73.8	79.4	0.49	73.6	60.6	0.35
KSMM-ld	68.9	61.7	0.35	75.8	72.7	0.49

SE: sensitivity; SP: specificity; MCC: Matthews correlation coefficient

3.2. Proteasomal models benchmarked on MHC I epitope prediction

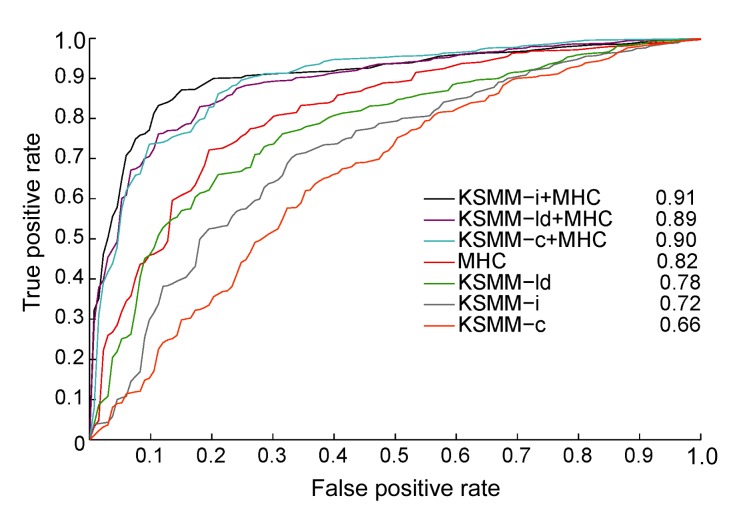
Using the MHCBN-test described in Section 2, we measured the suitability of different proteasome models for MHC I ligand identification (Fig. 1). Before evaluating the combination of proteasome and MHC I binding predictions, we used the thresholds when the sensitivity of cleavage prediction was 0.90. The highest corresponding specificities (true negative rates) of KSMM-c, KSMM-i, and KSMM-ld were 51%, 46%, and 64%, respectively. A sensitivity of 0.90 could significantly diminish false positives at the cost of a slight increase in false negatives. We filtered the MHCBN test by discarding ligands that had a prediction lower than the threshold. Then, we made a binding affinity prediction based on the reduced test set and generated an ROC graph. Comparing proteasome models alone (Fig. 1), KSMM-ld trained with MHC I ligands performed the best, with an AUC value of 0.78. KSMM-i again clearly gave a better prediction than KSMM-c (0.72 vs. 0.66). The MHC binding affinity predictive method was developed by training radial-based KSMM with MHCBN-train, which achieved an AUC value of 0.82. The joint combination of MHC and the cleavage predictions significantly enhanced the AUC values (~0.90). When combined with MHC, the difference between KSMM-i and KSMM-c was statistically significant, whereas the difference between KSMM-c and KSMM-ld was not. The increased AUC values of integral predictions resulted from a decrease in false positives. Compared to MHC I affinity prediction alone, over the entire range of true positive rates in the ROC calculation, the reduction in the false positive rate was 50% when combining KSMM-c, and 55% when combining KSMM-ld. The integration with KSMM-i led to an even larger reduction in the false positive rate (71%). The basis of this reduction is that the proteasome digestion of source protein into MHC I ligands has some additional degree of selectivity.

Fig. 1.

ROC performance curves for different prediction methods

Predictions were made on the MHCBN-test, and proteasome predictions were made by identifying HLA-A^*0201 epitopes in their source proteins. AUC values are given based on the methods shown in the box. The different prediction methods were: KSMM-i/c/ld +MHC, the combined proteasome predictions+MHC I epitope prediction; MHC, radial-based KSMM alone in Eq. (6) trained with MHCBN-train; KSMM-i/c/ld, the constitutive, immunoproteasome, and MHC I ligand cleavage algorithms

3.3. Weight coefficients of the linear iCP and cCP models

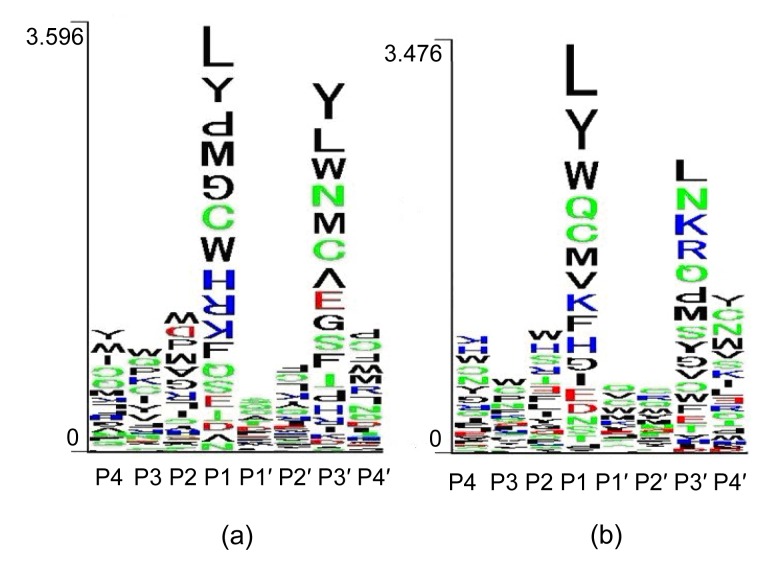
Besides those AAs at P1/P1′, AAs nearby also have a great influence on the choice of proteasomal cleavage (Toes et al., 2001). This explains why cleavage happens for certain P1/P1′ compositions, while other identical P1/P1′ compositions are ignored. Each score of the optimal plane w ^* in Eq. (9) corresponds to a kind of AA in a sequence position, and the sum of these scores is the predicted usage of the cleavage site. Hence, the weight coefficient w ^* can be seen as the impact of each AA in a sequence position on the cleavage site usage. For the 8-residue window of cCP and iCP in vitro data, we calculated w ^* with a linear function in Eq. (6). The values of w ^* are shown in Fig. 2.

Fig. 2.

Weight coefficients of AAs in cleavage-site adjacent regions for constitutive (a) and immuno-type (b) proteasomes

Each symbol column corresponds to a sequence position close to a possible cleavage site between P1 and P1′. The colors of AA symbols represent their physicochemical characteristics: black, neutral and hydrophobic; blue, basic; green, neutral and polar; red, acidic. The upright or upside-down AA symbol represents a positive or negative weight coefficient of w ^*, respectively. The height of the symbol is proportional to the absolute w ^* value of the AA (Note: for interpretation of the references to color in this figure legend, the reader is referred to the web version of this article)

4. Discussion

The 20S proteasome is shaped like a hollow barrel containing 4 layers of rings, each composed of seven subunits. The 2 inner rings each have 7 β subunits. Among them, the β ₁, β ₂, and β ₅ subunits are proteolytically active, and each has an NH₂-terminus Thr1 playing a critical role in the hydrolysis of peptide bonds. Protein substrate is degraded not only by single active subunits, but also by cooperation between two active subunits (Wenzel et al., 1994). The protein substrate within the proteasome is fully unfolded (Sorokin et al., 2009). According to the ‘molecular ruler’ of Wenzel et al. (1994), the length of the degradation products is related to the distance between active sites. We computed the distances between the active sites of mouse 20S cCP and iCP (Table 4). Distances between active sites of iCP were a little longer (0.04–0.26 nm) than those between active sites of cCP. Toes et al. (2001) reported that cCP and iCP generated peptides with an average lengths of 7.4 and 8.6 AAs, respectively. The average length of iCP production is about 1 AA longer than that of cCP production. On the basis of the correspondence between the length of unfolded protein sequence and the number of AAs in the sequence, as proposed by Coux et al. (1996), a length of 0.26 nm of the cleavage product is close to 1 AA. Therefore, the different average fragment lengths generated by cCP and iCP production may relate to the gap between the active sites of cCP and iCP.

Table 4.

Distances between active sites of mouse 20S cCP and iCP

cCP PDB id 3UNE		Distance between active sites of mouse 20S cCP (nm)
		(Thr1) β 1c	(Thr1) β 2c	(Thr1) β 5c
β ring	(Thr1) β 1c		2.75	6.11
	(Thr1) β 2c	2.75		6.17
	(Thr1) β 5c	6.11	6.17
β * ring	(Thr1) β * 1c	2.77	4.87	5.66
	(Thr1) β * 2c	4.87	6.37	3.93
	(Thr1) β * 5c	5.66	3.93	4.76
iCP PDB id 3UNH		Distance between active sites of mouse iCP (nm)
		(Thr1) β 1i	(Thr1) β 2i	(Thr1) β 5i
β ring	(Thr1) β 1i		2.79	6.26
	(Thr1) β 2i	2.79		6.33
	(Thr1) β 5i	6.26	6.33
β * ring	(Thr1) β * 1i	3.03	5.05	5.86
	(Thr1) β * 2i	5.05	6.54	4.09
	(Thr1) β * 5i	5.86	4.09	4.99

The KSMM+pair coefficient method achieved accuracies of 75.0%, 72.3%, and 83.1% using cCP, iCP, and MHC I ligand data, respectively (Table 2). These results are comparable to those of SVM. This demonstrates that the KSMM+pair coefficient method could serve as a protein-protein interaction predictive algorithm. Using Saxová’s test set as a benchmark, we found that the predictive performance of our optimal iCP and cCP and MHC C-terminus cleavage models was superior to that of the reference models (Holzhütter and Kloetzel, 2000; Nussbaum et al., 2001; Keşmir et al., 2002) (Table 3). Our cleavage models also helped improve HLA-A^*0201 peptide identification when integrated with MHC I binding predictions (Fig. 1), i.e., the AUC values increased from 0.82 to 0.91. The improved AUC values indicate that the 8-residue, 4 residues on each side of the cleavage/non-cleavage site of immuno-, constitutive, or MHC I restricted C-terminus samples, could precisely reflect the information of cleavage fragments generated by 20S cCP and iCP. They also demonstrate that both MHC I ligands and proteasomal in vitro degradation bear a close resemblance to naturally processed digestion.

KSMM-i performed better than KSMM-c in cCP cleavage site identification (Table 2) and in single or combined HLA-A^*0201 peptide identification (Fig. 1). This suggests that, compared with cCP, iCP is more specific in cleavage site selection and generates MHC I ligands more efficiently. As for KSMM-ld, it can be regarded as another type of cCP cleavage model. Most of the MHC I epitopes are processed and eluted in an environment without inducing the expression of iCPs. Differences in the performance of KSMM-c, KSMM-i, and KSMM-ld in combined HLA-A^*0201 peptide identification were small (Fig. 1). This may result from the fact that the selectivity of the MHC I molecule may reduce the gap in MHC I ligand generation efficiency between iCP and cCP.

iCP and cCP in vitro digestion data could more accurately reflect the pure information of proteasomal cleavage fragments with respect to the C-terminus of MHC I restricted samples. This may be because MHC I restricted samples are likely to contain not only the information of proteasomal cleavage fragments, but also the information of peptides binding to MHC I and TAP transport (Liu et al., 2009). KSMM-ld is markedly better than KSMM-c/i in MHC I epitope identification (0.78 vs. 0.66 and 0.72, respectively; Fig. 1), but KSMM-ld is no better than KSMM-c or KSMM-i when combined with MHC-binding prediction. The MHC I and TAP binding information in the Antigen-human is responsible for the excellent performance of KSMM-ld in single MHC I epitope identification. In Fig. 2, the height of each AA symbol is proportional to its absolute w ^* value, which is the contribution of the AA in a sequence position to the usage of potential cleavage sites. The height of all the AA symbols stacked at each position along P4–P4′ is proportional to the sum of the corresponding absolute scores for the 20 possible AAs at the positions which are the contribution to possible cleavage sites. The AAs on adjacent positions of the cleavage site, i.e., P1, P3′ positions, have a distinct effect on the potential cleavage site, demonstrating that both cCP and iCP species are selective in the hydrolysis of peptide bonds.

For the purpose of interpreting the AA characteristics in cCP and iCP cleavage-site flanking positions (Fig. 2), the crystal structures of mouse 20S iCP and cCP (PDB id: 3UNE and 3UNH) were used to find AAs which make nonbonding contact with residue Thr1 of active subunits (i.e., where there is at least one AA atom at ≤0.5 nm distance from any other atom of Thr1) (Holzhütter and Kloetzel, 2000). Table 5 lists all the AAs making nonbonding contact with the Thr1 of active subunits. The AAs surrounding the active sites of 20S iCP and cCP differ in β ₁ and β ₅: the electropositive and basic AA Arg45 in β _1c is substituted by the neutral AA Leu45 in β _1i, and the neutral AA Ala46 in β _5c is substituted by the neutral AA Ser46 in β _5i. It may simply be that, compared to β _1c, the AAs surrounding the active site of the β _1i subunit are less electropositive and tend to be more neutral on the whole, preferring to cleave after the neutral AAs. The substitution of neutral Ala46 in β _5c by neutral Ser46 in β _5i makes little difference to the physicochemical characteristics surrounding the β ₅ active sites and does not alter the hydrolysis preference of β _5i. Relative to cCP, iCP preferentially cleaves peptides after nonpolar AAs (Seifert et al., 2010). So the cleavage difference between cCP and iCP may relate to the change in the physicochemical characteristics surrounding β ₁-subunit active sites.

Table 5.

Amino acids (AAs) making nonbonding contact (≤0.5 nm distance) with active sites of mouse 20S iCP and cCP

AA No.	AAs making nonbonding contact with their own Thr1
	β 1c	β 1i	β 2c	β 2i	β 5c	β 5i
1	Thr2	Thr2	Thr2	Thr2	Thr2	Thr2
2	Ile3	Ile3	Ile3	Ile3	Thr3	Thr3
3	Asp17	Asp17	Asp17	Asp17	Asp17	Asp17
4	Arg19	Arg19	Arg19	Arg19	Arg19	Arg19
5	Lys33	Lys33	Lys33	Lys33	Lys33	Lys33
6	Arg45	Leu45	Gly45	Gly45	Met45	Met45
7	Ser46	Ser46	Ala46	Ala46	Ala46	Ser46
8	Gly47	Gly47	Gly47	Gly47	Gly47	Gly47

PDB id: 3UNE for cCP and 3UNH for iCP. Neutral AAs are colored black, electropositive and basic AAs are colored blue, and electronegative and acidic AAs are colored red (Note: for interpretation of the references to color in this figure legend, the reader is referred to the web version of this article)

The AA specificities of the P1 position correspond to the integral binding characteristics of the S1 pockets of three active subunits (Fig. 2). A binding mechanism is common to all active sites of cCP and iCP (Huber et al., 2012). Its selectivity depends, apart from the reactive warhead, solely on the interactions with S1 pockets. According to this mechanism, besides the P1 position, the proteasomal selective specificities in the P3′ position also relate to the S1 pockets of active subunits. The length of the unfolded peptide between the cleavage site and the P3′ position is 3 AAs, which is about 1.2–1.6 nm. Distances between any pair of pocket centers of the six active subunits of two β rings have been calculated (Table 6). The Ser130 (Gly130) Cα atoms of active subunits, which are close to the S1 pocket centers, are used as the S1 pocket centers. Of all 12 pairs of distances for cCP and iCP, the distances between the S1 pockets centers of β ₁ and β ₁ ^* are 1.48 and 1.56 nm, resepctively, and fall within the range 1.2–1.6 nm; the remaining 11 distances both for cCP and iCP are much longer than 1.6 nm. The AA specificities of the P3′ position are associated with the preference of the S1 pocket of β ₁ ^*, and the AA specificities of the P1 position most probably reflect the characteristics of the S1 pocket of the β ₁ subunit. Together, this demonstrates the selectivity of the cCP and iCP for certain cleavage sites, and that this selectivity may be related to the hydrolysis characteristics of their β ₁ subunits.

Table 6.

Distances between S1 pocket centers of active subunits of mouse 20S cCP and iCP

cCP PDB id 3UNE		Distance between S1 pocket centers of active subunits of mouse 20S cCP (nm)
		(Ser130) β 1c	(Gly130) β 2c	(Ser130) β 5c
β ring	(Ser130) β 1c		2.83	5.79
	(Gly130) β 2c	2.83		6.29
	(Ser130) β 5c	5.79	6.29
β * ring	(Ser130) β * 1c	1.56	3.79	5.66
	(Gly130) β * 2c	3.79	6.04	4.43
	(Ser130) β * 5c	5.66	4.43	3.71
iCP PDB id 3UNH		Distance between S1 pocket centers of active subunits of mouse iCP (nm)
		(Ser130) β 1i	(Gly130) β 2i	(Ser130) β 5i
β ring	(Ser130) β 1i		2.94	10.7
	(Gly130) β 2i	2.94		11.0
	(Ser130) β 5i	10.7	11.0
β * ring	(Ser130) β * 1i	1.48	4.11	9.67
	(Gly130) β * 2i	4.11	11.5	10.9
	(Ser130) β * 5i	9.67	10.9	3.71

Ser130 (Gly130) Cα atoms of active subunits are used as the S1 pocket centers

Nevertheless, this leads to a contradiction. The in vitro cleavage samples are a collection of peptide fragments generated by three types of active subunits (‘caspase-like’ β ₁, ‘trypsin-like’ β ₂, and ‘chymotrypsin-like’ β ₅); and the AA specificity information reflected by Fig. 2 is also a comprehensive reflection of different hydrolysis characteristics of active subunits. This resulted in low predictive accuracies of the cCP and iCP models (Table 2). If more digestion data for the β _1i/β _1c-, β _2i/β _2c-, and β _5i/β _5c-subunits were available, a predictive model specific for a single active subunit could be established; this could improve the proteasomal predictive accuracy.

The following results may explain the apparent contradiction. Muchamuel et al. (2009) showed that β _1i/β _1c- and β _2i/β _2c-subunits have much higher activities than β _5i/β _5c-subunits; β _2i/β _2c-subunits harbor very spacious S1 pockets and therefore do not show marked specificities (Huber et al., 2012); however, functional data indicate that incorporation of i-subunits enhances the activity of β _1i (Nussbaum et al., 1998), thereby resulting in the stronger preference of iCPs for hydrophobic AAs at P1. All these results suggest that the β ₁ subunit is both specific and active, relative to the β ₂ and β ₅ subunits. These results are consistent with our conclusion.

Using the absolute amounts of AAs found in positions close to the cleavage sites generated by 20S proteasomes (6.135×10⁻⁹ mol cCP and 6.370×10⁻⁹ mol iCP cleavage sites in Toes et al. (2001), and 15.964×10⁻⁹ mol cCP and 9.164×10⁻⁹ mol iCP cleavage sites in Tenzer et al. (2004)), we calculated the log-odds ratios of all 20 AAs at P1 and P3′ (log-odds ratio, lg(f_i/p_i), where f_i is the frequency of occurrence of AA i at a certain position, and p_i is the background frequency of AA i in the Swiss-Prot database (Bairoch and Apweiler, 2000)). The sign of the log-odds ratio could reflect the preference of the position for the AA i, i.e., a positive sign ‘+’ implies that the AA i at this position is beneficial to the usage of the cleavage site, whereas a negative sign ‘−’ implies that the AA at this position is not. The analysis of yeast enolase degradation data (Toes et al., 2001) is shown in Table 7. The comparison of all 20 signs at P1 and P3′ shows that there are 16 identical signs at P1 and P3′ for cCP and 14 for iCP. This demonstrates that the preference for AAs at P1 and P3′ is the same for AAs at cCP and iCP (P<0.001 and P<0.05). This may be related to the selectivities of the two β ₁ subunits. The analysis of prion degradation data shows that there are 13 identical signs at P1 and P3′ for cCP and 10 for iCP (Tenzer et al., 2004). This result, to some extent, reflects a similar preference of cCP and iCP for AAs at P1 and P3′ (P>0.1 and P≥0.5). This may be due to the highly biased composition of AAs in the prion sequence, i.e., about 20% Gly and many repeat regions (Tenzer et al., 2004).

Table 7.

Signs of log-odds ratios at P1 and P3′ for cCP and iCP^*

AA	cCP		iCP
	P1	P3′	P1	P3′
Ala	+	+	+	+
Cys	−	−	−	−
Asp	+	+	−	−
Glu	+	+	−	−
Phe	−	−	+	−
Gly	−	+	−	+
His	−	−	−	−
Ile	+	−	+	−
Lys	−	+	−	−
Leu	+	+	+	+
Met	−	−	−	−
Asn	−	−	−	+
Arg	−	−	−	−
Pro	−	−	−	−
Arg	−	−	−	−
Ser	−	−	−	−
Thr	−	−	−	−
Val	+	+	−	+
Trp	−	−	−	−
Tyr	+	−	+	−

^* Signs of log-odds ratios reflect the preference of the position for the amino acid (AA) i; i.e., ‘+’ implies that AA i at this position is beneficial to the usage of the cleavage site, whereas ‘−’ implies it is not

5. Conclusions

The KSMM+pair coefficient method could serve as a competitive bioinformatic tool. The three proteasomal cleavage predictive models in this paper are reasonable when the window size is 8 AAs. The cCP and iCP in vitro cleavage data show additional specificities in the MHC I-peptide processing and presentation pathway. The cleavage specificities of cCP and iCP towards substrate proteins may be related to the physicochemical characteristics of their β ₁-subunit active sites.