Structure and flexibility within proteins as identified through small angle X-ray scattering

Abstract

Flexibility between domains of proteins is often critical for function. These motions and proteins with large scale flexibility in general are often not readily amenable to conventional structural analysis such as X-ray crystallography, nuclear magnetic resonance spectroscopy (NMR) or electron microscopy. A common evolution of a crystallography project, once a high resolution structure has been determined, is to postulate possible sights of flexibility. Here we describe an analysis tool using relatively inexpensive small angle X-ray scattering (SAXS) measurements to identify flexibility and validate a constructed minimal ensemble of models, which represent highly populated conformations in solution. The resolution of these results is sufficient to address the questions being asked: what kinds of conformations do the domains sample in solution? In our rigid body modeling strategy BILBOMD, molecular dynamics (MD) simulations are used to explore conformational space. A common strategy is to perform the MD simulation on the domains connections at very high temperature, where the additional kinetic energy prevents the molecule from becoming trapped in a local minimum. The MD simulations provide an ensemble of molecular models from which a SAXS curve is calculated and compared to the experimental curve. A genetic algorithm is used to identify the minimal ensemble (minimal ensemble search, MES) required to best fit the experimental data. We demonstrate the use of MES in several model and in four experimental examples.

Introduction

It has been estimated that over 50% of eukaryotic proteins contain unstructured regions that are over 40 amino acids in length (Vucetic et al. 2003) and growing evidence suggests that macromolecular flexibility will be an important part of the regulatory mechanism in many different biological systems.

Solving protein structures, which adopt multiple conformations using X-ray crystallography can be challenging. In the present study small angle X-ray scattering (SAXS) has been used to investigate conformational disorder of multi-modular proteins. This technique is indeed a fundamental tool for the study of biological molecules in solution. SAXS data collection is amenable to high throughput and there has been a significant improvement in data quality from low concentration samples (<1 mg/ml) (Hura et al. 2009). The theoretical basis for solution scattering was the subject of an excellent review (Koch et al. 2003). Here we briefly consider the most common situation for structure reconstruction in which samples are homogeneous, monodisperse, and lacking long-range interactions in solution. The nuance of this method is that it can provide structural information on molecules exhibiting some intrinsic disorder, flexibility or heterogeneity, all of which have typically constituted a major obstacle for the other classical structural methods (Putnam et al. 2007).

By combining domain structures from X-ray crystallography and nuclear magnetic resonance spectroscopy (NMR) and recent advances in computational approaches, SAXS has the potential to provide realistic information regarding large-scale rearrangement of the macromolecule using rigid body modeling.

In general, rigid body modeling involves preparing a large number of possible atomic models and comparing the predicted model to experimental data. The models can either be directly refined against experimental data (Petoukhov and Svergun 2005) or can be prepared independently, out of which then the best model structure is selected (Boehm et al. 1999; Forster et al. 2008).

Whether a protein has naturally built-in flexibility or a preference for a single conformation is often a critical aspect of its function. For the former type of macromolecule, attempting envelope reconstruction using ab initio approaches (Chacon et al. 1998; Svergun 1999) can be misleading and at best provides a model representing an average of the conformations (Putnam et al. 2007). A number of techniques can be used to generate atomic models that sample conformational space for use in fitting experimental scattering data. Monte Carlo techniques (Buey et al. 2007; Shell et al. 2007), methods based on exploration of the dihedral angles in the connections region (Akiyama et al. 2004) and molecular dynamics (MD) (Boehm et al. 1999) can all be employed. Development of ”constrained modeling” has continued over many years by Stephen Perkins' group (reviewed in Perkins and Bonner (2008)). This technique uses a large number of conformers that are built with “minimal MD” calculations applied only on the domains' connections. These models are filtered based on their agreement with parameters extracted from the experimental curve, such as the radius of gyration R_G, cross section R_xc and the overall fit of the theoretical scattering from the model to the experimental data (Aslam and Perkins 2001; Aslam et al. 2003; Gilbert et al. 2005, 2006). The single best-fit conformation is adopted as the potential solution structure.

While these methods significantly increase the number of realistic models to be vetted against experimental data, a single best-fit conformation cannot always fit the experimental data well. The lack of convergence of a single best-fit conformation has been shown to be correlated with conformational disorder rather than a limitation of the search space in the algorithm (Hammel et al. 2005). In the case of scattering from a heterogeneous population, the measured scattering is derived from the population-weighted thermodynamic ensemble. In the past few years, a large number of studies on proteins denoted as intrinsically unstructured/disordered have appeared and SAXS has played a key role in obtaining structural information for these challenging systems (Boehm et al. 1999; Aslam and Perkins 2001; Yuzawa et al. 2001; Mattinen et al. 2002; Aslam et al. 2003; Akiyama et al. 2004; Hammel et al. 2004, 2005; Bernado et al. 2005; Gilbert et al. 2005, 2006; Grishaev et al. 2005; von Ossowski et al. 2005; Nagar et al. 2006).

Moreover, several schemes have been used to prove the existence of heterogeneity in protein conformations and to characterize them. Using experimentally determined scattering and theoretical scattering from individual components (form factors), volume fractions in each conformation can be determined by solving a system of linear equations (Konarev et al. 2003). This technique is recently most frequently used to de-convolute experimental scattering profiles by using theoretical profiles of single components (Akiyama et al. 2004; Goettig et al. 2005; Graille et al. 2005; Vestergaard et al. 2005; Nowak et al. 2006a,b). In the minimal ensemble search (MES) approach described here, we use the same principle where the most appropriate mixture of components is identified using a genetic algorithm. The information content of a SAXS curve alone is low relative to that required to describe a complete ensemble of a flexible protein. Exploring the conformational space of the molecule with realistic MD motions which produce conformationally realistic models is a significant restraint on models which are entertained as possible members of an ensemble. However, this too is insufficient and MES-selected models do not represent the complete ensemble. Rather they are probable components of the population of many conformations that could occur in thermodynamic average.

The biggest challenge in trying to model conformational flexible systems using SAXS data is to avoid over-fitting the raw data. One strategy to avoid over-fitting the raw data with multiple models is to search for the minimal number of conformers that de-convolute experimental data. Another restraint which will help to not overfit raw data would be to explore the conformational space of the molecule with realistic MD motions which would produce realistic conformational models.

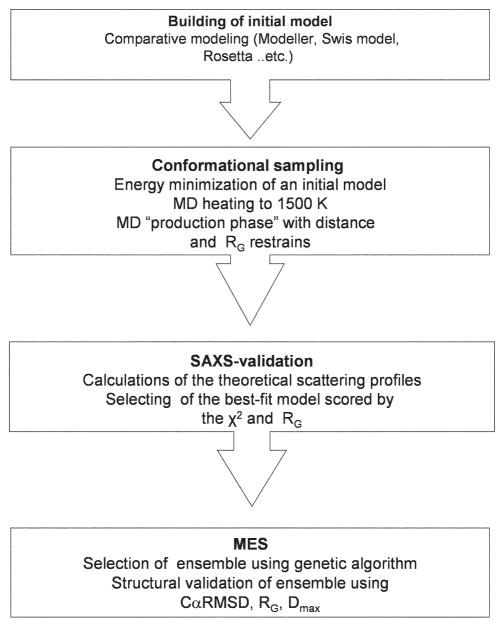
Here we describe a protocol for rigid body modeling called BILBOMD, which applies MD based conformational sampling followed by SAXS validation (see http://bl1231.als.lbl.gov/saxs_protocols/bilbomd.php). BILBOMD builds a large number of conformers using MD simulation applied on the domain connections where each conformer is validated based on the agreement with the parameters extracted from the experimental SAXS curve.

BILBOMD protocol implements a MES for the conformations contributing to the experimental scattering. These subsets of conformers (2 to 5 conformers) are selected using the genetic algorithm from a large (1000 to 15,000 conformers) pool of conformers build in the previous MD simulation (Fig. 1). Here we quantify the performance of the BILBOMD protocol using a benchmark of several artificial and four experimental systems. Consequently we provide guidance on how to distinguish a rigid system from a flexible one by comparing the structural properties of the MES-selected conformers.

Figure 1.

Schematic for BILBOMD strategy.

Theory and Methods

Conformational sampling using MD simulation

Conventional MD methods are computationally intensive. To effectively screen the entire conformational space of a multimodular protein, we develop a method for fast conformational sampling using the program CHARMM, version 33 b (Brooks et al. 1983). Using the CHARMM for MD simulation allows us to implement several efficiency enhancements, which increased the size of tractable conformational changes during the simulation. These include multiple timestep MD in which simulations are run at very high temperatures (Boehm et al. 1999; Yuzawa et al. 2001; Hammel et al. 2005; von Ossowski et al. 2005; Gilbert et al. 2006). Simulation at high temperature give the system additional kinetic energy which prevent the molecule from being trapped in a local minimum (Leach 2001). Additionally we reduce the number of nonbonded interaction terms that actually need to be computed. In our strategy we exclude electrostatic interactions between all atom pairs and, specifically, we exclude van der Waals terms using “ByGroup” algorithm. The basis of the efficiency of the ByGroup algorithm over a brute-force comparison of each atomic position with all others in the system is that it clusters atoms into chemical groups, initially ignoring the individual atoms themselves. This significantly reduces the number of pair potentials to be calculated. Effectively, ByGroup speeds up the calculation by reducing the particle density, what is done by simply redefining the particles. Once a list of group-group pairs satisfying the initial distance criterion is made, only atoms from this relatively short list are then considered for further atom-atom distance testing (MacKerel et al. 1998).

Before we can start conformational sampling we need to obtain an initial atomic model of the full-length protein assembly. If the protein assembly does not represent the experimentally determined structure, the initial model may be reconstructed by sequence homology modeling. Single domains for the initial model may be modeled by comparative modeling based on related structures. The alignments for comparative modeling may be obtained from the comprehensive database of structural alignments, (Marti-Renom et al. 2001). A model covering the entire sequence may be reconstructed using ‘automodel’ tools in MODELLER-9.0 package (Eswar et al. 2008) or the web application SWISS MODEL (Arnold et al. 2006).

In the MD simulation the initial model is taken as the starting point for the simulations. A common strategy is to perform the simulation on the domain connections and flexible loops.

The system is subjected to energy minimization with harmonic constraints on the protein atoms to clear all possible sterical hindrances potentially created in the previous comparative modeling step. In all cases the minimization is followed by heating up the MD simulation box to 1500 K keeping the protein atoms fixed. During the subsequent “phase of production”, only the atoms of the flexible domains connections are allowed to move, while the domains are treated as rigid bodies, with no internal motion. The simulations are performed in vacuum with a time step of 1 to 2 fs and the resulting conformers are recorded every 0.5 ps in a trajectory file. These conformations are automatically validated by subsequent calculations of the theoretical scattering profiles using the program CRYSOL (Svergun et al. 1995). It is not trivial to define at which step the MD simulation covers entire conformational space. In general these parameters depend on the size of the protein and the length of the flexible regions. However, based on inspection of the created conformations we believe that a pool of the 10,000 conformations for a multidomain 100 kDa protein is sufficient to sample the conformation space at a resolution relevant for SAXS data.

Several recent examples have demonstrated that more detailed structural information can be extracted utilizing SAXS data when additional constraints are imposed in the modeling (symmetry, intermolecular distances etc.) (Putnam et al. 2007). An advantage of the presented rigid body modeling protocol is its ability to use additional constraints to incorporate other information about the system, such as known distance constraints or constraints on R_G of constructed models.

On an average Linux-based cluster of 10 processors, the building and validation of the calculated SAXS profiles for 100 kDa size protein take 2 to 4 h.

MES

Considering the flexibility of domains, the coexistence of different conformations that contribute to the experimental scattering curve has to be taken into account. Based on the ensemble optimization method described by Bernado et al. (2007) we have developed an algorithm which searches for the minimal ensemble (MES) of the conformations from the pool of all generated conformations. The multiconformational scattering I(q) from such a minimal ensemble is computed by averaging the individual scattering patterns from the conformers.

$$\text{I}(\text{q})=1/\text{N}({\text{I}}_1(\text{q})+{\text{I}}_2(\text{q})+\dots ..+{\text{I}}_{\text{N}}(\text{q}))$$

I_1,2,3…N (q) are the scattering profiles from the single conformers and the momentum transfer q = 4π sinθ/λ where 2θ is the scattering angle and λ is the wavelength.

To select an appropriate ensemble from a pool of all generated conformations, a genetic algorithm based search is used. The scattering curves from all the structures in the pool are first pre-computed using CRYSOL program (Svergun et al. 1995) and the subsequent selection operators are performed using these scattering profiles and not the structures. The final model should best-fit the experimental curve I(q)_experiment minimizing the discrepancy χ² between the experimental and calculated multiconformational curve

$${\text{X}}^2=\frac{1}{\text{K}-1}\sum _{\text{j}=1}^{\text{K}}{\left[\frac{\mu \text{I}({\text{q}}_{\text{j}})-{\text{I}({\text{q}}_{\text{j}})}_{\text{experiment}}}{\sigma ({\text{q}}_{\text{j}})}\right]}^2$$

where K is the number of experimental points, σ(q) are standard deviations, and μ is a scaling factor (Bernado et al. 2007).

$$\mu =\frac{{\displaystyle \sum _{\text{j}=1}^{\text{K}}}\frac{{\text{I}({\text{q}}_{\text{j}})\text{I}({\text{q}}_{\text{j}})}_{\text{experiment}}}{{\sigma }^{\text{2}}({\text{q}}_{\text{j}})}}{{\displaystyle \sum _{\text{j}=1}^{\text{K}}}\frac{{\text{I}({\text{q}}_{\text{j}})}^2}{{\sigma }^{\text{2}}({\text{q}}_{\text{j}})}}$$

A common strategy with MES is to select 2, 3, 4 or 5 conformations that may be non-uniformly weighted. The weighting of the selected conformations is optional and allows us to distinguish conformational disordered systems and systems adopting multiple well-defined conformations.

Description of MES

A genetic algorithm (Holland 1975; Goldberg 1989) is used to find the protein ensemble that fits the experimental data best. The genetic algorithm evolves a population (multiset) of M ensembles, where each ensemble consists N = 2, 3, 4 or 5 generated conformations. The subsets are initially generated at random. In each iteration, a population of M new ensembles is first created using the operators of crossover and mutation, and the best ensembles from the original population and the new one are then selected to form the population of ensembles in the next iteration.

First, crossover is applied with probability p_c to pairs of ensembles in the current population; the pairs of ensembles to undergo crossover are selected at random. Members of the two ensembles participating in crossover are first randomly matched and each of the matched pairs of conformations is exchanged between the two ensembles with probability 50%. Exchanges are only performed when neither of the two resulting ensembles contains multiple identical conformations.

Mutation is then applied to each resulting ensemble. Mutation iterates through the selected conformations in the given ensemble and modifies each conformation randomly with probability p_m. Two types of modifications are used: i) change to a randomly selected conformation according to the uniform distribution over all conformations (with probability p_mr), and ii) change to a conformation randomly selected from the current population of ensembles (with probability 1 − p_mr). Similarly as in crossover, only modifications that do not yield ensembles with multiple identical conformations are allowed.

The M best ensembles are then selected from the original population of ensembles and the new one based on the discrepancy between the experimental and computed curves. The original population of ensembles is replaced with these best ensembles and the new iteration is executed unless a predefined maximum number of iterations, t_max, has been reached. The best ensemble in the last population of ensembles is then returned.

To estimate adequate parameter values and test the implemented MES technique, we ran the algorithm on several artificial data sets. Artificial data sets were created by randomly selecting N computed conformations and then setting the target conformation to be the average of the selected conformations. For artificial data, a perfect match can thus be obtained, unlike for most experimental data. Robust and efficient results were obtained with M = 10,000, p_c = 0.8, pm = 1/N, p_mr = 0.1, and t_max = 1000. Due to the stochastic nature of the genetic algorithm, each run may lead to a different selection of conformations; nonetheless, the results were found to be consistent with respect to both the structure as well as the quality of the fit.

Solution X-ray scattering data acquisition at the synchrotron radiation source

The production and purification of the chimeric scaffoldin (S4) were described elsewhere (Fierobe et al. 2002; Hammel et al. 2005). SAXS experiments were performed at the European Synchrotron Radiation Facility (Grenoble, France) on beamline ID02 as described in (Hammel et al. 2004).

Extracellular adherence protein (Eap) was expressed and purified according to the previously published method (Geisbrecht et al. 2006; Xie et al. 2006). SAXS experiments were performed at BioCAT beamline 18ID of the Advanced Photon Source of Argonne National Laboratory as described in (Hammel et al. 2007).

Mammalian polynucleotide kinase (mPNK) was prepared for SAXS experiments according to the protocol described in (Bernstein et al. 2005). Flavin reductase domain protein (FRDP) have been prepared based on standardized procedure of the Joint Center for Structural Genomics (Lesley et al. 2002). SAXS data collection of mPNK and FRDP were performed at the ALS beamline 12.3.1 LBNL (Berkeley, California) as described by Putnam et al. (2007, chapter 5).

Assessment of structural properties

The conformational disorder of the system can be analyzed by comparison of the structural diversity of the selected MES conformers. The level of the conformational disorder may be described using three measures: i) Pairwise structure alignment commonly uses root mean square deviation (RMSD) to measure the structural similarity. Therefore, the similarity of MES conformers can be defined by the mean deviation of each structure from the best-fit structure which has to be defined previously. The smaller the deviation from this structure the narrower the conformational space. For simplicity we used only RMSD of Cα atoms (CαRMSD). The best-fit conformer is assessed by the goodness of fit (lowest χ²) to the experimental data where the models that exceed R_G values of the experimental data by more than 20% are not taken into account. Each CαRMSD was obtained by superposing the model with best-fit structure and then computing the deviation between the structures. The CαRMSD values were calculated using the “COOR ORIENT” command of CHARMM (Brooks et al. 1983). ii) R_G and iii) maximal dimension (D_max) of models were calculated using the COOR RGYR or COOR MAXD commands of CHARMM (Brooks et al. 1983), respectively. The spread of the CαRMSD, R_G and D_max of MES conformers in relation to the values determined for all generated conformations may indicate flexibility of the system. Macromolecules with minimal flexibility may be identified by clustered values for CαRMSD, R_G and D_max of MES conformers. If the MES values cover the range of the entire pool, the system adopts a more disordered character.

Results

Robustness of MES

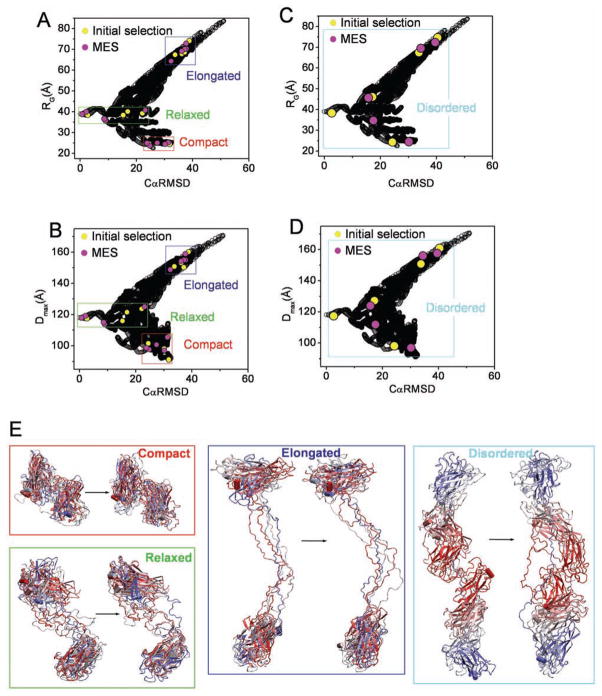
To emphasize robustness of MES, we created four artificial data sets for the cellulosome S4 system. We used S4 due to its ability to model different levels of conformational disorder. S4 contains a pair of globular domains connected with 50 residues long linker. An initial atomic model was built as described in Hammel et al. (2005). For each data set, representing compact, relaxed, extended or conformational disordered system, respectively, five conformations (form factors) have been selected (Fig. 2, yellow dots) from the entire pool of 15,000 conformations. We set the target profile to be the average of these selected form factors and perform MES in reverse action of de-convolution. Due to the stochastic nature of the genetic algorithm, each reverse de-convolution may lead to a different selection of conformations; nonetheless, the MES models were found to be similar with respect to the structural features CαRMSD, R_G and D_max. As shown in the Fig. 2 for all four data sets the re-selected models (pink dots) have a similar CαRMSD, R_G and D_max distribution with the models in the initial selection (yellow dots). Besides the similar distribution of the parameters, four out of five re-selected models are highly identical in the simulation of disordered system (Fig. 2C,D). In addition to the structural parameters, a visual inspection of the models show a striking similarity between the initial and MES-reselected models (Fig. 2E). These simulations show robustness of MES algorithm.

Figure 2.

Application of MES to the artificial data sets. A.–D. Graphs represents the comparison of R_G and D_max values for all 15,000 S4 models (black) with their CαRMSD values referenced to the single model as selected in Fig. 3. Initially selected models and MES re-selected models are highlighted with yellow and pink dots, respectively. Area of selection for the data sets representing compact (red), relaxed (green), elongated (blue) and disordered conformers (cyan) are highlighted with boxes. E. Models of initially selected conformers (left models) are compared to those re-selected in MES (right models). Models representing compact (red), relaxed (green), elongated (blue) and disordered (cyan) data sets have been superimposed on each other with no principle axis restrain using program Supcomb (Kozin and Svergun 2001).

Application of MES to experimental systems

We demonstrate the use of MES in the prediction of conformational disorder by using 4 experimental systems adopting different levels of conformational disorder.

The benchmark includes hybrid cellulosome S4, Eap, mPNK and FRDP (Table 1). The levels of the conformational disorder of these proteins are well known and established and are used as standards for our purpose. We performed a common BILBOMD protocol (Fig. 1) with the following four steps: 1. building of initial atomic model; 2. conformational sampling applying distance and R_G restrains; 3. validation of constructed conformers using experimental scattering curve; 4. MES. The structural properties of derived minimal ensemble have been monitored using the parameters CαRMSD, D_max and R_G.

Table 1.

Global scattering parameters

Protein	Mw (kDa)	RG (Å)	Dmax (Å)	χ2 best-fit / MES
S4	37	39.8 ± 0.2	∼150	24.6/7.7
Eap	50	40.5 ± 0.6	∼180	10.5/6.5
mPNK	54	35.3 ± 0.2	∼150	2.1/1.5
FRDP	82	31.6 ± 0.1	∼115	4.1/1.5

Mw, molecular weight given by the sequence; R_G, radius of gyration given by the Guinier approximation (Guinier and Fournet 1955); D_max, maximum protein distance estimated from P(r) function calculated by GNOM (Svergun 1992); χ² best-fit / MES, χ² for best-fit / MES model; S4, chimeric scaffoldin; Eap, extracellular adherence protein; mPNK, mammalian polynucleotide kinase; FRDP, flavin reductase domain protein.

Cellulosome S4

Cellulolytic bacteria living in anaerobic biotopes produce large extra-cellular multi-enzymatic complexes termed cellulosomes which efficiently degrade crystalline cellulose and related plant cell wall polymers. In our previous work (Hammel et al. 2005), the solution structure of cellulosome S4 was established using SAXS. The results from this analysis of the overall SAXS parameters, ab initio and rigid body modeling are consistent with an extended character of S4, occupying a large conformational space (Hammel et al. 2005).

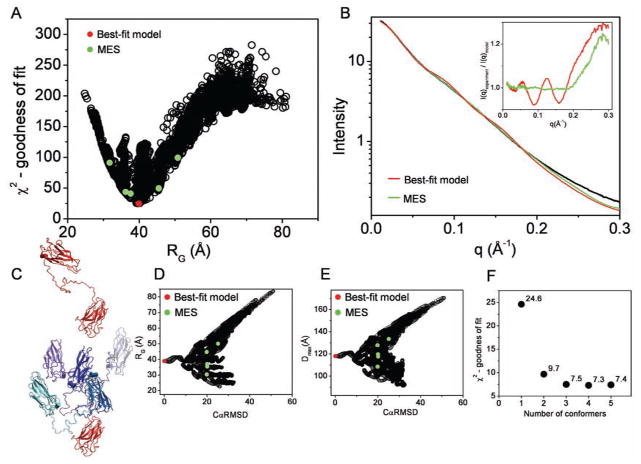
Here we used S4 to validate BILBOMD approach for the system adopting a large conformational disorder. S4 contains a pair of divergent cohesins from Clostridium cellulolyticum and Clostridium thermocellum which are connected with 50 residues long linker. 15,000 conformations were constructed by MD simulations and validated using the experimental scattering curve. The correlation between χ² and R_G, shown in Fig. 3A, indicate that the best-fit conformers have R_G values identical to those obtained from the experimental curve (Table 1). The best-fit model (χ² = 24.6) contains an extended S4 linker. Conformations contributing to the experimental scattering curve were identified using the MES approach (Fig. 3B). Already mixing two conformers fits the data significantly better (χ² = 9.7) then the single best-fit model. Additional improvement using a mixture of 3, 4 or 5 (χ² = 7.4) conformers has been obtained (Fig. 3F). Besides the visual inspection of the selected conformers (Fig. 3C), also a distribution of the CαRMSD, R_G, D_max in relation to the entire pool indicates that the S4 linker is flexible allowing unrestricted inter-cohesin motion (Fig. 3D,E). Comparison of the scattering profile of the best-fit and the MES fit shows that main improvement in the fit rose from the smoothness of the multiconformational profile. Smoothness of the experimental scattering profile is one of the main characteristic features of the intrinsic flexible protein (Hammel et al. 2005; von Ossowski et al. 2005). To improve the fitness for MES model, the multiconformational profile needs to reflect the smoothness of the experimental scattering curve. To emphasize smoothness of the MES profile, we compare calculated residuals (I(q)_experiment/I(q)_model) for MES ensemble with 5 conformers and the single best-fit model (Fig. 3B, inset).

Figure 3.

BILBOMD analysis of cellulosome scafoldin protein (S4). A. Graph represents the comparison of discrepancy (χ²) values for 15,000 S4 models with their R_G values. The value for the best-fit model is indicated by red dot. The green dots indicate the five MES conformers which are shown in the panel C. B. Experimental SAXS curve (black). Red and green lines represent theoretical scattering for the best-fit and MES ensemble, respectively. Inset – calculated residuals (I(q)_experiment/I(q)_model) for MES ensemble with 5 conformers and single best-fit model. C. The best-fit model for S4 (left panel). The five MES-selected models superimposed on the cohesin from Clostridium thermocellum colored red, showing conformational space adopted by cohesion from Clostridium cellulolyticum colored in blue (right panel). D., E. Graphs represents the comparison of R_G and D_max values for all 15,000 models with their CαRMSD values referenced to the best-fit model. The values for the best-fit model and MES-selected models are indicated by red and green dots, respectively. F. χ² values for MES fit in dependence to the number of selected conformers.

Of particular note for this experimental data is the high q deviation of calculated and experimental scattering. The residual flexibility of the terminal C- and N-terminus may lead to additional variability in the conformations and probably causes deviation in the high q range. Another explanation for this deviation could be that fitting experimental scattering at q > 0.25 Å⁻¹ is more problematic for spherical harmonic reconstructions (used in CRYSOL), as they do not account for the internal structure of the scattering particles (Putnam et al. 2007).

Eap

Eap of Staphylococcus aureus participates in a wide range of protein-protein interactions that facilitate the initiation and dissemination of Staphylococcal disease. The results from the SAXS analysis in our previous work show that Eap adopts an extended conformation in solution, where the linkers connecting four sequential Eap domains are solvent exposed (Hammel et al. 2007).

Comparative Raman spectroscopy experiments raised the possibility of the additional interactions between adjacent Eap domains (Hammel et al. 2007). Here we used the Eap experimental system as an example of a multimodular protein with restricted interdomain motion.

The initial model for the full-length Eap used in the BILBOMD modeling was constructed by connecting unique homology models for each individual Eap domain that were generated by virtue of the high sequence identity between the respective Eap domains (Geisbrecht et al. 2005) (see Theory and Methods).

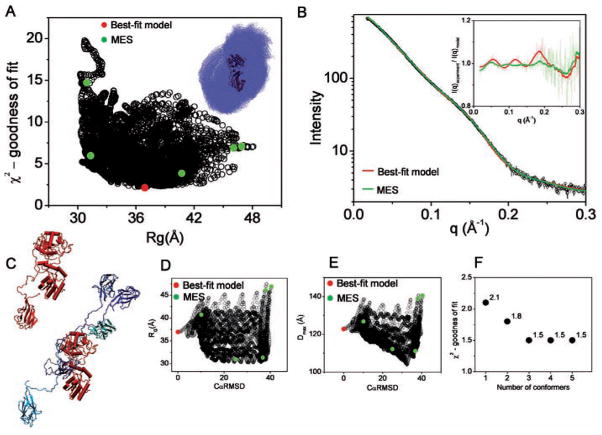
When no R_G constraints were applied in the MD simulation, the resulting Eap models were found to adopt both a highly stretched (D_max ∼ 200 Å, R_G ∼ 95 Å) and a compact conformation (D_max ∼ 100 Å, R_G ∼ 25 Å); these resulted in a poor fit to the experimental scattering curves with χ² > 100.

The correlation between χ² and R_G of 15,000 conformers shown in Fig. 4A indicates that the best-fit model has R_G value similar to that obtained from the experimental curve (Table 1). The best-fit model (χ² = 10.5) typified by an elon-gated arrangement shows Eap domains in close proximity with the interdomain distances ranged between 5–10 Å. (Fig. 4B). MES selected two conformers fitting data with the same goodness of fit (χ² = 10.5) as the best-fit model of one conformer. Improvement of the fit has been obtained for the mixture of 3 (χ² = 7.5), 4 (χ² = 6.9) or 5 (χ² = 6.5) conformers (Fig. 4F).

Figure 4.

BILBOMD analysis of extracellular adherence protein (Eap). A. Graph represents the comparison of discrepancy (χ²) values for 15,000 Eap models with their R_G values. The value for the best-fit model is indicated by red dot. The green dots indicate the five MES conformers. B. Experimental SAXS curve (black). Red and green lines represent theoretical scattering for the best-fit and MES ensemble, respectively. Inset – calculated residuals (I(q)_experiment/I(q)_model) for MES ensemble with 5 conformers and single best-fit model. C. The best-fit and five MES-selected model for Eap. The MES-selected models have been superimposed on each other with no principle axis restrain using program Supcomb (Kozin and Svergun 2001) (right panel). D., E. Graph represents the comparison of R_G and D_max values for all 15,000 models with their CαRMSD values referenced to the best-fit model. The values for the best-fit model and MES-selected models are indicated by red and green dots, respectively. F. χ² values for MES fit in dependence to the number of selected conformers.

As shown in the Fig. 3D,E the structural parameters R_G, D_max and CαRMSD for the MES ensemble are clustered in relation to the distribution of the parameters determined for the entire pool (Fig. 4D,E). Furthermore the visual inspection of the selected conformers (Fig. 4C) confirms that the Eap domains have a restricted interdomain motion. These results confirm our previous observations, suggesting that full-length Eap is held together by additional interactions between adjacent Eap domains (Hammel et al. 2007).

mPNK

mPNK is a critical DNA repair enzyme required for the processing of damaged DNA termini prior to completion of many DNA repair processes. Here we used the mPNK as a model system where the crystal structure of the entire molecule assembly is known and BILBOMD approach evaluates how the solution structures differ from crystal structures to establish biologically relevant solution conformation.

The crystal structure of mPNK (PDBid: 1yj5) reveals its overall architecture (Bernstein et al. 2005). The enzyme comprises of 3 functional domains, a kinase and phosphatase, closely associated within the catalytic segment and an N-terminal Forkhead-associated (FHA) domain. The FHA domain is attached by a 33-amino acid linker to catalytic segment. In the mPNK crystal structure, the linker electron density could not be defined, presumably due to disorder. The authors have proposed that the linker would act as a flexible tether between the FHA and catalytic segment in solution (Bernstein et al. 2005). This flexibility could be important in facilitating interactions between mPNK and its diverse protein partners and DNA substrates.

The missing linker-region was modeled using the strategy described in Theory and Methods. MD performed on the linker was used to determine the conformational distribution of FHA. 6000 conformations of mPNK were built in MD simulation (Fig. 5A, inset) and compared against the experimental SAXS data (Fig. 5A). The best-fit model (χ² = 2.1) is in an extended conformation (Fig. 5B). Multiple conformations of the protein contributing to the experimental scattering curve were compared using MES. A mixture of two conformers fit the experimental data better (χ² = 1.8) than the single best-fit model. Additional improvement using a mixture of 3 (χ² = 1.5), 4 (χ² = 1.5) or 5 (χ² = 1.5) conformers has been obtained (Fig. 5F). χ² values should not be validated in the absolute scale because they are weighted on the experimental standard deviation, σ, (see Theory and Methods). Calculated χ² values for mPNK models are relatively small values due to the larger σ, however, the relative improvement in-between single (χ² = 2.1) and three MES conformations (χ² = 1.5) is significant. The level of fitness improvement for MES model is obvious in the comparison of calculated residuals (I(q)_experiment/I(q)_model) for MES model with 5 conformers and the single best-fit model (Fig. 5B, inset).

Figure 5.

BILBOMD analysis of mammalian polynucleotide kinase (mPNK). A. Graph represents the comparison of discrepancy (χ²) values for 6000 mPNK models with their R_G values. The value for best-fit model is indicated by red dot. The green dots indicate the five MES conformers. Inset – the superimposition of all 6000 nPNK modeled comnformers. FHA domains are shown in blue dot representation. PK is shown in carton colored (red). B. Experimental SAXS curve (black). Red and green lines represent theoretical scattering for the best-fit and MES ensemble, respectively. Inset – calculated residuals (I(q)_experiment/I(q)_model) for MES ensemble with 5 conformers and single best-fit model. For better visualization the residuals have been smoothed. C. The best-fit model for mPNK (left panel). The five MES-selected models, representing conformational space of the FHA domain (colored blue). The models are superimposed on the PK structure colored red (right panel). D., E. Graph represents the comparison of R_G and D_max values for all 6000 models with their CαRMSD values referenced to the best-fit model. The values for the best-fit model and MES-selected models are indicated by red and green dots, respectively. F. χ² values for MES fit in dependence to the number of selected conformers.

Furthermore, the relative χ² improvement needs to be compared with respect to the size of the protein, rigid domains and length of the linkers. In the mPNK system the flexibility of relatively small FHA domain (10 kDa) may influence scattering much less than the flexibility of the four larger Eap domains (33 kDa) in the Eap protein. For these reasons we believe that the visual inspection of the MES models and the spread of the R_G, D_max, CαRMSD in relation to the distribution of the entire pool is the best method to suggest a level of the flexibility. Particularly for the mPNK system the spread of the R_G, D_max, CαRMSD values (Fig. 5D,E) caused by the different compactness of FHA domain (Fig. 5C) indicate that the FHA domain adopts a conformational disorder.

FRDP

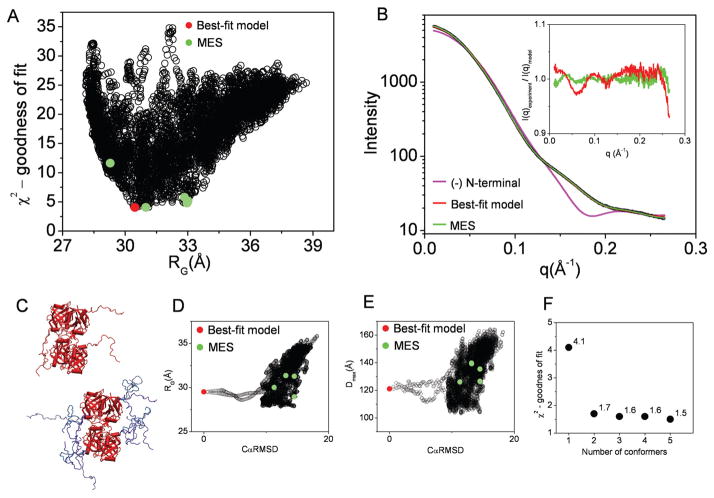
SIBYLS beamline has been concerned with the development of the data collection and analysis infrastructure for application of SAXS on a proteomic scale. Recently we have collected and processed SAXS data on a large number of proteins which had been previously prepared for a crystallographic based on structural genomics initiatives. We have shown that in many cases the solution structure differs from the crystal or homologues atomic structure only by a short extension on N- or C-terminal regions. Here we present the example of FRDP. FRDP monomer is a 17.5 kDa (155 residues) large protein. For the purpose of protein expression FRDP was cloned with additional 25 residues N-terminal HIS-tag. In solution, FRDP adopts a tetrameric state with the biological unit solved by crystallography (PDBid: 2qck) and here we show the influence of the short unstructured protein terminus on the experimental scattering profiles.

First, the missing HIS-tag regions which could not be defined in the crystal structure were constructed in each monomeric unit using the strategy described in Theory and Methods. 7000 conformations of the N-terminal unstructured region were constructed in MD simulation and the theoretical scattering profiles were utilized (Fig. 6A). The best-fit model (χ² = 4.1) shows the N-terminal HIS-tag in the disordered conformation (Fig. 6B) and dramatically improves the fit in the comparison to the structure missing HIS-tag regions (χ² = 48.6, Fig. 6C).

Figure 6.

BILBOMD analysis of Flavin reductase domain protein (FRDP). A. Graph represents the comparison of discrepancy (χ²) values for 7000 FRDP models with their R_G values. The value for best-fit model is indicated by red dot. The green dots indicate the five MES conformers. B. Experimental SAXS curve (black). The theoretical scattering profile for FRDP atomic structure missing flexible N-terminal extension (pink line). Red and green lines represent the theoretical scattering for the best-fit and MES ensemble, respectively. Inset – calculated residuals (I(q)_experiment/I(q)_model) for MES ensemble with 5 conformers and single best-fit model. C. The best-fit model for FRDP (left panel). The five MES-selected models (right panel). D., E. Graph represents the comparison of R_G and D_max values for all 7000 models with their CαRMSD values referenced to the best-fit model. The values for the best-fit model and MES-selected models are indicated by red and green dots, respectively. F. χ² values for MES fit in dependence to the number of selected conformers.

MES fit improved in comparison with the single best fit, giving χ² values 1.7, 1.6, 1.6 and 1.5 for a mixture of 2, 3, 4 and 5 conformers, respectively (Fig. 6F).

In this experimental system we show an example where the existence of disordered loops which are missing in the crystal structure has been visualized by SAXS. The dramatic improvement of the fitting comes from the simple addition of these loops to the crystallographically determined structure, where only a minor improvement could be achieved including multiple conformations of those loops (Fig. 6B, inset). The dramatic improvement of the fit by the adding the terminal HIS-tag to the FRDP atomic structure shows that small distortions in the molecular shape may have a huge impact on the scattering curve and consequently on the SAXS based rigid body modeling. To summarize, if a rigid body does not have a distinctive globular shape, a small distortion, like disordered N-terminus, can be sufficient to alter the scattering profile and, consequently, the match of the rigid body model to the experimental data.

Discussion

For bridging atomic resolution structures with SAXS data we developed an approach in which MD simulation is used to generate a wide range of macromolecular conformations from which theoretical scattering profiles are calculated and compared to the measured curve. Our BILBOMD protocol implements the ultimate speed-up steps using the CHARMM program. Fast evaluation of nonbonded interactions, larger time step size for the MD simulations and high (1500 K) temperature during MD simulation are the main sources of efficiency enhancement. The substantial advantage of using CHARMM scripting is to restrain modeling with the other stereochemical restraints derived from other experiments or global SAXS parameters like R_G and D_max.

The current challenge is to analyze the presence of multiple conformations of proteins contributing to the experimental scattering profile. Bernado and co-workers define an ensemble optimization method (EOM) in which a pool of possible conformations (N > 1000) is randomly generated to cover to the conformational space. A genetic algorithm is then applied to select subsets of 50 configurations that fit the experimental data (Bernado et al. 2007). Based on this basic principle we have developed the MES where the genetic algorithm is used to select a small number of conformers (2 to 5) from the pool of all conformations derived in MD sampling so that the best-fit to the experimental data is obtained. In the EOM method the optimal ensemble size has been determined for artificial data sets of the polyalanin chain ensemble. Bernado and coauthors show that the fitness improved dramatically with the number of conformers in the chromosome for small subset to reach a plateau around N = 10. We show that for all our experimental cases of multimodular proteins the fitness improved dramatically with the 2 conformers in the chromosome and reach a plateau for around N = 4 or 5 (see panels F in Figs. 3–6). We believe that the strategy to avoid over-fitting the raw data is to search for the minimal number of conformers that de-convolute experimental data. Although MES selects only a small number of conformers, we want to stress that for flexible proteins these conformers do not represent the only conformations in solution. The structural information that can be extracted is only the size, shape and conformational distribution even though MES employs a high resolution atomic model.

SAXS is often used to determine the overall size of multimodular or partially unfolded proteins by monitoring R_G (Doniach 2001). The experimentally established R_G determined for disordered systems is an overall size parameter being an average over all conformations in solution. The R_G distribution determined from the ensemble created by MES provides significantly more information about the system and consequently may suggest flexibility of systems.

Comparison of the structural properties of the selected models in the ensemble subset allowed us to suggest the degree of flexibility of the experimental system. As shown in the Fig. 2 the spread of the structural parameters R_G, D_max, CαRMSD for the MES ensemble in relation to those determined for the entire pool correlate strongly with the level of flexibility. The MES models for a protein with restricted flexibility like Eap show similar structural parameters as their best-fit model (Fig. 4). Those very similar structural parameters are not spread out in the entire conformational space, suggesting that the system is adopting a limited conformational space. In contrast, the MES-conformers for conformationally disordered systems like the S4 or FHA domain of mPNK show a broad range of R_G, D_max, CαRMSD spread over the entire conformational space (Figs. 3 and 5). To find an accurate quantitative validation for protein flexibility is a big challenge. Comparison of CαRMSD, R_G and D_max of MES conformers is not quantitatively accurate and needs to be compared within the context of the size of the protein, the rigid domains and the length of the linkers.

For example, if we assume that S4 and Eap have the same size of the flexible linkers (50 for S4, 47 for Eap) but S4 has a smaller molecular weight (S4 37 kDa, Eap 50 kDa) then the R_G values of the MES S4-conformers (30.1–50.0 Å versus 39.3–51.0 Å for Eap) may be described as significantly more spread out. A unique quantitative validation for protein flexibility remains an open problem; however, the validation of MES models may be used in the comparison of flexibility for the protein under different conditions.

Inspection of the conformational space searched is necessary. For extremely large systems containing a large number of domains, adequate conformational sampling is a key challenge. For these kinds of systems a different strategy may be employed. Conformational sampling may be done using parallel MD simulations launched with different initial models or using simulations under different distance/R_G constraints.

Studies have demonstrated situations in which more and more detailed structural information can be extracted utilizing SAXS data when additional constraints are being imposed on the reconstructions. An advantage of the rigid body modeling presented here is the ability of using additional constraints to incorporate additional information about the system, such as known distance constraints.

Techniques providing complementary information containing local distance or chain properties, like circular dichroism, fluorescence resonance energy transfer and NMR may appear extremely useful in combination with MES. Interdomain movement restriction, such as that observed in Eap domains (Hammel et al. 2007) may be tested with MES. Another example of symbiosis between crystallography and MES is shown in the mPNK example where the distance between the FHA and catalytic segment proposed by crystallography (Bernstein et al. 2005) was verified and corrected.

SAXS is an effective and important complement to crystallography as it can provide information on every sample, faster data collection than electron microscopy or NMR, and structural analysis of protein in solution. Furthermore, SAXS results provide an efficient and powerful way to identify an experimentally testable model of macromolecular interactions and conformations in solution. We expect that implementing MES in SAXS analysis substantially improves the definition of an intrinsic flexible proteins in its native state.