Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Sep 16;3:2666. doi: 10.1038/srep02666

Precisely aligned graphene grown on hexagonal boron nitride by catalyst free chemical vapor deposition

Shujie Tang 1, Haomin Wang 1,a, Yu Zhang 2, Ang Li 1, Hong Xie 1, Xiaoyu Liu 1, Lianqing Liu 2, Tianxin Li 3, Fuqiang Huang 4, Xiaoming Xie 1,b, Mianheng Jiang 1
PMCID: PMC3773621  PMID: 24036628

Abstract

To grow precisely aligned graphene on h-BN without metal catalyst is extremely important, which allows for intriguing physical properties and devices of graphene/h-BN hetero-structure to be studied in a controllable manner. In this report, such hetero-structures were fabricated and investigated by atomic resolution scanning probe microscopy. Moiré patterns are observed and the sensitivity of moiré interferometry proves that the graphene grains can align precisely with the underlying h-BN lattice within an error of less than 0.05°. The occurrence of moiré pattern clearly indicates that the graphene locks into h-BN via van der Waals epitaxy with its interfacial stress greatly released. It is worthy to note that the edges of the graphene grains are primarily oriented along the armchair direction. The field effect mobility in such graphene flakes exceeds 20,000 cm2·V−1·s−1 at ambient condition. This work opens the door of atomic engineering of graphene on h-BN, and sheds light on fundamental research as well as electronic applications based on graphene/h-BN hetero-structure.

Graphene has attracted enormous interest and intense research activities due to its rich physical properties in fundamental research and versatile potentiality to revolutionize many applications, especially in electronics and opto-electronics1,2. As the charge carriers in graphene are very sensitive to the underlying substrates, such as the surface roughness3, charge impurity4,5,6, surface phonon energy7, and the adsorbates8, long coherent length and high mobility of charge carriers are usually achieved on mechanically exfoliated graphene that is normally either suspended9,10 or transferred on h-BN11,12. As h-BN has a flat surface free of dangling bonds and charge impurities, the carrier scattering in graphene/h-BN can be greatly reduced. Compared to suspended graphene, graphene on h-BN has a physical support to avoid the mechanical collapsing, thus facilitates the subsequent processing. For these reasons, single crystal h-BN is believed to be an ideal substrate for graphene-based devices. Recent experiment showed that the weak periodic potential imposed by a supper-lattice on graphene/h-BN can generate extra Dirac cones in its energy dispersion13. Anderson localization was realized in ultra-high-quality graphene sandwiched by h-BN via tuning the carrier density14 and in the similar way a high on/off ratio of 106 was obtained in graphene transistor through h-BN barriers15. Moreover, theoretical calculation predicts that AB stacked graphene/h-BN structure could generate a tunable band gap16. However, graphene/h-BN devices in above experiments were fabricated by the direct transfer technology, which usually gives rise to a random orientation of graphene, not to mention its extremely low yield. The random stacking always leads to the uncertainty in the electronic properties of graphene/h-BN. Controllable synthesis of well-aligned graphene/h-BN is thus highly demanding.

Several reports on fabrication of graphene/h-BN hetero-structure are already available based on metal catalytic CVD process17,18, the process is quite similar to that of catalytic graphene growth on metal substrates19,20,21,22, however, the unavoidable transfer process added to the complexities to such approaches and lowered their significances. Thus far, only a few experiments were reported on the CVD growth of graphene on h-BN without metal catalysts23,24,25. Our earlier work has demonstrated 200 nm single crystal graphene grains on h-BN flakes24. It was found that graphene nucleates mainly at the defective sites of substrate. Carbon atoms accumulate around the nucleus and grow continuously into graphene domains. However, the detailed structures of the graphene domains and h-BN are rarely investigated. Especially, the graphene lattice registration to h-BN is yet unknown. To precisely measure the atomic feature of graphene, one may have to turn to scanning tunneling microscopy (STM), which is normally performed under ultrahigh vacuum environment and requires the sample to be conductive. As the h-BN substrate is insulating, scanning atomic force probe microscopy (AFM) provides an alternative, regardless of the conductivity of substrate and the height variation modulated from the local density of states26,27,28. Here we use atomic force microscope (AFM) to investigate the CVD-grown hetero-epitaxy of graphene on h-BN. The appearance of moiré interference pattern confirms that the graphene grains can align themselves precisely with the underlying h-BN substrate under optimized processes. This work opens the door for atomic engineering of graphene on h-BN, shedding light on many intriguing possibilities for fundamental research as well as device application on the graphene/h-BN hetero-structure.

Results

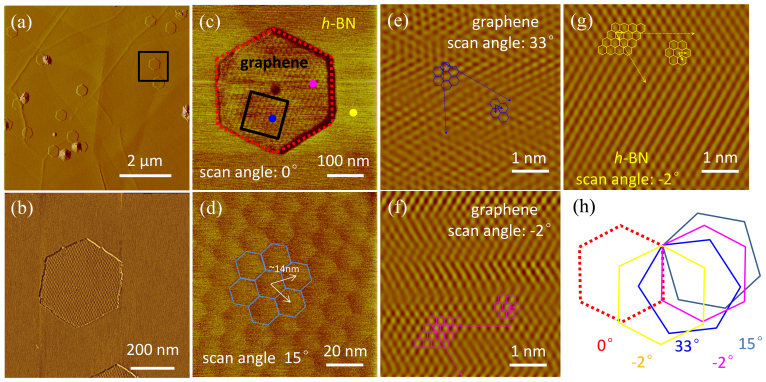
The graphene/h-BN samples were grown by dissociating methane (CH4) at a pressure of 12 mbar around 1200°C, as described in our earlier report24. Fig. 1a shows a typical AFM image of h-BN surface after CVD growth. Many single-layer graphene grains (see Fig. 1a) are formed in hexagonal shape on h-BN, typically with their opposite edges parallel. Their edges exhibit similar orientation signifying an epitaxial growth. A zoom-in view (Fig. 1b) reveals a sizable superstructure with the periodicity much larger than the lattice constants of both graphene and h-BN. A detailed investigation is followed to understand the geometric relation between graphene grain, lattice and the enormous periodicity. In order to reduce the influence of tip effect, graphene grains of moderate size are chosen as depicted in Fig. 1c and 1d. The superstructure has a hexagonal symmetry with lattice constant about 14 nm.

Figure 1. Determination of the rotational orientation of monolayer graphene with respect to h-BN.

Figure 1

Open in a new tab

(a) A typical topography of the graphene grains on h-BN surface. Almost all the grains are in hexagonal shape with the opposite sides parallel. The hexagons are aligned on the whole h-BN surface. It clearly indicates anisotropic growth of graphene; (b) A zoom-in view from the black box in panel (a). A sizable superstructure with a periodicity much larger than the lattice constant of both graphene and h-BN was observed on graphene; (c) Friction image of a single crystal graphene on h-BN. Dashed red line marks the edges of this grain; (d) A closer view (100 × 100 nm2) in the black box of (c), the superstructure exhibits hexagonal symmetry with lattice constant about 14 nm; Regular hexagons are superimposed on the images to demonstrate the giant lattice. The friction images (e), (f) and (g) show the atomic lattice of 5 × 5 nm2 area taken from the blue, pink and orange dot areas in panel(c), regular hexagons demonstrate the lattice of both graphene and h-BN, respectively. Zigzag directions (in dashed line) and lattice vectors (in solid line) are indicated by arrows. The atomic images are filtered to improve clarity, and the corresponding raw images of (e–g) are shown in supplementary materials. The small distortion in images (e) and (f) was due to slight slip in the movement of the AFM tip. The scanning angle of the tip is sometimes adjusted in order to obtain clear images with sample location fixed; (h) All the model hexagons with different scan angles in previous panels are rescaled for comparison. The hexagons are all parallel after correcting the scan angle.

In order to obtain the direct evidence for the correlation of the crystal structure and orientation, atomic-resolution friction measurements on the different locations of graphene/h-BN sample are carried out, and the friction images are shown in Figure 1e, 1f and 1g, respectively. Unless otherwise stated, all atomic-resolution friction images in the following part are taken in an area of 5 × 5 nm2. Fig. 1e and 1f, show the atomic lattice of the hexagonal graphene grain while Fig. 1g shows that of h-BN. Zigzag directions (in dashed line) and lattice vectors (in solid line) are indicated by arrows. The angle between the two zigzag directions is ~60°. Regular hexagons are superimposed on the images to demonstrate the lattice of graphene and h-BN. The characteristics of honeycomb lattice in both graphene and h-BN can be clearly observed. Figure 1h presents the representative models of hexagon in Figure 1c (grain hexagon with the scan angle 0°), 1d (superstructure hexagon with the scan angle 15°), 1e (graphene lattice hexagon with scan angle 33°), 1f (graphene lattice hexagon, with the scan angle −2°), and 1g (h-BN lattice hexagon with the scan angle −2°). The model hexagons with different scanning angles are rescaled for comparison. The fact that they are all parallel (after correcting the scan angle) verifies the epitaxy of graphene on h-BN from atomic level.

Normally there are two most energetically favorable edge configurations in graphene: zigzag and armchair29,30,31,32,33,34,35,36,37. As the neighboring zigzag and armchair edges sharing the same corner are exclusively 30°/90°/150° apart, the hexagonal graphene grains with 120° corners are solely armchair- or zigzag-edged. By comparing the hexagonal models in Fig. 1e and 1f with that in Fig. 1c, it is easy to find that the edges of graphene grain on h-BN are all along the armchair direction. Of course, the edge configuration is not microscopically clear because of the difficulty to obtain atomic resolution on the edge via friction AFM. Usually, zigzag edges are preferred in hexagonal graphene flakes grown on metal19,20,21,38. Although the mechanism is still under debate, the catalytic metal surface is believed to play an important role38,39,40,41,42. In addition, zigzag edges are always observed in graphene after metal-assisted anisotropic etching43,44,45 and hydrogen plasma etching46. Hydrogen partial pressure is very important in determining the configuration of graphene edges due to its multiple roles in edge reconstruction, and etching of graphene domains, as well as removal of surface-adsorbed C atoms47. A well-shaped, regular hexagonal hole with zigzag edges can also be obtained on SiO2-supported graphene via oxidation at 500°C33,48. These experiments indicate the superior thermal stability of zigzag edge to armchair one in etching process. Different from etching process, the formation of graphene edges involves higher partial pressure of carbon source. Density function calculations predict that armchair edges have lower formation energy than zigzag edges in the absence of metal surface49, supported by the observation of armchair edges in graphene islands formed on SiC (0001)34. It is believed that the higher density of states near the zigzag edge leads to higher formation energy while the armchair edge is free of boundary states49. Our findings seem to be consistent with this scenario.

The hexagonal superstructure in Figure 1b–d is believed to be moiré pattern whose periodicity depends on the lattice mismatch between graphene and h-BN, as reported in earlier scanning tunneling microscopic studies on mechanically exfoliated graphene13,50,51. Typical moiré pattern in graphene exhibits hexagonal symmetry and a periodicity of about 14 nm (as shown in Fig. 1d), and aligns with the underlying h-BN. The existence of moiré pattern gives us two strong indications. Firstly, in the conventional epitaxy, the top layer lattice is bonded and firmly locked to the substrate lattice, the film-substrate interplay results in an interfacial stress depending on the lattice mismatch and growth condition. Here in our case, the interfacial stress between graphene and the h-BN is relaxed, and the growth continues according to a so called van der Waals epitaxy. The substrate affects the hetero-epitaxial process only through the van der Waals (vdW) interaction52,53. it is necessary to mention that the film-substrate interaction is adequate to line up two lattices, but too weak to introduce crystallographically constrained epitaxy. Secondly, from the moiré periodicity one can determine precisely the lattice orientation between graphene and h-BN as we will do in the following section.

Discussion

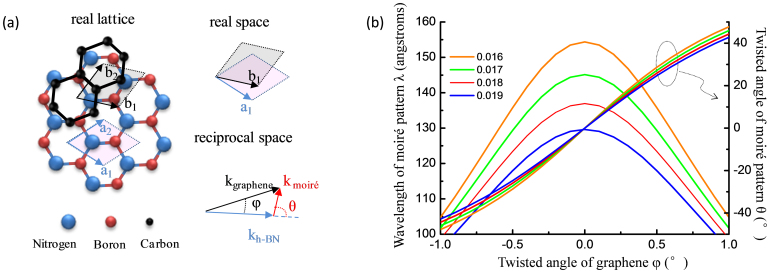
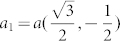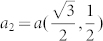The schematic in Fig. 2a is an explanation to moiré geometry. When h-BN is overlaid with a graphene layer, new symmetry may emerge leading to the moiré pattern. Its orientation and wavelength are fixed and can be derived mathematically. As shown in Fig. 2a, the hexagonal lattice of h-BN is defined by vectors (a1, a2), where a1 and a2 can be written as Inline graphic and Inline graphic, respectively. a represents the lattice constant of h-BN. Similarly, graphene lattice is represented by (b1, b2). The lattice of graphene is mis-oriented counterclockwise by an angle φ from the h-BN and shorter in length by a factor of δ. The factor δ denotes lattice mismatch between h-BN and graphene. Then the reciprocal lattice vector can be described as 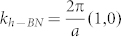Inline graphic for h-BN and 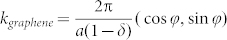Inline graphic for graphene, respectively. The reciprocal lattice vectors of the moiré pattern is given by: 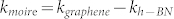Inline graphic. Therefore, the moiré pattern in real space has a wavelength 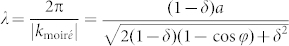Inline graphic and an mis-oriented angle 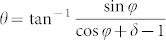Inline graphic to h-BN. Here we use 2.51 angstroms as the value of a. The wavelength of moiré pattern (λ) and its orientation relative to the h-BN (θ) as functions of mis-orientation angle between graphene and h-BN (φ) are plotted in Fig. 2b with lattice mismatch (δ) in the range 1.6% to 1.9%. (A more generalized analysis is presented in Fig. S6 and the subsequent description). It is found that the wavelength of moiré pattern decreases with the increase of the absolute value of δ. It reaches maximum when φ equals to zero. In the other words, moiré pattern in the maximal dimension can be observed when graphene grain aligns perfectly with the underlying h-BN. The estimated δ of 1.6 ~ 1.9% yields λ ranging from 13 to 15 nm, which is in good agreement with the measured value. We noticed that λ decays very fast with the increase of φ. When φ exceeds 5°, the moiré lattice constant drops to a value of less than 3 nm, beyond the limit of AFM (See supplementary materials Fig. S6d). Furthermore, the alignment of moiré pattern (θ) strongly depends on how much graphene is mis-orientated from h-BN (φ). A nonzero φ as small as 0.5° can cause a rotation of more than tens of degree for the moiré pattern. As the measurement error for lattice orientation is less than ±3° in our experiments (See Supplementary Materials content 4), the mis-orientation between graphene and h-BN should be less than 0.05°. That is to say, the graphene lattice is precisely aligned with that of the h-BN substrate.

Figure 2. Characteristics of moiré pattern on graphene/h-BN.

Figure 2

Open in a new tab

(a) Representation of a rotated monolayer graphene on h-BN surface. The honeycomb lattice, real lattice vectors and the corresponding reciprocal lattice vectors of both graphene and h-BN are plotted respectively. In the reciprocal space, moiré pattern vector kMoiré connects the h-BN reciprocal lattice vector kh-BN to the graphene reciprocal lattice vector kgraphene, φ is the rotation of kgraphene with respect to kh-BN, θ describes the relative rotation of kmoiré with respect to kh-BN; (b) Moiré pattern wavelength and its rotation angle with respect to the h-BN as a function of mis-orientation angle between graphene and h-BN (several lattice mismatch values are presented).

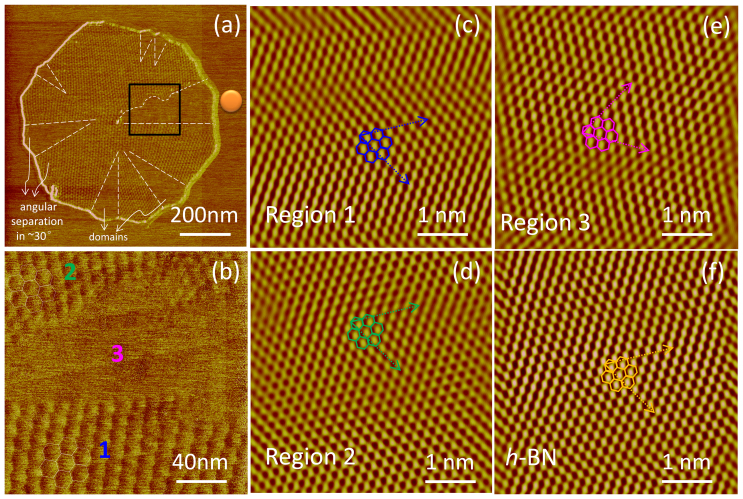
Additional information about the domain orientation comes from polycrystalline monolayer graphene on h-BN. The polycrystalline graphene can be encountered in samples grown at slightly lower temperature. As shown in Fig. 3a, the graphene flake is stitched with several domains where moiré patterns are missing (at least invisible to AFM). The moiré pattern shows discontinuity across different regions. It's obvious in region “1” and “2” while blank in region 3 as shown in a zoom-in view (Fig. 3b). A careful examination on region “1” and “2” found that their moiré patterns have a 12° angular difference although the graphene lattice in both regions seems to follow that in substrate pretty well (Fig. 3c, d and f). Recall from Fig. 2b, it is obvious that the moiré pattern rotation angle (θ) varies very sensitively on the lattice mis-orientation angle (φ). A rotation of moiré pattern by 12° corresponds to 0.2° graphene mis-orientation from h-BN, too small to be noticed by our AFM. On the contrary, the graphene lattice in region “3” is at 30° to the h-BN that causes a drop of moiré wavelength down to about 0.5 nm (See Fig. S6c and S6d), which is almost undetectable. We also noticed that the moiré patterns in neighboring domains are usually oriented away from each other by a large amount, typically near 30° (as shown Fig. 3a). This characteristic angle may correspond to a second lowest energy for graphene registry to h-BN, similar to the graphene/graphene stacking54. This phenomenon differs clearly from the earlier results of polycrystalline graphene grown on transitional metals where random lattice orientations were found among domains55,56,57. In all, lower temperature causes the growth of polycrystalline graphene in which the lattices are imperfectly aligned with the h-BN substrate. The large-angle grain boundaries may indicate a metastable state for graphene/h-BN epitaxy.

Figure 3. Friction imaging of polycrystalline monolayer graphene on h-BN.

Figure 3

Open in a new tab

(a) A typical polycrystalline graphene grown on h-BN. The graphene flake with giant moiré patterns is stitched with several domains where the moiré pattern is invisible. Dashed lines depict the shapes of the “blank” regions. The blank regions seem radiated from the center of the graphene flake; (b) Magnified friction images from the black box in panel (a). The moiré patterns exhibit discontinuity. Regular hexagons demonstrate the lattice of moiré pattern; (c), (d), (e) and (f) are the atomic scans (5 × 5 nm2) taken from the blue, pink, green and orange positions in panel (a) and (b), regular hexagons demonstrate the lattice of graphene and h-BN, respectively. Zigzag directions (in dashed line) and lattice vectors (in solid line) are indicated by arrows. The atomic images are filtered to improve clarity. Above images are measured with the same scan angle. In region “1” and “2”, their moiré patterns have a 12° angular difference although the graphene lattice in both regions seems to follow that in h-BN substrate pretty well. The graphene lattice in region “3” is rotated of about 30° with respect to the h-BN lattice. The corresponding unfiltered raw images of (c–f) are shown in Fig. S7.

It is noticed that defective sites are often found near the center of graphene flakes. This finding confirms our early conclusion that these sites are nucleation centers24. The carbon adatoms have extremely high mobility on h-BN at elevated temperatures hence only the defective sites or step edges can trap them to form nuclei. Compared with the inert surface of graphene, sites with dangling bonds are much more reactive to incoming atoms or fragments, consequently the growth of graphene continues laterally after nucleation.

The transport properties of graphene devices were measured with low-frequency lock-in technique. The field effect mobility extracted from two graphene samples is above 2 × 104 cm2·V−1·s−1 at ambient condition. The high values indicate that the carrier scattering is not significant at the graphene/h-BN interface. The preserved high mobility in graphene on the other hand proves that the interaction between graphene and h-BN is weak, further supporting our observation of epitaxy via van der Waals force.

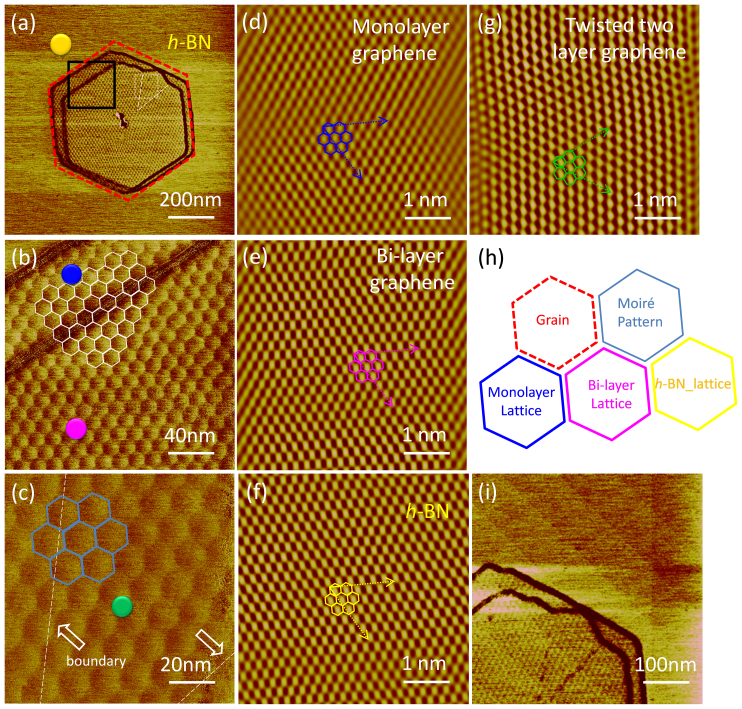
Under the growth conditions for monolayer graphene, double-layer graphene grains are occasionally seen, especially at increased partial pressure of carbon source CH4. Fig. 4a shows a friction image of the epitaxial bilayer graphene on h-BN. The top-layer nucleates about the same defects as the first layer. The smaller size of the top-layer stands for slower growth than the bottom one. The nearly perfect alignment between top- and bottom-layer hexagons implies one particular stacking order. The incoming carbon radicals tend to arrange themselves into thermodynamically stable AB stacking structure during epitaxy58. As shown in Figure 4b, clear moiré pattern observed on both terraces exhibits uninterrupted periodicity across the step edge. Atomically resolved AFM images on bottom-, top-layer graphene and h-BN substrate (Fig. 4d, 4e, and 4f) confirm that their crystal structures are well aligned with each other. The bilayer graphene is mainly in AB stacking as evidenced by Raman spectrum (See Fig. S11). We noticed that the up-right region between two white dashed lines in Fig. 4a is a graphene domain with lattice 30°-tilted (Fig. 4g), however, a closer look into the moiré pattern showed a continuous pattern across the boundary. The seemingly contradiction can be explained as follows: suppose that the bottom layer graphene is aligned precisely with the h-BN substrate, they will generate a moiré pattern with a periodicity around 14 nm. Then we put an additional graphene layer on top of this moiré pattern with a rotation angle of 30°, we will get another moiré pattern whose periodicity in reciprocal space is the difference in the reciprocal lattice vectors of the top graphene layer and the first moiré pattern. Due to the big difference between the reciprocal lattice vector of the graphene and the first moiré pattern, the wavelength of the second moiré pattern dropped to less than 2 nm regardless its orientation, which is difficult to be imaged by AFM. As a result, only the first moiré pattern is visualized, which overlaps continuously with moiré patterns on other regions across the boundary.

Figure 4. Investigation of the morphology of bilayer graphene grown on h-BN.

Figure 4

Open in a new tab

(a) A typical bilayer graphene on h-BN. Both the top and bottom layer of the bilayer are in hexagonal shape with the opposite sides parallel. The nearly perfect alignment between top- and bottom-layer hexagons can be observed. Dashed red line marks the grain edges of the bottom layer. To be noted that the right-up part of the top layer marked between two white dashed lines is a graphene domain with different lattice orientation; (b) Magnified friction image from the black box in panel (a) is shown. Moiré pattern on both terraces exhibits uninterrupted periodicity across the step edge; (c) Magnified friction image from the white box in panel (a) is shown. The dashed white lines represent the tilted interfaces of different domains in the top layer. Continuous moiré pattern was also observed on the graphene domains stitched together at tilted interfaces. Regular hexagons demonstrate the patterns; The friction images (d), (e), (f) and (g) show the (scan 5 nm × 5 nm) atomic lattices taken from the blue, pink, orange and green dots in panel(a), (b) and (c), some regular hexagons demonstrate the lattice of graphene and h-BN, respectively. Zigzag directions (in dashed line) and lattice vectors (in solid line) are indicated by arrows. The images are filtered to improve clarity; (h) All model hexagons in previous panels (except (g)) are rescaled for comparison and they are well aligned with each other. Hexagon model in (g) is obviously anticlockwise tilted for 30° from other one. It reveals that the graphene domain is twisted with its neighbor at almost 30°. Above images are measured under the same scan angle. The corresponding unfiltered raw images of (e–g) are shown in Fig. S8; (i) The boundaries of domains in the top layer of bilayer graphene were unveiled after powerful laser treatment under ambient condition, as the boundaries are more chemically reactive than the pristine graphene lattice.

In conclusion, we studied the micro-structural features of single crystal graphene grains grown on insulating h-BN with friction AFM. Moiré pattern was observed indicating the van der Waals epitaxial nature of such graphene. From the geometric analysis of moiré pattern and atomic images simultaneously acquired on graphene and substrate, it is determined that the lattice of graphene single crystals aligns precisely with that of h-BN within an error less than 0.05°. The edges of the graphene grains are found to be along armchair direction, consistent with the theoretical prediction for graphene grown on insulating substrates. Besides realizing graphene single crystal grain in micrometer size on h-BN, the present work uncovers a crucial issue about the graphene lattice registration on h-BN and might trigger more interests in fundamental as well as application studies with the atomically engineered graphene/h-BN hetero-structure.

While the current manuscript is being reviewed, we notice a related work by metal catalyzed CVD process done by Kim et al., published online18. They claim turbo-static stacking of graphene/h-BN/Cu and aligned h-BN/graphene/Cu with angular separation between graphene and h-BN smaller than 1 degree. We are updated that the very recent paper by Yang et al.59, grow epitaxial graphene on h-BN by plasma enhanced CVD after the first round review of our manuscript.

Methods

Graphene was deposited on the h-BN via chemical vapor deposition. Graphene samples were grown at 1200°C by flowing CH4:H2 at 5:5 s.c.c.m. for 60–300 minutes with pressure below 12 mbar. After growth, samples are cooled down to room temperature by keeping the argon flowing. The morphology, grain size, shape and crystallographic orientation of the CVD graphene can be recorded in contact mode (Veeco NanoScope V AFM). To obtain a high accuracy, calibration in atomic resolution was performed with newly cleaved highly ordered pyrolytic graphite (HOPG) before measurement. Parameters like integral gain, set-point and scan rate were adjusted to get high quality images. Several hours pre-scanning were carried out to warm up the scanner in order to obtain a high stability in imaging. See supplementary information for the details about fabrication, characterization and transport measurement of the graphene/h-BN hetero-structure.

Author Contributions

M.J. and X.X. directed the research work. H.W., X.X. and S.T. conceived and designed the experiments. S.T. fabricated the graphene samples. S.T. and Y.Z. performed the AFM experiments with support from T.L., L.L. and H.W. H.X. and X.L. fabricated the electronic devices. H.W. carried the transport measurements. H.W., A.L. and S.T. analyzed the data and designed the figures. H.W. performed the theoretical calculations. H.W., A.L., F.H., X.X. and M.J. co-wrote the manuscript and all authors contributed to the critical discussions of the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information:Precisely Aligned Graphene Grown on Hexagonal Boron Nitride by Catalyst Free Chemical Vapor Deposition

srep02666-s1.doc (17.8MB, doc)

Acknowledgments

We thank Z.X. Shen and Y. Cui from Stanford University for fruitful discussions. We acknowledge B. Gao for his support in transport measurement trials. The work in Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Science is partially supported by the National Science and Technology Major Projects of china (Grant No. 2011ZX02707), Chinese Academy of Sciences (Grant No. KGZD-EW-303), CAS International Collaboration and Innovation Program on High Mobility Materials Engineering, the National Natural Science Foundation of China (Grant No. 11104303, 11274333, 11204339 and 61136005), and the projects from Science and Technology Commission of Shanghai Municipality (Grant No. 12JC1410100 and 12JC1403900). Single crystal flakes from Momentive Performance Materials, Inc., USA is highly appreciated.

References

  1. Geim A. K. & Novoselov K. S. The rise of graphene. Nature Mater. 6, 183–191 (2007). [DOI] [PubMed] [Google Scholar]
  2. Novoselov K. S. et al. A roadmap for graphene. Nature 490, 192–200 (2012). [DOI] [PubMed] [Google Scholar]
  3. Katsnelson M. I. & Geim A. K. Electron scattering on microscopic corrugations in graphene. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 366, 195–204 (2008). [DOI] [PubMed] [Google Scholar]
  4. Adam S., Hwang E. H., Galitski V. M. & Das Sarma S. A self-consistent theory for graphene transport. Proc. Natl Acad. Sci. USA 104, 18392–18397 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Tan Y. W. et al. Measurement of Scattering Rate and Minimum Conductivity in Graphene. Phys. Rev. Lett. 99, 246803 (2007). [DOI] [PubMed] [Google Scholar]
  6. Chen J.-H., Jang C., Xiao S., Ishigami M. & Fuhrer M. S. Intrinsic and extrinsic performance limits ofgraphene devices on SiO2. Nature Nanotechnol. 3, 206–209 (2008). [DOI] [PubMed] [Google Scholar]
  7. Zhang Y. et al. Giant phonon-induced conductance in scanning tunnelling spectroscopy of gate-tunable graphene. Nature Phys. 4, 627–630 (2008). [Google Scholar]
  8. Wang H., Wu Y., Cong C., Shang J. & Yu T. Hysteresis of Electronic Transport in Graphene Transistors. ACS Nano 4, 7221–7228 (2010). [DOI] [PubMed] [Google Scholar]
  9. Du X., Skachko I., Barker A. & Andrei E. Y. Approaching ballistic transport in suspended graphene. Nature Nanotechnol. 3, 491–495 (2008). [DOI] [PubMed] [Google Scholar]
  10. Bolotin K. I., Sikes K. J., Hone J., Stormer H. L. & Kim P. Temperature-Dependent Transport in Suspended Graphene. Phys. Rev. Lett. 101, 096802 (2008). [DOI] [PubMed] [Google Scholar]
  11. Dean C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nature Nanotechnol. 5, 722–726 (2010). [DOI] [PubMed] [Google Scholar]
  12. Elias D. C. et al. Dirac cones reshaped by interaction effects in suspended graphene. Nature Phys. 8, 172–172 (2012). [Google Scholar]
  13. Yankowitz M. et al. Emergence of superlattice Dirac points in graphene on hexagonal boron nitride. Nature Phys. 8, 382–386 (2012). [Google Scholar]
  14. Ponomarenko L. A. et al. Tunable metal-insulator transition in double-layer graphene heterostructures. Nature Phys. 7, 958–961 (2011). [Google Scholar]
  15. Britnell L. et al. Field-Effect Tunneling Transistor Based on Vertical Graphene Heterostructures. Science 335, 947–950 (2012). [DOI] [PubMed] [Google Scholar]
  16. Giovannetti G., Khomyakov P. A., Brocks G., Kelly P. J. & van den Brink J. Substrate-induced band gap in graphene on hexagonal boron nitride: Ab initio density functional calculations. Phys. Rev. B 76, 073103 (2007). [Google Scholar]
  17. Oshima C., Itoh A., Rokuta E., Tanaka T., Yamashita K. & Sakurai T. A hetero-epitaxial-double-atomic-layer system of monolayer graphene/monolayer h-BN on Ni(111). Solid State Commun. 116, 37–40 (2000). [Google Scholar]
  18. Kim S. M., Hsu A., Araujo P. T., Lee Y.-H., Palacios T., Dresselhaus M. et al. Synthesis of Patched or Stacked Graphene and hBN Flakes: A Route to Hybrid Structure Discovery. Nano Lett. 13, 933–941 (2013). [DOI] [PubMed] [Google Scholar]
  19. Yu Q. et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nature Mater. 10, 443–449 (2011). [DOI] [PubMed] [Google Scholar]
  20. Gao L. et al. Repeated growth and bubbling transfer of graphene with millimetre-size single-crystal grains using platinum. Nature Commun. 3, 699 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Wu T. et al. Triggering the Continuous Growth of Graphene Toward Millimeter-Sized Grains. Adv. Func. Mater. 23, 198–203 (2012). [Google Scholar]
  22. Li X. et al. Graphene Films with Large Domain Size by a Two-Step Chemical Vapor Deposition Process. Nano Lett. 10, 4328–4334 (2010). [DOI] [PubMed] [Google Scholar]
  23. Son M., Lim H., Hong M. & Choi H. C. Direct growth of graphene pad on exfoliated hexagonal boron nitride surface. Nanoscale 3, 3089–3093 (2011). [DOI] [PubMed] [Google Scholar]
  24. Tang S. et al. Nucleation and growth of single crystal graphene on hexagonal boron nitride. Carbon 50, 329–331 (2012). [Google Scholar]
  25. Garcia J. M. et al. Graphene growth on h-BN by molecular beam epitaxy. Solid State Commun. 152, 975–978 (2012). [Google Scholar]
  26. Rong Z. Y. & Kuiper P. Electronic effects in scanning tunneling microscopy: Moiré pattern on a graphite surface. Phys. Rev. B 48, 17427–17431 (1993). [DOI] [PubMed] [Google Scholar]
  27. Campanera J. M., Savini G., Suarez-Martinez I. & Heggie M. I. Density functional calculations on the intricacies of Moiré patterns on graphite. Phys. Rev. B 75, 235449 (2007). [Google Scholar]
  28. Miller D. L. et al. Structural analysis of multilayer graphene via atomic moireacute interferometry. Physical Review B 81 (2010). [Google Scholar]
  29. Geim A. K. & Novoselov K. S. The rise of graphene. Nature Mater. 6, 183–191 (2007). [DOI] [PubMed] [Google Scholar]
  30. Neubeck S. et al. Direct determination of the crystallographic orientation of graphene edges by atomic resolution imaging. Appl. Phys. Lett. 97, 053110 (2010). [Google Scholar]
  31. Girit Ç. Ö. et al. Graphene at the Edge: Stability and Dynamics. Science 323, 1705–1708 (2009). [DOI] [PubMed] [Google Scholar]
  32. Jia X. et al. Controlled Formation of Sharp Zigzag and Armchair Edges in Graphitic Nanoribbons. Science 323, 1701–1705 (2009). [DOI] [PubMed] [Google Scholar]
  33. Nemes-Incze P., Magda G., Kamaras K. & Biro L. P. Crystallographically selective nanopatterning of graphene on SiO2. Nano Res. 3, 110–116 (2010). [Google Scholar]
  34. Rutter G. M., Guisinger N. P., Crain J. N., First P. N. & Stroscio J. A. Edge structure of epitaxial graphene islands. Phys. Rev. B 81, 245408 (2010). [Google Scholar]
  35. Okada S. Energetics of nanoscale graphene ribbons: Edge geometries and electronic structures. Phys. Rev. B 77, 041408 (2008). [Google Scholar]
  36. Nakajima T. & Shintani K. Molecular dynamics study of energetics of graphene flakes. J. Appl. Phys. 106, 114305 (2009). [Google Scholar]
  37. Gan C. K. & Srolovitz D. J. First-principles study of graphene edge properties and flake shapes. Phys. Rev. B 81, 125445 (2010). [Google Scholar]
  38. Luo Z., Kim S., Kawamoto N., Rappe A. M. & Johnson A. T. C. Growth Mechanism of Hexagonal-Shape Graphene Flakes with Zigzag Edges. ACS Nano 5, 9154–9160 (2011). [DOI] [PubMed] [Google Scholar]
  39. Shu H., Chen X., Tao X. & Ding F. Edge Structural Stability and Kinetics of Graphene Chemical Vapor Deposition Growth. ACS Nano 6, 3243–3250 (2012). [DOI] [PubMed] [Google Scholar]
  40. Coraux J. et al. Growth of graphene on Ir(111). New J. Phys. 11, 039801 (2009). [Google Scholar]
  41. Eom D. et al. Structure and Electronic Properties of Graphene Nanoislands on Co(0001). Nano Lett. 9, 2844–2848 (2009). [DOI] [PubMed] [Google Scholar]
  42. Yamamoto M., Obata S. & Saiki K. Structure and properties of chemically prepared nanographene islands characterized by scanning tunneling microscopy. Surf. Interface Analy. 42, 1637–1641 (2010). [Google Scholar]
  43. Ci L. et al. Controlled nanocutting of graphene. Nano Res. 1, 116–122 (2008). [Google Scholar]
  44. Campos L. C., Manfrinato V. R., Sanchez-Yamagishi J. D., Kong J. & Jarillo-Herrero P. Anisotropic Etching and Nanoribbon Formation in Single-Layer Graphene. Nano Lett. 9, 2600–2604 (2009). [DOI] [PubMed] [Google Scholar]
  45. Booth T. J. et al. Discrete Dynamics of Nanoparticle Channelling in Suspended Graphene. Nano Lett. 11, 2689–2692 (2011). [DOI] [PubMed] [Google Scholar]
  46. Shi Z. et al. Patterning Graphene with Zigzag Edges by Self-Aligned Anisotropic Etching. Adv. Mater. 23, 3061–3065 (2011). [DOI] [PubMed] [Google Scholar]
  47. Vlassiouk I. et al. Role of Hydrogen in Chemical Vapor Deposition Growth of Large Single-Crystal Graphene. ACS Nano 5, 6069–6076 (2011). [DOI] [PubMed] [Google Scholar]
  48. Krauss B. et al. Raman Scattering at Pure Graphene Zigzag Edges. Nano Lett. 10, 4544–4548 (2010). [DOI] [PubMed] [Google Scholar]
  49. Okada S. Energetics of nanoscale graphene ribbons: Edge geometries and electronic structures. Phys. Rev. B 77, 041408R (2008). [Google Scholar]
  50. Xue J. et al. Scanning tunnelling microscopy and spectroscopy of ultra-flat graphene on hexagonal boron nitride. Nature Mater. 10, 282–285 (2011). [DOI] [PubMed] [Google Scholar]
  51. Decker R. G. et al. Local Electronic Properties of Graphene on a BN Substrate via Scanning Tunneling Microscopy. Nano Lett. 11, 2291–2295 (2011). [DOI] [PubMed] [Google Scholar]
  52. Koma A., Sunouchi K. & Miyajima T. Fabrication and characterization of heterostructures with subnanometer thickness. Microelectron. Eng. 2, 129–136 (1984). [Google Scholar]
  53. Koma A. Van der Waals epitaxy—a new epitaxial growth method for a highly lattice-mismatched system. Thin Solid Films 216, 72–76 (1992). [Google Scholar]
  54. Shallcross S., Sharma S. & Pankratov O. A. Twist boundary in graphene: energetics and electric field effect. J. Phys. Condens. Matter. 20, 454224 (2008). [Google Scholar]
  55. Gao L., Guest J. R. & Guisinger N. P. Epitaxial Graphene on Cu(111). Nano Lett. 10, 3512–3516 (2010). [DOI] [PubMed] [Google Scholar]
  56. Wofford J. M., Nie S., McCarty K. F., Bartelt N. C. & Dubon O. D. Graphene Islands on Cu Foils: The Interplay between Shape, Orientation, and Defects. Nano Lett. 10, 4890–4896 (2010). [DOI] [PubMed] [Google Scholar]
  57. Zhao L. et al. Influence of copper crystal surface on the CVD growth of large area monolayer graphene. Solid State Commun. 151, 509–513 (2011). [Google Scholar]
  58. Yan K., Peng H., Zhou Y., Li H. & Liu Z. Formation of Bilayer Bernal Graphene: Layer-by-Layer Epitaxy via Chemical Vapor Deposition. Nano Lett. 11, 1106–1110 (2011). [DOI] [PubMed] [Google Scholar]
  59. Yang W. et al. Epitaxial growth of single-domain graphene on hexagonal boron nitride. Nature Mater (2013) http://dx.doi.org/10.1038/nmat3695. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information:Precisely Aligned Graphene Grown on Hexagonal Boron Nitride by Catalyst Free Chemical Vapor Deposition

srep02666-s1.doc (17.8MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES