Abstract
In order to understand the anomalous interface adhesion properties between graphene membranes and their substrates, we have developed a theoretical method to calibrate the interface adhesion energy of monolayer and multilayer graphene on substrates based on the bond relaxation consideration. Four kinds of interfaces, including graphene/SiO2, graphene/Cu, graphene/Cu/Ni and Cu/graphene/Ni, were taken into account. It was found that the membrane thickness and the interface confinement condition determine the adhesion energy. The relationship between the critical interface separation and the graphene thickness showed that the interface separation in the self-equilibrium state drops with decreasing membrane thickness. The size-dependent Young's modulus of graphene membrane and the interfacial condition were responsible for the novel interface adhesion energy. The proposed theory was expected to be applied to the design of graphene-based devices.
Graphene has received special attention in recent years because of its exceptional electronic, mechanical and thermal properties from both fundamental scientific issues and potentially technological applications including biosensors, nanomechanical and nanoelectronic devices, etc1,2. Supported on a substrate, the interfacial interaction between graphene and its substrate has been one of the key questions from both scientific and technological impetuses3,4. Up to now, a number of theoretical5,6,7,8 and experimental9,10,11,12 methods have been employed to address the interface adhesion energy between graphene and different types of substrates and further explore the underlying mechanism. Strikingly, the available results with regard to the adhesion energies in graphene membranes show the evident thickness dependence. For instance, Koenig et al.10 measured the adhesion energy is 0.45 ± 0.02 J/m2 for monolayer graphene on SiO2, which is higher than that of 0.31 ± 0.03 J/m2 for multilayer graphene with 2–5 layers using a pressurized blister test. Yoon et al.13 reported the adhesion energy of monolayer graphene on Cu is 0.72 ± 0.07 J/m2 by double cantilever beam fracture mechanics testing. On the other hand, according to the experimental configurations some researchers modeled the mechanics of a single layer of graphene adhered to a substrate14,15,16, and others studied the effect of membrane thickness and surface forces on the adhesion energy of graphene membranes grown on different substrates17,18,19,20,21. In addition, the substrate roughness (e.g., 1D sinusoidal surface grooves of the underlying substrate) has also been considered on interface interaction of graphene membranes22,23,24.
Despite recent progress in the fabrication and characterization of graphene membranes grown on different substrates, little is yet known about the elastic strain energy stored in the graphene owing to surface relaxation and its contribution is usually ignored easily. Furthermore, with shrinking the solid size of a material to nanoscale, a variety of physical quantifies of graphene membranes will be changed25,26,27. The atomic identities such as nature, length and strength of nanostructures deviated from the bulk case. Atoms at surface and interface regions have less atomic coordination numbers (CNs) and will become shorter and stronger27,28,29. For example, Lee et al.30 reported that the measured values of Young's modulus of single- and bilayer graphene, respectively, are 2.4 ± 0.4 and 2.0 ± 0.5 TPa, which is much larger than that of the bulk counterpart (~1.02 TPa)31. Moreover, Huang et al.32 calculated the thickness of graphene and single-wall carbon nanotubes directly from the interatomic potential and found the thickness and the related elastic moduli also depend on type of loading.
Accordingly, the lattice strain will take place spontaneously owing to large ratio of uncoordinated atoms located at the end parts and associated with higher energy state compared with the bulk counterpart. Importantly, the interface adhesion energy and other physical-chemical properties, including band offset and mechanical modulus, are determined on the self-equilibrium strain19,33,34,35. Therefore, it is necessary to put forward a comprehensive understanding between lattice strain and interface adhesion energy in graphene membranes under self-equilibrium state from the perspective of atomistic origin.
Focusing on the adhesion energy of substrate-supported graphene membranes, in this paper we develop a quantitative analytical method that describes the effects original from surface relaxation and interface misfit based on the atomic-bond-relaxation (ABR) consideration. Taking into account the free energy contributions including elastic strain energy stored in graphene membranes and van der Walls interaction between graphene and its substrate, we demonstrate that the adhesion energy depends on the membrane thickness and Young's modulus of graphene. The interface interaction is determined on the various system parameters. Our theoretical results suggest that the interface adhesion energy can be modulated via membrane thickness and various interface confinement conditions. Furthermore, the validity of our method is confirmed by the available evidences.
The schematic illustration of a multilayer graphene with volume V0, area Ag, and thickness tf grown on a substrate is shown in Fig. 1. r and h, respectively, are the distance between the film and the substrate, and the height between the top surface layer and the substrate. Theoretically, the total free energy Utotal of the graphene membrane can be divided into the van der Waals interaction energy Uvdw and the elastic strain energy Ue, i.e.,
Notably, the van der Waals interaction between a carbon and a substrate atom can be expressed by Lennard-Jones potential19,36: WLJ = −C1/r6 + C2/r12, where r is the distance between two atoms, C1 and C2 are the constants for the attractive and repulsive interactions. In general, we can assume that the interfacial van der Waals interaction between the substrate and the first graphene layer is predominant because the corresponding separation is much larger than the C-C bond length. Thus, the total interaction potential between graphene and substrate can be obtained by integrating all the atoms of film and substrate19: 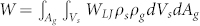 , where ρg represents the number of atoms per unit area of the monolayer graphene, ρs is the number of atoms per unit volume of the substrate and Vs is the substrate volume. Thus, the interfacial potential energy can be yielded as
, where ρg represents the number of atoms per unit area of the monolayer graphene, ρs is the number of atoms per unit volume of the substrate and Vs is the substrate volume. Thus, the interfacial potential energy can be yielded as
where r0 and Γ0 denote the interface separation under equilibrium state and the intrinsic adhesion energy per unit area in the bulk case, respectively19.
Figure 1. Schematic illustration of a multilayer graphene on substrate.
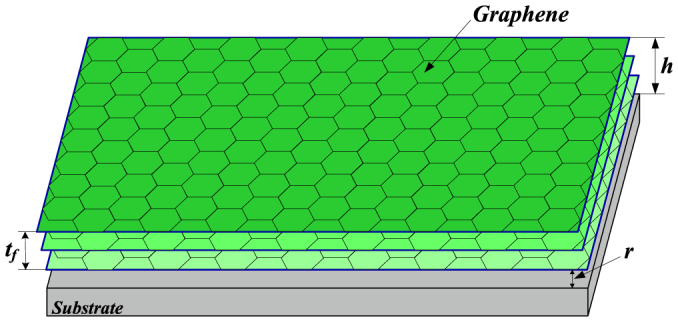
tf is the thickness of graphene membrane, r is the interface separation between graphene and substrate, h = r + tf is the height between the top layer of graphene and the substrate.
On the other hand, according to the continuum mechanics principle, the strain energy per unit area stored in graphene membranes can be given as
where Y(tf) and v are the thickness-dependent Young's modulus and the Poisson's ratio of the graphene membranes, respectively.
Physically, the strain stimulated by the surface and interface effects in nanostructures is one of the importantly fundamental quantities to a wide range of domains owing to inducing novel optical, electronic and mechanical properties as compared to those of the bulk counterpart37,38. For example, the bulk elastic moduli of nanoparticles have shown strain effects induced by the solid sizes and external stimuli such as pressure and temperature39. The related approach demonstrates that the mechanical modulus can be influenced by less-CNs and interlayer relaxation, which provides information on the measurable quantities and the atomic bond identities39. For graphite and graphene membranes, the well-studied bulk graphite offers a well-defined parameterization: a Young's modulus of 1.02 TPa and a interlayer distance of 0.335 nm. However, this viewpoint does not scale down to the monolayer40,41. For example, Zhang et al.41 found that the thicknesses of graphene membranes decrease from 0.331 to 0.082 nm with decreasing layers from five to one. It demonstrated that the bulk value of interlayer separation (0.335 nm) for graphite cannot be suitable for the graphene membranes. In addition, the effective CNs for bulk graphite is 5.335 based on the bond contraction relation by using a length of 0.142 nm for the C-C bond in graphite42. Therefore, in terms of the strain-dependent bulk elastic modulus of nanoparticles and taking further the strains original from the surface and interface effects into account, we can derive the Young's modulus of graphene membranes, i.e.,
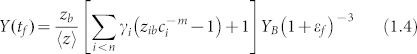 |
where YB is the Young's modulus of the bulk counterpart, m = 2.56 is the bond nature indicator25. 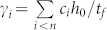 is the surface-to-volume ratio,
is the surface-to-volume ratio, 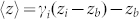 and zb are the mean CNs of the graphene and that of the bulk.
and zb are the mean CNs of the graphene and that of the bulk.
Considering the lattice strains induced by surface relaxation and interface misfit, as well as the van der Waals interaction between the graphene membrane and its substrate, the graphene membrane will be a self-equilibrium state, and the relationship between the critical interface separation r* and the membrane thickness tf can be obtained by setting 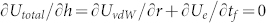 . Thus, we have
. Thus, we have
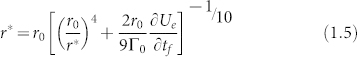 |
with
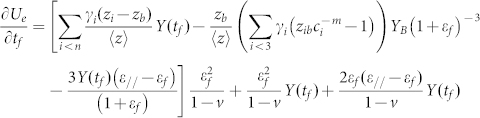 |
Consequently, the total free energy per unit area of the graphene membrane in self-equilibrium state can be obtained
Results
Single interface
In order to address the interface adhesion energy between graphene membrane grown on a substrate, we take graphene/SiO2 and graphene/Cu(111) with single interface and graphene/Cu/Ni and Cu/graphene/Ni with complex interfaces as examples to check the validity. Note that in our cases we assume that the graphene membranes are grown on the purity substrate as depicted in Figure 1.
Using Eq.(2.1) and (2.2), we first calculate the thickness-dependent in-plane strains in graphene/Cu(111) and graphene/SiO2 as well as the total strains in graphene membranes, as shown in Figure 2(a). The necessary parameters are listed in Tables 1. It is clear to see that both of the in-plane strains and the total strains in these two types of systems increase gradually with decreasing thickness. He et al.34 measured the strain in graphene on Cu(111) and found the mean compressive strain is 0.5% for the C-C bond length according to the Raman spectroscopy analysis. Evidently, the variation trend is consistent with our calculations. Also, the compressive strain in graphene/Cu is larger than that in graphene/SiO2 at fixed thickness owing to the different mismatch existing in two systems. Thus, it is concluded that the compressive strains in these two systems are mainly contributed to the coordination number imperfections in surface and the mismatched lattice in interface.
Figure 2. Thickness-dependent mean strains of (a) in-plane in graphene/Cu, graphene/SiO2, and the membranes, (b) in-plane in Cu/graphene/Ni, graphene/Cu/Ni, and the membranes.
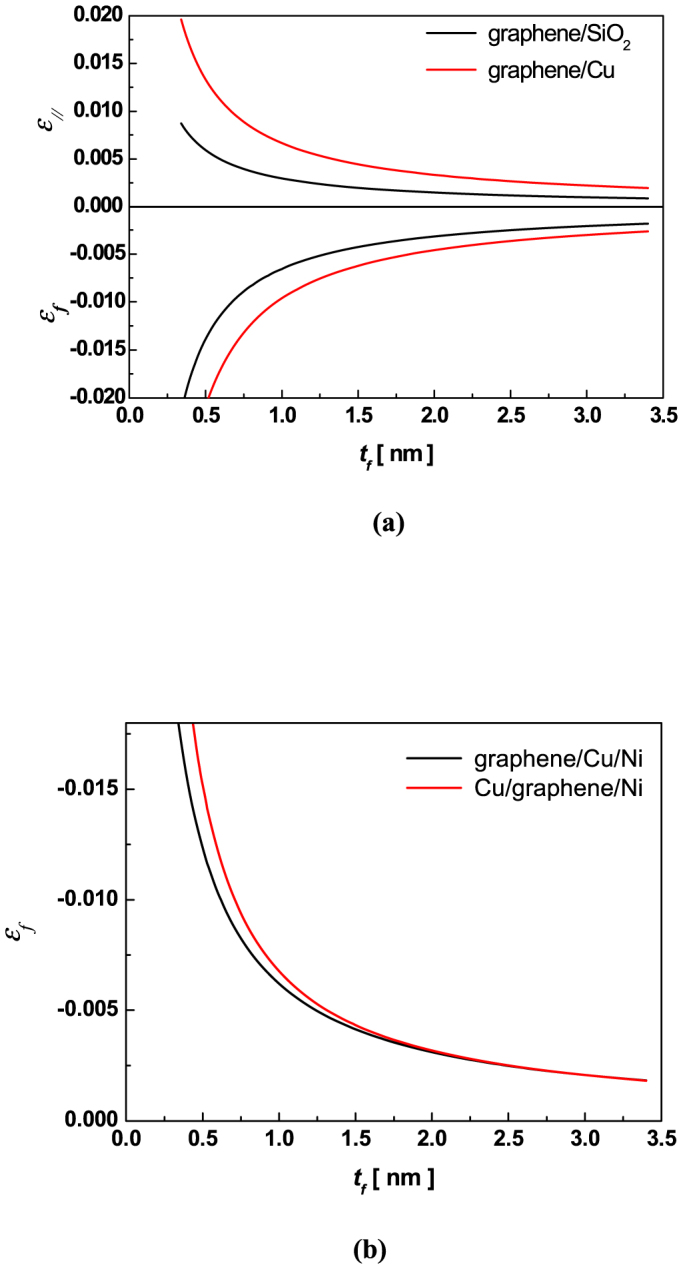
Table 1. Input parameters for calculations. r0, a, h0, E, v and YB are the interface equilibrium distance, in-plane lattice constant, bond length, binding energy per unit area, Poisson's ratio and Young's modulus, respectively.
Complex interface
On the other hand, Figure 2(b) shows the thickness-dependent mean strains of graphene membranes in graphene/Cu/Ni (the black line) and Cu/graphene/Ni (the red line), respectively. Clearly, the total strains of graphene in graphene/Cu/Ni and Cu/graphene/Ni increase with decreasing membrane thickness. It should be noted that the in-plane strain of graphene in graphene/Cu/Ni system can be calculated as follows: according to the definition of lattice strain, the in-plane strain of Cu is 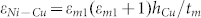 , where εm1 is the mismatch strain between Ni and Cu, and hCu is the mean bond length of Cu. Similarly, we can obtain the in-plane strain of the graphene, i.e.,
, where εm1 is the mismatch strain between Ni and Cu, and hCu is the mean bond length of Cu. Similarly, we can obtain the in-plane strain of the graphene, i.e., 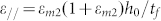 , here
, here 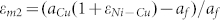 is the mismatch strain between Cu and graphene, aCu is the lattice constant of Cu. In addition, in the case of Cu/graphene/Ni, the in-plane strain can also be obtained as following: the in-plane strain of graphene in graphene/Ni interface is
is the mismatch strain between Cu and graphene, aCu is the lattice constant of Cu. In addition, in the case of Cu/graphene/Ni, the in-plane strain can also be obtained as following: the in-plane strain of graphene in graphene/Ni interface is 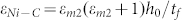 , and the in-plane strain of graphene in graphene/Cu interface is
, and the in-plane strain of graphene in graphene/Cu interface is 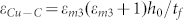 , where εm2 and εm3 are, respectively, the mismatch strains in Ni/graphene and Cu/graphene. Therefore, the in-plane strain of graphene in Cu/graphene/Ni system can be given by
, where εm2 and εm3 are, respectively, the mismatch strains in Ni/graphene and Cu/graphene. Therefore, the in-plane strain of graphene in Cu/graphene/Ni system can be given by 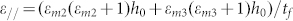 .
.
In our case we assume the Cu has a single layer in those two complex systems, which is in accord with Lahiri's consideration12. Similarly, Murayama43 reported that the misfit strain of Co layer in Cu/Co/Au/Cu(111) system increases with increasing Au-interlayer thickness and found that the in-plane strain in Co layer at the Co/Au interface gradually decreases as the Co thickness increases. Thus, it implies that the middle layers play the crucial role in the complex system.
Discussion
It is noted that the strain induced by surface effect and interface confinement condition of membranes would change the mechanical modulus due to different bond identities compared with the bulk counterpart. Using Eq.(1.4), we calculate the thickness-dependent Young's modulus (Y(tf)) of graphene membranes, as shown in Figure 3. It is found that the Young's modulus of graphene membrane increases dramatically with decreasing graphene thickness. Lee et al.30 demonstrated that the Young's modulus of single- and bilayer graphene are 2.4 ± 0.4 and 2.0 ± 0.5 TPa. Also, Tu et al.44 calculated the Young's modulus of multiwalled carbon nanotubes using local density approximation, and obtained the Young's modulus are, respectively, 1.7, 1.41, 1.29, and 1.23 TPa for 2–5 layers and 1.15 TPa for 8 layers. Importantly, our predictions are exceedingly well agreement with the experimental measurements and theoretical calculations.
Figure 3. Thickness dependence of the relative change of Young's modulus.
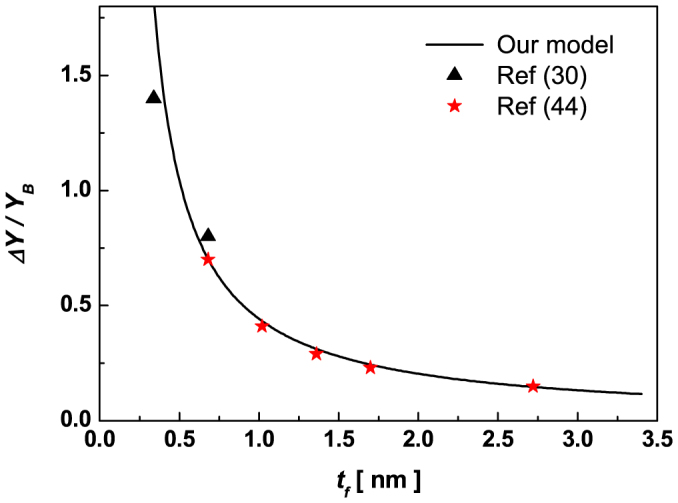
The solid line denotes the consequence of Eq. 1.4. The symbols in (a) represent the experimental results and calculations30,44.
Furthermore, the thickness dependence of Young's modulus will lead to the changes of elastic strain energy and total free energy of graphene membranes. Figure 4(a) shows the thickness-dependent van der Waals interaction energy and elastic strain energy in graphene/SiO2. Noticeably, these two energies show the opposite variation with thickness. Also, Figure 4 (b) shows the relationship among the total free energy, the number of layers and the interface separation in graphene/SiO2. Strikingly, the minimum of total free energies have obvious shift with number of layers of graphene membranes. Meanwhile, the relationship between the critical interface separation and the membrane thickness based on Eq. (1.5) is shown in Figure 4(b). Surprisingly, the variation of interface separation becomes lower with decreasing membrane thickness. When the thickness goes to infinite, the r* → r0. Therefore, it is concluded that the interface separation is influenced by the elastic relaxation of membrane. At the equilibrium state, the total free energy is negative, and the interface adhesion energy can be calculated as 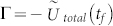 . As illustrated in Figure 4 (c), the interface adhesion energy of graphene/SiO2 shows the evident thickness effect. Clearly, the interfacial adhesion energy increases as the thickness decreases, which agrees very well with the experimental observations10.
. As illustrated in Figure 4 (c), the interface adhesion energy of graphene/SiO2 shows the evident thickness effect. Clearly, the interfacial adhesion energy increases as the thickness decreases, which agrees very well with the experimental observations10.
Figure 4. Thickness-dependent interface van der Waals interaction of graphene/SiO2 in (a), the total free energy of graphene/SiO2 as a function of interface separation in (b), and thickness-dependent adhesion energy of graphene/SiO2 in (c).
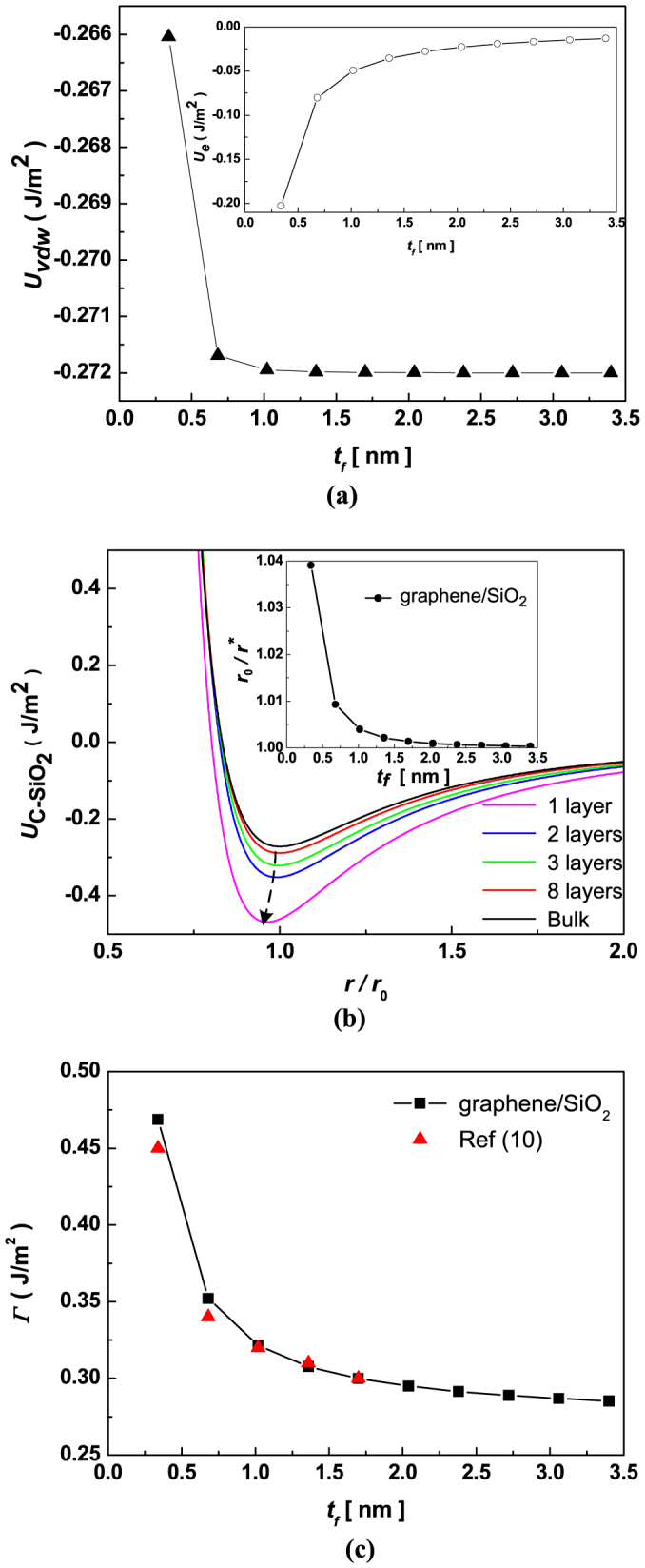
The inset in (a) is the elastic strain energy stored in graphene membranes grown on SiO2 under self-equilibrium state. The inset in (b) is the relationship between the critical interface separation and the membrane thickness. The symbols shown in (c) are the results measured by a pressurized blister test10.
Compared with the graphene/SiO2, the case of graphene/Cu shows the similar interface adhesion properties shown in Figure 5. The adhesion energy in graphene/Cu decreases with increasing membrane thickness, while the interface separation between graphene and Cu becomes larger with increasing thickness. However, the shift of interface separation is wider than that in graphene/SiO2. The main reason is that the mismatch in graphene/Cu is larger than that in graphene/SiO2. Thus, the elastic strain energy stored in graphene/Cu at self-equilibrium state is more remarkable compared to that in graphene/SiO2. Yoon et al.13 measured the adhesion energy of graphene/Cu is 0.72 ± 0.07 J/m2, which is larger than that of 0.45 ± 0.02 J/m2 in graphene/SiO2. The possible mechanism is that the electronic density in graphene/Cu interface is more remarkable than that in graphene/SiO2. Therefore, the interatomic force between graphene and Cu becomes stronger than the typical van der Waals force between graphene and SiO2. In our case, we take the combination from the interface misfit and surface relaxation in the graphene/substrate system, and further predict that the size-dependent adhesion energy in graphene/Cu and obtain the adhesion energies are 0.74, 0.40, 0.32, 0.29 and 0.27 J/m2 for the graphene thickness change from 1 layer to 5 layers. In addition, Lahiri et al.12 calculated the adhesion energy of Ni/graphene/Ni using density functional theory. They found that the adhesion energy can be expressed as a function of the thickness of Ni overlayer, from 3.5 to 3.0 J/m2 for the monolayer to three layers in Ni (overlayer)/graphene/Ni (substrate), which shows the size-dependent adhesion energy in the complex interface, and suggested that the overlayer has a large impact on interfacial adhesion energy.
Figure 5. Thickness-dependent interface van der Waals interaction of graphene/Cu in (a), the total free energy of graphene/Cu as a function of interface separation in (b), and thickness dependent adhesion energy of graphene/Cu in (c).
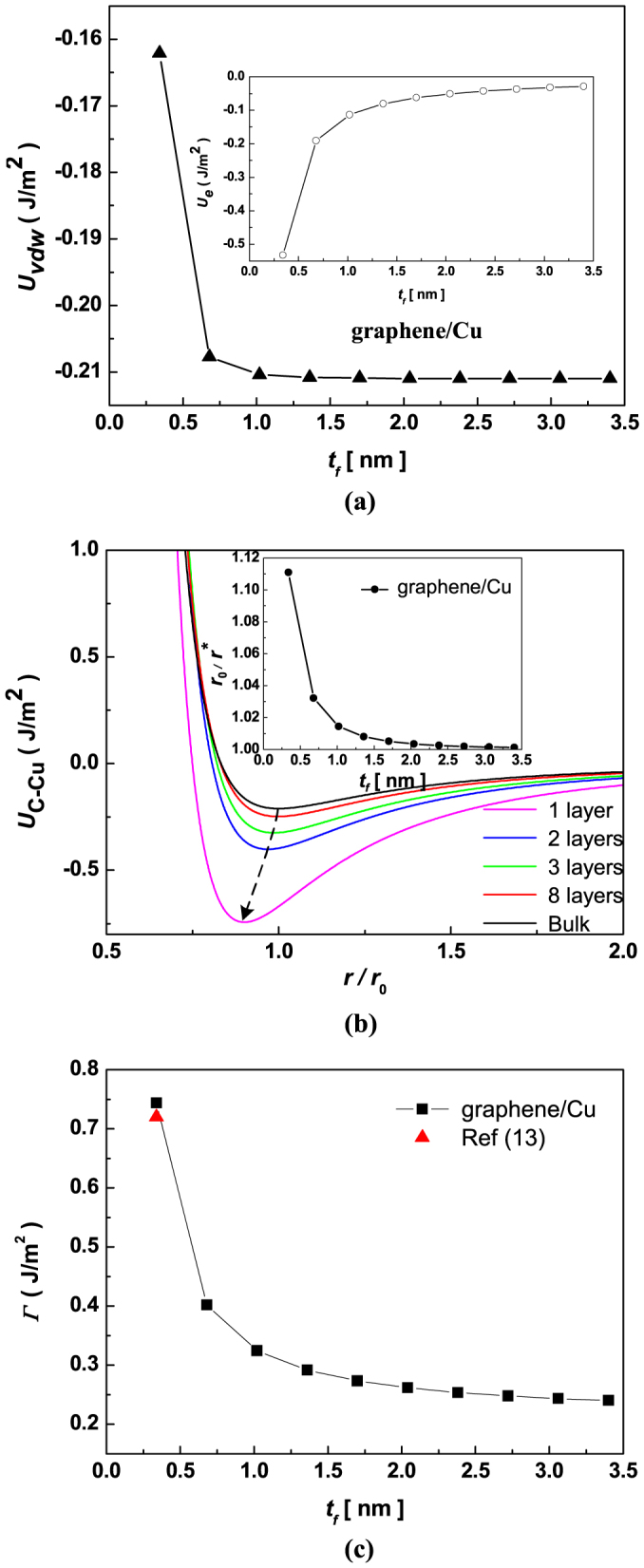
The inset in (a) is the elastic strain energy stored in graphene membranes grown on Cu under self-equilibrium state. The inset in (b) is the relationship between the critical interface separation and the membrane thickness. The symbols shown in (c) are the results measured by double cantilever beam fracture mechanics testing13.
To further confirm the consistency of our analysis, we consider the complex interface conditions in our case. Taking graphene/Cu/Ni and Cu/graphene/Ni as two examples in our considerations, we plotted the graphene thickness-dependent adhesion energy shown in Figure 6. Interestingly, we show that the interface separations between graphene and Cu in graphene/Cu/Ni and Cu/graphene/Ni are different despite they show the same trends in comparison with other cases. Lahiri et al.12 found the adhesion energy and the interfacial separation between graphene and Cu are 0.34 J/m2 and 0.312 nm in graphene/Cu/Ni whereas those are 0.51 J/m2 and 0.291 nm in Cu/graphene/Ni. The underlying mechanism is that the electronic density of Cu/graphene interface in Cu/graphene/Ni becomes larger than that of graphene/Cu interface in graphene/Cu/Ni, which leads to the results of adhesion in those systems different from each other. Interestingly, these results are consistent with our calculations. In fact, there are two types of interfaces in Cu/graphene/Ni, i.e., Cu/graphene and graphene/Ni. The coupling role original from two mismatch strains of Cu/graphene and graphene/Ni determines the equilibrium state of the system. Nevertheless, in graphene/Cu/Ni system, there is only a single interface that influences the final equilibrium state. Noticeably, the roles of Ni and Cu layers cannot be ignored. This is due to the mismatch between Cu and Ni would affect the Cu layer and further change the total free energy. Apparently, as plotted on Figure 6(a) and 6(b), the adhesion energy of Cu/graphene/Ni is larger than that of graphene/Cu/Ni owing to the difference of elastic properties, such as Young's modulus, Poisson's ratio and strain energy of the two systems. Therefore, the coupling role from surface and interface conditions has great effect on the interface adhesion properties in graphene membranes.
Figure 6. Dependence of adhesion energy on the membrane thickness for (a) graphene/Cu/Ni and (b) Cu/graphene/Ni.
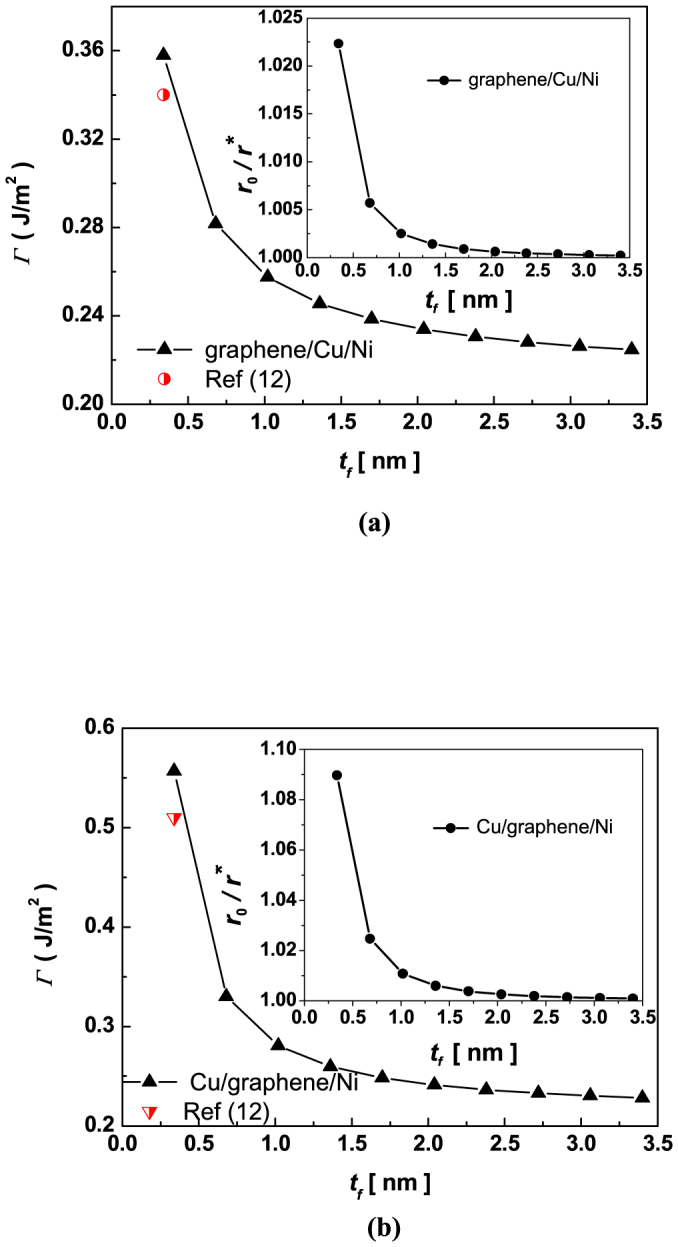
The insets in (a) and (b) are the relationship between the critical interface separation and the membrane thickness. The symbols shown in the (a) and (b) are from the experimental measurements12.
In summary, we have studied the interface adhesion energies of the graphene membranes on SiO2 and Cu substrates with single interface (graphene/Cu and graphene/SiO2) as well as Cu/graphene/Ni and graphene/Cu/Ni with complex interfaces on the basis of ABR consideration. Our theoretical results showed that the interface feature and the thickness effects play the dominant role for the interfacial adhesion energy in both of single and complex interfaces. The elastic relaxation energy stored in graphene membranes at the self-equilibrium state affects the physical properties such as the Young's modulus and the equilibrium separation between graphene and substrate. Likewise, different interface conditions would lead to the changes of adhesion energy. The theoretical predictions were consistent with the experimental measurements and the relevant calculations, which suggested that the developed method could be regarded as a theoretical tool to design the interface adhesion of graphene membranes in graphene-based nanomechanical and nanoelectronic devices.
Methods
General consideration on the strain energy stored in graphene membranes
According to the continuum mechanics, the mismatch strain in the interface will be taken place due to the lattice parameter difference between the graphene membranes and their substrates. It can be usually expressed as: εm = (as − af)/af. Thus, the compatibility of the deformation of two layers is determined by45,46, εf − εm = εs, where εf and εs are the mean biaxial strain stored in the in-plane direction of film and that in the substrate, respectively. In addition, the atomic bond length in the surface would contract spontaneously upon the elastic strain on account of imperfect coordination, which is under a more active energy state differently from that in the region of interface28,47,48. Therefore, the total strain stored in the graphene is
with
where εi is the strain in the surface layer, 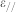 is the strain in the interface layer, n is the number of layers, tf and h0 represent the thickness of a film and the average bond length in bulk. Based on the bond length and bond energy correlation, the bond contraction coefficient
is the strain in the interface layer, n is the number of layers, tf and h0 represent the thickness of a film and the average bond length in bulk. Based on the bond length and bond energy correlation, the bond contraction coefficient 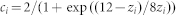 , with zi being the effective CNs in the ith atomic layer49. In addition, the
, with zi being the effective CNs in the ith atomic layer49. In addition, the 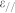 can be calculated as
can be calculated as
Assuming the deformation of the substrate can be ignored, i.e., the lattice strain in the substrate is zero (εs = 0), the strain energy will be concentrated in the graphene membranes. Therefore, the strain energy per unit area is given by
Author Contributions
Y.H., W.F.C. and W.B.Y. established the theoretical models and plotted all the figures. Y.H. wrote the paper. G.O. and G.W.Y. supervised the project and revised the paper. All authors discussed the results and commented on the manuscript.
Acknowledgments
We thank Prof. Chang Q. Sun for helpful discussions. This work was supported by the National Natural Science Foundation of China (Grant Nos. 11174076 and 91233203), the Hunan Provincial Natural Science Foundation of China (Nos. 12JJ1009 and 11JJ7001) and Scientific Research Fund of Hunan Provincial Education Department (No. 12A082).
References
- Geim A. K. Graphene: Status and prospects. Science 324, 1530–1534 (2009). [DOI] [PubMed] [Google Scholar]
- Neto A. H. C., Guinea F., Penes N. M. R., Novoselov K. S. & Geim A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009). [Google Scholar]
- Zhu Y. F., Dai Q. Q., Zhao M. & Jiang Q. Physicochemical insight into gap openings in graphene. Sci. Rep. 1, 1524 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren J. G. et al. Germanium-graphene composite anode for high-energy lithium batteries with long cycle life. J. Mater. Chem. A 1, 1821–1826 (2013). [Google Scholar]
- Khomyakov P. A. et al. First-principles study of the interaction and charge transfer between graphene and metals. Phys. Rev. B 79, 195425 (2009). [Google Scholar]
- Giovannetti G. et al. Doping graphene with metal Contacts. Phys. Rev. Lett. 101, 026803 (2008). [DOI] [PubMed] [Google Scholar]
- Fuentes-Cabrera M., Baskes M. I., Melechko A. V. & Simpson M. L. Bridge structure for the graphene/Ni(111) system: a first principles study. Phys. Rev. B 77, 035405 (2008). [Google Scholar]
- Adamska L., Addou R., Batzill M. & Oleynik I. I. Atomic and electronic structure of graphene/Sn-Ni(111) and graphene/Sn-Cu(111) surface alloy interfaces. Appl. Phys. Lett. 101, 051602 (2012). [Google Scholar]
- Gao L., Guest J. R. & Guisinger N. P. Epitaxial graphene on Cu (111). Nano Lett. 10, 3512–3516 (2010). [DOI] [PubMed] [Google Scholar]
- Koenig S. P., Boddeti N. G., Dunn M. L. & Bunch J. S. Ultra-strong adhesion of graphene membranes. Nat. Nanotech. 6, 543–546 (2011). [DOI] [PubMed] [Google Scholar]
- Lee I., Kim S., Yun J., Park I. & Kim T.-S. Interfacial toughening of solution processed Ag nanoparticle thin films by organic residuals. Nanotechnology 22, 485704 (2012). [DOI] [PubMed] [Google Scholar]
- Lahiri J. et al. Graphene growth and stability at nickel surfaces. New J. Phys. 13, 025001 (2011). [Google Scholar]
- Yoon T. et al. Direct measurement of adhesion energy of monolayer graphene as-grown on copper and its application to renewable transfer process. Nano Lett. 12, 1448–1452 (2012). [DOI] [PubMed] [Google Scholar]
- Vanin M. et al. Graphene on metals: a van der Waals density functional study. Phys. Rev. B 81, 081408 (2010). [Google Scholar]
- Xu Z. & Buehler M. J. Interface structure and mechanics between graphene and metal substrates: a first-principles study. J. Phys.: Condens. Matter 22, 485301 (2010). [DOI] [PubMed] [Google Scholar]
- Adamska L., Lin Y., Rose A. J., Batzill M. & Oleynik I. I. Atomic and electronic structure of single metal/graphene and complex metal/graphene/metal interfaces. Phys. Rev. B 85, 195443 (2012). [Google Scholar]
- Bunch J. S. & Dunn M. L. Adhesion mechanics of graphene membranes. Solid State Commun. 152, 1359–1364 (2012). [Google Scholar]
- Rudenko A. N., Keil F. J., Katsnelson M. I. & Lichtenstein A. I. Graphene adhesion on mica: role of surface morphology. Phys. Rev. B 83, 045409 (2011). [Google Scholar]
- Aitken Z. H. & Huang R. Effects of mismatch strain and substrate surface corrugation on morphology of supported monolayer graphene. J. Appl. Phys. 107, 123531 (2010). [Google Scholar]
- Gao W. & Huang R. Effect of surface roughness on adhesion of graphene membranes. J. Phys. D: Appl. Phys. 44, 452001 (2011). [Google Scholar]
- Lu Z. & Dunn M. L. van der Waals adhesion of graphene membranes. J. Appl. Phys. 107, 044301 (2010). [Google Scholar]
- Koskinen P. & Kit O. O. Efficient approach for simulating distorted materials. Phys. Rev. Lett. 105, 106401 (2010). [DOI] [PubMed] [Google Scholar]
- Scharfenberg S., Rocklin D. Z., Chialvo C., Weaver R. L., Goldbart P. M. & Mason N. Probing the mechanical properties of graphene using a corrugated elastic substrate. Appl. Phys. Lett. 98, 091908 (2011). [Google Scholar]
- Li T. & Zhang Z. Snap-through instability of graphene on substrates. Nanoscale Res. Lett. 5, 169–173 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun C. Q. Size dependence of nanostructures: impact of bond order deficiency. Prog. Solid State Chem. 35, 1–159 (2007). [Google Scholar]
- Ouyang G., Wang C. X. & Yang G. W. Surface energy of nanostructural materials with negative curvature and related size effects. Chem. Rev. 109, 4221–4247 (2009). [DOI] [PubMed] [Google Scholar]
- Sun C. Q. Thermo-mechanical behavior of low-dimensional systems: the local bond average approach. Prog. Mater. Sci. 54, 179–307 (2009). [Google Scholar]
- Ouyang G., Yang G. W., Sun C. Q. & Zhu W. G. Nanoporous structures: smaller is stronger. Small 4, 1359–1362 (2008). [DOI] [PubMed] [Google Scholar]
- Zhang A., Zhu Z., He Y. & Ouyang G. Structure stabilities and transitions in polyhedral metal nanocrystals: an atomic-bond-relaxation approach. Appl. Phys. Lett. 100, 171912 (2012). [Google Scholar]
- Lee J. U., Yoon D. & Cheong H. Estimation of Young's modulus of graphene by Raman spectroscopy. Nano Lett. 12, 4444–4448 (2012). [DOI] [PubMed] [Google Scholar]
- Lee C., Wei X., Kysar J. W. & Hone J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321, 385–388 (2008). [DOI] [PubMed] [Google Scholar]
- Huang Y., Wu J. & Hwang K. C. Thickness of graphene and single-wall carbon nanotubes. Phys. Rev. B 74, 245413 (2006). [Google Scholar]
- Zhang Z. & Li T. Graphene morphology regulated by nanowires patterned in parallel on a substrate surface. J. Appl. Phys. 107, 103519 (2010). [Google Scholar]
- He R. et al. Large physisorption strain in chemical vapor deposition of graphene on copper substrates. Nano Lett. 12, 2408–2413 (2012). [DOI] [PubMed] [Google Scholar]
- Zabel J. et al. Raman spectroscopy of graphene and bilayer under biaxial strain: bubbles and balloons. Nano Lett. 12, 617–621 (2011). [DOI] [PubMed] [Google Scholar]
- Israelachvili J. N. Intermolecular And Surface Forces, Academic press: London, 1992. [Google Scholar]
- Diao J., Gall K. & Dunn M. L. Surface-stress-induced phase transformation in metal nanowires. Nat. Mater. 2, 656–660 (2003). [DOI] [PubMed] [Google Scholar]
- Smith A. M., Mohs A. M. & Nie S. Tuning the optical and electronic properties of colloidal nanocrystals by lattice strain. Nat. Nanotechnol. 4, 56–63 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ouyang G., Zhu W. G., Sun C. Q., Zhu Z. M. & Liao S. Z. Atomistic origin of lattice strain on stiffness of nanoparticles. Phys. Chem. Chem. Phys. 12, 1543–1549 (2010). [DOI] [PubMed] [Google Scholar]
- Hemandez E., Goze C., Bernier P. & Rubio A. Elastic properties of C and BxCyNz composite nanotubes. Phys. Rev. Lett. 80, 4502–4505 (1998). [Google Scholar]
- Zhang D. B., Akatyeva E. & Dumitrică T. Bending ultrathin graphene at the margins of continuum mechanics. Phys. Rev. Lett. 106, 255503 (2011). [DOI] [PubMed] [Google Scholar]
- Yang X. X. et al. Raman spectroscopic determination of the length, strength, compressibility, Debye temperature, elasticity, and force constant of the C-C bond in graphene. Nanoscale 4, 502–510 (2012). [DOI] [PubMed] [Google Scholar]
- Murayama A., Hyomi K., Eickmann J. & Falco C. M. Strain dependence of the interface perpendicular magnetic anisotropy in epitaxial Co/Au/Cu(111) films. Phys. Rev. B 60, 15245–15250 (1999). [Google Scholar]
- Tu Z. C. & Ou-Yang Z.-C. Single-walled and multiwalled carbon nanotubes viewed as elastic tubes with the effective Young's moduli dependent on layer number. Phys. Rev. B 65, 233407 (2002). [Google Scholar]
- Zhu Z. M., Zhang A., He Y., Ouyang G. & Yang G. W. Interface relaxation and band gap shift in epitaxial layers. AIP Advances 2, 042185 (2012). [Google Scholar]
- Freund L. B. & Nix W. D. A critical thickness condition for a strained compliant substrate/epitaxial film system. Appl. Phys. Lett. 69, 173–175 (1996). [Google Scholar]
- Ouyang G., Sun C. Q. & Zhu W. G. Atomistic origin and pressure dependence of band gap variation in semiconductor nanocrystals. J. Phys. Chem. C 113, 9516–9519 (2009). [Google Scholar]
- Zhu Z. M., Zhang A., Ouyang G. & Yang G. W. Edge effect on band gap shift in Si nanowires with polygonal cross-sections. Appl. Phys. Lett. 98, 263112 (2011). [Google Scholar]
- Zhu Z. M., Zhang A., Ouyang G. & Yang G. W. Band gap tunability in semiconductor nanocrystals by strain: size and temperature effect. J. Phys. Chem. C 115, 6462–6466 (2011). [Google Scholar]
- Hossain M. Z. Chemistry at the graphene-SiO2 interface. Appl. Phys. Lett. 95, 143125 (2009). [Google Scholar]
- Dmitriev V., Torgashev V., Toledano P. & Salje E. K. H. Theory of SiO2 polymorphs. Europhys. Lett. 37, 553–558 (1997). [Google Scholar]


