Abstract
We demonstrate a unique shear-induced crystallization phenomenon above the equilibrium freezing temperature 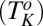 in weakly swollen isotropic
in weakly swollen isotropic 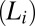 and lamellar
and lamellar 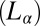 mesophases with bilayers formed in a cationic-anionic mixed surfactant system. Synchrotron rheological X-ray diffraction study reveals the crystallization transition to be reversible under shear (i.e., on stopping the shear, the nonequilibrium crystalline phase
mesophases with bilayers formed in a cationic-anionic mixed surfactant system. Synchrotron rheological X-ray diffraction study reveals the crystallization transition to be reversible under shear (i.e., on stopping the shear, the nonequilibrium crystalline phase 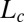 melts back to the equilibrium mesophase). This is different from the shear-driven crystallization below
melts back to the equilibrium mesophase). This is different from the shear-driven crystallization below 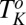 , which is irreversible. Rheological optical observations show that the growth of the crystalline phase occurs through a preordering of the
, which is irreversible. Rheological optical observations show that the growth of the crystalline phase occurs through a preordering of the 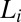 phase to an
phase to an 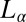 phase induced by shear flow, before the nucleation of the
phase induced by shear flow, before the nucleation of the 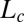 phase. Shear diagram of the
phase. Shear diagram of the 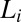 phase constructed in the parameter space of shear rate
phase constructed in the parameter space of shear rate 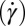 vs. temperature exhibits
vs. temperature exhibits 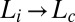 and
and 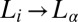 transitions above the equilibrium crystallization temperature
transitions above the equilibrium crystallization temperature 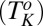 , in addition to the irreversible shear-driven nucleation of
, in addition to the irreversible shear-driven nucleation of 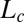 in the
in the 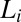 phase below
phase below 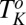 . In addition to revealing a unique class of nonequilibrium phase transition, the present study urges a unique approach toward understanding shear-induced phenomena in concentrated mesophases of mixed amphiphilic systems.
. In addition to revealing a unique class of nonequilibrium phase transition, the present study urges a unique approach toward understanding shear-induced phenomena in concentrated mesophases of mixed amphiphilic systems.
Keywords: shear-induced phase separation, strongly binding counterions, coagels
Shear is known to assist crystallization below the equilibrium freezing temperature in complex fluids like colloidal glasses (1, 2), dense granular suspensions (3), polymer melts (4, 5), micellar solutions of block copolymers (6), and multicomponent surfactant systems (7, 8). Shear-driven crystallization is equally relevant for simple fluids like bulk metallic glasses (9), molecular liquids (10), and atomic systems (11). The general understanding is that shear lowers the energy barrier for nucleation and accelerates the growth of a stable crystalline phase from a metastable, amorphous/isotropic solution at Peclet number 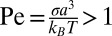 , where σ is the shear stress, a is the characteristic length scale, and
, where σ is the shear stress, a is the characteristic length scale, and 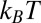 is the thermal energy (12). The crystalline phase primarily induced by the effect of flow on the internal structure and ordering of the constituents does not revert to the starting fluid state when the imposed shear is removed, indicating that the phenomenon is not a dynamic phase transition. In the present study, we report a unique phenomenon, where under steady shear, crystallization occurs above the equilibrium crystallization temperature
is the thermal energy (12). The crystalline phase primarily induced by the effect of flow on the internal structure and ordering of the constituents does not revert to the starting fluid state when the imposed shear is removed, indicating that the phenomenon is not a dynamic phase transition. In the present study, we report a unique phenomenon, where under steady shear, crystallization occurs above the equilibrium crystallization temperature 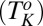 in an isotropic mesophase
in an isotropic mesophase 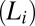 consisting of bilayers formed in a lyotropic surfactant system. Notably, above
consisting of bilayers formed in a lyotropic surfactant system. Notably, above 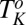 , when the imposed shear is removed, the crystalline phase melts back to the starting
, when the imposed shear is removed, the crystalline phase melts back to the starting 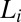 phase.
phase.
The studies were carried out in a cationic-anionic mixed surfactant system formed by SDS and the strong binding counter-ion paratoluene hydrochloride (PTHC) in water. At equilibrium, the organic counter-ion PTHC has the tendency to remain at the micelle–water interface, decreasing the spontaneous curvature of the micellar aggregates and transforming them from cylinders to bilayers (13, 14). The equilibrium phase behavior of the concentrated phases was investigated recently in this system, and a novel isotropic phase 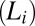 of bilayers was reported (15). The
of bilayers was reported (15). The 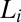 phase with short-range translational correlations occurs when the quasi–long-range positional order of the
phase with short-range translational correlations occurs when the quasi–long-range positional order of the 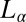 phase is destroyed at higher temperatures or at higher concentrations of counter-ions through the creation of defects in the bilayer. Further, it was proposed that the optically isotropic
phase is destroyed at higher temperatures or at higher concentrations of counter-ions through the creation of defects in the bilayer. Further, it was proposed that the optically isotropic 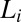 phase is made up of bilayers with pores/randomly connected passages. Importantly, this phase was reported to exhibit flow birefringence, suggesting that the symmetry of the phase can be broken by shear. Here, we report from in situ synchrotron rheological X-ray scattering measurements and rheological optical studies in the
phase is made up of bilayers with pores/randomly connected passages. Importantly, this phase was reported to exhibit flow birefringence, suggesting that the symmetry of the phase can be broken by shear. Here, we report from in situ synchrotron rheological X-ray scattering measurements and rheological optical studies in the 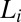 and
and 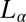 phases of a lyotropic mixed surfactant system, a unique shear-induced phase transition to a crystalline phase above the equilibrium freezing temperature, which is reversible under shear. We construct a shear diagram (Fig. 1) in the parameter space of shear rate and temperature, which reveals, in addition to crystallization (region III, Fig. 1), the observation of an
phases of a lyotropic mixed surfactant system, a unique shear-induced phase transition to a crystalline phase above the equilibrium freezing temperature, which is reversible under shear. We construct a shear diagram (Fig. 1) in the parameter space of shear rate and temperature, which reveals, in addition to crystallization (region III, Fig. 1), the observation of an 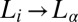 transition (region II, Fig. 1) in a concentrated isotropic mesophase above a low critical shear rate of 0.05 s−1. In Fig. 1, (R) and (IR) are used to emphasize the reversible nature and irreversible nature of the phases, respectively, on stopping the shear. The high-resolution powder X-ray diffraction data obtained for the nonequilibrium
transition (region II, Fig. 1) in a concentrated isotropic mesophase above a low critical shear rate of 0.05 s−1. In Fig. 1, (R) and (IR) are used to emphasize the reversible nature and irreversible nature of the phases, respectively, on stopping the shear. The high-resolution powder X-ray diffraction data obtained for the nonequilibrium 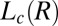 phases in region III were indexed to a triclinic lattice (Figs. 2 and 3). By following the growth kinetics, we show that the crystalline phase nucleates in the shear-induced
phases in region III were indexed to a triclinic lattice (Figs. 2 and 3). By following the growth kinetics, we show that the crystalline phase nucleates in the shear-induced 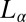 phase (Fig. 4), with a higher concentration of the organic counter-ions compared with the starting
phase (Fig. 4), with a higher concentration of the organic counter-ions compared with the starting  phase at rest. Consequently, we propose that the driving mechanism for the formation of the
phase at rest. Consequently, we propose that the driving mechanism for the formation of the 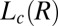 phase is the shear-induced redistribution of the hydrophobic counter-ions in the bilayers of the
phase is the shear-induced redistribution of the hydrophobic counter-ions in the bilayers of the 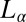 phase.
phase.
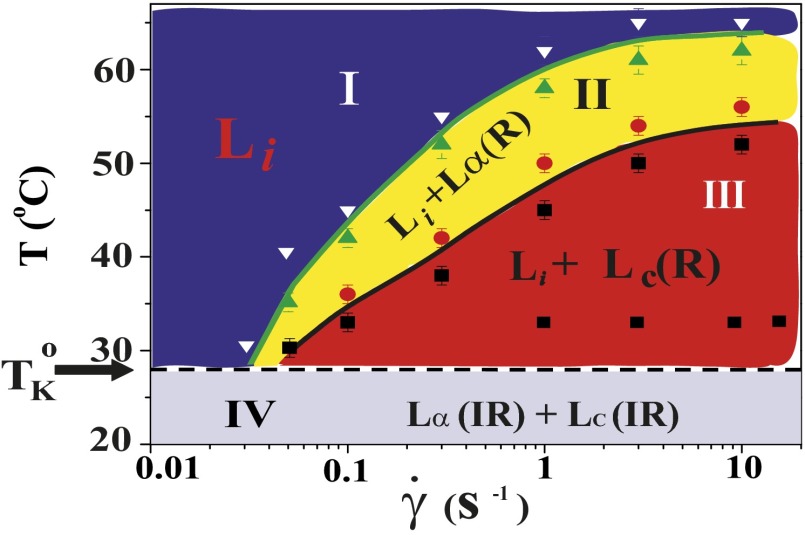
Fig. 1.
Shear diagram for the isotropic phase 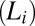 . Region III (shaded in red) demonstrates the coexistence of
. Region III (shaded in red) demonstrates the coexistence of 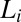 with the shear-induced crystalline phase
with the shear-induced crystalline phase 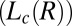 . Coexistence of the
. Coexistence of the 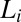 and
and 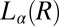 phases is observed in region II (shaded in yellow). The crystalline
phases is observed in region II (shaded in yellow). The crystalline 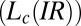 and lamellar
and lamellar 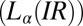 phases nucleate irreversibly in the
phases nucleate irreversibly in the 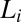 phase under shear (region IV, shaded in blue) below
phase under shear (region IV, shaded in blue) below 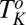 . Only the transitions above
. Only the transitions above 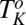 (indicated by the dashed line) are reversible under shear. The approximate boundaries demarcating different regions are shown by solid lines. The data points corresponding to the final phases, constructed from the stress relaxation measurements, are shown by different symbols indicating
(indicated by the dashed line) are reversible under shear. The approximate boundaries demarcating different regions are shown by solid lines. The data points corresponding to the final phases, constructed from the stress relaxation measurements, are shown by different symbols indicating 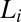 (inverted white triangles),
(inverted white triangles), 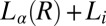 (green triangles and red circles), and
(green triangles and red circles), and 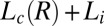 (black squares).
(black squares).
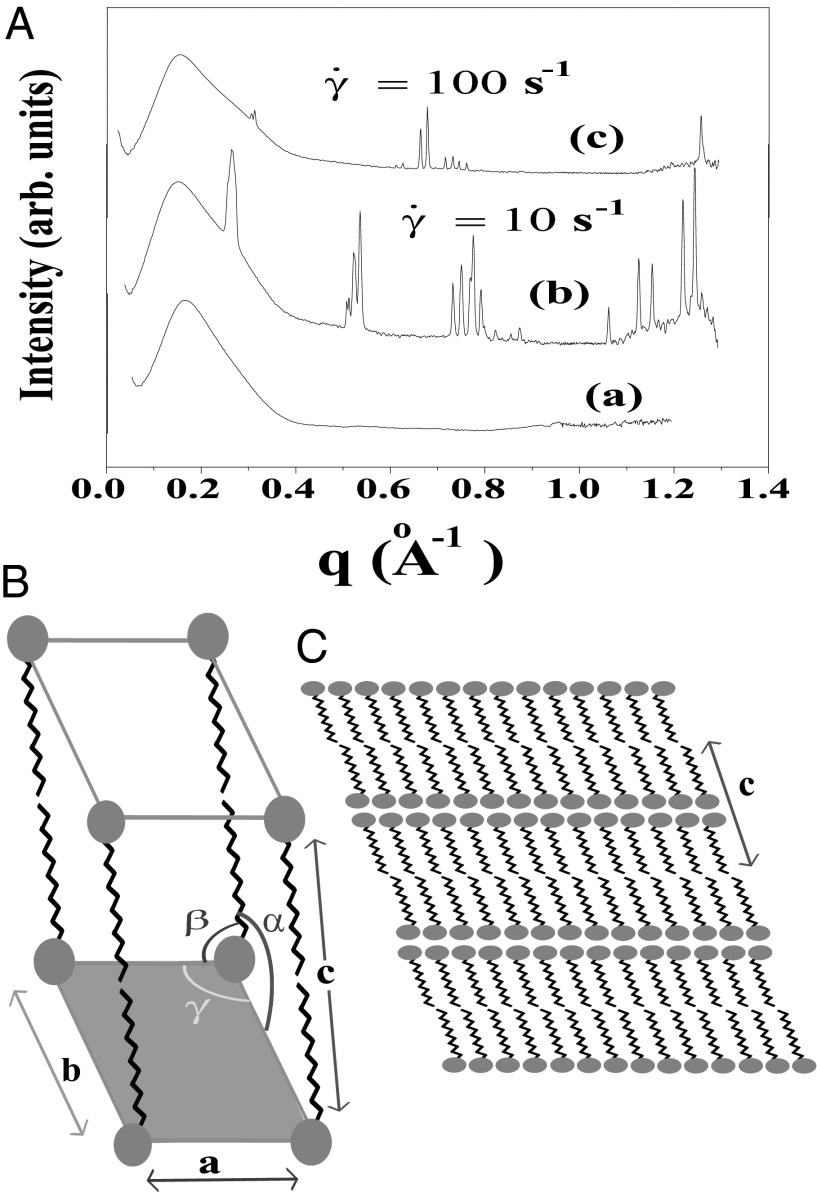
Fig. 2.
X-ray diffraction pattern of the equilibrium  phase (corresponding to region I, Fig. 1) and shear-induced crystalline
phase (corresponding to region I, Fig. 1) and shear-induced crystalline 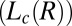 phases (corresponding to region III, Fig. 1). (A) Diffraction pattern from the
phases (corresponding to region III, Fig. 1). (A) Diffraction pattern from the 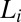 phase at rest at T = 33 °C is shown in curve a; Rheo-SAXS data in the radial geometry obtained at T = 33 °C indicate the coexistence of the
phase at rest at T = 33 °C is shown in curve a; Rheo-SAXS data in the radial geometry obtained at T = 33 °C indicate the coexistence of the 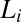 and
and 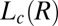 phases for samples sheared at (i) 10 s−1 in curve b and (ii) 100 s−1 in curve c. arb., arbitrary. There is a shift in peak positions and relative intensities of the Bragg peaks in curve c with respect to curve b indicates a change in the structure of
phases for samples sheared at (i) 10 s−1 in curve b and (ii) 100 s−1 in curve c. arb., arbitrary. There is a shift in peak positions and relative intensities of the Bragg peaks in curve c with respect to curve b indicates a change in the structure of 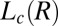 with the shear rate. A triclinic unit cell (B) and a schematic sketch of the proposed crystalline structure (C) are illustrated.
with the shear rate. A triclinic unit cell (B) and a schematic sketch of the proposed crystalline structure (C) are illustrated.
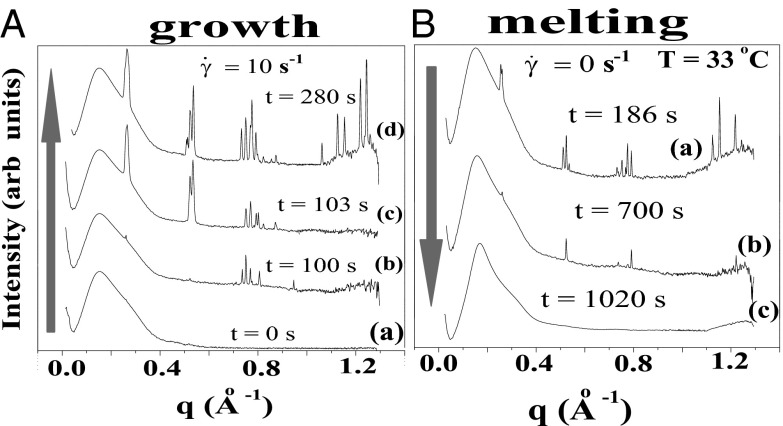
Fig. 3.
Time-resolved Rheo-SAXS data of the 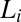 phase (corresponding to region III, Fig. 1) in the radial geometry at T = 33 °C indicates growth of the
phase (corresponding to region III, Fig. 1) in the radial geometry at T = 33 °C indicates growth of the 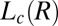 phase with time, at 10 s−1, in which the times shown correspond to that from the start of shear (A) and melting of the
phase with time, at 10 s−1, in which the times shown correspond to that from the start of shear (A) and melting of the 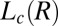 phase at 33 °C on stopping the shear, in which the times shown correspond to that from the stoppage of shear (B).
phase at 33 °C on stopping the shear, in which the times shown correspond to that from the stoppage of shear (B).
Fig. 4.
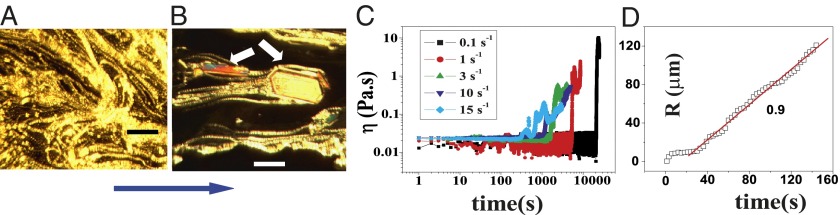
Stress relaxation and rheological optical measurements in the 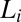 phase. Polarizing optical micrographs at different times after the onset of shear at
phase. Polarizing optical micrographs at different times after the onset of shear at 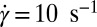 , T = 33 °C, shows the growth of shear-induced
, T = 33 °C, shows the growth of shear-induced 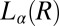 identified from the oily streak texture in the
identified from the oily streak texture in the 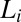 phase (indicated by the dark optically isotropic background) (A); growth of birefringent crystallites [
phase (indicated by the dark optically isotropic background) (A); growth of birefringent crystallites [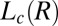 , indicated by arrows] in the
, indicated by arrows] in the 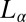 phase (B) (Scale bars in A and B, 200 microns); viscosity (η) as a function of time (t) at different shear rates
phase (B) (Scale bars in A and B, 200 microns); viscosity (η) as a function of time (t) at different shear rates 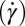 measured in a cone-plate geometry, T = 33 °C (C); and increase in the radius R of the crystal with time, under conditions as described in the main text (D).
measured in a cone-plate geometry, T = 33 °C (C); and increase in the radius R of the crystal with time, under conditions as described in the main text (D).
The proposed mechanism is very different from the shear-reversible crystallization reported in colloidal hard sphere fluids (16) in a large-amplitude oscillatory shear (LAOS) at Pe > 1, where the shear-induced ordering is determined by the balance between Brownian forces and the interparticle interactions, with the range of interaction set by the applied strain amplitude. So far, shear-induced phase transitions reported in bilayer-forming amphiphilic systems have shown that an isotropic sponge phase 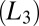 of interconnecting bilayers can transform to a lamellar phase
of interconnecting bilayers can transform to a lamellar phase 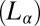 consisting of a stack of bilayers with 1D quasi–long-range positional order (17) or that a dilute
consisting of a stack of bilayers with 1D quasi–long-range positional order (17) or that a dilute 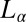 phase is shear-transformed to a collapsed surfactant-rich
phase is shear-transformed to a collapsed surfactant-rich 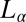 phase with very little water between the bilayers, coexisting with excess solvent (18). In this context, the studies have been restricted to the swollen
phase with very little water between the bilayers, coexisting with excess solvent (18). In this context, the studies have been restricted to the swollen 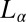 or
or 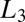 phase with highly flexible bilayers dominated by steric repulsion, where the transitions occur due to shear-induced suppression of thermal fluctuations above a critical shear rate of
phase with highly flexible bilayers dominated by steric repulsion, where the transitions occur due to shear-induced suppression of thermal fluctuations above a critical shear rate of 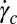 (19). Because
(19). Because 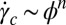 , where ϕ is the surfactant volume fraction and the exponent n lies (18) in the range of 1.5–3, the transitions are absent for ϕ > 0.3 within the experimentally accessible range of shear rates (∼1,000 s−1) (20). Our present study is different from the earlier studies on sponge phases because it examines the role of steady shear in weakly swollen, concentrated (ϕ > 0.5) isotropic phases (15, 21) in driving a nonequilibrium transition from isotropic
, where ϕ is the surfactant volume fraction and the exponent n lies (18) in the range of 1.5–3, the transitions are absent for ϕ > 0.3 within the experimentally accessible range of shear rates (∼1,000 s−1) (20). Our present study is different from the earlier studies on sponge phases because it examines the role of steady shear in weakly swollen, concentrated (ϕ > 0.5) isotropic phases (15, 21) in driving a nonequilibrium transition from isotropic 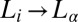 (R)/
(R)/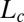 (R) at Pe ≪ 1. The structural transition is feasible through a shear-induced segregation/microphase separation of the hydrophobic counter-ions in bilayers to tune the spontaneous curvature at the bilayer–water interface. Counter-ion redistribution under shear is equally relevant for different classes of mixed amphiphilic systems, where shear drives a change in microstructure of the micellar aggregates transforming them from cylinders into bilayers (22, 23), or vice versa (24, 25), in a flow field or shear promotes the formation of pores in vesicles (26) through the partial segregation of amphiphiles in the bilayers. A microphase separation driven by shear flow can manifest in concentrated mesophases as shear-induced phase transitions, a possibility that, to our knowledge, was completely unexplored until the present work.
(R) at Pe ≪ 1. The structural transition is feasible through a shear-induced segregation/microphase separation of the hydrophobic counter-ions in bilayers to tune the spontaneous curvature at the bilayer–water interface. Counter-ion redistribution under shear is equally relevant for different classes of mixed amphiphilic systems, where shear drives a change in microstructure of the micellar aggregates transforming them from cylinders into bilayers (22, 23), or vice versa (24, 25), in a flow field or shear promotes the formation of pores in vesicles (26) through the partial segregation of amphiphiles in the bilayers. A microphase separation driven by shear flow can manifest in concentrated mesophases as shear-induced phase transitions, a possibility that, to our knowledge, was completely unexplored until the present work.
Results and Discussion
Shear Diagram of the  Phase.
Phase.
All rheological measurements (unless otherwise stated) were carried out on the 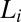 phase prepared at a composition
phase prepared at a composition 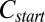 , where the PTHC-to-SDS molar ratio (α) is 1.5 and the overall surfactant weight fraction (ϕ) is 0.4. Our studies clearly established that at rest or at low shear rates, the crystalline phase
, where the PTHC-to-SDS molar ratio (α) is 1.5 and the overall surfactant weight fraction (ϕ) is 0.4. Our studies clearly established that at rest or at low shear rates, the crystalline phase 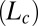 could be obtained by cooling the
could be obtained by cooling the 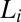 phase below 14 °C. On heating, the
phase below 14 °C. On heating, the 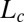 phase melts at 28 °C, which is identified as the equilibrium freezing temperature or Krafft temperature
phase melts at 28 °C, which is identified as the equilibrium freezing temperature or Krafft temperature 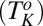 . Because the
. Because the 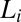 phase can be supercooled down to 14 °C, it explains the absence of the
phase can be supercooled down to 14 °C, it explains the absence of the 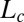 phase in the equilibrium phase diagram of the study by Pal et al. (15). The attractive interactions giving rise to a weakly swollen behavior result in the coexistence of the
phase in the equilibrium phase diagram of the study by Pal et al. (15). The attractive interactions giving rise to a weakly swollen behavior result in the coexistence of the 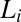 phase with excess solvent, which is a characteristic feature of a class of amphiphilic systems that form coacervate phases (21). To study shear-induced nonequilibrium phenomena in such systems, it is reasonable to isolate them from the excess solvent (more details on the sample composition and equilibrium phase behavior are provided in SI Appendix, SI Text, Figs. S1 and S2, and Tables S1 and S2). The main result of our study is the nonequilibrium phase behavior of the
phase with excess solvent, which is a characteristic feature of a class of amphiphilic systems that form coacervate phases (21). To study shear-induced nonequilibrium phenomena in such systems, it is reasonable to isolate them from the excess solvent (more details on the sample composition and equilibrium phase behavior are provided in SI Appendix, SI Text, Figs. S1 and S2, and Tables S1 and S2). The main result of our study is the nonequilibrium phase behavior of the 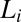 phase summarized in Fig. 1, obtained by combining polarizing optical microscopy with stress relaxation measurements. To construct the shear diagram (Fig. 1) reproducibly, the following protocol was established. The vial containing the sample prepared at the composition
phase summarized in Fig. 1, obtained by combining polarizing optical microscopy with stress relaxation measurements. To construct the shear diagram (Fig. 1) reproducibly, the following protocol was established. The vial containing the sample prepared at the composition 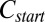 was placed in a water bath at a fixed temperature T, and the phase-separated
was placed in a water bath at a fixed temperature T, and the phase-separated 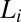 was loaded into the cone-plate geometry at the same temperature. The sample compositions at rest for the phase-separated
was loaded into the cone-plate geometry at the same temperature. The sample compositions at rest for the phase-separated 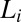 have been determined at three different temperatures (SI Appendix, Fig. S1 and Table S1). Each data point in the shear diagram was constructed by carrying out stress relaxation measurements at a fixed shear rate (with a waiting time of 1 s for each data point). The above protocol was repeated for many different temperatures. The notable features of the shear diagram (
have been determined at three different temperatures (SI Appendix, Fig. S1 and Table S1). Each data point in the shear diagram was constructed by carrying out stress relaxation measurements at a fixed shear rate (with a waiting time of 1 s for each data point). The above protocol was repeated for many different temperatures. The notable features of the shear diagram (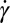 vs. T) are the
vs. T) are the  (region III) (see Movie S1), and
(region III) (see Movie S1), and 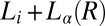 (region II) transitions occurring well above
(region II) transitions occurring well above 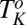 . The
. The 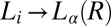 transition observed in region II is shear-reversible (Movie S2), and the textures observed under shear confirm that the transition to the
transition observed in region II is shear-reversible (Movie S2), and the textures observed under shear confirm that the transition to the 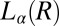 phase is not accompanied by the formation of onions. Region IV shows the shear-irreversible
phase is not accompanied by the formation of onions. Region IV shows the shear-irreversible 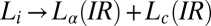 transition below
transition below 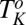 , to form a gel consisting of a percolating network of plate-like crystals with solvent trapped in the interstitial regions, known as a coagel phase (27). In region III, the optical micrographs confirm the appearance of an oily streak texture corresponding to the
, to form a gel consisting of a percolating network of plate-like crystals with solvent trapped in the interstitial regions, known as a coagel phase (27). In region III, the optical micrographs confirm the appearance of an oily streak texture corresponding to the 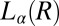 phase (Fig. 4A), accompanied by a sharp increase in viscosity in stress relaxation measurements (Fig. 4C) and the subsequent growth of crystallites of
phase (Fig. 4A), accompanied by a sharp increase in viscosity in stress relaxation measurements (Fig. 4C) and the subsequent growth of crystallites of 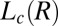 in
in 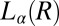 (Fig. 4B). The criterion for reaching the steady state is that at a given temperature and shear rate, within the maximum time over which the samples have been sheared, which is 20,000 s (∼6 h), the shear-induced phases identified from the optical texture do not evolve any further. However, any further evolution of viscosity and the crystallite size with time, under shear, are not taken into account when constructing the shear diagram. For shear rates <0.1 s−1, the data points (Fig. 1) at boundaries I and II between the
(Fig. 4B). The criterion for reaching the steady state is that at a given temperature and shear rate, within the maximum time over which the samples have been sheared, which is 20,000 s (∼6 h), the shear-induced phases identified from the optical texture do not evolve any further. However, any further evolution of viscosity and the crystallite size with time, under shear, are not taken into account when constructing the shear diagram. For shear rates <0.1 s−1, the data points (Fig. 1) at boundaries I and II between the 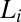 and
and 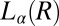 phases and at boundaries II and III between the
phases and at boundaries II and III between the 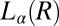 and
and 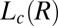 phases were obtained by shearing the samples for 40,000 s (12 h). The solid line demarcating regions II and III in Fig. 1, where the
phases were obtained by shearing the samples for 40,000 s (12 h). The solid line demarcating regions II and III in Fig. 1, where the 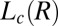 phase melts, indicates a positive shift in the Krafft temperature under shear. A similar shear diagram constructed by means of a parallel-plate geometry is given in SI Appendix, Fig. S3. Because the main focus of the present study is the crystallization observed above
phase melts, indicates a positive shift in the Krafft temperature under shear. A similar shear diagram constructed by means of a parallel-plate geometry is given in SI Appendix, Fig. S3. Because the main focus of the present study is the crystallization observed above 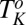 , all the results outlined in the remaining sections below will pertain to region III of Fig. 1.
, all the results outlined in the remaining sections below will pertain to region III of Fig. 1.
Structure of Lc (R) Phases.
Rheological small angle x-ray scattering (Rheo-SAXS) measurements were carried out at 33 °C (>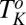 , corresponding to region III in Fig. 1) to determine the structure of the shear-induced crystalline phases. At zero shear, the diffraction pattern of the
, corresponding to region III in Fig. 1) to determine the structure of the shear-induced crystalline phases. At zero shear, the diffraction pattern of the 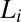 phase, which consists of a broad peak (Fig. 2A, curve a) with an average d-spacing of 41.0 Å, fitted well to the model for the
phase, which consists of a broad peak (Fig. 2A, curve a) with an average d-spacing of 41.0 Å, fitted well to the model for the 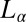 phase (15). The model parameters (SI Appendix, Table S2) indicate that the number of correlated bilayers is ∼2 for the
phase (15). The model parameters (SI Appendix, Table S2) indicate that the number of correlated bilayers is ∼2 for the 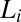 phase compared with ∼13 in the weakly swollen
phase compared with ∼13 in the weakly swollen 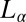 phase of the same system. On shearing the
phase of the same system. On shearing the 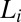 phase at 33 °C (which is significantly much above
phase at 33 °C (which is significantly much above 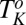 ) at a shear rate
) at a shear rate 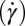 of 10 s−1, sharp crystalline peaks appear in the small- and wide-angle regions, coexisting with the broad peak corresponding to the
of 10 s−1, sharp crystalline peaks appear in the small- and wide-angle regions, coexisting with the broad peak corresponding to the 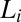 phase (Fig. 2A, curve b and Fig. 3A, curves b–d). Because the crystals that form are likely to be oriented along flow, the time-resolved structures of the crystallites are obtained from the analysis of diffraction data obtained in a radial geometry that gives a powder pattern (SI Appendix, Fig. S8A). The diffraction peaks obtained after a shearing time of t = 100 s (Fig. 3A, curve b) were indexed to a triclinic structure (Fig. 2B) with lattice parameters of a = 8.4 Å, b = 8.8 Å, and c = 24.4 Å and α = 96.0°, β = 91°, and γ = 102°, with a unit cell volume of 1,758 Å3. Interestingly, the crystalline peak positions, as well as their relative intensities, are seen to evolve under shear. The subsequent diffraction peaks obtained at t = 103 s (Fig. 3A, curve c) were indexed to a triclinic structure (Fig. 2B) with lattice parameters a = 9.7 Å, b = 12.8 Å, and c = 24.4 Å and α = 79.0°, β = 79°, and γ = 89° with a unit cell volume of 2,942 Å3. The crystalline peaks (Fig. 3A, curve d) obtained after 280 s (when a final steady state with no further temporal evolution of the peak positions or relative intensities is reached) were indexed to a triclinic structure with lattice parameters a = 13.3 Å, b = 16.6 Å, and c = 25.2 Å and α =101.0°, β = 100°, and γ = 107°, with a corresponding unit cell volume of 5,087 Å3 (SI Appendix, Fig. S5 and Table S3). Hence, under shear with time, although the crystal lattice remains the same, the unit cell volume increases by increasing the area of the a–b plane, keeping the length of the c axis nearly constant. The sharp peaks in the wide-angle region (Fig. 2A) confirm that the alkyl chains of SDS are in a crystalline state and the proposed crystalline phase consists of bilayers (Fig. 2C), with the bilayer thickness (corresponding to lattice parameter c) determined by the tilt of crystalline alkyl chains of SDS molecules and the lattice parameters a and b determined by the in-plane ordering, as well as the tilt of the chains, as proposed in SDS crystal phases (28). We surmise that a shear-driven increase in the number of surfactant molecules forming the basis of the triclinic lattice and the resulting change in the packing of the chains in the unit cell can give rise to the observed shift in peak positions and relative intensities with time. Accordingly, the significant increase in the lattice parameters a and b corresponding to the bilayer plane suggests a change in the composition (α) of the bilayers through incorporation of additional surfactant molecules and para toluidine hydrogen cations
phase (Fig. 2A, curve b and Fig. 3A, curves b–d). Because the crystals that form are likely to be oriented along flow, the time-resolved structures of the crystallites are obtained from the analysis of diffraction data obtained in a radial geometry that gives a powder pattern (SI Appendix, Fig. S8A). The diffraction peaks obtained after a shearing time of t = 100 s (Fig. 3A, curve b) were indexed to a triclinic structure (Fig. 2B) with lattice parameters of a = 8.4 Å, b = 8.8 Å, and c = 24.4 Å and α = 96.0°, β = 91°, and γ = 102°, with a unit cell volume of 1,758 Å3. Interestingly, the crystalline peak positions, as well as their relative intensities, are seen to evolve under shear. The subsequent diffraction peaks obtained at t = 103 s (Fig. 3A, curve c) were indexed to a triclinic structure (Fig. 2B) with lattice parameters a = 9.7 Å, b = 12.8 Å, and c = 24.4 Å and α = 79.0°, β = 79°, and γ = 89° with a unit cell volume of 2,942 Å3. The crystalline peaks (Fig. 3A, curve d) obtained after 280 s (when a final steady state with no further temporal evolution of the peak positions or relative intensities is reached) were indexed to a triclinic structure with lattice parameters a = 13.3 Å, b = 16.6 Å, and c = 25.2 Å and α =101.0°, β = 100°, and γ = 107°, with a corresponding unit cell volume of 5,087 Å3 (SI Appendix, Fig. S5 and Table S3). Hence, under shear with time, although the crystal lattice remains the same, the unit cell volume increases by increasing the area of the a–b plane, keeping the length of the c axis nearly constant. The sharp peaks in the wide-angle region (Fig. 2A) confirm that the alkyl chains of SDS are in a crystalline state and the proposed crystalline phase consists of bilayers (Fig. 2C), with the bilayer thickness (corresponding to lattice parameter c) determined by the tilt of crystalline alkyl chains of SDS molecules and the lattice parameters a and b determined by the in-plane ordering, as well as the tilt of the chains, as proposed in SDS crystal phases (28). We surmise that a shear-driven increase in the number of surfactant molecules forming the basis of the triclinic lattice and the resulting change in the packing of the chains in the unit cell can give rise to the observed shift in peak positions and relative intensities with time. Accordingly, the significant increase in the lattice parameters a and b corresponding to the bilayer plane suggests a change in the composition (α) of the bilayers through incorporation of additional surfactant molecules and para toluidine hydrogen cations 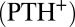 in the unit cell. At a shear rate of 10 s−1, the structure of the
in the unit cell. At a shear rate of 10 s−1, the structure of the 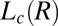 phase in the nonequilibrium steady state is the same as the equilibrium
phase in the nonequilibrium steady state is the same as the equilibrium 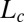 phase (SI Appendix, Fig. S7). The coexistence of
phase (SI Appendix, Fig. S7). The coexistence of 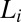 and
and 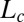 (R) phases was also observed at
(R) phases was also observed at 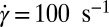 (Fig. 2A, curve c). Interestingly, there is a significant shift in positions of the Bragg peaks compared with the peak positions at lower shear rates (Fig. 2A, curve b), indicating a variance in the structure of
(Fig. 2A, curve c). Interestingly, there is a significant shift in positions of the Bragg peaks compared with the peak positions at lower shear rates (Fig. 2A, curve b), indicating a variance in the structure of 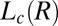 . The crystalline peaks were indexed again to a triclinic structure with different lattice parameters, where a = 11.6 Å, b = 20.5 Å, and c = 20.9 Å and α = 93°, β = 99°, and γ = 102°, with a unit cell volume of 4,795 Å3.
. The crystalline peaks were indexed again to a triclinic structure with different lattice parameters, where a = 11.6 Å, b = 20.5 Å, and c = 20.9 Å and α = 93°, β = 99°, and γ = 102°, with a unit cell volume of 4,795 Å3.
Nucleation, Growth, and Melting of Lc (R) Phases.
In situ synchrotron X-ray scattering, which is a powerful probe to resolve growth kinetics under shear, can give a reliable time scale for the onset of crystallization. In Rheo-SAXS measurements, the data acquisition was started at the onset of shear. At 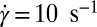 , the growth of the crystallite occurs after 100 s. The temporal evolution of the crystal volume [which is proportional to the integrated intensity
, the growth of the crystallite occurs after 100 s. The temporal evolution of the crystal volume [which is proportional to the integrated intensity 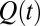 estimated from the first-order crystalline peak at q = 0.263 Å−1 as described in SI Appendix, Fig. S9] is given by
estimated from the first-order crystalline peak at q = 0.263 Å−1 as described in SI Appendix, Fig. S9] is given by 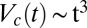 , suggesting that the growth law for the present system is similar to that seen during the crystal growth from a melt in hard sphere colloidal suspensions (29, 30). However, we admit that caution should be exercised when interpreting these results obtained by assuming a powder diffraction pattern from randomly oriented crystals. A partial alignment of the crystallites can occur due to the growth of
, suggesting that the growth law for the present system is similar to that seen during the crystal growth from a melt in hard sphere colloidal suspensions (29, 30). However, we admit that caution should be exercised when interpreting these results obtained by assuming a powder diffraction pattern from randomly oriented crystals. A partial alignment of the crystallites can occur due to the growth of 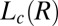 in an aligned
in an aligned 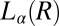 phase (evident in the diffraction patterns obtained in the tangential geometry at a time t = 134 s during the early stages of growth; SI Appendix, Fig. S8B), as well as from the time-dependent orientation of crystallites in the direction of flow. Nevertheless, from polarizing microscopy experiments (Fig. 4D), we have verified the linear growth law for the crystal size where the average radius of the crystallite R ∼ t (here, the time t is measured after the crystallite has grown to a size of 5 μm in a steady shear of 10 s−1) by monitoring the growth of a crystallite in an oscillatory shear (as soon as the steady shear is stopped, a strain amplitude γ = 10 at an angular frequency ω = 1 rad/s is applied to achieve strain rate amplitude γ ω of 10 s−1). It is interesting that the growth kinetics in the present system follow the Wilson–Frenkel model, which proposes that the growth rate is determined by the rate of adsorption of molecules at the crystal interface. As evident from Fig. 3B, on stopping the shear, the intensity of the crystalline peaks decreases gradually with time due to the melting of the
phase (evident in the diffraction patterns obtained in the tangential geometry at a time t = 134 s during the early stages of growth; SI Appendix, Fig. S8B), as well as from the time-dependent orientation of crystallites in the direction of flow. Nevertheless, from polarizing microscopy experiments (Fig. 4D), we have verified the linear growth law for the crystal size where the average radius of the crystallite R ∼ t (here, the time t is measured after the crystallite has grown to a size of 5 μm in a steady shear of 10 s−1) by monitoring the growth of a crystallite in an oscillatory shear (as soon as the steady shear is stopped, a strain amplitude γ = 10 at an angular frequency ω = 1 rad/s is applied to achieve strain rate amplitude γ ω of 10 s−1). It is interesting that the growth kinetics in the present system follow the Wilson–Frenkel model, which proposes that the growth rate is determined by the rate of adsorption of molecules at the crystal interface. As evident from Fig. 3B, on stopping the shear, the intensity of the crystalline peaks decreases gradually with time due to the melting of the 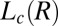 phase. The melting of the crystalline mass with time follows a sigmoidal curve of the functional form
phase. The melting of the crystalline mass with time follows a sigmoidal curve of the functional form 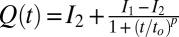 (SI Appendix, Fig. S9). After 1,000 s, only the broad peak from the
(SI Appendix, Fig. S9). After 1,000 s, only the broad peak from the 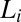 phase remains (Fig. 3B, curve c) confirming that the
phase remains (Fig. 3B, curve c) confirming that the 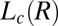 phase observed above
phase observed above 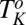 is an out-of-equilibrium phase, occurring only when an external shear field is imposed.
is an out-of-equilibrium phase, occurring only when an external shear field is imposed.
An important finding from the rheological optical measurements that gives further insight into the crystallization phenomenon is that the nucleation of the 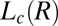 phase occurs in a shear-induced lamellar phase (Fig. 4 A and B). In Rheo-SAXS measurements, the partial alignment of the crystallites along the direction of flow (evident in the first-order crystalline peaks) in the tangential configuration at the early stages of growth (SI Appendix, Fig. S8B) is consistent with the alignment of bilayers of
phase occurs in a shear-induced lamellar phase (Fig. 4 A and B). In Rheo-SAXS measurements, the partial alignment of the crystallites along the direction of flow (evident in the first-order crystalline peaks) in the tangential configuration at the early stages of growth (SI Appendix, Fig. S8B) is consistent with the alignment of bilayers of 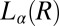 along the walls of the Couette and the growth of crystallites in
along the walls of the Couette and the growth of crystallites in 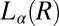 . X-ray diffraction peaks of
. X-ray diffraction peaks of  are not evident in Rheo-SAXS measurements when the
are not evident in Rheo-SAXS measurements when the 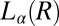 peaks overlap with
peaks overlap with 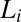 . This has been established by shearing the
. This has been established by shearing the 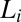 phase below
phase below 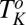 , where the final state after stopping the shear corresponds to the
, where the final state after stopping the shear corresponds to the 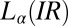 phase coexisting with
phase coexisting with 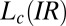 (SI Appendix, Fig. S7). Fig. 4C shows the viscosity (η) as a function of time (t) at different shear rates at 33 °C measured in a cone-plate geometry. At
(SI Appendix, Fig. S7). Fig. 4C shows the viscosity (η) as a function of time (t) at different shear rates at 33 °C measured in a cone-plate geometry. At 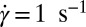 , although η at the onset of shear remains constant at 20 mPa/s, after shearing for ∼5,000 s (defined as a delay time
, although η at the onset of shear remains constant at 20 mPa/s, after shearing for ∼5,000 s (defined as a delay time 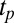 ), viscosity increases by two orders of magnitude accompanied by birefringent oily streaks corresponding to a lamellar texture as seen from the polarizing optical micrographs (Fig. 4A). Further shearing leads to the growth of birefringent crystallites only in the
), viscosity increases by two orders of magnitude accompanied by birefringent oily streaks corresponding to a lamellar texture as seen from the polarizing optical micrographs (Fig. 4A). Further shearing leads to the growth of birefringent crystallites only in the 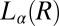 phase (Fig. 4B), reaching a final steady state with the coexistence of
phase (Fig. 4B), reaching a final steady state with the coexistence of 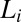 and
and 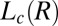 phases (Movie S1 A and B). On stopping the shear, the crystallites melt and the starting
phases (Movie S1 A and B). On stopping the shear, the crystallites melt and the starting 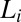 phase is recovered (Movie S1C). It is seen that at a fixed shear rate and temperature, the delay time
phase is recovered (Movie S1C). It is seen that at a fixed shear rate and temperature, the delay time 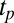 , which marks the incubation time for the onset of crystallization (identified from the sharp increase in viscosity as well as the optical micrographs), varies (SI Appendix, Figs. S10 and S11) as expected for a nucleation process (17). However, the onset of crystallization appears to require a minimum strain
, which marks the incubation time for the onset of crystallization (identified from the sharp increase in viscosity as well as the optical micrographs), varies (SI Appendix, Figs. S10 and S11) as expected for a nucleation process (17). However, the onset of crystallization appears to require a minimum strain 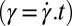 of 1,000, which is also consistent with the Rheo-SAXS data (Fig. 3A, curve b). Note that the shear-induced crystallization observed presently at γ > 1,000 should be contrasted with colloidal hard sphere fluids, where the phenomenon is absent under steady shear (16, 31). We further confirm that the
of 1,000, which is also consistent with the Rheo-SAXS data (Fig. 3A, curve b). Note that the shear-induced crystallization observed presently at γ > 1,000 should be contrasted with colloidal hard sphere fluids, where the phenomenon is absent under steady shear (16, 31). We further confirm that the 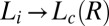 or
or 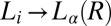 transition does not occur under oscillatory shear up to a strain amplitude of 10. This behavior is very different from colloidal systems (31) or block copolymers (32), where the phase transition occurs only due to a shear-induced ordering under LAOS.
transition does not occur under oscillatory shear up to a strain amplitude of 10. This behavior is very different from colloidal systems (31) or block copolymers (32), where the phase transition occurs only due to a shear-induced ordering under LAOS.
Shear-Reversible Crystallization in a Weakly Swollen 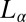 Phase Above
Phase Above 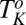 .
.
Having established that the growth of the 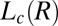 phase occurs only in the shear-induced
phase occurs only in the shear-induced 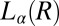 phase, it is important to verify whether
phase, it is important to verify whether 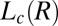 phases can also be induced by shearing an equilibrium
phases can also be induced by shearing an equilibrium 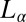 phase. We now show that a shear-reversible crystallization is also obtained in the
phase. We now show that a shear-reversible crystallization is also obtained in the 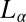 phase of the same system prepared at a different sample composition (α = 1, ϕ = 0.5). Here, the
phase of the same system prepared at a different sample composition (α = 1, ϕ = 0.5). Here, the 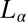 phase, which coexists with excess solvent (15), consists of a turbid dispersion of multilamellar vesicles (MLVs), as confirmed from polarizing microscopy observations. The diffraction pattern obtained from the
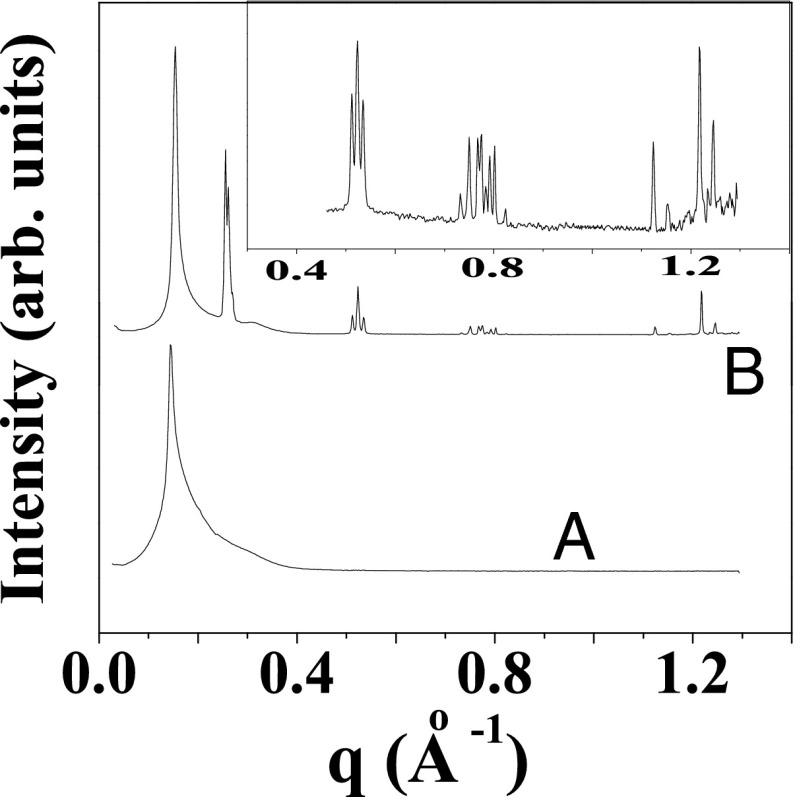
phase, which coexists with excess solvent (15), consists of a turbid dispersion of multilamellar vesicles (MLVs), as confirmed from polarizing microscopy observations. The diffraction pattern obtained from the  phase at rest at 33 °C shows a lamellar peak at 43.7 Å (Fig. 5, curve a). Only one diffraction peak is measured for the
phase at rest at 33 °C shows a lamellar peak at 43.7 Å (Fig. 5, curve a). Only one diffraction peak is measured for the 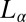 phase because the structure factor reaches the asymptotic value of 1 near the second-order peak. However, the second-order lamellar peak is present at lower temperatures (SI Appendix, Fig. S2). X-ray diffraction patterns of the
phase because the structure factor reaches the asymptotic value of 1 near the second-order peak. However, the second-order lamellar peak is present at lower temperatures (SI Appendix, Fig. S2). X-ray diffraction patterns of the 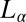 phase sheared at 30 s−1 reveal a lamellar peak with d-spacing of 40.1 Å, in addition to sharp crystalline peaks in the small- and wide-angle regions (Fig. 5, curve b) that were indexed to a triclinic lattice (SI Appendix, Fig. S6 and Table S4) with the same structure and lattice parameters as the equilibrium
phase sheared at 30 s−1 reveal a lamellar peak with d-spacing of 40.1 Å, in addition to sharp crystalline peaks in the small- and wide-angle regions (Fig. 5, curve b) that were indexed to a triclinic lattice (SI Appendix, Fig. S6 and Table S4) with the same structure and lattice parameters as the equilibrium 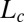 phase. Another feature evident in the Rheo-SAXS experiments on the
phase. Another feature evident in the Rheo-SAXS experiments on the 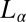 phase is the decrease of d-spacing under shear accompanied by a decrease in the width and increase in height of the lamellar Bragg peak, indicating an increased correlation between the bilayers. This decrease in d-spacing under shear in concentrated lamellar phases with MLVs can arise when the water can permeate across the bilayers of the vesicle to fill the interstitial volume, thus lowering the packing constraints under shear (33).
phase is the decrease of d-spacing under shear accompanied by a decrease in the width and increase in height of the lamellar Bragg peak, indicating an increased correlation between the bilayers. This decrease in d-spacing under shear in concentrated lamellar phases with MLVs can arise when the water can permeate across the bilayers of the vesicle to fill the interstitial volume, thus lowering the packing constraints under shear (33).
Fig. 5.
Tangential diffraction patterns obtained in Rheo-SAXS measurements of the 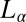 phase prepared at α = 1, ϕ = 0.5 at 33 °C:
phase prepared at α = 1, ϕ = 0.5 at 33 °C: 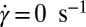 (A) and
(A) and 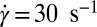 (B).
(B).
Proposed Mechanism for Shear-Reversible Crystallization.
Because the 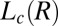 phase always nucleates in a nonequilibrium
phase always nucleates in a nonequilibrium 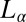 phase, we propose below a possible mechanism for the crystallization that occurs in two steps. In the first step, at a strain >1,000, the randomly connected bilayers of the
phase, we propose below a possible mechanism for the crystallization that occurs in two steps. In the first step, at a strain >1,000, the randomly connected bilayers of the 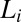 phase align along the direction of shear to form the
phase align along the direction of shear to form the 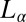 phase. We speculate that one possible pathway for this transition in the concentrated phase presently studied is through the disruption of bilayer passages by unbinding and redistributing the hydrophobic counter-ions. We further suggest that crystallization occurs in the second step, when the bilayers permeable to solvent under shear can get stretched, with the large deformation increasing the effective area of the bilayers, and hence the dynamic surface tension. The surface tension can be lowered by the absorption of hydrophobic counter-ions (which have a preference for the micelle–water interface) into the bilayers, from the solvent or through the redistribution of counter-ions within the bilayers between the stretched and unstretched regions. The crystalline phase is likely to nucleate in the
phase. We speculate that one possible pathway for this transition in the concentrated phase presently studied is through the disruption of bilayer passages by unbinding and redistributing the hydrophobic counter-ions. We further suggest that crystallization occurs in the second step, when the bilayers permeable to solvent under shear can get stretched, with the large deformation increasing the effective area of the bilayers, and hence the dynamic surface tension. The surface tension can be lowered by the absorption of hydrophobic counter-ions (which have a preference for the micelle–water interface) into the bilayers, from the solvent or through the redistribution of counter-ions within the bilayers between the stretched and unstretched regions. The crystalline phase is likely to nucleate in the  bilayers with a larger concentration of PTH+ ions. In our study, we have further provided direct experimental evidence through elemental analysis (SI Appendix, SI Text) for the increase in the concentration of the hydrophobic PTH+ counter-ions in the shear-induced crystalline phase
bilayers with a larger concentration of PTH+ ions. In our study, we have further provided direct experimental evidence through elemental analysis (SI Appendix, SI Text) for the increase in the concentration of the hydrophobic PTH+ counter-ions in the shear-induced crystalline phase 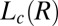 . At 33 °C, the α value of the
. At 33 °C, the α value of the 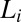 phase at rest is 1.5. However, the measured α for
phase at rest is 1.5. However, the measured α for 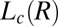 phases is always greater than 2 and the same as that in the supercooled
phases is always greater than 2 and the same as that in the supercooled 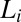 (SI Appendix, Table S1) phase, where the growth of the
(SI Appendix, Table S1) phase, where the growth of the 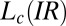 phase occurs under shear. It is noteworthy in this context that the
phase occurs under shear. It is noteworthy in this context that the 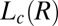 and
and 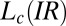 phases have the same triclinic structure with identical lattice parameters. The evolution of the crystal structure under shear (Fig. 3A), as discussed earlier, also supports the proposed change in composition of the bilayers under shear. In addition, the linear growth law (Fig. 4D and SI Appendix, Fig. S9) lends additional support to the proposed mechanism, indicating that the crystal growth kinetics are determined by the adsorption of PTH+ ions at the
phases have the same triclinic structure with identical lattice parameters. The evolution of the crystal structure under shear (Fig. 3A), as discussed earlier, also supports the proposed change in composition of the bilayers under shear. In addition, the linear growth law (Fig. 4D and SI Appendix, Fig. S9) lends additional support to the proposed mechanism, indicating that the crystal growth kinetics are determined by the adsorption of PTH+ ions at the 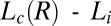 interface. Moreover, a shear-induced crystallization through a change in composition of the bilayers, where the crystalline phase can nucleate only in bilayers with α > 2, can further explain the absence of a single-phase region for
interface. Moreover, a shear-induced crystallization through a change in composition of the bilayers, where the crystalline phase can nucleate only in bilayers with α > 2, can further explain the absence of a single-phase region for 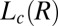 in the shear diagram (Fig. 1).
in the shear diagram (Fig. 1).
The proposed mechanism involves both a change in spontaneous curvature as well as the stretching of bilayers under shear. In ionic surfactant systems with oppositely charged strong binding counter-ions (22–24), when the shear effect on the aggregate structure was taken into account in the deformation energy of a free bilayer (25) through a shear-dependent contribution of spontaneous curvature 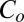 arising from unbinding of counter-ions, the resultant shear diagram obtained by minimizing the free energy could predict a shear-induced vesicle-to-micelle transition. Similarly, in mixed lipid/surfactant systems, shear-induced partial segregation within the bilayer of the initially evenly distributed amphiphiles is believed to give rise to a change in spontaneous curvature and the membrane line tension leading to pore formation (26). Our study suggests that an analogous phenomenon of shear-induced modification of spontaneous curvature can drive phase transitions in concentrated bilayer-forming mesophases. It is also worthwhile to note that shear-induced stretching in MLVs (34), which are highly permeable to water, leads to formation of entangled tubular vesicles at low shear rates, with applied strain being the control parameter for the onset of transition. The strain value of ∼1,000 for the vesicle-to-tubule transition is comparable to that required for the onset of crystallization in the system under study.
arising from unbinding of counter-ions, the resultant shear diagram obtained by minimizing the free energy could predict a shear-induced vesicle-to-micelle transition. Similarly, in mixed lipid/surfactant systems, shear-induced partial segregation within the bilayer of the initially evenly distributed amphiphiles is believed to give rise to a change in spontaneous curvature and the membrane line tension leading to pore formation (26). Our study suggests that an analogous phenomenon of shear-induced modification of spontaneous curvature can drive phase transitions in concentrated bilayer-forming mesophases. It is also worthwhile to note that shear-induced stretching in MLVs (34), which are highly permeable to water, leads to formation of entangled tubular vesicles at low shear rates, with applied strain being the control parameter for the onset of transition. The strain value of ∼1,000 for the vesicle-to-tubule transition is comparable to that required for the onset of crystallization in the system under study.
In the equilibrium phase diagram of the SDS/PTHC/water system, because 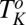 of the
of the 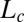 phase increases with α (SI Appendix, Fig. S13), the increase in the melting point of the crystalline phase with the shear rate as evident in the shear diagrams of the
phase increases with α (SI Appendix, Fig. S13), the increase in the melting point of the crystalline phase with the shear rate as evident in the shear diagrams of the 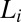 phase (Fig. 1) is likely to arise from a shear rate-dependent increase in α of the
phase (Fig. 1) is likely to arise from a shear rate-dependent increase in α of the 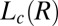 phase. The
phase. The 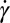 -dependent shift in the composition of the shear-induced phase is also consistent with the different lattice parameters obtained for
-dependent shift in the composition of the shear-induced phase is also consistent with the different lattice parameters obtained for 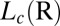 phases formed at different shear rates (Fig. 2A, curves b and c). It should also be noted, however, that the transitions occur only for shear rates in the range of 0.05–100 s−1. It is important to note that the
phases formed at different shear rates (Fig. 2A, curves b and c). It should also be noted, however, that the transitions occur only for shear rates in the range of 0.05–100 s−1. It is important to note that the 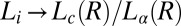 transitions discussed in the present study also occur when the
transitions discussed in the present study also occur when the 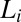 phase is sheared in the presence of excess solvent, indicating that the solvent phase does not contribute to the transition (SI Appendix, Fig. S12). Shear-reversible crystallization above
phase is sheared in the presence of excess solvent, indicating that the solvent phase does not contribute to the transition (SI Appendix, Fig. S12). Shear-reversible crystallization above 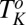 was also observed for single-phase samples of
was also observed for single-phase samples of 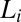 (Movie S3).
(Movie S3).
Conclusions and Perspectives
To summarize, we have shown a unique shear-reversible, first-order transition from an isotropic phase to crystalline/lamellar phases in a mixed amphiphilic system. The occurrence of these transitions in the highly concentrated mesophases (with ϕ > 0.5) above a low critical shear rate (∼0.05 s−1) suggests that the mechanism driving the shear-induced transitions in the present system with a limited swelling behavior should be very different from that of the swollen lamellar or sponge phase. Because the 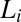 phase under study is proposed to form through the proliferation of dislocations in the
phase under study is proposed to form through the proliferation of dislocations in the 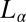 phase (15), it is relevant in this context to address the role of the imposed shear field in suppressing the dislocations, thus stabilizing the
phase (15), it is relevant in this context to address the role of the imposed shear field in suppressing the dislocations, thus stabilizing the 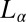 phase. It is worthwhile to mention here that earlier studies on the effect of shear on dislocation loops have yielded conflicting results near the smectic-A/nematic transition (35, 36). By following the kinetics of nucleation under shear, we also show that an
phase. It is worthwhile to mention here that earlier studies on the effect of shear on dislocation loops have yielded conflicting results near the smectic-A/nematic transition (35, 36). By following the kinetics of nucleation under shear, we also show that an  phase forms as a pretransition before the onset of crystallization. This is not surprising, considering that the
phase forms as a pretransition before the onset of crystallization. This is not surprising, considering that the 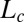 phase has a lamellar structure with crystalline alkyl chains. This is similar to the appearance of the 1D phase as a precursor for the 3D shear-induced crystalline phase, which has been observed, for instance, in the form of string-like structures in dense colloidal suspensions (31, 37) or a smectic phase in melts of flexible polymers (5).
phase has a lamellar structure with crystalline alkyl chains. This is similar to the appearance of the 1D phase as a precursor for the 3D shear-induced crystalline phase, which has been observed, for instance, in the form of string-like structures in dense colloidal suspensions (31, 37) or a smectic phase in melts of flexible polymers (5).
In the context of multicomponent surfactant systems, understanding the role of lamellar ordering induced by shear will be an important step toward controlling the microstructure of the different shear-induced crystalline structures in coagel phases. Although the kinetics of lamellar-to-coagel transitions have been studied under static conditions, there are relatively few reports of these studies under shear. In the shear diagram (Fig. 1, region IV) presented in our study, we further show that the final shear-thickened state obtained from the starting 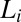 phase consists of the coagel phase below
phase consists of the coagel phase below 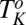 , whereas the percolating network of crystalline platelets is absent above
, whereas the percolating network of crystalline platelets is absent above 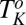 , although the crystal structures are identical at
, although the crystal structures are identical at 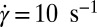 . This suggests that formation of coagel phases proceeds in two stages, where shear promotes the formation of
. This suggests that formation of coagel phases proceeds in two stages, where shear promotes the formation of 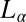 in the first stage, and subsequently the nucleation of crystalline platelets, and in the second stage, the platelets percolate to form a 3D network above a critical volume fraction of the crystallites. In industrial manufacturing processes, mixing (shear) is an important control parameter because it homogenizes multicomponent systems as well as enhancing the kinetics of crystallization. The present finding may be of interest to the food processing industry, where the solidification of edible fats and oils is essential when manufacturing margarine, reduced fat spreads, ice cream, chocolate (38), and honey (39), or in consumer industry when manufacturing bar soaps, personal care creams, toothpastes, and lubricant greases (40).
in the first stage, and subsequently the nucleation of crystalline platelets, and in the second stage, the platelets percolate to form a 3D network above a critical volume fraction of the crystallites. In industrial manufacturing processes, mixing (shear) is an important control parameter because it homogenizes multicomponent systems as well as enhancing the kinetics of crystallization. The present finding may be of interest to the food processing industry, where the solidification of edible fats and oils is essential when manufacturing margarine, reduced fat spreads, ice cream, chocolate (38), and honey (39), or in consumer industry when manufacturing bar soaps, personal care creams, toothpastes, and lubricant greases (40).
Another outcome of the present study is the possible role of shear-induced phase segregation of amphiphiles within the bilayers in driving the crystallization. The role of microphase separation driven by shear flow in concentrated mesophases has not been incorporated in any of the theoretical models for nonequilibrium phase transitions in bilayer-forming amphiphilic systems comprising surfactants, block copolymers, and microemulsions. Understanding shear as a strategy to control the spontaneous curvature of bilayers of mixed amphiphilic systems is also expected to have significant applications in the design of novel drug delivery systems (41), controlling the permeability of bilayers in onion phases used for encapsulation, in addition to tuning the viscosity during flow processing of surfactant-based products in consumer industry.
Materials and Methods
Ternary solutions of SDS and PTHC (purchased from Sigma-Aldrich and used without further purification) at the desired molar ratio 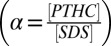 of the two components and at the total surfactant weight fraction
of the two components and at the total surfactant weight fraction 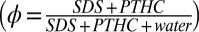 were prepared in deionized water. Rheological measurements were carried out on samples prepared at (i) α = 1.5, ϕ = 0.4 and (ii) α = 1, ϕ = 0.5. Rheo-SAXS measurements were performed at the SWING beamline of the SOLEIL synchrotron (Proposal 20110293) using a fixed energy of 15 keV and a sample-to-detector distance of 898.42 mm. An MCR-501 rheometer (Anton Paar) equipped with a Couette cell (with a rotating inner cylinder and a temperature-controlled static outer cylinder, gap = 0.2 mm) was mounted on the SAXS beamline (42). The 2D scattering patterns with the X-ray beam parallel or perpendicular to the flow direction (tangential or radial geometry) were recorded on an AVIEX CCD camera formed by four detectors, and appropriate corrections were applied to the data (SI Appendix, Fig. S4).
were prepared in deionized water. Rheological measurements were carried out on samples prepared at (i) α = 1.5, ϕ = 0.4 and (ii) α = 1, ϕ = 0.5. Rheo-SAXS measurements were performed at the SWING beamline of the SOLEIL synchrotron (Proposal 20110293) using a fixed energy of 15 keV and a sample-to-detector distance of 898.42 mm. An MCR-501 rheometer (Anton Paar) equipped with a Couette cell (with a rotating inner cylinder and a temperature-controlled static outer cylinder, gap = 0.2 mm) was mounted on the SAXS beamline (42). The 2D scattering patterns with the X-ray beam parallel or perpendicular to the flow direction (tangential or radial geometry) were recorded on an AVIEX CCD camera formed by four detectors, and appropriate corrections were applied to the data (SI Appendix, Fig. S4).
The shear diagram (Fig. 1) was constructed through polarizing optical microscopy measurements in a stress-controlled rheometer (MCR 102; Anton Paar) with a temperature-controlled cone-plate geometry (cone diameter = 25 mm, cone angle = 2°). Preshearing was avoided when loading the samples, and a humidity chamber was used to prevent evaporation of solvent. Images were recorded on an eight-bit color CCD camera (0.75C, 1,200 × 980 pixels; Lumenera) fitted with a microscope objective (20×/0.28 N.A.; Mitutoyo).
Supplementary Material
Acknowledgments
We acknowledge SOLEIL (Gif-sur-Yvette, France) for provision of synchrotron radiation facilities, and we thank Florian Meneau for assistance in using beamline SWING. We thank M. Mani for technical assistance with shear cells and Santosh Prasad Gupta for preliminary Rheo-SAXS experiments in the laboratory. A.K.S. thanks the Council for Scientific and Industrial Research (CSIR) for research support through the Bhatnagar Fellowship. R.K. thanks the Department of Science and Technology (DST) for the Ramanujan Fellowship. V.R. thanks the CSIR for the Senior Research Fellowship and DST for travel support for Rheo-SAXS experiments at SOLEIL.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1304777110/-/DCSupplemental.
References
- 1.Shereda LT, Larson RG, Solomon MJ. Boundary-driven colloidal crystallization in simple shear flow. Phys Rev Lett. 2010;105(22):228302–228305. doi: 10.1103/PhysRevLett.105.228302. [DOI] [PubMed] [Google Scholar]
- 2.Wu YL, Derks D, van Blaaderen A, Imhof A. Melting and crystallization of colloidal hard-sphere suspensions under shear. Proc Natl Acad Sci USA. 2009;106(26):10564–10569. doi: 10.1073/pnas.0812519106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tsai JC, Voth GA, Gollub JP. Internal granular dynamics, shear-induced crystallization, and compaction steps. Phys Rev Lett. 2003;91(6):064301–064304. doi: 10.1103/PhysRevLett.91.064301. [DOI] [PubMed] [Google Scholar]
- 4.Li L, Lambreva D, de Jeu WH. Lamellar ordering and crystallization in a symmetric block copolymer. J Macromol Sci, Chem. 2004;B43(1):59–70. [Google Scholar]
- 5.Li L, de Jeu WH. Shear-induced smectic ordering in the melt of isotactic polypropylene. Phys Rev Lett. 2004;92:075506–075509. doi: 10.1103/PhysRevLett.92.075506. [DOI] [PubMed] [Google Scholar]
- 6.Phoon CL, Higgins JS, Allegra G, van Leeuwen P, Staples E. Shear induced crystallization and melting of a micellar solution. Proc R Soc Lond A Math Phys Sci. 1993;442:221–230. [Google Scholar]
- 7.Mazzanti G, Guthrie SE, Marangoni AG, Idziak SHJ. A conceptual model for shear-induced phase behavior in crystallizing cocoa butter. Crystal Growth and Design. 2007;7:1230–1241. [Google Scholar]
- 8.Mazzanti G, Marangoni AG, Idziak SHJ. Modeling phase transitions during the crystallization of a multicomponent fat under shear. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;71(4 Pt 1):041607–041618. doi: 10.1103/PhysRevE.71.041607. [DOI] [PubMed] [Google Scholar]
- 9.Lohwongwatana B, Schroers J, Johnson WL. Strain rate induced crystallization in bulk metallic glass-forming liquid. Phys Rev Lett. 2006;96(7):075503–075506. doi: 10.1103/PhysRevLett.96.075503. [DOI] [PubMed] [Google Scholar]
- 10.Gray RA, Warren PB, Chynoweth S, Michopoulos Y, Pawley GS. Crystallization of molecular liquids through shear-induced nucleation. Proc R Soc Lond A Math Phys Sci. 1995;448:113–120. [Google Scholar]
- 11.Heyes DM. Shear thinning and thickening of the Lennard-Jones liquid. A molecular dynamics study. J Chem Soc Faraday Trans 2. 1986;82:1365–1383. [Google Scholar]
- 12.Onuki A. Phase transitions of fluids in shear flow. J Phys Condens Matter. 1997;9:6119–6157. [Google Scholar]
- 13.Hassan PA, Raghavan SR, Kaler EW. Microstructural changes in SDS micelles induced by hydrotropic salt. Langmuir. 2002;18:2543–2548. [Google Scholar]
- 14.Ghosh SK, Rathee V, Krishnaswamy R, Raghunathan VA, Sood AK. Re-entrant phase behavior of a concentrated anionic surfactant system with strongly binding counterions. Langmuir. 2009;25(15):8497–8506. doi: 10.1021/la804330x. [DOI] [PubMed] [Google Scholar]
- 15.Pal A, Pabst G, Raghunathan VA. Defect-mediated lamellar-isotropic transition of amphiphilic bilayers. Soft Matter. 2012;8:9069–9072. [Google Scholar]
- 16.Ackerson BJ, Pusey PN. Shear-induced order in suspensions of hard spheres. Phys Rev Lett. 1988;61:1033–1036. doi: 10.1103/PhysRevLett.61.1033. [DOI] [PubMed] [Google Scholar]
- 17.Leon E, Bonn D, Meunier J, Al-Kahwaji A, Kellay H. Shear-induced first-order sponge-to-lamellar transition in a lyotropic surfactant system. Phys Rev Lett. 2001;86:938–941. doi: 10.1103/PhysRevLett.86.938. [DOI] [PubMed] [Google Scholar]
-
18.Porcar L, Hamilton WA, Butler PD. Scaling of structural response of
 sponge phases in the “sweetened” cetylpyridinium/hexanol/dextrose/brine system. Langmuir. 2003;19(26):10779–10794. [Google Scholar]
sponge phases in the “sweetened” cetylpyridinium/hexanol/dextrose/brine system. Langmuir. 2003;19(26):10779–10794. [Google Scholar] - 19.Cates ME, Milner ST. Role of shear in the isotropic-to-lamellar transition. Phys Rev Lett. 1989;62(16):1856–1859. doi: 10.1103/PhysRevLett.62.1856. [DOI] [PubMed] [Google Scholar]
- 20.Kleman M. The lamellar and sponge phases of dilute surfactant systems: Structures and defects at equilibrium and under shear. Pramana - Journal of Physics. 1999;53:107–119. [Google Scholar]
- 21.Pal A, Bharath P, Dastidar SG, Raghunathan VA. Collapse and coacervation of a lamellar phase by inter-headgroup bridging. Soft Matter. 2012;8:927–930. [Google Scholar]
- 22.Danino D, Talmon Y, Zana R. Cryo-TEM of thread-like micelles: On-the-grid microstructural transformations induced during specimen preparation. Colloids Surf A Physicochem Eng Asp. 2000;169:67–73. [Google Scholar]
- 23.Zheng Y, et al. Cryo-TEM imaging the flow-induced transition from vesicles to threadlike micelles. J Phys Chem B. 2000;104:5263–5271. [Google Scholar]
- 24.Mendes E, et al. Shear-induced vesicle to wormlike micelle transition. J Phys Chem B. 1997;101:2256–2258. [Google Scholar]
- 25.Mendes E, Menon SVG. Vesicle to micelle transitions in surfactant mixtures induced by shear. Chem Phys Lett. 1997;275:477–484. [Google Scholar]
- 26.Bernard A, et al. Shear-induced permeation and fusion of lipid vesicles. J Colloid Interface Sci. 2005;287:298–306. doi: 10.1016/j.jcis.2004.12.019. [DOI] [PubMed] [Google Scholar]
- 27.Sein A, Verheij JA, Agterof WGM. Rheological characterization, crystallization, and gelation behavior of monoglyceride gels. J Colloid Interface Sci. 2002;249:412–422. doi: 10.1006/jcis.2002.8287. [DOI] [PubMed] [Google Scholar]
- 28.Coiro VM, Manigrasso M, Mazza F, Pochetti G. Structure of a triclinic phase of sodium dodecyl sulfate monohydrate. A comparison with other sodium dodecyl sulfate crystal phases. Acta Crystallogr C. 1987;43:850–854. [Google Scholar]
- 29.Palberg T. Crystallization kinetics of repulsive colloidal spheres. J Phys Condens Matter. 1999;11:R323–R360. [Google Scholar]
- 30.Aastuen DJW, Clark NA, Cotter LK, Ackerson BJ. Nucleation and growth of colloidal crystals. Phys Rev Lett. 1986;57:1733–1737. doi: 10.1103/PhysRevLett.57.1733. [DOI] [PubMed] [Google Scholar]
- 31.Besseling TH, et al. Oscillatory shear-induced 3D crystalline order in colloidal hard-sphere fluids. Soft Matter. 2012;8:6931–6939. [Google Scholar]
- 32.Koppi KA, Tirrell M, Bates FS. Shear-induced isotropic-to-lamellar transition. Phys Rev Lett. 1993;70(10):1449–1452. doi: 10.1103/PhysRevLett.70.1449. [DOI] [PubMed] [Google Scholar]
- 33.Nettesheim F, Zipfel J, Lindner P, Richtering W. Influence of sodium dodecyl sulfate on structure and rheology of aqueous solutions of the nonionic surfactant tetraethyleneglycol-monododecyl ether (C12E4) Colloids Surf A Physiochem Eng Asp. 2001;183-185:563–575. [Google Scholar]
- 34.Shahidzadeh N, Bonn D, Aguerre-Chariol O, Meunier J. Large deformation of giant floppy vesicles in shear flow. Phys Rev Lett. 1998;81:4268–4271. [Google Scholar]
- 35.Safinya CR, Sirota EB, Plano RJ. Nematic to smectic-A phase transition under shear flow: A nonequilibrium synchrotron X-ray study. Phys Rev Lett. 1991;66(15):1986–1989. doi: 10.1103/PhysRevLett.66.1986. [DOI] [PubMed] [Google Scholar]
- 36.Fujii S, Ishii Y, Komura S, Lu CYD. Smectic rheology close to the smectic-nematic transition. Europhys Lett. 2010;90:64001–64006. [Google Scholar]
- 37.Cheng X, Xu X, Rice SA, Dinner AR, Cohen I. Assembly of vorticity-aligned hard-sphere colloidal strings in a simple shear flow. Proc Natl Acad Sci USA. 2012;109(1):63–67. doi: 10.1073/pnas.1118197108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bruin S, Jongen ThRG. Food process engineering: The last 25 years and challenges ahead. Comprehensive Reviews in Food Science and Food Safety. 2003;2:42–81. doi: 10.1111/j.1541-4337.2003.tb00015.x. [DOI] [PubMed] [Google Scholar]
- 39.Chen Y, Lin C, Wu F, Chen H. Rheological properties of crystallized honey prepared by a new type of nuclei. J Food Process Eng. 2009;32:512–527. [Google Scholar]
- 40.Raut JS, Naik VM, Singhal S, Juvekar VA. Soap: The polymorphic genie of hierarchically structured soft condensed-matter products. Ind Eng Chem Res. 2008;47:6347–6353. [Google Scholar]
- 41.Holme MN, et al. Shear-stress sensitive lenticular vesicles for targeted drug delivery. Nat Nanotechnol. 2012;7:536–543. doi: 10.1038/nnano.2012.84. [DOI] [PubMed] [Google Scholar]
- 42.De Silva JP, et al. RheoSAXS studies of anisotropic complex fluids under shear. J Phys Conf Ser. 2010;247:012052–012061. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.