Cellular capsules as a tool for multicellular spheroid production and for investigating the mechanics of tumor progression in vitro

Significance

Tumor growth intrinsically generates pressure onto the surrounding tissues, which conversely compress the tumor. These mechanical forces have been suggested to contribute to tumor growth regulation. We developed a microfluidic technique to produce 3D cell-based assays and to interrogate the interplay between tumor growth and mechanics in vitro. Multicellular spheroids are grown in permeable elastic capsules. Capsule deformation provides a direct measure of the exerted pressure. By simultaneously imaging the spheroid by confocal microscopy, we show that confinement induces a drastic cellular reorganization, including increased motility of peripheral cells. We propose that compressive stress has a beneficial impact on slowing down tumor evolution but may have a detrimental effect by triggering cell invasion and metastasis.

Abstract

Deciphering the multifactorial determinants of tumor progression requires standardized high-throughput preparation of 3D in vitro cellular assays. We present a simple microfluidic method based on the encapsulation and growth of cells inside permeable, elastic, hollow microspheres. We show that this approach enables mass production of size-controlled multicellular spheroids. Due to their geometry and elasticity, these microcapsules can uniquely serve as quantitative mechanical sensors to measure the pressure exerted by the expanding spheroid. By monitoring the growth of individual encapsulated spheroids after confluence, we dissect the dynamics of pressure buildup toward a steady-state value, consistent with the concept of homeostatic pressure. In turn, these confining conditions are observed to increase the cellular density and affect the cellular organization of the spheroid. Postconfluent spheroids exhibit a necrotic core cemented by a blend of extracellular material and surrounded by a rim of proliferating hypermotile cells. By performing invasion assays in a collagen matrix, we report that peripheral cells readily escape preconfined spheroids and cell–cell cohesivity is maintained for freely growing spheroids, suggesting that mechanical cues from the surrounding microenvironment may trigger cell invasion from a growing tumor. Overall, our technology offers a unique avenue to produce in vitro cell-based assays useful for developing new anticancer therapies and to investigate the interplay between mechanics and growth in tumor evolution.

In any multicellular organism, cells experience a 3D environment provided by the neighboring cells and the ECM. Even though the vast majority of in vitro cell biology studies are performed using cell monolayers cultured on flat substrates, there is growing evidence that 2D cell cultures fail to recapitulate the architecture of living tissues, and may thus bias the cellular response to external cues or cell-integrated signals (1). In particular, it is believed that the poor predictability in tumor responsiveness to new therapeutic agents that have been evaluated on cell monolayers originates from the lack of tissue-specific properties of 2D cultures. Since the 1980s, multicellular spheroids (MCSs) have been proposed as 3D in vitro models of avascular solid microtumors (2), and MCSs embedded in ECM-like gels (3) have been further used to investigate the mechanisms of cell invasion. In biomedical research, these MCS-based assays represent a promising alternative that overcomes the limitations of 2D cell cultures and avoids systematic animal testing. Formation of a MCS is generally performed using conventional methods, such as the hanging drop method, gyratory rotation, or liquid overlay cultures (4), whose main drawbacks are their low yield and the difficulty in controlling the size of the cellular aggregates. The recent advent of microscale photolithography has led to various sophisticated attempts to automate MCS production using microarrays (5), microwells (6), or microfluidic devices (7, 8). However, these emerging techniques have not yet progressed beyond the proof-of-concept stage, principally due to difficulty in achieving gentle cell culture conditions (8). In this context, we have developed a simple and reproducible method to prepare size-controlled spheroids amenable to quantitative biophysical study. Our technique, which is adapted from a process for making liquid core hydrogel capsules (9), is based on a microfluidic coextrusion device. Similar to previous work in the field of transplantation, we used alginate as a biocompatible polymeric material, which undergoes gelation in the presence of divalent cations (10). However, in contrast to the majority of those works where cells are embedded in solid alginate beads, our cellular capsule technology consists of encapsulating cells in an aqueous core enclosed by a hydrogel shell in gentle, oil-free conditions. The permeability of the gel allows free flow of nutrients into the capsule and cell proliferation in a scaffold-free environment. In addition to characterizing the kinetics of encapsulated MCS growth, we demonstrate the extended capabilities of the method by using the capsules as elastic confining compartments. Because the geometry of the hollow sphere sets the elastic properties of the capsule, capsule deformation upon cell division is a direct readout of the pressure applied by the expanding MCS onto the surrounding medium of controlled rigidity. Conversely, the compressive restoring force exerted by the capsule directs cellular reorganization within the spheroid, leading to the formation of a solid-like core of denatured proteins and a peripheral rim of highly motile cells whose phenotype resembles that of invasive cells.

Results

Microfluidic-Assisted Formation of Alginate Microcapsules.

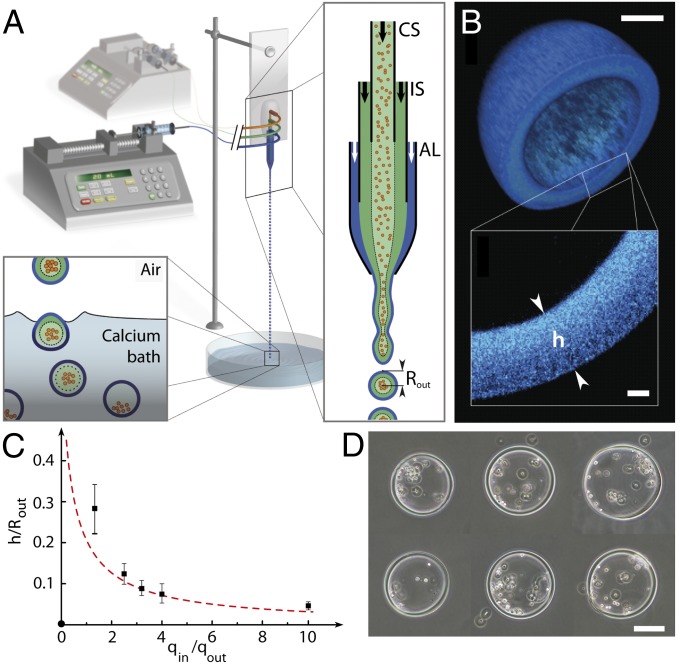
The protocol for preparing cellular microcapsules is inspired by the process developed for millimeter-sized liquid pearl fabrication (9, 11) and adapted to fulfill cell culture requirements. The basic operating principle consists of generating hydrogel shells enclosing a suspension of cells by coextrusion (Fig. 1A). More precisely, the microfluidic device is assembled by cocentering three glass capillaries. The cell suspension flows into the innermost capillary, whereas a solution of alginate is injected into the outermost tapered capillary. Gelation of the alginate shell occurs off-chip in a calcium bath. An intermediate capillary filled with a calcium-free solution serves as a barrier to diffusion of calcium released from intracellular stores, and thus avoids blockage of the chip. To produce submillimetric capsules, we have modified the mode of droplet formation. At a high enough flow rate, the liquid emerges as a jet (12), which breaks up downstream into droplets due to capillary instability (13) (Movie S1). At first order, the drop radius is set by the diameter of the jet or by the equivalent exit orifice (14). Confocal imaging using alginate doped with a fluorescent polymer confirmed the core-shell structure of the capsule and allowed accurate measurement of the shell thickness h (Fig. 1B). More interestingly, h can be tuned by varying the ratio between the inner flow rate q_in (sum of cell suspension and intermediate solution flow rates) and the outer flow rate q_out of the alginate solution. Changes in q_in/q_out mostly have an impact on the aspect ratio h/R_out (Fig. 1C), with R_out being the outer capsule radius. The height of fall was empirically adjusted to minimize coalescence between two consecutive drops before gelation, and thus to reduce the fraction of larger ellipsoidal-shaped capsules (Fig. S1 and SI Materials and Methods). Another control parameter is the initial number of cells per capsule, which can be set by altering the cell suspension density (Fig. 1D). For most operating conditions, the flow rate of liquid exiting the orifice is set in the range of 50–100 mL/h, and nozzles are microengineered with a diameter of ∼100 μm, which leads to a production rate higher than 10³ s⁻¹, with a mean capsule radius of 100–150 μm (SI Discussion and Equations), and shell thickness variable between 5 and 35 μm. In the present work, we have not exploited the high-throughput capabilities of the technology; instead, we have selected individual capsules to investigate the growth of encapsulated spheroids.

Fig. 1.

Operating principle of the microfluidic device and characterization of the alginate microcapsules. (A) Schematic of the microfluidic platform, which is composed of an external fluidic injection system, coextrusion microdevice, and off-chip gelation bath. An enlarged view of the chip (Right) shows the three-way configuration, with cell suspension (CS), intermediate solution (IS), and alginate solution (AL), respectively, flowing into the coaligned capillaries. The inlets of the chip are connected to three syringes controlled by two syringe pumps. The compound liquid microdroplets fall into a 100-mM calcium bath. Calcium-mediated gelation of the alginate shell freezes the structure of the capsule, and cells remain encapsulated. (B) Confocal image of an alginate capsule stained with high-molecular-weight fluorescent dextran. (Inset) Magnified view of the capsule wall. (C) Plot of the capsule aspect ratio h/R_out as a function of the ratio between the inner flow rate q_in = q_CS + q_IS and outer flow rate q_out = q_AL. Black dots represent experimental data. The red dashed line is the theoretical curve derived from volume conservation (SI Materials and Methods). Notations are indicated in A and B. (D) Representative phase-contrast micrographs of individual capsules encapsulating cells. (Scale bars: B, 50 μm; D, 100 μm.)

Cell Encapsulation and MCS Growth.

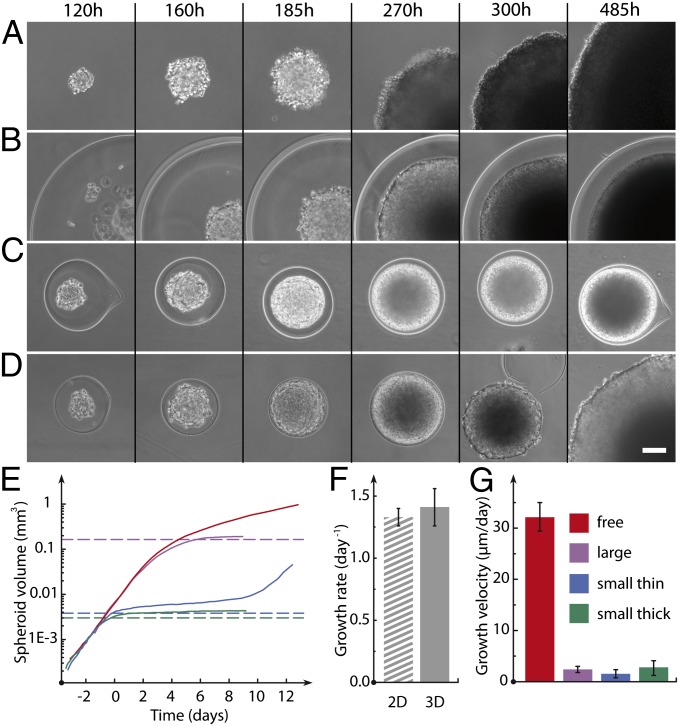
Typically, we generated capsules containing a few tens of cells (Fig. 1D and SI Materials and Methods). We checked that the survival rate following encapsulation was identical to that of trypsinized cells cultured in a Petri dish, indicating that neither shear through the device nor exposure to the calcium bath was harmful to the cells (Fig. S2). To test the capabilities of our approach for MCS formation, we monitored the fate of encapsulated cells over several days in standard culture conditions. Most commonly, we used the CT26 mouse colon carcinoma cell line, which is known to form MCSs readily when seeded on agarose cushions (15). Images were taken by time-lapse, phase-contrast microscopy (Fig. 2 A–D), and MCS volumes V(t) were derived from radii measurements R(t) assuming spherical geometry at all growth stages (Fig. 2E). Nonencapsulated growing spheroids were used as a control. As previously reported, and theoretically interpreted (16), freely growing spheroids exhibit an initial exponential growth characterized by an average doubling time of τ = 17 ± 1 h (Fig. 2F), which is followed by a power-law volume increase: 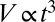. The transition between these two stages is regulated by the availability of nutrients that penetrate the spheroid by diffusion, and thus by the spheroid size. Deviation from exponential growth occurs for R_c ∼ 200 μm (V_c ∼ 0.03 mm³; Fig. 2E), in agreement with previous estimates for the diffusion distance of oxygen in tissues (17, 18). As the tumor MCS grows further, a layered structure becomes visible: A dark necrotic core is surrounded by a thin viable rim. Beyond the crossover region (200 μm < R < 350 μm), the spheroid shows a purely surface growth regime characterized by a radius expansion velocity of 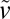= 32 ± 3 μm⋅d⁻¹ (Fig. 2G), which is in agreement with growth velocities measured previously in conditions of standard nutrient and oxygen concentration (16). In the case of encapsulated cells, we first observed that cells occupy an increasing volume of the capsule (Fig. 2 B–D and Movie S2). When cells fill the capsule, confluence is reached and is detectable as a smoothening of the MCS contour. More quantitatively, the volume increase rate is indistinguishable from that of freely growing MCSs before confluence (Fig. 2 E and F), indicating that the access to nutrients required for normal growth is not compromised by the hydrogel shell. This observation is consistent with alginate permeability characterized by a molecular cutoff of molecular mass of ∼150 kDa for globular proteins (19, 20).

Fig. 2.

Confined and free growth of spheroids. Sequences of phase-contrast micrographs show free growth of a spheroid (A) and confined growth of a spheroid encapsulated in large and thick (B; h = 100 μm, R = 407 μm), small and thick (C; h = 38 μm, R = 151 μm), and small and thin (D; h = 7 μm, R = 129 μm) alginate shells. The thin capsule ultimately bursts. Time is recorded from encapsulation. (Scale bars: 50 μm.) (E) Representative log-linear time plots of spheroid volume in conditions of free growth (red) and confined growth in a large capsule (purple), in a small and thick capsule (blue), and in a small and thin capsule (green). (F) Growth rate for CT26 cells cultured in a Petri dish (2D) and as spheroids (3D) before confluence (early stages). The 3D growth rate is derived from MCS volume increase normalized by the actual volume. (G) Growth velocity measured in the late stages of CT26 spheroid growth.

We then focused on the postconfluence stages of MCS growth. We varied capsule size and shell thickness. Here, we distinguish small thick capsules (R₀ ∼ 100 μm < R_c, h/R₀ ∼ 0.25), small thin capsules (R₀ ∼ 100 μm < R_c, h/R₀ ∼ 0.08), and large thick capsules (R₀ ∼ 350 μm > R_c, h/R₀ ∼ 0.25). The volumetric evolution of MCSs confined in thick capsules displays common features irrespective of capsule radius; once confluence is reached, the spheroid size seems to level off (Fig. 2E). Closer inspection reveals that growth is not stalled, per se, but is instead significantly slowed down. The spheroid is still expanding with an average growth velocity (∼ micrometers per day) reduced by one order of magnitude compared with freely growing spheroids (Fig. 2G). The main difference between large and small capsules lies in the actual structure of the spheroids: A dark core, which originates from a limitation in nutrient diffusion, becomes visible in large spheroids before confluence, whereas a strongly light-absorbing core is observed to nucleate concomitantly with confluence in small spheroids (Fig. 2 B–D and Movie S2). This core ends up covering the major fraction of the capsule, leaving a thin rim of a few cell layers. Because the MCS radius remains below the oxygen diffusion distance of about 200 μm, this peculiar cellular response suggests alterations in division and death rates induced by confinement. All experiments discussed hereafter were therefore performed on capsules of radius R₀ < 150 μm to decouple nutrient-limited and confinement-induced effects. When spheroids are cultured in thinner capsules, the sequence of growth patterns is similar, except capsule deformation is increased. Thin capsules display maximal dilations of ∼40% in the radius before they burst within 8–12 d (Fig. 2D and Movie S3). Upon rupturing, the spheroid resumes growth with a rate comparable to that of free spheroids.

We also succeeded in preparing spheroids derived from HeLa cells, which have a low propensity to form 3D aggregates, and from murine sarcoma S180 cells expressing low levels of E-cadherin, and thus exhibiting weak cell–cell adhesions (21) (Fig. S3 and Movie S4). The ability to grow spheroids under these conditions suggests that confinement itself and the cell-repellent nature of the gel (10) favor 3D multicellular assembly. Bare unconfined spheroids can readily be recovered upon alginate dissolution in PBS. Dissolution mediated by calcium/sodium exchange requires 1 h for bulk alginate gel (22), but disassembly of ∼20-μm-thick shells is completed in less than 10 min (Movie S5). At this stage, bare cohesive MCSs can be used for various applications, such as high-throughput screening of drugs.

Impact of Confinement on the Internal Cellular Organization of Spheroids.

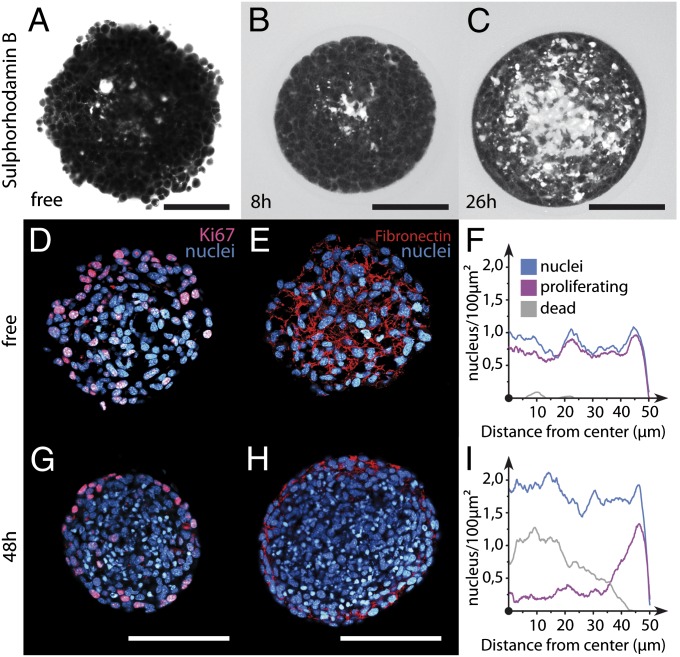
To gain mechanistic insight into the influence of confinement on MCS growth, we investigated the structural differences between free and encapsulated spheroids at a cellular and molecular level. First, we used a water-soluble dye, sulforhodamine B (SRB), that accumulates in the extracellular space. By two-photon microscopy (Fig. 3), we observed that (i) a bright core is nucleated only a few hours after confluence and (ii) it spreads outward in a fractal-like manner within 2 d. At longer time points, the labeled core occupies the largest fraction of the spheroid, whereas the first three to four peripheral cell layers remain unstained. As a control, a free spheroid of the same size (R ∼ 150 μm) showed very little staining. This experiment confirms that the appearance of an SRB-sensitive core composed of extracellular or released protein material is induced solely by confinement. Alternative imaging of encapsulated MCS labeled with a membrane-sensitive dye, FM4-64 (Fig. S4 and Movie S6), shows an increasing occurrence of necrotic events once the spheroid becomes effectively compressed. The confinement-induced core is therefore also composed of permeabilized cells.

Fig. 3.

Imaging of the internal cellular organization of growing spheroids under elastic confinement. Snapshots taken by two-photon imaging of free (A) and encapsulated (B and C) spheroids stained with the polar dye SRB are shown. Time t = 0 corresponds to confluence. Confocal images of free (D and E) and confined (G and H) spheroids after cryosection and immunolabeling for DAPI (blue), KI67 (magenta), and fibronectin (red). Quantification of cell nucleus (blue), proliferating cell (purple), and dead cell (gray) radial densities for free (F) and confined (I) CT26 spheroids. (Scale bars: A–C, 50 μm; D, E, G, and H, 100 μm.)

We then complemented live imaging with specific fluorescence staining of MCS cryosections. Comparison was made between free and confined spheroids. DAPI staining shows that the nuclei are smaller in confined MCSs (Fig. 3 D and G), leading to a cell density twice as large as in the freely growing spheroids (Fig. 3 F and I). We also examined cell proliferation by staining with KI-67 (AbCys) (Fig. 3 D and G). As expected, cell proliferation is homogeneously distributed throughout small free MCSs (Fig. 3F). In contrast, in confined MCSs, cell division mostly occurs in the peripheral rim (Fig. 3I). Consistently, very bright DAPI-stained nuclei identified as dead cells are mainly visible in the core of the confined spheroids. Similarly, fibronectin staining is fibrillar and homogeneously distributed in free spheroids, whereas it is restricted to the peripheral region of the confined spheroid (Fig. 3 E and H). Staining for vimentin, laminin, or collagen is also negative or very faint in the central region of the postconfluent spheroids (Fig. S5), suggesting that extracellular proteins nonspecifically labeled by SRB (Fig. 3 B and C) may be in a denatured state.

Mechanical Analysis of the Growth of Elastically Confined Spheroids.

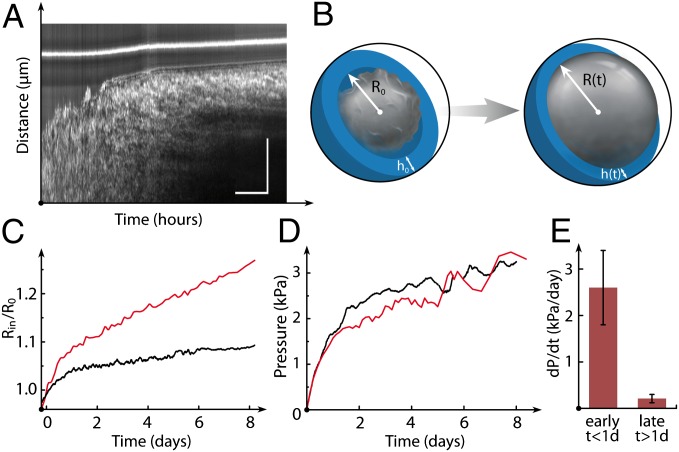
As mentioned above, the growth of encapsulated spheroids is not arrested at confluence and causes capsule dilation (Fig. 4A). If shell thickness is reduced, capsule bursting may occur. In this case, the initial capsule size is instantaneously recovered with a variation of less than 3% (Fig. 2B and Movie S3), which suggests that the alginate gel behaves as an elastic solid with negligible plasticity. Using assays such as atomic force microscopy indentation and osmotic swelling, we measured the Young’s modulus of alginate gels to be E = 68 ± 21 kPa (Fig. S6, SI Materials and Methods, and SI Discussion and Equations) and observed no hysteresis, indicating negligible viscosity. Capsules can thus serve directly as elastic sensors of MCS growth (Fig. 4B). Capsule stiffness k_caps is determined both by bulk elasticity and by shell thickness: k_caps 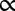E × h. The postconfluence deformation of the capsule thus becomes a direct readout of the pressure exerted by the expanding spheroid. As a first approximation, we consider the capsules as thin-walled pressurized vessels in the framework of isotropic linear elasticity. The pressure that inflates the shell is given by (23):

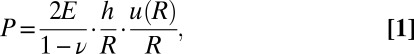where u(R) is the radial displacement at a distance R_in ≤ R ≤ R_out from the center of the capsule and ν is the Poisson’s ratio. As the spheroid grows, the capsule radius R(t) increases and the shell thickness h(t) decreases according to volume conservation of the shell (ν = 1/2; Fig. S7 and SI Discussion and Equations). The actual experimental conditions require additional corrections, however. For thin capsules, the assumption of linear elasticity does not apply because strains exceed 20%. A phenomenological dependence of the Young’s modulus on strain was taken into account for nonlinear elasticity and strain hardening (SI Discussion and Equations). For thick capsules (h/R ∼ 0.25), the complete formalism of thick-walled vessel theory was used (SI Discussion and Equations). In practice, we placed individual capsules in custom-made drift-free observation chambers (Fig. S8) and we monitored the evolution of the mean inner capsule radius R_in(t) normalized by the unstressed radius R_in(t = 0) (Fig. 4C). Although deformation traces for thin and thick capsules are strikingly distinguishable, we find that pressure curves essentially collapse within experimental error (Fig. 4D) and exhibit two main features. First, pressure builds up rapidly during the first 24 h after confluence (Fig. 4E; dP/dt = 2.4 ± 0.5 kPa⋅d⁻¹). Then, at a threshold pressure P_th = 2.2 ± 0.5 kPa, there is a drastic drop in pressure increase, which reaches a steady value as low as dP/dt = 0.2 ± 0.08 kPa⋅d⁻¹ (Fig. 4E). Altogether, these results demonstrate that the mechanics of growing spheroids can be quantitatively and dynamically characterized by measuring the deformation of the elastic capsules.

Fig. 4.

Quantitative mechanical analysis of postconfluent spheroid growth. (A) Phase-contrast intensity plot as a function of time and radial distance from the MCS center. The bright line is the outer wall of the capsule. (Scale bars: 20 h and 50 μm.) (B) Drawing of encapsulated spheroid and capsule deformation suggesting the use of the shell as a mechanical sensor. R₀ and h₀ are the initial capsule radius and shell thickness, respectively. (C) Representative time plots show the influence of capsule stiffness (via shell thickness) on MCS growth. The radius of the spheroid R_in is normalized to the undeformed inner radius R₀ vs. time (h = 8 μm, red; h = 28 μm, black). (D) Pressure exerted by the spheroid on the capsule wall vs. time (h = 8 μm, red; h = 28 μm, black). (E) Statistical analysis (n = 40, including 23 thin capsules and 17 thick capsules). The rate of pressure increase within 1 d following confluence and at later stages is shown.

Impact of Compressive Stress on Cell Migration at the Periphery of Confined Spheroids.

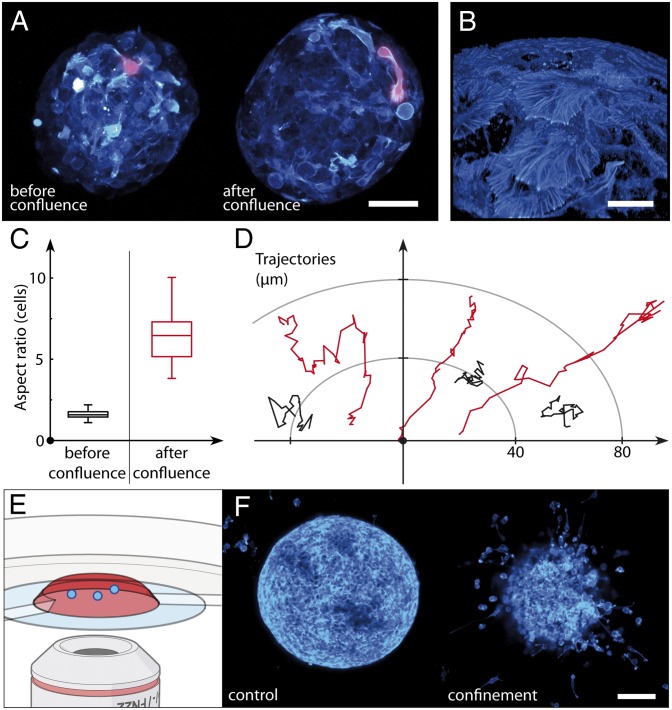
Even under prolonged confinement and after capsule dissolution, spheroids conserve a well-defined cellular organization composed of a solid-like core made of denatured proteins and cell debris and a rim of proliferative cells (Movie S7 and Fig. S9). By focusing on these peripheral cells, we then tested whether confinement affects cell motility. We imaged CT26 cells stably transfected with LifeAct-mCherry (provided by R. Gaudin; Institut Curie, Unit 932, Paris, France) before and after confluence (Fig. 5A and Movie S8). Initially, cells are fairly round (Fig. 5C) and moderately mobile, as shown by their random walk-like trajectories (Fig. 5D). Once confluence is reached, most peripheral cells become elongated (Fig. 5C) and highly migratory (Fig. 5D). They exhibit persistent motions within the peripheral cell layer of the spheroid, with a characteristic velocity on the order of 5 μm⋅h⁻¹. They form long and thin protrusions tipped with lamellipodia and filopodia, which move parallel to the surface of the inner border of the capsule (Movie S9). Lamellipodia and filopodia are also observed in fixed cells stained with fluorescent phalloidin (Fig. 5B and Movie S10).

Fig. 5.

Impact of elastic confinement on cell motility at the periphery of growing spheroids. (A) Confocal live imaging of an encapsulated spheroid grown from cells stably transfected with LifeAct-mCherry. Maximum intensity projections of the confocal stacks [a hot look-up table acquired using Fiji is shown (cyan)]. One representative cell is colored magenta before and after confluence to highlight the features quantified in C. (B) Enlarged view of the surface of a fixed spheroid imaged by confocal microscopy after staining with phalloidin-Alexa 488 (Hot LUT, cyan). (C) Box plot shows the aspect ratio of cells before and after confluence (n = 94, five spheroids). (D) Representative projected trajectories of the center of mass of cells moving at the periphery of spheroids. The time interval is 15 min. (E) Cartoon describing cell migration assay. Spheroids (blue) are embedded in collagen matrix (red) in a Petri dish. (F) Confocal image taken 48 h after implantation in collagen for spheroids grown freely (control) and in a capsule past confluence after shell dissolution (confined). (Scale bars: A, 50 μm; B, 10 μm; F, 100 μm.)

A priori, the elongated morphology and enhanced motility could be due to cells squeezing between the alginate shell and the solid MCS core or could correspond to a phenotypic change toward a mechanosensitive hypermotile phenotype. In the first case, shell dissolution would be expected to abolish cell elongation and reduce migration. In the second case, these features should be conserved after compression release. To distinguish between both hypotheses, we recovered bare spheroids by shell dissolution and performed a 3D motility assay by embedding them in a collagen matrix. Control preconfluent spheroids were observed to grow while keeping a smooth boundary with the matrix (Fig. 5F, Left and Movie S11). In contrast, individual cells or small clusters of cells readily escape postconfluent spheroids only few hours after implantation (Fig. 5F, Right and Movie S12).

Discussion

Hydrogels have been used extensively for cell culture, tissue transplantation (24), and drug release (10). We designed a unique approach to achieve massive production of cell-encapsulating hollow, permeable, and elastic alginate shells. We demonstrate that this method allows efficient preparation and long-term culture of MCSs, considered as the minimal in vitro system that mimics microtumors. In contrast to classical methods (4), our technique overcomes the disadvantages of low production rate and size variability. By comparison with more recent strategies based on microarrays (5) and microfluidics (25), our technique does not require lithography equipment or the use of an oil phase and viscosity enhancer that results in decreased cell viability (8).

Although tumor development is undoubtedly controlled by genetic alterations and biochemical factors, it is now accepted that mechanical cues sensed by or transduced to the stroma may also assist tumor progression (26, 27). Long hypothesized on the basis of general mechanisms for cell mechanosensitivity, the influence of mechanical stress exerted by the environment was demonstrated in a pioneer in vitro work on spheroids embedded in agarose matrix (28). Jain and colleagues (28) observed a twofold increase in cellular packing density and evaluated growth-inhibitory stress in the range of 5–15 kPa from the phenomenological strain energy function of agarose. The existence of a pressure value at which spheroids reach a stationary size was then theoretically formalized, termed “homeostatic pressure” (29), and experimentally addressed by applying osmotic pressure to spheroids (30). On initial consideration, our results are roughly consistent with the main outcomes of these experimental reports. However, the main differences are threefold. First, from a methodological point of view, we have replaced bulk hydrogel with hollow hydrogel spheres, whose controlled geometry provides a more straightforward way to probe quantitatively the dynamical relationship between mechanics and growth of the spheroids. Second, the pressure threshold above which spheroid growth drastically drops is found to be lower, on the order of 2 kPa, which could be a cell line-specific effect. Third, even though first-order analysis may lead us to confirm the existence of a plateau phase of growth inhibition, closer examination of the late stages of confined growth reveals that MCS growth is not completely suppressed. We observe fast growth transiently after confluence, followed by a much slower expansion with a velocity decreased to ∼2 μm⋅d⁻¹, which is barely detectable if not monitored over a long time period. Although interpreted as saturation pressures, similar gently sloping plateaus can be inferred from data reported by Helmlinger et al. (28). In a more recent work, Munn and colleagues (31) showed that the growth of MCSs implanted in agarose gel was accompanied by necrosis but that upon induction of cracks in the agarose matrix, cell proliferation could be resumed due to stress release. Similarly, we have found that the elastic shell-restoring force prompts important changes and leads to a layered structure of the spheroid. More importantly, we show that the steady-state spheroid structure is composed of a compact solid-like core made of cellular debris cemented by presumably denatured proteins and surrounded by a 20-μm-thick rim of proliferative cells. This observation may lead us to speculate about the superior physiological relevance of our cellular capsules over free spheroids as tumor/microenvironment mimics, because tumors are often detected as a palpable stiffening of the tissue (26), whereas the nutrient-limited necrotic core of free large spheroids does not exhibit any solid-like feature.

To explain why elastically confined spheroids do not reach a well-defined stationary size but continue to grow very slowly, we need to revisit the assumptions underlying the homeostatic pressure notion (29). Briefly, a steady-state pressure is reached when the division rate, which is decreased upon compression, is balanced by the apoptosis rate, which is enhanced upon stress. The main hypotheses are that the spheroid is considered as a homogeneous incompressible viscoelastic liquid under external pressure and that dividing cells double their volume, whereas the volume of apoptotic cells instantaneously drops to zero. Evidently, dead cells do not vanish instantaneously. Moreover, we observed significant increase in cellular packing, suggesting compressibility of the spheroid. Using a modified version of a two-rate model (30, 32), we will present a simplified description of spheroid growth in conditions of elastic confinement. For the sake of simplicity, cell addition dominantly occurs in the outer rim of thickness λ with a doubling rate k_s, and cell disappearance is localized in the core at a rate α⋅k_v, with k_v being the net difference between death and division rates in bulk, and α << 1, a prefactor that accounts for only partial disappearance over observation times of a few days. The growth equation thus reads:

where N is the total number of cells and N_s is the number of cells in the surface proliferative rim.

In the slow postconfluent growth phase, assuming λ constant R >> λ and taking into account variation of cell density 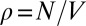, one obtains:

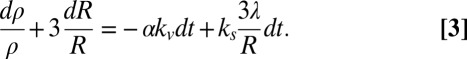By defining a compression bulk modulus of the spheroid 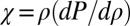, Eq. 3 reduces to:

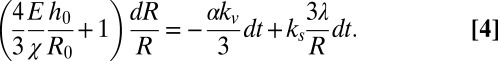If one neglects volume loss due to dead cells (α << 1), we express the growth velocity v = dR/dt as:

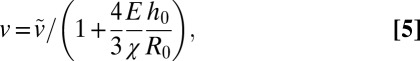where 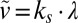is the characteristic growth velocity in the absence of confinement.

Eq. 5 shows that for “strong” confinement (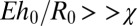), v is inversely proportional to the capsule aspect ratio, which is in good agreement with experimental data (Fig. 2G). Taking 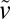= 32 μm⋅d⁻¹ and v = 2 μm⋅d⁻¹ for thick capsules (h₀/R₀ ∼ 0.2), one finds 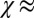1 kPa, in good agreement with previously reported values (16, 33).

More interestingly, we have demonstrated that these moderate pressure levels (∼kilopascals) induce a drastic stimulation of protrusion formation and cell motility at the spheroid periphery. This phenotypic change leads to cells swiftly disseminating through the surrounding collagen matrix, which may also suggest an enhanced propensity to escape the tumor. This result extends to a more physiologically relevant 3D tumor MCS configuration and the recent proposal that mechanical compression of 2D cancer cell monolayers confined on adhesive micropatterns generates “leader cells” that exhibit an invasive phenotype (34). We thus believe that these cellular capsules, which allow integration of mechanical cues from the tumor environment, may pave the way for further comprehension of the cellular and molecular bases of tumor development.

Materials and Methods

Detailed experimental methods can be found in SI Materials and Methods. The microfluidics device consists of three coaligned glass capillary tubes. The flow of the three fluid phases (Fig. 1) was controlled by syringe pumps. The gelation bath was composed of 100 mM calcium chloride. We most commonly used WT CT26 mouse colon carcinoma cells. Long-term imaging of MCS growth inside capsules and motility through 3D collagen matrix was performed by phase-contrast microscopy. For motility assays, alginate shells were first dissolved in PBS and spheroids were mounted in collagen matrix. We used confocal microscopy to visualize the peripheral cell layers and the core of growing spheroids. Morphometric measurements were obtained using ImageJ (National Institutes of Health) routines. Time-lapse, phase-contrast images were analyzed using a custom-made, gradient-based edge detection algorithm implemented in MATLAB (MathWorks).