Significance
Many forest insects undergo outbreaks, in which their densities rise from undetectable to extremely high. Outbreaks are widely assumed to be driven by specialist natural enemies such as infectious pathogens, but gypsy moth outbreaks show alternating severe and mild outbreaks in forests with a high percentage of oaks, a pattern that cannot be explained by host-pathogen models. We used an experiment to show that induced defenses in red oak reduce heterogeneity among gypsy moth larvae in the risk of virus infection, and extending standard models to allow for this effect produces alternating outbreaks, matching the data. The ability of our model to reproduce this complex pattern suggests that the role of induced defenses in insect outbreaks has been underestimated.
Keywords: host-pathogen model, Lymantria dispar, complex population dynamics, spatial model, hydrolyzable tannins
Abstract
Cyclic outbreaks of defoliating insects devastate forests, but their causes are poorly understood. Outbreak cycles are often assumed to be driven by density-dependent mortality due to natural enemies, because pathogens and predators cause high mortality and because natural-enemy models reproduce fluctuations in defoliation data. The role of induced defenses is in contrast often dismissed, because toxic effects of defenses are often weak and because induced-defense models explain defoliation data no better than natural-enemy models. Natural-enemy models, however, fail to explain gypsy moth outbreaks in North America, in which outbreaks in forests with a higher percentage of oaks have alternated between severe and mild, whereas outbreaks in forests with a lower percentage of oaks have been uniformly moderate. Here we show that this pattern can be explained by an interaction between induced defenses and a natural enemy. We experimentally induced hydrolyzable-tannin defenses in red oak, to show that induction reduces variability in a gypsy moth’s risk of baculovirus infection. Because this effect can modulate outbreak severity and because oaks are the only genus of gypsy moth host tree that can be induced, we extended a natural-enemy model to allow for spatial variability in inducibility. Our model shows alternating outbreaks in forests with a high frequency of oaks, and uniform outbreaks in forests with a low frequency of oaks, matching the data. The complexity of this effect suggests that detecting effects of induced defenses on defoliator cycles requires a combination of experiments and models.
Periodic outbreaks of forest-defoliating insects severely damage valuable timber and increase atmospheric CO2 levels by converting forests from carbon sinks to carbon sources (1). Decades of research have produced multiple hypotheses to explain defoliator outbreak cycles (2), but a decisive experiment to choose between competing hypotheses faces almost insurmountable logistical difficulties, because outbreaks occur at 5–30 y intervals and typically cover thousands of square kilometers (3). Efforts to support particular hypotheses have therefore instead relied on a mixture of observational field data, small-scale field and laboratory experiments, and mathematical models.
For example, the most widely accepted hypothesis is that defoliator cycles are driven by natural enemies. Support for this hypothesis comes first of all from observational data showing that defoliators experience high rates of infection by specialist pathogens and parasitoids in peak populations (2, 4) and high rates of attack by generalist predators and parasitoids in trough populations (5). Second, experimental data have confirmed key assumptions of defoliator–natural-enemy models, and the models produce long-period, large-amplitude cycles resembling time series of insect densities and defoliation levels (6).
Neither data nor models have provided meaningful support for an important alternative hypothesis, that defoliator cycles are driven by induced defenses. In many trees, antiherbivore defensive compounds increase in response to defoliation (7, 8), and such increases could in principle cause outbreaks to collapse. Direct toxic effects of induced defenses in experiments, however, are often weak, and the mechanisms underlying these defenses are often unknown or poorly understood (9). Moreover, there are no obvious signs of the effects of induced defenses in time series of defoliation or insect densities. Induced-defense models therefore provide no better an explanation for defoliator cycles than do natural-enemy models (10, 11), while additionally providing no explanation for mortality due to natural enemies. Given the successes of the natural-enemy hypothesis, these failures of the induced-defense hypothesis have led to the conclusion that induced defenses play little to no role in defoliator outbreak cycles (3). Here we argue that this conclusion is premature, by presenting evidence showing that induced defenses modulate outbreak cycles of the gypsy moth (Lymantria dispar) in North America.
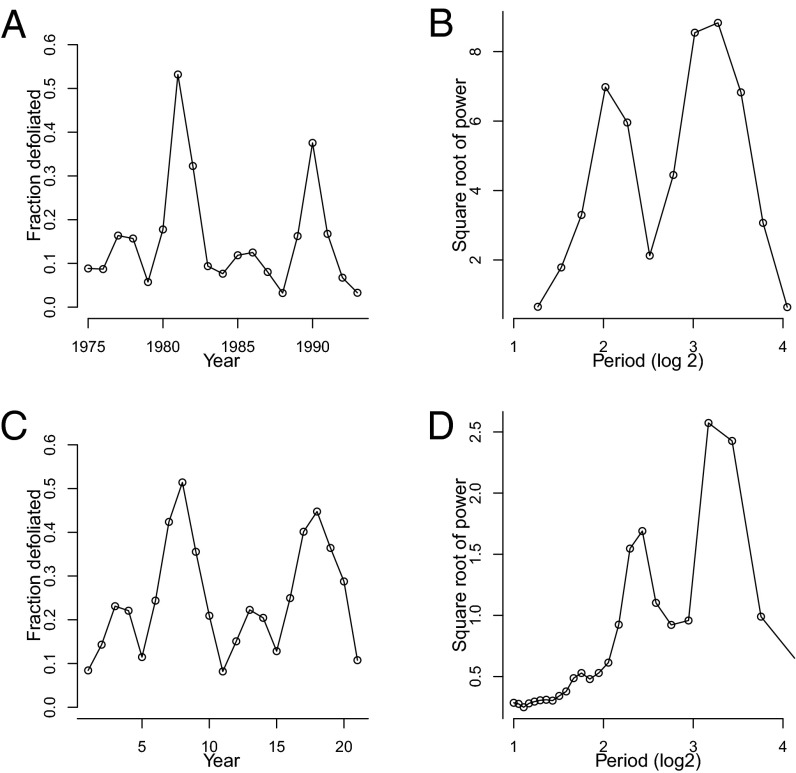
We suspected that induced defenses play a role in gypsy moth cycles because recent analyses of defoliation data have revealed that gypsy moth cycles differ between forest types (12). In oak–hickory (Quercus–Carya spp.) forests, in which the aboveground tree biomass is 43% oaks, severe outbreaks have alternated with mild outbreaks, leading to a strong subharmonic oscillation in time series of defoliation (Fig. 1 A and B). In oak–pine (Quercus–Pinus spp.) forests, in which the aboveground tree biomass is 15% oaks, outbreak severity has instead been roughly uniform, and there has been no subharmonic (Fig. 2 A and B). Logistic regression (12) and spatially smoothed autocorrelation (13) analyses have confirmed that these differences are statistically significant.
Fig. 1.
Outbreak dynamics in oak–hickory forests, in data (12), and in a spatial version of an outbreak model that includes induced defenses. A and C are defoliation time series in the data and in the model, respectively, and B and D are the corresponding power spectra. For the model we show a time series based on a single realization, but to ensure that the pattern holds up over multiple realizations, the spectrum for the model is an average over 100 realizations (SI Appendix, Figs. S6–S10 shows more realizations). Because the gypsy moth is an invader and because invasion dynamics could lead to confounding effects, the data are based only on areas that were completely infested by 1975, which in practice meant mostly the New England and Mid-Atlantic sections of the United States (12).
Fig. 2.
Outbreak dynamics in oak–pine forests. Again A and C are defoliation time series in the data and in the model, respectively, and B and D are the associated power spectra (SI Appendix, Figs. S11–S15 shows more model realizations).
This difference in outbreak cycles is unlikely to be due to differences in the physical environment, because climatic conditions are effectively identical between forest types and because the soil-moisture differences that determine forest composition have no direct effect on the gypsy moth (12). Meanwhile, simple natural-enemy models that include a specialist baculovirus pathogen (14) and a generalist predator (5) can reproduce qualitative features of gypsy moth cycles (6), but standard models do not produce a subharmonic. Bjornstad et al. (13) therefore extended a natural-enemy model to allow for spatial variability in generalist-predator attack rates. Their work suggests that the subharmonic requires some kind of spatial structure, but their model only produces a subharmonic if infected larvae are allowed to disperse and uninfected larvae are not allowed to disperse. In nature both infected and uninfected larvae disperse (15), so spatial variability in generalist predators does not appear to be a sufficient explanation.
We therefore considered whether the observed differences in outbreak dynamics between forest types could instead be due to differences in inducibility between genera of gypsy moth host trees. In the range of the gypsy moth in North America, defoliation induces hydrolyzable tannins in most oak species (16), including red oak (Quercus rubra) (17), black oak (Quercus velutina) (17), and chestnut oak (Quercus prinus) (18), whereas the effects of white-oak defoliation (Quercus alba) on gypsy moths are also likely due to increases in hydrolyzable tannins (19). Meanwhile, pines do not contain hydrolyzable tannins at all (20), whereas levels of hydrolyzable tannins in hickories are close to or equal to zero (21). The effects of induced hydrolyzable tannins on baculovirus transmission are therefore likely to be stronger in oak–hickory forests than in oak–pine forests because of the higher fraction of oaks in oak–hickory forests.
Direct toxic effects of induced defenses on gypsy moths are known to be relatively weak (22), but like many baculoviruses (23), the gypsy moth virus is transmitted when host larvae consume virus-contaminated foliage. Induced hydrolyzable tannins in foliage can therefore alter a gypsy moth larva’s risk of infection, but as we will discuss, previous laboratory evidence for such effects (24) was not consistent with field data (14). Induced birch defenses (Betula pubescens ssp. czerepanovii) can similarly alter the responses of autumnal moth (Epirrita autumnata) larvae to artificially implanted plastic filaments in the laboratory (25), but efforts to detect induction effects on autumnal moths in the field were likewise unsuccessful. Also, there is no obvious signature of induced defenses in time series of autumnal moth defoliation (26).
Accordingly, for differences in host-plant inducibility to explain the disparate dynamics of gypsy moth outbreaks in oak–hickory and oak–pine forests, induced hydrolyzable tannins in oaks must first of all affect baculovirus transmission in nature. We therefore carried out an experiment to test whether induced hydrolyzable tannins modulate baculovirus transmission under field conditions. Second, spatial variability in tree-species composition must explain the differences in outbreak dynamics between the two forest types. We therefore used a mathematical model to test whether the mechanism revealed by our field experiment produces alternating severe and mild outbreaks in simulated oak–hickory forests and consistently moderate outbreaks in oak–pine forests, as seen in the data for each forest type.
Results
A previous effort to induce hydrolyzable tannins using artificial defoliation was unsuccessful (27). We therefore induced hydrolyzable tannins by spraying foliage with the plant-signaling compound jasmonic acid (JA) (28), which had previously been used to induce hydrolyzable tannins in red-oak seedlings in the greenhouse (29). Hydrolyzable tannin levels in oak foliage in nature increase after budburst in defoliated trees and decline in undefoliated trees (17). We thus expected that induction effects would be manifest through statistically significant effects of week and through a treatment-by-week interaction. Statistical model parameters associated with these terms were indeed significantly different from zero (week, 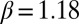 ,
, 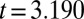 ,
, 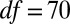 ,
, 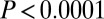 ; treatment-by-week interaction,
; treatment-by-week interaction, 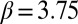 ,
, 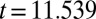 ,
, 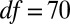 ,
, 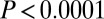 ; Table 1; mixed-effects repeated-measures model with JA treatment and week as fixed effects, and with tree and branch nested within a tree as random effects, so that separate intercept and slope terms were fitted for each branch). For the same reason, we expected that the effect of induction alone would not be significant, and again this expectation was upheld (
; Table 1; mixed-effects repeated-measures model with JA treatment and week as fixed effects, and with tree and branch nested within a tree as random effects, so that separate intercept and slope terms were fitted for each branch). For the same reason, we expected that the effect of induction alone would not be significant, and again this expectation was upheld (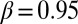 ,
, 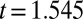 ,
, 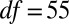 ,
, 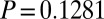 ). Hydrolyzable tannin concentrations in foliage of experimental branches therefore increased relative to controls, reaching levels that were indistinguishable from levels induced by natural defoliation (17). A similar but slightly weaker effect was seen in samples the following year (SI Appendix, section 1.2 and Fig. S1). The JA spray in our experiments was thus highly effective at inducing realistic increases in hydrolyzable tannins.
). Hydrolyzable tannin concentrations in foliage of experimental branches therefore increased relative to controls, reaching levels that were indistinguishable from levels induced by natural defoliation (17). A similar but slightly weaker effect was seen in samples the following year (SI Appendix, section 1.2 and Fig. S1). The JA spray in our experiments was thus highly effective at inducing realistic increases in hydrolyzable tannins.
Table 1.
Effects of experimental JA spray in this study, and natural defoliation in a previous study (17), on percent hydrolyzable tannin concentration in red oak foliage
| Induction method | Treatment | Pretreatment concentration, % | Posttreatment concentration, % |
| JA spray | JA | 19.7 ± 0.82 | 27.8 ± 0.82 |
| Control | 19.5 ± 0.74 | 15.9 ± 0.84 | |
| Natural defoliation | Defoliated | 23.30 ± 1.0 | 27.05 ± 1.4 |
| Ref. 17 | Control | 23.36 ± 0.9 | 19.54 ± 0.9 |
Pretreatment concentrations were significantly different between studies (treatments, 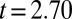 ,
, 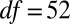 ,
, 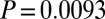 ; controls,
; controls, 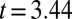 ,
, 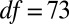 ,
, 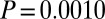 ), as were posttreatment control concentrations (
), as were posttreatment control concentrations (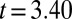 ,
, 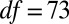 ,
,  ), reflecting natural background variability in hydrolyzable tannins. Posttreatment concentrations were nevertheless effectively identical in JA-sprayed and naturally defoliated branches (
), reflecting natural background variability in hydrolyzable tannins. Posttreatment concentrations were nevertheless effectively identical in JA-sprayed and naturally defoliated branches (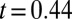 ,
,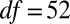 ,
, 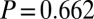 ), and controls in the two studies declined by similar magnitudes.
), and controls in the two studies declined by similar magnitudes.
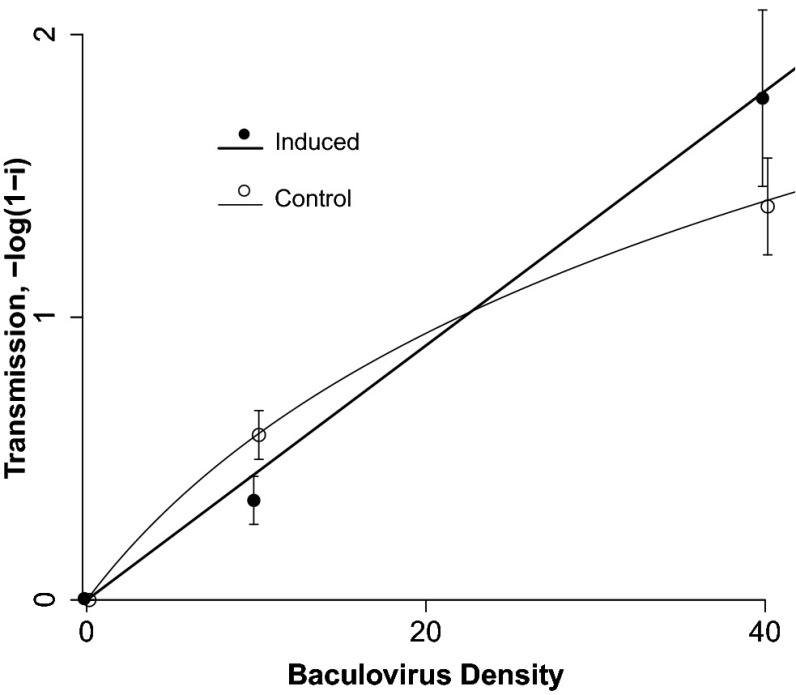
We then quantified infection rates on induced and noninduced foliage, by first allowing infected larvae to die on both types of foliage and then allowing uninfected larvae to feed on the foliage. The resulting data show that the induction of hydrolyzable tannins had a strong effect on infection rates, but the effect varied across virus densities. At the lower virus density, average infection rates were lower on induced foliage, but at the higher virus density, they were higher on induced foliage (Fig. 3). To confirm that these differences were not simply due to chance effects, we used maximum likelihood and nonlinear optimization routines to fit a range of competing transmission models to the data, such that different models made different assumptions about the effects of induction on transmission. We then used the Akaike Information Criterion (AIC) to choose between the models (30). This model selection procedure provided very strong evidence that transmission was a nonlinear function of virus density on control foliage (Table 2), as in previous experiments (31), and that it was a linear function on induced foliage.
Fig. 3.
Effects of induction on baculovirus transmission. Symbols indicate data, and lines indicate the best fit versions of Eq. 5. Note that on branches without virus-infected cadavers, the fraction infected was very close to 0 (one infected insect out of 1,710), and so the model fit is based on three virus densities. Virus densities are jittered so that error bars can be easily distinguished.
Table 2.
AIC analysis of the results of the field transmission experiment
| Model | AICc | ΔAICc | AICc WT |
| No treatment effect, linear model | 183.9 | 13.10 | 0.001 |
| No treatment effect, nonlinear model | 177.9 | 7.17 | 0.026 |
| JA linear, control linear | 186.0 | 15.22 | 0.001 |
| JA linear, control nonlinear | 170.8 | 0.00 | 0.940 |
JA nonlinear, control nonlinear—(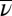 same, C different) same, C different) |
178.8 | 7.51 | 0.022 |
JA nonlinear, control nonlinear—(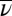 different, C same) different, C same) |
179.9 | 9.13 | 0.001 |
The best model is in boldface. The model for which transmission was linear on induced branches and nonlinear on control branches provided an overwhelmingly stronger explanation for the data, such that the AIC difference for the next-best model was more than 7 (some more complex models are not included because they converged on the best model; SI Appendix). Moreover, the second-best model that allowed for a treatment effect assumed that the infection rate function was nonlinear on both induced and noninduced branches, again with lower infection risk on JA-treated branches. The probability that induction lowered variability in infection risk was thus greater than 0.96 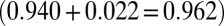 .
.
Previous work has shown that nonlinear virus transmission is due to high levels of variability in instantaneous infection risk between individuals (32). Because our AIC analysis demonstrates that induction produced linear virus transmission, it implies that induction strongly reduced variability in infection risk (Table 2). Reflecting the model-selection results, our estimate of variability in infection risk was low on induced foliage and high on noninduced foliage, and the respective confidence intervals did not overlap (SI Appendix, section 1.4 and Table S1, which also shows that there were detectable but weaker effects on average infection risk). Induction of hydrolyzable tannins thus sharply reduced variability in infection risk in the field.
Our field experiment confirmed that induced hydrolyzable tannins alter the transmission of the gypsy moth baculovirus in the field, but the spatial scale of our experiment was much smaller than the scale of naturally occurring outbreaks. Additional support for our hypothesis, however, comes from laboratory experiments and field observations. In simultaneous laboratory experiments, induced defenses affected both physiological susceptibility and risk of exposure (SI Appendix, section 1.5, Tables S2 and S3, and Fig. S3), the two main components of overall infection risk (31). These experiments provide mechanisms by which induced defenses affected transmission in our field experiment, suggesting that the results of that experiment were not simply due to some unknown experimental artifact.
The effects of induction in our experiments also help to resolve a contradiction between a previous laboratory experiment on induced defenses in gypsy moths and field observations of baculovirus epizootics. In a laboratory experiment by Hunter and Schultz (24), average susceptibility declined modestly as a result of induction, as it did in our experiments (note that there was no consideration of changes in variability in susceptibility in Hunter and Schultz’s experiment). The data from their experiment therefore imply that virus mortality should decline with increasing host density, but virus mortality in naturally occurring gypsy moth populations instead increases with increasing host density (14).
Because we explicitly accounted for variability in infection risk, our results instead imply that virus mortality will increase with host density, for reasons that are explained by epidemiological theory. In our field experiment, the decline in variability in infection risk was much more dramatic than the decline in the average infection risk (SI Appendix, Table S1). Epidemiological theory has shown that declines in variability lead to higher cumulative infection rates in epizootics, because reduced variability means that there are fewer individuals with both a higher than average risk and a lower than average risk, but the reduction in the number of individuals with a lower than average risk has a disproportionate effect on the epizootic (33). The reduction in variability due to induction should therefore cause the cumulative infection rate to rise more rapidly with increasing host density. The results of our field experiment are thus consistent with both Hunter and Schultz’s experiment and with observations of virus mortality at large scales in nature.
Most importantly, the effects seen in our experiments predict both the occurrence of the subharmonic in gypsy moth outbreaks in oak–hickory forests and the disappearance of the subharmonic in oak–pine forests. To show this, we first extended a nonspatial natural-enemy model to allow for an induced defense. The resulting model shows that induction leads to cycles with a longer period and a larger amplitude, demonstrating that the increase in the severity of density-dependent virus mortality due to induction has a destabilizing effect (SI Appendix, section 2.2 and Fig. S4).
As in Bjornstad et al.’s (13) nonspatial model, our nonspatial model showed no subharmonic, and so we extended our model to include spatial variability in inducibility. We also included stochasticity in the insect’s reproductive rate, to reflect the effects of stochastic fluctuations in weather, which are believed to synchronize gypsy moth outbreaks (34). The output of the spatial model then matches the difference in dynamics in gypsy moth outbreaks between forest types. In model forests that are 43% inducible, time series of defoliation show alternating severe and mild outbreaks, as in oak–hickory forests, whereas in model forests that are only 15% inducible, time series of defoliation show only moderate outbreaks, as in oak–pine forests (Figs. 1 and 2). Reflecting these features of the time series, the corresponding model power spectra show peaks at periods that are close to the corresponding peaks in the data power spectra.
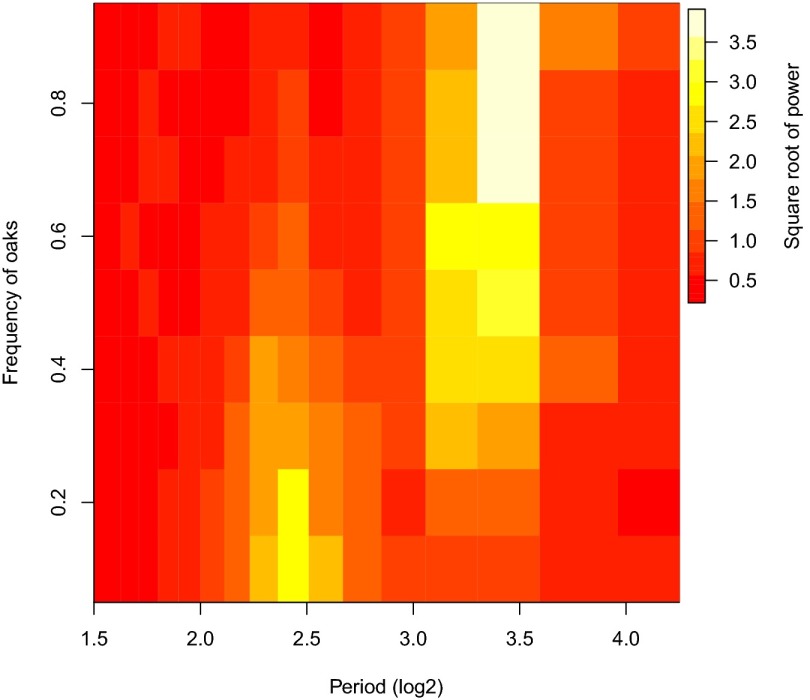
An important point is that because the model is stochastic, the model predictions necessarily vary between realizations or “runs.” We took this variability into account first of all by averaging model power spectra across realizations. Different time series, however, may give very similar power spectra (35), and so additional support for our argument is provided by the model’s ability to reproduce not just the data power spectra, but more specifically the alternation of mild and severe outbreaks in oak–hickory forests. Accordingly, it is important to also consider variability in this alternation, and so we examined a large number of additional realizations (SI Appendix, section 3.3 and Figs. S6–S10). In at least 50% of realizations of oak–hickory forests, the model shows at least two alternations of mild and severe outbreaks, meaning two each of severe and mild outbreaks in strict alternation, as seen in the data. Moreover, in almost every realization, there is at least one case in which a mild outbreak is followed by a severe outbreak, or vice versa. Meanwhile, in model oak–pine forests, alternation of severe and mild outbreaks never occurs (SI Appendix, Figs. S11–S15), and continuously increasing the frequency of inducible trees in the model leads to a gradual increase in the dominance of the longer period peak over the shorter period peak (Fig. 4). The model thus predicts that alternation of severe and mild outbreaks should occur frequently in oak–hickory forests, but that the alternation can be disrupted by stochasticity, whereas stochasticity never causes alternation to appear by chance in oak–pine forests (in SI Appendix, section 3.3 and Fig. S16, we discuss why the fit to the oak–hickory data varies across realizations). The lack of clear alternation in oak–hickory forests since 1990 (12) suggests that stochasticity can indeed interrupt the pattern of alternation in such forests, but the introduction of the fungal pathogen Entomophaga maimaiga in the late 1980s may also have played a role (6).
Fig. 4.
Effects of oak frequency on the power spectrum of the defoliation time series in the spatial model. The colors show the square root of the power of each period, such that dark red indicates the lowest power and white indicates the highest power. The figure thus shows that, at a low frequency of oaks, only short period cycles occur, whereas at a high frequency of oaks, only long period cycles occur. The relative importance of short-period and long-period cycles then gradually shifts as the frequency of oaks increases, so that both short-period and long-period cycles are represented in the power spectrum at intermediate frequencies of oaks.
Initially, we assumed that net rates of gypsy moth reproduction were as high on pines, hickories, and other nonoak genera as on oaks, because defoliation during outbreaks is often equally severe on trees in all three genera (16). In nature, gypsy moth larval survival is often reduced on nonoaks (36), but in SI Appendix, section 2.3 and Fig. S18, we show that allowing for lower survival on nonoaks, in the form of a lower net reproductive rate, has only a minor effect on our model results. On the other hand, the subharmonic in oak–hickory forests disappears if we assume that differences between host trees affect only net reproduction and not induced defenses (SI Appendix, Fig. S19). Any model of a phenomenon as complex as defoliator population cycles will inevitably provide only a rough approximation of nature. The robustness of our model results nevertheless suggests that differences in gypsy moth cycles between forest types are best explained by the effects of induced defenses on pathogen transmission.
Discussion
As we have described, the hypothesis that induced defenses alter natural enemy attack rates is not new, but previous work relied largely on laboratory data that have been of little use in explaining infection rates in the field (24, 26). Our work is instead directly based on field data, beginning with our field experiment, and our experimental data are consistent with patterns of virus infection in naturally occurring epizootics. Crucial additional support is also provided by differences in defoliation levels between forest types. Meanwhile, the lack of evidence that induced defenses affect other insects may be a consequence of the lack of large-scale variation in tree-species composition within forests attacked by those insects (11, 26), rather than a true lack of effect of induced defenses. Given enough experimental data with which to estimate parameters, however, our models could in principle be used to detect effects of induced defenses in defoliation data even in the absence of variability in forest type.
An important feature of our work is that it combines models and experiments. The spatial and temporal scale of our experiments was nevertheless much smaller than the temporal and spatial scales of the data to which we compare our model predictions. We therefore note that the model parameters that determine the dynamics of the induced defenses were first fit to the experimental data, but then were adjusted to give a better fit to the defoliation data (SI Appendix, section 2.3). The model output thus does not depend on the accuracy of our experimental measurements, and so our experimental data and the predictions of our spatial model serve as stand-alone arguments that nevertheless complement each other.
Variability in plant quality similarly modifies the effects of predation on population cycles of herbivorous mammals (37), suggesting that interactions between natural enemies and resources may play a general role in animal population cycles. Our work also shows that forest diversity can have unexpected effects on insect population dynamics, with important consequences for the use of baculoviruses as environmentally benign insecticides for controlling forest pests (4). Previous work implied that induced defenses would interfere with control by reducing average infection risk (24), but our results instead show that induced defenses can increase infection rates by reducing variability in infection risk, thereby improving control. Reforestation practices that include highly inducible trees may therefore produce forests that can be defended more easily with baculoviruses, helping to maintain forests as carbon sinks rather than as defoliated carbon sources (1).
Materials and Methods
Studies of baculovirus transmission have historically relied only on laboratory dose-response experiments, in which larvae are fed moderate doses of a virus solution, and larvae that do not consume the entire dose are discarded. Larvae in nature instead often consume very high doses, and they can sometimes detect and avoid infectious cadavers (38). Because of these differences, laboratory dose-response experiments often cannot be used to predict the effects of plant defenses on baculovirus infection rates in the field (23). We therefore instead carried out a field transmission experiment, in which larvae were allowed to feed freely on foliage contaminated with virus-infected cadavers in the field (we also carried out simultaneous dose-response and feeding experiments, see SI Appendix, section 1.5).
In our field experiment, we first induced hydrolyzable tannin concentrations in eight experimental red oaks, such that on each tree three branches were randomly assigned to a JA spray treatment, and three branches were assigned to the non-JA control spray (additional control branches on unsprayed trees were identical to control branches on sprayed trees, SI Appendix, section 1.1). To quantify changes in hydrolyzable tannin concentrations, we collected samples at budburst, and again 3 wks later, 24 h before the initially uninfected larvae in the experiment began feeding on the branches (SI Appendix, section 1.1).
Next, we placed virus-infected larvae on each branch (treatments: 0, 10, 40 larvae per 0.2 m2 of foliage), and we allowed the infected larvae to die before adding 25 initially uninfected larvae. The initially uninfected larvae fed for 7 d, a period short enough to ensure that none died due to infection. The initially uninfected larvae were then reared in individual cups of artificial diet in the laboratory to determine whether or not they had become infected.
To analyze our data, we used an epidemic model that has been shown to provide a good description of virus epizootics in gypsy moth populations (39). This model is a standard Susceptible-Exposed-Infected-Recovered (SEIR) model (40), extended to allow for variability in infection risk (41).
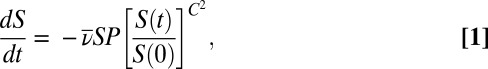 |
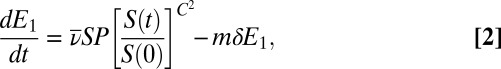 |
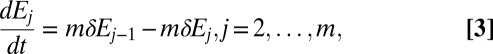 |
 |
Here S is the density of uninfected hosts, P is the density of infectious cadavers and 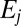 is the density of exposed hosts in class j. By including multiple exposed classes, the model allows for gamma distributed incubation times, with mean
is the density of exposed hosts in class j. By including multiple exposed classes, the model allows for gamma distributed incubation times, with mean 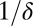 and variance
and variance 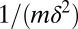 (40). Also,
(40). Also, 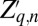 and C are the average and the coefficient of variation of the distribution of transmission rates ν (39), so that C measures variability in infection risk. When larvae reach the final exposed class, they die and become infectious cadavers P, which break down at rate μ.
and C are the average and the coefficient of variation of the distribution of transmission rates ν (39), so that C measures variability in infection risk. When larvae reach the final exposed class, they die and become infectious cadavers P, which break down at rate μ.
In our experiments, virus density is constant (38), so we can set 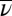 and solve Eq. 1 to produce an expression for the fraction infected during the experiment, i:
and solve Eq. 1 to produce an expression for the fraction infected during the experiment, i:
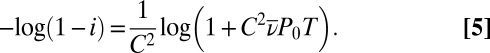 |
Here T is the length of the experiment and 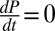 is the virus density. We then fit Eq. 5 to our data using maximum likelihood, and we used AICc to choose the version of the model that explained the data most parsimoniously, such that each version made different assumptions about the effects of induction on transmission (SI Appendix, section 1.4).
is the virus density. We then fit Eq. 5 to our data using maximum likelihood, and we used AICc to choose the version of the model that explained the data most parsimoniously, such that each version made different assumptions about the effects of induction on transmission (SI Appendix, section 1.4).
To explain our model of gypsy moth outbreaks, we note first that, like most outbreaking forest insects (42), gypsy moths have discrete generations and reproduce only once per year, and only larvae can become infected (23). Transmission thus ends before reproduction begins. Accordingly, to allow for multiple generations, we first use the epizootic model, Eqs. 1–4, to describe the within-generation baculovirus epizootic, and then we account for reproduction and other sources of mortality (6). The model is then:
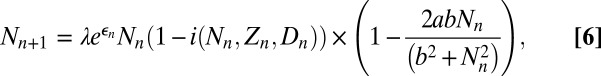 |
 |
Here 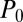 ,
, 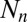 and
and 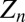 are the host and pathogen densities and the induced defense, respectively, in generation n. The insect reproductive rate is λ, and the fraction dying in the epidemic is
are the host and pathogen densities and the induced defense, respectively, in generation n. The insect reproductive rate is λ, and the fraction dying in the epidemic is 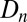 , as calculated using the SEIR model, Eqs. 1–4, integrated for 56 d, the approximate length of virus epizootics in gypsy moth populations (38). The normally distributed random variate
, as calculated using the SEIR model, Eqs. 1–4, integrated for 56 d, the approximate length of virus epizootics in gypsy moth populations (38). The normally distributed random variate 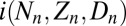 , which has mean 0 and standard deviation σ, allows for stochastic effects of weather, an important source of stochasticity in insect populations (43). The term
, which has mean 0 and standard deviation σ, allows for stochastic effects of weather, an important source of stochasticity in insect populations (43). The term 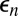 represents the fraction of insects surviving predation, as determined by a Type III functional response (6). The parameter ϕ is the overwintering impact of virus produced in generation n, including both survival and the relative susceptibility of hatchlings (38), while γ is the survival rate of virus produced in earlier generations. To allow for effects of the induced defense
represents the fraction of insects surviving predation, as determined by a Type III functional response (6). The parameter ϕ is the overwintering impact of virus produced in generation n, including both survival and the relative susceptibility of hatchlings (38), while γ is the survival rate of virus produced in earlier generations. To allow for effects of the induced defense 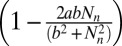 on virus transmission in generation n, we set the variability parameter in the epizootic Eqs. 1–4 to
on virus transmission in generation n, we set the variability parameter in the epizootic Eqs. 1–4 to 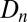 , where
, where 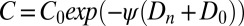 is the baseline variability and
is the baseline variability and 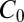 is the constitutive level of induced defenses, meaning the level reached in the absence of defoliation.
is the constitutive level of induced defenses, meaning the level reached in the absence of defoliation.
The induced hydrolyzable tannin concentration 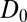 increases linearly with increasing insect density
increases linearly with increasing insect density 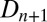 in the previous generation at rate α, to reflect the effects of defoliation. The tannin concentration is also a function of the previous generation’s value
in the previous generation at rate α, to reflect the effects of defoliation. The tannin concentration is also a function of the previous generation’s value 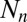 , which allows for the carryover effect that we observed in our experiments from one year to the next, with half-saturation constant β to reflect the constraints of plant physiology (44). Note that the effects of hydrolyzable tannins on transmission are much stronger than the effects of hydrolyzable tannins on host reproduction (22), and so here we follow previous authors in allowing for effects of tannins only on virus transmission (45).
, which allows for the carryover effect that we observed in our experiments from one year to the next, with half-saturation constant β to reflect the constraints of plant physiology (44). Note that the effects of hydrolyzable tannins on transmission are much stronger than the effects of hydrolyzable tannins on host reproduction (22), and so here we follow previous authors in allowing for effects of tannins only on virus transmission (45).
To extend the model to allow for spatial variability in forest composition, we combined the non-spatial model, Eqs. 6–8, with the spatial model of Abbott and Dwyer (46), which describes spatial gypsy moth dynamics as driven by a combination of the baculovirus and generalist predators. The Abbott and Dwyer model divides space into a grid, with dispersal between grid cells, which makes it easy to include stochastic variation in inducibility across space. Dispersal occurs through both ballooning and movement on automobiles (47), with the average dispersal distances determined from previous analyses of data on movement and spatial variability in gypsy moth-virus interactions (48, 49, and SI Appendix, section 2.3.1).
The spatial model is then:
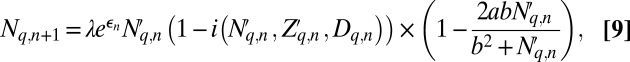 |
 |
Host density 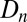 , cadaver density
, cadaver density 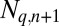 , and tannin content
, and tannin content 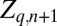 at location q in generation
at location q in generation 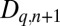 are thus dependent upon the post-dispersal densities of hosts
are thus dependent upon the post-dispersal densities of hosts 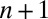 and cadavers
and cadavers 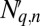 from the previous generation n.
from the previous generation n.
Supplementary Material
Acknowledgments
J. M. Bergelson, A. F. Hunter, and W. F. Morris made many helpful comments on the manuscript. Discussions between G. Dwyer and K. Haynes began as part of the Forest Insects Working Group at the National Institute for Mathematical and Biological Synthesis. Our work was supported by National Institutes of Health Grant R01GM096655.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1300759110/-/DCSupplemental.
References
- 1.Slaney GL, Lantz VA, MacLean DA. The economics of carbon sequestration through pest management: Application to forested landbases in New Brunswick and Saskatchewan, Canada. For Policy Econ. 2009;11(7):525–534. [Google Scholar]
- 2.Varley GC, Gradwell GR, Hassell MP. Insect Population Ecology: An Analytical Approach. Oxford, UK: Blackwell Scientific; 1973. [Google Scholar]
- 3.Liebhold A, Kamata N. Introduction—Are population cycles and spatial synchrony a universal characteristic of forest insect populations? Popul Ecol. 2000;42(3):205–209. [Google Scholar]
- 4.Moreau G, Lucarotti CJ. A brief review of the past use of baculoviruses for the management of eruptive forest defoliators and recent developments on a sawfly virus in Canada. Forest Chronicle. 2007;83(1):105–112. [Google Scholar]
- 5.Elkinton JS, et al. Interactions among gypsy moths, white-footed mice, and acorns. Ecology. 1996;77(8):2332–2342. [Google Scholar]
- 6.Dwyer G, Dushoff J, Yee SH. The combined effects of pathogens and predators on insect outbreaks. Nature. 2004;430(6997):341–345. doi: 10.1038/nature02569. [DOI] [PubMed] [Google Scholar]
- 7.Nykӓnen H, Koricheva J. Damage-induced changes in woody plants and their effects on insect herbivore performance: A meta-analysis. Oikos. 2004;104(2):247–268. [Google Scholar]
- 8.Barbehenn RV, Constabel CP. Tannins in plant-herbivore interactions. Phytochemistry. 2011;72(13):1551–1565. doi: 10.1016/j.phytochem.2011.01.040. [DOI] [PubMed] [Google Scholar]
- 9.Haukioja E. Plant defenses and population fluctuations of forest defoliators: Mechanism-based scenarios. Annales Zoologici Fennici. 2005;42(4):313–325. [Google Scholar]
- 10.Edelstein-Keshet L, Rausher MD. The effects of inducible plant defenses on herbivore populations. I. Mobile herbivores in continuous time. American Naturalist. 1989;133(6):787–810. [Google Scholar]
- 11.Turchin P, et al. Dynamical effects of plant quality and parasitism on population cycles of larch budmoth. Ecology. 2003;84(5):1207–1214. [Google Scholar]
- 12.Johnson DM, Liebhold AM, Bjornstad ON. Geographic variation in the periodicity of gypsy moth outbreaks. Ecography. 2006;29(3):367–384. [Google Scholar]
- 13.Bjornstad ON, Robinet C, Liebhold AM. Geographic variation in North American gypsy moth cycles: Subharmonics, generalist predators, and spatial coupling. Ecology. 2010;91(1):106–118. doi: 10.1890/08-1246.1. [DOI] [PubMed] [Google Scholar]
- 14.Woods SA, Elkinton JS. Bimodal patterns of mortality from nuclear polyhedrosis-virus in gypsy-moth (Lymantria-dispar) populations. J Invertebr Pathol. 1987;50:151–157. [Google Scholar]
- 15.Dwyer G, Elkinton JS. Host dispersal and the spatial spread of insect pathogens. Ecology. 1995;76(4):1262–1275. [Google Scholar]
- 16.Campbell RW, Sloan RJ. Forest stand responses to defoliation by gypsy moth. Forest Science. 1977;23(M19):1–34. [Google Scholar]
- 17.Schultz JC, Baldwin IT. Oak leaf quality declines in response to defoliation by gypsy moth larvae. Science. 1982;217(4555):149–150. doi: 10.1126/science.217.4555.149. [DOI] [PubMed] [Google Scholar]
- 18.Hunter MD, Schultz JC. Fertilization mitigates chemical induction and herbivore responses within damaged oak trees. Ecology. 1995;76(4):1226–1232. [Google Scholar]
- 19.Wold EN, Marquis RJ. Induced defense in white oak: Effects on herbivores and consequences for the plant. Ecology. 1997;78(5):1356–1369. [Google Scholar]
- 20.Hagerman AE. Extraction of tannins from fresh and preserved leaves. J Chem Ecol. 1988;14(2):453–461. doi: 10.1007/BF01013897. [DOI] [PubMed] [Google Scholar]
- 21.Wilken LO, Cosgrove FP. Phytochemical investigation of Carya illinoensis L. J Pharm Sci. 1964;53(4):364–368. doi: 10.1002/jps.2600530403. [DOI] [PubMed] [Google Scholar]
- 22.Schultz JC, Foster MA, Montgomery ME. Host plant-mediated impacts of a baculovirus on gypsy moth populations. In: Watt AD, Leather SR, Hunter MD, Kidd NAC, editors. Population Dynamics of Forest Insects. Andover, UK: Intercept Ltd; 1990. pp. 621–637. [Google Scholar]
- 23.Cory JS, Hoover K. Plant-mediated effects in insect-pathogen interactions. Trends Ecol Evol. 2006;21(5):278–286. doi: 10.1016/j.tree.2006.02.005. [DOI] [PubMed] [Google Scholar]
- 24.Hunter MD, Schultz JC. Induced plant defenses breached—Phytochemical induction protects an herbivore from disease. Oecologia. 1993;94(2):195–203. doi: 10.1007/BF00341317. [DOI] [PubMed] [Google Scholar]
- 25.Kapari L, Haukioja E, Rantala MJ, Ruuhola T. Defoliating insect immune defense interacts with induced plant defense during a population outbreak. Ecology. 2006;87(2):291–296. doi: 10.1890/05-0362. [DOI] [PubMed] [Google Scholar]
- 26.Klemola N, Klemola T, Markus MJ, Ruuhola T. Natural host-plant quality affects immune defence of an insect herbivore. Entomologia Experimentalis et Applicata. 2007;123(2):167–176. [Google Scholar]
- 27.D’Amico V, Elkinton JS, Dwyer G, Willis RB, Montgomery ME. Foliage damage does not affect within-season transmission of an insect virus. Ecology. 1998;79(3):1104–1110. [Google Scholar]
- 28.Baldwin IT. Jasmonate-induced responses are costly but benefit plants under attack in native populations. Proc Natl Acad Sci USA. 1998;95(14):8113–8118. doi: 10.1073/pnas.95.14.8113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Allison SD, Schultz JC. Differential activity of peroxidase isozymes in response to wounding, gypsy moth, and plant hormones in northern red oak (Quercus rubra L.) J Chem Ecol. 2004;30(7):1363–1379. doi: 10.1023/b:joec.0000037745.66972.3e. [DOI] [PubMed] [Google Scholar]
- 30.Burnham KP, Anderson DR. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. New York: Springer; 2002. [Google Scholar]
- 31.Dwyer G, Firestone J, Stevens TE. Should models of disease dynamics in herbivorous insects include the effects of variability in host-plant foliage quality? Am Nat. 2005;165(1):16–31. doi: 10.1086/426603. [DOI] [PubMed] [Google Scholar]
- 32.Elderd B, Dushoff J, Dwyer G. Does natural selection on disease susceptibility play a role in insect outbreaks? Am Nat. 2008;172(6):829–842. doi: 10.1086/592403. [DOI] [PubMed] [Google Scholar]
- 33.Anderson RM, May RM. Infectious Diseases of Humans: Dynamics and Control. Oxford: Oxford Univ Press; 1991. [Google Scholar]
- 34.Peltonen M, Liebhold AM, Bjornstad ON, Williams DW. Spatial synchrony in forest insect outbreaks: Roles of regional stochasticity and dispersal. Ecology. 2002;83:3120–3129. [Google Scholar]
- 35. Chatfield C The Analysis of Time Series, 5th Ed (Chapman & Hall, Boca Raton, FL)
- 36.Barbosa P, Krischik VA. Influence of alkaloids on the feeding preference of eastern deciduous forest trees by the gypsy moth, Lymantria dispar. Am Nat. 1987;130(1):53–69. [Google Scholar]
- 37.Krebs CJ, et al. Impact of food and predation on the snowshoe hare cycle. Science. 1995;269(5227):1112–1115. doi: 10.1126/science.269.5227.1112. [DOI] [PubMed] [Google Scholar]
- 38.Fuller E, Elderd BD, Dwyer G. Pathogen persistence in the environment and insect-baculovirus interactions: Disease-density thresholds, epidemic burnout, and insect outbreaks. Am Nat. 2012;179(3):E70–E96. doi: 10.1086/664488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dwyer G, Elkinton JS, Buonaccorsi JP. Host heterogeneity in susceptibility and disease dynamics: Tests of a mathematical model. Am Nat. 1997;150(6):685–707. doi: 10.1086/286089. [DOI] [PubMed] [Google Scholar]
- 40.Keeling MJ, Rohani P. Modeling Infectious Diseases in Humans and Animals. Princeton, NJ: Princeton Univ Press; 2007. [Google Scholar]
- 41.Dwyer G, Dushoff J, Elkinton JS, Levin SA. Pathogen-driven outbreaks in forest defoliators revisited: Building models from experimental data. Am Nat. 2000;156(2):105–120. doi: 10.1086/303379. [DOI] [PubMed] [Google Scholar]
- 42.Hunter AF. Ecology, life history, and phylogeny of outbreak and non-outbreak species. In: Cappuccino N, Price PW, editors. Population Dynamics: New Approaches and Synthesis. Amsterdam: Academic; 1995. pp. 41–64. [Google Scholar]
- 43.Williams DW, Liebhold AM. Influence of weather on the synchrony of gypsy moth (Lepidoptera:Lymantriidae) outbreaks in New England. Environ Entomol. 1995;24(5):987–995. [Google Scholar]
- 44.Karban R, Baldwin IT. Induced Responses to Herbivory. Chicago: Univ of Chicago Press; 1997. [Google Scholar]
- 45.Foster MA, Schultz JC, Hunter MD. Modelling gypsy moth-virus-leaf chemistry interactions: Implications of plant quality for pest and pathogen dynamics. J Anim Ecol. 1992;61(3):509–520. [Google Scholar]
- 46.Abbott KC, Dwyer G. Using mechanistic models to understand synchrony in forest insect populations: The North American gypsy moth as a case study. Am Nat. 2008;172(5):613–624. doi: 10.1086/591679. [DOI] [PubMed] [Google Scholar]
- 47.Liebhold AM, Halverson JA, Elmes GA. Gypsy-moth invasion in North America—A quantitative analysis. Journal of Biogeography. 1992;19(5):513–520. [Google Scholar]
- 48.Hunter AF, Elkinton JS. Effects of synchrony with host plant on populations of a spring-feeding Lepidopteran. Ecology. 2000;81(5):1248–1261. [Google Scholar]
- 49. Fujita PA (2007) Combining Models with Empirical Data to Examine Dispersal Mechanisms in the Gypsy Moth-Nucleopolyhedrovirus Host-Pathogen System. PhD dissertation (Univ of Chicago, Chicago)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.