Confounding control in a non-experimental study of STAR*D data: Logistic regression balanced covariates better than boosted CART

Abstract

Purpose

Propensity scores, a powerful bias-reduction tool, can balance treatment groups on measured covariates in non-experimental studies. We demonstrate the use of multiple propensity score estimation methods to optimize covariate balance.

Methods

We used secondary data from 1,292 adults with non-psychotic major depressive disorder in the Sequenced Treatment Alternatives to Relieve Depression trial (2001–2004). After initial citalopram treatment failed, patient preference influenced assignment to medication augmentation (n=565) or switch (n=727). To reduce selection bias, we used boosted classification and regression trees (BCART) and logistic regression iteratively to identify two potentially optimal propensity scores. We assessed and compared covariate balance.

Results

After iterative selection of interaction terms to minimize imbalance, logistic regression yielded better balance than BCART (average standardized absolute mean difference across 47 covariates: 0.03 vs. 0.08, matching; 0.02 vs. 0.05, weighting).

Conclusions

Comparing multiple propensity score estimates is a pragmatic way to optimize balance. Logistic regression remains valuable for this purpose. Simulation studies are needed to compare propensity score models under varying conditions. Such studies should consider more flexible estimation methods, such as logistic models with automated selection of interactions or hybrid models using main effects logistic regression instead of a constant log-odds as the initial model for BCART.

Introduction

In non-experimental studies, propensity scores (PSs) are used increasingly to address potential selection bias and confounding [1–6]. The PS is a person’s probability of receiving a particular treatment, given pre-treatment characteristics. By measuring important confounders, including them in a PS model, and balancing treatment groups on the PS, analysts can achieve balance on measured pre-treatment characteristics, and therefore a treatment effect estimate (relative risk or risk difference) that is unbiased under the assumption of no unmeasured confounding [7–11].

The research literature describes several PS estimation methods [2, 5, 6, 8, 12–15]. Logistic regression is the conventional choice, but non-parametric methods such as classification and regression trees (CART) have potential advantages: they automatically incorporate interactions, model non-linear associations easily, and may yield more accurate estimates when modeling complex relations [14]. However, studies comparing CART with logistic regression have had mixed results [14, 15]. Boosted CART (BCART) may compare more favorably to logistic regression. BCART uses machine learning to combine multiple simple classification trees, improving prediction [16, 17], yielding more stable estimates when there are many covariates [16], and reducing vulnerability to overfitting [15, 18]. BCART may also be less sensitive than logistic regression to collinearity [16].

Theoretical work and simulation studies have evaluated different PS estimation methods [14, 17] and have quantified the bias reduction due to PS matching [13, 19–21] under certain conditions. However, studies have not fully described which PS estimation methods minimize bias under which circumstances. Further, applied researchers cannot detect bias directly and therefore must seek instead to optimize covariate balance [22]. In this report, we use an empirical example from the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) trial [23] to demonstrate how covariate balance can be optimized under real-world conditions using multiple PS estimation methods. The STAR*D trial provides an appropriate example because it was a large effectiveness study with clinically relevant comparisons that were not randomized. Using the STAR*D data, we optimized between-group covariate balance with both logistic regression and BCART. Comparing these methods not only made substantive analyses possible but also generated questions and hypotheses for future simulation studies.

Methods

Sample and data

The original STAR*D study (2001–2004) enrolled 4,041 outpatients with non-psychotic major depressive disorder [23, 24]. Of these, 1,439 participants discontinued initial citalopram monotherapy because of side effects, lack of recovery after at least 9 weeks, or individual choice, and entered second-line treatment. Second-line treatment options included four treatment strategies: augmenting citalopram with another antidepressant agent (bupropion SR or buspirone), switching to an alternative antidepressant (bupropion SR, sertraline, or venlafaxine XR), augmenting with cognitive therapy, or switching to cognitive therapy. The original study’s equipoise randomization scheme allowed each participant to select acceptable treatment strategies; patients were randomized to a treatment within the categories they had selected. Using a public-release dataset available through the National Institute of Mental Health, the current study examines data from the 1,292 participants who received either medication augmentation (n=565) or an antidepressant switch (n=727).

The University’s Biomedical Institutional Review Board determined that the current study did not require its approval.

Measures

Our primary balance measure was the average standardized absolute mean (ASAM) difference across 47 covariates that we selected based on empirical evidence and theory. ASAM difference was calculated by subtracting each of the 47 comparison group means from the corresponding treatment group mean, taking the absolute value of each difference, dividing each absolute difference by the pooled standard deviation of the covariate, and then computing the mean of the standardized absolute differences [16, 25].

As auxiliary balance measures, we used statistics developed by Rubin [26]: B, the absolute standardized mean difference on the PS logit; R, the variance ratio (augment/switch) for the PS logit; the percentage of variance ratios on the 47 covariates that were in the severe range (augment variance divided by switch variance <0.5 or >2); and the percentage of variance ratios on covariates that were in the moderate range (≥0.5 but <.8, or >1.25 but ≤2). Variance ratios were based on residual variance, after regressing each covariate on the PS logit in a linear or logistic model. To calculate PS-weighted statistics, we used means x̅_w = (1 / Σ_i w_i) × Σ_i w_ix_i and variances s²_w = (1 / ((Σ_i w_i) − 1)) × Σ_i (w_i(x_i − x̅_w)²), where w_i is the weight corresponding to observation i and x_i is the covariate value or PS logit for observation i. Good covariate balance is indicated by an R value near 1 and values of the other statistics near zero.

Statistical analysis

The original STAR*D design allowed randomized comparisons of treatment options within, but not between, the augment and switch arms. We wished to estimate the effect of medication augmentation versus switching in the population of patients receiving augmentation. Because patient preference influenced assignment to these treatment categories, we sought to balance the groups on pre-treatment characteristics using PSs.

After addressing missingness, we used BCART and logistic regression in iterative procedures to identify two potentially optimal PSs. In both matched and weighted samples, we compared the BCART and logistic PSs to determine which method yielded better covariate balance and therefore would better support a comparison of medication augmentation with medication switching. We also assessed the sensitivity of treatment effect estimates (described below) to the choice of PS estimation method.

Missing data imputation

Although 82% of observations had at least one missing value, only 5% of data values were missing, making our data well-suited for imputation to avoid a biased complete-case analysis [27–30]. Assuming missingness at random, we employed the expectation-maximization method in SAS PROC MI (SAS Institute, Cary, NC), including 95 relevant variables in the imputation model and using pre-imputation diagnostics to avoid multicollinearity.

Propensity score estimation

For the logistic models we used SAS version 9.2. For PS estimation and balance checking, covariates (including interactions) should be selected based on theory and prior evidence about their relations with the outcome [31], as they were in the current study. However, Rosenbaum and Rubin recommended adding interaction and quadratic terms to optimize balance on the selected set of covariates [8]. Therefore, we employed a forward stepwise procedure to add 30 product terms to the logistic model, out of 1,101 candidates. (Quadratic terms for the 27 dichotomous covariates were excluded.) We chose 30 as the number of interaction terms because we believed that 30 would exceed the number of interaction terms that most analysts would add manually and that 30 terms would address residual imbalance sufficiently while keeping computational burden reasonable. At each step we selected the model that minimized covariate imbalance (weighted ASAM difference, described below). We automated this procedure because an automated approach can optimize balance [16] and provides a meaningful comparison with the inherently automated BCART model. Further, this approach allows the inclusion of interaction terms that improve covariate balance but might not be obvious choices for a researcher.

The BCART model was created using Ridgeway’s “gbm” package for R software, which creates a non-linear model for the log-odds of treatment assignment, starting with the constant log-odds calculated for the whole sample and iteratively improving the model by adding simple regression trees [32, 33]. Each regression tree is created by identifying an optimal combination of covariate cutpoints to predict the residuals from the previous iteration. For example, a two-level tree might first split the sample into two age groups and then split the lower age group based on a cutpoint for number of weeks of first-line treatment. The final model is the sum of the constant log-odds of treatment assignment and the incremental adjustments contributed by the series of regression trees. We specified a maximum tree depth of 2 (i.e., allowed only main effects and 2-way interactions). Based on recommendations by McCaffrey and colleagues [16], we set the shrinkage parameter to 0.0005 and used a 50% subsample of the data to fit each tree. We specified a maximum of 20,000 iterations and stopped the algorithm when weighted ASAM difference (described in the following paragraph) was minimized.

Propensity score implementation

To create the matched sample we used a 5-to-1 digit PS matching algorithm [34], which made 5 passes through the augment group in random order, starting with a caliper of ±0.000005 and widening the caliper by a factor of 10 after each pass, ending with ±0.05. During each pass, one-to-one caliper matching was performed without replacement, considering potential matches in random order. When assumptions are met, the resulting matched sample can be used to estimate the treatment effect in the treated [7, 35, 36]. To allow the same type of estimates based on weighting, we assigned a weight of 1 to each treated (augment) observation and a weight of PS / (1 − PS) to each untreated (switch) observation [16, 37]. Because matching is resource-intensive, we used these weights to calculate ASAM difference after each iteration of the logistic and BCART models.

Sensitivity of treatment effect estimates to propensity score estimation methods

We used SAS procedures FREQ and SURVEYFREQ to estimate the effect of treatment on depression remission (as measured by Quick Inventory of Depression Symptomatology-Self Report [QIDS-SR₁₆] scores after second-line treatment). We assessed the sensitivity of the resulting risk ratios (RRs) to PS estimation method.

Results

The first 6 rows of Table 1 summarize between-group balance before propensity scoring and after using each combination of PS estimation and implementation methods. The imbalance before propensity scoring is evident in the ASAM difference of 0.20 standard deviations, B values (i.e., standardized mean differences on the PS logit) near 2, R values in or near the severe range, and the 21% of covariate variance ratios in the moderate-to-severe range.

Table 1.

Covariate balance by propensity score estimation and implementation method

Estimation Method	Application Method	ASAM Difference	B*	R*	% Severe Variance Ratio†	% Moderate Variance Ratio†
BCART	Before Implementation	0.20	1.98	0.52	2.10	19.10
BCART	Matching	0.08	0.00	0.98	4.30	19.10
BCART	Weighting	0.05	0.41	0.72	0.00	8.50
Logistic	Before Implementation	0.20	1.68	0.28	2.10	19.10
Logistic	Matching	0.03	0.01	0.98	0.00	4.30
Logistic	Weighting	0.02	0.04	1.06	0.00	8.50
Logistic Without Interactions	Before Implementation	0.20	1.67	0.38	2.10	19.10
Logistic Without Interactions	Matching	0.04	0.01	0.98	0.00	6.40
Logistic Without Interactions	Weighting	0.06	−0.12	0.82	0.00	10.60

ASAM difference = average standardized absolute mean difference across covariates; B = standardized difference between treatment conditions on mean propensity score logit; BCART = boosted classification and regression trees; R = variance ratio (treatment/comparison) for propensity score logit

^*B and R vary between estimation methods even before application because they are conditioned on the estimated propensity score.

^†Severe range is <.5 or >2; moderate range is >=.5 but <.8, or >1.25 but <=2. Covariates are conditioned on the propensity score logit before variance ratios are calculated (26).

Every permutation of propensity scoring methods improved covariate balance. However, using weights to apply the BCART PS resulted in relatively poor balance according to the B statistic and moderately severe imbalance according to the R statistic. Regardless of PS implementation method (matching or weighting), the balance statistics obtained under the logistic model were equal or superior to those obtained under the BCART model. In a sensitivity analysis using a main effects logistic model, this pattern generally persisted (last 3 rows of Table 1), though the results for weighting were mixed. Compared with BCART, logistic regression resulted in a lower c-statistic (i.e., area under the receiver operating characteristic curve [38]; 0.88 vs. 0.90) and a larger matched sample (n=538 vs. 470).

Table 2 reports balance on selected characteristics before and after implementing the logistic PS. Before propensity scoring, the augment and switch groups resembled each other closely on sociodemographic variables (e.g., age 41.6 [12.7] and 42.4 [12.8] respectively) and somewhat closely on depression history variables (e.g., number of lifetime major depressive episodes 5.3 [8.0] and 6.4 [10.3] respectively) but differed markedly on characteristics at the end of first-line treatment (e.g., treatment duration 11.9 [2.9] vs. 8.0 [4.2] weeks; citalopram dose 55.1 [10.9] vs. 41.5 [17.7] mg/day; QIDS-SR₁₆ depressive severity 11.4 [4.9] vs. 13.2 [4.9]; percentage discontinuing first-line treatment due to side effects 10.2% vs. 62.7%). After PS implementation, minimal differences remained.

Table 2.

Participant characteristics before and after implementing logistic propensity scores, United States, 2001–2004

	Pre-Propensity Score		After Propensity Score Matching		After Propensity Score Weighting
	Augment N = 565	Switch N = 727	Augment N = 269	Switch N = 269	Augment N = 565	Switch N = 727
Age (yr)	41.6 (12.7)	42.4 (12.8)	42.0 (12.6)	42.6 (12.8)	41.6 (12.7)	40.9 (13.2)
Female sex (%)	58.8	58.7	58.0	59.1	58.8	61.1
Age at first major depressive episode (yr)	25.1 (14.0)	24.9 (13.9)	25.4 (14.2)	25.7 (14.6)	25.1 (14.0)	24.6 (14.2)
No. of major depressive episodes	5.3 (8.0)	6.4 (10.3)	6.4 (9.6)	6.1 (9.5)	5.3 (8.0)	5.3 (8.0)
Duration of first-line treatment (wk)	11.9 (2.9)	8.0 (4.2)	10.8 (3.2)	11.0 (2.8)	11.9 (2.9)	11.9 (3.0)
Citalopram dose during first-line treatment (mg/day)	55.1 (10.9)	41.5 (17.7)	53.1 (12.7)	53.1 (12.4)	55.1 (10.9)	54.0 (11.3)
QIDS-SR16 score at end of first-line treatment	11.4 (4.9)	13.2 (4.9)	12.5 (5.1)	12.5 (4.8)	11.4 (4.9)	11.5 (4.7)
Exited first-line treatment due to side effects (%)	10.2	62.7	19.0	19.9	10.2	10.6

QIDS-SR₁₆ = the 16-item Quick Inventory of Depressive Symptomatology, Self-Report (scores can range from 0 to 27; higher scores indicate increased severity of depressive symptoms)

Statistics reported are Mean (SD) unless otherwise indicated.

The crude RR for remission favored augmentation (RR: 1.41, 95% confidence interval [CI]: 1.19 to 1.67). In the PS-matched sample, treatment effect estimates were identical between PS estimation methods (Table 3), but in the weighted sample, the logistic PSs resulted in a 3% larger treatment effect estimate (ratio 1.28/1.24=1.03).

Table 3.

Treatment effect estimates for augmentation versus switching by propensity score estimation and implementation method

	Risk Ratio (95% CI)
Estimation Method	Matched Sample	Weighted Sample
BCART	1.00 (0.73, 1.37)	1.24 (0.94, 1.65)
Logistic	1.00 (0.75, 1.34)	1.28 (0.97, 1.69)

BCART = boosted classification and regression trees; CI = confidence interval. Crude risk ratio was 1.41 (95% CI: 1.19 to 1.67).

To explore whether the differences in residual imbalance between BCART and logistic regression resulted from grossly different treatment of covariates in the two estimation models, we described the BCART model in more detail and compared the balance results for individual covariates. Of the 19,002 trees included in the final model, 999 (5.3%) were “main effect” trees with splits on only one variable. Although all 47 covariates were used in the BCART model, only 18 (38.3%) were used in main effect trees. The gbm package reports relative influence, a measure of the reduction in sum of squared error attributable to each covariate [32, 39], normalized to sum to 100. Relative influence ranged from 0.02 to 45.7 with a median of 0.34 (mean, 2.13; standard deviation, 6.85), indicating that some covariates influenced the BCART model more strongly than others. Although the covariates used in main effect trees accounted for 94.2% of the total reduction in sum of squared error, the main effect trees themselves accounted for only 2.3%. Compared with logistic regression, BCART achieved a very similar pattern of results across the 47 covariates (r=.98 for both absolute and relative changes in ASAM difference with matching, r=.99 for absolute and relative changes with weighting). Absolute change in ASAM difference using the BCART PSs was correlated with relative influence in the BCART model (r=−0.70 and r=−0.72 for matching and weighting respectively) and also with the proportion of trees in which each covariate was included at level 1 (r=−0.76 and r=−0.78 respectively) (P<.0001).

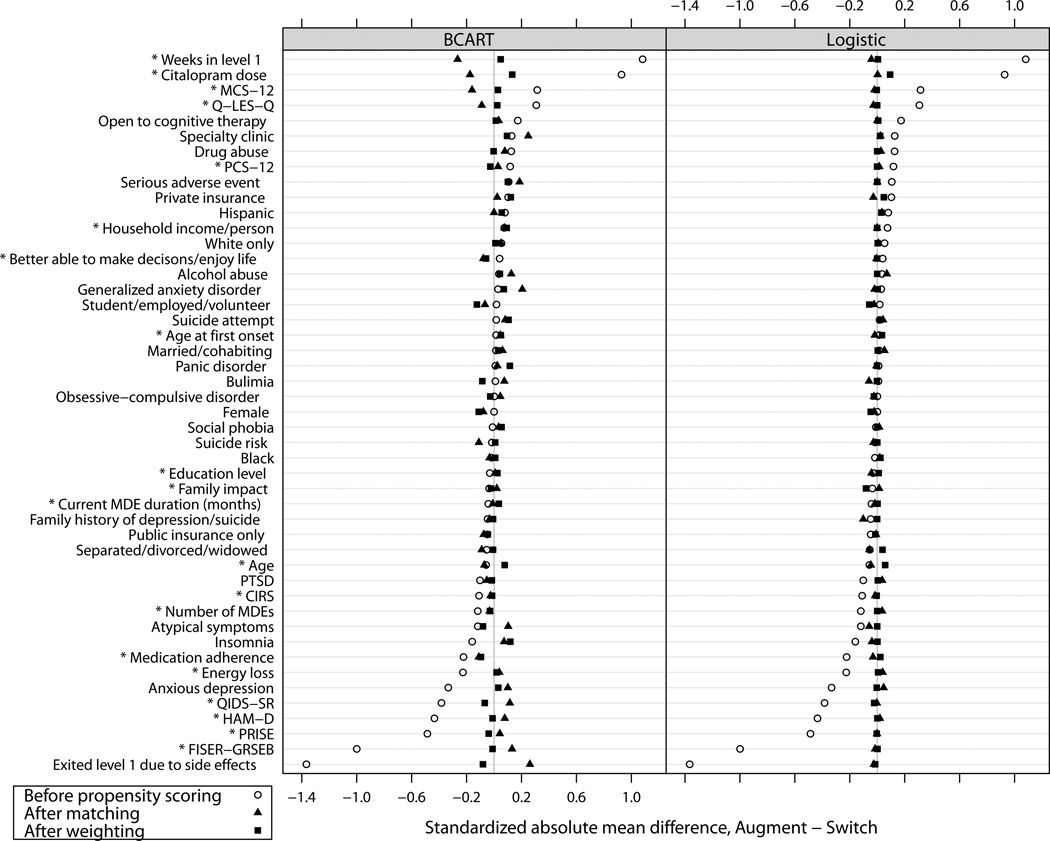
Figure 1 shows the standardized differences on individual covariates before and after PS implementation. Despite the similarity between the BCART and logistic PSs in patterns of absolute and relative change on individual covariates, generally the PSs from BCART resulted in slightly greater residual imbalance. For the covariates that had the largest imbalances before propensity scoring, matching on the BCART PSs appeared to result in over-correction (i.e., slight imbalance in the opposite direction). We examined dichotomous and continuous covariates separately (the latter are marked with asterisks in Figure 1). Although the covariates with the largest initial imbalances tended to be continuous, covariate type did not appear to explain the differences between the BCART results and the logistic regression results.

Figure 1. Balance on individual covariates before and after propensity score implementation.

* Continuous (versus dichotomous) covariate.

BCART=boosted classification and regression trees; CIRS=Cumulative Illness Rating Scale; FISER-GRSEB=Frequency and Intensity of Side Effects Rating/Global Rating of Side Effects Burden; HAM-D=Hamilton Depression Scale; MCS-12=Mental Component Summary (of the SF-12 Short-Form Health Survey); PCS-12=Physical Component Summary (of the SF-12 Short-Form Health Survey); PRISE=Patient-Rated Inventory of Side Effects; PTSD=post-traumatic stress disorder; QIDS-SR=Quick Inventory of Depressive Symptomatology-Self Report; Q-LES-Q= Quality of Life Enjoyment and Satisfaction Questionnaire

Discussion

We examined the effects of PS estimation methods on covariate balance in order to select a PS model for treatment effect estimation. In our STAR*D subsample, logistic regression provided better balance than BCART regardless of the PS implementation method used (matching or weighting). Logistic regression also resulted in a larger matched sample and therefore a more efficient matched comparison.

The better balance results from the logistic model were surprising given the perceived flexibility of BCART models. However, in a simulation study, Lee and colleagues found that in most scenarios main effects logistic regression yielded better covariate balance (i.e., lower ASAM differences) than BCART, on average [17]. Our findings are consistent with those simulation results. Importantly, Lee and colleagues also observed that main effects logistic regression yielded a skewed distribution of ASAM differences, in which outliers had large residual imbalance. Further, in their study, BCART generally resulted in similar average levels of balance with a more symmetric distribution, lower bias, lower standard errors, and higher 95% CI coverage. Their findings called into question the use of main effects logistic regression to estimate PSs and the use of ASAM difference as the sole measure of covariate balance. They noted that logistic regression might yield better results with more model calibration and/or a different measure of covariate balance. Our logistic model included multiple interaction terms designed to reduce residual imbalance, and we assessed balance using four measures other than ASAM difference.

It occurred to us that our findings might be explained in part by the different handling of main effects and interactions in the two methods. BCART automatically incorporated interactions, but not necessarily main effects or even all of the covariates. The logistic model, on the other hand, included all main effects by default, as well as 30 selected product terms. As it turned out, BCART put relatively little weight on main effects. However, by using key variables in many trees, BCART generated a pattern of balance improvements on individual covariates that was similar to the pattern generated by the logistic regression procedure. Despite the similar patterns of results, BCART generally resulted in slightly greater residual imbalance on individual covariates. On average, the differences in residual imbalance were small.

The stepwise procedure we used to select interactions for the logistic model was more complicated than the manual procedures that might typically be used for logistic PS models. Interestingly, when we ran the logistic model without interactions as a sensitivity analysis, it was inferior to the full logistic model but generally equivalent to or slightly better than the BCART model in terms of covariate balance.

Despite the better covariate balance achieved by logistic regression as compared with BCART, our treatment effect estimates were not sensitive to PS estimation method. Possibly the difference in balance (.03 to .05 standard deviations depending on implementation method) was too small to have a meaningful impact. Alternatively, the additional imbalance associated with BCART may have involved covariates unrelated to depression remission (unlikely given the careful selection of covariates) or covariates with offsetting effects on remission. The weighted treatment effect estimates did differ from the matched estimates, because there was some treatment effect heterogeneity and these two samples represented different populations. Even though we found little difference between PS estimation methods in treatment effect estimates, optimizing balance remains important because even a small imbalance on a strong risk factor can bias treatment effect estimates substantially.

This study is subject to certain limitations. First, it is based on a single empirical sample, so its primary contributions are demonstrating a pragmatic approach to PS estimation and identifying questions (below) for future simulation studies, rather than establishing differences among methods. Second, our selection of balance statistics was somewhat arbitrary, as standards for assessing balance have not yet been established. We addressed this limitation by using several balance statistics with face validity. In fact, we obtained similar results with 3 measures not reported here: ASAM difference with an arcsine transformation for dummy variables; ASAM difference with each covariate weighted in proportion to its association with the outcome; and distribution of the percent change in the treatment effect estimate after additionally adjusting for each covariate, one at a time, in the analysis model (a measure of residual confounding) [40]. Third, we included an arbitrary degree of flexibility in the logistic regression approach. We could have included more or fewer interaction terms, greater interaction depth, or splines. We anticipated that 30 product terms would suffice to address the residual imbalance associated with the main effects model. Fourth, and similarly, in the BCART procedure we allowed only main effects and two-way interactions. Some authors have recommended allowing higher-level interactions; for example, McCaffrey and colleagues recommended allowing up to four-way interactions [16]. However, when we did so (not shown), it did not improve covariate balance compared with our primary BCART model, based on ASAM difference, the B and R statistics, and variance ratios on individual covariates. Fifth, although careful covariate selection and balance optimization lead to better control for measured confounders, we were unable to measure bias in treatment effect estimates because the true treatment effect is unknown. ASAM difference has been shown to be only moderately correlated with bias under a variety of data generating models [17]. Although we employed a variety of balance measures, these measures may be imperfect proxies for bias. Finally, we imputed missing values under the plausible assumption of missingness at random. In settings where this assumption is implausible, more sophisticated methods for imputation should be considered [41].

Logistic regression may not always yield better covariate balance than BCART. Future studies should use both simulated and empirical data to explore further why and under what circumstances this is the case. Because the two methods handle main effects and interactions differently, their relative performance may depend on conditions such as covariate distributions, the functional forms of relations between covariates and treatment (or outcome), and the presence or absence of interactions in the true treatment or outcome model. Along with the main effects logistic regression used in previous simulations [14, 17], it would be worth testing more complex models such as the automated model presented here, or perhaps a hybrid model that uses main effects logistic regression instead of a constant log-odds as the initial model for BCART. Researchers who use propensity scoring and consumers of research findings, including clinicians, would benefit from these investigations and also from further standardization of PS estimation methods and balance statistics.

Conclusion

Using data from the STAR*D study, including many continuous covariates carefully selected to capture risk for the outcome of interest, we compared a logistic model with forward stepwise selection of interactions to a boosted CART model. Although both were designed to optimize covariate balance, the logistic model achieved better balance in both PS-matched and PS-weighted samples. Until more is known about which models perform best under which circumstances, a pragmatic approach is to compare multiple PS estimates in order to optimize between-group balance on risk factors affecting treatment assignment.

List of abbreviations and acronyms

ASAM difference

average standardized absolute mean difference

BCART

boosted classification and regression trees

CART

classification and regression trees

CI

confidence interval

PS

propensity score

RR

risk ratio

STAR*D

Sequenced Treatment Alternatives to Relieve Depression