Force spectroscopy of complex biopolymers with heterogeneous elasticity

Abstract

Cellular biopolymers can exhibit significant compositional heterogeneities as a result of the non-uniform binding of associated proteins, the formation of microstructural defects during filament assembly, or the imperfect bundling of filaments into composite structures of variable diameter. These can lead to significant variations in the local mechanical properties of biopolymers along their length. Existing spectral analysis methods assume filament homogeneity and therefore report only a single average stiffness for the entire filament. However, understanding how local effects modulate biopolymer mechanics in a spatially resolved manner is essential to understanding how binding and bundling proteins regulate biopolymer stiffness and function in cellular contexts. Here, we present a new method to determine the spatially varying material properties of individual complex biopolymers from the observation of passive thermal fluctuations of the filament conformation. We develop new statistical mechanics-based approaches for heterogeneous filaments that estimate local bending elasticities as a function of the filament arc-length. We validate this methodology using simulated polymers with known stiffness distributions, and find excellent agreement between derived and expected values. We then determine the bending elasticity of microtubule filaments of variable composition generated by repeated rounds of tubulin polymerization using either GTP or GMPCPP, a nonhydrolyzable GTP analog. Again, we find excellent agreement between mechanical and compositional heterogeneities.

Biopolymers often exhibit spatially varying material properties as a consequence of compositional heterogeneities. Cytoskeletal filaments such as actin and microtubules have mechanical and kinetic properties that are tightly regulated by the binding of a diverse class of proteins. The mechanisms by which local mechanical properties of the filament are augmented is a question of fundamental importance in cell biology. Yet, probing the function of such actin and microtubule associated proteins at the single filament level presents significant experimental challenges. Although a number of methods have been developed to extract materials properties from homogeneous polymers using the shapes of individual filaments subjected to thermal fluctuations or applied load,^1–8 none of these has allowed for measurement of heterogeneous polymers.

We discuss here a new method for the study of local mechanical properties of individual complex biological filaments while measuring simultaneously the filament composition and configurations. Using a statistical mechanical analysis of the shape fluctuations of individual heterogeneous filaments, we gain insight into the mechanical roles played by the distribution of stabilization agents and associated proteins in determining the properties of complex biopolymers. We test our proposed methodology by performing a number of validation studies that demonstrate that our approach correctly reconstructs the spatially varying stiffness of a simulated ensemble of images of biopolymers subjected to thermal fluctuations. We then show how our method can be used in practice by analyzing experimental images of diffusing microtubules that have been generated using different stabilization agents to produce diblock or triblock copolymers with variable composition along their length. Our method successfully detects variations in material properties that are strongly correlated with microtubule composition, which is independently determined using fluorescence labeling to indicate the difference in stabilization agent. To our knowledge, our methodology provides the first quantitative analysis of the mechanics of heterogeneous filaments. We expect this powerful new approach to be useful in probing how filament binding proteins influence the local mechanical properties of biopolymers.

1 Results and discussion

1.1 Statistical mechanics of heterogeneous biopolymers

To investigate the mechanics of heterogeneous biopolymers, we use a modified Kratky–Porod Worm-Like Chain (WLC) model to characterize the local elastic mechanics.^9,18,21 This corresponds to associating with any given biopolymer configuration x(s) the energy

$$E_{\text{bend}}[\mathit{x}]=\frac{1}{2}\underset{0}{\overset{L}{\int }}k(s){(\mathrm{\theta ̇}(s))}^2\mathrm{d}s.$$ (1)

The θ(s) refers to the local tangent angle of the filament, θ̇(s) = dθ/dsdenotes the derivative of the tangent angle in s, where s is the arc-length along the filament. The κ(s) is the bending modulus of the biopolymer at location s. In this representation, a reference point is needed to uniquely determine the contour location and we use by convention x₀ = x(0). From this information, the biopolymer configuration is given by

$$\mathit{x}(s)=\underset{0}{\overset{s}{\int }}\tau (\theta (s\prime ))\mathrm{d}s\prime +{\mathit{x}}_0.$$ (2)

The tangent vector τ for a given angle θ is given by τ(θ) = (cos(θ), sin(θ)).

We remark that our choice of the modified Kratky–Porod WLC model given in eqn (1) is most appropriate for stiff biopolymers, such as microtubules, that have a persistence length that exceeds the contour length and for biopolymers that are under relatively weak two dimensional confinement (as in the experiments we shall consider in this work). When these conditions are not met, there are many well-known situations in which the Kratky–Porod WLC model can break-down, requiring a more involved description of the biopolymer mechanics.^19,20 However, much of our subsequent analysis methodology is independent of the precise functional form of the energy and can be readily adapted for use with alternative descriptions of the biopolymer mechanics.

At thermodynamic equilibrium, such a biopolymer has thermal fluctuations exhibiting the Gibbs–Boltzmann distribution with the probability density

$${\rho }_{\text{bend}}[\mathit{x}]=\frac{1}{Z}\text{exp}[-E_{\text{bend}}[\mathit{x}]/k_{\mathrm{B}}T]$$ (3)

where T is the temperature, k_B is the Boltzmann constant, and Z denotes the partition function, see ref. 10. The fluctuations governed by the Gibbs–Boltzmann distribution provide the key link between the local bending modulus κ(s) and the local effective persistence length L_p(s) by κ (s) = L_p(s)/k_BT. Here, L_p has the interpretation consistent with the persistence length that would be obtained for a long homogeneous biopolymer if it was constructed to have the bending modulus κ as in ref. 1.

In practice, we obtain contour configurations by processing an ensemble of fluorescence images obtained experimentally for a passively fluctuating biopolymer. This is achieved by minimizing a utility function which ensures a maximum of overlap between the contour and the fluorescence signal. For this purpose we use

$$U[\mathit{x},\mathit{I}]=-\underset{0}{\overset{L}{\int }}\underset{\Omega }{\int }k(|\mathit{y}-\mathit{x}(s)|)\mathit{I}(\mathit{y})\mathrm{d}\mathit{y}\mathrm{d}s.$$ (4)

The I = I(y) gives the fluorescence image intensity parameterized over the spatial domain Ω. The L is the contour length. The k(r) is a smoothing kernel that vanishes for r > r₀. We use the following kernel function,

$$k(r)=\{\begin{array}{cc}\alpha [1+\text{cos}(\pi r/r_0)]\hfill & r\le r_0\hfill \\ 0\hfill & r>r_0\hfill \end{array}.$$ (5)

The utility function is then minimized using steepest descent for the contour. For more details see ref. 1.

We emphasize that the image processing step is used solely to obtain an ensemble of contour configurations for the subsequent analysis and does not depend on the particular choice of mechanical model. This has the convenient property that other mechanical models can also be easily considered within our methodology without the need for additional image processing steps.

To handle biopolymer configurations in practice, we expand the representative contour in terms of a finite basis of Chebyshev orthogonal polynomials

$$\theta (s)=\sum _n{a}_n{T}_n(s).$$ (6)

Each T_n(s) is a polynomial of degree n satisfying the orthonormal inner-product condition 〈T_i,T_j〉 = δ _ij, where δ _ij is the Kronecker delta-function and 〈·〉 is the Chebyshev-weighted inner product.¹¹ In this representation, the contour configuration is uniquely determined by the degrees of freedom (a,x₀). The term a denotes the composite vector of coefficients with [a]_n = a_n.

To develop the statistical mechanics of heterogeneous biopolymers when the contour has this representation, it is convenient to express the energy as

$$E_{\text{bend}}[\mathit{a}]=\frac{1}{2}{\mathit{a}}^{T}S\mathit{a}{S}_{ij}=\underset{0}{\overset{L}{\int }}k(s){Ṫ}_i(s){Ṫ}_j(s)\mathrm{d}s.$$ (7)

The S denotes the stiffness matrix of the biopolymer modes. The Gibbs–Boltzmann distribution can be expressed using this coefficient representation as

$${\rho }_{\text{bend}}[\mathit{a}]=\frac{1}{\mathrm{Z̃}}\text{exp}[-\frac{{\mathit{a}}^{T}S\mathit{a}}{2k_{\mathrm{B}}T}]$$ (8)

where Z̃ is the partition function of this representation. In this form, we see that ρ_bend has the convenient form of a multivariate Gaussian with mean zero and covariance

$$\langle \mathit{a}{\mathit{a}}^T\rangle =k_{\mathrm{B}}T{S}^{-1}.$$ (9)

This provides the key expression that allows for the heterogeneous stiffness to be estimated from the empirical covariance of the Chebyshev coefficients obtained from the ensemble of experimental fluorescence images. In practice, a method must be developed to construct κ(s) from such statistics.

1.2 Spectral analysis of heterogeneous filaments

Heterogeneous biopolymers present a number of challenges for the analysis of filament stiffness from the passive fluctuations of biopolymer shape. Although it is tempting to expand κ (s) in an orthogonal polynomial basis using eqn (1), then to attempt inversion of the resulting linear system to obtain κ (s), we have found in practice that this approach is very sensitive to noise. As with many ill-posed problems, such as the inverse heat equation, this sensitivity arises from the lack of regularity requirements on the function κ(s), which can result upon inversion in highly erratic functions that are highly sensitive to small errors in the covariance spectrum. Despite this, in most practical circumstances one is primarily interested in the leading-order variations in the function rather than the fine-scale variations that often either approach the limits of the underlying physical assumptions in modeling or are a product primarily of noise in the measurement.

To extract such leading-order features, while avoiding the need to directly invert the fluctuation spectrum, we develop a method to estimate κ(s) that works in real-space, making use of only local information about the undulations of the filament within a small window that slides along the biopolymer contour. We refer to our approach as the sliding window method. While our approach can be thought of as an effective filter for the extraction of κ (s) from the biopolymer covariance spectrum, it has the distinct advantage that the function obtained has a rather straight-forward physical interpretation. The function κ (s) gives the equivalent bending modulus of a homogeneous worm-like chain that would exhibit this same covariance spectrum over the sub-segment window under consideration.

1.3 Sliding window method

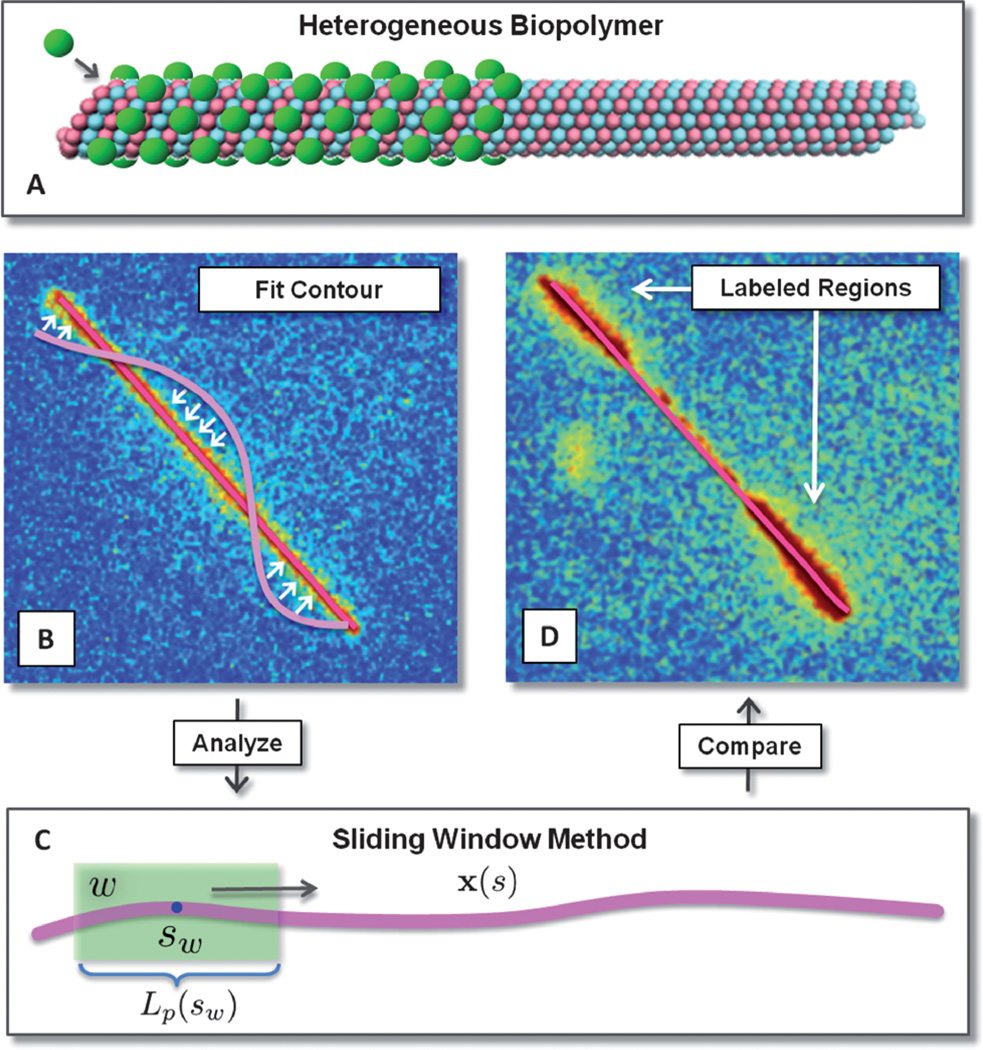
We seek to extract κ (s) or equivalently L_p(s) the effective local persistence length of the filament related by L_p(s) = κ (s)k_BT. For this purpose, consider a sub-segment W of the polymer of length L and width w < L centered at s_W.We call this interval W a window, and calculate the persistence length L_p(s_W) by considering the sample of contours restricted to W. We then slide W from the beginning to end of the contour and interpolate these values to get a smoothly varying heterogeneous persistence length L_p(s). This analysis is illustrated in Fig. 1.

Fig. 1.

Schematic of heterogeneous biopolymer analysis. Fluorescence imaging, contour fitting, and processing. (A) Biopolymers can exhibit heterogeneous material properties for many reasons including binding of regulatory proteins, defects in polymer microstructure, or differences in stabilization agents. (B) Contours are represented by a continuous curve expanded in a Chebyshev polynomial basis and fit to the images by maximizing the overlap with fluorescence via the utility function in eqn (4) and steepest descent. (C) Heterogeneous elastic stiffness coefficients are determined locally using a window over which the spectrum of fluctuations is estimated and a stiffness attributed. (D) The heterogeneous stiffness locally attributed to the biopolymer is then compared with heterogeneous regions that were specifically labeled with a distinguishable fluorophore.

An important consideration is the choice of the size of the window w, since the stiffness determined by our analysis will represent the heterogeneous material properties averaged over this length scale. Depending on the level of resolution sought, the image quality, and the sources of sampling error, the width of the window W could be varied as the window slides through the contour to control the trade-off between these effects. In this initial presentation of the methodology, we shall keep the window width fixed throughout, and study the effects of different choices of window sizes. In general, we find an intermediate window width is optimal. In the case of very small windows, care must be taken for a meaningful persistence length to be obtained that actually reflects the bending configurations of the biopolymer and not artifacts and noise in the fluorescence image. The point-spread function and quality of the optics along with the lateral distribution of fluorophores also sets a lower bound on the length-scales on which the images of biopolymers contain meaningful information. On the other hand, making the window too large is not particularly useful, as this results in significant averaging of local material properties, and therefore a distortion of the fine-scale variations and features we seek to characterize. We investigate these trade-offs for a known ensemble of polymer configurations below.

When performing analysis with the sliding window method we have found that it is often useful to consider windows that overlap in position in order to provide a more continuous description of how material properties vary along the contour. For this purpose the elasticity attributed at location s may be obtained from several overlapping windows and combined through averaging to obtain an effective persistence length L̄_p(s). Let L_p(s) be the persistence length over the windows W_i such that s ∈ W_i. We then weight the average of this persistence length by the distance between s and s_Wi. More precisely,

$${\mathrm{L̄}}_{\mathrm{p}}(s)=\sum _i{\alpha }_i(s)L_{\mathrm{p}}(s_{w_i})/\sum _i{\alpha }_i(s){\alpha }_i(s)=1-{(s-s_{w_i}/(w/2))}^2.$$ (10)

This procedure provides an effective persistence length at any location s along the contour in the full range [0, L].

1.4 Validation studies

An important test of any spectral analysis methodology is to determine how it performs on a known ensemble of contour configurations. This not only serves to validate the proposed methodology and implementation but also to give an indication of the roles played by adjustable methodological parameters, and an estimate of uncertainties in measured parameters. For this purpose, we performed two sets of validation studies to investigate the performance of the spectral analysis methods for known ensembles. In the first case, we consider a diblock copolymer that has a smaller persistence length on its left half than on its right half. For the second case, we consider a triblock copolymer that has a segment in the center with a significantly larger persistence length than the two neighboring sub-segments.

To perform our validation studies, we generated a numerical dataset of M heterogeneous contours constructed by stitching together piecewise homogeneous contours of different persistence lengths end to end. We ensure that no kinks form in the amalgamated contour by rotating each contour so their tangent angles match at their endpoints. This does not affect the stiffness since the WLC energy is invariant to rotation. We then approximate each amalgamated contour with a single contour of high resolution, using Chebyshev interpolation where necessary.

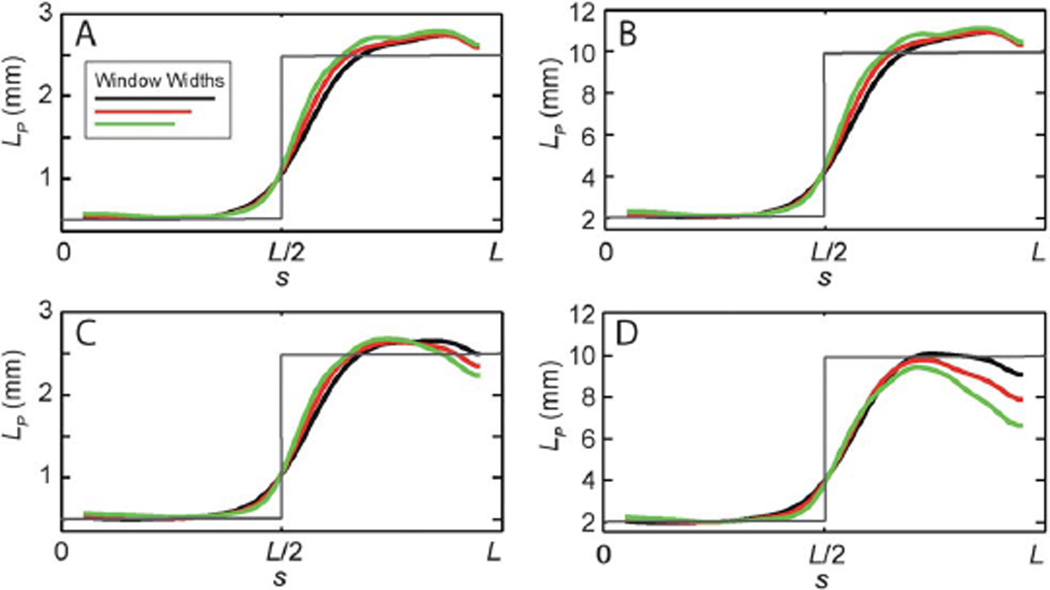
For the diblock copolymer, we considered two ensembles with stiffnesses $L_{\mathrm{p}}^{\mathrm{A}}(0)=0.5\mathrm{m}\mathrm{m}{L}_{\mathrm{p}}^{\mathrm{A}}(L)=2.5\mathrm{m}\mathrm{m}$ and $L_{\mathrm{p}}^{\mathrm{B}}(0)=2\mathrm{m}\mathrm{m}{L}_{\mathrm{p}}^{\mathrm{B}}(L)=10\mathrm{m}\mathrm{m}$ with M = 500 (Fig. 2, panels A and B, respectively). In both cases, to investigate the transition region between the two different persistence lengths, we varied the window width in the analysis method over the range L/4 to L/6. To identify effects of absolute stiffness, we used the same random number generator to create both ensembles. This results in stiffness variations that are qualitatively similar in the two cases, and verify that even very stiff polymers, with persistence lengths on the order of 10 mm, can be analyzed with this approach.

Fig. 2.

Validation of methodology on simulated images of diblock copolymers, and the effects of window size and noise. To validate the methodology we show results for the sliding window method for simulated ensembles of contours (M = 500) that are generated with known heterogeneous elasticity (shown in gray). Persistence lengths are determined using three window widths (L/4 in black, L/5 in red, and L/6 in green). Results for a diblock copolymer, with (A) L_p(0) = 0.5 mm, L_p(L) = 2.5 mm, and no image noise, (B) L_p(0) = 2.0 mm, L_p(L) = 10 mm, and no image noise, (C) L_p(0) = 0.5 mm, L_p(L) = 2.5 mm, and σ_b/I_c = 1/6, and (D) L_p(0) = 2.0 mm, L_p(L) = 10 mm, σ_b/I_c = 1/6 are shown.

We then subjected the ensembles to additional noise to simulate the type of image artifacts that commonly arise as a result of background fluorescence (Fig. 2, panels C and D). To introduce background noise, we perturbed each pixel located on the contour by a random value having mean μ_c = 0 and variance σ_c², and perturbed each pixel not located on the contour by a random value with mean μ_b = 0 and σ_b² = σ_c². Here, we fix σ_b/ I_c = 1/6 where I_c is the characteristic intensity difference between the contour and background. Again, we find good agreement between the expected and determined values for both ensembles and for all window widths.

The primary effect of window size is to determine the sharpness of the transition region between the regions of different persistence lengths. Although the effect is modest, the transition width varies approximately linearly in the window size, possibly leading to systematic effects. An important issue that also arises in experimental images, is that the quality of elasticity estimates declines at the end-points of the biopolymer. These regions are often poorly resolved in fluorescence images and without special care can unduly contribute to persistence length estimates.¹ Even in the simulated images, we find that agreement with the expected values decreases when approaching the contour edges, particularly in images subjected to background noise. This effect is more pronounced in the stiffer filaments, since the intrinsic filament fluctuations are of smaller amplitude, and thus noise has a larger influence on the measured elastic parameters. An important feature of the real-space sliding window method is that windows farther from the end-points are estimated completely independently and do not suffer from localized artifacts near the end-points. This can serve as an advantage even in the determination of the stiffness of filaments that are not compositionally heterogeneous, since the stiffness determined from the filament interior may provide a more robust estimate of the homogeneous persistence length.

To investigate the role of the window width when resolving more complicated heterogeneities, we consider the case of a triblock copolymer with L_p(0) = L_p(L) = 0.5 mm, and L_p(1/2) = 2.5 mm. The width of the stiffer middle sub-segment size was varied from ℓ = L/3 to L/10 and the window width was varied from w = L/4 to L/8; in all cases M = 500. For w comparable to or smaller than ℓ, we find that the analysis methodology robustly estimates the persistence lengths of the heterogeneous biopolymer (see Fig. 3). The primary role of the window width is to smooth the transition regions between these heterogeneous regions. As the sub-segment size becomes smaller than the window width, we find that the persistence length values are averaged with those of the neighboring region, leading to a systematic underestimate of the actual stiffness. In all cases, the heterogeneity is still detected, but one must be careful to interpret the estimated persistence length values in terms of a spatially averaged material property.

Fig. 3.

Validation of methodology on simulated images of triblock copolymers, and the effects of window size. To validate the methodology we show results for the sliding window method for simulated ensembles of contours (M = 500, no image noise) generated with known heterogeneous elasticity (in gray), with L_p(0) = L_p(L) = 0.5 mm, and L_p(L/2) = 2.5 mm. The width of the stiffer middle sub-segment size was varied from ℓ = L/3 to L/10 and persistence lengths determined using four window widths (L/4 in black, L/5 in red, L/6 in green, and L/8 in blue).

1.5 Heterogeneous biopolymers

To demonstrate the effectiveness of our approach in practice using experimental images, we generated microtubules with variable composition by repeated rounds of tubulin polymerization using either GTP, the normal nucleotide to induce microtubule growth, or GMPCPP, a non-hydrolyzable GTP analog. Prior studies have indicated that microtubules polymerized with GMPCPP are substantially stiffer than those polymerized by GTP,^12–14 so we anticipated that the GTP-rich and GMPCPP-rich tubulin blocks would have different stiffnesses even when contained within the same microtubule. To generate such filaments, we used a mixture of unlabeled and rhodamine-labeled tubulin, to enable visualization of the entire microtubule contour. To form the stiffer GMPCPP-rich blocks, we polymerized 2 µM of tubulin with 0.5 mM GMPCPP in a standard microtubule assembly buffer at 35 °C for three hours. In this assembly reaction, we added green fluorescent HiLyte tubulin at a 1 : 5 molar ratio of HiLyte-labeled tubulin to unlabeled tubulin. Thus, the microtubules are labeled with two fluorophores: rhodamine, which enables visualization of the entire contour, and HiLyte, which will specifically label the GMPCPP-rich block, allowing us to correlate microtubule composition and mechanics. After the first round of polymerization, the microtubules were pelleted in a microcentrifuge, and resuspended in fresh assembly buffer. To induce the growth of GTP-rich tubulin blocks onto the plus-end of the microtubule, we then combined in a 50 µL reaction: 50 µM tubulin (a mixture of rhodamine and unlabeled tubulin, but no fluorescent HiLyte tubulin), 2 mM GTP, and 14 µL of the GMPCPP microtubule solution, which provides seeds upon which GTP–tubulin dimers bind, thereby elongating the microtubule. Unlike microtubules polymerized by GMPCPP, microtubules polymerized by GTP require additional stabilization to maintain constant length; thus to stabilize the microtubules, we included taxol, a small-molecule inhibitor that prevents microtubule dynamics. After the second round of polymerization, the microtubules were again centrifuged to remove any remaining free tubulin and resuspended in assembly buffer supplemented with GTP and taxol. This protocol reliably produces microtubules with an average length of 15–20 µm and with distinct regions of GMPCPP-rich and GTP-rich blocks.

Microtubules were then diluted into fresh assembly buffer supplemented with taxol, casein (a blocking protein added to prevent non-specific binding of microtubules to the coverslip), and an enzymatic oxygen scavenging system to minimize the effects of photobleaching. A small volume of this solution is sandwiched between a clean glass coverslip and slide such that the gap distance between the two surfaces is 3 µm; this narrow gap ensures that most microtubules are in focus and oriented parallel to the coverslip surface. These filaments are then visualized using a custom-built fluorescence microscope with dual color excitation at 488 nm and 532 nm. Once a candidate filament was identified, a single snapshot of the HiLyte–tubulin distribution was obtained using the 488 nm excitation. Under this imaging condition, no signal from the rhodamine fluorophore was observed, so this image serves to provide a map of the GMPCPP-rich blocks only. The candidate filament was briefly observed to ensure that the center of mass was freely diffusing, and no portion of the microtubule adhered to the surface. The excitation wavelength was then switched to 532 nm, which enabled visualization of the rhodamine fluorophores, which were present during both the GMPCPP and GTP polymerization, and thus observed along the entire length of the microtubule. Movies with 200–400 frames of freely fluctuating filaments were collected using an air-cooled EMCCD camera (Andor iXon) at a frame rate of 5.8 frames per second. Photobleaching of the rhodamine fluorophores prevented imaging over longer times.

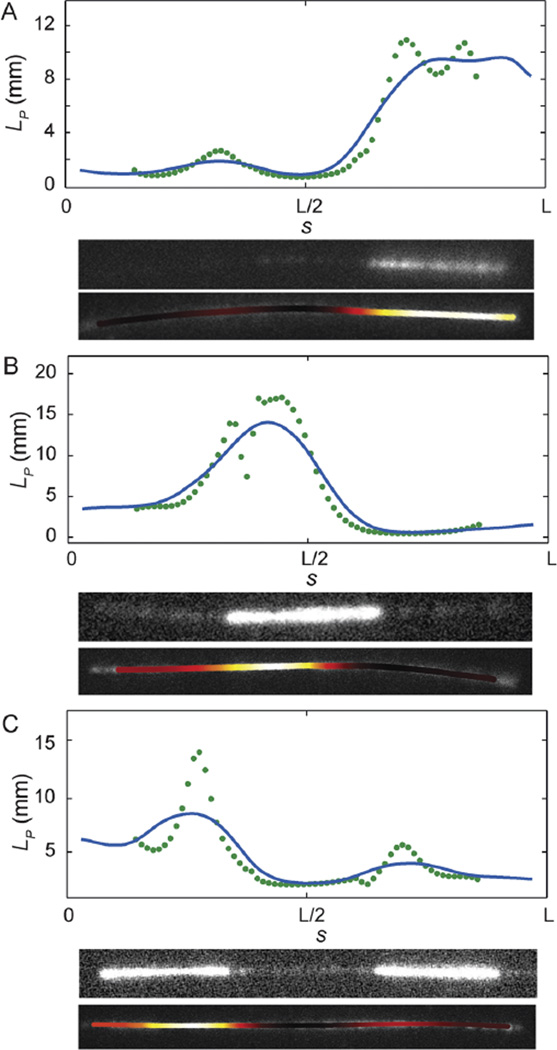
To determine the stiffness of the heterogeneous microtubules, we employed the sliding window method with a fixed window size of L/4 using the rhodamine signal only. As shown with three representative filaments in Fig. 4, we found strong correlation between filament stiffness and composition. In each panel, we plot persistence length as a function of arc-length, display the image of the filament obtained using the HiLyte tubulin signal, and also display an intensity map in which the stiffest regions of the polymer are brightest. In all cases, we found that the HiLyte tubulin signal, which labels the GMPCPP-rich block, was found in the stiffest regions of the microtubule. It is important to note that the filament stiffness is determined using the rhodamine signal only, which does not correlate with nucleotide state, and no information about the GMPCPP distribution is included in the analysis. The majority of the filaments are diblocks, with one GMPCPP-rich end, and one GTP-rich end joined somewhere near the middle of the microtubule, as shown in Fig. 4A. However, a variety of other compositions are possible. In Fig. 4B, GTP-rich blocks extend from both ends of the GMPCPP-rich block; in Fig. 4C, it appears that two GMPCPP seeds have annealed to form one long microtubule with an internal GDP block. The stiffer regions, which we assign to GMPCPP-rich blocks, have an average persistence length of ≈8 to 15mmand softer regions, which we assign to GTP-rich blocks have an average persistence length of ≈1 to 3 mm; this is consistent with independent measurements of microtubule stiffness using homogeneous filaments.¹⁴

Fig. 4.

Experimental results. Shown are the results of the sliding window method for experimental ensembles of images of three fluctuating microtubules. The heterogeneous stiffness measured locally for the biopolymer correlates strongly with the biopolymer composition, as indicated by the fluorescence imaging of the GMPCPP-rich block. In each panel, we plot persistence length as a function of arc length. We also display the image of the filament obtained using the HiLyte tubulin signal, which was introduced with the GMPCPP tubulin, and an intensity map in which the stiffest regions of the polymer are colored white, which then transitions to yellow, orange, deep red, and black as filament stiffness decreases. In each case, we find very good correlation between the GMPCPP-rich blocks and regions of increased stiffness. The data points are from the sliding window method with window width L/4 and the blue curve gives the effective local persistence length L̄_p(s) (see eqn (10)).

2 Conclusions

We presented a new statistical mechanics-based approach to determine the spatially varying material properties of complex biopolymers from the observation of passive thermal fluctuations. To achieve robust estimates of the local bending elasticity of the filament, our analysis is performed in real-space by employing a sliding window over which the fluctuation spectrum is analyzed. This results in a robust method to estimate the local bending elasticity as a function of the filament arc-length. To validate our approach, and to investigate the role played by methodological parameters, we analyze a simulated ensemble of biopolymer configurations with known mechanical properties. Through comparison of the results of our method with the known heterogeneous bending elasticities, we reported the effects of image noise and window size, and demonstrated that the properties of di- and triblock copolymers can be reliably determined, even for fairly small sample sizes of 500 images and in the presence of background noise. Using experimental data for microtubule filaments that were polymerized using different types of stabilization, we have shown that our methods detect heterogeneous bending elasticities that correlate closely with compositional heterogeneities. Our heterogeneous bending stiffness estimates also agree closely with independent measurements of the stiffness of homogeneous polymers subjected to similar stabilization methods. We expect the new spectral analysis methods we introduced for heterogeneous biopolymers to be useful in investigations of a wide class of problems in biophysics, including the determination of the effects of bundling or the non-uniform binding of associated proteins to cytoskeletal polymers or nucleic acids.

3 Materials and methods

3.1 Microtubule preparation

Bovine brain tubulin was purified as previously described.^15,16 From this, rhodamine-labeled tubulin (0.14 mole rhodamine per mole tubulin) was prepared by carboxyrhodamine labeling (Molecular Probes) as described.¹⁷ Rhodamine labeled tubulin and unlabeled tubulin were mixed at a 1 : 5 molar ratio respectively in all microtubule polymerizations.

Heterogeneous microtubules consisted of a GMPCPP stabilized portion and a taxol stabilized portion. GMPCPP microtubules were polymerized first in a 100 µL reaction at 2 µMtubulin (which included a 1 : 5 molar ratio of green fluorescent HiLyte (Cytoskeleton) tubulin to unlabeled tubulin), 0.5 mM GMPCPP in PEM80 buffer for 3 hours at 35 °C. This was then spun down at 14 000 rpm for 10 minutes in a microcentrifuge, and reconstituted to 20 µL in PEM80. To polymerize GTP taxol stabilized ends on the GMPCPP seeds we then combined in a 50 µL reaction: 50 µM tubulin, 2 mM GTP, and 14 µL of the GMPCPP microtubule solution. This solution was incubated for ten minutes at 35 °C. Taxol stabilized polymerization was then performed by a 3-step taxol addition (1 µM, 7 µM, and 20 µM), each addition was followed by a ten minute incubation period at 35 °C. The solution was then centrifuged again and reconstituted into PEM80 buffer containing 2 mM GTP and 20 µM taxol, and the resultant microtubules were used within 24 hours.

3.2 Fluctuation assay to measure microtubule stiffness

The heterogeneous microtubules (average length 15–20 µm) were diluted into a PEM80 (80 mM Pipes, 1 mM EGTA, 4 mM MgCl₂) solution containing 1% mercaptoethanol with an oxygen scavenging system (glucose, glucose oxidase, and catalase) and 1.5 mg mL⁻¹ casein (added to passivate the glass surface). A small amount of the microtubule solution (2.6 µL) was sandwiched between a clean glass slide and a cover glass cleaned by exposure to plasma in a plasma cleaner (Harrick PDC-32G) for ten minutes at 18 Watts. Gentle pressure was applied to spread the solution over the entire area of the cover slip and the chamber was sealed with VALAP wax (equal parts Vaseline, lanolin and paraffin). The resulting chamber depth was 3 µm. The sample was imaged using a custom built TIRF (total internal reflection fluorescence) microscope and EMCCD camera (Andor iXon). The TIRF excitation beam was aligned to a slightly subcritical incident angle resulting in a mixed TIRF-epifluorescence mode. Because of this the excitation region extended across the chamber depth while still retaining a portion of the noise reduction inherent in TIRF. Images were taken at 5.8 frames per second at a magnification of 44 nm per pixel. Images were collected until the microtubule was photo-bleached (typically 200–400 images per movie).