Batch Mode Reinforcement Learning based on the Synthesis of Artificial Trajectories

Abstract

In this paper, we consider the batch mode reinforcement learning setting, where the central problem is to learn from a sample of trajectories a policy that satisfies or optimizes a performance criterion. We focus on the continuous state space case for which usual resolution schemes rely on function approximators either to represent the underlying control problem or to represent its value function. As an alternative to the use of function approximators, we rely on the synthesis of “artificial trajectories” from the given sample of trajectories, and show that this idea opens new avenues for designing and analyzing algorithms for batch mode reinforcement learning.

1 Introduction

Optimal control problems arise in many real-life applications, such as engineering [40], medicine [41,35,34] or artificial intelligence [43]. Over the last decade, techniques developed by the Reinforcement Learning (RL) community [43] have become more and more popular for addressing those types of problems. RL was initially focusing on how to design intelligent agents able to interact with their environment so as to optimize a given performance criterion [43]. Since the end of the nineties, many researchers have focused on the resolution of a subproblem of RL: computing high performance policies when the only information available on the environment is contained in a batch collection of trajectories. This subproblem of RL is referred to as batch mode RL [18].

Most of the techniques proposed in the literature for solving batch mode RL problems over large or continuous spaces combine value or policy iteration schemes from the Dynamic Programming (DP) theory [2] with function approximators (e.g., radial basis functions, neural networks, etc) representing (state-action) value functions [7]. These approximators have two main roles: (i) to offer a concise representation of state-action value functions defined over continuous spaces and (ii) to generalize the information contained in the finite sample of input data. Another family of algorithms that has been less studied in RL adopts a two stage process for solving these batch mode RL problems. First, they train function approximators to learn a model of the environment and, afterwards, they use various optimization schemes (e.g., direct policy search, dynamic programming) to compute a policy which is (near-)optimal with respect to this model.

While successful in many studies, the use of function approximators for solving batch mode RL problems has also drawbacks. In particular, the black box nature of this approach makes performance analysis very difficult, and hence severely hinders the design of new batch mode RL algorithms presenting some a priori desired performance guarantees. Also, the policies inferred by these algorithms may have counter-intuitive properties. For example, in a deterministic framework, for a fixed initial state, and when there is in the input sample a trajectory that has been generated by an optimal policy starting from this initial state, there is no guarantee that a function approximator-based policy will reproduce this optimal behavior. This is surprising, since a simple “imitative learning” approach would have such a desirable property.

The above observations have lead us to develop a new line of research based on the synthesis of “artificial trajectories” for addressing batch mode RL problems. In our approach, artificial trajectories are rebuilt from the tuples extracted from the given batch of trajectories with the aim of achieving an optimality property. In this paper, we revisit our work on this topic [19–23], with the objective of showing that these ideas open avenues for addressing many batch mode RL related problems. In particular, four algorithms that exploit artificial trajectories will be presented. The first one computes an estimate of the performance of a given control policy [22]. The second one provides a way for computing performance guarantees in deterministic settings [19]. The third one leads to the computation of policies having high performance guarantees [20, 23], and the fourth algorithm presents a sampling strategy for generating additional trajectories [21]. Finally, we highlight connections between the concept of artificial trajectory synthesis and other standard batch mode RL techniques.

The paper is organized as follows. First, Section 2 gives a brief review of the field of batch mode RL. Section 3 presents the batch mode RL setting adopted in this paper and several of the generic problems it raises. In Section 4, we present our new line of research articulated around the synthesis of artificial trajectories. Finally, Section 5 proposes to make the link between this paradigm and existing batch mode RL techniques, and Section 6 concludes.

2 Related Work

Batch mode RL techniques are probably rooted in the works of Bradtke and Barto [6] and Boyan [4] related to the use of least-squares techniques in the context of Temporal Difference learning methods (LSTD) for estimating the return of control policies. Those works have been extended to address optimal control problems by Lagoudakis and Parr [27] who have introduced the Least-Square Policy Iteration (LSPI) algorithm that mimics the policy iteration algorithm of the DP theory [2]. Several papers have proposed some theoretical works related to least-squares TD-based algorithms, such as for example Nedić and Bertsekas [36] and Lazaric et al. [29,30].

Another algorithm from the DP theory, the value iteration algorithm, has also served as inspiration for designing batch mode RL algorithms. For example, Ormoneit and Sen have developed a batch mode RL algorithm in 2002 [37] using kernel approximators, for which theoretical analyses are also provided. Reference [12] proposes an algorithm that combines value iteration with any type of regressors (e.g., regression trees, SVMs, neural networks). Reference [13] has named this algorithm Fitted Q Iteration (FQI) and provides a careful empirical analysis of its performance when combined with ensembles of regression trees.

References [40, 28] and [44] study the performances of this FQI algorithm with (deep) neural networks and CMACs (Cerebella Model Articulator Controllers). The Regularized FQI algorithm proposes to use penalized least-squares regression as function approximator to limit the model-complexity of the original FQI algorithm [17]. Extensions of the FQI algorithm to continuous action spaces have also been proposed [1]. More theoretical works related with FQI have also been published [33, 10].

Applications of these batch mode RL techniques have already lead to promising results in robotics [38,3,45], power systems [14], image processing [15], water reservoir optimization [9,8], medicine [34,16,26] and driving assistance strategies [39].

3 Batch Mode RL: Formalization and Typical Problems

We consider a stochastic discrete-time system whose dynamics is given by

$$x_{t+1}=f(x_t+u_t+w_t)\forall t\in \{0,\dots ,T-1\}$$

where x_t belongs to a state space ⊂ ℝ^d, Where ℝ^d is the d – dimensional Euclidean space and T ∈ ℕ\{0} denotes the finite optimization horizon. At every time t ∈ {0,…, T − 1}, the system can be controlled by taking an action u_t ∈ , and is subject to a random disturbance w_t ∈ drawn according to a probability distribution p (·)¹. To each system transition from time t to t + 1 is associated a reward signal:

$$r_t=\rho (x_t,u_t,w_t)\forall t\in \{0,\dots ,T-1\}.$$

Let h : {0, …,T−1} × → be a control policy. When starting from a given initial state x₀ and following the control policy h, an agent will get a random sum of rewards signal R^h (x₀):

$$\begin{array}{c}{R}^h(x_0,w_0,\dots ,w_{T-1})=\sum _{t=0}^{T-1}\rho (x_t,h(t,x_t),w_t)\\ \text{with}{x}_{t+1}=f(x_t,h(t,x_t),w_t)\forall t\in \{0,\dots ,T-1\}\\ w_t\sim p\mathcal{W}(\cdot ).\end{array}$$

In RL, the classical performance criterion for evaluating a policy h is its expected T–stage return:

Definition 1 (Expected T–stage Return)

$$J^h(x_0)=\underset{w_0,\dots ,w_{T-1}\sim p\mathcal{W}(.)}{\mathbb{E}}[R^h(x_0,w_0,\dots ,w_{T-1})],$$

but, when searching for risk-aware policies, it is also of interest to consider the value at risk criterion:

Definition 2 (T–stage Value at Risk)

Let b ∈ ℝ and c ∈ [0, 1[.

$$J_{\mathit{\text{VaR}}}^{h,(b,c)}(x_0)=\{\begin{array}{l}-\infty \text{if}P(R^h(x_0,w_0,\dots ,w_{T-1})<b)>c,\\ J^h(x_0)\text{otherwise}.\end{array}$$

The central problem of batch mode RL is to find a good approximation of a policy h* that optimizes one such performance criterion, given the fact that the functions f, ρ and p (·) are unknown, and thus not accessible to simulation. Instead, they are “replaced” by a batch collection of n ∈ ℕ\{0} elementary pieces of trajectories, defined according to the following process.

Definition 3 (Sample of transitions)

Let

$${\mathcal{P}}_n={\{(x^l,u^l)\}}_{l=1}^n\in {(\mathcal{X}\times \mathcal{U})}^n$$

be a given set of state-action pairs. Consider the ensemble of samples of one-step transitions of size n that could be generated by complementing each pair (x^l, u^l) of _n by drawing for each l a disturbance signal w^l at random from p (.), and by recording the resulting values of ρ(x^l, u^l, w^l) and f(x^l, u^l, w^l). We denote by _n ( _n, w¹,…,wⁿ) one such “random” set of one-step transitions defined by a random draw of n disturbance signals w^l l = 1 … n. We assume that we know one realization of the random set _n ( _n, w¹,…,wⁿ), that we denoted by _n:

$${\mathcal{F}}_n={\{(x^l,u^l,r^l,y^l)\}}_{l=1}^n$$

where, for all l ∈ {1,…, n},

$$\begin{array}{l}\forall l\in \{1,\dots ,n\},r^l=\rho (x^l,u^l,w^l),\\ y^l=f(x^l,u^l,w^l),\end{array}$$

for some realizations of the disturbance process w^l ∼p (·).

Notice first that the resolution of the central problem of finding a good approximation of an optimal policy h* is very much correlated to the problem of estimating the performance of a given policy. Indeed, when this latter problem is solved, the search for an optimal policy can in principle be reduced to an optimization problem over the set of candidate policies. We thus will start by addressing the problem of characterizing the performance of a given policy.

It is sometimes desirable to be able to compute policies having good performance guarantees. Indeed, for many applications, even if it is perhaps not paramount to have a policy h which is very close to the optimal one, it is however crucial to be able to guarantee that the considered policy h leads to high-enough cumulated rewards. The problem of computing such policies will also be addressed later in this paper.

In many applications, one has the possibility to move away from a pure batch setting by carrying out a limited number of experiments on the real system in order to enrich the available sample of trajectories. We thus also consider the problem of designing strategies for generating optimal experiments for batch mode RL.

4 Synthesizing Artificial Trajectories

We first formalize the concept of artificial trajectories in Section 4.1. In Section 4.2, we detail, analyze and illustrate on a benchmark how artificial trajectories can be exploited for estimating the performances of policies. We focus in Section 4.3 on the deterministic case, and we show how artificial trajectories can be used for computing bounds on the performances of policies. Afterwards, we exploit these bounds for addressing two different problems: the first problem (Section 4.4) is to compute policies having good performance guarantees. The second problem (Section 4.5) is to design sampling strategies for generating additional system transitions.

4.1 Artificial Trajectories

Artificial trajectories are made of elementary pieces of trajectories (one-step system transitions) taken from the sample _n. Formally, an artificial trajectory is defined as follows:

Definition 4 (Artificial Trajectory)

An artificial trajectory is an (ordered) sequence of T one-step system transitions:

$$[(x^{l_0},u^{l_0},r^{l_0},y^{l_0}),\dots ,(x^{l_{T-1}},u^{l_{T-1}},r^{l_{T-1}},y^{l_{T-1}})]\in {\mathcal{F}}_n^T$$

where

$$l_t\in \{1,\dots ,n\},\forall t\in \{0,\dots ,T-1\}.$$

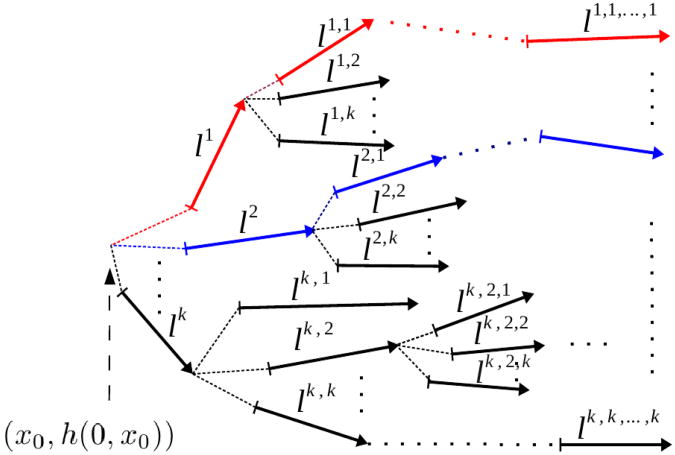
We give in Figure 1 an illustration of one such artificial trajectory.

Fig. 1.

An example of an artificial trajectory rebuilt from 4 one-step system transitions from _n.

Observe that one can synthesize n^T different artificial trajectories from the sample of transitions _n. In the rest of this paper, we present various techniques for extracting and exploiting “interesting” subsets of artificial trajectories.

4.2 Evaluating the Expected Return of a Policy

A major subproblem of batch mode RL is to evaluate the expected return J^h(x₀) of a given policy h. Indeed, when such an oracle is available, the search for an optimal policy can be in some sense reduced to an optimization problem over the set of all candidate policies. When a model of the system dynamics, reward function and disturbances probability distribution is available, Monte Carlo estimation techniques can be run to estimate the performance of any control policy. But, this is indeed not possible in the batch mode setting. In this section, we detail an approach that estimates the performance of a policy by rebuilding artificial trajectories so as to mimic the behavior of the Monte Carlo estimator. We assume in this section (and also in Section 4.3) that the action space is continuous and normed.

4.2.1 Monte Carlo Estimation

The Monte Carlo (MC) estimator works in a model-based setting (i.e., in a setting where f, ρ and p (.) are known). It estimates J^h(x₀) by averaging the returns of several (say p ∈ ℕ₀) trajectories which have been generated by simulating the system from x₀ using the policy h. More formally, the MC estimator of the expected return of the policy h when starting from the initial state x₀ writes:

Definition 5 (Monte Carlo Estimator)

$${\mathbb{M}}_p^h(x_0)=\frac{1}{p}\sum _{i=1}^p\sum _{t=0}^{T-1}\rho (x_t^i,h(t,x_t^i),w_t^i)$$

With ∀t ∈ {0,…,T − 1}, ∀i ∈ {1,…,p},

$$\begin{array}{c}{w}_t^i\sim p\mathcal{W}(.),\\ x_0^i=x_0,\\ x_{t+1}^i=f(x_t^i,h(t,x_t^i),w_t^i).\end{array}$$

The bias and variance of the MC estimator are:

Proposition 1 (Bias and Variance of the MC Estimator)

$$\begin{array}{c}\underset{w_t^i\sim p\mathcal{W}(.),i=1\dots p,t=0\dots T-1}{\mathbb{E}}[{\mathbb{M}}_p^h(x_0)-J^h(x_0)]=0,\\ \underset{w_t^i\sim p\mathcal{W}(.),i=1\dots p,t=0\dots T-1}{\mathbb{E}}[{({\mathbb{M}}_p^h(x_0)-J^h(x_0))}^2]=\frac{{\sigma }_{R^h}^2(x_0)}{p}.\end{array}$$

where ${\sigma }_{R^h}^2(x_0)$ denotes the assumed finite variance of R^h (x₀, w₀,…,w_T-1):

$${\sigma }_{R^h}^2(x_0)=\underset{w_0,\dots ,w_{T-1}\sim p\mathcal{W}(.)}{\mathit{\text{Var}}}[R^h(x_0,w_0,\dots ,w_{T-1})]>+\infty .$$

4.2.2 Model-free Monte Carlo Estimation

From a sample _n, our model-free MC (MFMC) estimator works by rebuilding p ∈ ℕ \ {0} artificial trajectories. These artificial trajectories will then serve as proxies of p “actual” trajectories that could be obtained by simulating the policy h on the given control problem. Our estimator averages the cumulated returns over these artificial trajectories to compute its estimate of the expected return J^h(x₀). The main idea behind our method amounts at selecting the artificial trajectories so as to minimize the discrepancy of these trajectories with a classical MC sample that could be obtained by simulating the system with policy h.

To rebuild a sample of p artificial trajectories of length T starting from x₀ and similar to trajectories that would be induced by a policy h, our algorithm uses each one-step transition in _n at most once; we thus assume that pT ≤ n. The p artificial trajectories of T one-step transitions are created sequentially. Every artificial trajectory is grown in length by selecting, among the sample of not yet used one-step transitions, a transition whose first two elements minimize the distance – using a distance metric Δ in × – with the couple formed by the last element of the previously selected transition and the action induced by h at the end of this previous transition. Because we do not re-use one-step transitions, the disturbances associated with the selected transitions are i.i.d., which provides the MFMC estimator with interesting theoretical properties (see Section 4.2.3). Consequently, this also ensures that the p rebuilt artificial trajectories will be distinct.

Algorithm 1 MFMC algorithm to rebuilt a set of size p of T–length artificial trajectories from a sample of n one-step transitions.

Input: n, h(., .),x0, Δ(., .),T,p

Let denote the current set of not yet used one-step transitions in n; Initially,

← n;

for i = 1 to p (extract an artificial trajectory) do

t ← 0;

$x_t^i\leftarrow x_0$;

while t < T do

$u_t^i\leftarrow h(t,x_t^i)$;

$\mathcal{H}\leftarrow \underset{(x,u,r,y)\in \mathcal{G}}{\text{arg min}}\Delta ((x,u),(x_t^i,u_t^i))$;

$l_t^i$ ← lowest index in n of the transitions that belong to ;

t ← t + 1;

$x_t^i\leftarrow y^{l_t^i}$;

$\mathcal{G}\leftarrow \mathcal{G}\backslash \left\{\right(x^{l_t^i},u^{l_t^i},r^{l_t^i},y^{l_t^i}\left)\right\}$; \\ do not re-use transitions

end while

end for

Return the set of indices ${\{l_t^i\}}_{i=1,t=0}^{i=p,t=T-1}$.

A tabular version of the algorithm for building the set of artificial trajectories is given in Table 1. It returns a set of indices of one-step transitions ${\{l_t^i\}}_{i=1,t=0}^{i=p,t=T-1}$ from _n based on h, x₀, the distance metric Δ and the parameter p. Based on this set of indices, we define our MFMC estimate of the expected return of the policy h when starting from the initial state x₀:

Definition 6 (Model-free Monte Carlo Estimator)

$${\mathcal{M}}_p^h({\mathcal{F}}_n,x_0)=\frac{1}{p}\sum _{i=1}^p\sum _{t=0}^{T-1}{r}^{l_t^i}.$$

Figure 2 illustrates the MFMC estimator. Note that the computation of the MFMC estimator ${\mathcal{M}}_p^h({\mathcal{F}}_n,x_0)$ has a linear complexity with respect to the cardinality n of _n, the number of artificial trajectories p and the optimization horizon T.

Fig. 2.

Rebuilding three 4-length trajectories for estimating the return of a policy.

4.2.3 Analysis of the MFMC Estimator

In this section we characterize some main properties of our estimator. To this end, we study the distribution of our estimator ${\mathcal{M}}_p^h({\stackrel{\sim }{\mathcal{F}}}_n({\mathcal{P}}_n,w^1,\dots ,w^n),x_0)$, seen as a function of the random set ${\stackrel{\sim }{\mathcal{F}}}_n({\mathcal{P}}_n,w^1,\dots ,w^n)$; in order to characterize this distribution, we express its bias and its variance as a function of a measure of the density of the sample _n, defined by its “k–dispersion”; this is the smallest radius such that all Δ-balls in × of this radius contain at least k elements from _n. The use of this notion implies that the space × is bounded (when measured using the distance metric Δ).

The bias and variance characterization will be done under some additional assumptions detailed below. After that, we state the main theorems formulating these characterizations. Proofs are given in [22].

Assumption: Lipschitz continuity of the functions f, ρ and h

We assume that the dynamics f, the reward function ρ and the policy h are Lipschitz continuous, i.e., we assume that there exist finite constants L_f, L_ρ and L_h ∈ ℝ⁺ such that:

$$\begin{array}{l}\forall (x,x\prime ,u,u\prime ,w)\in {\mathcal{X}}^2\times {\mathcal{U}}^2\times \mathcal{W},\\ {║f(x,u,w)-f(x\prime ,u\prime ,w)║}_{\mathcal{X}}\le L_f({║x-x\prime ║}_{\mathcal{X}}+{║u-u\prime ║}_{\mathcal{U}}),\\ |\rho (x,u,w)-\rho (x\prime ,u\prime ,w)|\le L_{\rho }({║x-x\prime ║}_{\mathcal{X}}+{║u-u\prime ║}_{\mathcal{U}}),\\ {║h(t,x)-h(t,x\prime )║}_{\mathcal{U}}\le L_h{║x-x\prime ║}_{\mathcal{X}},\forall t\in \{0,\dots ,T-1\},\end{array}$$

where ║.║ and ║.║ denote the chosen norms over the spaces and , respectively.

Assumption: × is bounded

We suppose that × is bounded when measured using the distance metric Δ.

Definition 7 (Distance Metric Δ)

$$\forall (x,x\prime ,u,u\prime )\in {\mathcal{X}}^2\times {\mathcal{U}}^2,\Delta ((x,u),(x\prime ,u\prime ))={║x-x\prime ║}_{\mathcal{X}}+{║u-u\prime ║}_{\mathcal{U}}.$$

Given k ∈ ℕ\{0} with k ≤ n, we define the k–dispersion, α_k( _n) of the sample _n:

Definition 8 (k–Dispersion)

$${\alpha }_k({\mathcal{P}}_n)=\underset{(x,u)\in \mathcal{X}\times \mathcal{U}}{\text{sup}}{\Delta }_k^{{\mathcal{P}}_n}(x,u),$$

where ${\Delta }_k^{{\mathcal{P}}_n}(x,u)$ denotes the distance of (x, u) to its k–th nearest neighbor (using the distance metric Δ) in the _n sample.

Definition 9 (Expected Value of ${\mathcal{M}}_p^h(\stackrel{\sim }{\mathcal{F}}({\mathcal{P}}_n,w^1,\dots ,w^n),x_0)$)

We denote by $E_{p,{\mathcal{P}}_n}^h(x_0)$ the expected value:

$$E_{p,{\mathcal{P}}_n}^h(x_0)=\underset{w^1,\dots ,w^n\sim p\mathcal{W}(.)}{\mathbb{E}}\left[{\mathcal{M}}_p^h\right({\stackrel{\sim }{F}}_n({\mathcal{P}}_n,w^1,\dots ,w^n),x_0\left)\right].$$

We have the following theorem:

Theorem 1 (Bias Bound for ${\mathcal{M}}_p^h({\stackrel{\sim }{\mathcal{F}}}_n({\mathcal{P}}_n,w^1,\dots ,w^n),x_0)$)

$$|J^h(x_0)-E_{p,{\mathcal{P}}_n}^h(x_0)|\le C{\alpha }_{\mathit{\text{pT}}}({\mathcal{P}}_n)\mathit{\text{with}}C=L_{\rho }\sum _{t=0}^{T-1}\sum _{i=0}^{T-t-1}{(L_f(1+L_h))}^i.$$

The proof of this result is given in [22]. This formula shows that the bias is bounded closer to the target estimate if the sample dispersion is small. Note that the sample dispersion itself actually only depends on the sample _n and on the value of p (it will increase with the number of trajectories used by our algorithm).

Definition 10 (Variance of ${\mathcal{M}}_p^h({\stackrel{\sim }{\mathcal{F}}}_n({\mathcal{P}}_n,w^1,\dots ,w^n),x_0)$)

We denote by $V_{p,{\mathcal{P}}_n}^h(x_0)$ the variance of the MFMC estimator defined by

$$V_{p,{\mathcal{P}}_n}^h(x_0)=\underset{w^1,\dots ,w^n\sim p\mathcal{W}(.)}{\mathbb{E}}\left[{\left({\mathcal{M}}_p^h\right({\stackrel{\sim }{\mathcal{F}}}_n({\mathcal{P}}_n,w^1,\dots ,w^n),x_0)-E_{p,{\mathcal{P}}_n}^h(x_0))}^2\right]$$

and we give the following theorem:

Theorem 2 (Variance Bound for ${\mathcal{M}}_p^h({\stackrel{\sim }{\mathcal{F}}}_n({\mathcal{P}}_n,w^1,\dots ,w^n),x_0)$)

$$V_{p,{\mathcal{P}}_n}^h(x_0)\le {(\frac{{\sigma }_{R^h}(x_0)}{\sqrt{p}}+2C{\alpha }_{\mathit{\text{pT}}}({\mathcal{P}}_n))}^2\mathit{\text{with}}C=L_{\rho }\sum _{t=0}^{T-1}\sum _{i=0}^{T-t-1}{(L_f(1+L_h))}^i.$$

The proof of this theorem is given in [22]. We see that the variance of our MFMC estimator is guaranteed to be close to that of the classical MC estimator if the sample dispersion is small enough.

• Illustration

In this section, we illustrate the MFMC estimator on an academic problem. The system dynamics and the reward function are given by

$$x_{t+1}=\text{sin}(\frac{\pi }{2}(x_t+u_t+w_t))$$

and

$$\rho (x_t,u_t,w_t)=\frac{1}{2\pi }{e}^{-\frac{1}{2}(x_t^2+u_t^2)}+w_t$$

with the state space being equal to [−1,1] and the action space to [−1,1]. The disturbance w_t is an element of the interval $\mathcal{W}=[-\frac{∊}{2},\frac{∊}{2}]$ with ∊ = 0.1 and p is a uniform probability distribution over this interval. The optimization horizon T is equal to 15. The policy h whose performances have to be evaluated is

$$h(t,x)=-\frac{x}{2},\forall x\in \mathcal{X},\forall t\in \{0,\dots ,T-1\}.$$

The initial state of the system is set x₀ = −0.5.

For our first set of experiments, we choose to work with a value of p = 10 i.e., the MFMC estimator rebuilds 10 artificial trajectories to estimate J^h(−0.5). In these experiments, for different cardinalities $n_j={(10j)}^2=m_j^{2}j=1\dots 10$, we build a sample _nj = {(x^l,u^l)} that uniformly cover the space × as follows:

$$x^l=-1+\frac{2j_1}{m_j}\text{and}{u}^l=-1+\frac{2j_2}{m_j}{j}_1,j_2\in \{0,\dots ,m_j-1\}.$$

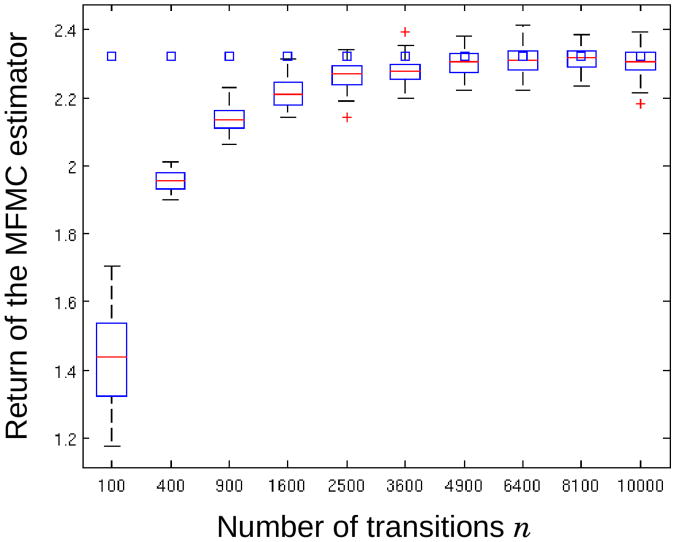
Then, we generate 50 random sets ${\mathcal{F}}_{n_j}^1,\dots ,{\mathcal{F}}_{n_j}^{50}$ Over _nj and run our MFMC estimator on each of these sets. The results of this first set of experiments are gathered in Figure 3. For every value of n_j considered in our experiments, the 50 values computed by the MFMC estimator are concisely represented by a boxplot. The box has lines at the lower quartile, median, and upper quartile values. Whiskers extend from each end of the box to the adjacent values in the data within 1.5 times the interquartile range from the ends of the box. Outliers are data with values beyond the ends of the whiskers and are displayed with a red + sign. The squares represent an accurate estimate of J^h(−0.5) computed by running thousands of Monte Carlo simulations. As we observe, when the samples increase in size (which corresponds to a decrease of the pT–dispersion α_pT( _n)) the MFMC estimator is more likely to output accurate estimations of J^h(−0.5). As explained throughout this paper, there exist many similarities between the model-free MFMC estimator and the model-based MC estimator. These can be empirically illustrated by putting Figure 3 in perspective with Figure 4. This latter figure reports the results obtained by 50 independent runs of the MC estimator, each one of these runs using also p = 10 trajectories. As expected, one can see that the MFMC estimator tends to behave similarly to the MC estimator when the cardinality of the sample increases.

Fig. 3.

Computations of the MFMC estimator with p = 10, for different cardinalities n of the sample of one-step transitions. For each cardinality, 50 independent samples of transitions have generated. Squares represent J^h (x₀).

Fig. 4.

Computations of the MC estimator with p = 10. 50 independent runs have been computed.

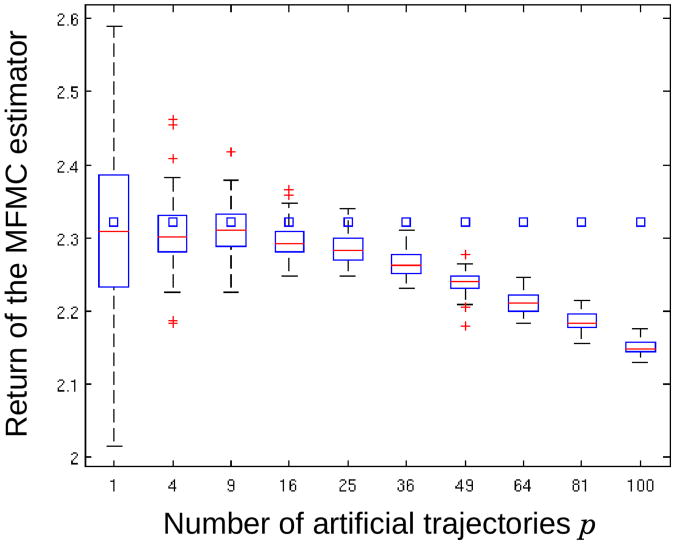
In our second set of experiments, we choose to study the influence of the number of artificial trajectories p upon which the MFMC estimator bases its prediction. For each value p_j = j² j = 1 … 10 we generate 50 samples ${\mathcal{F}}_{\mathrm{10,000}}^1,\dots ,{\mathcal{F}}_{\mathrm{10,000}}^{50}$ of one-step transitions of cardinality 10, 000 (using the sample ₁₀₀₀₀ defined in the first set of experiments) and use these samples to compute the MFMC estimator. The results are plotted in Figure 5. This figure shows that the bias of the MFMC estimator seems to be relatively small for small values of p and to increase with p. This is in accordance with Theorem 1 which bounds the bias with an expression that is increasing with p.

Fig. 5.

Computations of the MFMC estimator for different values of the number p of artificial trajectories extracted from a sample of n = 10, 000 tuples. For each value of p, 50 independent samples of transitions have generated. Squares represent J^h (x₀).

In Figure 6, we have plotted the evolution of the values computed by the model-based MC estimator when the number of trajectories it considers in its prediction increases. While, for small numbers of trajectories, it behaves similarly to the MFMC estimator, the quality of its predictions steadily increases with p, while it is not the case for the MFMC estimator whose performances degrade once p crosses a threshold value. Notice that this threshold value could be made larger by increasing the size of the samples of one-step system transitions used as input of the MFMC algorithm.

Fig. 6.

Computations of the MC estimator for different values of the number of trajectories p. For each value of p, 50 independent runs of the MC estimator have been computed. Squares represent J^h(x₀).

4.2.4 MFMC Estimation of the value at risk

In order to take into consideration the riskiness of policies - and not only their good performances “on average” -, one may prefer to consider a Value-at-Risk–type performance criterion instead of expected return. Notice that this type of criterion has received more and more attention during the last few years inside the RL community [11,31,32].

If we consider the p artificial trajectories that are rebuilt by the MFMC estimator, the value at risk $J_{\mathit{\text{VaR}}}^{h,(b,c)}(x_0)$ can be efficiently approximated by the value ${\stackrel{\sim }{J}}_{\mathit{\text{VaR}}}^{h,(b,c)}(x_0)$ defined as follows:

Definition 11 (Estimate of the T–stage Value at Risk)

Let b ∈ ℝ and c ∈[0, 1[.

$${\stackrel{\sim }{J}}_{\mathit{\text{VaR}}}^{h,(b,c)}(x_0)=\{\begin{array}{cc}-\infty & \text{if}\frac{1}{p}{\sum }_{i=1}^p{\mathbb{I}}_{\{{\mathbf{r}}^i<b\}}>c,\\ {\mathcal{M}}^h({\mathcal{F}}_n,x_0)& \text{otherwise}\end{array}$$

where rⁱ denotes the return of the i–th artificial trajectory:

$${\mathbf{r}}^i=\sum _{t=0}^{T-1}{r}^{l_t^i}.$$

4.3 Artificial Trajectories in the Deterministic Case: Computing Bounds

From this subsection to the end of Section 4, we assume a deterministic environment. More formally, we assume that the disturbances space is reduced to a single element = {0} which concentrates the whole probability mass p (0) = 1. We abusively use the convention:

$$\forall (x,u)\in \mathcal{X}\times \mathcal{U},f(x,u)=f(x,u,0),\rho (x,u)=\rho (x,u,0).$$

We still assume that the functions f, ρ and h are Lipschitz continuous. Observe that, in a deterministic context, only one trajectory is needed to compute J^h(x₀) by Monte Carlo estimation. We have the following result:

Proposition 2 (Lower Bound from the MFMC)

Let ${[(x^{l_t},u^{l_t},r^{l_t},y^{l_t})]}_{t=0}^{T-1}$ be an artificial trajectory rebuilt by the MFMC algorithm when using the distance measure Δ. Then, we have

$$|{\mathcal{M}}_1^h({\mathcal{F}}_n,x_0)-J^h(x_0)|\le \sum _{t=0}^{T-1}{L}_{Q_{T-t}}\Delta ((y^{l_{t-1}},h(t,y^{l_{t-1}})),(x^{l_t},u^{l_t}))$$

where

$$L_{Q_{T-t}}=L_{\rho }\sum _{i=0}^{T-t-1}{(L_f(1+L_h))}^i$$

and y^l−1 = x₀.

The proof of this theorem can be found in [19]. Since the previous result is valid for any artificial trajectory, we have:

Corollary 1 (Lower Bound from any Artificial Trajectory)

Let ${[(x^{l_t},u^{l_t},r^{l_t},y^{l_t})]}_{t=0}^{T-1}$ be any artificial trajectory. Then,

$$J^h(x_0)\ge \sum _{t=0}^{T-1}{r}^{l_t}-\sum _{t=0}^{T-1}{L}_{Q_{T-t}}\Delta ((y^{l_{t-1}},h(t,y^{l_{t-1}})),(x^{l_t},u^{l_t}))$$

This suggests to identify an artificial trajectory that leads to the maximization of the previous lower bound:

Definition 12 (Maximal Lower Bound)

$$L^h({\mathcal{F}}_n,x_0)=\underset{{[(x^{l_t},u^{l_t},r^{l_t},y^{l_t})]}_{t=0}^{T-1}\in {\mathcal{F}}_n^T}{\text{max}}\sum _{t=0}^{T-1}{r}^{l_t}-\sum _{t=0}^{T-1}{L}_{Q_{T-t}}\Delta ((y^{l_{t-1}},h(t,y^{l_{t-1}})),(x^{l_t},u^{l_t})).$$

Note that in the same way, a minimal upper bound can be computed:

Definition 13 (Minimal Upper Bound)

$$U^h({\mathcal{F}}_n,x_0)=\underset{{[(x^{l_t},u^{l_t},r^{l_t},y^{l_t})]}_{t=0}^{T-1}\in {\mathcal{F}}_n^T}{\text{min}}\sum _{t=0}^{T-1}{r}^{l_t}+\sum _{t=0}^{T-1}{L}_{Q_{T-1}}\Delta ((y^{l_{t-1}},h(t,y^{l_{t-1}})),(x^{l_t},u^{l_t})).$$

Additionaly, we can prove that both the lower and the upper bound are tight, in the sense that they both converge towards J^h(x₀) when the dispersion of the sample of system transitions _n decreases towards zero.

Proposition 3 (Tightness of the Bounds)

$$\begin{array}{r}\exists C_b>0:J^h(x_0)-L^h({\mathcal{F}}_n,x_0)\le C_b{\alpha }_1({\mathcal{P}}_n)\\ U^h({\mathcal{F}}_n,x_0)-J^h(x_0)\le C_b{\alpha }_1({\mathcal{P}}_n)\end{array}$$

where α₁( _n) denotes the 1 – dispersion of the sample of system transitions _n.

This result is proved in [19]. Note that the computation of both the maximal lower bound and minimal upper bound can be reformulated as a shortest path problem in a graph, for which the computational complexity is linear with respect to the optimization horizon T and quadratic with respect to the cardinality n of the sample of transitions _n.

4.3.1 Extension to Finite Action Spaces

The results given above can be extended to the case where the action space is finite (and thus discrete) by considering policies that are fully defined by a sequence of actions. Such policies can be qualified as “open-loop”. Let Π be the set of open-loop policies:

Definition 14 (Open-loop Policies)

$$\Pi =\{\pi :\{0,\dots ,T-1\}\to \mathcal{U}\}$$

Given an open-loop policy π, the (deterministic) T–stage return of π writes:

$$J^{\pi }(x_0)=\sum _{t=0}^{T-1}\rho (x_t,\pi (t))$$

With

$$x_{t+1}=f(x_t,\pi (t)),\forall t\in \{0,\dots ,T-1\}.$$

In the context of a finite action space, the Lipschitz continuity of f and ρ is: ∀(x, x′, u) ∈ ² × ,

$${║f(x,u)-f(x\prime ,u)║}_{\mathcal{X}}\le L_f{║x-x\prime ║}_{\mathcal{X}},|\rho (x,u)-\rho (x\prime ,u)|\le L_{\rho }{║x-x\prime ║}_{\mathcal{X}}.$$

Since the action space is not normed anymore, we also need to redefine the sample dispersion.

Definition 15 (Sample Dispersion)

We assume that the state space is bounded, and we define the sample dispersion α*( _n) as the smallest α such that

$$\exists \alpha >0:\underset{x\in \mathcal{X}}{\text{sup}}\underset{l\in \{1,\dots ,n\}}{\text{min}}{║x^l-x║}_{\mathcal{X}}\le \alpha .$$

Let π ∈ Π be an open-loop policy. We have the following result:

Proposition 4 (Lower Bound - Open-loop Policy π)

Let ${[(x^{l_t},u^{l_t},r^{l_t},y^{l_t})]}_{t=0}^{T-1}$ be an artificial trajectory such that

$$u^{l_t}=\pi (t)\forall t\in \{0,\dots ,T-1\}.$$

Then,

$$J^{\pi }(x_0)\ge \sum _{t=0}^{T-1}{r}^{l_t}-\sum _{t=0}^{T-1}{L}_{Q_{T-t}}^{\prime }{║y^{l_{t-1}}-x^{l_t}║}_{\mathcal{X}}.$$

where

$$L_{Q_{T-t}}^{\prime }=L_{\rho }\sum _{i=0}^{T-t-1}{(L_f)}^i.$$

A maximal lower bound can then be computed by maximizing the previous bound over the set of all possible artificial trajectories that satisfy the condition u^l_t = π(t) ∀t ∈ {0,…,T − 1}. In the following, we denote by ${\mathcal{F}}_{n,\pi }^T$ the set of artificial trajectories that satisfy this condition:

$${\mathcal{F}}_{n,\pi }^T=\{{[(x^{l_t},u^{l_t},r^{l_t},y^{l_t})]}_{t=0}^{T-1}\in {\mathcal{F}}_n^T|u^{l_t}=\pi (t)\forall t\in 0,\dots ,T-1\}$$

Then, we have:

Definition 16 (Maximal Lower Bound - Open-loop Policy π)

$$L^{\pi }({\mathcal{F}}_n,x_0)=\underset{{[(x^{l_t},u^{l_t},r^{l_t},y^{l_t})]}_{t=0}^{T-1}\in {\mathcal{F}}_{n,\pi }^T}{\text{max}}\sum _{t=0}^{T-1}{r}^{l_t}-\sum _{t=0}^{T-1}{L}_{Q_{T-t}}^{\prime }{║y^{l_{t-1}}-x^{l_t}║}_{\mathcal{X}}.$$

Similarly, a minimal upper bound U^π ( _n, x₀) can also be computed:

Definition 17 (Minimal Upper Bound - Open-loop Policy π)

$$U^{\pi }({\mathcal{F}}_n,x_0)=\underset{{[(x^{l_t},u^{l_t},r^{l_t},y^{l_t})]}_{t=0}^{T-1}\in {\mathcal{F}}_{n,\pi }^T}{\text{min}}\sum _{t=0}^{T-1}{r}^{l_t}+\sum _{t=0}^{T-1}{L}_{Q_{T-t}}^{\prime }{║y^{l_{t-1}}-x^{l_t}║}_{\mathcal{X}}.$$

Both bounds are tight in the following sense:

Proposition 5 (Tightness of the Bounds - Open-loop Policy π)

$$\exists C_b^{\prime }>0:J^{\pi }(x_0)-L^{\pi }({\mathcal{F}}_n,x_0)\le c_b^{\prime }\alpha \ast ({\mathcal{P}}_n),U^{\pi }({\mathcal{F}}_n,x_0)-J^{\pi }(x_0)\le C_b^{\prime }\alpha \ast ({\mathcal{P}}_n).$$

The proofs of the above stated results are given in [20].

4.4 Artificial Trajectories for Computing Safe Policies

Like in Section 4.3.1, we still assume that the action space is finite, and we consider open-loop policies. To obtain a policy with good performance guarantees, we suggest to find an open-loop policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }\in \Pi$ such that:

$${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }\in \underset{\pi \in \Pi }{\text{arg max}}{L}^{\pi }({\mathcal{F}}_n,x_0).$$

Recall that such an “open-loop” policy is optimized with respect to the initial state x₀. Solving the above optimization problem can be seen as identifying an optimal rebuilt artificial trajectory ${\left[\right(x^{l_t^{\ast }},u^{l_t^{\ast }},r^{l_t^{\ast }},y^{l_t^{\ast }}\left)\right]}_{t=0}^{T-1}$ and outputting as open-loop policy the sequence of actions taken along this artificial trajectory:

$$\forall t\in \{0,\dots ,T-1\},{\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }(t)=u^{l_t^{\ast }}.$$

Finding such a policy can again be done in an efficient way by reformulating the problem as a shortest path problem in a graph. We provide in [20] an algorithm called CGRL (which stands for “Cautious approach to Generalization in RL”) of complexity (n²T) for finding such a policy. A tabular version of the CGRL is given in Table 2 and an illustration that shows how the CGRL solution can be seen as a shortest path in a graph is also given in Figure 7. We now give a theorem which shows the convergence of the policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ towards an optimal open-loop policy when the dispersion α* ( _n) of the sample of transitions converges towards zero.

Fig. 7.

A graphical interpretation of the CGRL algorithm. The CGRL solution can be interpreted as a shortest path in a specific graph.

Theorem 3 (Convergence of ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$)

Let * (x₀) be the set of optimal open-loop policies:

$$\mathcal{J}\ast (x_0)=\underset{\pi \in \Pi }{\text{arg max}}{J}^{\pi }(x_0),$$

Algorithm 2 CGRL algorithm.

Input: ${\mathcal{F}}_n={\{(x^l,u^l,r^l,y^l)\}}_{l=1}^n,L_f,L_{\rho },x_0,T$

Initialization:

D ← n × (T − 1) matrix initialized to zero;

A ← n–dimensional vector initialized to zero;

B ← n–dimensional vector initialized to zero;

Computation of the Lipschitz constants ${\left\{L_{Q_N}^{\prime }\right\}}_{N=1}^T$:

$L_{Q_1}^{\prime }=L_{\rho }$;

for k = 2 … T do

$L_{Q_k}^{\prime }\leftarrow L_{\rho }+L_f{L}_{Q_{k-1}}^{\prime }$;

end for

t ← T − 2;

while t > −1 do

for i = 1 … n do

$j_0\leftarrow \underset{j\in \{1,\dots ,n\}}{\text{arg max}}{r}^j-L_{Q_{T-t-1}}^{\prime }{║y^i-x^j║}_{\mathcal{X}}+B(j)$;

$m_0\leftarrow \underset{j\in \{1,\dots ,n\}}{\text{max}}{r}^j-L_{Q_{T-t-1}}^{\prime }{║y^i-x^j║}_{\mathcal{X}}+B(j)$;

A(i) ← m0;

D(i, t + 1) ← j0; \\ best tuple at t + 1 if in tuple i at time t

end for

B ← A;

t = t −1;

end while

Conclusion:

S ← (T + 1)–length vector of actions initialized to zero;

$l\leftarrow \underset{j\in \{1,\dots ,n\}}{\text{arg max}}{r}^j-L_{Q_T}^{\prime }{║x_0-x^j║}_{\mathcal{X}}+B(j)$;

$S(T+1)\leftarrow \underset{j\in \{1,\dots ,n\}}{\max }{r}^j-L_{Q_T}^{\prime }{║x_0-x^j║}_{\mathcal{X}}+B(j)$; \\ best lower bound

S(1) ← ul; \\ CGRL action for t = 0.

for t = 0 … T − 2 do

l′ ← D(l, t + 1);

S(t + 2,:) ← ul′; other CGRL actions

l ← l′;

end for

Return: S

and let us suppose that *(x₀) ≠ Π (if *(x₀) = Π, the search for an optimal policy is indeed trivial). We define

$$∊(x_0)=\underset{\pi \in \Pi \backslash \mathcal{J}\ast (x_0)}{\text{min}}\left\{\right(\underset{\pi \prime \in \Pi }{\text{max}{J}^{{\pi }^{\prime }}}(x_0))-J^{\pi }(x_0)\}.$$

Then,

$$(C_b^{\prime }{\alpha }^{\ast }({\mathcal{P}}_n)<∊(x_0))\Rightarrow {\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }\in \mathcal{J}\ast (x_0).$$

The proof of this result is also given in [20].

• Illustration

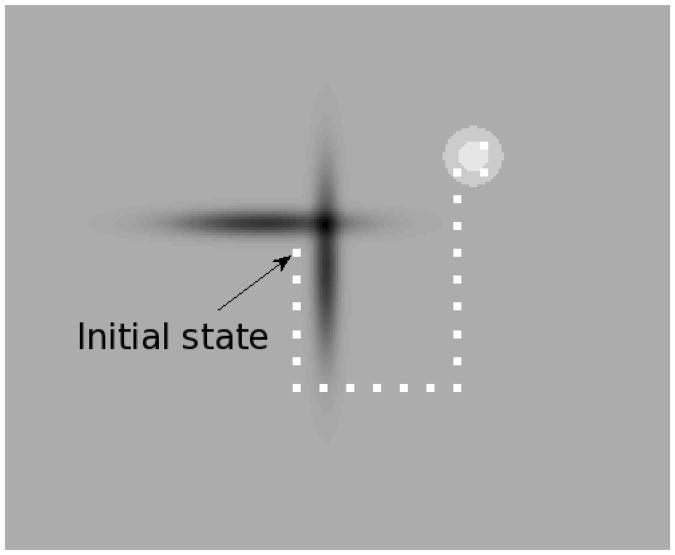
We now illustrate the performances of the policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ computed by the CGRL algorithm on a variant of the puddle world benchmark introduced in [42]. In this benchmark, a robot whose goal is to collect high cumulated rewards navigates on a plane. A puddle stands in between the initial position of the robot and the high reward area (see figure 8). If the robot is in the puddle, it gets highly negative rewards. An optimal navigation strategy drives the robot around the puddle to reach the high reward area. Two datasets of one-step transitions have been used in our example. The first set contains elements that uniformly cover the area of the state space that can be reached within T steps. The set ′ has been obtained by removing from the elements corresponding to the highly negative rewards. The full specification of the benchmark and the exact procedure for generating and ′ are given in [20]. On Figure 9, we have drawn the trajectory of the robot when following the policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$. Every state encountered is represented by a white square. The plane upon which the robot navigates has been colored such that the darker the area, the smaller the corresponding rewards are. In particular, the puddle area is colored in dark grey/black. We see that the policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ drives the robot around the puddle to reach the high-reward area – which is represented by the light-grey circles.

Fig. 8.

The Puddle World benchmark. Starting from x₀, an agent has to avoid the puddles and navigate towards the goal.

Fig. 9.

CGRL with .

Figure 10 represents the policy inferred from by using the (finite-time version of the) Fitted Q Iteration algorithm (FQI) combined with extremely randomized trees as function approximators [13]. The trajectories computed by the policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ and FQI algorithms are very similar and so are the sums of rewards obtained by following these two trajectories. However, by using ′ rather that , the policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ and FQI algorithms do not lead to similar trajectories, as it is shown on Figures 11 and 12. Indeed, while the policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ still drives the robot around the puddle to reach the high reward area, the FQI policy makes the robot cross the puddle. In terms of optimality, this latter navigation strategy is much worse. The difference between both navigation strategies can be explained as follows. The FQI algorithm behaves as if it were associating to areas of the state space that are not covered by the input sample, the properties of the elements of this sample that are located in the neighborhood of these areas. This in turn explains why it computes a policy that makes the robot cross the puddle. The same behavior could probably be observed by using other algorithms that combine dynamic programming strategies with kernel-based approximators or averagers [5,25,37]. The policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ generalizes the information contained in the dataset, by assuming, given the intial state, the most adverse behavior for the environment according to its weak prior knowledge about the environment. This results in the fact that it penalizes sequences of decisions that could drive the robot in areas not well covered by the sample, and this explains why the policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ drives the robot around the puddle when run with ′.

Fig. 10.

FQI with .

Fig. 11.

CGRL with ′.

Fig. 12.

FQI with ′.

4.4.1 Taking Advantage of Optimal Trajectories

In this section, we give another result which shows that, in the case where an optimal trajectory can be found in the sample of system transitions, then the policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ computed by the CGRL algorithm is also optimal.

Theorem 4 (Optimal Policies computed from Optimal Trajectories)

Let ${\pi }_{x_0}^{\ast }\in \mathcal{J}\ast (x_0)$ be an optimal open-loop policy. Let us assume that one can find in _n a sequence of T one-step system transitions

$$[(x^{l_0},u^{l_0},r^{l_0},x^{l_1}),(x^{l_1},u^{l_1},r^{l_1},x^{l_2}),\dots ,(x^{l_{T-1}},u^{l_{T-1}},r^{l_{T-1}},x^{l_T})]\in {\mathcal{F}}_n^T$$

such that

$$\begin{array}{l}{x}^{l_0}=x_0,\\ u^{l_t}={\pi }_{x_0}^{\ast }(t)\forall t\in \{0,\dots ,T-1\}.\end{array}$$

Let ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ be such that

$${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }\in \underset{\pi \in \Pi }{\text{arg max}}{L}^{\pi }({\mathcal{F}}_n,x_0).$$

Then,

$${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }\in {\mathcal{J}}^{\ast }(x_0).$$

Proof Let us prove the result by contradiction. Assume that ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$ is not optimal. Since ${\pi }_{x_0}^{\ast }$ is optimal, one has:

$$J^{{\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }}(x_0)<J^{{\pi }_{x_0}^{\ast }}(x_0).$$ (1)

Let us now consider the lower bound ${\mathcal{B}}^{{\pi }_{x_0}^{\ast }}({\mathcal{F}}_n,x_0)$ on the return of the policy ${\pi }_{x_0}^{\ast }$ computed from the sequence of transitions

$$[(x^{l_0},u^{l_0},r^{l_0},x^{l_1}),(x^{l_1},u^{l_1},r^{l_1},x^{l_2}),\dots ,(x^{l_{T-1}},u^{l_{T-1}},r^{l_{T-1}},x^{l_T})]\in {\mathcal{F}}_n^T.$$

By construction of this sequence of transitions, we have:

$$\begin{array}{l}{\mathcal{B}}^{{\pi }_{x_0}^{\ast }}({\mathcal{F}}_n,x_0)=\sum _{t=0}^{T-1}{r}^{l_t}-\sum _{t=0}^{T-1}{L}_{Q_{T-t}}^{\prime }{║x^{l_t}-x^{l_t}║}_{\mathcal{X}}\\ =\sum _{t=0}^{T-1}{r}^{l_t}\\ =J^{h_{x_0}^{\ast }}(x_0)\end{array}$$

By definition of the policy ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }\in \underset{\pi \in \Pi }{\text{arg max}}{L}^{\pi }({\mathcal{F}}_n,x_0)$, we have:

$$L^{{\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }}({\mathcal{F}}_n,x_0)\ge {\mathcal{B}}^{{\pi }_{x_0}^{\ast }}({\mathcal{F}}_n,x_0)=J^{{\pi }_{x_0}^{\ast }}(x_0).$$ (2)

Since $L^{{\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }}({\mathcal{F}}_n,x_0)$ is a lower bound on the return of ${\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }$, we have:

$$J^{{\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }}(x_0)\ge L^{{\widehat{\pi }}_{{\mathcal{F}}_n,x_0}^{\ast }}({\mathcal{F}}_n,x_0).$$ (3)

Combining inequalities 2 and 3 yields a contradiction with inequality 1.

4.5 Rebuilding Artificial Trajectories for Designing Sampling Strategies

We suppose in this section that additional system transitions can be generated, and we detail hereafter a sampling strategy to select state-action pairs (x, u) for generating f(x, u) and ρ(x, u) so as to be able to discriminate rapidly – as new one-step transitions are generated – between optimal and non-optimal policies from Π. This strategy is directly based on the previously described bounds.

Before describing our proposed sampling strategy, let us introduce a few definitions. First, note that a policy can only be optimal given a set of one-step transitions if its upper bound is not lower than the lower bound of any element of Π. We qualify as “candidate optimal policies given ” and we denote by Π ( , x₀) the set of policies which satisfy this property:

Definition 18 (Candidate Optimal Policies Given )

$$\Pi (\mathcal{F},x_0)=\{\pi \in \Pi |\forall \pi \prime \in \Pi ,U^{\pi }(\mathcal{F},x_0)\ge L^{\pi \prime }(\mathcal{F},x_0)\}.$$

We also define the set of “compatible transitions given ” as follows:

Definition 19 (Compatible Transitions Given )

A transition (x, u, r, y) ∈ × × ℝ × is said compatible with the set of transitions if

$$\forall (x^l,u^l,r^l,y^l)\in \mathcal{F},(u^l=u)\Rightarrow \{\begin{array}{l}|r-r^l|\le L_{\rho }{║x-x^l║}_{\mathcal{X}},\\ {║y-y^l║}_{\mathcal{X}}\le L_f{║x-x^l║}_{\mathcal{X}}.\end{array}$$

We denote by ( ) ⊂ × × ℝ × the set that gathers all transitions that are compatible with the set of transitions .

Our sampling strategy generates new one-step transitions iteratively. Given an existing set _m of m ∈ ℕ\{0} one-step transitions, which is made of the elements of the initial set _n and the m-n one-step transitions generated during the first m-n iterations of this algorithm, it selects as next sampling point (x^m+1,u^m+1) ∈ × , the point that minimizes in the worst conditions the largest bound width among the candidate optimal policies at the next iteration:

$$(x^{m+1},u^{m+1})\in \underset{(x,u)\in \mathcal{X}\times \mathcal{U}}{\text{arg min}}\{\underset{(r,y)\in ℝ\times \mathcal{X}s.t.(x,u,r,y)\in \mathcal{C}({\mathcal{F}}_m)\pi \in \Pi ({\mathcal{F}}_m\cup \{(x,u,r,y)\},x_0)}{\text{max}}{\delta }^{\pi }({\mathcal{F}}_m\cup \{(x,u,r,y)\},x_0)\}$$

where

$${\delta }^{\pi }(\mathcal{F},x_0)=U^{\pi }(\mathcal{F},x_0)-L^{\pi }(\mathcal{F},x_0).$$

Based on the convergence properties of the bounds, we conjecture that the sequence (Π( _m, x₀))_m∈ℕ converges towards the set of all optimal policies in a finite number of iterations:

$$\exists m_0\in \mathbb{N}\backslash \{0\}:\forall m\in \mathbb{N},(m\ge m_0)\Rightarrow \Pi ({\mathcal{F}}_m,x_0)=\mathcal{J}\ast (x_0).$$

The analysis of the theoretical properties of the sampling strategy and its empirical validation are left for future work.

• Illustration

In order to illustrate how the bound-based sampling strategy detailed above allows to discriminate among policies, we consider the following toy problem. The actual dynamics and reward functions are given by:

$$\begin{array}{l}f(x,u)=x+u,\\ \rho (x,u)=x+u.\end{array}$$

The state space is included in ℝ. The action space is set to

$$\mathcal{U}=\{-0.20,-0.10,0,+0.10,+0.20\}.$$

We consider a time horizon T = 3, which induces 5³ = 125 different policies. The initial state is set to x₀ = −0.65. Consequently, there is only one optimal policy, which consists in applying action +0.20 three times.

In the following experiments, the $\underset{(x,u)\in \mathcal{X}\times \mathcal{U}}{\text{arg min}}$ and $\underset{(r,y)\in ℝ\times \mathcal{X}s.t.(x,u,r,y)\in \mathcal{C}({\mathcal{F}}_m)}{\text{max}}$ operators, whose computation is of huge complexity, are approximated using purely random search algorithms (i.e. by randomly generating feasible points and taking the optimum over those points). We begin with a small sample of n = 5 transitions (one for each action)

$$\{(0,-0.20,\rho (0,-0.20),f(0,-0.20)),(0,-0.10,\rho (0,-0.10),f(0,-0.10)),(0,0,\rho (0,0),f(0,0)),(0,0.10,\rho (0,0.10),f(0,0.10)),(0,0.20,\rho (0,0.20),f(0,0.20))\}$$

and iteratively augment it using our bound-based sampling strategy. We compare our strategy with a uniform sampling strategy (starting from the same initial sample of 5 transitions). We plot in Figure 13 the evolution of the empirical average number of candidate optimal policies (over 50 runs) with respect to the cardinality of the generated sample of transitions ². We empirically observe that the bound-based sampling strategy allows to discriminate policies faster than the uniform sampling strategy. In particular, we observe that, on average, bound-based strategy using 40 samples provides discriminating performances that are equivalent to those of the uniform sampling strategy using 80 samples, which represents a significant increase. Note that in this specific benchmark, one should sample 5 + 25 + 125 = 155 state-action pairs (by trying all possible policies) in order to be sure to discriminate all non-optimal policies.

Fig. 13.

Evolution of the average number of candidate optimal policies with respect to the cardinality of the generated samples of transitions using our bound-based sampling strategy and a uniform sampling strategy (empirical average over 50 runs).

4.6 Summary

We synthesize in Figure 14 the different settings and the corresponding results that have been presented in Section 4. Such results are classified in two main categories: stochastic setting and deterministic setting. Among each setting, we explicit the context (continuous/finite action space) and the nature of each result (theoretical result, algorithmic contribution, empirical evaluation) using a color code.

Fig. 14.

A schematic presentation of the results presented in Section 4. algorithm.

5 Towards a New Paradigm for Batch Mode RL

In this concluding section, we highlight some connexions between the approaches based on synthesizing artificial trajectories and a more standard batch mode RL algorithm, the FQI algorithm [13] when it is used for policy evaluation. From a technical point of view, we consider again in this section the stochastic setting that was formalized in Section 3. The action space is continuous and normed, and we consider a given closed-loop, time varying, Lipschitz continuous control policy h: {0, …, T − 1} × → .

5.1 Fitted Q Iteration for Policy Evaluation

The finite horizon FQI iteration algorithm for policy evaluation (FQI-PE) works by recursively computing a sequence of functions ${({\widehat{Q}}_{T-t}^h(.,.))}_{t=0}^{T-1}$ as follows:

Definition 20 (FQI-PE Algorithm)

• ∀(x, u) ∈ × .

$${\widehat{Q}}_0^h(x,u)=0\forall (x,u)\in \mathcal{X}\times \mathcal{U},$$

• For t = T − 1…0, build the dataset $D={\left\{\right(i^l,o^l\left)\right\}}_{l=1}^n$:

$$\begin{array}{c}{i}^l=(x^l,u^l)\\ o^l=r^l+{\widehat{Q}}_{T-t-1}^h(y^l,h(t+1,y^l))\end{array}$$

and use a regression algorithm to infer from D the function ${\widehat{Q}}_{T-t}^h$:

$${\widehat{Q}}_{T-t}^h=\mathcal{R}\mathcal{A}(D).$$

The FQI -PE estimator of the policy h is given by:

Definition 21 (FQI Estimator)

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)={\widehat{Q}}_T^h(x_0,h(0,x_0)).$$

5.2 FQI using k–Nearest Neighbor Regressors: an Artificial Trajectory Viewpoint

We propose in this section to use a k–Nearest Neighbor algorithm (k–NN) as regression algorithm . In the following, for a given state action couple (x, u) ∈ × , we denote by l_i(x, u) the lowest index in _n of the i-th nearest one step transition from the state-action couple (x, u) using the distance measure Δ. Using this notation, the k–NN based FQI-PE algorithm for estimating the expected return of the policy h works as follows:

Definition 22 (k–NN FQI-PE Algorithm)

• ∀(x, u) ∈ × ,

$${\widehat{Q}}_0^h(x,u)=0,$$

• For t = T − 1…0, ∀(x, u) ∈ × ,

$${\widehat{Q}}_{T-t}^h(x,u)=\frac{1}{k}\sum _{i=1}^k(r^{l_i(x,u)}+{\widehat{Q}}_{T-t-1}^h(y^{l_i(x,u)},h(t+1,y^{l_i(x,u)})\left)\right).$$

The k–NN FQI-PE estimator of the policy h is given by:

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)={\widehat{Q}}_T^h(x_0,h(0,x_0)).$$

One can observe that, for a fixed initial state x₀, the computation of the k–NN FQI-PE estimator of h works by identifying (k + k² + … + k^T) non-unique one-step transitions. These transitions are non-unique in the sense that some transitions can be selected several times during the process. In order to concisely denote the indexes of the one-step system transitions that are selected during the k–NN FQI-PE algorithm, we introduce the notation l^{i₀,i₁, … i_t} for refering to the transition l_it (y^{li₀, … i_t−1}, h(t, y^{li₀, … i_t−1})) for i₀, … i_t ∈ {1, … k}, t ≥ 1 with l^i₀ = l_i0(x₀, h(0, x₀)). Using these notations, we illustrate the computation of the k–NN FQI-PE Estimator in Figure 15. Then, we have the following result:

Fig. 15.

Illustration of the k–NN value iteration algorithm in terms of artificial trajectories.

Proposition 6 (k–NN FQI-PE using Artificial Trajectories)

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)=\frac{1}{K^T}\sum _{i_0=1}^k\cdots \sum _{i_{T-1}=1}^k(r^{l^{i_0}}+r^{l^{i_0,i_1}}+\dots +r^{l^{i_0,i_1,\dots ,i_{T-1}}}).$$

where the set of rebuilt artificial trajectories

$$\left\{\right[(x^{l^{i_0}},u^{l^{i_0}},r^{l^{i_0}},y^{l^{i_0}}),\dots ,(x^{l^{i_0,\dots ,i_{T-1}}},u^{l^{i_0,\dots ,i_{T-1}}},r^{l^{i_0,\dots ,i_{T-1}}},y^{l^{i_0,\dots ,i_{T-1}}})\left]\right\}$$

is such that ∀t ∈ {0, …, T − 1}, ∀ (i₀, …,i_t) ∈ {1, …, k}^{t + 1},

$$\Delta \left(\right(y^{l^{i_0,\dots ,i_{t-1}}},h(t,y^{l^{i_0,\dots ,i_{t-1}}})),(x^{l^{i_0,\dots ,i_t}},u^{l^{i_0,\dots ,i_t}}\left)\right)\le {\alpha }_k({\mathcal{P}}_n).$$

Proof We propose to prove by induction the property

$${\mathcal{H}}_t:{\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)=\frac{1}{k^t}\sum _{i_0=1}^k\dots \sum _{i_{t-1}=1}^k(r^{l^{i_0}}+\dots +r^{l^{i_0,\dots ,i_{t-1}}}+{\widehat{Q}}_{T-t}^h(y^{l^{i_0,\dots ,i_{t-1}}},h(t,y^{l^{i_0,\dots ,i_{t-1}}})\left)\right).$$

Basis: According to the definition of the k–NN estimator, we have:

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)=\frac{1}{k}\sum _{i_0=1}^k(r^{l^{i_0}}+{\widehat{Q}}_{T-1}^h(y^{l^{i_0}},h(1,y^{l^{i_0}})\left)\right),$$

which proves ₁.

Induction step: Let us assume that _t is true for t ∈ {1,…, T − 1}. Then, we have:

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)=\frac{1}{k^t}\sum _{i_0=1}^k\dots \sum _{i_{t-1}=1}^k(r^{l^{i_0}}+\dots +r^{l^{i_0,\dots ,i_{t-1}}}+{\widehat{Q}}_{T-t}^h(y^{l^{i_0,\dots ,i_{t-1}}},h(t,y^{l^{i_0,\dots ,i_{t-1}}})\left)\right).$$ (4)

According to the definition of the k–NN FQI-PE algorithm, we have:

$${\widehat{Q}}_{T-t}^h(y^{l^{i_0,\dots ,i_{t-1}}},h(t,y^{l^{i_0,\dots ,i_{t-1}}}\left)\right)=\frac{1}{k}\sum _{i_t=1}^k(r^{l^{i_0,\dots ,i_{t-1,i_t}}}+{\widehat{Q}}_{T-t-1}^h(y^{l^{i_0,\dots ,i_{t-1},i_t}},h(t+1,y^{l^{i_0,\dots ,i_{t-1},i_t}})\left)\right)$$ (5)

Equations (4) and (5) give

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)=\frac{1}{k^t}\sum _{i_0=1}^k\dots \sum _{i_{t-1}=1}^k(r^{l^{i_0}}+\dots +r^{l^{i_0,\dots ,i_{t-1}}}+\frac{1}{k}\sum _{i_t=1}^k(r^{l^{i_0,\dots ,i_t}}+{\widehat{Q}}_{T-t-1}^h(y^{l^{i_0,\dots ,i_t}},h(t+1,y^{l^{i_0,\dots ,i_t}}))))=\frac{1}{k^t}\sum _{i_0=1}^k\dots \sum _{i_{t-1}=1}^k(\frac{1}{k}\sum _{i_t=1}^k(r^{l^{i_0}}+\dots +r^{l^{i_0,\dots ,i_{t-1}}})+\frac{1}{k}\sum _{i_t=1}^k(r^{l^{i_0,\dots ,i_t}}+{\widehat{Q}}_{T-t-1}^h(y^{l^{i_0,\dots ,i_t}},h(t+1,y^{l^{i_0,\dots ,i_t}}))))=\frac{1}{k^{t+1}}\sum _{i_0=1}^k\dots \sum _{i_{t-1}=1}^k\sum _{i_t=1}^k(r^{l^{i_0}}+\dots +r^{l^{i_0,\dots ,i_{t-1}}}+r^{l^{i_0,\dots ,i_t}}+{\widehat{Q}}_{T-t-1}^h(y^{l^{i_0,\dots ,i_t}},h(t+1,y^{l^{i_0,\dots ,i_t}}))),$$

which proves _t+1. The proof is completed by observing that

$${\widehat{Q}}_0^h(x,u)=0,\forall (x,u)\in \mathcal{X}\times \mathcal{U}$$

and by observing that the property

$$\Delta \left(\right(y^{l^{i_0,\dots ,i_{t-1}}},h(t,y^{l^{i_0,\dots ,i_{t-1}}})),(x^{l^{i_0,\dots ,i_t}},u^{l^{i_0,\dots ,i_t}}\left)\right)\le {\alpha }_k({\mathcal{P}}_n).$$

directly comes from the use of k–NN function approximators.

The previous result shows that the estimate of the expected return of the policy h computed by the k–NN FQI-PE algorithm is the average of the return of k^T artificial trajectories. These artificial trajectories are built from (k + k² + … + k^T) non-unique one-step system transitions from _n that are also chosen by minimizing the distance between two successive one-step transitions.

• Illustration. We empirically compare the MFMC estimator with the k–NN FQI-PE estimator on the toy problem presented in Section 4.2, but with a smaller time horizon T = 5. For a fixed cardinality n = 100, we consider all possible values of the parameter k (k ∈ {1,…, 100} since there are at most n nearest neighbours) and p (p ∈ {1,…, 20} since one can generate at most n/T different artificial trajectories without re-using transitions). For each value of p (resp. k), we generate 1000 samples of transitions using a uniform random distribution over the state action space. For each sample, we run the MFMC (resp. the k–NN FQI-PE estimator). As a baseline comparison, we also compute a 1000 runs of the MC estimator for every value of p. Figure 16 (resp. 17 and 18) reports the obtained empirical average (resp. variance and mean squared error).

Fig. 16.

Empirical average observed for the MC estimator, the MFMC estimator and the k–NN FQI-PE estimator for different values of k and p (k ∈ {1,…, 100}, p ∈ {1,…, 20}, 1000 runs for each value of k, p).

We observe in Figure 16 that (i) the MFMC estimator with p ∈ {1,…, 3} is less biased than the k–NN FQI-PE estimator with any value of k ∈ {1,…, 100} and (ii) the bias of the MFMC estimator increases faster (with respect to p) than the bias of the k–NN FQI-PE estimator (with respect to k). The increase of the bias of the MFMC estimator with respect to p is suggested by Theorem 1, where an upper bound on the bias that increases with p is provided. This phenomenon seems to affect the k–NN FQI-PE estimator (with respect to k) to a lesser extent. In Figure 17, we observe that the k–NN FQI-PE estimator has a variance that is higher than that of the MFMC estimator for any k = p. This may be explained by the fact that for samples of n = 100 transitions, one-step transitions are often re-used by the k–NN FQI-PE estimator, which generates dependence between artificial trajectories. We finally plot in Figure 18 the observed empirical mean squared error (sum of the squared empirical bias and empirical variance) and observe that in our specific setting, the MFMC estimator offers for values of p ∈ {1,2,3,4} a better bias versus variance compromise than the k–NN FQI-PE estimator with any value of k.

Fig. 17.

Empirical variance observed for the MC estimator, the MFMC estimator and the k–NN FQI-PE estimator for different values of k and p (k ∈ {1,…, 100}, p ∈ {1,…, 20}, 1000 runs for each value of k, p).

Fig. 18.

Empirical mean square error observed for the MC estimator, the MFMC estimator and the k–NN FQI-PE estimator for different values of k and p (k ∈ {1,…, 100}, p ∈ {1,…, 20}, 1000 runs for each value of k, p).

5.3 Kernel-based and Other Averaging type Regression Algorithms

The results exposed in Section 5.2 can be extended to the case where the FQI-PE algorithm is combined with kernel-based regressors and in particular tree-based regressors. In such a context, the sequence of functions ${({\widehat{Q}}_{T-t}^h(.))}_{t=0}^T$ is computed as follows:

Definition 23 (KB FQI-PE Algorithm)

∀(x, u) ∈ × ,

$${\widehat{Q}}_0^h(x,u)=0,$$

For t = T – 1 … 0, ∀(x, u) ∈ × ,

$${\widehat{Q}}_{T-t}^h(x,u)=\sum _{l=1}^n{k}_{{\mathcal{F}}_n}((x,u),(x^l,u^l))(r^l+{\widehat{Q}}_{T-t-1}^h(y^l,h(t+1,y^l))),$$

with

$$k_{{\mathcal{F}}_n}((x,u),(x^l,u^l))=\frac{\Phi \left(\frac{\Delta ((x,u),(x^l,u^l))}{b_n}\right)}{{\sum }_{i=1}^n\Phi \left(\frac{\Delta ((x,u),(x^i,u^i))}{b_n}\right)},$$

where Φ: [0,1] → ℝ⁺ is a univariate non-negative “mother kernel” function, and b_n > 0 is the bandwidth parameter. We also suppose that ${\int }_0^1\Phi (z)\mathit{\text{dz}}=1$ and Φ(x) = 0 ∀x > 1.

The KB estimator of the expected return of the policy h is given by:

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)={\widehat{Q}}_T^h(x_0,h(0,x_0)).$$

Given an initial state x₀ ∈ , the computation of the KB FQI-PE algorithm can also be interpreted as an identification of a set of one-step transitions from _n. At each time step t, all the one-step transitions (x^l, u^l, r^l, y^l) that are not farther than a distance b_n from (x_t, h(t, x_t)) are selected and weighted with a distance dependent factor. Other one-step transitions are weighted with a factor equal to zero. This process is iterated with the output of each selected one-step transitions. An illustration is given in Figure 19 . The value returned by the KB estimator can be expressed as follows:

Fig. 19.

Illustration of the KB value iteration agorithm in terms of artificial trajectories.

Proposition 7

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)=\sum _{i_0=1}^n\dots \sum _{i_{T-1}=1}^n{\theta }_0^{0,i_0}{\theta }_1^{i_0,i_1}\dots {\theta }_{T-1}^{i_{T-2},i_{T-1}}(r^{i_0}+\dots +r^{i_{T-1}})$$

with

$$\begin{array}{l}{\theta }_0^{0,i_0}=k_{{\mathcal{F}}_n}((x_0,h(0,x_0)),(x^{i_0},u^{i_0})),\\ {\theta }_{t+1}^{i_t,i_{t+1}}=k_{{\mathcal{F}}_n}((y^{i_t},h(t+1,y^{i_t})),(x^{i_{t+1}},u^{i_{t+1}})),\forall t\in \{0,\dots ,T-2\}.\end{array}$$

Proof We propose to prove by induction the property

$${\mathcal{H}}_t:{\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)=(\sum _{i_0=1}^n\dots \sum _{i_t=1}^n{\theta }^{0,i_0}{\theta }^{i_0,i_1}\dots {\theta }^{i_{t-1},i_t}(r^{i_0}+\dots +r^{i_{t-1}}+{\widehat{Q}}_{T-t}^h(y^{i_{t-1}},h(t,y^{i_{t-1}}))\left)\right).$$

Basis: One has

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)=\sum _{i_0=1}^n{\theta }^{0,i_0}(r^{i_0}+{\widehat{Q}}_{T-t}^h(y^{i_0},h(1,y^{i_0}))),$$

which proves ₁.

Induction step: Let us assume that _t is true for t ∈ {1,…, T − 1}. Then, one has

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)=(\sum _{i_0=1}^n\dots \sum _{i_t=1}^n{\theta }^{0,i_0}{\theta }^{i_0,i_1}\dots {\theta }^{i_{t-2},i_{t-1}}(r^{i_0}+\dots +r^{i_{t-1}}+{\widehat{Q}}_{T-t}^h(y^{i_{t-1}},h(t,y^{i_{t-1}}))\left)\right).$$ (6)

According to the KB value iteration algorithm, we have:

$${\widehat{Q}}_{T-t}^h(y^{i_{t-1}},h(t,y^{i_{t-1}}))=\sum _{i_{t-1}=1}^k{\theta }^{i_{t-1},i_t}(r^{i_t}+{\widehat{Q}}_{T-t-1}^h(y^{i_t},h(t+1,y^{i_t}))).$$ (7)

Equations (6) and (7) give

$${\widehat{J}}_{\mathit{\text{FQi}}}^h({\mathcal{F}}_n,x_0)=\sum _{i_0=1}^n\dots \sum _{i_{t-1}=1}^n{\theta }^{0,i_0}\dots {\theta }^{i_{t-2},i_{t-1}}\times (r^{i_0}+\dots +r^{i_{t-1}}+\sum _{i_t=1}^n{\theta }^{i_{t-1},i_t}(r^{i_t}+{\widehat{Q}}_{T-t-1}^h(y^{i_t},h(t+1,y^{i_t}))))$$

Since ${\sum }_{i_t=1}^n{\theta }^{i_{t-1},i_t}=1$, one has

$${\widehat{J}}_{\mathit{\text{FQI}}}^h({\mathcal{F}}_n,x_0)=\sum _{i_0=1}^n\dots \sum _{i_{t-1}=1}^n{\theta }^{0,i_0}\dots {\theta }^{i_{t-2},i_{t-1}}\times ((\sum _{i_t=1}^n{\theta }^{i_{t-1},i_t})(r^{i_0}+\dots +r^{i_{t-1}})+\sum _{i_t=1}^n{\theta }^{i_{t-1},i_t}(r^{i_t}+{\widehat{Q}}_{T-t-1}^h(y^{i_t},h(t+1,y^{i_t})))=\sum _{i_0=1}^n\dots \sum _{i_{t-1}=1}^n{\theta }^{0,i_0}\dots {\theta }^{i_{t-2},i_{t-1}}\sum _{i_t=1}^n{\theta }^{i_{t-1},i_t}\times (r^{i_0}+\dots +r^{i_{t-1}}+r^{i_t}+{\widehat{Q}}_{T-t-1}^h(y^{i_t},h(t+1,y^{i_t})))$$

which proves _{t + 1}. The proof is completed by observing that ${\widehat{Q}}_0^h(x,u)=0,\forall (x,u)\in \mathcal{X}\times \mathcal{U}$.

One can observe through Proposition 7 that the computation of the KB estimate of the expected return of the policy h can be expressed in the form of a weighted sum of the return of n^T artificial trajectories. Each artificial trajectory

$$[(x^{i_0},u^{i_0},r^{i_0},y^{i_0}),(x^{i_1},u^{i_1},r^{i_1},y^{i_1}),\dots ,(x^{i_{T-1}},u^{i_{T-1}},r^{i_{T-1}},y^{i_{T-1}})]$$

is weighted with a factor ${\theta }_0^{0,i_0}{\theta }_1^{i_0,i_1}\dots {\theta }_{T-1}^{i_{T-2,i_{T-1}}}$. Note that some of these factors can eventually be equal to zero. Similarly to the k–NN estimator, these artificial trajectories are also built from the T × n^T non-unique one-step system transitions from _n.

More generally, we believe that the notion of artificial trajectory could also be used to characterize other batch mode RL algorithms that rely on other kinds of “averaging” schemes [24].

6 Conclusion

In this paper we have revisited recent works based on the idea of synthesizing artificial trajectories in the context of batch mode reinforcement learning problems. This paradigm shows to be of value in order to construct novel algorithms and performance analysis techniques. We think that it is of interest to revisit in this light the existing batch mode reinforcement algorithms based on function approximators in order to analyze their behavior and possibly create new variants presenting interesting performance guarantees.