Abstract
X-ray micro-CT is an important imaging tool for biomedical researchers. Our group has recently proposed a hybrid “true-color” micro-CT system to improve contrast resolution with lower system cost and radiation dose. The system incorporates an energy-resolved photon-counting true-color detector into a conventional micro-CT configuration, and can be used for material decomposition. In this paper, we demonstrate an interior color-CT image reconstruction algorithm developed for this hybrid true-color micro-CT system. A compressive sensing-based statistical interior tomography method is employed to reconstruct each channel in the local spectral imaging chain, where the reconstructed global gray-scale image from the conventional imaging chain served as the initial guess. Principal component analysis was used to map the spectral reconstructions into the color space. The proposed algorithm was evaluated by numerical simulations, physical phantom experiments, and animal studies. The results confirm the merits of the proposed algorithm, and demonstrate the feasibility of the hybrid true-color micro-CT system. Additionally, a “color diffusion” phenomenon was observed whereby high-quality true-color images are produced not only inside the region of interest, but also in neighboring regions. It appears harnessing that this phenomenon could potentially reduce the color detector size for a given ROI, further reducing system cost and radiation dose.
Keywords: Color/spectral-CT, micro-CT, photon-counting, statistical interior tomography
I. Introduction
Microimaging technology for small-animal studies has developed rapidly in the past decade due to its critical importance for systems biology and medicine. At present, biomedical research institutions and companies are extensively using microimaging tools, including x-ray micro-CT, micromagnetic resonance imaging (micro-MRI), micropositron emission tomography (micro-PET), microsingle photon emission computed tomography (micro-SPECT), microultrasound (micro-US), micro-optical scanners, etc. X-ray micro-CT is generally considered superior among these microimaging tools; it outperforms micro-MRI in terms of imaging speed and cost effectiveness, captures much finer features than micro-PET and micro-SPECT, brings much less artifacts than micro-US, and allows significantly deeper sample penetration than optical imaging.
However, a major limitation of current micro-CT scanners is insufficient contrast resolution for soft tissue. Energy-integrating detectors are a major cause for this limitation because the detected x-ray signals are accumulated over the entire source spectrum, which makes it difficult to utilize the energy-dependent property of x-ray attenuation [1]. In contrast, recently developed energy-resolved photon-counting detectors can resolve individual photons and their associated energies [2]. Photon-counting detectors can measure the x-ray attenuation under different spectral channels simultaneously using a conventional polychromatic x-ray source. Consequently, they are capable of revealing elemental composition of different materials. In addition, photon-counting detectors have an inherently higher signal-to-noise ratio (SNR) because electronic noise below the counting threshold does not increment the counter. These photon-counting detectors have been used to develop true-color CT systems that dramatically improve contrast resolution [3]-[9]. Here, “true color” is relative to the well-known pseudocolor images mapped from gray-scale images in clinical applications. True-color CT is also referred to as spectral, multienergy, spectroscopic, energy-selective or energy-sensitive CT.
Given innumerable potential applications of spectral x-ray CT (e.g., tissue characterization, functional studies, cellular and molecular imaging), the transition from gray scale to true color is almost certain to occur sooner or later. However, there are two major challenges in this process: detector cost and radiation dose. First, the spectral detection technology is not yet mature for large area, high resolution, uniform performance, and long duration operation. The replacement of a gray-scale x-ray detector array with a true-color spectral detector will be rather expensive in the near future. Second, radiation exposure is a public concern, and x-ray spectral detection would require much higher radiation dosage if each spectral channel requires the same exposure as that for a corresponding energy-integrating detector. These issues will require further research and refinement, but are far from terminal limitations.
While classic CT theory targets exact reconstruction of the sample’s entire cross section from complete projections, biomedical applications of CT and micro-CT often focus on smaller, internal regions of interest (ROIs). Unfortunately, classic CT theory cannot exactly reconstruct an internal ROI from truncated x-ray projections that only pass through the ROI because this “interior problem” does not have a unique solution [10]. However, in recent years it has been proven that the interior problem can be exactly solved if there is some additional prior information. One method is based on the truncated Hilbert transformation (THT) with a known subregion inside the ROI [11]-[16]. Another method is based on the compressive sensing (CS) theory, assuming a piecewise constant or polynomial ROI [17]-[19]. These “interior tomography” methods provide a way to exactly reconstruct an internal ROI with reduced radiation dose and detector size.
We propose that the detector cost and radiation dose problems of x-ray spectral micro-CT can be solved by applying interior tomography. Recently, we have designed a hybrid true-color micro-CT system that incorporates spectral imaging and interior tomography to improve micro-CT performance [20]. Our design adds a narrow-beam true-color imaging chain in the current micro-CT system using a small energy-resolved photon-counting detector. This hybrid system has three advantages: first, it keeps the conventional gray-scale imaging chain, which is necessary for a transition from gray-scale to true-color reconstruction and important for locating the ROI more accurately; second, it can provide higher contrast true-color ROI reconstruction with lower system cost and radiation dose; third, the gray-scale global reconstruction provides prior information for a better true-color ROI reconstruction.
The remainder of this paper is organized as follows. Section II describes the hybrid true-color micro-CT system; Section III presents the interior-color reconstruction algorithm; experimental results will be shown in Section IV; finally, we will discuss related problems and conclude this paper in Section V.
II. Hybrid True-Color Micro-CT
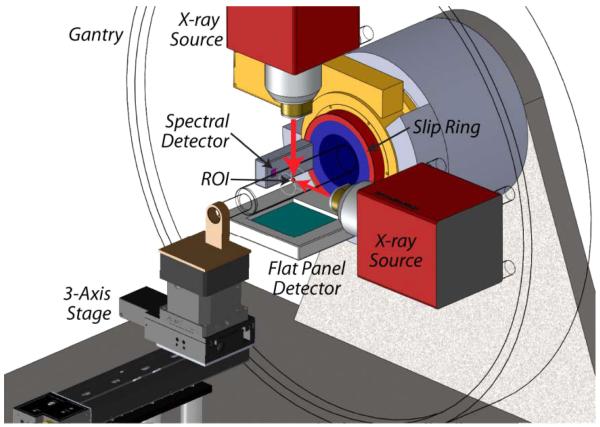
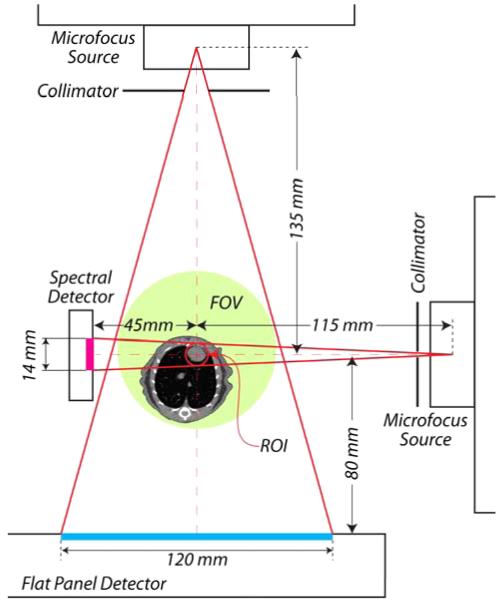
Recently, our group has designed a hybrid true-color micro-CT system [20]. The system consists of a wide-beam gray-scale imaging chain perpendicular to a narrow-beam true-color imaging chain on a rotating slip ring (see Fig. 1). The wide-beam imaging chain is designed to have a field of view (FOV) of radius 36 mm, which provides conventional projection data for global gray-scale imaging. The narrow-beam imaging chain is designed to have an FOV of radius 5 mm, which provides a set of spectral projection data for true-color ROI reconstruction (see Fig. 2).
Fig. 1.
3-D rendering of the hybrid true-color micro-CT system. A wide-beam gray-scale imaging chain and a narrow-beam true-color imaging chain are combined on a rotating gantry.
Fig. 2.
2-D sketch of the hybrid true-color micro-CT system. A wide-beam gray-scale imaging chain and a narrow-beam true-color imaging chain are combined on a rotating gantry.
The scanner’s multispectral photon-counting x-ray detector was selected as Medipix3. The Medipix is a series of state-of-the-art photon-counting detectors for x-ray microimaging, and the Medipix3 is the latest version of Medipix series with a higher energy resolution [21]-[25]. A single Medipix3 chip is employed in our design, and has 256×256 matrix of 55×55 μm pixels. The readout logic of Medipix3 supports eight energy thresholds for spectroscopic imaging. The gray-scale x-ray detector is a 120×120 mm sensitive area with a pixel size of 50×50 μm. The two x-ray tubes are identical and designed to allow the K-edge imaging of gold nanoparticles (GNP) at 80.7 KeV. The targets of this system are 50 μm spatial resolution, 20 Hounsfield unit (HU) noise deviation, 8 spectral channels, and up to 15 rotations per minute.
III. Methodology
A single global polychromatic (energy-integrating) projection dataset and several local spectral projection datasets can be obtained with our proposed hybrid imaging system. Conventional analytical or iterative reconstruction methods can be used to reconstruct the global projection data, while interior tomography methods can be used to reconstruct an interior ROI image on each channel from the local spectral projection data. An interior-color image can be rendered from this set of ROI reconstructions via image analysis methods; however, the gray-scale global reconstruction can be used to improve the performance of the interior-color reconstruction. We will next describe this reconstruction method in detail.
A. CS-Based Interior Tomography
We used CS-based interior tomography to reconstruct each spectral channel (energy threshold) for two reasons. First, CS-based interior tomography does not need a known subregion within the ROI, which is required by landmark-based methods and usually difficult to be exactly obtained, especially for determining the exact attenuations of a subregion on a different spectral channel. Second, CS-based interior tomography better accommodates the statistical property of the projections and performs better with noisy data, which is important for multi-energy data due to the lower counts and higher noise in each spectral channel. Recently, it has been demonstrated that the CS-statistical interior tomography (CS-SIT) performs very well in low count scenarios [26]. In this paper, we employ an enhanced CS-SIT algorithm for interior reconstruction on each spectral channel, aided by the gray-scale global reconstruction.
The detected photons of each spectral channel s(s = 1, …, S, S is the number of spectral channels) can be approximately modeled as a Poisson distribution
| (1) |
where is the measured data of the spectral channel s along the ith x-ray path, is the blank scan factor, is the integral of the x-ray linear attenuation coefficients, A = {aij} is the system matrix, is a distribution of linear attenuation coefficients, accounts for read-out noise, and I and J are the number of projections and pixels.
According to the CS-based interior tomography theory, a piecewise constant ROI can be exactly reconstructed from the locally truncated projections by minimizing the image total variation (TV). Combining the Poisson property of projection data and the TV regularization in the maximization of a posterior (MAP) framework, an ROI image on each spectral channel s can be exactly reconstructed via minimizing the following objective function:
| (2) |
where is the statistical weight for each x-ray path, is the estimated line integral, βs is the regularization parameter to balance the data fidelity and TV terms, and TV (μs) is the operator of computing TV of the reconstructed image.
B. Principle Component Analysis
After we obtain the reconstructed images of all spectral channels, next important task is to extract features from these reconstructions to render a color image μC. Principle component analysis (PCA) is a simple and effective method to identify independent information from highly correlated data [27]. It has been applied in spectral CT and performs well [6], [28], which is why we adopted this method in our study.
The sample’s attenuation coefficients are embedded in each spectral channel from the spectral image set . Identical materials should have the same pattern of attenuation change from one spectral channel to another (i.e., different energy thresholds). We aim to discriminate different materials by identifying these patterns through the PCA method, which will be briefly described.
First, we introduce a matrix M = {Msj} ∈ ℝS×J, , and the covariance of the images set in spectral domain is C = (1/(S − 1))MMT (the superscript “T” is the transpose operator). Applying singular value decomposition to C and arranging the eigenvalues in decreasing order, the corresponding eigenvectors form a new basis, which are called principal components. The matrix M can be transformed by this basis to form the principal component image (PC image) set , . We can use the first N PC images to discriminate between various materials.
Furthermore, we have a gray-scale global image μG with a good spatial resolution, which can be used for color mapping. Thus, we combined the PC images with the gray-scale global image to produce the final high-resolution color image μC.
As for color mapping, we can either adopt the RGB or HSV mapping. The red, green, blue components or the hue, saturation, value components of the final color image will be linear/nonlinear mapped from the PC images and gray-scale global image or the linear/nonlinear combinations of these images. Our team is working to optimize a general map scheme for better visualization based on computer vision theory.
C. Overall Workflow
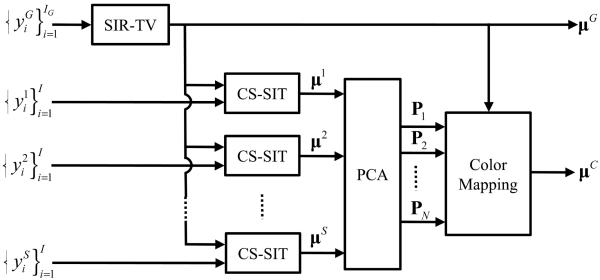
The overall workflow of the hybrid imaging system reconstruction algorithm is shown in Fig. 3.
Fig. 3.
Image reconstruction workflow for the hybrid true-color micro-CT system.
Global projection data are denoted as and IG is the number of global projections. In this case, the statistical iterative reconstruction method with a TV regularization constraint (SIR-TV) is used to reconstruct the gray-scale global image μG due to better performance for low count data. Due to the additional spectral imaging chain, the gray-scale chain should have reduced flux, and therefore reduced counts, to keep a reasonable overall dose for the combined imaging chains. Besides, SIR-TV and CS-SIT are identical except for the input data type. The reconstruction of μG by SIR-TV is to minimize the following objective function:
| (3) |
where is the statistical weight for each projection of this global data, and and βG are the estimated line integral and the regularization parameter of this case, respectively. Equation (3) can also be effectively and efficiently solved by the soft threshold filtering-based alternating minimization algorithm as (2). This global result μG will be used to regularize the interior color reconstruction.
On each spectral channel, the image μs is reconstructed by the CS-SIT with μG as the initial image. Then a PCA is performed on this set of spectral results . The first N PC-images are selected and combined with the global reconstruction μG to render a color image μC.
IV. Experimental Results
To evaluate the proposed reconstruction method and demonstrate the feasibility of the hybrid true-color micro-CT system, we first performed a numerical simulation experiment. Furthermore, the reconstruction method is validated using the datasets from spectral micro-CT scans of physical phantoms, in vitro human samples, and euthanized GNP-injected mice.
A. Numerical Simulation
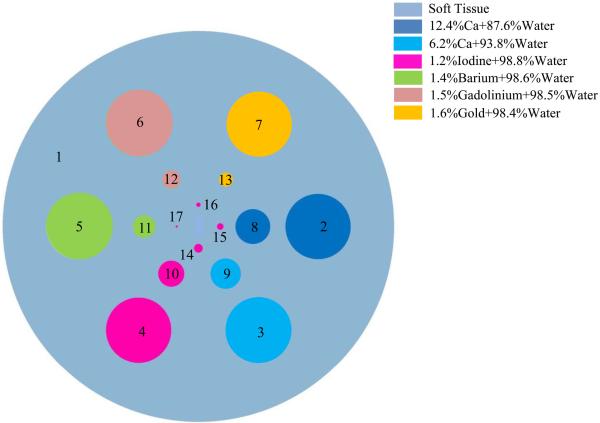
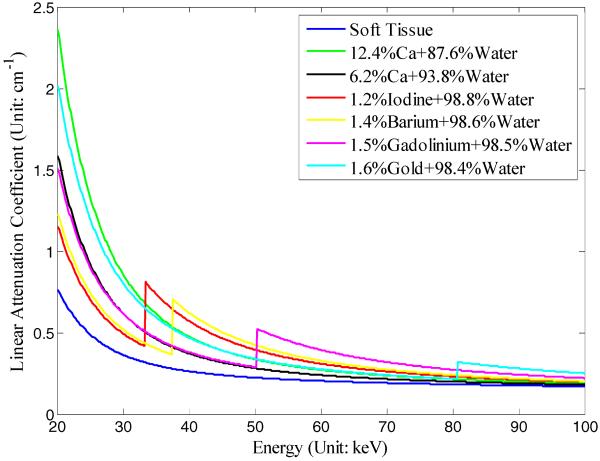
In this simulation, a cylindrical phantom was designed to evaluate the spatial and contrast resolution of the proposed hybrid system and reconstruction methodology; it contains several cylindrical inclusions of various radii and seven materials with different energy attenuation properties. The phantom parameters in transverse plane are shown in Fig. 4 and Table I. The concentration percentages of base materials are calculated by weight. The linear attenuation coefficients of the phantom materials are shown in Fig. 5.
Fig. 4.
Transverse plane of the cylindrical phantom with seven different materials.
TABLE I.
Cylindrical Phantom Geometry and Composition
| Object | Center (mm) | Radius (mm) |
Base Material |
|---|---|---|---|
| 1 | (0.000, 0.000) | 9.000 | Soft Tissue |
| 2 | (5.500, 0.000) | 1.500 | 12.4%Ca+87.6%Water |
| 3 | (2.750, −4.763) | 1.500 | 6.2%Ca+93.8%Water |
| 4 | (−2.750,−4.763) | 1.500 | 1.2%Iodine+98.8% Water |
| 5 | (−5.500, 0.000) | 1.500 | 1.4%Barium+98.6%Water |
| 6 | (−2.750, 4.763) | 1.500 | 1,5%Gadolinium+98.5%Water |
| 7 | (2.750, 4.763) | 1.500 | 1.6%Gold+98.4%Water |
| 8 | (5.500, 0.000) | 0.800 | 12.4%Ca+87.6%Water |
| 9 | (2.750, −4.763) | 0.700 | 6.2%Ca+93.8%Water |
| 10 | (−2.750,−4.763) | 0.600 | 1.2%Iodine+98.8%Water |
| 11 | (−5.500, 0.000) | 0.500 | 1.4%Barium+98.6%Water |
| 12 | (−2.750, 4.763) | 0.400 | 1.5%Gadolinium+98.5%Water |
| 13 | (2.750, 4.763) | 0.300 | 1.6%Gold+98.4%Water |
| 14 | (0.000,−1.000) | 0.200 | 1.2%Iodine+98.8%Water |
| 15 | (1.000, 0.000) | 0.150 | 1.2%Iodine+98.8%Water |
| 16 | (0.000, 1.000) | 0.100 | 1.2%Iodine+98.8%Water |
| 17 | (−1.000, 0.000) | 0.050 | 1.2%Iodine+98.8%Water |
Fig. 5.
Linear attenuation coefficients with respect to incident photon energy of the phantom materials in the numerical simulation.
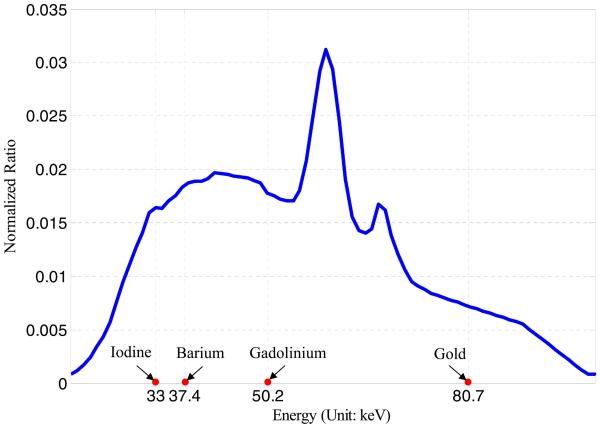
Both the wide-beam gray-scale imaging chain and narrow-beam color-scale imaging chain were simulated with a fan-beam geometry and equidistant detector. The virtual detectors were centered at the system origin and perpendicular to the lines from the system origin to its corresponding x-ray source. The distance from each source to the system origin was 115 mm. The wide-beam and narrow-beam imaging chain detectors have 540 and 256 detector elements, respectively, with an element width of 0.04 mm. Six hunderd equiangular projections were collected over 360°. The x-ray tube voltage was assumed as 120 kVp; its normalized emission spectrum is shown in Fig. 6. Taking into account the k-edges of materials in this phantom, which are iodine (33 keV), barium (37.4 keV), gadolinium (50.2 keV), and gold (80.7 keV), five spectral channels were selected in the color-scale imaging chain: ≤32 keV, 33–37 keV, 38–42 keV, 51–56 keV, and ≥81 keV. In order to simulate various noisy scenarios, both imaging chains were simulated with emitted photon counts along each x-ray path as 105, 5×104, 2×104, and 104. The emitted photon counts of the true-color imaging chain were calculated by weighting the tube spectrum distribution; thus, each spectral channel contained only about 10% of the total photons and resulted in more noise in the projection data.
Fig. 6.
Source photon emission spectra used for numerical simulation, which expresses the normalized ratios of photons with different energies. Four specific energies are denoted along the x-axis, which are the k-edges of iodine (33 keV), barium (37.4 keV), gadolinium (50.2 keV), and gold (80.7 keV).
The image reconstruction process was implemented following the workflow illustrated in Fig. 3. An ordered-subsets technique [29] and a fast iterative shrinkage threshold algorithm (FISTA) [30] were employed to speed up the iterative process. The reconstructed images are 600×600 pixels covering a region of 10×10 mm; the iteration count was fixed at 20. For comparison, images were also reconstructed by the conventional FBP (filtered-backprojection) method, which first smoothly extrapolates the truncated local projections to zeros and then performs global reconstruction in each spectral channel. A constant shift was imposed to each FBP reconstruction to make the central region match the original phantom image. Finally, the same PCA and color mapping scheme were used to render color images from the images reconstructed by the FBP method.
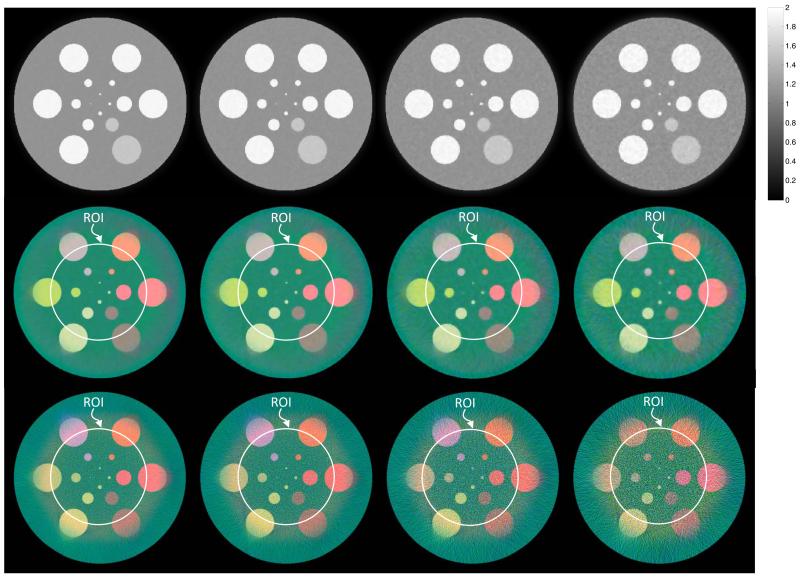
The reconstructed results are shown in Fig. 7. The gray-scale images are reconstructed from global projections via the SIR-TV method. In these gray-scale results, the materials “12.4%Ca+87.6%Water,” “1.2%Iodine+98.8%Water,” “1.4%Barium+98.6%Water,” “1.5%Gadolinium+98.5%Water,” and “1.6%Gold+98.4%Water” have similar gray scales, which cannot be discriminated between each other. However, in the true-color interior reconstructions by the proposed method, different materials are mapped into different colors and can be easily distinguished. Therefore, we can see that spectral scanning can provide color reconstructions with much higher contrast. At the same time, it can be seen that using the proposed method the true-color interior ROIs have the same noise and spatial resolution as the gray-scale reconstructions. When the emitted photon count decreases from 105 to 104, both the gray-scale and true-color results have increased noise and decreased spatial resolution. In the cases of 2×104 and 104 photons, the smallest inclusion is contaminated by the severe noise and cannot be recognized. It is worth noting that although the spectral scanning is only performed in the ROI, high-quality true-color reconstruction can be produced not only inside the ROI but also in neighboring regions. As for the true-color images based on the FBP reconstructions, there is much noise and the materials, such as “1.2%Iodine+98.8%Water” and “1.4%Barium+98.6%Water,” cannot be discriminated effectively, which is due to the inaccuracy of interior tomography by the FBP method in each spectral channel.
Fig. 7.
Reconstructed images in numerical simulation. The first to third rows are the global gray-scale reconstructions by SIR-TV, the true-color interior reconstructions by the proposed method, and the true-color results based on FBP reconstructions (with appropriate extrapolation and constant shift), respectively. From first to fourth columns are the results from the projections assuming 105, 5×104, 2×104, and 104 photons, respectively.
B. Phantom Experiment
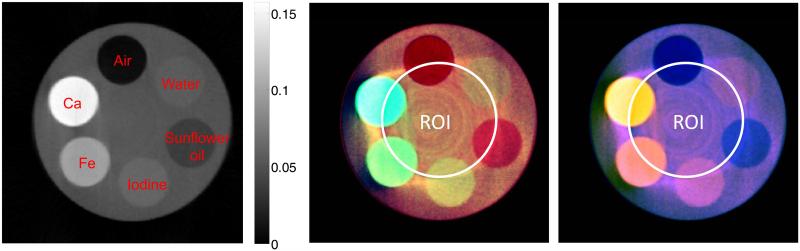
To further evaluate the proposed reconstruction algorithm and demonstrate the feasibility of the hybrid true-color micro-CT system, we designed a physical phantom. It is a Perspex cylinder of 10 mm diameter with six cylindrical inclusions of 2.5 mm diameter filled with solutions of 2.0M calcium chloride, 0.4M ferric nitrate, 0.02M iodinated water, sunflower oil, water, and air. This phantom was scanned by the state-of-the-art spectral micro-CT scanner—Medipix All Resolution System (MARS)—with a Medipix MXR Si detector [31]. The distances from the source to the system origin and the source to the detector are 141 and 203 mm, respectively. Two hundred and fifty equiangular projections were collected over 360° to form a full scan. We used the Medipix3 detector chip for this experiment; it has 256×256 elements of size 55×55 μm. The detector chip was horizontally translated for each projection to cover a wider FOV, producing a 438×256 projection for each view. The central slice was selected for image reconstruction with typical fan-beam geometry of 250 views and 438 equidistant detector cells. The x-ray source was selected as the Source-Ray SB-80-1K (Source-Ray Inc., New York), which has a minimum focal spot of 50 μm. The x-ray tube voltage and current was set to 50 kVp and 500 mA, respectively. Each spectral channel detects photons with energy greater than the selected threshold. Six energy thresholds were selected as approximately 9.8, 15.1, 20.4, 25.6, 30.9, and 36.2 keV. The acquired datasets were processed by flat-field correction and denoising processing. The dataset with the lowest energy threshold is assumed as the projection of gray-scale global imaging chain; other datasets are truncated to simulate the spectral ROI scanning. The ROI was located in the phantom center with a radius of 2.75 mm.
The reconstructed images are 500×500 pixels covering a region of 11.46×11.46 mm (see Fig. 8). The reconstruction results are similar to those of the previous phantom simulation experiment. Fig. 8 shows that the proposed algorithm performs very well for true-color image reconstruction in the ROI: the reconstructed materials have strong contrast between each other and can be easily discriminated in the color space. Additionally, it is shown that a good color reconstruction can also be obtained in the neighboring region of the ROI.
Fig. 8.
Interior color reconstruction results of a physical phantom. The right one is the gray-scale image reconstructed from global projections using the statistical iterative reconstruction method (SIR-TV); the middle and right one are the images of true-color interior reconstruction (CS-SIT) using two different color map schemes.
C. In Vitro Study
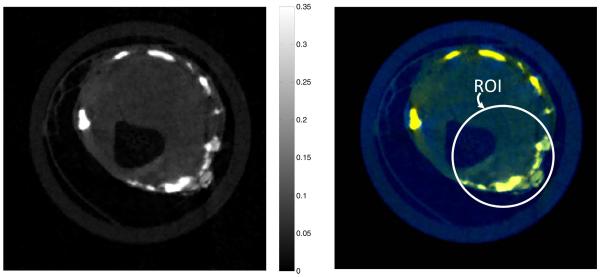
Another study to validate our proposed reconstruction technique was an in vitro human tissue scanned on the MARS micro-CT. An extracted human atheroma sample was placed in a plastic tube (15.8 mm diameter) and scanned using a quad-Medipix 3 detector (silicon layer, four detectors in 2×2 arrangement). The distance from the source to the system origin was 129.2 mm, and the distance from the source to the detector was 197.6 mm. Two hundred and fifty equiangular projections were collected over 360° to form a full scan. The central slice was picked for image reconstruction in typical fan-beam geometry. The x-ray source was Source-Ray SB-80-1K and the x-ray tube was set to 50 kVp and 500 mA with 1.8-mm aluminum filter. Four spectral channels were selected as ≥10, ≥16, ≥22, and ≥28 keV. The datasets were processed identically to the previous phantom experiment with the ROI (3.95 mm radius) located as shown in Fig. 9.
Fig. 9.
Results from the spectral scan of excised human atheroma sample; the left one is the global gray-scale reconstruction, and the right one is the true-color interior reconstruction.
The reconstructed images are 516×516 pixels covering a region of 18.56×18.56 mm. The gray-scale global image is reconstructed by the SIR-TV method. From Fig. 9, it can be seen that there are some plaque calcifications in this human atheroma sample. The plaque calcifications in the ROI can be easily discriminated in the color space. Besides, the plaque calcifications outside of the ROI can also be discriminated in this color-interior reconstruction.
D. GNP Mice Study
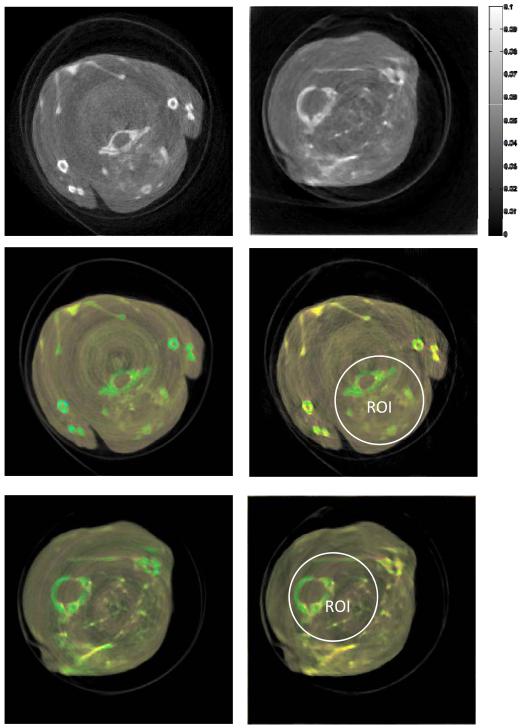
To evaluate the feasibility of the designed hybrid true-color micro-CT system for GNP-based applications, two euthanized mice were scanned on the MARS micro-CT with a Medipix MXR CdTe layer detector. The x-ray source was selected as the Source-Ray SB-120-400 (Source-Ray Inc., New York), which has a minimum focal spot of 75 μm. One mouse was injected with 0.2 mL of 15 nm Aurovist II GNP (Nanoparticles; Yaphank, NY) into the tail vein and was alive for ~3 h between injection and euthanasia. The second mouse was injected with 0.2 mL of 15 nm Aurovist II GNP (Nanoparticles; Yaphank, NY) in a direct cardiac puncture injection and immediate euthanasia. A representative sample of the scanned mice is shown in Fig. 10. The distances from the source to the system origin and the source to the detector are 158 and 255 mm, respectively. Three hundred and seventy-one equiangular projections were collected over 360° to form a full scan. Thirteen energy bins were collected with the source tube operated with 120 kVp and 175 mA. The detector chip was moved horizontally with overlapped pixels to cover a wider FOV of 34.89 mm diameter and correct for production defects in the detector sensor layer. Since there was significant noise in the sinogram, neighboring detector bins were merged to form a new sinogram of size 512×371. Next, we used the method in [32] to reduce ring artifact (see Fig. 11). As mentioned, the dataset with the lowest energy threshold was assumed to be the gray-scale projection from the global imaging chain. Other datasets were truncated to simulate spectral ROI scanning; the ROIs are indicated in Fig. 12 with a radius of 3.4 mm.
Fig. 10.
Photo of a BALB/C mouse used in this study after GNP injection.
Fig. 11.
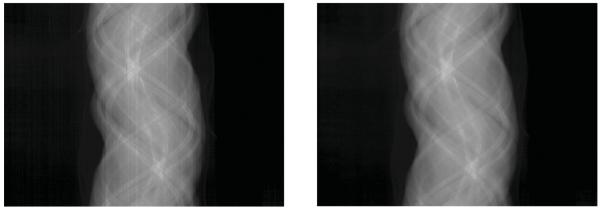
Sinogram ring artifacts reduction; the left one is the sinogram before preprocessing, and the right one is the sinogram after the ring artifacts removing.
Fig. 12.
Results from GNP mice studies. The first and second rows are the global gray-scale and true-color reconstruction results; and the third row is the color interior reconstructions. The left and right columns are the central slices from the mouse with tail vein injection of GNP and with direct cardiac puncture injection of GNP, respectively.
The reconstructed images are 512×512 pixels covering a region of 18.41×18.41 mm. The reconstructed results are shown in Fig. 12. The gray-scale global images for these two mice were reconstructed by the SIR-TV method. These image slices are of the mouse upper thorax and include the front limbs, thoracic vertebra, and scapula. The true-color reconstructions demonstrate that the GNP was present within the vascular structures of the upper thorax. It can be seen that the color interior tomography can nearly reproduce the same color result in ROI as with global reconstruction. The calcium in the bones and injected GNP have varying energy-specific attenuation properties compared to the background soft tissues which is represented as color variation in the PCA images.
V. Discussion and Conclusion
X-ray attenuation is both material and energy dependent. Conventional energy-integrating detectors measure x-ray attenuation along the path integrated in the whole energy spectrum. The resultant images from these detectors can be viewed as the weighted average of the material’s x-ray attenuation coefficients across the entire source spectrum, and do not capture energy-dependent characteristics. In many situations, the x-ray attenuation coefficients of different materials are similar in the conventional gray-scale CT, and it is hard to discriminate between these materials. As shown in our numerical simulations, “12.4%Ca+87.6%Water,” “1.2%Iodine+98.8%Water,” “1.4%Barium+98.6%Water,” “1.5%Gadolinium+98.5%Water,” and “1.6%Gold+98.4%Water” have similar gray scales. This phenomenon contributes to lower contrast for traditional gray-scale CT.
However, the photon-counting detectors are able to resolve incident photon energy and thus can measure the x-ray attenuation coefficients along the x-ray path in each spectral channel simultaneously. The energy-dependent property of x-ray attenuation is embedded in the spectral dataset, which can be used to extract additional information about the materials. One important feature is the material’s absorption edge (k-edge/L-edge), which produces a sudden increase in attenuation coefficient as the x-ray photon energy matches that of the material’s valence shell electrons. This kind of sudden change would be reflected in spectral data, while it would be concealed in energy-integrated scanning. Consequently, the contrast resolution will be improved significantly by using the photon-counting technique, which has been confirmed by our results in Section IV. However, the true-color CT technique is limited by the expense of photon-counting detector chips and higher radiation dose to provide each spectral channel with sufficient counts.
Interior tomography exactly reconstructs an interior ROI only from the data passing through the ROI, and can be applied to both decrease the detector size and reduce radiation dose. Considering that many imaging applications are focused on only a small ROI, it will be useful to incorporate the interior tomography and true-color techniques with modern CT systems; this is the motivation for our work reported in this paper. Our proposed hybrid true-color micro-CT system adds a narrow-beam spectral imaging chain into the conventional micro-CT system and aims to provide high contrast resolution in the ROI with a low system cost and radiation dose. From the results in Section IV, it can be seen that this system is feasible and can provide a high-quality color reconstruction. In the conventional gray-scale imaging chain, the noise and spatial resolution are related to the SNR of projection data, and, from the simulation experiment in Section IV, we can see that as the photon number is decreased from 105 to 104, the noise is increased and the spatial resolution is degraded. For the spectral data, usually the counts in each spectral channel are much lower than the energy-integrating projection datasets which will lead to higher noise and lower spatial resolution in the reconstruction. Fortunately, the gray-scale imaging chain can be used not only to provide global gray-scale image, but also to enhance the interior tomography in each spectral channel, and improve spatial resolution and suppress image noise. It can be seen from the simulation experiment that the interior color reconstructions can maintain the same spatial resolution and noise level as the gray-scale reconstruction.
Given all the results in Section IV, one can see that a high-quality true-color image is typically available in the neighboring region of the ROI, even as the spectral imaging chain only covers the ROI itself. We propose to name this phenomenon as “color diffusion,” which appears to benefit from stabilizing the interior tomography of each spectral channel aided by the global gray-scale reconstruction. Using this color diffusion phenomenon, we can potentially use a smaller true-color detector for a given ROI and thus reduce system cost. For example, if we wanted to reconstruct an ROI of radius 20.0 mm, we may choose a smaller true-color detector which only covers a 14.0 mm radius field of view.
At present, the Medipix photon-counting detector is the state-of-the-art spectral imaging technology and a very exciting research topic in the CT field. We believe that this technique will transform CT imaging from gray scale to true color by providing the spectral information for the imaging object. However, this technique is still under development and has some unsolved problems, such as the charge sharing which negatively affects the spectral data accuracy and hinders the absorption edge detection [33]. More efforts are needed to develop and improve photon-counting technology.
In conclusion, we proposed an image reconstruction method for a hybrid true-color micro-CT system, which has an additional spectral imaging chain based on a conventional micro-CT configuration. The spectral imaging chain incorporates an energy-resolving photon-counting detector and an interior tomography reconstruction technique. With the proposed reconstruction method, this system can provide a low noise, high spatial and contrast resolution true-color images with low system cost and radiation dose. Furthermore, the observed color diffusion can help to reduce the color detector size for a given ROI to further reduce system cost and radiation dose.
Acknowledgments
This work was supported in part by the National Institutes of Health/National Institute of Biomedical Imaging and Bioengineering under Grant EB011785 and a seed grant from the Wake Forest Institute for Regenerative Medicine.
Contributor Information
Qiong Xu, Institute of Image Processing and Pattern Recognition, Xi’an Jiaotong University, Xi’an, Shaanxi 710049, China; Department of Radiology, Division of Radiologic Sciences, Wake Forest University Health Sciences, Winston-Salem, NC 27157 USA (xjtuxqiong@gmail.com).
Hengyong Yu, Department of Radiology, Division of Radiologic Sciences and Biomedical Imaging Division, VT-WFU School of Biomedical Engineering and Sciences, Wake Forest University Health Sciences, Winston-Salem, NC 27157 USA.
James Bennett, Biomedical Imaging Division, VT-WFU School of Biomedical Engineering and Sciences, Virginia Tech, Blacksburg, VA 24061 USA (jrbennet@vt.edu).
Peng He, Biomedical Imaging Division, VT-WFU School of Biomedical Engineering and Sciences, Virginia Tech, Blacksburg, VA 24061 USA (hepeng_vvv@hotmail.com).
Rafidah Zainon, Department of Physics and Astronomy, University of Canterbury, Christchurch 8140, New Zealand (rafidah.zainon@pg.canterbury.ac.nz).
Robert Doesburg, Department of Physics and Astronomy, University of Canterbury, Christchurch 8140, New Zealand (robertd@actrix.co.nz).
Alex Opie, Department of Electrical and Computer Engineering, University of Canterbury, Christchurch 8140, New Zealand (alex.opie@pg.canterbury.ac.nz).
Mike Walsh, Department of Radiology, University of Otago, Christchurch 8011, New Zealand (michael.walsh@canterbury.ac.nz).
Haiou Shen, Biomedical Imaging Division, VT-WFU School of Biomedical Engineering and Sciences, Virginia Tech, Blacksburg, VA 24061 USA (hhshen@vt.edu).
Anthony Butler, Department of Radiology, University of Otago, Christchurch 8011, New Zealand; European Organization for Nuclear Research (CERN), Geneva 23, Switzerland (anthony@butler.co.nz).
Phillip Butler, Department of Physics and Astronomy, University of Canterbury, Christchurch 8140, New Zealand; European Organization for Nuclear Research (CERN), Geneva 23, Switzerland (phil.butler@canterbury.ac.nz).
Xuanqin Mou, Institute of Image Processing and Pattern Recognition, Xi’an Jiaotong University, Xi’an, Shaanxi 710049, China (xqmou@mail.xjtu.edu.cn).
Ge Wang, Biomedical Imaging Division, VT-WFU School of Biomedical Engineering and Sciences, Virginia Tech, Blacksburg, VA 24061; Wake Forest University Health Sciences, Winston-Salem, NC 27157 USA.
References
- [1].Alvarez RE, Macovski A. Energy-selective reconstructions in x-ray computerised tomography. Phys. Med. Biol. 1976;21:733–744. doi: 10.1088/0031-9155/21/5/002. [DOI] [PubMed] [Google Scholar]
- [2].Jakůbek J. Semiconductor pixel detectors and their applications in life sciences. J. Instrum. 2009;4:1–21. Article ID P03013. [Google Scholar]
- [3].Roessl E, Proksa R. K-edge imaging in x-ray computed tomography using multi-bin photon counting detectors. Phys. Med. Biol. 2007;52:4679–4696. doi: 10.1088/0031-9155/52/15/020. [DOI] [PubMed] [Google Scholar]
- [4].Feuerlein S, Roessl E, Proksa R, Martens G, Klass O, Jeltsch M, Rasche V, Brambs HJ, Hoffmann MHK, Schlomka JP. Multi-energy Photon-counting K-edge imaging: Potential for improved luminal depiction in vascular imaging. Radiology. 2008;249:1010–1016. doi: 10.1148/radiol.2492080560. [DOI] [PubMed] [Google Scholar]
- [5].Schlomka J, Roessl E, Dorscheid R, Dill S, Martens G, Istel T, B̈aumer C, Herrmann C, Steadman R, Zeitler G. Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography. Phys. Med. Biol. 2008;53:4031–4047. doi: 10.1088/0031-9155/53/15/002. [DOI] [PubMed] [Google Scholar]
- [6].Anderson N, Butler A, Scott NJA, Cook N, Butzer J, Schleich N, Firsching M, Grasset R, de Ruiter N, Campbell M. Spectroscopic (multi-energy) CT distinguishes iodine and barium contrast material in MICE. Eur. Radiol. 2010;20:2126–2134. doi: 10.1007/s00330-010-1768-9. [DOI] [PubMed] [Google Scholar]
- [7].Cormode DP, Roessl E, Thran A, Skajaa T, Gordon RE, Schlomka JP, Fuster V, Fisher EA, Mulder WJM, Proksa R. Atherosclerotic plaque composition: Analysis with multicolor CT and targeted gold nanoparticles. Radiology. 2010;256:774–782. doi: 10.1148/radiol.10092473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Wang X, Meier D, Mikkelsen S, Maehlum G, Wagenaar D, Tsui B, Patt B, Frey E. MicroCT with energy-resolved photon-counting detectors. Phys. Med. Biol. 2011;56:2791–2816. doi: 10.1088/0031-9155/56/9/011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Wang X, Meier D, Taguchi K, Wagenaar DJ, Patt BE, Frey EC. Material separation in x-ray CT with energy resolved photon-counting detectors. Med. Phys. 2011;38:1534–1546. doi: 10.1118/1.3553401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Natterer F. The Mathematics of Computerized Tomography. Society for Industrial Mathematics; Philadelphia, PA, USA: 2001. [Google Scholar]
- [11].Ye YB, Yu HY, Wei YC, Wang G. A general local reconstruction approach based on a truncated Hilbert transform. Int. J. Biomed. Imag. 2007;2007:1–8. doi: 10.1155/2007/63634. Article ID 63634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Ye YB, Yu HY, Wang G. Exact interior reconstruction with cone-beam CT. Int. J. Biomed. Imag. 2007;2007:1–5. doi: 10.1155/2007/10693. Article ID:10693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Ye YB, Yu HY, Wang G. Exact interior reconstruction from truncated limited-angle projection data. Int. J. Biomed. Imag. 2008;2008:1–6. doi: 10.1155/2008/427989. Article ID 427989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Yu HY, Ye Y, Wang G. Interior reconstruction using the truncated Hilbert transform via singular value decomposition. J. X-Ray Sci. Technol. 2008;16:243–251. [PMC free article] [PubMed] [Google Scholar]
- [15].Kudo H, Courdurier M, Noo F, Defrise M. Tiny a priori knowledge solves the interior problem in CT. Phys. Med. Biol. 2008;53:2207–2231. doi: 10.1088/0031-9155/53/9/001. [DOI] [PubMed] [Google Scholar]
- [16].Courdurier M, Noo F, Defrise M, Kudo H. Solving the interior problem of computed tomography using a priori knowledge. Inverse Problems. 2008;24:1–27. doi: 10.1088/0266-5611/24/6/065001. Article ID 065001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Yu HY, Wang G. Compressed sensing based interior tomography. Phys. Med. Biol. 2009;54:2791–2805. doi: 10.1088/0031-9155/54/9/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Yu HY, Yang JS, Jiang M, Wang G. Supplemental analysis on compressed sensing based interior tomography. Phys. Med. Biol. 2009;54:N425–N432. doi: 10.1088/0031-9155/54/18/N04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Yang JS, Yu HY, Jiang M, Wang G. High-order total variation minimization for interior tomography. Inverse Problems. 2010;26:1–29. doi: 10.1088/0266-5611/26/3/035013. Article ID 035013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Wang G. Computed tomography based imaging systems. US Patent Application, No. 12916458. 2010 Oct 29;
- [21].Bert C, Niederlöhner D, Giersch J, Pfeiffer KF, Anton G. Computed tomography using the Medipix1 chip. Nuclear Instrum. Methods Phys. Res. Section A: Accelerators, Spectrometers, Detectors Associated Equipment. 2003;509:240–250. [Google Scholar]
- [22].Llopart X, Campbell M, Dinapoli R, San Segundo D, Pernigotti E. Medipix2: A 64-k pixel readout chip with 55-μm square elements working in single photon counting mode. IEEE Trans. Nuclear Sci. 2002;49(5):2279–2283. [Google Scholar]
- [23].Firsching M, Takoukam Talla P, Michel T, Anton G. Material resolving X-ray imaging using spectrum reconstruction with Medipix2. Nuclear Instrum. Methods Phys. Res. Section A: Accelerators, Spectrometers, Detectors Associated Equipment. 2008;591:19–23. [Google Scholar]
- [24].Firsching M, Butler AP, Scott N, Anderson NG, Michel T, Anton G. Contrast agent recognition in small animal CT using the Medipix2 detector. Nuclear Instrum. Methods Phys. Res. Section A: Accelerators, Spectrometers, Detectors Associated Equipment. 2009;607:179–182. [Google Scholar]
- [25].Ballabriga R, Campbell M, Heijne E, Llopart X, Tlustos L. The Medipix3 prototype, a pixel readout chip working in single photon counting mode with improved spectrometric performance. IEEE Trans. Nuclear Sci. 2007 Oct;54(5):1824–1829. [Google Scholar]
- [26].Xu Q, Mou XQ, Wang G, Sieren J, Hoffman EA, Yu HY. Statistical interior tomography. IEEE Trans. Med. Imag. 2011 May;30(5):1116–1128. doi: 10.1109/TMI.2011.2106161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Jolliffe I. Principal Component Analysis (Springer Series in Statistics) 2nd ed. Springer; New York: 2002. [Google Scholar]
- [28].Butzer J, Butler A, Butler P, Bones P, Cook N, Tlustos L. Medipix imaging—Evaluation of datasets with PCA; Image and Vision Computing New Zealand, IVCNZ 2008.2008. pp. 1–6. [Google Scholar]
- [29].Kamphuis C, Beekman F. Accelerated iterative transmission CT reconstruction using an ordered subsets convex algorithm. IEEE Trans. Med. Imag. 1998 Dec;17(6):1101–1105. doi: 10.1109/42.746730. [DOI] [PubMed] [Google Scholar]
- [30].Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imag. Sci. 2009;2:183–202. [Google Scholar]
- [31].Butzer J, Anderson N, Tipples R, Cook N, Melzer T, Butler P. Bio-medical X-ray imaging with spectroscopic pixel detectors. Nuclear Instruments and Methods in Physics Research A. 2008;591(1):141–146. [Google Scholar]
- [32].Raven C. Numerical removal of ring artifacts in microtomography. Rev. Sci. Instrum. 1998;69:2978–2980. [Google Scholar]
- [33].Kalemci E, Matteson J. Investigation of charge sharing among electrode strips for a CdZnTe detector. Nuclear Instrum. Methods Phys. Res. Section A: Accelerators, Spectrometers, Detectors Associated Equipment. 2002;478:527–537. [Google Scholar]