Rational temporal predictions can underlie apparent failures to delay gratification

Abstract

An important category of seemingly maladaptive decisions involves failure to postpone gratification. A person pursuing a desirable long-run outcome may abandon it in favor of a short-run alternative that has been available all along. Here we present a theoretical framework in which this seemingly irrational behavior emerges from stable preferences and veridical judgments. Our account recognizes that decision makers generally face uncertainty regarding the time at which future outcomes will materialize. When timing is uncertain, the value of persistence depends crucially on the nature of a decision-maker’s prior temporal beliefs. Certain forms of temporal beliefs imply that a delay’s predicted remaining length increases as a function of time already waited. In this type of situation, the rational, utility-maximizing strategy is to persist for a limited amount of time and then give up. We show empirically that people’s explicit predictions of remaining delay lengths indeed increase as a function of elapsed time in several relevant domains, implying that temporal judgments offer a rational basis for limiting persistence. We then develop our framework into a simple working model and show how it accounts for individual differences in a laboratory task (the well-known “marshmallow test”). We conclude that delay-of-gratification failure, generally viewed as a manifestation of limited self-control capacity, can instead arise as an adaptive response to the perceived statistics of one’s environment.

Introduction

Valuable long-run rewards, such as career advancement, physical fitness, financial stability, and recovery from addiction, require persistence in the face of short-run costs. People’s behavior in pursuing such outcomes can appear curiously self-contradictory. A person may initially opt to delay gratification (e.g., by sticking to a diet, saving for retirement, or quitting smoking). However, the same person may later give in, abandoning the long-run outcome in favor of an immediate reward that was available all along (Ainslie, 1975; Mischel & Ebbesen, 1970; Schelling, 1984; Strotz, 1955).

A vivid example of this type of reversal occurs in the famous delay-of-gratification (DG) laboratory paradigm introduced by Mischel and colleagues (Mischel & Ebbesen, 1970; Mischel, Ebbesen, & Zeiss, 1972). The paradigm typically involves offering a four-year-old child a choice between two food rewards. The child can either wait to receive a preferred reward (usually 10–20 minutes), or receive a less-preferred reward immediately. Children often start out waiting for the preferred reward, but subsequently give up and accept the lesser reward instead.

The DG paradigm appears to capture a striking failure of rational decision making. In economic terms, behavior seems to violate the principle of stationarity (Fishburn & Rubinstein, 1982). If the large reward were worth waiting for, the child should wait the necessary time. If not, the child should choose the small reward at the outset. Intermediate behavior—first waiting and then quitting—seems to reveal an impulsive, dynamically inconsistent decision process.

In the present paper we challenge the standard assumption that quitting after first waiting necessarily reflects unstable preferences. We outline a framework in which these reversals emerge from dynamically consistent preferences and rational, utility-maximizing choices.

Although we will center our discussion on the classic DG paradigm, our interest is in characterizing aspects of persistence behavior that are shared across several real-life situations such as those involving diet, education, finances, and addiction. The DG paradigm provides a useful point of reference because, by design, it captures the essential structure of such situations. The paradigm is, as Metcalfe and Mischel (1999) described it, “a prototype for the study of willpower” (p3).

To set the stage, we briefly review several of the most widely accepted theoretical explanations for delay-of-gratification failure in the literature to date.

Theoretical perspectives on delay-of-gratification failure

Dual systems

One influential idea is that reversals emerge from interactions between two internal systems that compete to govern behavior. Different theoretical frameworks characterize these systems as hot vs. cool (Metcalfe & Mischel, 1999), affective vs. deliberative (Loewenstein & O’Donoghue, 2005) or Pavlovian vs. instrumental (Dayan, Niv, Seymour, & Daw, 2006).

In the hot/cool framework, for example, the cool system is viewed as supporting deliberation and tending to favor persistence, while the hot system is considered reflexive and emotional, facilitating rapid action but tending to undermine persistence. This idea is motivated by findings that waiting times in the DG paradigm can be increased by removing rewards from view, by providing distracting activities, or by encouraging children to think about the rewards in a non-appetitive manner (Mischel & Ebbesen, 1970; Mischel et al., 1972; Mischel & Moore, 1973; Mischel & Baker, 1975). All these manipulations can be viewed as ways to reduce hot-system activation.

A principal goal of the hot/cool framework is to explain why behavior varies across individuals and across contexts. For example, why does one person wait longer than another? Other approaches have focused more directly on the dynamics of preference change: for example, why would a decision maker quit after a period of waiting rather than simply selecting the immediate reward when it was first offered?

Strength and depletion

A strength and depletion framework offers a specific explanation for quitting after first waiting. The idea is that temptation-related impulses need to be suppressed by a self-regulatory mechanism (Baumeister & Heatherton, 1996), which weakens the more it is used (Baumeister, Bratslavsky, Muraven, & Tice, 1998; Muraven, Tice, & Baumeister, 1998). The balance of power between the impulsive and regulatory systems therefore shifts over time. A person who initially possessed the self-regulatory strength to resist a temptation might succumb once that strength was partially depleted. Such a dynamic has begun to be incorporated in formal economic models of choice (Fudenberg & Levine, 2012; Ozdenoren, Salant, & Silverman, 2012; Loewenstein & O’Donoghue, 2005).

Environmental cuing

Another possibility is that preferences are influenced by cues in the immediate environment (Dayan et al., 2006; Bernheim & Rangel, 2004; Laibson, 2001; Loewenstein & O’Donoghue, 2005). Cuing can occur in dual-system frameworks: for example, reward stimuli in close proximity might increase the influence of hot, affective, or Pavlovian control. On this view, dynamic inconsistency can be attributed to changes in one’s external surroundings. However, cuing requires additional assumptions in order to explain reversals in situations like the DG paradigm, where the external environment remains unchanged between the time of the initial choice to wait and the later choice to quit.

Hyperbolic discounting

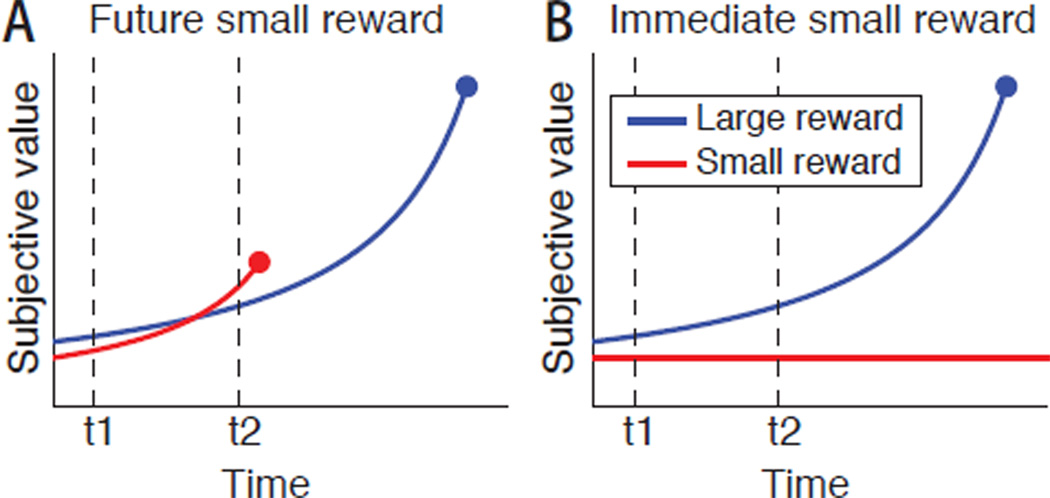
Hyperbolic temporal discounting functions offer an explanation for dynamic inconsistency in many settings (Ainslie, 1975; Frederick, Loewenstein, & O’Donoghue, 2002; Laibson, 1997; Strotz, 1955). Hyperbolic discounting implies that future rewards gain subjective value in an accelerating manner as they draw nearer, with the soonest rewards gaining value the fastest (Mazur, 1987). If someone initially preferred the later of two rewards, the mere passage of time could reverse this preference (Ainslie, 1975; see Figure 1A).

Figure 1.

Predictions of a hyperbolic discounting model. Panel A shows a scenario in which this model predicts preference reversals. Two rewards are available at specific times in the future. At t1 the decision maker prefers the larger, later reward, but by t2 this preference reverses. Panel B shows a scenario more like the DG task, with the small reward continuously and immediately available. The small-reward value in the illustration is set to match its initial value in Panel A, so the choice at the beginning of the interval is the same. Time passage only increases the margin of preference for the larger, later alternative. Note that Panel B represents a scenario in which the delayed reward’s timing is known, even though, as we discuss below, participants in the standard DG paradigm lack this information.

However, hyperbolic discounting fails to explain reversals in situations structured like the DG paradigm. Here, the sooner reward is not set for a specific future timepoint, but instead is always available immediately. Because the sooner reward never draws any nearer, its subjective value does not increase as time passes (see Figure 1B). To explain delayed quitting in the DG paradigm (and in real-life situations with the same type of structure), a mechanism other than hyperbolic discounting is needed.

A normative perspective

Here we propose a rational prediction framework to account for reversals during delay of gratification. Unlike cuing and hyperbolic discounting, our framework directly explains reversals in situations structured like the DG paradigm. Unlike the depletion framework, our proposal holds that reversals emerge from a single, self-consistent valuation system. Later in the paper we discuss how our framework also might begin to explain the types of individual differences and situational effects that are the main purview of the hot/cool framework.

At the outset, we emphasize that we intend our framework to apply to persistence decisions in general, not specifically or exclusively to persistence by four-year-olds in DG experiments. We focus on the DG paradigm because it provides a concrete and vivid empirical demonstration of persistence failure, together with a large amount of available data. Our aim, however, is to develop a framework that applies across a wide range of situations that involve waiting for delayed rewards.

We begin by posing a normative question: how long should a decision maker be willing to wait for a delayed reward before giving up? The answer to this question is complicated by the existence of temporal uncertainty. Decision makers are often unsure how long it will take for an awaited outcome to materialize. This is true of a person waiting for a city bus or a phone call, as well as one waiting to see the payoff of a diet or a practice regimen.

Temporal uncertainty is also present in the DG laboratory paradigm. Even though the large reward’s delay has a fixed value in any given experiment (e.g., 15 minutes), participants themselves lack this information. The original instructions described the task’s timing as follows:

I have to go out of the room for a while and when I come back you can eat those [cookies] all up. You can take them off the table and eat them right up. But, you know, sometimes, I’m gone a long time and if you want to bring me back you can. (Mischel & Ebbesen, 1970, p. 332)

The delay’s duration is unspecified except as “a while,” and potentially “a long time.” Subsequent studies used similar descriptions. Far from being an oversight or an idiosyncrasy, the omission of timing information is a key aspect of the paradigm’s face validity. The DG paradigm is intended to examine processes that govern the pursuit of meaningful long-run outcomes, which commonly involve uncertain, open-ended delays. Open-ended timing also figures into other laboratory indices of persistence, such as measures of how long someone will squeeze a handgrip or work on impossible puzzles (Muraven et al., 1998).

Despite this, temporal uncertainty in the DG paradigm has proven easy to overlook. It plays no role in the theoretical explanations reviewed above. One prominent early discussion (Ainslie, 1975) elided the issue entirely, stating that each participant in the DG experiments “was told he could have a food he preferred if he waited for 15 min or an unpreferred food immediately whenever he wanted to stop waiting,” (p. 475).

To address the normative question, we need to consider what a decision maker believes about the length of the delay. Different types of temporal beliefs carry very different implications for the amount of time one should wait before giving up. Rachlin (2000) eloquently expressed the intuition that we shall develop:

In a normal situation, where buses come on a fixed schedule, the time left until the coming of the bus would vary inversely with the time elapsed. But a New York street corner at eleven o’clock on a cold night is far from normal. … Where waiting time is completely unpredictable, as at the bus stop and in delay-of-gratification experiments, we would expect estimates of time left to vary directly with time elapsed. The longer you have already waited for the bus, the longer you expect to wait. As time goes by, therefore, the larger reward recedes farther and farther into the distance…Children with flatter discount functions delay gratification longer than those with steeper discount functions, and people waiting for the bus hail taxis one by one in order of the flatness of their discount functions. (Rachlin, 2000, pp. 46–47)

That is, the passage of time can increase the anticipated remaining length of a delay. In the next section we focus on the prediction problem that arises during delay of gratification.

Time prediction during delay of gratification

Temporal uncertainty and adaptive prediction

Probabilistic beliefs

We will assume that even when a delay is unknown, a decision maker still holds beliefs and would judge some delay lengths as more likely than others. We represent these beliefs in the form of a subjective probability distribution. Because we do not know the shape of this distribution a priori, our strategy will be to examine several qualitatively different possibilities.

The basic idea that decision makers maintain temporal beliefs in probabilistic form is supported by extensive evidence. When animals experience variable-interval reward schedules, for example, their response rates come to track the true probability of reward over time (Bateson & Kacelnik, 1995; Catania & Reynolds, 1968). In “variable foreperiod” studies of motor preparedness in humans (Nickerson, 1965), cued responses are fastest at times when cues are most probable.

Probabilistic beliefs also inform explicit judgments. When participants compare time intervals, their judgments are influenced by the full distribution of intervals they have encountered in the same environment (Jazayeri & Shadlen, 2010). When participants predict how long real-world events (lifespans, Congressional careers, etc.) will last, their judgments—at least at the group level—faithfully reflect the true duration statistics of the relevant domain (Griffiths & Tenenbaum, 2006). When multiple observations of a time interval are available, these observations appear to be aggregated in a Bayesian manner to support predictions (Griffiths & Tenenbaum, 2011).

Dynamic updating

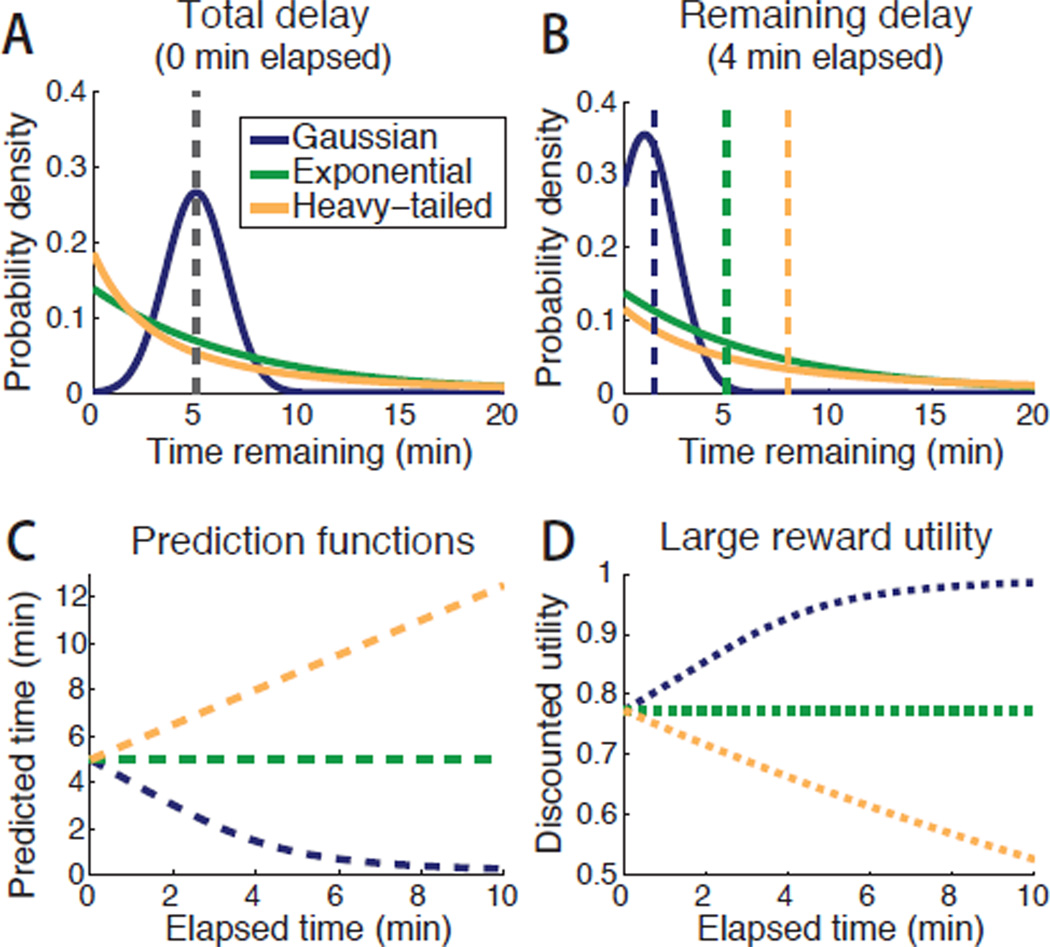
We represent a decision maker’s initial beliefs as a cumulative probability distribution, denoted F(t). For any potential delay length t, F(t) equals the subjectively held probability of the reward arriving at t or earlier. Three example distributions are shown in Figure 2A in terms of their density functions.

Figure 2.

Effect of temporal beliefs on reward evaluation. A: Three hypothetical distributions, representing different forms of temporal beliefs a decision maker might hold at the outset of the task. Depicted are a Gaussian (blue), exponential (green) and generalized Pareto distribution (orange). Each implies an initial predicted delay of 5 min (gray). B: Remaining-time distributions after 4 min of waiting. The Gaussian is truncated, the exponential remains identical, and the generalized Pareto is rescaled. Dashed lines represent updated median-based predictions. C: Remaining-delay estimates as a function of time waited. D: The delayed reward’s discounted utility (as a proportion of its undiscounted magnitude) as a function of time waited (discount rate δ = 0.95).

We next consider how beliefs change as the delay unfolds. As time passes, the original belief distribution can be translated into a remaining-time distribution. This updating process arises as a straightforward statistical problem in survival and reliability analysis (e.g., Elandt-Johnson & Johnson, 1980), and can also be described in terms of Bayesian inference (Caves, 2000; Griffiths & Tenenbaum, 2006). Briefly, if an interval t_past elapses without the reward arriving, this rules out total delays shorter than t_past while leaving unchanged the relative probabilities of longer delays (see Figure 2A–B for examples, and see Appendix for details). For example, if a certain electronic component were originally expected to last 5–10 years, and were still working after 8 years, then at that point it would be expected to last 0–2 more years.

At any given time, we can summarize the belief distribution in terms of a point prediction, denoted t^*. This point prediction is the person’s “best guess” about the length of the remaining delay. Following earlier work (Griffiths & Tenenbaum, 2006; Hayden & Platt, 2009), we set it to the median of the remaining-time distribution. (The mean, when it can be calculated, gives similar results.) Plotting the change in t^* as time passes yields the prediction function (borrowing terminology from Griffiths & Tenenbaum, 2006; see Figure 2C). The prediction function shows how the predicted remaining delay changes as a function of time elapsed.

To summarize, we assume that people start out believing that some delays are more likely than others and then update their beliefs as time passes by eliminating those delays that have already been exceeded. The next three sections examine the prediction functions that emerge from three qualitatively different forms of prior temporal beliefs.

Gaussian beliefs

First, suppose the decision maker’s prior beliefs are Gaussian. That is, the unknown delay length is thought to be normally distributed around some expected value. Figure 2A shows a Gaussian distribution with mean μ = 5 min and standard deviation σ = 1.5 min (implicitly truncated at zero). In the DG paradigm, this might represent a scenario in which the child interpreted “a while” as meaning, “five minutes, give or take a minute or two.”

The associated prediction function is plotted in Figure 2C. The predicted remaining delay grows shorter as time elapses. Even if the elapsed time exceeds the original predicted delay, the reward is still perceived as drawing progressively nearer. Gaussian beliefs might characterize a real-life situation such as waiting for the end of a lecture: the longer it runs, the less time one expects is left. In the context of the DG paradigm, Gaussian beliefs would offer no reason to reverse one’s original preference for the delayed reward. Assessed in terms of its discounted utility, the awaited reward should only grow more attractive as time passes.

Exponential beliefs

Alternatively, suppose that the decision maker believed the delayed reward had a constant probability of occurrence per unit time (i.e., a flat hazard rate). For example, the child might think there was some chance of the experimenter returning immediately, and might maintain this same level of expectancy over time. This would imply an exponential delay-length distribution, with some rate parameter λ.

A distribution of this type is shown in Figure 2A, with λ chosen so that, like above, the predicted delay is initially 5 min. Because exponential distributions are memoryless, predictions are not influenced by the passage of time. As time passes, the awaited reward is perpetually predicted to be five minutes away (Figure 2C). This would resemble a real-life situation such as predicting how many more dice rolls it will take to roll a seven.

Exponential prior beliefs constitute the only scenario in which time passage would have no effect on the predicted remaining delay. Similarly to Gaussian beliefs, exponential beliefs would offer no reason to reverse one’s original patient choice.

Generalized Pareto beliefs

As a third possibility, suppose initial beliefs take the form of a heavy-tailed distribution, such as a power function. A heavy-tailed density has more mass in its upper tail than an exponential function, and assigns greater probability to extreme values. Figure 2A shows an example, a generalized Pareto distribution. In the context of the DG paradigm, it would represent a child who thinks the delay will likely be short, but could potentially be extremely long. The distribution shown is parameterized to predict a 5-min delay initially, like the previous examples.

The predicted remaining delay increases linearly as time passes (see Figure 2C). This is a well-recognized property of power-function distributions (see, e.g., Griffiths & Tenenbaum, 2006; Gott, 1993). The anticipated wait is longer after some time has passed than when the interval began. Similar properties have been noted for other types of high-variance timing distributions (see, e.g., Dasgupta & Maskin, 2005). A real life situation that might be characterized by heavy-tailed beliefs is waiting for a reply to an email. You might initially expect a very quick reply, but if it does not come quickly you might infer that it will take substantially longer. In the DG paradigm, a lengthening of the predicted delay could justify a reversal of one’s original decision to wait (Rachlin, 2000).

Translating predictions into decisions

Approach

So far we have shown that, under some circumstances, people’s predictions of the remaining delay can lengthen as a function of time already waited. Intuitively, such lengthening predictions could justify failures to persist. Next we make this intuition concrete by showing how temporal beliefs may be translated directly into theoretical waiting times. Waiting times depend not only on temporal beliefs, but also on the value of the rewards and the rate of temporal discounting. For specific values of these parameters, we can calculate how long a utility-maximizing decision maker would persist before giving up.

Discounted utility

We base our predictions on a simple economic utility model (Equation 1). The model incorporates temporal discounting; that is, a reward at a shorter delay would be preferred to an identical reward at a longer delay.

$$U=m{\delta }^{t^{*}}$$ (1)

Here, U is discounted utility, m is reward magnitude, t^* is the predicted delay, and δ is the discount rate (0 < δ < 1). The occurrence of temporal discounting is documented by extensive behavioral evidence, and can also be justified on normative grounds (for a review, see Frederick et al., 2002). We use exponential (rather than hyperbolic) discounting in order to emphasize that our framework does not depend on violations of stationarity (Fishburn & Rubinstein, 1982). Using this function we can translate each prediction function in Figure 2C into a pattern of change in the utility of the delayed reward (see Figure 2D). Utility rises over time under Gaussian beliefs, holds constant under exponential beliefs, and deteriorates under heavy-tailed beliefs.

Decision rule

For illustration, we consider a scenario in which the decision maker initially predicts a 5-min delay, but the reward actually arrives in 10 min. We model the initial prediction as arising from either the Gaussian or heavy-tailed distribution shown in Fig. 2A (omitting the exponential case, with the understanding that exponential and Gaussian distributions make similar predictions about reversal behavior). We assign the immediate reward a magnitude of 1 and a delay of zero.

We use a deterministic decision rule. The decision maker always selects the higher-utility alternative. Because the immediate reward’s utility is fixed at 1, the choice depends on the evaluation of the delayed reward. The decision maker waits if U > 1, and quits as soon as U ≤ 1.

We compute theoretical waiting times across ranges of values for the delayed reward’s magnitude (m ranging from 1–2), and the per-minute discount rate (δ ranging from 0.91–0.99). These values capture a range of time preferences, from no delay tolerance at all (m = 1) to acceptance of delays exceeding 60 min (m = 2, δ = 0.99). These ranges are intended to be roughly plausible for the DG paradigm. If the large reward is twice the size of the small reward (e.g., 2 marshmallows vs. 1), then, allowing for diminishing marginal utility, its undiscounted utility should lie between 1 and 2. Empirical estimates of discounting usually imply per-minute discount rates near unity, but much steeper discounting occurs in children experiencing delays directly (Scheres et al., 2006).

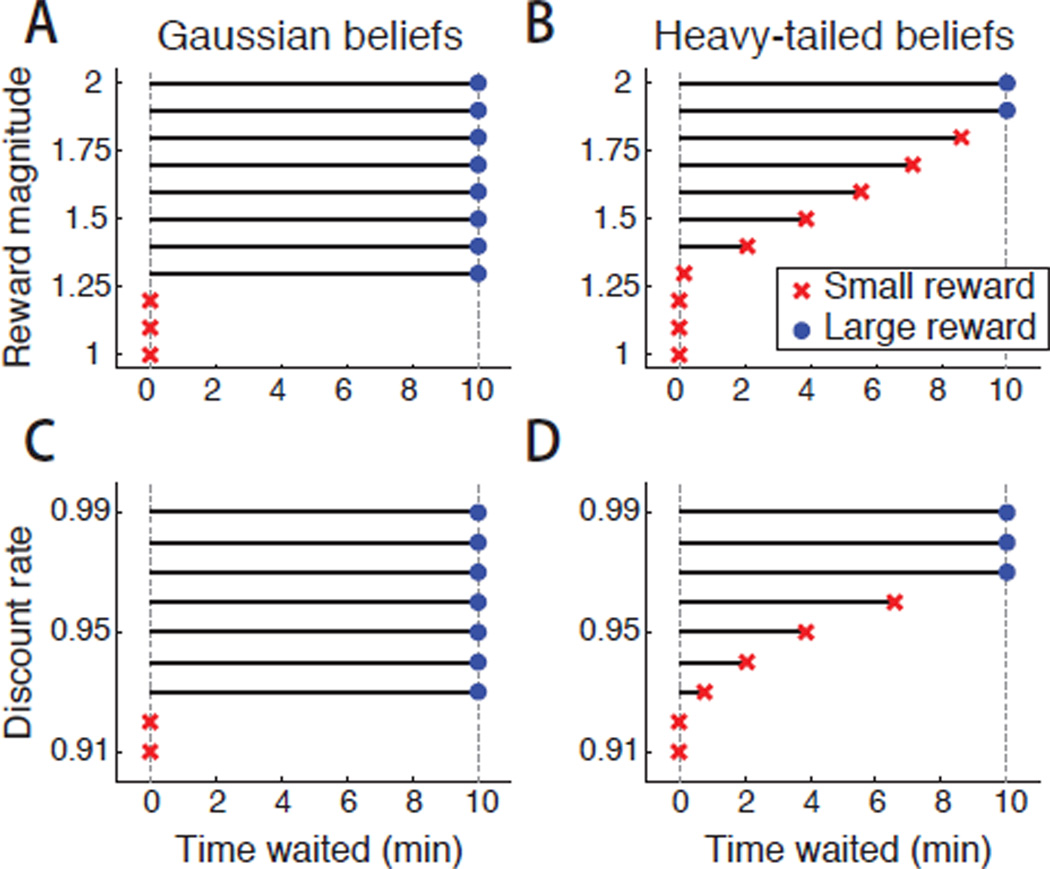
Figure 3 shows how theoretical waiting times vary as a function of temporal beliefs, discount rates, and reward magnitudes. Because both belief distributions predict a 5-min delay at the outset of the task, they always agree on whether the decision maker begins to wait. However, subsequent behavior is very different. Under Gaussian beliefs a decision maker who begins to wait always goes on to obtain the large reward. Under heavy-tailed beliefs the same decision maker may quit after a delay.

Figure 3.

Waiting times, calculated analytically, for a utility-maximizing decision maker holding the temporal beliefs in Fig. 2A. Marker shape denotes the outcome obtained. Waiting times are longer for more valuable delayed rewards (A, B) and for shallower temporal discounting functions (C, D). Under Gaussian beliefs (A, C), a decision maker who begins waiting always persists. Under heavy-tailed beliefs (B, D) a decision maker may begin waiting but later reverse this decision. The delayed reward’s magnitude is set to 1.5 in Panels C and D; the discount rate is set to 0.95 in Panels A and B.

In the context of heavy-tailed temporal beliefs, multiple factors can underlie differences in waiting times across individuals. One factor is the relative evaluation of the two rewards: individuals wait longer if they initially preferred the delayed reward by a greater margin (see Figure 3B). A second factor is the discount rate: individuals wait longer if their discounting function is shallower (Rachlin, 2000; see Figure 3D). Heavy-tailed temporal beliefs set up conditions under which these factors exert a graded influence on waiting times.

Discussion

Certain forms of temporal beliefs can cause an anticipated delay to lengthen as time passes. This occurs because time passage rules out short delays, while much longer delays remain possible. An increase in the predicted delay reduces a reward’s discounted utility. Failing to persist under these circumstances would not reflect dynamic inconsistency, but would instead be a rational response to new information. If one originally believed the reward might have arrived by now, its failure to do so warrants an updated estimate of when it might arrive in the future.

Our framework points to three concrete factors that, from a normative perspective, should influence persistence: temporal beliefs, discount rate, and reward magnitude. While the importance of these factors may appear intuitive, they differ starkly from the standard theoretical explanations reviewed above. We argue that recognizing these rational influences might reduce the number of situations in which it seems necessary to posit capacity limitations, dual-system competition, or other intrinsic sources of dynamic inconsistency. A rational prediction framework could also be expanded to incorporate factors that might be reassessed with the passage of time in other situations (e.g., the disutility of waiting, or the risk of the delayed reward never arriving).

The effect of temporal beliefs on persistence has recently been examined experimentally (McGuire & Kable, 2012). When experimental participants directly experienced a heavy-tailed distribution of time intervals, they become less persistent and more likely to show reversals, just as a rational prediction framework predicts. Later in the present paper we show how our framework might also address naturally occurring individual differences in the DG paradigm. First, however, we consider a more fundamental question. The next section examines whether decision makers actually hold heavy-tailed temporal beliefs about situations that require persistence.

Characterizing temporal beliefs

Background

So far we have shown that if decision makers held heavy-tailed temporal beliefs, this would offer a simple and rational explanation for reversals during delay of gratification. But do people really hold beliefs of this form? Indirect evidence suggests they might. Time intervals associated with many real-world human activities are well fit by heavy-tailed functions. Examples include the interval between receiving an email and replying (Barabási, 2005), between successive mentions of the same name in a newspaper (J. R. Anderson & Schooler, 1991), and between hospital admission and discharge (Harrison & Millard, 1991). When Griffiths and Tenenbaum (2006) asked participants to predict how long they would remain on hold in a phone call, median predictions were best fit by heavy-tailed beliefs.

Heavy-tailed prior beliefs have also been recommended, on theoretical grounds, as appropriate defaults when an event’s timing is unknown (Caves, 2000; Gott, 1994; Jeffreys, 1983). Heavy-tailed functions can arise from mixtures of exponentials (Sozou, 1998), and therefore are applicable if one believes an event is generated by a random process with an unknown underlying rate. Sozou (1998) shows that hyperbolic discounting functions can be explained by assuming decision makers hold heavy-tailed beliefs about the timing of an unpredictable event (specifically, in this case, an event that could cancel an expected reward).

In sum, indirect evidence suggests decision makers might bring heavy-tailed temporal beliefs to the evaluation of open-ended delayed rewards. Here we test this hypothesis directly. We conducted two survey studies of temporal prediction, using an empirical strategy developed in previous work (Griffiths & Tenenbaum, 2006). It is possible to characterize people’s temporal beliefs by asking them to predict the durations of in-progress events that are known to have lasted a specific amount of time so far. Using this strategy, we probe people’s beliefs about situations that are commonly thought to challenge self-control. The studies were conducted with adults, since our goal is to examine the possibility of a highly general link between temporal beliefs and behavioral persistence. (Additional work would be necessary to determine whether young children’s temporal cognition operates similarly; see further discussion below).

We have simple directional hypotheses. Under heavy-tailed beliefs the predicted time left should increase with time elapsed. Under Gaussian beliefs it should decline.

Study 1

Overview

In a web-based survey, adult respondents read about a hypothetical DG experiment in which a less-preferred reward was available immediately but a more-preferred reward would be delivered when an experimenter returned after a delay. A series of prompts asked respondents to imagine they had already waited a certain length of time and to predict how much more time remained. (Respondents were asked to imagine that they themselves were participating in the experiment; they were not asked to take the perspective of a child.) As a control condition, a different group of participants read a scenario adapted directly from previous work (Griffiths & Tenenbaum, 2006), which asked them to predict the time remaining in an unfamiliar movie.

Participants, materials, and procedure

A total of 390 unique participants were recruited via Amazon Mechanical Turk (http://www.mturk.com), restricting to the United States. Participants were 66% female, with mean age 35.2 (SD = 13.2), consistent with previously reported demographics (Buhrmester, Kwang, & Gosling, 2011). Each participant was paid $0.20 to complete the 5-min survey, which was administered using Qualtrics software (http://www.qualtrics.com), and analyzed in Matlab (The MathWorks, Natick, MA).

Each respondent read a scenario describing either a DG experiment or a movie in progress. On 8 subsequent screens, participants were asked to imagine that the movie or the delay had been underway for a specific length of time (2, 10, 20, 30, 40, 70, 100, or 130 min), and to predict how much longer it would continue. A ninth screen checked attentiveness, instructing participants to leave the response field empty (no participant failed this catch trial by entering a response).

Participants were randomly divided among four conditions. In the Delay-Sequential and Movie-Sequential conditions (each n = 65), participants encountered the eight elapsed times in ascending order. In the Delay-Random and Movie-Random conditions (each n = 130), participants saw the elapsed times in one of eight random orders, forming a counterbalanced Latin-square design (n = 16–17 per cell). The random-order conditions allow us to perform a between-subject analysis using the first trial only, to guard against any effect of repeated queries.

Results and discussion

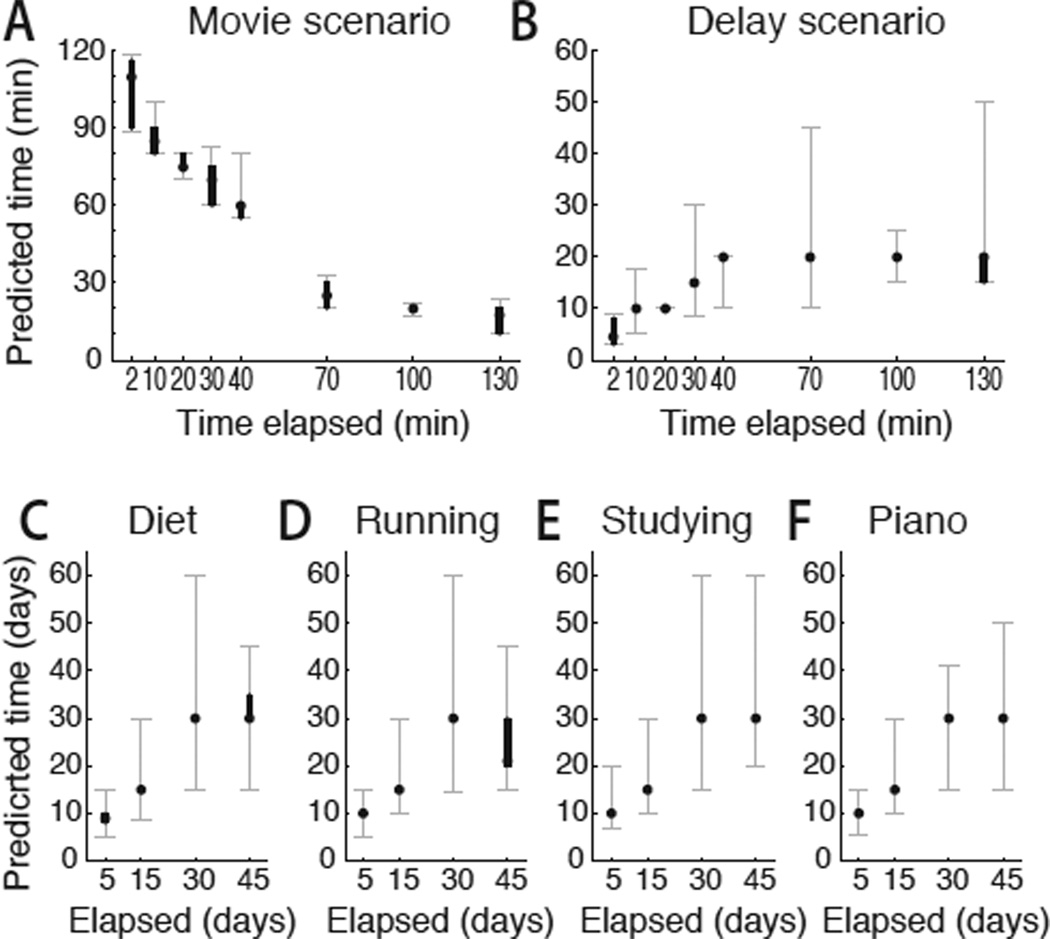
We first examine responses on the first trial in the random-order conditions. Across participants, we calculated the Spearman rank correlation between elapsed time and predicted time left. For the movie scenario, time-left estimates correlated negatively with elapsed time (Spearman ρ = −0.87, p < 0.001; see Figure 4A), replicating previous findings (Griffiths & Tenenbaum, 2006) and presumably reflecting participants’ knowledge about the roughly Gaussian distribution of movie run times. For the delay scenario, in contrast, time-left estimates correlated positively with elapsed time (Spearman ρ = 0.46, p < 0.001; see Figure 4B). This finding directly supports our hypothesis that an anticipated delay may lengthen as a function of time waited. The effect also holds if we consider only the shortest 4 elapsed times (2–30 min; ρ = 0.44, n = 65, p < 0.001).

Figure 4.

Judgments of time remaining as a function of time elapsed, for scenarios involving temporally uncertain future events. Points show the median response across participants. Gray error bars show the interquartile range. Black error bars show bootstrapped 68% confidence intervals for the median (analogous to ±1 standard error), which in some cases contain only one value. Data in A–B reflect each participant’s first trial in the random-order conditions of Study 1. A: For the time left until the end of a movie, estimates decline as a function of time elapsed. B: For the time left in a delay-of-gratification experiment, estimates rise. Panels C–F show results of Study 2. Responses reflect estimates of how much longer it would take to achieve a long-run outcome, given no noticeable progress after the specified elapsed time. In all four scenarios, predicted remaining delays rise as a function of time elapsed.

In the sequential-order conditions we evaluated the equivalent effect on a within-subject basis. We calculated Spearman’s ρ for each participant individually (correlating the 8 elapsed time values with an individual’s 8 predicted delays), and tested the median single-subject ρ against zero using a nonparametric Wilcoxon signed-rank test. Time-left estimates again declined with elapsed time for the movie scenario (median ρ = −0.99, signed-rank p < 0.001) and rose with elapsed time for the delay scenario (median ρ = 0.55, signed-rank p < 0.001).

To summarize, judgments of time left increased as a function of time elapsed in an open-ended waiting scenario. The empirical functions in Figure 4 correspond to the theoretical prediction functions in Figure 2C. While the observed pattern is consistent with a heavy-tailed belief distribution, it also supports our central argument independently of this. A lengthening predicted delay is sufficient to imply that discounted utility declines with time waited, offering a rational basis for reevaluating one’s original choice to persist. The exact cognitive algorithms people use to make these types of predictive judgments are an active topic of research (for thorough overviews, see, e.g., Griffiths & Tenenbaum, 2006, 2011). The difference between the movie and delay conditions establishes that judgments depended on the scenario content.

For the DG scenario, the shorter elapsed times are arguably more realistic than the longer times (although Mischel & Ebbesen, 1970, do mention pilot work in which waiting times exceeded an hour). For all the analyses described above, participants made their responses to shorter times before they encountered longer times, mitigating any concern that long elapsed-time values might have caused participants not to take the task seriously.

Study 2

Overview

A second experiment tested a broader range of domains in which self-control intuitively seems relevant. Four scenarios asked participants to imagine that they had begun some regimen in hopes of achieving a long-run objective, but had not yet succeeded after a given period of time. Participants were asked to predict the time left before they would succeed.

Participants, materials, and procedure

A total of 256 participants were recruited in the same manner as Study 1, and were paid $0.15 for completing the 3-minute web-based survey. Participants were 56% female, with mean age 32.7 (SD = 11.8).

Four scenarios asked respondents to imagine that they were (1) dieting in hopes of losing weight, (2) running in hopes of improving their mile time, (3) studying in hopes of improving their LSAT score, or (4) practicing piano in hopes of playing a piece without mistakes. Each scenario was associated with a different length of time that had elapsed without the desired outcome having yet occurred (5, 15, 30, or 45 days). The assignment of times to scenarios followed a counterbalanced Latin-square design (n = 63–65 per cell). A fifth screen asked participants to leave the response field blank. Two participants (0.8%) failed this catch trial by entering responses and were replaced. Data were analyzed for each scenario separately, using between-subject Spearman rank correlation tests.

Results and discussion

Predicted time left increased with elapsed time in all four scenarios (ρs = 0.46–0.53, ps < 0.001; see Figure 4C–F). The effect also holds when examining only the two shortest elapsed times in a Wilcoxon rank-sum test (5 vs. 15 days; all ps < 0.001). We conclude that lengthening temporal predictions characterize a variety of naturalistic domains in which self-control is typically assumed to play a role. Our findings imply that even an individual with stable preferences and no self-control limitations would still sometimes reverse his or her own previous patient choices.

Fitting empirical waiting times

Variability in delay times

The previous two sections showed that a rational prediction framework can explain why people would sometimes reverse their previous decisions and fail to persist toward delayed gratification. However, much previous research has focused, not merely on the occurrence of reversals, but on differences in persistence across individuals and situations (Mischel, Shoda, & Peake, 1988; Shoda, Mischel, & Peake, 1990). Accounting for these differences is a chief aim of the hot/cool framework (Metcalfe & Mischel, 1999). In this section we examine how a rational prediction framework could accommodate individual differences.

As discussed above, our framework identifies three specific influences on waiting times. The first is a person’s temporal beliefs, which dictate how the predicted delay will change as time passes. The second is the delayed reward’s perceived magnitude. People who initially prefer the delayed reward by a greater margin will wait longer (see Figure 3B). The third is an individual’s temporal discount rate. Steeper discounters will wait less, because the rising delay will have a greater impact on their evaluation of the delayed reward (see Figure 3D).

In the present section we translate our framework into a simple working model, and show that it successfully fits an empirical distribution of waiting times. We do not view the quality of the fit in itself as discriminative (other successful models could undoubtedly be formulated). However, the results qualify our framework as one viable explanation for the patterns of individual differences observed empirically. To our knowledge, hot/cool and depletion models have not yet been formulated at a level of detail that would permit this type of direct evaluation.

Delay-of-gratification data

Data source

We used data from a large longitudinal study (the National Institute of Child Health and Human Development Study of Early Child Care and Youth Development [NICHD-SECCYD]; for further details see, e.g., Belsky et al., 2007). The data set includes waiting times for a sample of 961 individuals (51.6% female) who completed a version of the classic DG task (Mischel & Ebbesen, 1970) at age 4.

Experimental procedure

Each child first practiced using a bell to call the experimenter. Then the child selected a snack (animal crackers, pretzels, or M&Ms). After verifying that the child preferred a larger amount to a smaller amount, the experimenter placed both amounts in front of the child and explained that he or she would leave the room. The child could either wait for the experimenter to return and then eat the larger snack, or could stop early and eat the smaller snack. The large reward was delivered after 7 min. The task stopped if the child rang the bell, ate the food, called for help, or tried to leave the room. The main dependent variable was the number of seconds before one of these events occurred.

For our purposes, it is important to know how the delay was described to the child. According to the instructional materials, the experimenter said, “I need to leave the room for a few minutes to do some work,” and later said, “I have to go out of the room for several minutes to do some work on my own.” “Several minutes” is arguably more specific than “a while” (Mischel & Ebbesen, 1970), but it remains the case that, as in previous studies, the precise duration was left unspecified and open-ended.

Descriptive results

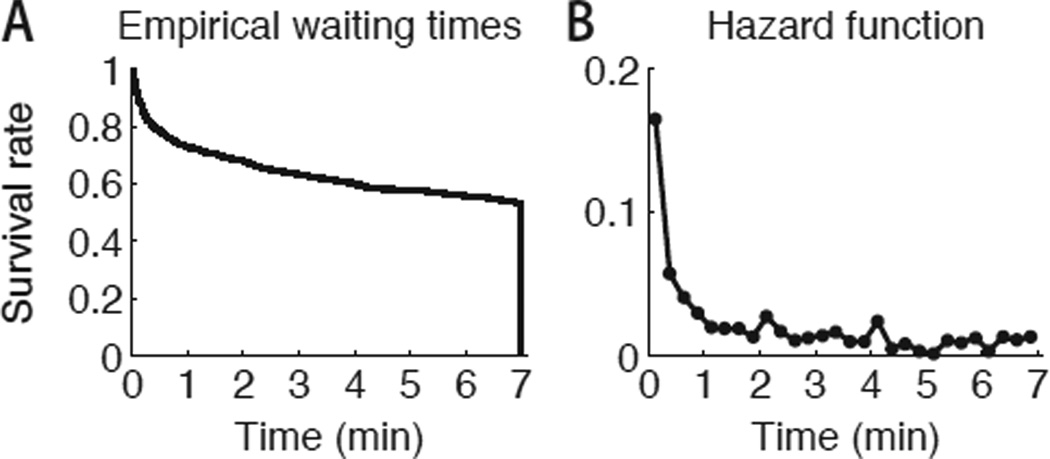
Of 961 children, 514 (53.5%) waited 7 min and received the large reward. Those who stopped earlier showed an asymmetrical distribution of waiting times (median = 36 sec, interquartile range = 8–147.25 sec). The empirical distribution is shown in Figure 5A. Its most prominent feature is a declining hazard rate, which is plotted directly in Figure 5B. Most of the children who give up do so early. A child’s probability of quitting declines the longer he or she has already waited.

Figure 5.

Distribution of waiting times in empirical delay-of-gratification data. A: Survival function, plotting the proportion of participants who are still waiting for the large reward at each point in the delay period. Those who were still waiting at the 7-min mark received the large reward. B: Empirical hazard function, calculated using 15-sec time bins. Each point plots the number of participants who stopped waiting during that bin, as a proportion of those who were still waiting at the beginning of the bin.

This pattern is already somewhat surprising in light of theories of persistence failure that posit an exhaustible self-control resource (Baumeister et al., 1998; Muraven et al., 1998). Although we are aware of no detailed predictions in this regard, such an account might intuitively imply that the probability of giving up would increase over time.

In the remainder of this section we will evaluate decision models in terms of their ability to match the empirical distribution in Figure 5A.

Developing a predictive model

Overview

Here we translate our rational prediction framework into a generative model that we can evaluate against empirical data. This process involves two steps. First we consolidate the terms of the model developed above, ultimately leaving only two free parameters. Second, we introduce variability across individuals.

Model simplification

Our premises are that the predicted time remaining, t^*, increases as a linear function of elapsed time, t_past, and that temporal discounting is exponential. (We obtain very similar results if we assume that discounting is hyperbolic; see Appendix.) With minor simplifications (see Appendix), this leads to the following expression for the delayed reward’s utility as a function of t_past:

$$U(t_{\text{past}})=m{D}^{t_{\text{past}}}$$ (2)

As above, m refers to the magnitude of the delayed reward. The parameter D controls the change over time in the delayed reward’s utility. It combines information about both the discount rate and the rate of increase in t^*. D is bounded between 0 and 1. Equation 2 resembles a discounting function because, under generalized Pareto beliefs, there is a linear relationship between elapsed time and remaining time. We will refer to D as the rate of deterioration in the delayed reward’s utility.

To generate waiting times, we need to identify the value of t_past at which an individual will give up waiting, for particular values of m and D. We set the utility of the immediate alternative to 1, and posit that the decision maker deterministically maximizes utility. So long as m ≥ 1 and 0 < D < 1, we can calculate the waiting time by setting Equation 2 equal to 1:

$$t_{\text{past}}=-\frac{\text{ln}m}{\text{ln}D}$$ (3)

If the resulting waiting time exceeds 7 min, the decision maker receives the delayed reward and the waiting time is recorded as 7 min.

Two sources of population variability

We introduce individual differences by allowing either m or D to vary across a population of decision makers. For m, this can be done by assuming a Gaussian distribution with mean μ_m and standard deviation σ_m. This represents the idea that some individuals might value the large reward more highly than others (relative to the small reward) when the choice is first presented.

Representing population variability in D requires an additional step. D cannot be Gaussian because it is bounded between 0 and 1. We use the logistic function, which maps real values to the unit interval, and set D as the logistic transformation of a Gaussian random variable X:

$$D=\frac{e^X}{1+e^X}$$ (4)

We characterize X in terms of its mean μ_X and standard deviation σ_X. Thus, the final model may have up to 4 parameters: μ_m, σ_m, μ_X, and σ_X. To examine only one source of variability at a time, we fit the model with either σ_m or σ_X fixed at zero.

Model fitting

Procedure

To test the model, we generated 961 waiting times (matching the size of the empirical data set) for a given set of parameter values. The values of m or X across samples reflected the relevant Gaussian distribution; we calculated D for each sample using Equation 4, and then calculated waiting times using Equation 3. The resulting distribution of waiting times was evaluated against the empirical data in Figure 5A.

We quantified the mismatch between the simulated and empirical data in terms of the Cramér-von Mises statistic T, which measures the overall difference between two cumulative distributions (T. W. Anderson, 1962). We used an automated optimization algorithm to search for parameters that minimized T (fminsearch in Matlab; The MathWorks, Natick, MA). We tested a grid of initialization values, iterating over {1, 2, 3} for each parameter.

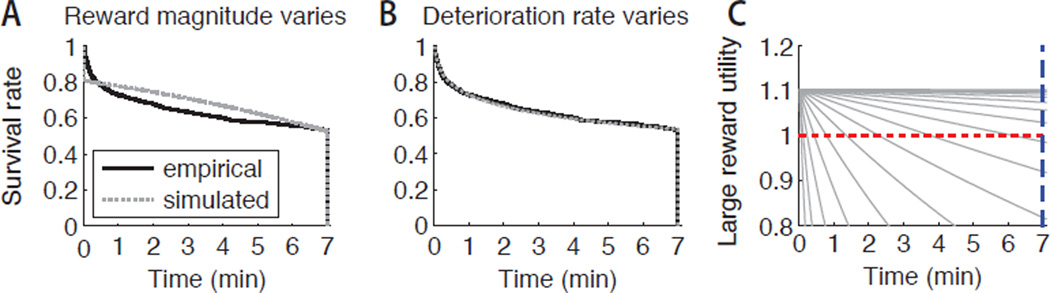
Variability in reward magnitude (m)

First we fit the model with variability solely in m, which controls the decision maker’s initial appraisal of the large reward. We optimized three free parameters, μ_m, μ_X, and σ_m, setting σ_X to zero. The result, shown in Figure 6A, failed to match the qualitative shape of the empirical distribution. The best-fitting T = 1.05 indicated that the simulated and empirical distributions were significantly different (p = 0.004). Best-fitting parameters were μ_m = 1.34, μ_X = 3.23, and σ_m = 0.39. These results offer little indication that variability in m alone can satisfactorily account for individual differences in waiting times.

Figure 6.

Results from fitting a rational prediction model to delay-of-gratification data. A: A model with individual variability in the delayed reward’s subjective magnitude m yields a qualitatively poor match. B: A model with individual variability in the delayed reward’s deterioration rate D fits successfully. C: Utility timecourses for the population of decision makers under the model in Panel B. Utility deteriorates at different rates for different individuals (gray lines). A decision maker quits when utility crosses below the red line (the value of the immediate reward), or, alternatively, obtains the delayed reward if the function first crosses the blue line.

This conclusion depends, of course, on our choice of a Gaussian distribution for m. The distribution for m could be tailored to match the data arbitrarily closely. For now we take the view that the waiting times data impose too few constraints to justify departing from default Gaussian assumptions (but see further discussion below).

Variability in the deterioration rate (D)

Next we tested a model with variability solely in the parameter D, which controls the rate of deterioration in the delayed reward’s utility over time. We optimized three free parameters, μ_m, μ_X, and σ_X, while leaving σ_m fixed at zero. As Figure 6B shows, this version of the model is successful, achieving T = 0.01, which indicates no significant difference between the distributions (p = 0.99). Best-fitting parameter values are μ_m = 1.10, μ_X = 4.62, and σ_X = 3.86. Taken at face value, the best-fitting model treats the delayed reward as initially preferred by only a small margin (1.10 times the value of the immediate reward), and posits high variability in the rate at which its utility deteriorates. The values of μ_X and σ_X imply a median deterioration rate D of 0.9902 (per minute elapsed) for the population, and interquartile range 0.8826–0.9993.

Figure 6C illustrates the internal workings of the best-fitting model in more detail. Solid lines depict utility over time, plotted for every 5th percentile (from 5 to 95) in the population. The red dashed line marks the utility of the immediate reward, while the blue dashed line marks the delayed reward’s arrival time. A decision maker quits if the utility timecourse crosses the red line before it reaches the blue line. The model instantiates something similar to Rachlin’s (2000) image in the passage quoted above, of decision makers giving up “one by one in order of the flatness of their discount functions.”

It is important to recognize that the model in this form is quite flexible. The successful fit therefore does not represent confirmation of a narrow model-derived prediction, but instead reflects that a rational prediction framework can accommodate a range of phenomena, including the findings of real delay-of-gratification experiments.

Discussion

Formulating a simple working model allowed us to examine two possible loci for individual differences within our framework: variability either in the large reward’s initial utility (m), or in the rate at which its utility deteriorates (D). As it happens, both these possibilities correspond to accounts of delay-of-gratification behavior previously suggested by Rachlin (2000). One idea is that children derive social reward merely from fulfilling the experimenter’s perceived expectation that they wait. If children differed in their sensitivity to social incentives, this would enter our model in the form of variability in m. Alternatively, individuals might differ in their discount functions or temporal beliefs, which would correspond to variability in D.

Either account depends crucially on the proposition that, from the decision maker’s perspective, the predicted remaining delay lengthens as time passes. Lengthening temporal predictions set up a situation in which individuals wait longer for outcomes that are more valuable, or that are discounted less steeply.

Our results suggest that real waiting times are not readily explained by Gaussian variability in the delayed reward’s perceived magnitude, but could potentially emerge from variability in the delayed reward’s deterioration rate. We cannot yet, however, isolate the specific contributions of discount rates and temporal beliefs; this remains a significant outstanding research objective. A general limitation of the approach we have adopted in this section is that waiting-time data exert only rather soft constraints on the underlying decision process. Our main aim in presenting this modeling exercise is to make clear that accounts positing limited self-control are not the only way to account for existing data on waiting times during delay of gratification.

While our simplified framework appears sufficient to fit the data, it could be elaborated in many ways. A more detailed model might allow for random noise, both in measurement and in the decision process itself, and might permit multiple parameters to vary simultaneously across individuals. It would be particularly interesting to examine the possibility that individuals hold qualitatively different prior temporal beliefs (compare, e.g., panels A and B of Figure 3). It is unlikely that such complexity could be supported on the basis of waiting times data alone. Instead, testing more elaborate models will require direct empirical measurement (or manipulation) of the model’s internal variables, such as temporal beliefs and discount rates (see, e.g., McGuire & Kable, 2012).

General discussion

Calibrating persistence

We have proposed that apparent delay-of-gratification failures in many contexts can emerge from a rational and self-consistent decision process. When the timing of events is uncertain, the expected remaining length of a delay can increase with time waited. This means that persistence is not beneficial under all circumstances. Adaptive behavior requires, not maximizing one’s level of persistence, but calibrating it appropriately to one’s environment.

The idea that persistence could sometimes become excessive has not, of course, escaped mention in the existing self-control literature (see Baumeister & Scher, 1988, for a review, and see McFarlin, Baumeister, & Blascovich, 1984, for relevant empirical work). Baumeister and Heatherton (1996) mention the pursuit of unrequited love as an example, while Mischel (1974) suggests excessive persistence might characterize “an emotionally constricted person whose gratifications are perpetually postponed” (p. 254). We argue that the need to curtail persistence does not arise only in exceptional cases of obsession or emotional constriction. Rather, limiting persistence is an extremely general requirement of living in an uncertain world (Dasgupta & Maskin, 2005; Fawcett, McNamara, & Houston, 2012; McFarlin et al., 1984; Rachlin, 2000). We propose that waiting is difficult, not just because people have self-control deficiencies, but because calibrating persistence is a genuinely complex problem. As previous authors have commented:

Although persistence is often regarded as a virtue, misguided persistence can waste time and resources and can therefore defeat one’s chances of success at superordinate goals…Rather than assuming that persistence is generally adaptive, the issue should be conceptualized as making judgments about when persistence will be effective and when it will be useless or even self-defeating. (Baumeister & Scher, 1988, pp. 12–13)

Previous evidence supporting a rational prediction framework

There is a surprising degree of precedent for the view that persistence failure emerges from a rational cost-benefit evaluation, both in the original DG paradigm and in other situations like it. Mischel, Ayduk, and Mendoza-Denton (2003) argue compellingly that children make their initial choice to wait by integrating costs and benefits, but maintain that the ensuing delay interval presents a test of self-control capacity. We contend that the delay period, too, could be understood in terms of a continual reassessment of costs and benefits.

One key prediction of our framework is that it should be possible to influence waiting behavior by manipulating people’s temporal beliefs. We tested this prediction in recent empirical work (McGuire & Kable, 2012) by giving decision makers direct experience with different distributions of delay lengths. Individuals who experienced a uniform time-interval distribution, which theoretically should promote high persistence, became willing to wait longer for rewards than those who experienced a heavy-tailed distribution.

A corollary of this is that even in the original DG paradigm, performance might change through learning if the same child is tested multiple times. This corresponds closely to what is actually observed. Mischel and colleagues (1988) report surprisingly low test-retest reliability for the DG paradigm (r = 0.22), and mention temporal learning across sessions as one potential explanation.

A further implication of our framework is that persistence failure should be sensitive to the magnitudes of the outcomes at stake. As Figure 3B shows, small delayed rewards should elicit immediate quitting while large delayed rewards should elicit successful persistence. Reversals (first waiting, then quitting) should occur only in between. Consistent with this, Mischel (1974) describes carefully calibrating the sizes of incentives: “Pretesting is necessary (and was conducted) to find items in the particular choice situation that are different enough in subjective value to assure that the children will be willing to delay for their preferred choice to some degree, yet similar enough to prevent most of them from waiting up to the criterion time.” (p. 265). This description implies that behavior remains sensitive to costs and benefits throughout the delay.

Finally, waiting times should depend on other factors that affect the value of the outcomes, such as risk. As a rational prediction framework would predict, greater risk (i.e., less trust in the experimenter) makes children less likely to select a delayed reward when it is first offered (Mahrer, 1956), and also less persistent once they start waiting (Kidd, Palmeri, & Aslin, 2012).

Situational and longitudinal correlates of waiting times

Much existing research focuses on associations between waiting times and other variables, including (1) experimental manipulations of the task context, (2) longitudinal measures of individual differences, and (3) a child’s focus of attention while waiting. Most of the relevant experimental findings specifically involve the original DG paradigm, although the underlying cognitive processes are assumed to be highly general. Here we outline how a rational prediction framework might address these relationships.

Waiting times can be increased by removing the rewards from view (Mischel & Ebbesen, 1970; but see Rodriguez, Mischel, & Shoda, 1989 for a non-replication), by offering distractions (Mischel et al., 1972), or by encouraging the child to think of the rewards in an abstract, non-consummatory manner (Mischel & Baker, 1975). These manipulations are thought to work by deactivating “hot” decision-making systems (Metcalfe & Mischel, 1999; Mischel et al., 2003). An alternative worth exploring, however, is that these manipulations also work by altering the perceived passage of time. Subjective time can speed up with attention and arousal (Zakay & Block, 1997). In our framework, faster subjective time passage would lead to shorter waiting times. An explanation based on subjective timing would imply that the same delay should feel longer if rewards are visible than if they are not. A study that assessed this (in 8-year-olds) reached exactly this conclusion (Miller & Karniol, 1976).

Waiting times also correlate with diverse metrics of cognitive and social ability assessed years later (Mischel et al., 1988; Seeyave et al., 2009; Shoda et al., 1990). The standard view is that these correlations reflect a stable trait of self-control capacity. However, other traits might also underlie these correlations. One candidate is temporal discount rate, which varies across individuals and shows trait-like stability over time (Kirby, 2009; Ohmura, Takahashi, Kitamura, & Wehr, 2006). In our framework, steeper discounting leads to shorter waiting times. Like waiting times, discount rates are correlated with cognitive ability (Shamosh & Gray, 2008). Individuals might also differ in their temporal beliefs, or in their awareness of the passage of time (Miller & Karniol, 1976; Mischel, 1961; Zauberman, Kim, Malkoc, & Bettman, 2009).

A third correlate is a child’s focus of attention while waiting. Children who spend more time looking at task stimuli (particularly the bell that serves as the termination signal) quit sooner (Eigsti et al., 2006; Rodriguez et al., 1989). One interpretation is that attention to choice stimuli drives hot-system activation (Metcalfe & Mischel, 1999). An alternative, however, is that attentional focus is a reflection, rather than the cause, of an ongoing reevaluation process. This interpretation is compatible with recent findings regarding the role of visual attention in the evaluation of choice alternatives (Kim, Seligman, & Kable, 2012; Krajbich, Armel, & Rangel, 2010).

Cognition, emotion, and phenomenology

A potential objection is that our proposal reserves no specific role for emotion in driving persistence failures. Tasks like the DG paradigm are often construed as affectively laden struggles, and existing theories explicitly appeal to affect as a part of the mechanistic basis for self-control failure (Loewenstein, 1996; Metcalfe & Mischel, 1999). In this regard, an account based on rational prediction might seem intuitively unsatisfying.

Our mathematical framing of the problem should not be misinterpreted as implying we believe decision makers engage in explicit numerical reasoning. Abundant evidence—pertaining to adults, infants, and nonhuman animals—indicates that statistical learning and inference take place implicitly (Aslin, Saffran, & Newport, 1998; Catania & Reynolds, 1968; Gallistel & Gibbon, 2000; Gopnik, Sobel, Schulz, & Glymour, 2001; Griffiths & Tenenbaum, 2006; Körding & Wolpert, 2004; Saffran, Aslin, & Newport, 1996; Trommershäuser, Landy, & Maloney, 2006; Turk-Browne, Jungé, & Scholl, 2005). Accordingly, nothing in our account requires that persistence decisions be free of affect. We find it highly plausible that distress or frustration might accompany the perceived lengthening of a delay. If affect helps drive the choice to quit, this would support a view of affect as facilitating adaptive decision-making, not impeding it (Bechara, Damasio, Tranel, & Damasio, 1997; Cosmides & Tooby, 2000; Kurzban, 2010).

Other forms of dynamic reassessment

While we have focused specifically on the reassessment of delay, other types of cost might also be reassessed as a function of elapsed time. One is the risk of the delayed reward never arriving. This type of risk was deliberately minimized in the original DG experiments (the importance of risk, or “trust,” having been documented previously; Mahrer, 1956). If the DG paradigm is modified to add risk, children indeed wait less time for less reliable experimenters (Kidd et al., 2012). Our framework could easily be extended to incorporate the risk of non-reward. Adding risk would introduce new ways of justifying persistence failure on normative grounds (Fawcett et al., 2012; McFarlin et al., 1984). Risk assessment is potentially relevant to the types of persistence scenarios we examined in Study 2; after a long period of unsuccessful dieting, for example, one might infer that success will never come. From a practical standpoint, there may be little difference between a reward that takes an extremely long time and one that never comes at all.

Decision makers also might dynamically reassess the disutility of waiting (i.e., the cost per unit time). If one is initially unsure how costly or unpleasant it will be to wait, one might need to estimate this from direct experience as the interval unfolds. This type of estimation might play an especially important role in tasks that require enduring pain or physical exertion, the cost of which might be hard to predict and might fluctuate. Incorporating dynamic utility estimation would require elaborating on the simple discounting model that we have used to characterize the cost of delay time. One implication of this is that merely supplying exact timing information would not necessarily be enough to eliminate delayed quitting. Even in the absence of temporal uncertainty, rational decision makers might still reverse themselves if they were dynamically estimating the disutility of delay.

Limitations

An important limitation on our framework’s scope is that it neither explains nor predicts self-constraining behavior. Self-constraining refers to locking in one’s current choice, limiting what alternatives will be available in the future (Ainslie, 1975; Gul & Pesendorfer, 2004; Schelling, 1984; Strotz, 1955). Decision makers might choose to self-constrain if they wish to guard against a shift in their own preferences. Because our framework posits stable preferences, self-constraining is not expected. Indeed, the essence of our argument is that a choice to begin waiting need not imply a commitment to wait indefinitely.

We take it as established that human decision makers are sometimes genuinely inconsistent, and sometimes do prefer to self-constrain (Ariely & Wertenbroch, 2002; Houser, Schunk, Winter, & Xiao, 2010; Trope & Fishbach, 2000). In particular, when the local environment changes, preferences may shift as a result of cuing effects (Bernheim & Rangel, 2004; Laibson, 2001). However, a key step toward understanding genuine preference instability is to delineate as narrowly as possible the situations in which it occurs. Our account of delay of gratification highlights a category of decisions in which, we argue, superficially inconsistent behavior can be more naturally understood in different terms.

A second limitation is that much of the evidence to which we refer (including our survey studies) pertains to adults, not children. This fits our primary objective, which is to address the general phenomenon of persistence failure while referring to the DG paradigm as an especially elegant and influential case. However, it leaves unresolved the developmental question of whether our framework explains delay of gratification in children. A potential future direction would be to assess temporal predictions in real time (this might be impractical with 4-year-olds but feasible with older children). Another would be to see if children change their waiting behavior in response to direct experience with time intervals (cf. McGuire & Kable, 2012).

Conclusions

When the timing of events is uncertain, decision makers face a nontrivial problem of deciding how long to pursue delayed rewards before giving up. The utility-maximizing course of action is usually not to persist indefinitely. Even a decision maker with infinite self-control would sometimes need to place limits on persistence. This suggests that research seeking to understand genuine preference instability and self-control failure might focus on a narrower range of situations than usually supposed.

The present research carries implications for efforts to modify persistence behavior. A rational prediction framework shows how waiting times should depend on reward magnitudes and temporal discount rates. This implies that interventions affecting discount rates (e.g., Senecal, Wang, Thompson, & Kable, 2012), might influence delay of gratification. Our framework also shows that persistence should depend on temporal beliefs, which may be highly malleable in response to new experience. Initial work (McGuire & Kable, 2012) suggests that domain-specific temporal learning rapidly influences willingness to persist. Future work should extend these findings to longer durations and new types of decision environments.

These recommendations differ from those that emerge from other explanatory frameworks. Other frameworks suggest improving persistence by acquiring strategies to manage hot/cool interactions (Metcalfe & Mischel, 1999), or by cultivating self-regulatory strength (Baumeister, Gailliot, DeWall, & Oaten, 2006). We propose a renewed focus on rational factors—reward magnitudes, discount rates, and temporal beliefs—that enter into the underlying computational problem.

Appendix

Mathematical details

Belief updating

General belief updating

Here we specify how probabilistic beliefs are updated based on the passage of time. We use t for the remaining delay until a reward will be delivered. F₀(t) is a cumulative distribution representing the decision maker’s beliefs about the delay before any time has yet elapsed. Our goal is to find an updated distribution, F_tpast(t), that characterizes beliefs about the remaining delay after the passage of some interval t_past.

To do this, we shift the original distribution leftward by t_past, truncate it at zero, and renormalize. Equation 5 gives the expression for the updated distribution.

$$F_{t_{\text{past}}}(t)=\{\begin{array}{cc}\frac{F_0(t_{\text{past}}+t)-F_0(t_{\text{past}})}{1-F_0(t_{\text{past}})}& \text{if}t\ge 0\hfill \\ 0\hfill & \text{otherwise}\end{array}$$ (5)

Equation 5 matches standard procedures in survival and reliability analysis (e.g., Elandt-Johnson & Johnson, 1980), and is similar to Bayesian approaches described previously (Griffiths & Tenenbaum, 2006; Caves, 2000). From here on, we leave it implicit that the remaining-time distribution only has support for nonnegative values of t. The next three sections work through this updating procedure for specific distributional forms.

Gaussian beliefs

First we consider the case in which the decision maker’s prior beliefs take the form of a Gaussian distribution with mean μ and standard deviation σ. Beliefs at the outset of the interval are described by Equation 6. (We use Φ for the standard normal cumulative distribution function and Φ⁻¹ for this function’s inverse.)

$$F_0(t)=\mathrm{\Phi }\left(\frac{t-\mu }{\sigma }\right)$$ (6)

Substituting Equation 6 into Equation 5 gives a truncated Gaussian distribution, which characterizes the decision maker’s beliefs upon reaching t_past(Equation 7).

$$F_{t_{\text{past}}}(t)=\frac{\mathrm{\Phi }(\frac{t_{\text{past}}+t-\mu }{\sigma })-\mathrm{\Phi }(\frac{t_{\text{past}}-\mu }{\sigma })}{1-\mathrm{\Phi }(\frac{t_{\text{past}}-\mu }{\sigma })}$$ (7)

Next we wish to obtain the decision maker’s median-based prediction (denoted t^*) as a function of t_past. The median has a cumulative probability of 0.5, so we identify t^* by setting Equation 7 equal to 0.5. This yields the following prediction function.

$$t^{*}=\mu -t_{\text{past}}+\sigma {\mathrm{\Phi }}^{-1}(0.5+0.5\mathrm{\Phi }(\frac{t_{\text{past}}-\mu }{\sigma }\left)\right)$$ (8)

Exponential beliefs

Next we consider an exponential belief distribution with rate parameter σ, which has the following cumulative function.

$$F_0(t)=1-e^{-\lambda t}$$ (9)

The median of an exponential distribution equals (ln 2)/λ. For illustration, we choose a value of lambda that makes an initial prediction of 5 minutes, matching the Gaussian distribution above: λ = (ln 2)/5 = 0.14.

Consistent with the memoryless nature of exponential distributions, substituting Equation 9 into Equation 5 just produces Equation 9 again. The updated distribution is unchanged, and the prediction function is constant.

Generalized Pareto beliefs

A generalized Pareto distribution is governed by the following cumulative distribution function, with shape parameter k and scale parameter σ:

$$F_0(t)=1-{(1+\frac{kt}{\sigma })}^{-1/k}$$ (10)

A third parameter, governing location, is set to zero and omitted, meaning that we always assume the minimum possible delay is zero. The distribution shown for illustration has shape parameter k = 0.81 and scale parameter σ = 5.38. The median equals σ(2^k − 1)/k. The chosen parameters once again imply an initial median-based prediction of a 5-minute delay.

Substituting Equation 10 into Equation 5 yields the following remaining-time distribution:

$$F_{t_{\text{past}}}(t)=1-{(1+\frac{kt}{\sigma +k{t}_{\text{past}}})}^{-1/k}$$ (11)

Comparing Equations 10 and 11 shows that the remaining-time distribution can itself be described as a generalized Pareto distribution. The new distribution’s scale parameter, σ_updated can be defined in terms of the original parameters as σ_updated = σ + kt_past. That is, the scale parameter increases as a linear function of t_past, with slope k.

The median of the remaining-time distribution, expressed in terms of the original parameters, is given in Equation 12:

$$t^{*}=t_{\text{past}}(2^k-1)+\frac{\sigma (2^k-1)}{k}$$ (12)

The prediction is linear in t_past. If k > 0, it increases as time passes.

Waiting time

We use the discounting function in Equation 1 to translate the predicted delay, t^*, into discounted utility. We assume that the small reward has a utility of 1, and that the decision maker continues waiting so long as the delayed reward’s utility exceeds 1.

Waiting times are calculated using a three step process. First we evaluate whether the small reward is preferred at the start of the interval. If so, it is selected with a waiting time of 0 min. If not, we evaluate the choice at the end of the interval (10 min elapsed). If the larger reward is still preferred, it is obtained with a waiting time of 10 min. (Here we are relying on the fact that the prediction functions under consideration are monotonic.)

If the waiting time falls between 0 and 10 min, we can directly calculate the time at which U = 1. This only occurs for heavy-tailed beliefs. We start by setting Equation 1 equal to 1, and solving for t^*, to identify the value of the predicted delay at which the decision maker gives up:

$$t^{*}=-\frac{\text{ln}m}{\text{ln}\delta }$$ (13)

Next we substitute Equation 12 into Equation 13 and solve for t_past. This gives an expression for the elapsed time at which the decision maker should quit:

$$t_{\text{past}}=\frac{-\text{ln}m}{(2^k-1)\text{ln}\delta }-\frac{\sigma }{k}$$ (14)

As a technical point, we have assumed throughout that the decision maker first makes a point prediction of the remaining delay, and then uses this prediction to assess utility. We could alternatively reverse the order of these steps: we could assume that the decision maker translates the full remaining-time distribution into a probability distribution over discounted utility, and takes its median. The result would be the same, because delay and utility are monotonically related (the median delay corresponds to the median utility).

Modeling empirical waiting times

Exponential discounting

In this section we describe the simplified version of our model with which we fit empirical waiting times. The model assumes that temporal beliefs take the form of a generalized Pareto distribution. As shown above, this implies that the predicted remaining time t^* is a linear function of t_past(see Equation 12). We can express this relationship more simply by using a for the intercept (the predicted delay when the task begins) and b for the slope.

$$t^{*}=b{t}_{\text{past}}+a$$ (15)

As a practical matter, increasing the intercept a has the same effect on utility as decreasing the large reward’s magnitude, m. The data give us no way to distinguish a fixed increase in a from a fixed decrease in m. We therefore make the simplifying assumption that a can be approximated as zero and omitted. This means any effect of a is folded into the value of m. Empirical results in Figure 4B suggest that a small value for a may indeed be plausible (that is, decision makers might at first expect the delay to be short). From here forward we use the following approximation:

$$t^{*}\approx b{t}_{\text{past}}$$ (16)

We assume that the large reward’s discounted utility, U, is computed according to Equation 1. U can be expressed as a function of t_past:

$$U(t_{\text{past}})=m{\delta }^{b{t}_{\text{past}}}$$ (17)

Provided the immediate reward has a utility of 1, the decision maker will choose to continue waiting as long as U(t_past) > 1.

Equation 17 contains three possible loci for individual differences. Individuals might differ in their temporal beliefs (b), their discount rate (δ), or their appraisal of the delayed reward (m). All three of these parameters are interpretable and theoretically motivated within our framework. However, their influence on waiting times overlaps. In particular, b and δ cannot be separately identified. We can simplify the model by defining a single parameter D = δ^b, relying on the fact that δ^bt_past = (δ^b)^t_past = D^t_past. Because b is positive while δ is bounded between 0 and 1, D is also bounded between 0 and 1. The reduced, 2-parameter model is shown in main-text Equation 2.

Hyperbolic discounting

We also constructed a version of the model using hyperbolic (rather than exponential) discounting. Equation 18 shows a hyperbolic function (Mazur, 1987):

$$V=\frac{m}{1+k{t}^{*}}$$ (18)

V is the delayed alternative’s subjective value, k now refers to the hyperbolic discounting parameter, m is the delayed reward’s magnitude, and t^* is the predicted remaining delay. Like above, we can take advantage of the linear relationship between elapsed and remaining time (again using the approximation in Statement 16) to describe V as a function of t_past.

$$V=\frac{m}{1+kb{t}_{\text{past}}}$$ (19)

To identify the time at which the decision maker will quit, we set V = 1 and solve for t_past.

$$t_{\text{past}}=\frac{m-1}{kb}$$ (20)

We can express Equation 20 in terms of a single free parameter K = kb/(m − 1). K corresponds to the deterioration rate in a hyperbolic model. Quitting times can then be expressed as t_past= 1/K. The hyperbolic parameter k is generally found to be lognormally distributed across individuals. If b and m are constant, then K will also be lognormal.

We set K = e^X, where X is a Gaussian random variable with mean μ_X and standard deviation σ_X. Fitting these two parameters using the same procedure as in the main text, we obtain a best-fitting T = 0.04, indicating no significant difference between the empirical and simulated distributions (p = 0.94). The best-fitting parameters are μ_X = −2.25 and σ_X = 3.52.

The hyperbolic formulation offers additional intuition regarding the model’s scope and flexibility. If K is lognormal, waiting times will also be lognormal (because the reciprocal of a lognormally distributed random variable is itself lognormal). The fit succeeds because the empirical waiting times are indeed well characterized as a lognormal function censored at the 7-min mark. The model would fail to match data that diverged from this general form.