A Framework for Identifying Distinct Multipollutant Profiles in Air Pollution Data

Abstract

BACKGROUND

The importance of describing, understanding and regulating multi-pollutant mixtures has been highlighted by the US National Academy of Science and the Environmental Protection Agency. Furthering our understanding of the health effects associated with exposure to mixtures of pollutants will lead to the development of new multi-pollutant National Air Quality Standards.

OBJECTIVES

Introduce a framework within which diagnostic methods that are based on our understanding of air pollution mixtures are used to validate the distinct air pollutant mixtures identified using cluster analysis.

METHODS: S

ix years of daily gaseous and particulate air pollution data collected in Boston, MA were classified solely on their concentration profiles. Classification was performed using k-means partitioning and hierarchical clustering. Diagnostic strategies were developed to identify the most optimal clustering.

RESULTS

The optimal solution used k-means analysis and contained five distinct groups of days. Pollutant concentrations and elemental ratios were computed in order to characterize the differences between clusters. Time-series regression confirmed that the groups differed in their chemical compositions. The mean values of meteorological parameters were estimated for each group and air mass origin between clusters was examined using back-trajectory analysis. This allowed us to link the distinct physico-chemical characteristics of each cluster to characteristic weather patterns and show that different clusters were associated with distinct air mass origins.

CONCLUSIONS

This analysis yielded a solution that was robust to outlier points and interpretable based on chemical, physical and meteorological characteristics. This novel method provides an exciting tool with which to identify and further investigate multi-pollutant mixtures and link them directly to health effects studies.

1. Introduction

The importance of considering multi-pollutant mixtures in air pollution was highlighted in 2004 by the National Academies of Science (NAS) (NRC 2004). In response, the EPA is working to develop a multi-pollutant air quality management plan. The importance of such a strategy is described in their Multi-Pollutant Report of 2008 (U.S. EPA 2008). Adopting a multi-pollutant approach is extremely challenging due to the highly complex interactions between source emissions, atmospheric processes and effects on human health and ecosystems. One of the key components of a multi-pollutant approach is the ability to capture the multivariate relationship between pollutants at a given site. A better grasp of these relationships will increase our understanding of the interaction between pollutants as well as further our understanding of the human health effects related to exposure to these complex mixtures.

On a given day, the relationship between pollutants at a receptor site reflects the interplay between the types of sources, the meteorological conditions governing the transport, transformation and removal of the emitted pollutants and the chemical reactions between pollutants. Grouping days with similar chemical profiles allows for the identification of distinct pollution paradigms at a given site. The days with common physico-chemical properties and meteorological conditions can then be separately described and investigated. Subsequently, the acute health effects observed on different groupings of days can be investigated in order to identify the mixtures posing higher health risks. The identified pollutant profiles can also be used in future health effects studies of PM_2.5 mass by including the mixture type as an effect modifier. This approach will permit identification of toxic multi-pollutant mixtures, thus enhancing our understanding of pollutant combinations that pose higher risks to public health.

This article presents a framework that allows for identification of distinct multi-pollutant profiles and the validation of these clusters using diagnostic criteria. First, cluster analysis is used to identify distinct groupings within the days of observation. There are a large number of possible clustering algorithms, the ones considered here are hierarchical clustering methods and k-means partitioning. Second, diagnostic strategies are presented that allow for the validation of the clustering results. These strategies include goodness of fit measures that are internal and external to the data being clustered, the physico-chemical properties of the clusters and meteorological properties of the clusters. Finally we use back-trajectory analysis to explore differences in air mass origin between clusters.

Cluster analysis has not been previously used to identify distinct multi-pollutant profiles at a given site or across sites. In the environmental health field, hierarchical clustering has been used to identify sources based on the grouping of analytes (Kavouras et al. 2001). It has also been used to provide a description of regional chemical and transport processes associated with particular regimes and can inform which sources may be most important in the development of pollution episodes. Beaver and Palazoglu (2006) used an aggregated solution of k-means cluster analysis to characterize classes of ozone episodes occurring in the San Francisco bay. Pakalapati, et al (2006) used hierarchical clustering and sequencing to group air flow patterns associated with elevated ozone concentrations. Cluster analysis has also been used to cluster back trajectories to identify different classes of synoptic regimes over the duration of the trajectories (Taubman et al, 2006, Comrie et al 1996).

In this paper, cluster analysis of monitoring data collected in the city of Boston between 2004 and 2009 will be used to group days that have similar multi-pollutant profiles. These clusters will then be described according to their physico-chemical characteristics. Furthermore, the differences in meteorological conditions associated with each cluster will be identified using local weather data as well as backwards trajectory analysis. It is anticipated that this novel approach to air pollution analysis will allow for better understanding of the different multi-pollutant mixtures that comprise population exposures and may result in better characterization of health effects associated with exposure to mixtures.

2. Methods

2.1 Data Collection

PM_2.5, particle number (PN), elemental and organic carbon (EC/OC) samples were collected at the Harvard Supersite in Boston, MA. The site (42°20′ north latitude, 71°06′ west longitude) is located on the roof of the Countway Library (a six-floor building) of the Harvard Medical School in downtown Boston. This site is located within one block of a four-lane street with truck traffic and with two major highways nearby: Interstate 90 (I-90) is approximately 1.5 km to the north and Interstate 93 (I-93) is approximately 3 km to the south.

Data used in this analysis were collected between January 1^st 2004 and December 31^st 2009. Daily integrated PM_2.5 samples were collected using Harvard Impactors with Teflon filters and were subsequently analyzed by x-ray fluorescence for elemental content. Particle number was measured hourly by condensation particle counter (CPC). In this analysis, the hourly values were averaged to obtain 24-hour values. Black carbon was measured by Aethalometer. Daily sulfate (SO₄⁻) concentrations were reconstructed using the mass of elemental sulfur measured in the XRF analysis by assuming that sulfur was mostly present in the form of ammonium sulfate

The concentrations of the gaseous pollutants nitrogen oxides (NO and NO₂) and ozone (O₃) were obtained from Boston area EPA monitoring stations. The hourly values were averaged to estimate daily concentrations if at least 18 hours of measurements were collected per day. The monitoring stations used were Harrison Av., Chelsea, Lynn, Kenmore and Breman Street for the nitrogen oxides and Harrison Av., Chelsea, Lynn and Waltham for O₃. The daily values from these stations were averaged together to obtain overall daily values. Because concentrations of O3, NO and NO2 can be highly dependent on localized sources, it was determined that the best course of action would be to average across the nearby stations in order to get a more representative value over the region. Ideally, the same monitoring station would have daily gaseous and PM_2.5 composition data and averaging across sites would not be necessary.

The analysis presented in this paper was performed in 3 distinct steps. The first step was preparing the data for clustering by selecting the appropriate variables to include in the analysis, normalizing the variables and removing any days with missing values. The second step was selecting the appropriate clustering algorithm. The clustering algorithms considered were the Hartigan and Wong (1979) k-means algorithm, Ward’s hierarchical clustering (Ward 1963), single-linkage (nearest neighbor) hierarchical clustering and complete-linkage (furthest neighbor) hierarchical clustering (Cormack, 1971). The best algorithm was determined to be the method that produced clusters with the largest between to within variability ratio (SSB/SSW). The SSB/SSW indicates how distinct each cluster is from the rest of the data set. Once the appropriate algorithm was selected, the optimal number of clusters was determined and the physico-chemical differences between the clusters were examined in order to ensure that the results were meaningful in the context of environmental health research. All analyses were conducted in R v2.13.0.

2.2 Data Preparation

The initial data set contained 2,192 days of measurements taken between January 2004 and December 2009. 450 days with missing data in at least one of the variables of interest were removed (Table 1). Thus, there was a total of 1,742 days with complete observations in the study period. July 2^nd, 3rd, 4^th and 5^th of every year of interest were excluded because of the potentially influential high potassium peaks due to fireworks. Furthermore, June 6^th 2007 was excluded due an extreme value of potassium (8 times the standard deviation) and September 9^th 2009 was excluded due to an extreme value of zinc (10 times the standard deviation). In total, there were 1,716 days included in the analysis.

Table 1.

Description of Excluded Days

	# Days
Total Number of days	2192
MISSING	450
Elemental Composition	186
Particle Number (PN)	166
Black Carbon (BC)	51
Elemental & PN	28
Elemental & BC	8
PN & BC	8
Elemental & PN & BC	3
July 4th weekend	24
Outliers	2
Final Data Set	1716

The variables used in the clustering were PN, O₃, SO₄⁻, Ni, V, Zn, K, Si, Ca, Fe, BC, NO, and NO₂. Other elements obtained as part of the speciation of the filters were considered as possible clustering variables but were excluded either because of the analytical measurement was judged to be unreliable (for example CO) or because a large proportion of the measurements were below the detection limit.

In order to prevent bias due to widely varying scales of the individual variables, each variable was expressed as a modified Z-score as shown in Equation 1. The advantage of using a modified Z-score is that outlier values have less influence on the result of the clustering. Because environmental data tends to be log-normally distributed, this approach was preferred to using a Z-score.

$$Z_i=\frac{X_i-\mathit{Median}(X)}{\mathit{Median}(X_i-\mathit{Median}(X))}$$ Equation 1 - Modified Z-score

2.3 Clustering

The goal of the analysis was to group together days in the observation period having similar pollutant profiles. Unsupervised cluster analysis encompasses a broad range of algorithms that identify multivariate patterns in data sets. The output of the algorithm may be “hard” if each observation is attributed to only one cluster or “fuzzy” if an observation may be assigned to a certain degree to more than one cluster. In this analysis, we were interesting in identifying a “hard” solution so that each day was uniquely assigned to a single cluster. Three broad categories of clustering algorithms that can be used for this purpose are hierarchical, partitioning and model based clustering algorithms. Preliminary investigation demonstrated that our data was not well classified by the model-based clustering algorithms, because the data did not meet the multivariate distribution assumptions required by these models. Thus we opted to investigate the application of the partitioning and hierarchical models to the dataset.

2.4 Clustering Algorithms

2.4.1 K-means Clustering

The k-means algorithm used was developed by Hartigan and Wong. It seeks to partition M points in N dimensions into K clusters. This iterative algorithm searches for a local solution that minimizes the Euclidean distance between the observations and the cluster centers.

Advantages of the k-means algorithm are that it is easily implemented, has been used in a wide range of applications and is computationally efficient (Steinley 2006, Jain et al 1999). It has also been suggested that this algorithm is somewhat less sensitive to outliers than hierarchical clustering methods (Punj and Stewart, 1983). A major obstacle in using k-means is that the number of clusters (k) must be assigned a priori based either on pre-existing knowledge of the data or observable characteristics of the data set. In our application, there was no pre-existing knowledge of the number of unique clusters of multi-pollutant profiles. We therefore chose to run the algorithm for all values of k in the range of 2 to 8 clusters. When selecting the number of clusters, the more parsimonious solutions were favored for reasons of interpretability and to ensure adequate power in later epidemiological time-series analysis.

We used two complimentary methods to inform our choice for the value of k. The first was the Davies-Bouldin index(DB; Davies-Bouldin 1979) described in Equation 2. Small values of the DB index reflect relatively compact clusters having clustering centers that are relatively far from each other. Therefore, the value of k that minimizes the value of the DB index is the preferred one.

$$DB=\frac{1}{n}\sum _{i=1,i\ne j}^{n}max\left(\frac{{\sigma }_i+{\sigma }_j}{d(c_i,c_j)}\right)$$ Equation 2 – DB Index

Where,

• n is the number of clusters

• σ_i is the average distance of observation in cluster i to the center c_i

• σ_j is the average distance of observation in cluster j to the center c_j

• d(c_i, c_j) is the distance between the cluster centers

The second method considers the variability of synoptic weather observations within each cluster of a given solution. Daily synoptic weather observations have been shown to be account for a significant proportion of the variability of both gaseous and particulate composition of air pollution on a given day (McGregor and Bamzelis (1995), Cheng and Li (2010), Gebhart et al. (2001), Wise and Comrie (2005)). The weather parameters considered were dry bulb temperature (T), relative humidity (RH), wind speed (WS), wind direction (WD) and boundary layer height at midday (ZIM). The percent change in overall deviation for each solution was calculated as follows:

$$\%\mathit{Change}in\mathit{Overall}\mathit{Deviation}=\sum _{i=1}^5\left[\sum _{j=1}^k\frac{1}{{\mathit{SSW}}_i}{\mathit{SSW}}_{ij}-1\right]$$

Where: SSW represents the sum of squared errors

• i represents the weather parameter (T, RH, WS, WD, ZIM)

• j represents the individual cluster (1 to k)

The percent change in overall deviation represents how effectively different solutions capture the synpoptic weather patterns that lead to development of characteristic weather profiles. This conforms to the guidelines set forth by Jain et al. (1999) which indicates that domain knowledge is the most reliable way to determine the optimum clustering for a given problem.

Using these two criteria together ensure that the selection of the value of k is based on both characteristics that are internal to the dataset (DB) as well as criteria that are external to the dataset (Overall Deviation of Weather). When the two criteria indicated a different optimal number of clusters, solutions with fewer clusters were favored. This was both for reasons of interpretability of the solution as well as to increase the power of future epidemiological investigations.

To ensure that the solution selected was not a local minimum, the k-means algorithm was run 1,000 times with 1,000 different random initial seeds. The solution with the lowest sum of squares within (SSW) was retained as the best solution for the given conditions. The large number of initial seed values helped to ensure that the solution did not correspond to a local minimum (Steinley, 2006).

The k-means algorithm used was implemented in the kmeans function of the stats package in R v. 2.13.0.

2.4.2 Hierarchical Clustering

Hierarchical clustering differs from partitioning algorithms such as k-means in that it results in a nested series of partitions that can be represented by a dendogram. All three algorithms considered in this analysis were agglomerative, meaning that they build the hierarchy by successive merging of cluster elements, starting with the individual observation points. When deciding which set of points to merge, different hierarchical methods use different criteria. The advantage of hierarchical algorithms is that the number of clusters in the solution does not need to be selected a-priori; rather the cluster dendogram is cut after analysis to represent the desired number of clusters.

Single-linkage hierarchical clustering is also known as closest neighbor linkage. This recursive algorithm begins by assigning each of the observations to separate clusters. It then recursively merges together the clusters that are closest to each other. The distance between two clusters is defined as the distance between the two closest elements of these clusters. A disadvantage of this algorithm is that it can result in a cluster that consists of a chain of single elements that are close to each other even though the elements of the cluster as a whole are distant (Sokal and Sneath, 1963).

Complete-linkage hierarchical clustering is similar to single-linkage. However, it uses a different distance measure. The distance between two clusters is defined as the distance between the two cluster elements that are furthest from each other. This method does not have the tendency to produce chaining. However, as the number of members of the cluster increases, the probability of a new element being added to the cluster decreases (Blashfield 1976). This can lead to incorrect classification of elements.

Ward’s method (1963) is an agglomerative process that begins with 1 cluster for every observation and then iteratively combines the points that lead to the minimal increase in the sum of squares. Because this method is agglomerative, the solution reached is constrained by the previous choices made by the algorithm. Therefore, for a given number of clusters, the solution reached by the Ward method is often not the solution that has the minimal sum of squares error. An advantage of this method is that it produces clusters that are relatively compact. It is criticized for sometimes producing clusters that are too small for the given data (Cormack 1971).

These three algorithms were run using the implementation in the hclust function of the stats package in R v. 2.13.0.

2.5 Sensitivity Analysis

Sensitivity analysis was performed in order to determine whether outlier observation days were driving the clustering results. The method used was to create 100 test data sets in which 170 (10%) of the observations days were randomly removed. The test data sets were then clustered using the same method as the complete data set. The dates were compared between the test clusters and the real clusters in order to determine the percent of days that were misclassified in the test data sets. Misclassification was defined to mean that a date belonged to a different cluster in the test data set than it did in the initial cluster results. It was assumed that a low percentage of misclassification would indicate that the clustering was not being driven by outlier values. The mean and standard deviation of the misclassification for the 100 test data sets was reported.

2.6 Back Trajectories

Back-trajectory paths were calculated using the HYSPLIT model (v. 4.9) developed by National Oceanic and Atmospheric Administration (NOAA). The meteorological archive used was the Eta Data Assimilation System with 40 km resolution (EDAS40). For every hour of every day from 2004–2009, a 84 hour back-trajectory was computed in HYSPLIT from the starting coordinates of the sampling site and a vertical height of 750 m. The vertical movement of air parcels within the system was modeled using an isentropic assumption (Draxler and Rolph (2003), Rolph (2003), Rolph (1990)).

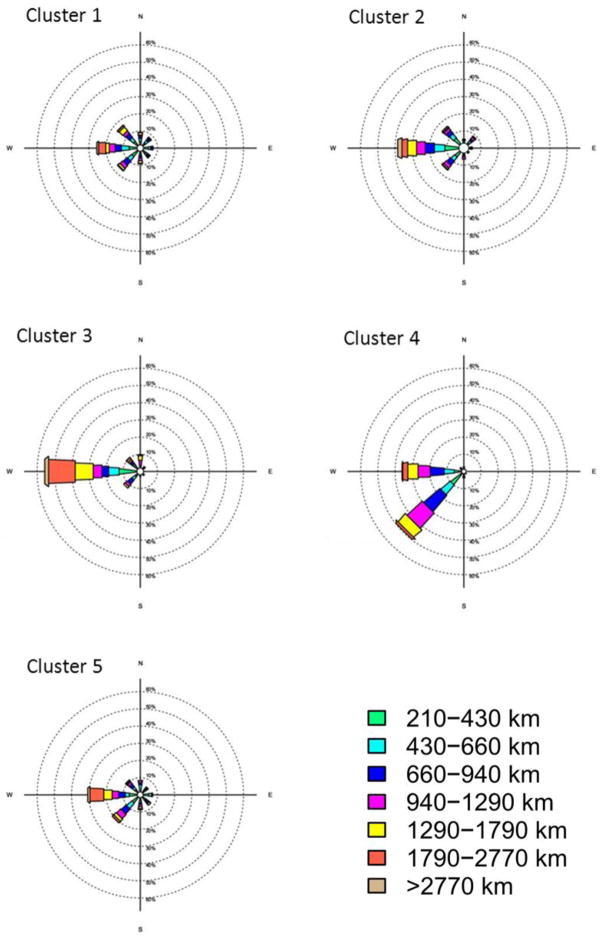
Back-trajectory points for each cluster where plotted on wind rose graph with 8 quadrants corresponding to the direction of the trajectory with respect to Boston. The distance of the trajectory with respect to Boston was displayed using colored bars on each radial segment. This plotting was done in R v. 2.13.0 using the rose2 function of the heR package written by Klepeis (2004).

3. Results

3.1 Algorithm Selection

Single-link and complete-link hierarchical clustering both produced solutions (for number of clusters (k) between 2 and 8) where over 90% of the observations belonged to a single cluster. This is not consistent with physico-chemical knowledge of discrete air pollution regimes.

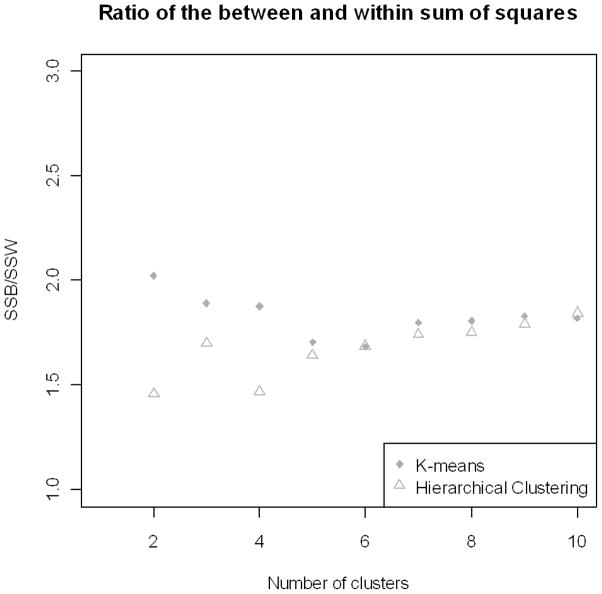
The ratio of the between sum of squares error (SSB) to the within sum of squares error (SSW) was used to compare the clustering solutions produced by the Ward method and k-means. Based on the results shown in Figure 1, k-means and the Ward method both show similar values of the SSB/SSW for values of k greater than 5. For values of k less than 5, k-means appears to perform better than the Ward method. In order to determine the degree of difference between the Ward’s and k-means classifications, the results were compared using the Rand index (Rand, 1971). This index measures the degree of similarity between different clustering solutions and ranges between 0 and 1, where 0 indicates complete disagreement and 1 indicates complete agreement. Table 2 shows that for values of k between 2 and 10, there is a fairly high degree of agreement between the two methods. Since, the k-means has a better SSB/SSW ratio for values of k less than 6 (the more parsimonious solutions) and because the k-means algorithm has the added advantage that it is a computationally faster algorithm for large datasets, we elected to use this method for the analysis.

Figure 1.

SSB/SSW criteria for selecting clustering method

Table 2.

Comparing Ward’s clustering and K-means clustering using the Rand Index

# Cluster (k)	Rand Index
2	0.75
3	0.81
4	0.73
5	0.77
6	0.78
7	0.81
8	0.84
9	0.84
10	0.84

3.2 K-Means Analysis of the data

3.2.1 Selecting k

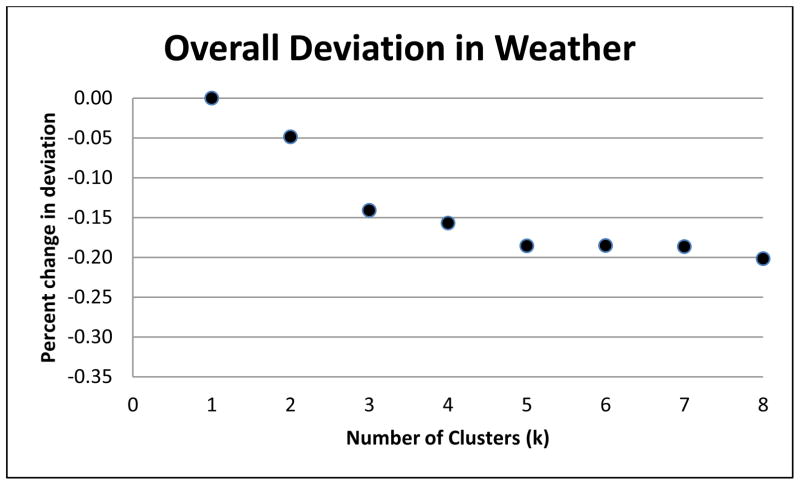
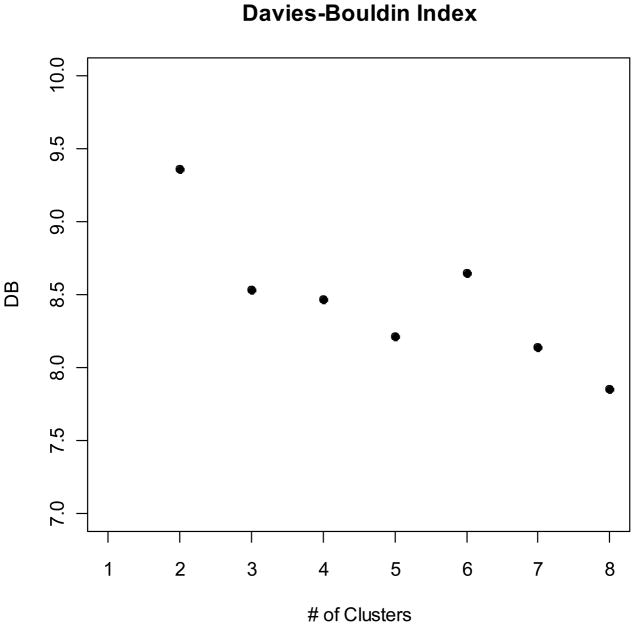
The first step in analyzing this data using k-means clustering was selecting the correct number of clusters. The two criteria of cluster fit used were the DB index and the overall percent change in weather deviation. The overall percent change in weather deviation decreased as k increases for values between 2 and 8 (Figure 2). However, the greatest decrease is at k=5. The gains by increasing the number of clusters past 5 are small. The DB index, which measures the relative compactness of the clusters in multi-dimensional Euclidean space, suggests that the most compact cluster is obtained for the 8 cluster solution (Figure 3). However, the DB index for the 5 cluster solution compares well to the 8 cluster solution and has the added advantage of being a more parsimonious solution.

Figure 2.

Overall Deviation in Weather Parameters. For each value of k, the overall deviation is described as the percent change in deviation as compared to the total variability in the dataset.

Figure 3.

DB index for values of k between 2–8

Both the internal and external criteria for selecting k indicate that the 5 cluster solution is a reasonable choice for this data set. The 5 cluster solution was selected over the 8 cluster solution because both criteria indicated that the adding of 3 additional clusters did not significantly improve the goodness of the classification. The 5 cluster solution of the k-means algorithm is further interpreted below.

3.2.2 Chemical Characteristics

The mean and standard deviation of pollutants included in the cluster analysis as well as some elements that were not included but were deemed important in the interpretation are presented in Table 3. A regression was run for each clustering variable in order to determine whether pollutant concentration profiles were significantly different between the groups. The trend component was removed using a penalized spline. The p-values represent how well the cluster accounts for concentrations observed in the de-trended data. Even using the conservative Bonferoni correction (p<0.004), the observed means between clusters are significantly different.

Table 3.

Chemical Characteristics of the Clusters

N	Cluster 1 740 Days	Cluster 2 366 Days	Cluster 3 107 Days	Cluster 4 159 Days	Cluster 5 344 Days	P-Values
	Mean SD	Mean SD	Mean SD	Mean SD	Mean SD
PM2.5 (μg/m3)*	5.49 (2.23)	8.63 (3.12)	15.92 (5.05)	20.29 (5.47)	9.49 (3.49)	<0.0001
PN (#)	15774 (8090)	15535 (5921)	27048 (10155)	10304 (3945)	26105 (11449)	<0.0001
O3 (ppb)	24.30 (7.49)	28.83 (9.36)	11.16 (7.28)	39.99 (10.30)	18.69 (7.39)	<0.0001
CO (ppm)*	0.24 (0.11)	0.29 (0.12)	0.58 (0.21)	0.26 (0.13)	0.35 (0.15)	<0.0001
NO (ppm)	9.66 (4.06)	10.83 (5.09)	43.47 (17.57)	7.28 (2.64)	17.54 (7.53)	<0.0001
NO2 (ppm)	13.23 (3.59)	17.14 (4.14)	27.56 (4.86)	16.52 (4.01)	20.19 (4.75)	<0.0001
BC (μg/m3)	0.42 (0.19)	0.65 (0.27)	1.27 (0.46)	0.97 (0.33)	0.70 (0.26)	<0.0001
Sulfate (μg/m3)	1.59 (0.89)	2.24 (1.07)	3.81 (1.58)	7.73 (2.48)	2.64 (1.16)	<0.0001
Ni (ng/m3)	1.13 (0.94)	1.40 (0.98)	5.39 (3.49)	2.13 (1.24)	3.92 (2.24)	<0.0001
V (ng/m3)	1.23 (1.18)	1.52 (1.22)	6.99 (7.00)	3.60 (2.68)	4.54 (2.90)	<0.0001
Se (ng/m3)*	0.36 (0.61)	0.29 (0.55)	0.84 (1.06)	0.85 (1.04)	0.61 (0.90)	<0.0001
Cu (ng/m3)*	1.36 (1.19)	2.73 (3.08)	4.15 (1.88)	2.42 (1.47)	2.32 (2.39)	<0.0001
Zn (ng/m3)	6.20 (3.22)	11.09 (5.85)	24.26 (11.35)	10.98 (5.01)	12.99 (7.06)	<0.0001
K (ng/m3)	25.02 (10.00)	40.24 (15.47)	66.22 (23.99)	48.85 (21.05)	40.24 (16.61)	<0.0001
Si (ng/m3)	18.64 (12.41)	56.79 (27.10)	49.17 (33.26)	68.70 (45.11)	26.07 (16.29)	<0.0001
Ca (ng/m3)	15.70 (8.49)	32.96 (12.42)	37.19 (17.33)	34.65 (13.98)	26.12 (9.51)	<0.0001
Fe (ng/m3)	36.30 (13.09)	73.73 (22.85)	109.06 (46.53)	78.45 (25.09)	61.07 (23.77)	<0.0001
Na (ng/m3)*	91.84 (100.82)	112.09 (104.92)	158.36 (93.92)	271.20 (145.71)	111.33 (82.98)	<0.0001
Al (ng/m3)*	12.05 (6.79)	26.53 (11.53)	25.43 (12.77)	41.72 (21.03)	16.39 (8.10)	<0.0001

^*These variables were not included in the cluster analysis, but their means and SD are presented to facilitate cluster interpretation. The p-values correspond to a time-series regression testing whether those specific elements are different between the 5 clusters.

To aid in cluster interpretation, we also calculated pollutant concentration ratios of selected species (Table 4). These ratios served as diagnostic tools to aid in attributing the 5 multi-pollutant mixtures to certain types of pollution regimes. Specifically: 1) higher Fe/Si ratios indicate a larger road dust contribution, relative to soil dust (assuming no impact of Fe point sources, such as steel mills); 2) higher K/Si ratios indicate a larger contribution from wood burning vs. soil dust (days around July 4 were excluded because K is also emitted by fireworks); 3) higher sulfate/PM_2.5 ratios indicate a sulfate-dominated system, reflecting predominance of power plant emissions vs. traffic and biogenic emissions; 4) higher NO/NO₂ ratio indicates predominance of fresh primary emissions; 5) higher BC/PM_2.5 indicates higher proportion of primary emissions; and 6) higher PN to PM_2.5 mass ratios, an index of size, indicate a particle size distribution with a relatively greater number of smaller particles. These diagnostic ratios permit simple comparisons between cluster types.

Table 4.

Pollutant Ratios

	Cluster 1	Cluster 2	Cluster 3	Cluster 4	Cluster 5
Fe/Si	1.95	1.30	2.22	1.14	2.34
K/Si	1.34	0.71	1.35	0.71	1.54
BC/Sulfate	0.27	0.29	0.33	0.13	0.26
NO/NO2	0.73	0.63	1.58	0.44	0.87
NO2/BC	31.35	26.55	21.73	17.00	28.94
NO2/O3	0.54	0.59	2.47	0.41	1.08
Su/PM25	0.29	0.26	0.24	0.38	0.28
BC/PM25	0.08	0.07	0.08	0.05	0.07
PN/PM25	4.57	4.06	5.84	4.53	5.60

To further facilitate the comparison between the clusters, normalized concentration (NC) values were calculated for each cluster using Equation 3. These NC values allow us compare the relative proportion of each pollutant within a cluster while controlling for the PM_2.5 concentration within that cluster (Table 5). This makes it possible to determine whether a certain pollutant is proportionally higher relative to PM_2.5 in a given cluster than in the other clusters. A normalized concentration of 1.0 indicates that the ratio of a pollutant to the PM_2.5 in a given cluster is the same as the mean ratio of that pollutant to PM_2.5 in the entire data set.

Table 5.

Normalized pollutant concentrations

	Cluster 1 740 days	Cluster 2 366 days	Cluster 3 107 days	Cluster 4 159 days	Cluster 5 344 days
PN (#)	1.43	0.90	0.85	0.25	1.37
O3	1.60	1.21	0.25	0.71	0.71
NO	1.18	0.84	1.83	0.24	1.24
NO2	1.30	1.07	0.93	0.44	1.15
BC	1.10	1.07	1.14	0.68	1.05
Sulfate	0.98	0.88	0.81	1.29	0.94
Ni	0.88	0.69	1.44	0.45	1.76
V	0.79	0.63	1.56	0.63	1.70
Fe	1.03	1.33	1.07	0.60	1.00
Zn	1.00	1.13	1.35	0.48	1.21
K	1.13	1.16	1.04	0.60	1.06
Si	0.88	1.70	0.80	0.87	0.71
Ca	1.05	1.40	0.85	0.62	1.01

$${NC}_{\mathit{Cluster}(i)}=\frac{\overline{{\mathit{Pollutant}}_{\mathit{Cluster}(\iota )}}/\overline{PM{2.5}_{\mathit{Cluster}(\iota )}}}{\overline{{\mathit{Pollutant}}_{\mathit{all}}}/\overline{PM{2.5}_{\mathit{all}}}}$$ Equation 3 - Calculating normalized concentrations (NC)

3.2.3 Elemental and organic carbon

Elemental carbon (EC) and organic carbon (OC) were only measured on 875 days out of the 1,716 days used in the analysis. Although these species could not be included in the cluster analysis due to the large number of missing values, the mean, SD and EC/OC ratio was calculated for the days in each cluster that had EC and OC measurements (Table 6). Higher EC/OC ratios indicate a larger contribution of primary emissions from traffic and other local combustion sources.

Table 6.

EC/OC mean and SD for the clusters the days that had EC/OC data

N	Cluster 1 740 Days	Cluster2 366 Days	Cluster 3 107 Days	Cluster 4 159 Days	Clusters 5 344 Days
Elemental Carbon (EC)	0.52 (0.16)	0.26 (0.10)	0.51 (0.18)	0.38 (0.13)	0.81 (0.26)
Organic Carbon (OC)	3.79 (1.16)	2.54 (0.99)	4.50 (1.18)	3.56 (1.12)	4.96 (1.51)
EC/OC	0.14	0.10	0.11	0.11	0.16

3.2.4 Weather Parameters Associated with Clusters

It was expected that the chemical differences seen within the different clusters would be related to changes to specific weather patterns in the local Boston area. Although none of the weather related variables were included in the cluster analysis, local and regional meteorological conditions govern the transport, transformation and removal of the emitted air pollutants. Shown in Table 7 is the mean and standard deviations of local weather related variables. The daily mean temperature ranges from 4.8–22.9 C, the mean RH from 59.4–70.0%, the wind speed from 3.1–5.7 m/s, the water vapor pressure from 7.0–19.6 mbar and the boundary layer height from 303.5–583.0 m. A time-series regression confirmed that these variables are all significantly different between the groups.

Table 7.

Weather Characteristics of the Clusters

N	Cluster 1 740 Days	Cluster 2 366 Days	Cluster 3 107 Days	Cluster 4 159 Days	Cluster 5 344 Days	P-values
	Mean SD	Mean SD	Mean SD	Mean SD	Mean SD
Temp (C)	9.3 (9.1)	13.7 (8.4)	5.2 (6.6)	22.9 (4.5)	4.8 (7.5)	<0.0001
RH (%)	65.0 (16.7)	59.4 (14.3)	69.5 (14.1)	70.0 (10.9)	68.1 (16.7)	<0.0001
Wind Speed (m/s)	5.7 (1.8)	4.4 (1.3)	3.1 (1.0)	4.5 (1.2)	4.5 (1.4)	<0.0001
Water Vapor Pressure (mbar)	9.2 (5.8)	10.5 (5.8)	6.8 (3.9)	19.6 (4.7)	7.0 (4.8)	<0.0001
Boundary Layer Height (m)	583.0 (271.3)	476.6 (203.5)	303.5 (182.0)	418.2 (146.4)	408.7 (213.9)	<0.0001

The p-values correspond to a time-series regression testing whether those specific weather variables are significantly different between the 5 clusters. None of these variables were included in the cluster analysis.

3.2.5 Temporal Characteristics

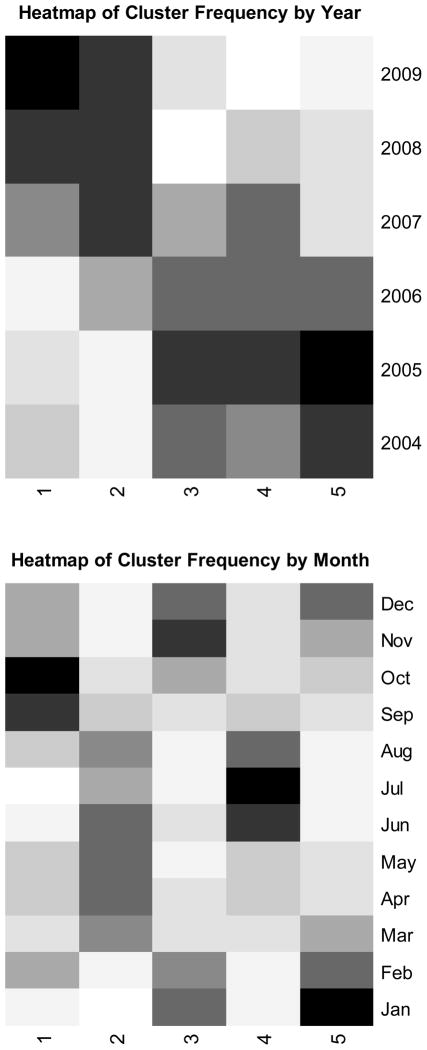
The yearly and monthly distributions of the clusters differed significantly. These distributions are presented in Table 8 and as heatmaps in Figure 4. The heatmaps clearly show seasonal patterns within each cluster. For example, cluster 4 shows a strong tendency to occur in the summer months of June, July and August. However, there are days that belong to cluster 4 that occur all throughout the year. This suggests that although the conditions that lead to the formation of the mixture captured by cluster 4 occur most often in the summer months, they also occur during other times of the year and a division of the days of exposure based solely on season would result in some important misclassification.

Table 8.

Temporal Distribution of the Clusters

YEAR	Cluster 1	Cluster 2	Cluster 3	Cluster 4	Cluster 5	Total Days
2004	121	39	27	32	104	323
2005	85	30	24	30	86	255
2006	68	46	18	24	61	217
2007	129	84	18	33	36	300
2008	174	91	8	26	37	336
2009	163	76	12	14	20	285
January	48	5	18	0	65	136
February	75	11	18	0	59	163
March	69	59	4	6	40	178
April	53	46	3	8	15	125
May	57	54	1	11	13	136
June	32	35	2	28	3	100
July	36	35	0	50	8	129
August	67	47	0	38	10	162
September	75	25	2	12	19	133
October	91	23	11	3	24	152
November	75	17	28	2	43	165
December	62	9	20	1	45	137

Figure 4.

Heatmaps of Temporal Distributions. Darker colors represent higher frequencies.

3.2.6 Results of Back-Trajectory Analysis

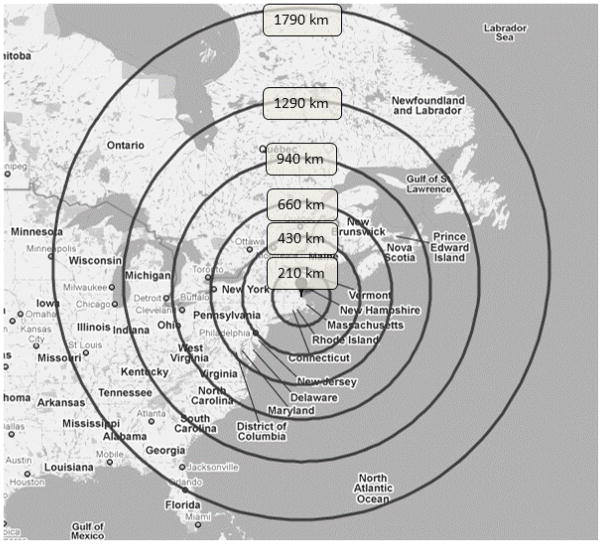
Back-trajectory analysis yielded 41,184 trajectories each with up to 84 hours of back-trajectory data (depending on the completeness of the weather data). Figure 5 shows the direction and distance from Boston of the trajectories located between 0 and 500 m above ground level in the 84 hours prior to arriving in Boston. The distance from Boston (in meters) is represented by the colors used in the rose. Figure 6 shows the location of the different radial distances from Boston on a map of the continent. Clusters 3 and 4 show the most differences in the back-trajectory locations. Cluster 3 is clearly associated with trajectories coming from the West whereas Cluster 4 is clearly associated with trajectories coming from the South West.

Figure 5. Back trajectory visualization.

The legend bar in these figures corresponds to the distance (m) from the Boston sampling location that the back trajectories were located. The direction of the bars on the figure corresponds to the direction of the back-trajectories. The length of the bars on the figure correspond fraction of the total trajectories that came from a given direction. Only trajectories that were between 0 and 500 meters from ground level are presented in this figure.

Figure 6.

Radial distances from Boston

3.2.7 Sensitivity Analysis

The sensitivity analysis confirmed that the clustering obtained is not dependent on a small number of outlier values. Randomly removing 10% of the observation resulted in an average of 10% (from 8%–12%) fewer days per cluster and misclassification of dates in the test data sets averaged of 5%, with a standard deviation of 5%. We therefore concluded that the observed clustering was not driven by a few outlier data points.

4. Discussion

Clustering of 6 years of daily concentration data from the Harvard Boston air pollution supersite yielded a solution with 5 distinguishable groups of days. This solution was both interpretable and robust to the inclusion of outlier points. These clusters differed in both their chemical properties, local prevailing weather conditions and back-trajectory direction and distance from Boston. Diagnostic ratios as well as normalized concentrations were used in order to further distinguish and describe the differences between the clusters. Below is a detailed description of the individual characteristics of each cluster.

4.1 Cluster description

• Cluster 1 (740 days) occurred mostly during early spring or mid-fall and was characterized by low PM_2.5 concentrations and relatively higher O₃ and PN. High O₃ concentrations in conjunction with low PM_2.5 mass and species levels might suggest intrusion of stratospheric O₃, since tropopause folding which can occur more frequently during the spring and fall (Nastrom et al 1989, Chung and Dann 1985). The high size index (PN/PM_2.5) indicates more ultrafine particles, which is expected for relatively low pollution days with low levels of accumulation-mode particles. This cluster was associated with the highest boundary layer height, which effectively increases the mixing volume over Boston and dilutes any ambient pollution. The wind rose plot (Figure 5) does not show a clear pattern in the direction of the back-trajectories that were between 0 and 500 meters above ground level before their arrival in Boston. However, 40% of the trajectories that were between 1500 and 2000 meters before their arrival in Boston were from the NW direction in this cluster. Furthermore, a large proportion of these NW trajectories were more than 2,000 km away from Boston 48-hours prior to the measurement day. Combined with the high wind speed on those days, we can hypothesize that relatively pollution free clean NW winds coming to the Boston area resulted in the lower overall concentrations in this cluster. The relatively higher EC/OC and BC/PM_2.5 ratios in this cluster suggest the higher impact of traffic emissions, possibly local, on this mixture.

• Cluster 2 (366 days) occurred less frequently in colder months. Most pollutant concentrations in this cluster were within the average range except for Fe, K, Si and Ca which were all elevated. This is especially clear when looking at the normalized concentrations, which accounts for the difference in total mass between the clusters. These elements, when present together indicate that some of the mass observed is attributable to suspension and re-suspension of crustal materials. The low Fe/Si and K/Si ratios confirm the prevalence of crustal materials in this cluster. The low frequency of this cluster in the winter months may be related to the ground being snow covered or wet due to precipitation and thus limiting crustal material suspension. The back-trajectory analysis indicated that the air masses on the days in this cluster generally came from either the NW or W direction and at 48h were on average 1,500 km from Boston.

• Cluster 3 (107 days) was characterized by elevated normalized concentrations of Ni, V, Zn, BC and NO. The NO/NO₂ ratio and BC/PM_2.5 ratio were both elevated with respect to other clusters which might indicate the presence of primary emissions. However, the average EC/OC ratio and high NO₂/O₃ ratio suggest a mix of fresh and aged primary pollutants on those days. The trajectory analysis shows that the air parcels were mainly from the west, and the distance suggests that many were coming from the Great Lakes region, which included cities like Cleveland and Chicago. This cluster occurred almost entirely in the winter months and occurred more often in the earlier years of the observation period. We hypothesize that a portion of the measured pollutants on these days corresponds to long range transport of pollutants from the Great Lakes region during winter months. The back-trajectory analysis confirms that 48 hours prior to these sampling day, 20% of the trajectories originated in the Chicago area. Overall, 60% of the trajectories originated from the West of Boston. The low boundary height on those days contributed to the concentration of the pollutants and the relatively high mass on those days.

• Cluster 4 (159 days) was characterized by its higher sulfate, PM_2.5 and Se concentrations and lower PN and size index. It occurred more frequently during the warm season. This cluster reflects sulfate episodes that are largely associated with SW winds. This is confirmed by the back trajectory analysis. The higher levels of Se suggest coal emissions. The lower PN concentration in conjunction with the higher PM_2.5 mass concentration and size index as compared to the other clusters suggest that particles are mostly in the accumulation mode. Particles in the accumulation mode provide a large particle surface area for heterogeneous coagulation of the freshly generated ultrafine particles. The backwards trajectory analysis indicates that 48 hours prior to arriving in Boston 20% of the air masses on these days were in western Ohio, an area where several major coal-powered generation plants are located. It also demonstrates that 50% of the trajectories that were between 0 and 500 meters prior to their arrival in Boston were located to the South West of Boston. The emergence of this cluster confirms that on some days, the pollutant mixture in Boston is dominated by primary and secondary pollutants transported from these regions.

• Cluster 5 (344 days) is characterized by a high EC/OC ratio as well as high normalized concentrations of PN, Ni and V. It occurred mostly in the winter months and had low average daily temperatures. The high Fe/Si ratio suggests a strong contribution of road dust and the high K/Si ratios suggests a contribution of wood burning. Although both clusters 3 and 5 have high normalized concentrations of Ni and V, which are associated with the combustion of heating oil, cluster 5 is different from cluster 3 in that it has a much higher size index, suggesting that cluster 5 had a higher proportion of local emissions than cluster 3. This is further confirmed by the higher EC/OC ratio in cluster 5. The back trajectory analysis confirms that the air masses in cluster 5 come from a different location than in cluster 3. In cluster 3, the air masses are predominantly from the W. In cluster 5, there is no clear predominant back-trajectory direction. This might suggest that the pollution observed on these days is associated with local sources and not related to transported pollution. Unlike cluster 3, cluster 5 increases in frequency over the course of the observation period.

4.2 Interpreting Cluster Analysis Results

The normalized concentrations, presented in Table 5, allow for direct examination of how the composition of PM_2.5 varies between clusters. This allows us to begin exploring how the short-term health effects of PM_2.5 are modified by its chemical composition. Cluster 2 and cluster 5 have extremely similar mean PM_2.5 concentrations and standard deviations (Table 3), however, there are important differences in the composition between the two clusters. From the normalized concentrations results, Cluster 2 is enriched in Silica, Iron and Calcium whereas cluster 5 is enriched in Nickel and Vanadium. From a health perspective, this implies that exposure to the same concentration of PM_2.5 from cluster 2 and cluster 5 might produce significantly different health effects. Nickel and Vanadium have been associated with both daily mortality rates as well as with cardiovascular mortality (Lippman et al. 2006, Zhang et al (2009)). On the other hand, Si, Fe and Ca present together in cluster 2 suggest that these particles contain a higher proportion of particles from soil origins. Laden et al. (2000) demonstrated that when PM_2.5 exposure was deconstructed using factor analysis, factors high in soil elements showed no association with daily mortality. Therefore, there are reasons to believe that exposure to PM_2.5 on days belonging to Cluster 2 would not produce the same response as exposure on days belonging to Cluster 5.

Incorporating the cluster type of a given day in epidemiological studies is an exciting application of this new method. Zanobetti and Schwartz (2009), used Poisson regression to examine the association between mean (day of death and previous day) PM_2.5 with daily deaths in 112 cities in the United States. Within each city, a season-specific model was constructed. Season is thought to be an important effect modifier of PM_2.5, after controlling for temperature, because of differences in composition between seasons (Franklin et al. 2008) as well as differences in the penetration of particles indoors (Janssen et al. (2002)). By including cluster type as an interaction term of PM_2.5 we would be able to explicitly model the effect of particle composition differences on the response to PM_2.5 independent other seasonally variable parameters, such as particle penetration. Furthermore, using clusters analysis instead of season to distinguish between differences in PM_2.5 composition will result in less misclassification as the cluster is directly based on the daily chemical composition.

This paper presents the results of cluster analysis in the setting of a single city. In a multi-city study, one of the challenges will be constructing clusters for each city. There is strong evidence that temporal changes in PM_2.5 composition occur across the entire United States (Bell et al. 2007). This implies that the temporal cluster analysis technique presented here will be useful in identifying the important multi-pollutant profiles for cities across the United States. However, because there are aspects of cluster analysis that are inherently subjective, maintaining uniform criteria for selecting the best clustering solution for each location will be key in interpreting results. The k-means method proposed in this paper along with the methodology for selecting the optimal number of clusters, provides a systematic way of selecting clustering solutions. Thus, it will be possible to extend this methodology to other locations.

5. Conclusions

We have introduced a new approach which uses cluster analysis to identify distinct air pollutant mixtures. To date, cluster analysis has been mostly used to group pollutants based on their source origins. However, in this paper we used cluster analysis to classify sampling days into groups based on their pollutant concentration profiles. The type of sources impacting a receptor and their relative impact, as reflected by the observed pollution characteristics on a given day, are governed by meteorology. Therefore, pollutant concentration relationships should be similar on days with similar meteorological conditions. For each cluster of days we estimated pollutant concentrations and elemental ratios to better characterize differences among the 5 groups. In addition, for each group we estimated the mean values of different meteorological parameters and examined the origin of air masses using back-trajectory analysis. This made it possible to link the distinct physico-chemical characteristics of each cluster to certain weather patterns. As shown by our analysis, the identified clusters of days were associated with different air mass origins. Overall we have demonstrated that our analysis yielded a solution that is both robust to outlier points and interpretable based on chemical, physical and meteorological characteristics. As a result, this novel method provides an exciting new tool with which to identify and further investigate multi-pollutant mixtures and link them directly to health effects studies.

5.1 Limitations

There are several limitations of this approach. Firstly, we did not consider model any based approaches to clustering. Model based clustering assumes a multivariate normal distribution which is not the case for environmental data. A potential solution would be to log transform the data. However, this would minimize the prominence of extreme pollution episodes which we want to capture as a separate regime. A second important limitation of this analysis was that it was not possible to include the EC/OC values in the analysis due to data completeness. Repeating this analysis on a different data set that also included EC/OC might improve the clustering and interpretability, since these species are significant contributors to the total mass.

5.2 Future applications

We expect that further investigation of the associations between acute health effects and the different types of mixtures can provide meaningful information about combinations of pollutants and/or types of sources posing higher risks. We also expect clustering larger data sets that include more than one sampling site over time may yield important information on both temporal and spatial changes in pollutant mixtures.

Highlights.

• We present a novel framework for identifying multi-pollutant profiles at a single sampling site.

• Daily data collected from 2004–2009 was grouped using k-means and hierarchical cluster analysis.

• The validity of the solutions was determined using the pollutant means, ratios and weather parameters.

• Back-trajectory analysis confirmed that origin of the air masses in each cluster were different.

• Sensitivity analysis confirmed that clustering was not driven by outlier points in the data.

Abbreviations

NAS

National Academies of Science

EPA

Environmental Protection Agency

PM_2.5

Particle matter with a diameter of 2.5 micrometers or less

EC

Elemental Carbon

OC

Organic Carbon

CPC

Condensation Particle Counter

DB

Davies-Bouldin

SSB

Sum of Squares Between

SSW

Sum of Squared Within

SSI

Simple Structure Index

NC

Normalized Concentration