Improving the identification of High Frequency Oscillations

Abstract

Objective

High Frequency Oscillations (HFOs), including Ripples (80–250 Hz) and Fast Ripples (250– 500 Hz), can be recorded from intracranial macroelectrodes in patients with intractable epilepsy. We implemented a procedure to establish the duration for which a stable measurement of rate of HFOs is achieved.

Methods

To determine concordance, Kappa coefficient was computed. The information gained when increasing the duration was analyzed in terms of HFO rates and ranking of channels with respect to HFO and spike rates.

Results

In a group of 30 patients, Kappa was 0.7 for ripples, 0.7 for fast ripples and 0.67 for spikes. Five minutes provided the same information as 10 min in terms of rates in 9/10 patients and with respect to ranking of channels in 8/10 patients; 5/30 patients did not achieve stable measurements of HFOs or spikes and needed marking for 10 min.

Conclusion

We propose that 5 min provides in most cases the same information as a longer interval when identifying HFOs and spikes in slow wave sleep, and present methods to identify when this is not the case.

Significance

This procedure is useful to control for consistency between readers and to evaluate if the selected interval provides stable information, for automatic and visual identification of events.

1. Introduction

High Frequency Oscillations (HFOs), referred to as Ripples (80– 250 Hz) and Fast Ripples (250–500 Hz), are EEG signals recorded from intracranial electrodes in patients with intractable epilepsy. It had been traditionally thought that only signals with frequency components up to the gamma band (40–80 Hz) have a clinical meaning. However, recent findings in rodents and humans showed a possible relation of HFOs with epileptogenesis (Bragin et al., 1999a,b; Staba et al., 2002; Khalilov et al., 2005; Jirsch et al., 2006; Urrestarazu et al., 2007; Jacobs et al., 2008).

Even though no formal definition exists, HFOs recorded with macroelectrodes can be characterized by oscillations of at least four cycles, with a typical duration of 80–100 ms for ripples and 30–50 ms for fast ripples, which can be clearly distinguished from the background activity (Jacobs et al., 2008), and with an interevent interval of around 25 ms. These EEG patterns occur spontaneously and can be identified more frequently during slow wave sleep (SWS, Staba et al., 2004; Bagshaw et al., 2009).

Based on these features, HFOs are visually identified by experienced readers or automatically marked by ripple detectors (Staba et al., 2002; Khalilov et al., 2005; Worrell et al., 2008) and sometimes visually validated (Worrell et al., 2008). However, given the lack of a complete definition, subjectivity is inevitable, sometimes resulting in poor agreement among reviewers. Visual marking is also highly time consuming, taking around 10 h to visually mark HFOs in a 10-channel 10-min recording. The current practice of marking 10-min episodes (Staba et al., 2002; Urrestarazu et al., 2007; Bagshaw et al., 2009; Jacobs et al., 2008) is an appropriate duration in the sense that stable SWS sections of this duration can be found in most patients with implanted electrodes. When using automatic detection 10- to 30-min intervals are selected (Staba et al., 2002, 2007; Worrell et al., 2008). It is possible, however, that the same amount of information could be obtained with shorter intervals.

The rates of HFOs are the most commonly used measure of HFO occurrence and are believed to be associated with the seizure onset zone (SOZ), not only during seizure generation but also interictally. Indeed, in interictal periods, higher rates of HFOs were observed in the SOZ (Bragin et al., 1999b; Urrestarazu et al., 2007) than in other areas, in particularly linked to epileptogenic lesions (Jacobs et al., 2008), and showed to be higher in atrophic hippocampus (Staba et al., 2007). The ranking of channels according to rate indicates the relative importance of a channel with respect to the others for each patient, providing an assessment independent of absolute rates.

A procedure is proposed to minimize the EEG duration that needs marking in order to obtain reliable estimates in terms of rates of HFOs and ranking of channels with respect to rates, and to assess concordance between readers. This procedure is useful for visually marked EEG as well as to ensure that a stable measurement is achieved with automatic detectors.

2. Methods

2.1. Patient selection and visual marking

Forty patients with medically intractable epilepsy underwent depth electrode implantation at the Montreal Neurological Hospital between September 2004 and December 2007 because their epileptogenic region could not be localized with non-invasive means. The mean age was 41.7 years (range 20–59). Twenty five were lesional and 15 non-lesional patients. Eighteen patients had seizures originating from mesio-temporal lobe structures and 22 had seizures originated from extra temporal structures (11 neocortical temporal areas, 6 frontal, 3 occipital and 2 centroparietal). All patients had complex partial seizures during the investigation, and 4 patients additionally had generalized tonic–clonic seizures during the investigation. The position of the electrodes was selected exclusively for clinical reasons. During some nights, the depth EEG (SEEG), recorded with the Harmonie system (Stellate, Montreal, Canada), was low-pass filtered at 500 Hz and sampled at 2000 Hz, allowing for the identification of HFOs. All patients gave informed consent in agreement with the Research Ethics Board of the Montreal Neurological Institute and Hospital.

Two experienced readers visually identified and marked HFOs and spikes in all patients. The marking of ripples and fast ripples was performed by vertically splitting the screen in two, and using an 80 Hz high-pass filter on the left half and a 250 Hz high-pass filter on the right. A ripple was marked if an event was clearly visible on the side of the 80 Hz filter and did not occur or show the same shape on the side of the 250 Hz filter, as it is defined as a distinct event between 80 and 250 Hz. An event was identified as a fast ripple if it was visible in the 250 Hz filter. Ripples and fast ripples were only regarded as such if their amplitude was clearly higher than the baseline of the investigated channel and they consisted of at least four consecutive oscillations (Jacobs et al., 2008). Spikes were marked independently of HFOs on a standard EEG display. All SEEG channels functioning properly were marked using a bipolar montage, resulting in 7–58 channels per patient. The first 10 patients were selected for the development and evaluation of the methods. To this end, their SEEG was visually marked during 10 min of SWS. For the remaining 30 patients, 5 min were marked. In the patients for whom the analysis showed that 5 min was not sufficient to reach a stable measurement, 10 min were marked and re-evaluated.

2.2. Sufficient interval and concordance evaluation

In order to improve the identification of HFOs and spikes in SEEG, we developed a procedure to ensure a minimum degree of concordance across reviewers and to determine whether the obtained information was representative of the EEG of each patient. We define a stable measurement as a measurement that does not change over time (i.e.: the measured rate and ranking of channels remain the same for the different interval lengths). Thus, the marked EEG was considered to be stable at a particular interval if the amount of information obtained in that interval was equivalent to the information of the whole marked EEG in terms of rate of HFOs and spikes and also in terms of ranking of channels according to the rates of HFOs and spikes.

The procedure can be divided in two steps (Fig. 1), evaluating the agreement between reviewers, then assessing when a stable measurement of the rates and ranking of channels according to the rates is achieved for the marked interval.

Fig. 1.

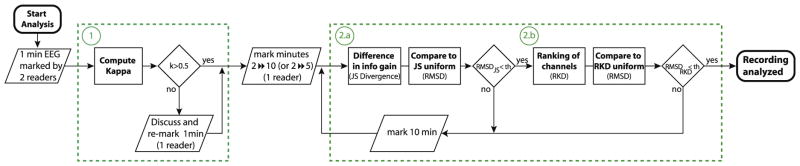
Diagram of the complete process. First step: Assessing concordance between readers based on Kappa coefficient (1). Second step: Evaluating if an interval is representative of the whole marked EEG, in terms of rates (2a) and ranking of channels (2b).

2.3. Inter-observer agreement

To determine concordance, the first minute of each EEG was marked by two reviewers. Cohen’s Kappa coefficient (Cohen, 1960) was computed for this first minute in each channel. This coefficient measures the degree of agreement between two reviewers, taking into account the agreements made by chance. Kappa < 0 reflects that the agreement is due to chance and κ = 1 indicates complete agreement. Kappa = 0.5 reflects moderate agreement, and was chosen as the threshold of concordance (Landis and Koch, 1977). Thus, channels with κ < 0.5 were reviewed and discussed jointly by the two reviewers to reach similar marking criteria. They were then remarked by the reviewer that also marked the remaining EEG.

2.4. Stable measurement assessment

An interval was considered representative of the whole EEG if marking this interval resulted in the same amount of information as marking the whole reference interval. This was assessed by two independent methods, Jensen–Shannon (JS) Divergence and Ranking Distance (RKD). The JS Divergence measures the relative information gained when comparing the rate of identified events found in different intervals and in the complete interval (the “true distribution”). The RKD allowed us to identify the changes in the ranking of the identified events for the same intervals.

To determine at which interval length a stable measurement was achieved in most patients, different durations, ranging from 6 s to 9.5 min, were compared against the 10 min “gold standard”. In addition, in order to ensure that there was no bias towards the beginning or end of the 10-min interval, 10 random start points were used for each interval length. For the second group of patients (marked during 5 min) the different intervals ranged between 6 s and 4.5 min and were compared against the 5-min interval.

For this second group of patients, the marked 5-min interval was considered stable if an interval of half the length (2.5 min) provided the same information as the 5-min interval (i.e.: if at 2.5 min the RMSD_JS and the RMSD_RKD were smaller than the threshold). Thus, if this condition was not met, we cannot determine if the 5-min interval is stable and therefore 10 min were marked for that patient.

2.4.1. JS Divergence

For evaluating the interval length providing stable measurement of rates, the information gained when increasing the interval duration was analyzed in terms of difference in the rate of events. If the rates are time invariant, the law of diminishing returns applies: increasing interval length results in decreasing gain in information. One well known way to measure the information gain is the Kullback–Leibler (KL) Divergence or relative entropy. The KL Divergence quantifies the difference in information gained when using a given distribution (Q) instead of the “true” distribution (P). In our case, P represents the percentage of epochs that contain a given event in the 10-min interval, while Q represents the percentage of epochs that contain a given event for the different time intervals (t). The epoch length was chosen as 50 ms for all types of events. Thus, for each of the possible events ripple, fast ripple, spikes and no event:

$$\begin{array}{l}{D}_{\text{KL}}(P\Vert Q_t)=\sum _{ev}P(ev)log\frac{P(ev)}{Q_t(ev)}\\ \text{where}ev=\text{ripple},\text{fast}\text{ripple},\text{spikes}\text{or}\text{no}\text{event}\end{array}$$ (1)

$$\begin{array}{l}P=\left[\begin{array}{c}{R}_{10min}\\ {FR}_{10min}\\ {Sp}_{10min}\\ {\mathit{noEv}}_{10min}\end{array}\right]Q_t=\left[\begin{array}{c}{R}_{tmin}\\ {FR}_{tmin}\\ {Sp}_{tmin}\\ {\mathit{noEv}}_{tmin}\end{array}\right]\\ \text{where}\text{interval}t=0.1,0.5,1,1.5,\dots ,9,9.5,10min\end{array}$$

Because we are trying to obtain the distance in terms of information gain between the 10-min interval (our “gold standard”) and the different interval, a true metric or distance function was needed. A true metric has the following properties: it is non-negative (d(x, y) ≥ 0); it is zero if and only if the two inputs are equal (d(x, y) = 0 iff x = y); it is symmetric (d(x, y) = d(y, x)); and satisfies the triangle inequality (d(x, z) ≤ d(x, y) + d(y, z)). The KL divergence satisfies the first two properties but it is a non-symmetric measure and does not satisfy the triangle inequality (Cover and Thomas, 1991). Moreover, it is possible that for certain epochs there would be no event of a particular type, which would make Q_t equal zero, and the KL Divergence infinite. Thus, the JS Divergence was used instead (Lin, 1991). The JS Divergence is a symmetric and smoothed version of the KL Divergence, defined as

$$D_{\text{JS}}(t)=\frac{1}{2}{D}_{\text{KL}}(P\Vert M_t)+\frac{1}{2}{D}_{\text{KL}}(Q_t\Vert M_t)$$ (2)

where $M_t=\frac{1}{2}(P+Q_t)$. Another advantage of the JS Divergence is that its square root $({\text{ND}}_{\text{JS}}(t)=\sqrt[2]{D_{\text{JS}}(t)})$ is bounded (not infinite) and satisfies the triangle inequality (Endres and Schindelin, 2003). Therefore, we used this true metric for calculation. The ND_JS was computed for each patient and each channel.

2.4.2. Ranking Distance

Not only are the rates per minute important, but so are the ranking of channels according to rates of HFOs (from highest to lowest HFO rate). To determine how the different durations affected the ranking of channels, we implemented an algorithm to measure the distance between two sequences, in our case rankings. The Ranking Distance (RKD) measures the difference between two rankings as the sum of the cost associated with each channel that is not in the “correct” position (with respect to the ranking of the whole interval, our “gold standard”).

$$\begin{array}{l}\text{RKD}(t)=\sum _{i=1}^{\#\text{Channs}}\sum _{j={\text{Pos}}_t}{C}_{ij}\\ \text{where}\text{interval}t=0.1,0.5,1,1.5,\dots ,9,9.5,10min\end{array}$$ (3)

where Pos_t are the new position in the ranking, #Channs the number of channels for that patient. The matrix cost (C) measures the cost of being in a different position in the ranking, and was computed as the difference in rates of those channels in the “true” ranking. Thus, C_ij is the cost associated with being in position j in the ranking instead of in position i.

$$\begin{array}{l}C=\left[\begin{array}{cccc}0& \dots & C_{1j}& C_{1N}\\ C_{i1}& 0& C_{ij}& C_{iN}\\ ⋮& ⋮& \ddots & ⋮\\ C_{N1}& \dots & C_{Nj}& 0\end{array}\right]\\ \text{where}i=1,2,\dots ,\#\text{Channs}\text{and}j=1,2\dots ,\#\text{Channs}\end{array}$$

where

$$C_{ij}=\frac{\mid \#{Ev}_i-\#{Ev}_j\mid }{K}$$ (4)

where #Ev_i is the rate of events in channel i for the whole EEG, K is a normalizing constant and C_ij equals C_ji. By using this cost function, the change in position is taken into consideration as well as the importance of the change as represented by the difference in rate between channels. The RKD score was normalized by dividing by a constant (K) such that a RKD score equals 0 only when the rankings are the same, while a RKD score of 1 represents total discrepancy. The RKD is computed for each type of event (ripple, fast ripple and spike) for each patient.

2.4.3. Root mean square difference

In order to decide when a stable measurement is achieved for each patient, we needed a thresholding approach that was consistent for both methods. Given that the ND_JS was calculated for each channel and that the RKD score was calculated for each type of event, we implemented for each of them the root mean square difference (RMSD), which provided a single value for each patient and for each interval.

As a reference distribution and to compute the threshold, we choose a uniform distribution of events with the same number of events as the real data. A uniform distribution of events is the ideal distribution in this case since it has the same rate at any interval length (i.e.: we obtain a stable measurement of the rate) and, therefore, the difference in information gained and the difference in ranking would be minimal across the different intervals. For each channel, 10 uniform distributions were produced by distributing randomly but uniformly the same number of total events as the real data over a 10-min interval. On the other hand, a beta distribution of the events with parameters α = 3 and β = 1 was used to represent the case when most of the events occur at the end of the interval, and therefore the selected interval will not provide a stable measurement of the rates. In this way, one good and one bad possible distribution of events were taken into consideration.

Thus, to assess when a stable measurement is obtained in terms of the information gained in each patient, the ND_JS obtained from the data was compared with the ND_JS obtained from a uniform distribution with the same rate of events in the 10-min interval (same R_{10 min}, FR_{10 min}, and Sp_{10 min}). The ND_JS was computed for the real and corresponding uniform distributions, for each channel and for each starting point. The RMSD between ND_JS of each channel and the mean ND_JS of the 10 uniform distributions corresponding to the same channel and starting point (see above), was computed for each patient.

$$\begin{array}{l}{\text{RMSD}}_{\text{JS}}(t)=\sqrt[2]{\sum _{c,st}{({\text{ND}}_{{\text{JS}}_{c,st}}^{\text{real}}(t)-{\text{ND}}_{{\text{JS}}_{c,st}}^{\text{unif}}(t))}^2}\\ \text{for}\text{interval}t=0.1,0.5,1,\dots ,9.5,10min\end{array}$$ (5)

where c are all possible channels of a patient and st are all the possible starting points. Thus, the analysis of stability was done independently for each patient based on the comparison of the ND_JS obtained for the patient and the ND_JS that corresponds to a uniform distribution with the same total number of events.

For selecting the threshold, the RMSD_JS between the ND_JS of each uniform distribution and the mean ND_JS of all the uniform distributions (across the patients marked for 10 min) was computed, resulting in only one reference RMSD_JS(t) value for each interval. It represents the variability of uniform distributions among patients. Because around 40% of the channels had a rate smaller than 1/min considering the complete marked interval (93/240 channels with ripples, 49/100 channels with fast ripples, and 122/304 channels with spikes for the first group of patients), and in order to have at least 1 event representative of the uniform distribution, we chose a 2-min interval as the interval in which to compute the threshold. The threshold (thRMSD_JS) was then empirically chosen as two times the reference RMSD_JS(t), for t = 2 min. For example, if for a patient the RMSD_JS(t ≥ 3 min) < thRMSD_JS, intervals longer than 3 min were considered equivalent to the uniform distribution in terms of information gain, and therefore a 3-min interval was representative of the whole segment of EEG, with no information gained by marking more than 3 min.

An equivalent approach was followed to assess when a stable measurement was reached in terms of ranking of channels. For each patient, the RMSD of the obtained RKD score with respect to the mean RKD score obtained by 10 uniform distributions was performed, similar to the approach followed for the JS Divergence.

$$\begin{array}{l}{\text{RMSD}}_{\text{RKD}}(t)=\sqrt[2]{\sum {({\text{RKD}}_{ev,st}^{\text{real}}(t)-{\text{RKD}}_{ev,st}^{\text{unif}}(t))}^2}\text{for}\text{interval}t\\ =0.1,0.5,1,\dots ,9.5,10min\end{array}$$ (6)

where ev are all possible events (ripples, fast ripples and spikes) and st are all the possible starting points. A stable measurement was considered to be achieved for a patient at a certain interval, in terms of ranking of channels, when the RMSD_RKD was smaller than the threshold. Following the same thresholding approach used for JS Divergence, the threshold (thRMSD_RKD) was set as two times the reference RMSD_RKD(t), for t = 2 min. As before, the reference RMSD_RKD(t) was obtained from the RKD scores based on all the uniform distributions for all patients with respect to the averaged RKD score of the uniforms.

3. Results

3.1. Inter-reviewer agreement

This was assessed by two reviewers marking the first minute of each recording. In the first 10 patients, the average κ was 0.6 for ripples, 0.56 for fast ripples and 0.49 for spikes. In order to improve concordance across readers, all channels with κ < 0.5 were discussed and new criteria were developed. For instance, the gain selected to mark spikes was redefined, whether to consider polyspikes as individual spikes or as one group was decided, and agreement regarding spiky baselines was achieved. The new criteria were considered for the remarking of the channels with low kappa, by one of the readers, and for the second group of patients (30 patients). For the second group, κ was higher: 0.7 for ripples, 0.7 for fast ripples and 0.67 for spikes, showing a clear improvement particularly for spikes.

When analyzing the common features of the jointly marked events, we observed that those HFOs that were identified by both reviewers were those that clearly stand out from the baseline. Moreover, when analyzing those channels with κ around 0.5, we found that the markings were consistent between reviewers and that the overall rates remained similar. In the case of channels with spiky (or bumpy) baselines, it was important to agree on the display gain to have good agreement. There was also sometimes disagreement in the duration of the marked HFOs. In the case of spikes, the use of a common gain to mark was the main factor of improvement. In addition, special attention was paid to avoid the erroneous marking of sleep spindles as events.

3.2. Sufficient interval

3.2.1. Initial assessment of the methods

Once concordance was evaluated for the first minute, the same 10 patients were marked for the remaining 9 min by one reviewer, and the different intervals were compared against the 10-min interval to assess the interval length at which a representative information of the whole EEG was reached. Because the JS Divergence and the RK Distance measure different aspect of the obtained information, they can be considered complementary; thus, patient’s markings had to provide a stable measurement in both methods at a particular interval length.

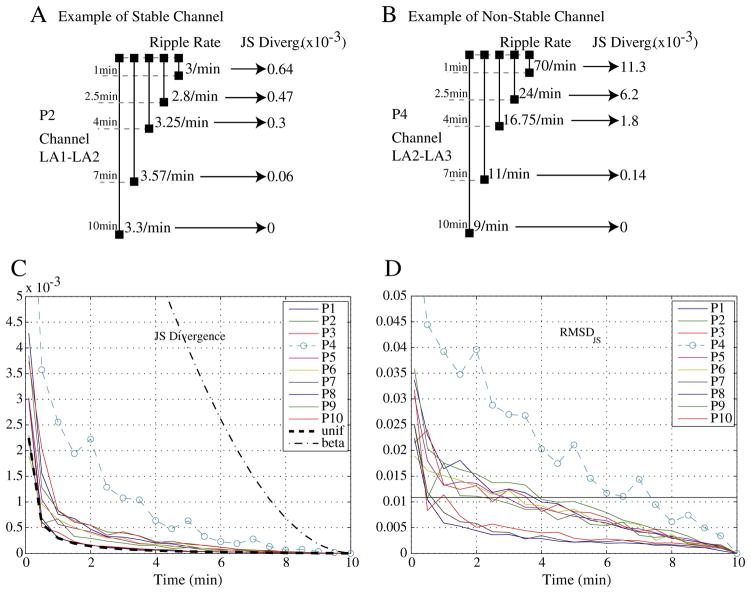
In 9 of the 10 patients, an interval of less than 5 min provided the same information as an interval of 10 min, as measured by the JS Divergence (example in Fig. 2A). For patient P4 (Fig. 2B), for whom this was not the case, only at an interval of 7.5 min was the RMSD_JS smaller than the threshold (Fig. 2D). Furthermore, if we compare the averaged JS Divergence, across channels for each patient, with the averaged JS Divergence, across channels and across patients, for a uniform and a beta (α = 3, β = 1) distributions, it can be observed that for all subjects but P4 the mean JS Divergence is similar to the mean JS Divergence for the uniform distributions (Fig. 2C). On the contrary, the mean JS Divergence for P4 resembles more the mean JS Divergence for the beta distribution.

Fig. 2.

The JS Divergence establishes the information gained when increasing the interval length. Top: Example of ripple rate for different intervals in one channel and the obtained JS Divergence (which is obtained by pooling ripple, fast ripple and spike rates). (A) Example of a stable channel. (B) Example of a non-stable channel. Bottom: (C) Comparison of the mean JS Divergence across channels, for the real markings, for a uniform distribution and for a beta distribution (α = 3, β = 1). (D) Root mean square difference (RMSD_JS) between ND_JS (root square of JS Divergence) obtained from the real marking of events and ND_JS that would be obtained if a uniform distribution of the events was used instead. Patient with a dashed line and a symbol (o) have a RMSD_JS(t ≥ 5 min) > thRMSD_JS. The thRMSD_JS equals twice the RMSD_JS for all uniform distributions at 2-min interval. A 10-min interval is considered as the “gold” standard.

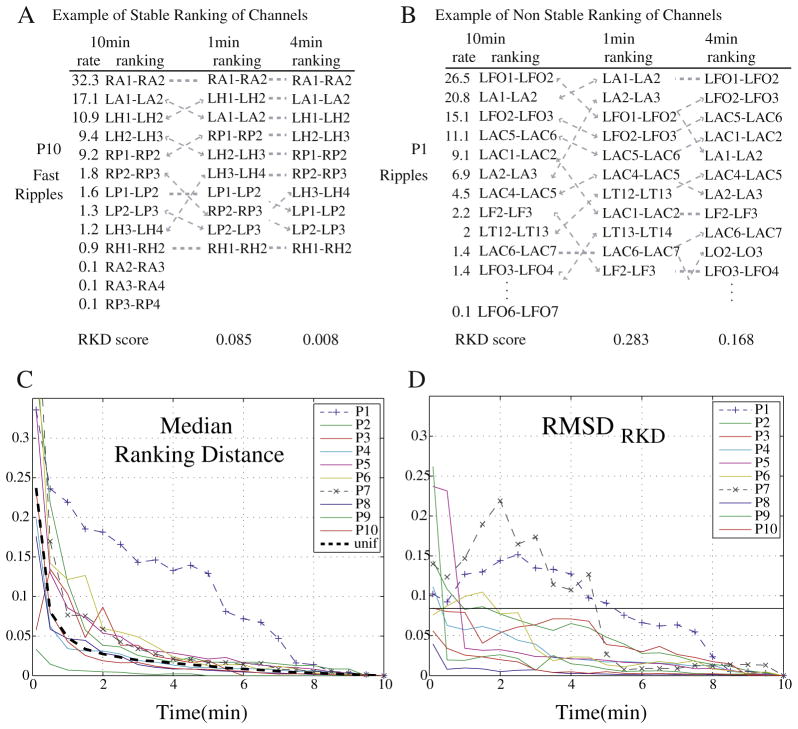
When assessing when a stable measure is obtained regarding the ranking of channels, 8 of 10 patients achieved a stable measurement before 5 min as measured by the RKD (examples in Figs. 3A and B). The RMSD_RKD measures the difference between the obtained RKD and the RKD of a uniform distribution and was smaller than threshold for intervals smaller than 2 min for 8 of the 10 patients. One patient (P7) only obtained an RMSD_RKD value smaller than threshold at 5-min intervals, while another (P1) only at 5.5 min (Fig. 3D). Furthermore, when analyzing the median value of the RKD (across different event types and different starting points) all but patient P1 showed a distribution similar to the uniform distribution for intervals of 4 min or longer (Fig. 3C).

Fig. 3.

The Ranking Distance (RKD) measures the difference in ranking for different intervals. Top: Example of difference in ranking and corresponding RKD scores, for 1 min and 4 min intervals. (A) Example of a stable ranking (patient P10 and fast ripples). (B) Example of non-stable ranking (patient P1 and ripples). Bottom: (C) Median RKD (across starting points and type of event) for each patient when comparing with the ranking of channels for the 10-min interval. (D) RMSD_RKD of the RKD score when comparing the obtained score for each interval with the corresponding RKD score for a uniform distribution. Patients with a dashed line and a symbol (+ or ×) have a RMSD_RKD(t ≥ 5 min) > thRMSD_RKD. The thRMSD_RKD equals twice the RMSD_RKD for all uniform distributions at 2-min interval. A 10-min interval is considered as the “gold” standard.

Thus, a stable measurement of the rates and ranking of channels is achieved for intervals smaller than 5 min for most patients, showing that an interval smaller than 5 min would provide the same relevant information as a 10-min interval for most patients. In particular, in terms of the relative information gained (RMSD_JS), a stable measurement is achieved for intervals smaller than 5 min for all patients but one. Moreover, in three patients no information was gained if analyzing intervals longer than 2 min. On the other hand, the ranking of channels (RMSD_RKD) remained stable for durations longer than 3 min in most patients. Thus, to ensure that the marked interval is representative of the whole EEG for most patients with respect to rates and ranking of channels, 5 min was selected as the interval length to be marked from now on.

3.2.2. Evaluation of the same patients for a 5-min interval

Since we showed that 5 min is a sufficient interval for most patients, we repeated the same analysis in this group of 10 patients considering the first 5 min as the “gold” standard, resulting in similar conclusions. This further validates the hypothesis that 5 min of marking was sufficient and shows consistency of the methods. Indeed, when these 10 patients were considered to be marked for 5 min and analyzed, the conclusion according to the JS Divergence was that for patient P1 and P4 the RMSD_JS was smaller than the threshold only at 4-min intervals (Fig. 4A). Moreover, the RMSD_RKD indicated that for 2 patients (P1 and P7), marking only 5 min was not enough (Fig. 4B). Thus, for the 3 patients for whom the previous analysis concluded that more than 5 min were necessary, the same conclusion was reached. Therefore, these methods seem appropriate to evaluate the length that is sufficient to mark to ensure that all relevant information is captured.

Fig. 4.

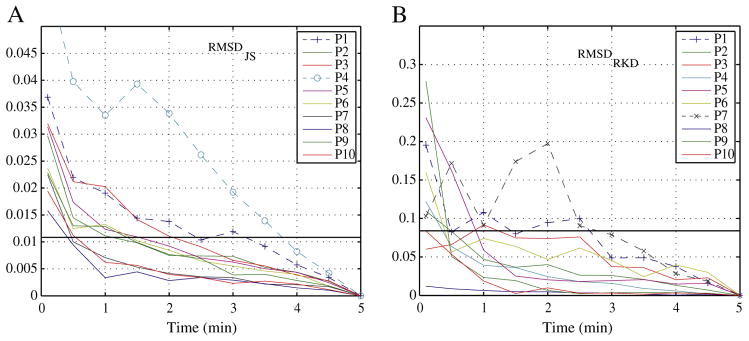
When using the procedure to assess if 5 min provide stable measurements for the first group of patients, three patients (P1, P4, and P7) do not present stable measurements as indicated by either (A) RMSD_JS or (B) RMSD_RKD (did not have a RMSD smaller than threshold at t ≤ 2.5 min). These are the same three that only reached a stable measurement after 5-min intervals comparing with 10 min.

3.2.3. Evaluation of additional patients marked during 5 min

The second group, consisting of 30 patients, was visually marked during 5 min and their stability evaluated. For five of these patients, a 5-min interval was not sufficient to provide consistent information in terms of information gained or stability in the ranking of rates of HFOs and spikes (Fig. 5). Because we are comparing with 5 min as the “gold standard” a stable measurement must be reached well before the 5-min interval for an interval to be considered representative of the whole EEG. Thus, if there is not stable measurement at 2.5-min intervals, we cannot determine whether 5 min are stable or not. According to the RMSD_RKD, four patients (P2, P5, P13 and P26) did not obtain an RMSD_RKD smaller than threshold before 3-min intervals. In addition, for one patient (P29), the RMSD_JS remained within the vicinity of the threshold at 2.5 min. As before, an interval was considered representative of the whole marked EEG (in this case 5 min), only when this was indicated by the RMSD_JS and the RMSD_RKD. Therefore, these five patients were marked for 10 min. The analysis of the 10-min interval for these five patients indicates that three of them were actually only stable after 5-min intervals. Indeed, in terms of information gain, the patient (P29) that did not clearly achieved stability before only achieved a RMSD_JS smaller than threshold at 5.5-min interval when marked for 10 min. Moreover, the stability with respect to the ranking of channels was achieved after 5 min by two of the remarked patients (P2 and P13) and at 2-min interval for the other three.

Fig. 5.

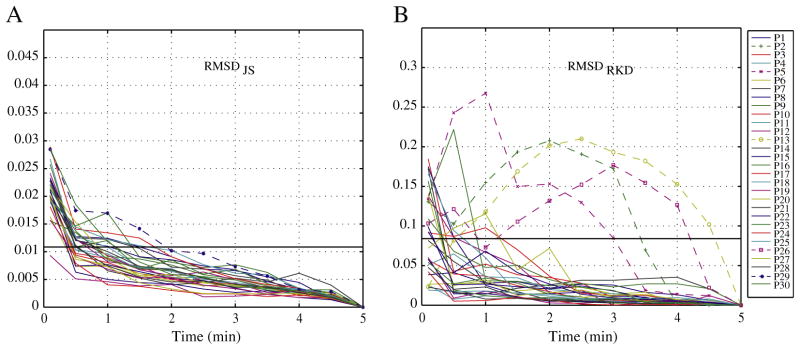
Evaluation of the second group of patients (30 patients) marked for 5 min. (A) RMSD_JS. All patients reached stable measurements at 2.5 min according to the JS Divergence, but 1 patient (P29) remained too close to the threshold, and was decided to be marked for 10 min. (B) RMSD_RKD. Four patients did not achieve stability in the ranking of channels and were thus marked for 10 min.

4. Discussion

We propose a new procedure to assess whether a stable measurement is achieved when identifying HFOs and spikes from intracranial recordings with macroelectrodes. The procedure is suitable to improve the visual identification of the events as well as to ensure stable measurements when using automatic detectors. The methods were first evaluated for 10 patients whose EEG was visually marked, considering a 10-min interval as the “gold standard”. It was possible to establish that intervals smaller than 5 min were representative of the whole EEG in most patients. From then on, this procedure is routinely used to evaluate the stability of the rates in all the patients when marked for 5 min. The incorporation of a measure of agreement among reviewers for the first minute improves consistency in the markings and allowed us to become less dependent of the reviewer that marks the complete file.

Until now, our group (Urrestarazu et al., 2007; Bagshaw et al., 2009; Jacobs et al., 2008) and others (Staba et al., 2002) have chosen 10 min as the interval to select. Ten minutes seem a reasonable interval given that, from a practical perspective, a longer interval would not be feasible to mark and that SWS is not usually stable for longer periods in patients with implanted electrodes. When using automatic detectors, 20 to 30-min intervals are also selected (Staba et al., 2007). However, no attempt had been made to assess if those intervals were necessary, or if shorter intervals might be sufficient. Moreover, no systematic approach was used to assess whether stable measurements are obtained during the selected intervals. We reported on a method to establish for how long it is reasonable to mark events, to ensure that the relevant information is obtained.

A secondary aim of this study was to help in the formal characterization of HFOs. At present, a few automatic HFOs detectors exist (Staba et al., 2002; Khalilov et al., 2005), but given the lack of a formal definition of HFOs, assessing the performance of an automatic detector is difficult. Thus, by helping to provide a more complete definition of HFOs we hope to help in a better characterization of HFOs, which could lead to the future development of robust automatic detection of these events. For example, the new criteria agreed upon after reviewing the channels with low kappa and the subsequent improvement of the results suggests that the proposed procedure could help towards a standard definition of HFOs. For instance, the recognition of channels with spiky baselines (particularly the deepest hippocampus channels), will allow for the proper recognition and particular analysis of these channels. If not considered apart from the rest, these channels could influence the training of automatic detectors. In addition, in some cases with disagreement, we observed that different subjective thresholds were used by the two reviewers for marking each patient. This is a good indicator that the signal to noise ratio of the HFOs was not consistent across patients and that it has to be taken into account when designing an automatic detector. Furthermore, discrepancies with respect to the duration of the HFOs were observed in some cases, when one reviewer marked one event while the other marked two. It would be important to define not only a minimum duration, but also an end point of an HFO. Therefore, by incorporating a measure of information stability together with a better characterization of HFOs, we aim to improve the reliability of automatic detectors.

Given that different start points can be used for the analysis, the procedure could also tell us which interval/s within the complete marked interval are those that are not stable. This aspect was not explored in detail in this paper, but could be particularly useful to determine which intervals provide stable measurements when using automatic detectors. There are many reasons for an interval of any length not to be stable. For instance, a patient can change sleep stage, there could be a change in the baseline, and there could be even changes in rates or ranking of channels due to a change in the epileptic activity. In those cases, it would be possible to use these methods to analyze different intervals, to separate between intervals and utilize only the selected ones for the subsequent processing. Previous studies showed correlation with the SOZ, suggesting that the ranking of channels and HFO rates may be able to distinguish between SOZ and non-SOZ areas (Jacobs et al., 2008). The RK Distance could also be used to assess a difference in ranking of channels in terms of rates between different types of events (e.g.: ranking of ripples vs. ranking of spikes), or channel location. Further investigation in this direction could provide a better understanding of the characteristics of HFOs.

A valid measurement of HFO events is essential for clinical use such as the identification of epileptic or potentially epileptic regions during intracranial investigations. This could help the delineation of the surgical extent and in the prediction of surgical outcome if post-surgical outcomes are evaluated. This would be possible, according to our results, after evaluating only 5 min of EEG.

Finally, this study was limited to events marked during SWS using a bipolar montage. Given that the largest amount of HFOs occur during SWS (Staba et al., 2004; Bagshaw et al., 2009), we decided to develop and test our methods in events marked during this stage. Even though the procedure can be used for other stages and montages, the conclusions cannot be generalized without further validation. Moreover, we assumed that 10 min provide a stable measurement and used only one 10-min interval per patient as the “gold standard”. The methodology we propose can be applied to any interval length and future studies using an automatic detector for different intervals could provide further validation.

In conclusion, the procedure presented in this study provides an approach to assess the duration of EEG that must be interpreted to obtain a representative measurement of HFO and spike rates from intracranial recordings with macroelectrodes in patients with epilepsy, and to optimize the time needed to mark these events. We propose that 5 min provides, in most cases, the same information as a longer interval, in terms of a stable measurement of rates and ranking of channels. We present a method to identify when this is not the case and thus more data needs to be marked. The following procedure is suggested for each patient: 1 min is marked by two readers (which could be human readers or an automatic approach) and concordance is evaluated. Once there is good agreement in the first minute, the remaining 4 min are marked by one of the reviewers and the 5-min interval is then evaluated for stability. When a stable measurement of the rates is not obtained within the 5-min interval, the following 5 min are also marked, and so on. These methods are useful to control for consistency between reviewers and to evaluate if the selected interval provides consistent information, or if a longer one is needed. Moreover, this procedure ensures a stable measurement in terms of rates and ranking of channels, when automatically detecting HFOs and spikes.