Abstract
Objective
We aim to automatically detect fast oscillations (40–200 Hz) related to epilepsy on scalp EEG recordings.
Methods
The detector first finds localized increments of the signal power in narrow frequency bands. A simple classification based on two features, a narrowband to wideband signal amplitude ratio and an absolute narrowband signal amplitude, then allows for an important reduction in the number of false positives.
Results
When compared to an expert, the performance in 15 focal epilepsy patients resulted in 3.6 false positives per minute at 95% sensitivity, with at least 40% of the detected events being true positives. In most of the patients the channels showing the highest number of events according to the expert and the automatic detector were the same.
Conclusions
A high sensitivity is achieved with the proposed automatic detector, but results should be reviewed by an expert to remove false positives.
Significance
The time required to mark fast oscillations on scalp EEG recordings is drastically reduced with the use of the proposed detector. Thus, the automatic detector is a useful tool in studies aiming to create a better understanding of the fast oscillations visible on the scalp.
Keywords: Fast oscillation, Automatic detection, Scalp EEG, Interictal, Focal epilepsy
1. Introduction
Fast oscillations (FOs) are oscillations visible in EEG signals at frequencies higher than the conventional clinical range of analysis. Recent studies suggest that they may play an important role in normal and pathological brain function. In epileptic patients high frequency oscillations were found in intracranial EEG recordings, both with microelectrodes (Bragin et al., 1999a,b; Staba et al., 2002) and macroelectrodes during ictal (Jirsch et al., 2006) and interictal intervals (Urrestarazu et al., 2007; Jacobs et al., 1893; Worrell et al., 2008; Crepon et al., 2010). The high frequency oscillations appear to be a good indicator of the seizure onset zone (Zijlmans et al., 2009), and are possibly related to the outcome of epilepsy surgery (Jacobs et al., 2010).
The possibility to study high frequency oscillations noninvasively in scalp EEG recordings would help the development of more clinical applications. Early studies reported fast oscillations in scalp EEG of only a small percentage of epileptic patients (Rodin et al., 1976; Nealis and Duffy, 1978). In the past few years there have been several reports of fast oscillations in scalp EEG (Kobayashi et al., 2004, 2010; Inoue et al., 2008; Wu et al., 2008; Yamazaki et al., 2009; Andrade-Valença et al., 2011). Interictal fast oscillations were specific in identifying children with epilepsy and localized ictal onsets (Wu et al., 2008). Ictal gamma activity was recorded on scalp EEG during epileptic spasms (Kobayashi et al., 2004; Inoue et al., 2008). Frequencies in the ripple band (80–200 Hz) were observed in children suffering from status epilepticus during sleep (Kobayashi et al., 2010). Recently, fast oscillations in the gamma band were identified in 15/15, and in the ripple band (80–200 Hz) in 12/15 patients with focal epilepsy during non-REM sleep scalp EEG recordings (Andrade-Valença et al., 2011).
In this work we study fast oscillations (FOs) in the 40–200 Hz range in scalp EEG signals. Note that this is not exactly the same frequency band as the 80–450 Hz high frequency oscillations (HFOs) band from intracranial recordings. The high sampling rate necessary to record this fast activity leads to recordings with large amounts of data. The amplitude of the fast oscillations is generally very low. The visual detection and marking of events in these recordings by human reviewers is therefore a very time consuming task, and subjectivity in the results is unavoidable. Several automatic detectors have been proposed to aid in the detection of HFOs in intracranial recordings (Staba et al., 2002; Gardner et al., 2007; Crepon et al., 2010; Zelmann et al., 2010). We propose an algorithm specially designed to automatically detect FOs in scalp EEG recordings. The main difference with existing HFO detectors is a processing in narrow frequency bands that should help in the detection of events in a high amplitude scalp EEG background. We evaluated the performance of the proposed detector with data from 15 focal epilepsy patients. The FOs in the fast gamma (40–80 Hz) and ripple (80–200 Hz) bands were marked by an expert and reported in a previous study (Andrade-Valença et al., 2011).
2. Methods
In order to design our detector, we adopted the following qualitative definition of an FO: an oscillation that stands out of the background, with an approximately sinusoidal shape, a duration of at least four cycles, and a frequency between 40 and 200 Hz. The four cycle minimum duration has been adopted in our previous studies involving FOs (Andrade-Valença et al., 2011) and HFOs (Jacobs et al., 1893; Zelmann et al., 2009, 2010; Zijlmans et al., 2009).
The automatic detector works in two stages, the first, the predetector, aims to separate the background from non-background, and the second consists in a classification of the previously detected events, in order to distinguish FOs from artifacts.
2.1. Pre-detection stage
The pre-detection consists in identifying localized power increments in narrow frequency bands. The separation in narrow bands ensures that the shape of a detected event in a given band will be approximately sinusoidal, as required by the adopted FO definition. The algorithm is described qualitatively in this section, and in Appendix A we provide the implementation details. In Fig. 1 we show a diagram of the pre-detection stage. The notation in the figure corresponds to the notation in Appendix A.
Fig. 1.
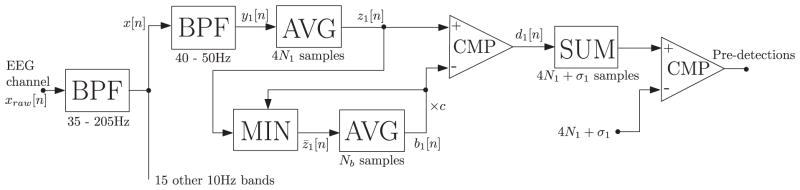
Diagram of the pre-detection processing. The passband of the band-pass filters (BPF) in indicated below the corresponding block. Below the averaging (AVG) and adding (SUM) blocks we indicate the number of involved samples. The comparing (CMP) blocks have unit output if the difference between inputs is grater than zero, and zero output otherwise.
The raw EEG signal has much larger power content at low frequencies than at the fast gamma and ripple bands in which we are interested. The first step of the pre-detector is a bandpass filter between 35 and 205 Hz; the resulting signal will be called broadband signal. The broadband bandpass filtering allows the use of filters with less attenuation in the next processing step (multiple narrowband filters), reducing the computational load because the broadband filtering is performed once whereas there are many narrowband filters.
Assuming the FOs have a duration of four cycles, the duration will be between 100 ms and 20 ms for FOs with central frequency between 40 and 200 Hz, respectively. The bandwidth of a signal is not smaller than approximately the inverse of its duration, the exact value depending on the signal shape. Then, the bandwidth of the FOs will vary in the range from approximately 10–50 Hz. We detect these FOs by identifying localized power increments in narrow frequency bands. In this way we have an increased sensitivity compared to existing intracranial HFO detectors (Staba et al., 2002; Crepon et al., 2010; Gardner et al., 2007; Zelmann et al., 2010) that look for a power increase in the whole frequency band of interest; the increase in power in a narrow band coincident with the FO’s bandwidth is greater than the increment in a wider band. Then, the narrowbands used to detect the FOs should not be wider than the bandwidth of these FOs. On the other hand, frequency bands narrower than the FO’s bandwidth will not deteriorate the performance of the detector, but may lead to a computation load larger than necessary. We adopt narrowbands of constant bandwidth equal to 10 Hz (the narrowest expected FO bandwidth), as a trade-off between computational load and design simplicity. This means that FOs with high central frequency will be detected in more than one frequency band simultaneously, but this does not affect the performance of the detector.
In each frequency band we compute the RMS value of the signal in a moving window of duration equal to 4 cycles of the center frequency of the band, and compare it to a moving threshold. An event or candidate FO is detected every time the RMS value of the signal is above the threshold during a time interval equal to four cycles of the central frequency of the band plus the effective duration of the impulse response of the narrowband filters. These filters have an impulse response with a shape that could be confused with an FO, and any glitch or fast transient in the broadband signal generates a confounding event in the narrow bands. The duration of these events is equal to the effective duration of the filter response. On the other hand, if an FO is present in the broadband signal, when filtered by the narrowband filter its duration also increases by an amount equal to the effective duration of the impulse response. Then, by selecting only oscillations lasting longer than fours cycles plus this effective duration, we avoid false positives related to fast transients in the original signal.
The moving threshold is proportional to the background signal level, with proportionality constant c. The background signal level is computed based on the RMS signal of the previous step, averaged in a causal moving window of length tb. Since we are interested in the background level, the RMS signal is limited to the threshold value before averaging, i.e. samples of the RMS signal with values higher than the threshold value are replaced by this threshold value, and the resulting signal is averaged in a window of length tb. In this way high RMS values not corresponding to background are excluded from the background level computation. Alternatively, a median filter could be used, but the computation of the moving average of the limited signal is less computationally demanding. The algorithm is not sensitive to changes of the parameters tb and c within a certain range, as shown in Appendix B. The values selected for these parameters are tb = 30 s and c = 2.5.
Several detections can occur almost simultaneously at different frequency bands. We implement a channel level detector by joining all the detected events in different frequency bands. Also, we consider consecutive oscillations separated by less than a certain time interval tsep as a single FO. Since in scalp EEG the measured electric potential distribution is spatially spread by the scalp, we expect events to be detected simultaneously in several channels. We form a subject level detector joining all events at different frequencies and channels, occurring at almost the same time, i.e. with separation less than tsep between them. The performance of the algorithm is not affected by the choice of this parameter within a certain range (see Appendix B), we select a value of tsep = 50 ms.
2.2. Classification
By design, the pre-detection stage has very high sensitivity, but the false positive rate of pre-detections is also high. In order to reduce the number of false pre-detections, a classification step is necessary. We implement this classification on the subject level pre-detector results.
Two major types of false pre-detections can be found in the pre-detection stage results. The first type consists of artifacts, such as muscle artifacts, glitches, or power-line interference. The second type are events which look like background. These events may have a power increase in a frequency band relative to the background, but the amplitude of the signal is still very small compared to other bands, and the event goes unnoticed in the broadband signal (35–205 Hz).
We select two features for a classification of the pre-detections in true and false positives. To obtain the first feature we compute the ratio of the maximum absolute value of the broadband signal, to the maximum absolute value of the signal in the narrow frequency band in which an event was detected. The feature used for the classification is the maximum value of this ratio among all the individual events that form a subject level detection. This feature is useful to discriminate between true positive pre-detections and several types of false positive pre-detections: glitches with much higher maximum absolute value in the broadband signal than in the narrowband signals, muscle artifacts showing a simultaneous power increment in all the narrowband signals, and low amplitude oscillations in narrowband signals with lower background than the rest of the bands. The threshold (Threshold A) will be selected based on the value of this feature in the events marked by the expert.
The second feature is the maximum of the RMS value of the narrowband signal, among all the individual events that are part of a subject level pre-detection. The events with RMS value lower than a threshold are considered false positive pre-detections. The threshold value (Threshold B) will be selected based on the value of the feature in the events marked by the expert. Low amplitude pre-detections could also be avoided by rising the threshold of the pre-detection stage, but a better overall performance of the automatic detector is achieved when using the proposed feature.
Since there are only two parameters in the classification, it is easy to find the optimum values based on events marked by an expert. We simply select the threshold values that minimize the number of false positive detections for any given number of true positive detections.
2.3. Performance metrics
We describe next the different quantities we adopt to evaluate the performance of the automatic detector. We are interested in two aspects of the detector performance. The first aspect is the performance in time, i.e. quantifying simultaneous expert’s marks and automatic detections, and the second aspect is the performance in space, i.e. quantifying to what degree the expert’s marks and automatic detections occur in the same channels. This is important since one of the purposes of the automatic detector is to determine which channels present a high number of FOs, in order to relate them to the epileptogenic zone (Andrade-Valença et al., 2011). In both aspects, time and space performance, we provide metrics that assume the expert’s marks are the gold standard and metrics to compare expert’s marks and automatic detections without assuming one of them is a gold standard.
2.3.1. Time performance
The time performance of the detector is analyzed at the subject level (i.e. to determine if there are simultaneous automatic detections and expert’s marks in any channel), and at the channel level. When considering the channel level detector, it is not clear if an automatic detection occurring at the same time as an expert’s mark but in a different channel should be considered as a true or false positive. We report then the strict channel level performance considering these events as false positives, and the loose channel level performance considering them as true positives.
Both expert’s marks and automatic detections are very short compared to the total duration of the recordings, and any performance metric based on true negative epochs would be quite meaningless since almost all the recording corresponds to true negatives. Hence, the reported performance metrics are derived from positive events. Also, note that in some cases a long expert’s mark can be detected by the automatic detector twice, and vice-versa. Hence, the number Ntp of true positive automatic detections is not exactly the same as the number Ndem of detected expert’s marks. Ndem is the number of expert’s marks which overlap with one or more automatic detections, and Ntp is the number of automatic detections which overlap with one or more expert’s marks.
When the expert’s marks are considered the gold standard we report the sensitivity (S) and the proportion of the automatic detections that are true positives, called positive predicted (PP) value. The sensitivity as a function of the positive predicted value is sometimes called precision-recall (PR) curve (Temko et al., 2011). The sensitivity and positive predicted values are computed as
| (1) |
| (2) |
where Nexpert is the total number of expert’s marks (detected plus undetected by the automatic detector), Ndem is the number of detected expert’s marks, Nauto is the total number of automatic detections (true plus false positives), and Ntp is the number of true positive automatic detections.
The other important measure we report is the false positive rate (FPR) per minute,
| (3) |
where Nfp = Nauto − Ntp is the number of false positive automatic detections and T is the total duration of the recordings in minutes.
For comparing both detectors assuming none of them is perfect we report the positive agreement (PA) (Cicchetti and Feinstein, 1990; Aarabi et al., 2007),
| (4) |
2.3.2. Space performance
Another point of interest is whether the high frequency activity is detected at the same channels by the automatic detector and the human expert. To evaluate this channel involvement we compare, for each subject level event, which channels exhibit fast oscillations.
Assuming the expert’s marks are the gold standard, we compute for each subject level event the spatial sensitivity (Se) and specificity (Sp) as
| (5) |
| (6) |
where Aexpert is the number of active channels (channels in which an FO is detected) according to the expert’s marks, Iexpert the number of inactive channels according to the expert’s marks, and Aboth and Iboth the number of active and in active channels according to both expert’s marks and automatic detections. Note that for each subject level event we have a sensitivity and specificity value. We report the average value of all these events.
In order to relate them to the epileptogenic zone it is useful to determine which channels present a high number of FOs. Then, the relative number of events in the different channels when using the automatic detector should be as close as possible to the one derived from the expert’s marks. To quantify this aspect of the performance we report the ranking distance (RD) (Zelmann et al., 2009). The ranking distance compares the ordering of the channels according to the number of detected FOs. The expert’s marks are considered the gold standard, a RD of 1 indicates the same ordering, RD = 0 corresponds to the reverse ordering, and the RD value weights the order difference by the difference in number of FOs between channels. A random ordering of the channels will almost always result in a RD very close to 0.5.
When the expert’s marks are not considered as gold standard, we report the comparison between the detectors using the positive agreement (P) and negative agreement (N),
| (7) |
| (8) |
where Aauto and Iauto are the number of active and inactive channels according to the automatic detector. For each subject level expert’s mark we get a positive and negative agreement value, and we report their average value.
We also report the Cohen’s Kappa coefficient κ (Cohen, 1960) as a comparison between the expert and the automatic detector, but the correction due to chance agreement in the Kappa coefficient computation is unrealistic (Maclure and Willett, 1987; Cicchetti and Feinstein, 1990; Guggenmoss-Holzmann, 1993; Hutchinson, 1993). This chance correction assumes the detections of each reviewer are independent random choices, not a realistic model if there are true events in the data that lead to correlated detections. In this particular case the correction is even more questionable since the automatic detection thresholds are selected based in the expert’s marks, thus the detectors are clearly not independent. Then, we believe it is better to compare detectors using the positive and negative agreement measures.
2.4. Data
To evaluate the performance of the detector we compare it with EEG recordings marked by a human expert. Fast gamma and ripple oscillation had been previously marked in scalp EEG recordings of 15 patients with focal epilepsy (Andrade-Valença et al., 2011). The patients (31.7 ± 11.6 years old, 13 women) underwent EEG-telemetry investigation at the Montreal Neurological Institute (MNI). The study was approved by the MNI and Hospital Research Ethics Committee and all patients signed an informed consent. The clinical purpose of EEG-telemetry included determination of seizure classification and epilepsy syndrome, and pre-surgical evaluation. The only inclusion criterion was the presence of at least 1 spike per minute during a previous record. The duration of epilepsy in the 15 patients was 12.6 ± 8.8 years. The age of the patients at the first epileptic seizure was 18.5 ± 11.6 years. No lesion was detected at the MRI in 9/15 (60%) patients. A seizure onset zone was identified in 8/15 (53.3%) patients; in 6/15 (40%) the discharge at the beginning of the seizure was not localized or lateralized; and one patient did not show any clinical seizure or ictal discharge.
Recordings were performed using the Harmonie monitoring system (Stellate, Montreal, Canada), with scalp electrodes placed according to the International 10–20 system, with additional zygomatic electrodes and electrodes at F9/F10, T9/T10, and P9/P10, and reference CPz. The EEG signals were acquired at a 600 Hz sampling rate, with a low pass antialiasing filter with 200 Hz cutoff frequency. For each patient, 30 min of non-REM sleep recordings were marked in a 31-channel bipolar montage. For marking the fast oscillations, the channels were displayed with the time scale at 250 mm/s. The computer screen was split to show the scalp EEG with the high-pass filter at 40 Hz and at 80 Hz simultaneously, thus removing the “standard” EEG and showing only fast activity. After all events were marked, the EEG was reviewed a second time by the same reviewer for verification.
Some channels were left out in the original study (Andrade-Valença et al., 2011) due to malfunction or continuous artifacts. We excluded the same channels and used the same montage in order to work with exactly the same data. One patient presented several bursts of almost continuous high frequency activity spread in many channels lasting between 1 and 10 s. The expert did not mark the individual FOs in these bursts, so all the automatic detections corresponding to subject level events with duration above 1s were excluded for this patient during the performance evaluation.
As mentioned at the end of Section 2.3 the threshold values for the classification stage are selected based on the expert’s marks. The number of marks varies in a large range among the patients (between 3 and 421 subject level events per patient), and the number of patients is not too large. Then, to make the threshold selection and evaluate the performance of the automatic detector, instead of separating the patients in training and test groups we adopted a jackknife, or leave one out approach (Efron, 1982). With this approach, the threshold levels for the classification stage are computed for each patient based in the expert’s marks of the other 14 patients.
To get the threshold values for any patient and any desired sensitivity, we compare the results of the pre-detection stage in the rest of the patients to the expert’s marks. First, we compute the number of true positive pre-detections that should pass the classification stage to get the desired sensitivity, given the number of expert’s marks in the 14 patients set. Then, the threshold values are varied to minimize the number of false positive pre-detections with maximum ratio of broadband to narrowband signal amplitude lower than Threshold A and maximum RMS value larger than Threshold B, always for the previously computed number of true positive pre-detections fulfilling the same conditions.
3. Results
A scatter plot showing the feature values of the events after the pre-detection stage is shown in Fig. 2. True and false positive pre-detections are shown in different colors, and lines showing the optimum threshold values to achieve 95% sensitivity after classification are also shown in the figure. We checked that the outliers of the true positive pre-detection cluster are not all from the same patient, but from several different ones. The pre-detection stage results for the 15 patients yields a 99.5% sensitivity, and a rate of 115 false positive pre-detections per minute at the subject level. The number of false positives is drastically reduced at the classification stage, giving a more reasonable number of false positive automatic detections. The processing of each 30 min recording of the 31 channels takes around 5 min of computing time in a standard desktop computer. The precise value depends on the number of FO pre-detections in the recording.
Fig. 2.
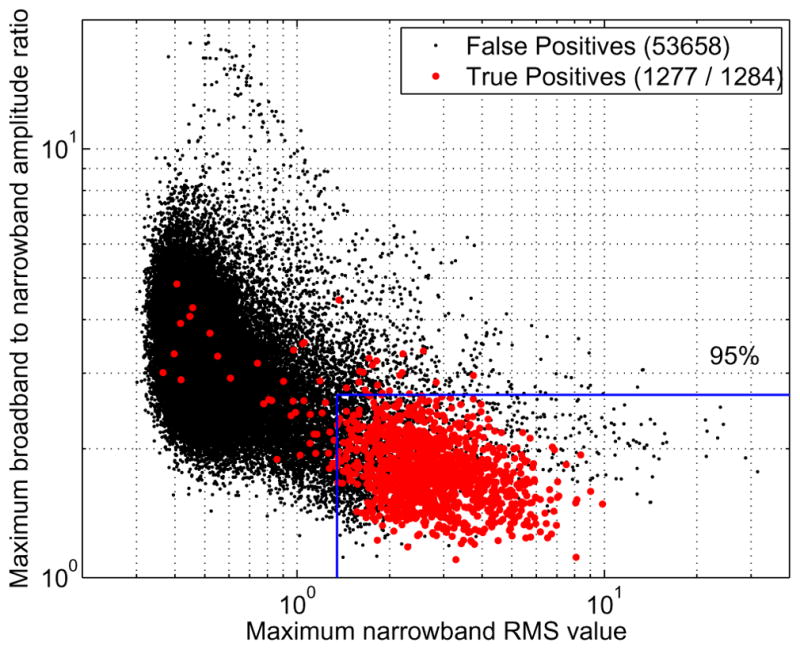
Feature values of the events after the detection stage, for the 15 patients set. Each point corresponds to a subject level event, and is either a true or false positive based on the expert’s marks. The number of events is given in the legend. An example of threshold values used for the classification is also shown, corresponding to the optimum threshold values to obtain 95% sensitivity considering all the patients as training data.
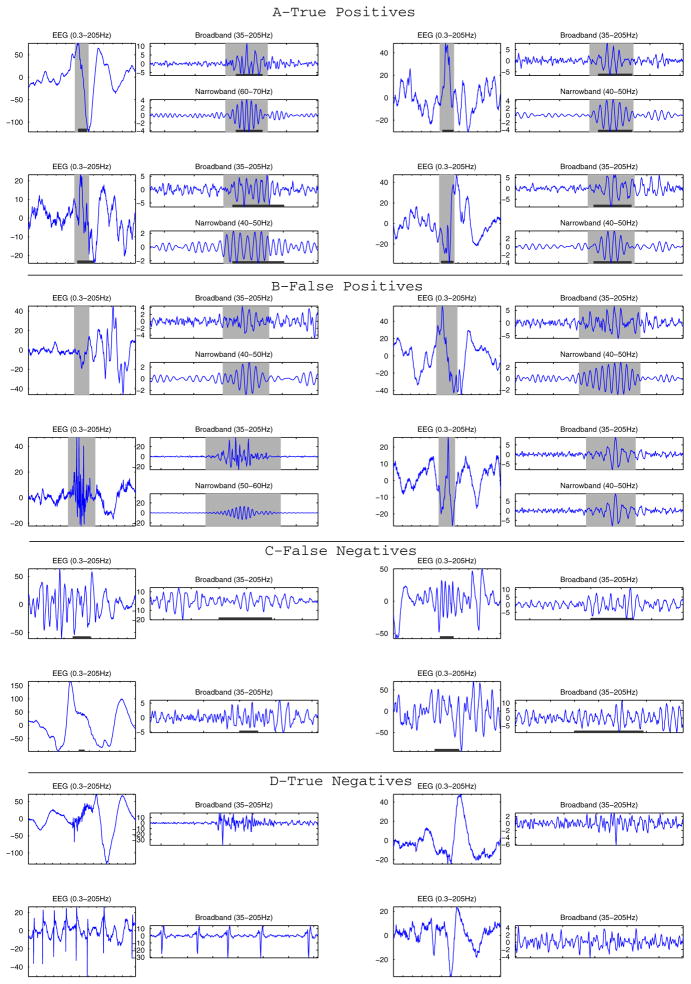
In Fig. 3 we show examples of true and false positive and negative events after the classification stage, i.e. of the results of the automatic detector. We see in the figure that some false positives are artifacts, while others could be actual FOs. Regarding the false negatives, i.e. events marked by the expert but not detected, some seem rather clear FOs, but others are weak and do not stand out of the background very much, although when reviewed at subject level most of them do seem to be actual FOs. We must point out that given the high sensitivity of the detector, the number of false negative or missed events is low. The shown true negatives are examples of glitches, artifacts, and weak signals that were correctly excluded from the pre-detection results.
Fig. 3.
(A) Example of true positive events illustrating clear events marked by the expert and identified by the detector. (B) Examples of false positive events; some look like genuine FOs that may have been missed by the expert and others are clearly part of artefacts. (C) Example of false negatives: these events marked by the expert but were not very clear and probably for this reason were missed by the detector. (D) True negatives show transients that were not marked by the expert and not detected. Gray background indicates detections of the automatic detector and dark lines at the bottom of the figures are expert’s marks. The EEG signal (0.3–205 Hz) and the broadband signal (35–205 Hz) are shown for each event, and the narrowband signal at which an event was detected are shown for the true and false positive detections. The Amplitude is given in μV, the ticks in the time axes correspond to 100 ms intervals.
In Fig. 4 we show performance curves for the detector. The curves are obtained by first computing the optimum thresholds for each desired sensitivity and then computing the resulting positive predicted and positive agreement values. We also show the curves that would be obtained if the thresholds for the classification were computed using all the patients, instead of the leave one out approach. The difference between both curves is small, which indicates that the threshold selection is robust with not too much patient to patient variation.
Fig. 4.
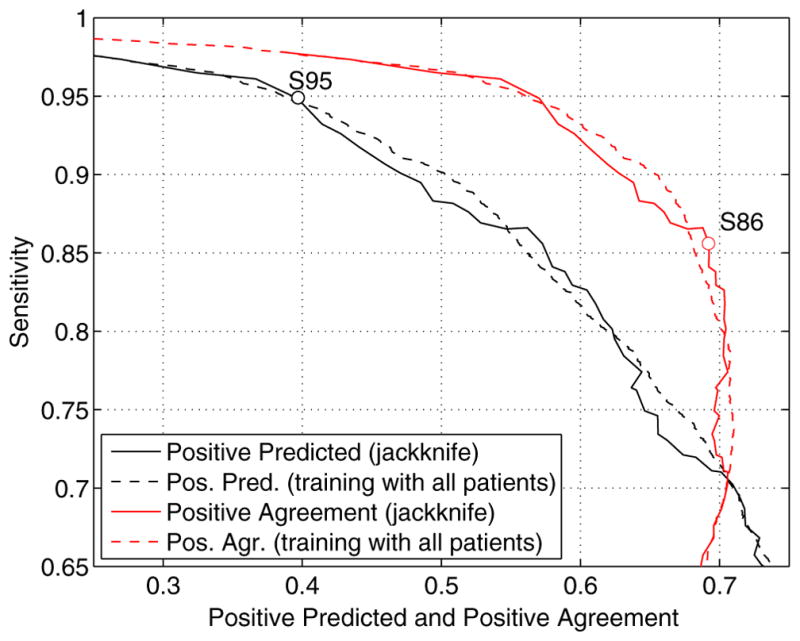
Performance curves of the automatic detector. Sensitivity vs. positive predicted and sensitivity vs. positive agreement curves are shown. The curves obtained with a jackkinfe approach (leave one out) are the curves used in the rest of the study. The curves obtained when training with all the patients are shown for comparison purposes. Two possible operating points (S95 and S86) are indicated in the curves.
Any point on the performance curve can be selected as an operating point, but points at which the slope of the curve changes are good options. Two possible operating points are indicated on the curves. When the expert’s marks are considered the Gold Standard a high sensitivity is desired. The operating point is selected in this case near the point of 95% sensitivity and 40% positive predicted, where there is a change in the slope of the S vs. PP curve. The threshold values for each patient are then selected to have the desired 95% sensitivity in the remaining 14 patients. We will denote this operating point as S95. When comparing the expert and the automatic detector without considering any of them as a gold standard, the selected operating point is near the point of 86% sensitivity and 69% positive agreement. Near this point there is a change in the S vs. PA curve, and the positive agreement is almost at its maximum. The individual threshold values are selected to get an 86% sensitivity; this operating point will be called S86.
Details of the subject level performance for the automatic detector are given in Table 1, for the S86 and S95 operating points. In the latter case the performance is also reported for each patient. The overall performance is not computed as an average of the different patients, but based in all the expert’s marks and automatic detections, even though the threshold values for the classification are different for each patient, as seen in the table. The actual sensitivity achieved in each patient is almost always high. Only in Patient J the sensitivity is low, and in this patient only 3 events were marked by the expert. One of these events is too weak and another too short to be detected by the automatic detector. We can also see in the table that the overall subject level false positive rate is 1.6 per minute at S86 operating point, and 3.6 per minute at S95, with values between 1.0 and 7.4 per minute for the different patients.
Table 1.
Subject level detector performance. Overall results for S86 and S95 operating points and patient to patient results at S95. The given values correspond to the threshold levels TH A and TH B ([μV]) of the classification stage, number of expert’s marks (Nexpert) and automatic detections (Nauto), sensitivity (S), false positive rate per minute (FPR), positive predicted (PP) and positive agreement (PA).
| Patient | TH A | TH B | Nexpert | Nauto | S (%) | FPR | PP (%) | PA (%) |
|---|---|---|---|---|---|---|---|---|
| S86 | 1284 | 1755 | 85.6 | 1.6 | 57.3 | 69.2 | ||
| S95 | 1284 | 2794 | 94.9 | 3.6 | 39.7 | 57.0 | ||
| A | 2.97 | 1.34 | 12 | 69 | 83.3 | 2.0 | 14.5 | 24.7 |
| B | 3.03 | 1.35 | 12 | 162 | 100 | 5.0 | 7.4 | 13.8 |
| C | 3.01 | 1.34 | 37 | 82 | 97.3 | 1.5 | 43.9 | 60.5 |
| D | 3.03 | 1.34 | 41 | 175 | 100 | 4.2 | 23.4 | 38.0 |
| E | 3.38 | 1.40 | 153 | 212 | 93.5 | 2.4 | 65.6 | 77.3 |
| F | 3.38 | 1.44 | 74 | 136 | 85.1 | 2.4 | 46.3 | 60.0 |
| G | 3.03 | 1.34 | 55 | 203 | 98 | 4.2 | 27.1 | 42.2 |
| H | 3.38 | 1.34 | 169 | 390 | 99 | 7.4 | 43.3 | 60.3 |
| I | 2.85 | 1.34 | 241 | 303 | 92.5 | 4.0 | 60.7 | 74.8 |
| J | 2.97 | 1.34 | 3 | 170 | 33.3 | 5.0 | 0.6 | 1.2 |
| K | 3.01 | 1.35 | 42 | 101 | 90.5 | 2.1 | 36.6 | 52.4 |
| L | 3.03 | 1.34 | 26 | 129 | 100 | 3.5 | 20.2 | 33.5 |
| M | 3.13 | 1.34 | 212 | 288 | 96.7 | 4.5 | 47.9 | 68.6 |
| N | 3.13 | 1.34 | 84 | 226 | 98.8 | 4.3 | 35.4 | 52.6 |
| O | 2.97 | 1.34 | 123 | 148 | 93.5 | 1.0 | 79.1 | 85.6 |
The channel level performance of the detector is reported on Table 2. We see that the strict channel level performance is worse than the subject level, and the loose channel level a little better. Again the worst results correspond to the patient with rare channel marks. The overall strict and loose false detection rates are 0.19 and 0.10 per channel per minute respectively at S86, and 0.51 and 0.29 per minute at S95.
Table 2.
Channel level detector performance. Overall results for S86 and S95 operating points and patient to patient results at S95, for both strict and loose channel level performance. The given values correspond to the number of expert’s marks (Nexpert) and automatic detections (Nauto), sensitivity (S), false positive rate per minute (FPR), positive predicted (PP) and positive agreement (PA).
| Pat. | Nexpert | Nauto |
S (%)
|
FPR
|
PP (%)
|
PA (%)
|
||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strict | Loose | Strict | Loose | Strict | Loose | Strict | Loose | |||
| S86 | 6879 | 5876 | 68.9 | 94.7 | 0.19 | 0.10 | 55.3 | 76.3 | 62.6 | 86.2 |
| S95 | 6879 | 11052 | 85.6 | 98.3 | 0.51 | 0.29 | 37.3 | 65.0 | 55.8 | 77.8 |
| A | 54 | 198 | 68.5 | 96.3 | 0.17 | 0.15 | 18.7 | 29.3 | 29.4 | 43.7 |
| B | 61 | 338 | 88.5 | 100 | 0.33 | 0.30 | 16.0 | 21.9 | 27.1 | 33.8 |
| C | 116 | 302 | 87.9 | 99.1 | 0.24 | 0.14 | 32.5 | 62.3 | 47.8 | 72.5 |
| D | 425 | 729 | 77.6 | 100 | 0.49 | 0.32 | 33.9 | 56.2 | 50.0 | 72.4 |
| E | 1428 | 1828 | 83.5 | 98.5 | 1.07 | 0.19 | 45.6 | 90.5 | 62.3 | 94.0 |
| F | 240 | 418 | 69.6 | 90.0 | 0.29 | 0.16 | 37.8 | 64.8 | 49.4 | 74.0 |
| G | 159 | 548 | 89.3 | 99 | 0.41 | 0.30 | 23.2 | 43.8 | 38.0 | 56.3 |
| H | 398 | 1233 | 88.7 | 99.2 | 1.32 | 0.80 | 26.0 | 55.5 | 41.3 | 66.2 |
| I | 685 | 959 | 83.6 | 96.2 | 0.53 | 0.23 | 49.0 | 77.9 | 63.4 | 85.5 |
| J | 5 | 389 | 20.0 | 40.0 | 0.37 | 0.37 | 0.3 | 1.0 | 0.5 | 1.5 |
| K | 75 | 286 | 84.0 | 94.7 | 0.24 | 0.18 | 21.7 | 42.0 | 34.6 | 52.9 |
| L | 102 | 367 | 91.2 | 100 | 0.33 | 0.24 | 24.0 | 43.6 | 38.6 | 55.9 |
| M | 1223 | 1782 | 88.4 | 99.4 | 1.03 | 0.46 | 40.6 | 73.3 | 60.0 | 84.0 |
| N | 277 | 815 | 97.1 | 99.6 | 0.61 | 0.38 | 30.8 | 56.9 | 47.6 | 67.8 |
| O | 1631 | 860 | 87.6 | 98.7 | 0.23 | 0.06 | 75.1 | 93.0 | 83.3 | 96.7 |
In Table 3 we show the results comparing the channel involvement during the marked events, between the expert and the automatic detector. The mean number of channels involved in a subject level event is almost the same for the automatic detector at S86 and the expert. At S95 the average number of active channels is 1.5 times higher than in the case of the expert’s marks. This difference in the number of active channels explains the higher sensitivity and lower specificity of the automatic detector at the S95 operating point, compared to the S86. There is much less difference in the automatic detector performance at different operating points when comparing the expert reviewer and the automatic detector without considering the former a gold standard. This indicates that at S86 there are as many active channels as in the expert reviewer results, but not necessarily the same ones.
Table 3.
Channel involvement results. Overall results for S86 and S95 operating points and patient to patient results at S95. Number of active channels (expert’s marks Aexpert and automatic detections Aauto), sensitivity (Se) and specificity (Sp), and positive (Pa) and negative (Na) agreement regarding channel involvement, Cohen’s κ coefficient and ranking distance (RD). All the values except the RD correspond to the average among all the subject level true positive events.
| Pat. | Aexpert | Aauto | Se (%) | Sp (%) | Pa (%) | Na (%) | κ | RD |
|---|---|---|---|---|---|---|---|---|
| S86 | 3.8 | 3.6 | 64.0 | 95.6 | 60.3 | 94.9 | 0.56 | 0.16 |
| S95 | 3.8 | 5.7 | 82.2 | 89.5 | 63.1 | 92.6 | 0.57 | 0.19 |
| A | 4.5 | 4.8 | 53.8 | 93.1 | 48.3 | 93.3 | 0.43 | 0.28 |
| B | 5.1 | 6.2 | 85.5 | 91.9 | 76.0 | 94.2 | 0.71 | 0.38 |
| C | 3.0 | 5.1 | 86.2 | 89.9 | 64.4 | 93.8 | 0.59 | 0.10 |
| D | 8.1 | 10.0 | 76.8 | 78.8 | 62.4 | 81.4 | 0.45 | 0.48 |
| E | 6.7 | 10.8 | 74.3 | 74.8 | 52.5 | 81.0 | 0.37 | 0.24 |
| F | 3.1 | 3.6 | 68.5 | 94.2 | 56.0 | 95.2 | 0.53 | 0.04 |
| G | 2.6 | 4.3 | 88.6 | 92.4 | 65.3 | 95.3 | 0.62 | 0.08 |
| H | 2.1 | 4.0 | 88.8 | 89.6 | 61.5 | 93.7 | 0.57 | 0.09 |
| I | 2.5 | 3.3 | 81.8 | 95.7 | 68.0 | 97.0 | 0.66 | 0.04 |
| J | 1.7 | 1.3 | 33.3 | 97.7 | 22.2 | 97.2 | 0.21 | 0.50 |
| K | 1.8 | 2.9 | 81.1 | 95.2 | 56.5 | 97.0 | 0.54 | 0.07 |
| L | 3.6 | 6.2 | 96.1 | 89.0 | 66.0 | 93.6 | 0.61 | 0.18 |
| M | 4.0 | 6.5 | 81.0 | 87.8 | 59.9 | 91.9 | 0.53 | 0.11 |
| N | 3.1 | 5.7 | 97.4 | 88.9 | 69.0 | 93.6 | 0.64 | 0.04 |
| O | 6.0 | 6.3 | 82.2 | 95.4 | 76.5 | 95.9 | 0.73 | 0.14 |
The ranking distance results are an important end point, and are also reported in Table 3. In this case the channel ordering derived from the expert reviewer is the gold standard, and the analysis is not restricted to true positives. To have an idea of the range of RD values, in a different study involving HFO detection in recordings with depth electrodes (SEEG), the RD value between two human reviewers was 0.07 after joint review of intervals with important differences (Zelmann et al., 2009). In this study, at the S95 operating point, we have 8 patients with RD below 0.11, and only two patients with RD near 0.5. One of them has only 5 channel level expert’s marks. Given that the number of false positives in this patient is almost 80 times larger (see Patient J in Table 3), it is natural that the results are equivalent to selecting a random ordering. The other patient with RD near 0.5 (patient D) has expert’s marks (and automatic detections) distributed among all the channels. It is the patient that presented long bursts of distributed fast activity spanning all the channels, which were excluded from the performance analysis. Almost no difference is found in the performance of the automatic detector at different operating points. This indicates that the events left out when changing the operating point to a lower overall sensitivity have a similar spatial distribution than the rest of the events.
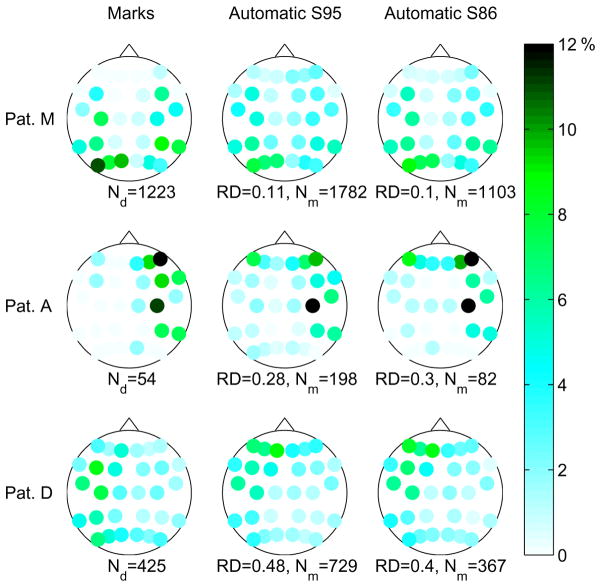
More details regarding the channels presenting FOs is shown in Fig. 5. The figure shows the proportion of channel level events at different channels, for 3 of the 15 patients. The color/gray level scale indicates the proportion of events corresponding to each channel. Results are shown for the expert’s marks and the S95 and S86 operating points of the automatic detector. In general, the results of the automatic detector are more spatially spread. We observe that in patients with low RD, such as Patient M in Fig. 5, the channels with a high proportion of automatic detections are the same as the ones with high proportion of expert’s marks, even though this proportion is not as high given the more spatially spread distribution of automatic detections. In patients with RD around 0.3, such as Patient A, there are some more channels with high proportion of automatic detections compared to channels with high proportions of expert’s marks, presumably due to artifacts. As expected, the channels with high proportion of expert’s marks also have a high proportion of automatic detections. Patient D, with RD around 0.5, shows a distribution of involved channels with the maximum in different channels than the expert’s marks, the pattern of marks is much more spatially spread than in other patients. In the figure we can also see that there is no significant improvement of the automatic detector at S86 compared to the S95, as mentioned earlier. The patients in Fig. 5 were selected to show results with different RD values. In the Supplementary Fig. S1 we show the same diagrams for all the patients, and it can be seen than in most patients the channels with a high proportion of events are the same according to the expert and the automatic detector.
Fig. 5.
Channel involvement results. Every dot corresponds to a bipolar channel on the scalp. The color/gray level of the dots indicates the proportion of events in that particular channel. Left: distribution of expert’s marks. Center and right: distribution of detections of automatic detector at operating points S95 and S85, respectively. The total number of events is given below each diagram, as well as the ranking distance (RD) value for the automatic detector. Results are shown for three patients with different RD values.
The expert also marked the interictal spikes, and in Table 4 we present results regarding the co-occurrence of spikes and FOs. There are 20704 channel-level marked spikes in the recordings, and 17% have simultaneous fast activity according to the expert’s marks. This represents 70% of all the marked high frequency events. The percentage of spikes with simultaneous fast activity is higher for the automatic detector at S95. From the table we also see that the percentage of automatic detections that occur at the same time as a spike is lower for the automatic detector.
Table 4.
Co-occurence of spikes and FOs. Percentage of the 20704 spikes with simultaneous high frequency activity, total number of channel level events and percentage of them occuring at the same time as a spike.
| Detector | Spikes with FOs (%) | Number of FOs | FOs with spikes (%) |
|---|---|---|---|
| Expert | 16.9 | 6879 | 70.3 |
| Auto. S86 | 16.3 | 5876 | 54.9 |
| Auto. S95 | 26.2 | 11052 | 47.0 |
We also studied the frequency of the detected events. In Fig. 6 we present the number of events detected at each frequency band, before grouping them in channel or subject level events. We separate the events belonging to true positive and false positive subject level events of the automatic detector at S95. From the figure there seems to be no reason to treat differently the fast gamma (40–80 Hz) and ripple (80–200 Hz) bands.
Fig. 6.
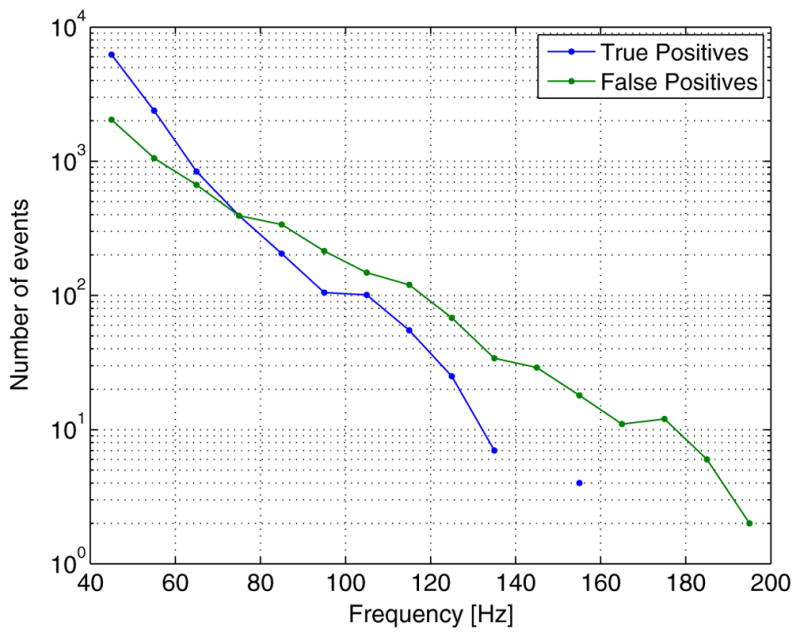
Number of detected events at different frequency bands. True positives and false positives of the automatic detector at operating point S95.
4. Discussion
We believe that fast oscillations in scalp recordings may be clinically relevant in epilepsy (Andrade-Valença et al., 2011). More studies are necessary to investigate this potential. We present an automatic scalp FO detector to be used as a tool in future studies. In order to replace the time consuming marking of the EEG recordings by human reviewers, the automatic detector should produce a similar output. Hence, this work focuses in the comparison between the human expert and the automatic detector.
In scalp EEG signals the frequency band under study is affected by the presence of muscle artifacts (Whitham et al., 2007), such as eye saccades (Yuval-Greenberg et al., 2008). To minimize these artifacts the analyzed recordings correspond to non-REM sleep. This reduces the number of artifacts, but some are still present. The expert reviewer distinguishes them by their irregular morphology compared to the more sinusoidal shape of the fast oscillations. Extreme care was taken in the marking procedure, and each mark was reviewed by the same expert at different time scales and frequency bands to exclude artifacts. The automatic detector also looks for events with sinusoidal shape, and was carefully designed to avoid detections associated to sharp transients, which are another possible source of false detections. Examples of these sharp transients can be seen in some of the true negative examples of Fig. 3. The automatic detector and the expert’s marks show a good agreement even though they use different filters, indicating that the FOs are not likely to be filtering artifacts. Another strong evidence supporting this is that most of the FOs can be seen in the unfiltered EEG signal, as shown in the true positives’ EEG signal (0.3–205 Hz) in Fig. 4. Finally, we also checked that the expert’s marks and automatic detections are not artifacts produced by sleep phenomena, such as sleep spindles or vertex waves.
The proposed automatic scalp FO detector shows a good performance in the tested group of patients. The sensitivity is high in all the patients with a reasonable number of clear FOs. The ordering of the channels based on the number of detected FOs is almost equal to the ordering based on the expert’s marks in more than half of the patients. Nevertheless, since for several patients the channel ordering is different than the expert’s, we consider that a review of the automatic detector results by a human expert is necessary. This is a common necessity also for intracranial HFO detectors (Staba et al., 2002; Gardner et al., 2007; Crepon et al., 2010; Zelmann et al., 2010). Given the limited experience with scalp FOs, we believe that a review of the automatic detector results by a human expert is necessary regardless of performance. The patients with more differences between the expert and the automatic detector, such as patients A and J, have a low number of expert’s marks. It seems reasonable that a human reviewer would unconsciously relax the qualitative requirements to find FOs in a recording with very few events compared to a recording with many events.
For the proposed detector we consider the S95 operating point a better choice than a lower sensitivity one. The number of events to be reviewed may be larger, but the chance of undetected FOs will be smaller. With an average number of less than 3.6 detected subject level events per minute, and at least 40% true positives, the review of the results will be much faster than manual marking. The classification stage implemented in the detector is a simple thresholding based on two features. We tried other options, such as clustering algorithms, and other features. We found that the improvements were only marginal, and every included feature could only identify a few extra false positives. Since the results should be checked by an expert anyway, we prefer this simple classification rather than using more features and risk an algorithm too finely tuned to our particular data.
Some of the results of the automatic detector at the S95 operating point suggest that a proportion of the false positive events could actually be FOs not marked by the reviewer (see some of the false positive examples in Fig. 3). The average number of active channels during subject level events is 1.5 times larger for the automatic detector at S95 than for the expert (see Table 3). The same 1.5 times increment is observed in the proportion of spikes with simultaneous automatic detections in Table 4. This supports the idea that the automatic detector at this operating point is more sensitive than the expert, detecting weaker but probably real FOs (note that for the automatic detector operating at S86 the proportion of spikes with simultaneous fast activity for the automatic detector is 0.95 times that of the expert, and the same 0.95 proportion is observed when comparing the average number of active channels in the subject level events). Also, almost no difference is found in the ranking distance of the automatic detector at both operating points (see Table 3 and Fig. 5). Again, this indicates that the events left out when changing the thresholds to obtain a lower sensitivity, have a similar spatial distribution than the rest of the events. Thus, probably an important proportion of them are actually weak FOs and not artifacts. Hence, the false positive rate is expected to be lower than the reported value.
A large proportion of the FOs (47–70%) occur at the same time as a spike. This provides a strong evidence for a relationship between FOs and epilepsy. Note that these spikes are a small fraction of the total spikes (16–26%), and they may be more specific in localizing the seizure onset zone (Andrade-Valença et al., 2011). We are quite confident that the detected events do not correspond to artifacts associated to bandpass filtering of the spikes since they can be seen in the unfiltered EEG signal in the true positive examples shown in Fig. 4. No evident difference, other than the presence of the FOs, was noted between the morphology of both groups of spikes.
There is a very marked decrease in the number of events as the frequency increases, part of this may be due to the fact that a non-ideal 200 Hz cutoff frequency antialiasing filter was used for the signal acquisition. This means that frequencies near 200 Hz may be attenuated up to 50% of their original amplitude. This does not affect the pre-detection stage of the automatic detector since amplitudes are compared to the background level in each frequency band. But it does affect both features in the classification stage, leading to an increased pruning of the attenuated higher frequency events. Higher sampling frequency recordings would allow a more accurate evaluation of the number of events as a function of the frequency. Finally, the figure also shows that for the expert’s marks (true positives) this decrease in number of events at higher frequencies is even more pronounced. This may mean that the higher frequency false positives correspond to artifacts, but it could also be explained if we consider that at frequencies above 150 Hz there are fewer than 4 samples per cycle, and the human expert may not consider the resulting signals as “sinusoidal” in shape, failing to mark such high frequency events.
The proposed algorithm was able to detect the events marked by the reviewer, which were limited to 150 Hz. Given the large number of patients with activity in the fast-gamma and ripple band, it would be of interest to investigate oscillations in the fast ripple band. To maintain a good performance with higher sampling rates, some modifications may be necessary in the algorithm. Non-uniform frequency bands in the detection stage, wider for higher frequencies, would help to reduce the computational burden. Also, frequency dependent thresholds may be necessary in the classification stage to detect higher frequency oscillations with potentially lower amplitudes. The same modified algorithm could also be used to detect HFOs in intracranial EEG recordings, and in magnetoencephalography (MEG) signals.
The presence of FOs on EEG scalp recording may seem unlikely considering that from intracranial studies it is known that the generators of HFOs are rather small, in the order of 1 cm3 or less (Bragin et al., 1999b; Crepon et al., 2010). A much larger area of synchronized cortex (at least 6–9 cm2) has been reported to be required for interictal spikes to be visible on the scalp (Tao et al., 2007). It is important to note that the skull and other tissues between the brain and the scalp do not attenuate the frequencies up to several KHz any more than the standard EEG frequencies below 40 Hz (Hämäläinen et al., 1993, Oostendorp et al., 2000).
A possible explanation of why there are visible HFOs on scalp recordings is that, on rare occasions, high frequency oscillations may occur simultaneously in larger brain regions (Crepon et al., 2010). To contribute significantly to a scalp event, such distant events would have to be synchronized and the above study did not address this issue. Another possibility is that some of the fast oscillation generators can produce a noticeable scalp potential with a smaller cortical area than a spike. The amplitude of the marked FOs in the analyzed recordings was about ten times smaller than the amplitude of the interictal spikes. A smaller generator for the scalp FOs than for the spikes could be the reason of this smaller amplitude. As to why they can be seen on the scalp, we found that the physiological noise level is lower in higher frequency bands than in the frequency band associated to the spikes (3–40 Hz), at least during non-REM sleep. A low frequency signal from a small generator may then be lost in the background noise in scalp recordings, but a generator of the same size could produce a fast oscillation that would stand clearly out of the (high frequency) background. In fact, we found in our scalp recordings that the spikes, fast gamma, and ripple oscillations have all a similar signal to noise ratio in their respective frequency bands. Simultaneous scalp and intracranial EEG recordings and/or combined EEG/MEG recordings may help create a better understanding of the scalp fast oscillations. The automatic detector described in this work would be a useful tool in such studies.
Supplementary Material
HIGHLIGHTS.
Fast oscillations present in scalp EEG signals can be detected automatically.
The fast oscillations are characterized by local increments of power in narrow frequency bands.
There is a high agreement between an expert reviewer and the automatic detector regarding the channels with the highest proportion of fast oscillations.
Acknowledgments
This study was funded by Canadian Institute of Health Research Grants MOP-102710 and MOP-10189.
Appendix A
In this section we give details regarding the pre-detection stage of the automatic detector, describing the algorithm used to detect the individual events in each channel and frequency band. These events will then be grouped to obtain the channel and subject level pre-detections. In Fig. 1 we show a diagram of the pre-detection stage, with the signal and parameter notations used below.
Let xraw [n] be the sequence of samples corresponding to any channel of the unprocessed EEG, sampled at 600 Hz. The detector algorithm is as follows:
-
Filter all the channels with a bandpass filter
(9) where x[n] is the sequence of bandpass filtered samples which we call broadband signal, hbp[n] is the impulse response of the bandpass filter, and {·*·}[n] is the convolution operator. The bandpass filter is an equiripple FIR filter of order 120, with pass-band from 35 Hz to 205 Hz, and transition bands of 10 Hz. The resulting stop-band attenuation is 40 dB, and pass-band ripple 0.1 dB.
-
Separate each channel in narrow frequency bands
(10) where yk[n] are the sequences we call narrowband signals, and hk[n] are the impulse responses of the narrowband filters. The filters are equiripple FIR filters of order 300, with pass-band from (30 + 10k) to (40 + 10k) Hz, transition bands 5 Hz wide, and a weighting factor 10 times larger for the low frequencies stop-band than for the other bands, resulting in approximately 60 dB attenuation in the low frequencies stop-band, 40 dB attenuation in the high frequencies stop-band, and 0.1 dB ripple in the pass-band. The effective duration of the filter impulse response is given for even order filters by(11) where N is the filter order. All the specified narrowband filters have effective duration σk between 18 and 19 samples.
-
Compute the RMS value of the signal in each frequency band, for an interval centered at each sample and with duration equal to four cycles of the central frequency of the band
(12) where Nk is the number of samples in one cycle of the central frequency of the band, i.e. the integer nearest to (35 + 10 k)/600.
-
Compute the moving background level bk[n] as
(13) where Nb is the number of samples in the background moving window, i.e. the integer nearest tb*600, and z̄k[n] is the moving RMS value signal zk[n] limited by the moving threshold value, i.e.(14) where c is the proportionality constant that sets the threshold based on the moving background level. Note that the background level corresponding to sample n is computed based on a window from n − 2Nk − Nb + 1 to n − 2Nk, so its based on previous values of the background level and RMS signal, and (13) and (14) can be implemented causally. The recursive implementation of (13) as(15) is adopted for computational efficiency. The 2Nk delay of the background window is to avoid an overlap with the window for the RMS value computation in (12).
-
Compute the detection indicator signal dk[n] as
(16) The individual events detected in frequency band k are all the sequences of ones in dk[n] which are at least 4Nk + σk samples long.
Appendix B
As seen in Section 2.1, there are three parameters involved in the pre-detection stage; the length tb of the averaging window in the computation of the background level, the proportionality constant c to obtain the threshold value, and the minimum separation tsep between events at channel and subject level.
The algorithm is insensitive to changes in a large range of values of tb and tsep. We tested values in the range 10 s < = tb < = 60 s and found no noticeable change in the performance, and the same conclusion could be drawn for changes in tsep between 25 and 100 ms. We selected values in the center of the range for both parameters; tb = 30 s and tsep = 50 ms. In the Supplementary Fig. S2, we show performance curves for different parameter values. The proportionality constant c should be chosen as low as possible to have a high sensitivity, but if it is too low there will be detections at some frequency band and channel almost anytime, leading to very long and unrepresentative channel and subject level events. We found that a value of 2.5 leads to almost 100% sensitivity in every tested patient, without continuous spurious detections. If a higher parameter value is used, the positive agreement and positive predicted values will deteriorate at high sensitivities, but remain almost unchanged at low sensitivities. A low parameter value may show excellent positive agreement and positive predicted values at high sensitivity, but the reason is simply that there are almost continuous detections. For lower sensitivities these performance measures degrade very quickly since large intervals of data including both true and false positives are discarded. A reasonably stable performance is found in the range c = 2.25 to c = 2.75. See performance curves for different parameter values in the Supplementary Fig. S2.
Footnotes
5. Disclosure
- Dr. von Ellenrieder received financial support from the Consejo Nacional de Investigaciones Científicas y Tecnológicas (CONICET), and Universidad Nacional de La Plata, Argentina.
- Dr. Andrade–Valença has received scholarship support from CIHR MOP-102710 and CIHR MOP-10189.
- Dr. Dubeau is a co-investigator of CIHR Grants MOP-102710 and MOP-10189 and associate editor from Epileptic Disorders.
- Dr. Gotman is the PI of CIHR Grants MOP-102710 and MOP-10189.
References
- Aarabi A, Grebe R, Wallois F. A multistage knowledge-based system for EEG seizure detection in newborn infants. Clin Neurophysiol. 2007;118:2781–97. doi: 10.1016/j.clinph.2007.08.012. [DOI] [PubMed] [Google Scholar]
- Andrade-Valença L, Dubeau F, Mari F, Zelmann R, Gotman J. Interictal scalp fast oscillations as a marker of the seizure onset zone. Neurology. 2011;77:524–31. doi: 10.1212/WNL.0b013e318228bee2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bragin A, Engel J, Jr, Wilson CL, Fried I, Mathern GW. Hippocampal and entorhinal cortex high-frequency oscillations (100–500 Hz) in human epileptic brain and in kainic acid-treated rats with chronic seizures. Epilepsia. 1999a;40:127–37. doi: 10.1111/j.1528-1157.1999.tb02065.x. [DOI] [PubMed] [Google Scholar]
- Bragin A, Engel J, Jr, Wilson CL, Vizentin E, Mathern GW. Electrophysiologic analysis of a chronic seizure model after unilateral hippocampal KA injection. Epilepsia. 1999b;40:1210–21. doi: 10.1111/j.1528-1157.1999.tb00849.x. [DOI] [PubMed] [Google Scholar]
- Bragin A, Engel J, Jr, Wilson CL, Fried I, Buzsaki G. High frequency oscillations in human brain. Hippocampus. 1999b;9:137–42. doi: 10.1002/(SICI)1098-1063(1999)9:2<137::AID-HIPO5>3.0.CO;2-0. [DOI] [PubMed] [Google Scholar]
- Cicchetti DV, Feinstein AR. High agreement but low kappa: II. Resolving the paradoxes. J Clin Epidemiol. 1990;43:551–8. doi: 10.1016/0895-4356(90)90159-m. [DOI] [PubMed] [Google Scholar]
- Cohen J. A coefficient of agreement for nominal scales. Educ Psychol Measure. 1960;20:37–46. [Google Scholar]
- Crepon B, Navarro V, Hasboun D, Clemenceau S, Martinerie J, Baulac M, et al. Mapping interictal oscillations greater than 200 Hz recorded with intracranial macroelectrodes in human epilepsy. Brain. 2010;133:33–45. doi: 10.1093/brain/awp277. [DOI] [PubMed] [Google Scholar]
- Efron B. The jackknife, the bootstrap and other resampling plans. Philadelphia: Society for Industrial and Applied Mathematics; 1982. [Google Scholar]
- Gardner AB, Worrell GA, Marsh E, Dlugos D, Litt B. Human and automated detection of high-frequency oscillations in clinical intracranial EEG recordings. Clin Neurophysiol. 2007;118:1134–43. doi: 10.1016/j.clinph.2006.12.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guggenmoss-Holzmann I. How reliable are chance-corrected measures of agreement? Stat Med. 1993;12:2191–205. doi: 10.1002/sim.4780122305. [DOI] [PubMed] [Google Scholar]
- Hämäläinen M, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV. Magnetoencephalography – theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Modern Phys. 1993;65:413–97. [Google Scholar]
- Hutchinson TP. Focus on Psychometrics. Kappa muddles together two sources of disagreement: tetrachoric correlation is preferable. Res Nurs Health. 1993;16:313–6. doi: 10.1002/nur.4770160410. [DOI] [PubMed] [Google Scholar]
- Inoue T, Kobayashi K, Oka M, Yoshinaga H, Ohtsuka Y. Spectral characteristics of EEG gamma rhythms associated with epileptic spasms. Brain Dev. 2008;30:321–8. doi: 10.1016/j.braindev.2007.10.003. [DOI] [PubMed] [Google Scholar]
- Jacobs J, LeVan P, Chander R, Hall J, Dubeau F, Gotman J, et al. Interictal high-frequency oscillations (80–500 Hz) are an indicator of seizure onset areas independent of spikes in the human epileptic brain. Epilepsia. 1893;49:1893–907. doi: 10.1111/j.1528-1167.2008.01656.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs J, Zijlmans M, Zelmann R, Chatillon CE, Hall J, Olivier A, et al. High-frequency electroencephalographic oscillations correlate with outcome of epilepsy surgery. Ann Neurol. 2010;67:209–20. doi: 10.1002/ana.21847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jirsch JD, Urrestarazu E, LeVan P, Olivier A, Dubeau F, Gotman J. High-frequency oscillations during human focal seizures. Brain. 2006;129:1593–608. doi: 10.1093/brain/awl085. [DOI] [PubMed] [Google Scholar]
- Kobayashi K, Oka M, Akiyama T, Inoue T, Abiru K, Ogino T, et al. Very fast rhythmic activity on scalp EEG associated with epileptic spasms. Epilepsia. 2004;45:488–96. doi: 10.1111/j.0013-9580.2004.45703.x. [DOI] [PubMed] [Google Scholar]
- Kobayashi K, Watanabe Y, Inoue T, Oka M, Yoshinaga H, Ohtsuka Y. Scalp-recorded high-frequency oscillations in childhood sleep-induced electrical status epilepticus. Epilepsia. 2010;50:2190–4. doi: 10.1111/j.1528-1167.2010.02565.x. [DOI] [PubMed] [Google Scholar]
- Maclure M, Willett WC. Misinterpretation and misuse of the kappa statistic. Am J Epidemiol. 1987;126:161–9. doi: 10.1093/aje/126.2.161. [DOI] [PubMed] [Google Scholar]
- Nealis JG, Duffy FH. Paroxysmal beta activity in the pediatric electroencephalogram. Ann Neurol. 1978;4:112–6. doi: 10.1002/ana.410040204. [DOI] [PubMed] [Google Scholar]
- Oostendorp TF, Delbeke J, Stegeman DF. The conductivity of the human skull: results of in vivo and in vitro measurements. IEEE Trans Biomed Eng. 2000;47:1487–92. doi: 10.1109/TBME.2000.880100. [DOI] [PubMed] [Google Scholar]
- Rodin E, Smid N, Mason K. The grand mal pattern of Gibbs, Gibbs and Lennox. Electroenceph Clin Neurophysiol. 1976;40:401–6. doi: 10.1016/0013-4694(76)90191-7. [DOI] [PubMed] [Google Scholar]
- Staba RJ, Wilson CL, Bragin A, Fried I, Engel J. Quantitative analysis of high-frequency oscillations 80–500 Hz. 2002. [DOI] [PubMed] [Google Scholar]
- Tao JX, Baldwin M, Hawes-Ebersole S, Ebersole JS. Cortical substrates of scalp EEG epileptiform discharges. J Clin Neurophysiol. 2007;24:96–100. doi: 10.1097/WNP.0b013e31803ecdaf. [DOI] [PubMed] [Google Scholar]
- Temko A, Thomas E, Marnane W, Lightbody G, Boylan GB. Performance assessment for EEG-based neonatal seizure detectors. Clin Neurophysiol. 2011;122:474–82. doi: 10.1016/j.clinph.2010.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urrestarazu E, Chander R, Dubeau F, Gotman J. Interictal high-frequency oscillations (100–500 Hz) in the intracerebral EEG of epileptic patients. Brain. 2007;130:2354–66. doi: 10.1093/brain/awm149. [DOI] [PubMed] [Google Scholar]
- Whitham EM, Pope KJ, Fitzgibbon SP, Lewis T, Clark CR, Loveless S, et al. Scalp electrical recording during paralysis: Quantitative evidence that EEG frequencies above 20 Hz are contaminated by EMG. Clin Neurophysiol. 2007;118:1877–88. doi: 10.1016/j.clinph.2007.04.027. [DOI] [PubMed] [Google Scholar]
- Worrell GA, Gardner AB, Stead SM, Hu S, Goerss S, Cascino GJ, et al. High-frequency oscillations in human temporal lobe:simultaneous microwire and clinical macroelectrode recordings. Brain. 2008;131:928–37. doi: 10.1093/brain/awn006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu JY, Koh S, Sankar R, Mathern GW. Paroxysmal fast activity: an interictal scalp EEG marker of epileptogenesis in children. Epilepsy Res. 2008;82:99–106. doi: 10.1016/j.eplepsyres.2008.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamazaki M, Chan D, Tovar-Spinoza Z, Go C, Imai K, Ochi A, et al. Interictal epileptogenic fast oscillations on neonatal and infantile EEGs in hemimegalencephaly. Epilepsy Res. 2009;83:198–206. doi: 10.1016/j.eplepsyres.2008.11.008. [DOI] [PubMed] [Google Scholar]
- Yuval-Greenberg S, Tomer O, Keren AS, Nelken I, Deouell LY. Transient induced gamma-band response in EEG as a manifestation of miniature saccades. Neuron. 2008;58:429–41. doi: 10.1016/j.neuron.2008.03.027. [DOI] [PubMed] [Google Scholar]
- Zelmann R, Zijlmans M, Jacobs J, Chatillon CE, Gotman J. Improving the identification of high frequency oscillations. Clin Neurophysiol. 2009;120:1457–64. doi: 10.1016/j.clinph.2009.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zelmann R, Mari F, Jacobs J, Zijlmans M, Chander R, Gotman J. Automatic detector of high frequency oscillations for human recordings with macroelectrodes. 32nd Annual International Conference of the IEEE EMBS; 2010. pp. 2329–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zijlmans M, Jacobs J, Zelmann R, Dubeau F, Gotman J. High-frequency oscillations mirror disease activity in patients with epilepsy. Neurology. 2009;72:979–86. doi: 10.1212/01.wnl.0000344402.20334.81. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.