Abstract
We develop a Bayesian model for the alignment of two point configurations under the full similarity transformations of rotation, translation and scaling. Other work in this area has concentrated on rigid body transformations, where scale information is preserved, motivated by problems involving molecular data; this is known as form analysis. We concentrate on a Bayesian formulation for statistical shape analysis. We generalize the model introduced by Green and Mardia for the pairwise alignment of two unlabeled configurations to full similarity transformations by introducing a scaling factor to the model. The generalization is not straight-forward, since the model needs to be reformulated to give good performance when scaling is included. We illustrate our method on the alignment of rat growth profiles and a novel application to the alignment of protein domains. Here, scaling is applied to secondary structure elements when comparing protein folds; additionally, we find that one global scaling factor is not in general sufficient to model these data and, hence, we develop a model in which multiple scale factors can be included to handle different scalings of shape components.
Keywords: Morphometrics, protein bioinformatics, similarity transformations, statistical shape analysis, unlabeled shape analysis
1. Introduction
The shape of an object is the information about the object which is invariant under the full similarity transformations of rotation, translation and rescaling. In order to compare the shapes of objects, we first seek to align them in some optimal registration. In statistical shape analysis, objects often are reduced to a set of points, known as landmarks, in d dimensions and thus can be represented as m × d point configurations, where m is the number of landmarks. Let X be such a configuration of points; the points on X are xj, j = 1, … , m, where are the rows of X, with each row therefore giving the coordinates of point xj. We shall consider the problem of pairwise alignment, where the objective is to align one configuration, such as X above, with another configuration, Y, say, where the rows of Y are yj, j = 1, … , m, the locations of the points of Y.
Labeled shape analysis assumes a known, one-to-one correspondence between the points on X and Y, labeled such that xj matches yj, j = 1, … , m. Since the configurations may be presented in arbitrary registrations, it is necessary first to filter out the similarity transformations so that only the shape information of interest remains. Mathematically, the problem is to find c, A and τ such that
where c > 0 is a scaling parameter, A is a d × d rotation matrix and is a translation vector. Of course, in practical situations, the point locations will be observed with error, so the statistical problem is to find an optimal solution to an equation of the form
where Σ is a d × m matrix of errors. The least squares solution to this problem is the Procrustes solution [Dryden and Mardia (1998)].
A much more challenging problem, which has been the subject of recent research interest, is that of unlabeled shape analysis, where the correspondence between landmarks is not known and often the configurations have different numbers of landmarks. Specifically, we have an m × d configuration X which we wish to align with an n × d configuration Y, with m ≠ n in general. To keep track of the correspondence between landmarks, an m × n matching matrix M (mjk) is introduced, where mjk = 1 if xj is matched to yk and 0 otherwise. Thus, the problem is to simultaneously estimate the matching matrix M as well as to solve the alignment problem described above for the labeled case. It is usually assumed that any point on a configuration can match at most one point on the other, so that any row or column of M contains at most one nonzero entry. Then the number of matched points, 0 ≤ L ≤ min(m, n), say, is and is not known. Thus, even for relatively small m and n, the number of possible matchings given by M is large, which makes the problem very challenging. Therefore, searching over all possible M and optimizing over transformation parameters to find a global solution is not computationally feasible. Green and Mardia (2006) developed a Bayesian solution to this problem, where the transformation, error and matching parameters were all treated as unknown parameters and samples from the joint posterior were drawn using MCMC. Although their model conceptually could handle similarity transformations, their applications focused on rigid-body alignment (i.e., no scaling parameter c)—inclusion of the scaling parameter c requires considerable attention, and it is the purpose of the present paper to address this problem. In particular, we reformulate the likelihood, which we find is necessary for good performance, and derive the full conditional distribution for the scaling parameter together with methods to sample from it.
Other solutions to the unlabeled alignment problem have been proposed. One such method is to maximize a likelihood over the transformation parameters conditional on a given matching, and then to propose a different matching given the transformation parameters, and alternate between these two steps; such methods have been used by Rodriguez and Schmidler (2013) and Dryden, Hirst and Melville (2007). Kent, Mardia and Taylor (2010) proposed a method based on the EM algorithm, with the missing data being the labels representing the matching between points. One problem with the methods which alternate between matching and optimizing is that they can depend on the initialization of the matching and can become trapped in local modes [Dryden, Hirst and Melville (2007), Kenobi and Dryden (2010)]. Schmidler (2007) developed a fast matching method based on an approximation using geometric hashing, and Srivastava and Jermyn (2009) tackled the unlabeled problem by looking for objects of predefined shape classes in cluttered point clouds, where the points are samples from the outline of a shape.
An issue with methods in which the transformation parameters are maximized out of the likelihood is that the alignment is considered “correct,” and uncertainty in this alignment is not fully propagated [Wilkinson (2007)]. Therefore, it is desirable to consider a fully Bayesian formulation, in which uncertainty in all the parameters is correctly handled. Such a formulation for the case of unlabeled similarity shape is the subject of this paper. Theobald and Wuttke (2006) considered a Bayesian model but concentrated on the labeled case and rigid-body transformations. For more discussion on these points, and a deeper comparison of the different methods, see, for example, the reviews by Green et al. (2010) and Mardia and Nyirongo (2012).
The paper is structured as follows: in Section 2 we briefly review the model of Green and Mardia (2006) and introduce our generalization of the model to full similarity transformations, with details of the resulting conditional distribution for the scale factor c. We also develop a model which can handle two scaling factors, which we find is necessary to model the protein data in our applications. Section 3 gives two illustrative examples: in the first we consider the alignment of rat skulls, a data set which has been analyzed previously in the shape analysis literature. In the second example we introduce a novel application to the alignment of protein domains based on a representation using their secondary structure elements (beta strands and alpha helices). With this representation, some scaling may allow for improved alignments between proteins which have the same overall fold, but whose corresponding secondary structure elements may be of different lengths; examples include homologous proteins which have evolved from a common ancestor. We conclude the paper with a discussion in Section 4. Additional results and material are provided in the Appendix and in the supplementary material [Mardia et al. (2013)].
2. The model
Consider a pair of configurations of points in d dimensions, X and Y, where X consists of m points and Y of n points. The configurations X and Y can be represented by m × d and n × d matrices, respectively, where the rows of X are , j = 1, … , m, and the rows of Y are k = 1, … , n. In the model developed by Green and Mardia (2006) for unlabeled landmarks,
where μ represents the (hidden) true point locations in some space V of volume v, of which the observed configurations are noisy realisations; the variance of the noise terms is σ2Id. The ψ and η are labels indexing the mapping between the observed locations and μ. In particular, if ψj = ηk, then xj and yk are both generated by the same point of μ and are therefore regarded as matched. The mapping can be represented by a m × n matrix M with elements mjk = I(ψj = ηk), where I(·) is the indicator function; M is one of the parameters of interest about which to draw inference. Each point on X may be matched to at most one point on Y and vice versa. Therefore, each row and column of M may contain at most one nonzero entry. Note that the case of labeled landmarks is the special case where M is known.
2.1. Likelihood
For our full similarity transformation model, we consider a different formulation to that of Green and Mardia (2006). Rather than considering one configuration being transformed into the space of the other, we initially consider a more “symmetrical” formulation where both configurations are transformed into μ-space, which can be thought of as an “average space.” Specifically, we have
| (1) |
where c > 0 is a scale parameter, B is a d × d rotation matrix and τ1, are translation vectors; BT denotes the transpose of B. We have
and
where the ε represent errors in the observed point locations. Assuming Gaussian errors, so ε1j, ε2k ~ N(0, σ2 Id), results in model (1). (We note that other error structures, such as heavy-tailed distributions, could be used, and this is computationally feasible. This would allow for the possibility of outliers. However, this would have the undesirable effect of including matches which are far apart after transformation, so the standard notion of robustness is not meaningful for alignment.) We denote the density of the error terms by f (ε) = φ(ε/σ)/σd, where φ(·) is the standard normal distribution in d dimensions. We now derive the full likelihood of the observed data. The points on μ are regarded as uniformly distributed over the region V. Assuming boundary effects can be ignored, then the likelihood contribution of the unmatched X points is therefore
Similarly, the contribution of the unmatched Y points is
and the contribution of the matched points between X and Y is
We have
the density of ε1j − ε2k. Here, and . The complete likelihood, p(x, y; M, B, τ1, τ2, σ, c), is then
Also, , which results from a model in which the unobserved μ points are realizations of a homogeneous Poisson process over the region V [Green and Mardia (2006)]. This process is thinned so that each μ point generates an observed point of exactly one of the following forms: on X only, on Y only, on both X and Y, or not observed. The μ points generating an observation on X and Y are the matched points. The probabilities of the thinned process are parameterized by κ, which can be regarded as the propensity of points to be matched a priori. In particular, larger values of κ give a stronger prior preference to larger numbers of matched points.
Combining these terms, the joint model p(M, B, τ1, τ2, σ, c, x, y) is proportional to
This can be written as
| (2) |
where and . The parameter can be regarded as the variance of the errors in X-space, and the term in the exponent above is of the same form as the transformation of the Y points into X-space as in Green and Mardia (2006), with the scaling parameter c now included. Note that the exponent of c is now as opposed to nd, as would result from strictly following the original formulation in Green and Mardia (2006); we find our novel formulation provides much better performance when dealing with full similarity shape. [Note that, although Green and Mardia (2006) provided a general formulation which could deal with similarity transformations, they focused on rigid body transformations only in their practical applications; the implementation was not considered.] Intuitively, it is plausible to expect that the exponent of c should depend on the number of matched points L, rather than the fixed quantity nd, and that is the case with our formulation; this is a possible explanation for the improved performance.
2.2. Prior distributions and MCMC updates
Priors for the parameters A, τ, σc and M are of the same form as in Green and Mardia (2006). The rotation matrix A has a matrix-Fisher prior distribution, where and the parameter F0 is a d × d matrix. A is parameterized by one angle θ when d = 2, and by Eulerian angles, θ12, θ13, θ23, say, in the case d = 3. In our examples of Sections 3.1 and 3.2, we use a uniform prior on A, which is the special case where F0 is the d × d matrix of zeroes. A then has a uniform prior with respect to the invariant measure on SO(3), the Haar measure, where SO(3) is the special orthogonal group of all d × d rotation matrices. With our parameterization, this measure is cos(θ13)dθ12 dθ13 dθ23. For the translation vector τ, we have , where μτ is a mean vector and a covariance matrix, with Id the d × d identity matrix. For the noise parameter σc, we have , where . The matching matrix M is parameterized by κ > 0, with as described above.
We perform inference by generating samples from the posterior distribution (2) using MCMC. Updates for the parameters A, τ, σ and M take the same form as in Green and Mardia (2006), with the necessary adjustments being made to the various terms to include the scale factor c where appropriate. We now concentrate on the scale parameter c.
From (2), the conditional distribution of c is proportional to
| (3) |
where is the number of matched points. Adopting a gamma prior on c with parameters αc and λc, so that , we have the conditional distribution
| (4) |
where and
This distribution is a member of the generalized exponential family of distributions introduced by Lye and Martin (1993). In particular, it is in the form of the generalized gamma distribution of Creedy and Martin (1994), who used these distributions for modeling the stationary distribution of prices in economic models. This generalized gamma distribution has the form
| (5) |
for c > 0, where ζi, i = 1, … , 4 are parameters and η is a constant. Here we have the special case ζ4 = 0 in (5), which we shall denote as the halfnormal-gamma distribution. We are not aware of other work which considers this particular distribution or methods to simulate from it. We use a Metropolis step, and also devise an acceptance-rejection algorithm, details of which are in the supplementary material [Mardia et al. (2013)]. Note that the choice of a gamma prior led to conjugacy, since both the likelihood term in (3) and the conditional posterior for c are of halfnormal-gamma form; therefore, our acceptance-rejection method can be used to generate exact samples from this full conditional distribution. In our applications, we have used the Metropolis method to perform updates for c, which we give details of here. A proposal value c′ is generated, given the current value c, from the distribution
where
and is the mode of the conditional distribution (4). The acceptance probability for the Metropolis step is
The choice of proposal distribution is motivated by a general principle of normal approximations to members of the exponential family of distributions. Details are given in the Appendix, where, in particular, we show ω2 to be an approximate variance for the halfnormal-gamma conditional distribution of c under such a normal approximation. The success of the Metropolis method will depend on how well the proposal distribution approximates the target distribution. Hence, in situations where this normal approximation is less adequate, the acceptance-rejection method may be more efficient. However, we find the Metropolis method is perfectly adequate for our examples (where the configurations have a relatively small numbers of points) and as such is used throughout.
2.3. The two-scale model
We now develop a model which allows for more than one scaling parameter, motivated by our protein folding applications in Section 3.2. Suppose there are two sets of points, groups 0 and 1, say, with the points in each group subject to different transformations.We assume that matched points, where mjk = 1, are from the same group. Introduce class labels , j = 1, … , m, to denote the group of point xj, and likewise for the Y points. For group 0 we have
and
and similarly for the group 1 points. Let m0 and n0 denote the number of X and Y points, respectively, in group 0, and similarly for m1 and n1. Also let L0 and L1 be the number of matched points in group 0 and 1, respectively. Using similar arguments to those in Section 2.1, the joint model p(M, A, τ0, τ1, σc0, σc1, c0, c1, x, y) is proportional to
where and , and likewise for group 1 parameters. We assume that both groups have the same rotation ; if there is no translation (as in our protein applications in Section 3.2), this assumption corresponds to a model where the entire configurations are first rotated by A, before the appropriate scaling is applied to each individual element. This is exactly the behavior we require in the protein alignment applications of Section 3.2 when using our representation of protein secondary structure. Assuming that the priors for the scale and noise parameters are independent and have the same form as previously, then the updates for the Markov chain have the same form, with the relevant updates for the transformation parameters for each group naturally depending on only the points in that group. Additionally, we also propose a switch of the class labels at each iteration of the chain. For identifiability of the groups, we set c1 > c0.
3. Applications
3.1. Rat growth (labeled landmarks)
In growth data, the interest is to assess changes in shape over time. Here, size is a key concept, since growth leads to an increase in the object’s overall size, while its shape may remain the same. Hence, scaling information is highly relevant and must be taken into account during the alignment process.
We illustrate our method on data relating to the growth of a rat’s skull. The data are described in Bookstein [(1991), page 67] and the references therein, and have been analyzed by many other authors including Kent et al. (2001), Kent and Mardia (2002) and Kenobi, Dryden and Le (2010). The data consist of m = 8 landmark locations in d = 2 dimensions on the skulls of 21 laboratory rats measured at 8 timepoints between the ages of 7 and 150 days. The correspondence between landmarks is known, hence, this is an example of labeled shape analysis. Since the measurements are on the same rat at different ages, we would expect clear differences in the size of the rat and, hence, there may be a change in scale, as well as possible changes in shape. The real interest is in changes in shape over time, but the configurations from each timepoint must first be registered by removing the information not relating to shape. Since the rat will grow over time, it is necessary to remove size information and, hence, the full similarity transformations must be used in the registration.
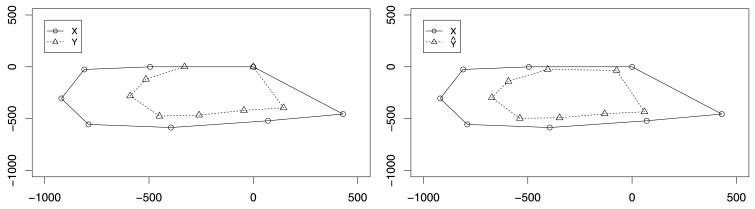
To highlight the need to include scaling in the alignment, we first consider using only a rigid-body transformation. In Figure 1 we see the initial configurations of the rat at the first and last time point, and the registered configurations using only rotation and translation as in the original method of Green and Mardia (2006). Here, the need for scaling is evident when comparing the fit to that obtained by using the full similarity transformation (Figure 2, bottom right).
Fig. 1.
Pairwise alignment between the rat configurations at timepoints 1 and 8 using only rotation and translation. The left panel shows the unregistered configurations, and the right panel the registered configurations; the need for scaling is clearly apparent.
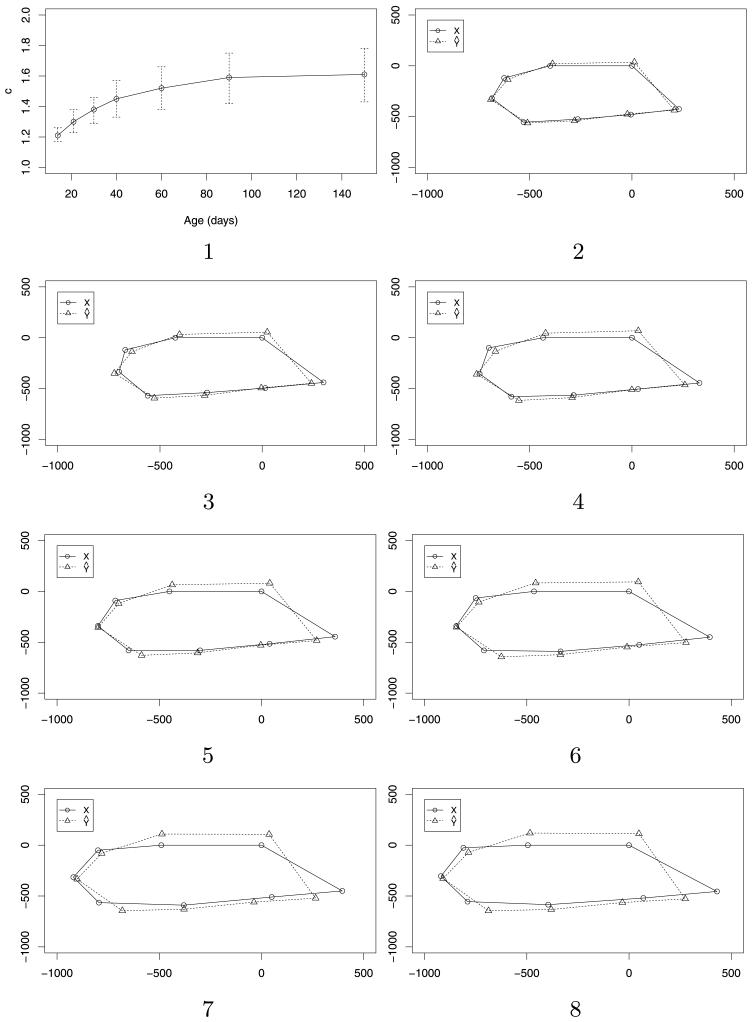
Fig. 2.
Pairwise alignments between the rat configurations at timepoints 2 to 8 and timepoint 1. In panel 1, the posterior medians for the scale factor c are plotted against the age of the rat, together with 95% posterior intervals. Panels 2 to 8 show the corresponding superpositions, ordered chronologically, with panel 2 showing the alignment between timepoints 2 and 1 and so on; in each case the dashed line represents the estimated superposition of the skull at the first timepoint onto the skull at the later timepoint (solid line).
We illustrate our method of full similarity shape alignment on one rat [labeled 1 in Bookstein (1991)] by comparing the shape at timepoints 2 to 8 with the shape at the first timepoint. We set a diffuse prior on the translation τ, with μτ equal to the difference in centroids and στ = 1000. We use an exponential prior for c with mean 1, and set α = 1 and β = 8, but find that the results are robust to these settings for α and β. In each case, we denote the younger rat configuration by Y and the older one by X.
Panel 1 of Figure 2 shows the posterior median of the scale factor c from each of the seven pairwise alignments of the youngest rat configuration with the older ones, together with a 95% posterior interval. Here we clearly see an initially rapid increase in the scale factor, slowing as the rat gets older. Panels 2 to 8 show the corresponding superpositions of the younger rat configuration () onto the older one (X), with the transformation obtained using the posterior mean estimates of A, τ and c. As well as an increase in size, there is also evidence of a change in shape, as seen by the progressively looser fits as the rat gets older. In particular, the skull becomes longer and thinner as the rat gets older.
3.2. Aligning protein domains
3.2.1. Proteins and secondary structure
We now consider an application to the alignment of protein domains. A protein is a chain of amino acid residues, and there are 20 different amino acid types. An amino acid consists of a structure common to all amino acid types, plus an additional side-chain structure which determines which of the 20 types it is. In particular, every amino acid contains an alpha-carbon (Cα) atom, and one possible representation of protein shape is the configuration of Cα atoms. Indeed, the first statistical work involving 3-d protein data in bioinformatics began with Wu et al. (1998), who used the alpha-carbon (Cα) atom of each amino acid residue as a landmark location.
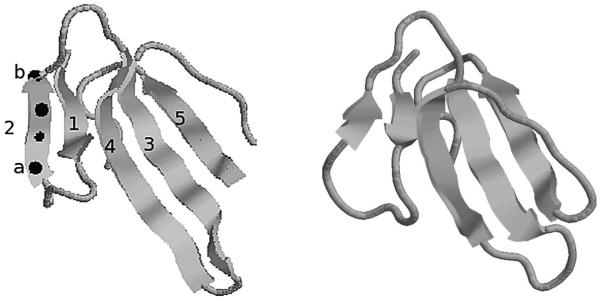
We use a representation based on the secondary structure elements of a protein. At the secondary structure level, a protein can be represented in terms of β strands and α helices (the two main secondary structure elements), which are themselves sub-chains of amino acid residues. The spatial arrangement of these elements, together with their connectivity, determine the fold of the protein, which is crucial to the biological activity of the protein. An example is shown in the left panel of Figure 3, the domain 2VLWA00 which we use in our examples below. The arrows represent beta strands, which are labeled 1–5 to indicate the sequence order in which they appear in the chain, each made up of a number of amino acid residues. For illustration, we have shown the positions of the Cα atoms of each residue on the strand labeled 2, represented by the dark spheres (not to scale); this particular strand has 4 residues and hence 4 Cα atoms. The beta strands are joined together by further regions of the amino acid chain, known as loops, represented here by the thin strings. For a thorough introduction to protein secondary structure, see, for example, Branden and Tooze (1999), Chapter 2.
Fig. 3.
Left: the domain 2VLWA00. The domain consists of 5 beta stands, labeled 1–5 to denote their sequence order in the chain. The locations of the Cα atoms (the dark spheres) from strand 2 are shown for illustration; this strand has 4 residues and hence 4 Cα atoms. Right: the domain 1FASA00.
One possible approach is to represent an element by the centroid of the Cα atoms from the residues of the element. The protein would then be reduced to a configuration of points, with each point representing the centroid of one element. However, applying scaling to this representation would also scale the distances between secondary structure elements in the packing arrangement of the protein. This is not satisfactory since these distances should be preserved. Where scaling is really required is in the comparison of the lengths of the elements. Two proteins sharing the same fold may have a very similar spatial arrangement of secondary structure elements, but the lengths of the elements may be longer in one than the other. Hence, we consider an approach using vectors to represent secondary structure elements, where each distinct element is represented by a vector from the origin to a single point. Scaling a configuration then only alters the length of each vector. The vector representation is found by taking the difference between the start and end points of the principal axis through the element, found using the method described in Taylor, Thornton and Turnell (1983) as follows. For any particular element (a beta strand say), the locations of the Cα atoms are taken to form a data cloud in three dimensions, and the principal axis (essentially the first principal component) is calculated. The start and end points of each element are then found by orthogonally projecting the Cα atom of the first and last residues onto this axis; the difference between these two points is then the point (vector) representing the element. For example, relating to Figure 3, to find the point representing the strand labeled 2, the principal axis through the 4 Cα atoms is first found. The start point of the strand is then found by projecting the Cα atom from the first residue of the element (labeled a) onto this axis; similarly, the end point of the strand is found by projecting the Cα atom from the last residue of the element (labeled b) onto the axis. The difference between the end and start points is then the vector representing this strand. In this example, there are 5 strands and, hence, there will be 5 points in total representing the protein, each found using the procedure above. Notationally, we represent the start point of the jth element of one protein by x1j and the end point by x2j. The jth row of configuration X is then xj = x2j − x1j, with a similar definition for the kth row of the second protein, Y, say, yk.
To address the particular challenges faced in the protein examples, we make two alterations to the methodology used in the paper thus far. First, the ordering of the secondary structure elements is important, as proteins which evolve from a common ancestor do so via the insertion/deletion of amino acid residues, and ultimately possibly secondary structure elements. As such, the parts which are conserved/common between two proteins will be placed in the same order relative to each other. Hence, we only allow proposed updates to the matching matrix M which preserve the sequence order of the elements. Second, in contrast to traditional applications in shape analysis, there is no reason why we should expect a single global scaling factor to be appropriate, since different pairs of secondary structure elements may require different scaling. Therefore, we propose a model with two scaling factors, which are sufficient to provide a good fit to the data in our examples, as each configuration has only a relatively small number of points (a maximum of ten). This model could be readily extended to handle a general number of scalings, which may be required for configurations with a larger number of points.
3.2.2. Illustrative examples
We illustrate this approach using 3 protein domains each consisting of beta strands: 2VLWA00, 1FASA00 and 1M9ZA00, which are classified in the same superfamily (CATH code 2.10.60.10) in the CATH database [Orengo et al. (1997)]; the domain names refer to their respective CATH identification labels. Since they are classified in the same CATH superfamily, they have the same fold and, hence, the domains should possess a high degree of structural similarity. However, the individual strands will not necessarily have the same length, so some scaling may be required to produce a good alignment of the individual structural elements (points). We provide two examples, namely, the domain 2VLWA00 aligned with each of the domains 1FASA00 and 1M9ZA00.
Our first example is the pair of domains 2VLWA00 (configuration X) and 1FASA00 (configuration Y), each of which consists of five beta strands; the structures are shown in Figure 3. We used the settings α = β = 1 throughout this section for the prior of σ−2. For the scale factor c, we have an exponential prior with the mean parameter taken as 1 (αc = 5, λc = 5) and we use κ = 100,000. We do not allow for translation, since translation is removed when taking the difference between start and end points of an element. The matches obtained and their respective probabilities are given in Table 1. We see that each pair of points matches with high probability. The posterior median of c0 is 1.06, with 95% posterior interval (0.75, 1.56), and the posterior median of c1 is 1.64, with 95% posterior interval (1.38, 2.14). These results highlight the ability of the model to capture the different scaling required for different elements, which we now explore further.
Table 1. Matches from an alignment of the secondary structures of 2VLW (X) and 1FAS (Y).
| Match | x | y | prob | ∥x∥/∥y∥ | prob (no scale) | prob (global scale) | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.989 | 2.41 | 0.869 | 0.983 | 0.17 |
| 2 | 2 | 2 | 0.945 | 2.70 | 0.701 | 0.958 | 0.15 |
| 3 | 3 | 3 | 0.968 | 1.62 | 0.347 | 0.965 | 0.08 |
| 4 | 4 | 4 | 0.980 | 1.59 | 0.414 | 0.970 | 0.10 |
| 5 | 5 | 5 | 0.924 | 1.02 | 0.672 | 0.512 | 0.98 |
Column 5 of Table 1 shows the length ratios of the matched points prior to any scaling. This suggests that some scaling is certainly necessary, and further still that varying amounts of scaling may be necessary for different pairs of points to provide the best fit to the data. We now consider the improvement in fit offered by first introducing one scaling factor, and the further improvement offered by adding a second scaling factor. The matches obtained using no scaling and one global scale factor are shown in columns 6 and 7 of Table 1, respectively. For the case of one global scale factor, where the posterior median of c is 1.54, with 95% posterior interval (1.25, 1.85), the model is clearly not sufficient to capture all the matches with high probability. In particular, the match between x5 and y5 has a much lower posterior probability of 0.512; this can be explained due to the ratio of lengths being 1.02, in comparison to the other ratios, which are 1.59 and above. However, the inclusion of a scaling parameter offers a clear improvement over the case where no scaling is applied whatsoever, as seen by the substantially lower matching probabilities obtained when no scaling is used.
Looking purely at the length ratios of the matched points, one might consider whether a model with three groups might be necessary. Column 8 of Table 1 shows the empirical proportion of the iterations that each pair of matched points were in group 0 (the group with the smaller scale factor), say. These proportions suggest that the points are separated into two clear groups, with the match between x5 and y5 being accounted for in its own group, and that group 1 can accommodate the other matches; this evidence, together with the posterior probabilities, suggests that two scaling factors are sufficient in this case. The model could readily accommodate more scaling factors, but given the small number of points in this example, this appears excessive and risks overfitting.
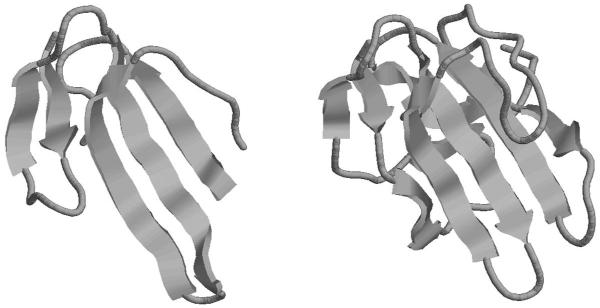
To illustrate further the power of the unlabeled method, we now consider an example with an unequal number of points (secondary structure elements). The domains are 2VLWA00 from the previous example (configuration X) which has five beta strands, and 1M9ZA00 (configuration Z) which has ten beta strands; the structures are shown in Figure 4. Even with the full possible matching of five points, the matching between individual strands is not obvious. (In the previous example, there is only one possible matching matrix M consistent with five matches, due to the ordering constraint.) The posterior matches in this example, for the cases of two scaling factors and one global scaling factor, are shown in Table 2. For the first case, five matches are found with high posterior probabilities. The empirical proportion of the iterations each match spent in group 0 is again shown, in column 7 of Table 2. As in the first example, the model clearly separates the matches into two groups, with the match requiring a smaller scaling factor being accommodated in group 0; the matching probabilities for the global scale model show that this match is neglected when only one scaling factor is used. We note that the beta strand represented by x5 is in group 0 in both cases; this strand is consistently smaller in domain 2VLWA00 than in the other domains we have considered. This evidence again suggests that one global scale factor is not sufficient to capture all possible matches with high probability, but that a two-scale model is adequate.
Fig. 4.
Left: the domain 2VLWA00, which has 5 beta strands, from the first example. Right: the domain 1M9ZA00, which has 10 beta strands.
Table 2. Matches from an alignment of the secondary structures of 2VLW (X) and 1M9Z (Z), for the cases of two scaling factors and one global scaling factor.
| Match | x | z | prob (two scale) | prob (global scale) | ∥x∥/∥z∥ | |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.990 | 0.975 | 1.29 | 0.07 |
| 2 | 2 | 4 | 0.988 | 0.980 | 1.11 | 0.04 |
| 3 | 3 | 5 | 0.997 | 0.985 | 1.47 | 0.04 |
| 4 | 4 | 6 | 0.990 | 0.981 | 1.19 | 0.06 |
| 5 | 5 | 9 | 0.957 | 0.179 | 0.81 | 0.99 |
3.3. Sensitivity to prior settings and computational issues
The role of and sensitivity to the parameters κ and β were discussed in Green and Mardia (2006); higher values of κ encourage more matches, and β is an inverse scale parameter for the noise variance, with larger values leading to generally fewer matches. Here, we concentrate on the sensitivity of our results to the prior settings for the scaling parameters. We consider three cases, namely, αc = 0.1, 5.0, 10.0; in each case, we set λc = αc, giving a prior mean of 1, with larger values of αc corresponding to a smaller prior variance. The matches obtained for our first protein example, the pair 2VLW-1FAS, are shown in Table 3. The effect on the parameters c0 and c1 can be seen in Table 4.
Table 3. Matches from an alignment of the secondary structures of 2VLW (X) and 1FAS (Y) for three different prior settings.
| Match | x | y | prob (case 1: αc = 0.1) | prob (case 2: αc = 5) | prob (case 3: αc = 10) |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.989 | 0.989 | 0.981 |
| 2 | 2 | 2 | 0.954 | 0.945 | 0.935 |
| 3 | 3 | 3 | 0.933 | 0.968 | 0.955 |
| 4 | 4 | 4 | 0.950 | 0.980 | 0.967 |
| 5 | 5 | 5 | 0.783 | 0.924 | 0.947 |
Table 4. Posterior summaries of c0 and c1 for 2VLW (X) and 1FAS (Y) for three different prior settings.
| Parameter | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| c 0 | 1.14 (0.76, 1.74) | 1.06 (0.75, 1.56) | 1.06 (0.75, 1.47) |
| c 1 | 1.71 (1.45, 3.30) | 1.64 (1.38, 2.14) | 1.61 (1.34, 1.91) |
For the second protein example, the pair 2VLW-1M9Z, the matches obtained are shown in Table 5 and the effect on the parameters c0 and c1 can be seen in Table 6. For both pairs, the matching probabilities are generally lower in case 1 (when the prior information on c is weak), although the overall alignment is still good. Results are robust for larger values of αc, and further results (not shown) show that the results remain robust for even larger values of αc = λc, with the posterior values of c moving slightly closer to the prior mean of 1; this is to be expected as the prior variance gets smaller, resulting in a more informative prior. However, the results change by only a small amount, suggesting that the data carry a lot of information.
Table 5. Matches from an alignment of the secondary structures of 2VLW (X) and 1M9Z (Y) for three different prior settings.
| Match | x | y | prob (case 1) | prob (case 2) | prob (case 3) |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.958 | 0.990 | 0.981 |
| 2 | 2 | 4 | 0.871 | 0.988 | 0.907 |
| 3 | 3 | 5 | 0.919 | 0.997 | 0.920 |
| 4 | 4 | 6 | 0.936 | 0.990 | 0.957 |
| 5 | 5 | 9 | 0.882 | 0.957 | 0.923 |
Table 6. Posterior summaries of c0 and c1 for 2VLW (X) and 1M9Z (Y) for three different prior settings.
| Parameter | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| c 0 | 0.82 (0.68, 1.21) | 0.82 (0.70, 1.15) | 0.83 (0.70, 1.15) |
| c 1 | 1.18 (1.08, 3.13) | 1.17 (1.09, 1.41) | 1.17 (1.08, 1.37) |
The implementation of our method does not come with a particularly high computational cost. The most computationally extensive aspect of our examples, the unlabeled two-scale model, was implemented in C++ and ran in 10 seconds on a desktop PC with a 3.10 GHz processor.
4. Discussion
In this paper we have presented a Bayesian model for the pairwise alignment of two point configurations under full similarity transformation. The fully Bayesian approach allows for uncertainty in the transformation parameters to be correctly propagated, which is a key conceptual difference between our method and others. We note that isotropic errors have been assumed throughout, but this has been standard practice in shape analysis [Dryden and Mardia (1998)]; Theobald and Wuttke (2006) have considered nonisotropic errors in the case of labeled landmarks. Our emphasis here has been on both the labeled and unlabeled cases.
The work presented here has concentrated on the pairwise alignment of two configurations. Ruffieux and Green (2009) generalized the method of Green and Mardia (2006) to develop a fully Bayesian model for the alignment of multiple configurations under rigid body transformations; a natural extension might therefore be to incorporate our methodology developed in this paper within their model.Mardia et al. (2011) addressed the problem of multiple alignment under rigid body transformations by embedding a pairwise alignment method within a multi-stage algorithm, and their methodology could easily be adapted to incorporate the extension to the full similarity shape introduced here.
Finally, an important part of our work is the novel application to the alignment of proteins, using a representation based on secondary structure elements. This application required the development of our model to handle more than one scaling factor, since different elements may require different scaling. The use of one global scaling factor has been standard practice in shape analysis [Dryden and Mardia (1998)]. We find that two scaling factors is sufficient for our needs; our proteins have only a small number of points, and including more scaling parameters would come at the cost of overfitting, which our results suggest is unnecessary. However, our method could be readily extended to include more scaling factors as needed. This would introduce issues such as model choice and comparison, and such matters are left for future work.
Supplementary Material
Acknowledgments
Fallaize acknowledges EPSRC funding for his research studies. We thank Peter Green for helpful comments, and the Editor, Associate Editor and anonymous referee for their comments which helped to improve a previous version of the paper.
APPENDIX: EXPONENTIAL FAMILY AND NORMAL APPROXIMATIONS
A.1. A normal approximation
Here we give a normal approximation for the exponential family of distributions, motivated by our requirement for an efficient proposal distribution for the Metropolis method described in Section 2.2. Consider the curved exponential family for a continuous random variable X with density
The second log derivative with respect to x is
We assume that the family is convex so that there is a single mode at and uniformly. Then for large a1(θ), we postulate that
| (6) |
where is the mode of the distribution. A heuristic explanation follows intuitively using the exchangeability of x and θ. For the maximum likelihood estimate of θ, it is well known that for a large sample size n we have , where I (θ) is the Fisher information, , and l(θ; x) is the log-likelihood function. Consider now interchanging the roles of x and θ, treating θ as a variable and x as a parameter. Since x and θ are exchangeable by conjugacy, we may write
which is equivalent to (6) and hence gives a heuristic demonstration of the result. The validity of this approximation is confirmed below in various cases where a normal approximation is well known. [Note that in the case of the normal distribution with mean μ and variance σ2 the approximation is exact as required, with X ~ N(μ, σ2).]
A.1.1. Gamma
Consider the gamma distribution with density . We have and the mode is , giving the approximation . The standard approximation is , so the two are approximately the same for large α.
A.1.2. Von Mises
For the von Mises distribution, we have f (x, μ) = K × exp{κ cos(x − μ)}, 0 < x, μ < 2π. The mode is ; thus, , and the approximation is , which is a well-known normal approximation to the von Mises distribution [Mardia and Jupp (2000), page 38].
A.1.3. Halfnormal-gamma
For the halfnormal-gamma distribution, we have
and
leading to an approximate variance given by . Recall that the mode is . We therefore have the approximation . We find the approximation to be better for larger r and δ; even for small r, the approximation is good for positive values of δ, but less good for relatively large negative values of δ. Further details are given in the supplementary material.
Contributor Information
Kanti V. Mardia, Department of Statistics, University of Leeds, Leeds, LS2 9JT, United Kingdom, K.V.Mardia@leeds.ac.uk, stuart@maths.leeds.ac.uk
Christopher J. Fallaize, School of Mathematical Sciences, University of Nottingham, Nottingham, NG7 2RD, United Kingdom, Chris.Fallaize@nottingham.ac.uk
Stuart Barber, Department of Statistics, University of Leeds, Leeds, LS2 9JT, United Kingdom, K.V.Mardia@leeds.ac.uk, stuart@maths.leeds.ac.uk.
Richard M. Jackson, Institute of Molecular and Cellular Biology, University of Leeds, Leeds, LS2 9JT, United Kingdom R.M.Jackson@leeds.ac.uk
Douglas L. Theobald, Department of Biochemistry, Brandeis University, 415 South St, Waltham, Massachusetts 02454-9110, USA, dtheobald@gmail.com.
REFERENCES
- Bookstein F. Morphometric Tools for Landmark Data: Geometry and Biology. Cambridge University Press; Cambridge: 1991. [Google Scholar]
- Branden C, Tooze J. Introduction to Protein Structure. 2nd ed. Garland; New York: 1999. [Google Scholar]
- Creedy J, Martin VL. A model for the distribution of prices. Oxford Bulletin of Economics and Statistics. 1994;56(1):67–76. [Google Scholar]
- Dryden IL, Hirst JD, Melville JL. Statistical analysis of unlabeled point sets: comparing molecules in chemoinformatics. Biometrics. 2007;63:237–251. doi: 10.1111/j.1541-0420.2006.00622.x. [DOI] [PubMed] [Google Scholar]
- Dryden IL, Mardia KV. Statistical Shape Analysis. Wiley; Chichester: 1998. [Google Scholar]
- Green PJ, Mardia KV. Bayesian alignment using hierarchical models, with applications in protein bioinformatics. Biometrika. 2006;93(2):235–254. [Google Scholar]
- Green PJ, Mardia KV, Nyirongo VB, Ruffieux Y. Bayesian modelling for matching and alignment of biomolecules. In: O’Hagan A, West M, editors. The Oxford Handbook of Applied Bayesian Analysis. Oxford University Press; Oxford: 2010. pp. 27–50. [Google Scholar]
- Kenobi K, Dryden IL. Bayesian matching of unlabelled point sets using Procrustes and configuration models. 2010 Available at http://arxiv.org/pdf/1009.3072.
- Kenobi K, Dryden IL, Le H. Shape curves and geodesic modelling. Biometrika. 2010;97(3):567–584. [Google Scholar]
- Kent JT, Mardia KV. Modelling strategies for spatial-temporal data. In: Lawson AB, Denison DGT, editors. Spatial Cluster Modelling. Chapman and Hall; London: 2002. pp. 213–226. [Google Scholar]
- Kent JT, Mardia KV, Taylor CC. Technical Report. University of Leeds; 2010. Matching unlabelled configurations and protein bioinformatics. [Google Scholar]
- Kent JT, Mardia KV, Morris RJ, Aykroyd RG. Functional models of growth for landmark data. In: Mardia KV, Aykroyd RG, editors. Proceedings in Functional and Spatial Data Analysis. Leeds University Press; Leeds: 2001. pp. 109–115. [Google Scholar]
- Lye J, Martin VL. Robust estimation, nonnormalities and generalized exponential distributions. Journal of the American Statistical Association. 1993;88:261–267. [Google Scholar]
- Mardia KV, Jupp PE. Directional Statistics. Wiley; Chichester: 2000. [Google Scholar]
- Mardia KV, Nyirongo VB. Bayesian hierarchical alignment methods. In: Hamelryck T, Mardia KV, Ferkinghoff-Borg J, editors. Bayesian Methods in Structural Bioinformatics. Springer; New York: 2012. pp. 209–232. [Google Scholar]
- Mardia KV, Nyirongo VB, Fallaize CJ, Barber S, Jackson RM. Hierarchical Bayesian modeling of pharmacophores in bioinformatics. Biometrics. 2011;67:611–619. doi: 10.1111/j.1541-0420.2010.01460.x. [DOI] [PubMed] [Google Scholar]
- Mardia KV, Fallaize CJ, Barber S, Jackson RM, Theobald DL. Supplement to “Bayesian alignment of similarity shapes”. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orengo CA, Michie AD, Jones DT, Swindells MB, Thornton JM. CATH: A hierarchic classification of protein domain structures. Structure. 1997;5:1093–1108. doi: 10.1016/s0969-2126(97)00260-8. [DOI] [PubMed] [Google Scholar]
- Rodriguez A, Schmidler S. Bayesian protein structural alignment. Annals of Applied Statistics. 2010 doi: 10.1214/14-AOAS780. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruffieux Y, Green PJ. Alignment of multiple configurations using hierarchical models. Journal of Computational and Graphical Statistics. 2009;18(3):756–773. [Google Scholar]
- Schmidler SC. Fast Bayesian shape matching using geometric algorithms. In: Bernardo JM, Bayarri J, Berger JO, Dawid AP, Heckerman D, Smith AF, West M, editors. Bayesian Statistics. Vol. 8. Oxford University Press; Oxford: 2007. pp. 471–490. [Google Scholar]
- Srivastava A, Jermyn IH. Looking for shapes in two-dimensional cluttered point clouds. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2009;31(9):1616–1629. doi: 10.1109/TPAMI.2008.223. [DOI] [PubMed] [Google Scholar]
- Taylor WR, Thornton JM, Turnell WG. An ellipsoidal approximation of protein shape. Journal of Molecular Graphics. 1983;1(2):30–38. [Google Scholar]
- Theobald DL, Wuttke DS. Empirical Bayes hierarchical models for regularizing maximum likelihood estimation in the matrix Gaussian Procrustes problem. Proceedings of the National Academy of Sciences. 2006;103(49):18521–18527. doi: 10.1073/pnas.0508445103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkinson DJ. Discussion to Schmidler. 2007. 2007. [Google Scholar]
- Wu TD, Schmidler SC, Hastie T, Brutlag DL. Regression analysis of multiple protein structures. Journal of Computational Biology. 1998;5(3):585–595. doi: 10.1089/cmb.1998.5.585. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.