EFFECTIVELY SELECTING A TARGET POPULATION FOR A FUTURE COMPARATIVE STUDY

Abstract

When comparing a new treatment with a control in a randomized clinical study, the treatment effect is generally assessed by evaluating a summary measure over a specific study population. The success of the trial heavily depends on the choice of such a population. In this paper, we show a systematic, effective way to identify a promising population, for which the new treatment is expected to have a desired benefit, utilizing the data from a current study involving similar comparator treatments. Specifically, using the existing data, we first create a parametric scoring system as a function of multiple multiple baseline covariates to estimate subject-specific treatment differences. Based on this scoring system, we specify a desired level of treatment difference and obtain a subgroup of patients, defined as those whose estimated scores exceed this threshold. An empirically calibrated threshold-specific treatment difference curve across a range of score values is constructed. The subpopulation of patients satisfying any given level of treatment benefit can then be identified accordingly. To avoid bias due to overoptimism, we utilize a cross-training-evaluation method for implementing the above two-step procedure. We then show how to select the best scoring system among all competing models. Furthermore, for cases in which only a single pre-specified working model is involved, inference procedures are proposed for the average treatment difference over a range of score values using the entire data set, and are justified theoretically and numerically. Lastly, the proposals are illustrated with the data from two clinical trials in treating HIV and cardiovascular diseases. Note that if we are not interested in designing a new study for comparing similar treatments, the new procedure can also be quite useful for the management of future patients, so that treatment may be targeted towards those who would receive nontrivial benefits to compensate for the risk or cost of the new treatment.

1. INTRODUCTION

In comparing a new treatment with a control via a randomized clinical trial, the assessment of the treatment efficacy is usually based on an overall summary measure over a specific study population. To increase the chance of success of the study, it is important to choose an appropriate study population for which the new treatment is expected to have non-trivial overall benefits that compensate for its risks and/or costs. In this paper we are interested in developing strategies which identify such a patient population using the data from a current study for comparing similar treatments. Even when we are not interested in designing another new study for comparing similar treatments, the new proposal provides a systematic, efficient procedure for the management of future patients, so that treatment may be targeted towards those who would receive nontrivial benefits to compensate for the risk or cost of the new treatment.

As an example, one of the very first trials to evaluate the added value of a potent protease inhibitor, indinavir, for HIV patients, was conducted by the AIDS Clinical Trials Group (ACTG). This randomized, double-blind study, ACTG 320 (Hammer et al., 1997), compared a three-drug combination (indinavir, zidovudine and lamivudine) with the standard two-drug combination (zidovudine and lamivudine). There were 1156 patients enrolled in the study. One of the endpoints was the CD4 count, measured 24 weeks after randomization. The overall estimated mean difference between the new treatment and control over the entire study population was 81 cells/mm³. Although the overall efficacy from the three-drug combination group is highly statistically significant, the new therapy may not work for all future patients. Moreover, there are nontrivial toxicities and serious concerns about the development of protease inhibitor resistance mutations. For instance, suppose that having an expected treatment benefit representing a week 24 CD4 count increase of 100 cells/mm³ relative to the control would be sufficient to compensate for the costs and risks of using the new therapy. The question, then, is how to identify such a subpopulation efficiently via the patient’s “baseline” covariates.

Various novel quantitative methods have been proposed to deal with the problem of heterogeneous treatment effects. For cases with a single covariate, Song and Pepe (2004), assuming a monotone relationship between the covariate and the treatment difference, proposed a procedure to obtain an optimal division of the population for determining which future patients should receive the treatment or control. Song and Zhou (2011) generalized this method for censored event time data. Janes et al. (2011) gave a practical guidance on using the marker-by-treatment predictiveness curves for treatment selection. Moreover, Bonetti and Gelber (2000, 2005) stratified patients utilizing a moving average procedure to obtain subject-specific nonparametric estimates for the treatment difference. For cases with multiple covariates, Cai et al. (2011) proposed a systematic two stage method for personalized treatment selection using a parametric scoring system for estimating the subject-specific treatment difference, followed by a nonparametric smoothing technique at the second stage. However, it is not clear how to utilize their procedure to efficiently identify a group of future patients who would have a desired overall treatment benefit. Moreover, there are no procedures available in the literature for comparing different scoring systems for treatment differences with multiple covariates.

Note that if the scoring system is built using data from the control group only, one may not be able to effectively identify a target population which has a desirable overall treatment benefit. For example, high-risk patients may not necessarily experience the greatest benefit from a new treatment. Thus for the present problem, even when considering only a single covariate, a first step is to create a scoring system for estimating the treatment difference; one can then use such a system to effectively identify a target population. However, unlike the prediction problem in the one sample case, none of the existing procedures in the literature which use scores for estimating treatment differences can be utilized to directly evaluate the performance of competing scoring systems. This difficulty arises from the fact that each study subject was assigned to receive either the new treatment or control, but not both. That is, the treatment difference is not observable at an individual level. Therefore, it is not clear how to compare, at the patient level, the observed treatment difference to its predicted counterpart.

For the case of a single treatment group, Moskowitz and Pepe (2004) generalize the idea of positive predictive values (PPV) and negative predictive values to accommodate a single continuous covariate and a binary outcome, and propose a graphical method to summarize predictive accuracy. In this paper, we generalize the notion of PPV to handle the present problem of treatment selections with multiple baseline covariates. Specifically, we first generate various parametric or semi-parametric scoring systems for estimating the subject-specific treatment differences using baseline markers, and then select the “best” one among all the candidate models. Various criteria are utilized for model selection based on, for example, the concordance between the observed and expected treatment differences via a cross-validation procedure to avoid potentially bias due to overoptimism. We then show how to define a target patient population, which can be used to identify future patients who would benefit from the new treatment for the purpose of designing inclusion/exclusion criteria for enrollment in future clinical trials. Our procedure does not require the usage of nonparametric smoothing techniques, which can be quite unstable when the sample size is not large. Furthermore, when there is only a single pre-specified working model involved, we propose inference procedures after model fitting for the treatment differences over a range of score values. Lastly, we illustrate our methods using the data from the above HIV study as well as censored survival time data from a large cardiovascular trial to compare the efficacy of Angiotensin-converting-enzyme inhibitors (ACEi) to a conventional therapy for patients with stable coronary heart disease and preserved left ventricular function (Braunwald et al., 2004).

2. SELECTING THE TARGET SUBPOPULATION VIA A SCORING SYSTEM

Suppose that each subject in a comparative study was randomly assigned to one of two groups, denoted by G = 0 (control) or 1 (treatment). Let π_k = pr(G = k) for k = 0, 1. Let Z be the patient’s p-dimensional vector of baseline covariates, and Y_(k) be the response variable or a function thereof, if the subject had been assigned to Group k, k = 0, 1. For each subject, only Y = GY₍₁₎ + (1 − G)Y₍₀₎ can potentially be observed. Assume that a larger Y indicates a better clinical outcome. For ease of presentation, we first consider the non-censored case that for each subject, we can observe the triplet (Y, G, Z) completely.

Now, let μ_k(Z) = E(Y_(k)∣Z) be the expected response for patients in Group k, conditional on Z. Furthermore, let the treatment difference D(Z) = μ₁(Z) − μ₀(Z). The data, {(Y_i, G_i, Z_i); i = 1, …, n}, consist of n independent copies of (Y, G, Z). Suppose that D̂(Z) is an estimator for D(Z). Let Z⁰ be the covariate vector for a future patient randomly drawn from the same population of the current study. Also let $Y_{(k)}^0$ be the potential response of this patient if assigned to Group k, k = 0, 1. Consider the subgroup of subjects such that D̂(Z⁰) ≥ c, where c is some fixed constant. That is, this subgroup of subjects has an estimated treatment difference no less than c. Let AD(c) be the average treatment difference for this subgroup of subjects:

$$E\left((Y_{(1)}^0-Y_{(0)}^0)\mid \widehat{D}({\mathit{Z}}^0)\ge c\right),$$ (1)

where the expectation is with respect to $Y_{(k)}^0$ and Z⁰, and also {(Y_i, G_i, Z_i); i = 1, …, n}.

Note that AD(c) depends on the sample size n. The AD(c) can be estimated by

$$\widehat{\mathit{AD}}(c)=\frac{{\sum }_{i=1}^n{Y}_{i}I\{\widehat{D}({\mathit{Z}}_i)\ge c,G_i=1\}}{{\sum }_{i=1}^{n}I\{\widehat{D}({\mathit{Z}}_i)\ge c,G_i=1\}}-\frac{{\sum }_{i=1}^n{Y}_{i}I\{\widehat{D}({\mathit{Z}}_i)\ge c,G_i=0\}}{{\sum }_{i=1}^{n}I\{\widehat{D}({\mathit{Z}}_i)\ge c,G_i=0\}},$$ (2)

where I(·) is the indicator function. Note that $\widehat{\mathit{AD}}(c)$ may not be stable when c is in the upper tail of the distribution of D̂(Z⁰).

As a function of c, $\widehat{\mathit{AD}}(c)$ can be quite useful for identifying patients who can expect specific levels of benefit from the new treatment relative to the control. As an example, consider the ACTG 320 study discussed in the Introduction. For simplicity, let Y be the CD4 count at week 24 and Z be a vector consisting of two baseline covariates, log(CD4) and log₁₀(RNA). These two measures have been shown to be highly predictive of various clinical outcomes relevant to HIV disease. One may obtain D̂(Z) by the difference of two estimates μ̂₀(Z) and μ̂₁(Z) based on two separate additive linear regression models, as given in Table 1. The resulting score for estimating the treatment difference is given by

$$\widehat{D}(\mathit{Z})=-120.61+12.57\log (\mathrm{CD}4)+29.13{\log }_{10}(\mathrm{RNA}).$$

Table 1.

Estimated (Est) regression coefficients, their standard errors (SE) and p-values by fitting two separate linear regression models to the ACTG 320 data with week 24 CD4 as the response and log(CD4) and log₁₀(RNA) as the baseline covariates

Covariates	Two-drug			Three-drug
	Est	SE	p-value	Est	SE	p-value
Intercept	-17.04	24.13	0.48	-137.66	40.91	<0.01
log(CD4)	43.05	2.31	<0.01	55.62	3.83	<0.01
log10(RNA)	-9.98	4.05	0.01	19.16	6.85	0.01

Note that a patient with high baseline CD4 and RNA values is expected to benefit more from the new treatment. Figure 1(a) provides the estimated $\widehat{\mathit{AD}}(c)$ in (2) over a range of values c. As discussed in the Introduction, the new treatment, a three-drug combination, demonstrated an impressive overall efficacy benefit with regards to week 24 CD4 count. However, there were concerns about the cost of the new therapy, as well as the potential for toxicity and/or development of drug resistance. Suppose that, in order to compensate for such non-trivial risks, one would like to treat future patients whose anticipated benefit from the new treatment, relative to the two-drug combination, could be considered “clinically” significant. For example, a meaningful benefit may be defined as an overall CD4 count difference, between the two treatments, of 100 cells/mm³ at week 24. From Figure 1(a), $\widehat{\mathit{AD}}(77)=100$, thus this subset of patients would be composed of patients with Z⁰ such that D̂(Z⁰) ≥ 77.

Figure 1.

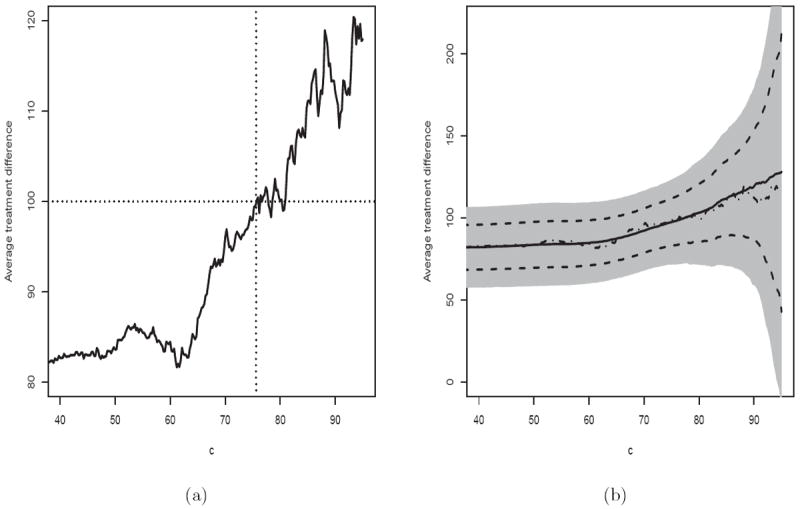
Estimated average treatment difference for patients with D̂(Z) ≥ c using the scoring system built with two baseline covariates, log(CD4) and log₁₀(RNA), for the ACTG 320 data. (a) Without cross-validation. (b) With cross-validation (Solid: point estimate with cross-validation; Dotted Dash: point estimate without cross-validation; Dashed: 95% pointwise confidence interval; Shaded: 95% simultaneous confidence interval).

Now, let us consider the case that the response variable may not be observed completely. For instance, let T be an event time and Y = I(T ≥ t₀), where t₀ is a specific time point of interest. Often T may be censored by a censoring variable C, which is assumed to be indeendent of T and Z given G. For each subject, the observable quantities are (X, Δ, G, Z), where X = min(T, C) and Δ = I(T ≤ C). The data, {(X_i, Δ_i, G_i, Z_i); i = 1, …, n}, consist of n independent copies of (X, Δ, G, Z). For this case, the AD(c) can be estimated by the difference in Kaplan-Meier survival probabilities, i.e.,

$$\widehat{\mathit{AD}}(c)=\prod _{t=0}^{t_0}\left\{1-\frac{{\sum }_{i=1}^{n}d{N}_{i,c}^{(1)}(t)}{{\sum }_{i=1}^n{Y}_{i,c}^{(1)}(t)}\right\}-\prod _{t=0}^{t_0}\left\{1-\frac{{\sum }_{i=1}^{n}d{N}_{i,c}^{(0)}(t)}{{\sum }_{i=1}^n{Y}_{i,c}^{(0)}(t)}\right\},$$ (3)

where $N_{i,c}^{(k)}(t)=I(X_i\le t,\widehat{D}({\mathit{Z}}_i)\ge c,G_i=k){\mathrm{\Delta }}_i$, and $Y_{i,c}^{(k)}(t)=I(X_i\ge t,\widehat{D}({\mathit{Z}}_i)\ge c,G_i=k)$, k = 0, 1; i = 1, …, n. Note that Π here denotes a product integral operator.

If one is interested in a global treatment contrast measure rather than t₀-year survival rates, the standard hazard ratio estimate may be utilized for building a scoring system. However, when the proportional hazards assumption is violated, it is not clear which parameter this model-based estimate would converge to (Kalbfleisch and Prentice, 1981; Lin and Wei, 1989; Xu and O’Quigley, 2000). The overall mean survival time is generally difficult to estimate well due to censoring. On the other hand, one may consider the restricted mean survival time up to a specific time point (Irwin, 1949; Andersen et al., 2004), say, τ₀, as an overall measure for quantifying survivorship. Note that this mean value is simply the area under the corresponding Kaplan-Meier curve, truncated at time τ₀. To this end, for the present problem, we let Y = min(T, τ₀). It is straightforward to show that the corresponding AD(c) can be estimated by

$$\widehat{\mathit{AD}}(c)={\mathit{\int }}_0^{{\tau }_0}\left[\prod _{s=0}^t\left\{1-\frac{{\sum }_{i=1}^{n}d{N}_{i,c}^{(1)}(s)}{{\sum }_{i=1}^n{Y}_{i,c}^{(1)}(s)}\right\}\right]\mathit{dt}-{\mathit{\int }}_0^{{\tau }_0}\left[\prod _{s=0}^t\left\{1-\frac{{\sum }_{i=1}^{n}d{N}_{i,c}^{(0)}(s)}{{\sum }_{i=1}^n{Y}_{i,c}^{(0)}(s)}\right\}\right]\mathit{dt},$$ (4)

using the fact that $E\{\min (T,{\tau }_0)\mid \widehat{D}({\mathit{Z}}^0)\ge c\}={\mathit{\int }}_0^{{\tau }_0}\mathrm{pr}(T>t\mid \widehat{D}({\mathit{Z}}^0)\ge c)\mathit{dt}$.

Given a particular scoring system, a plot like Figure 1(a) is useful for identifying the target patient population who would benefit from the new treatment at various levels of interest. However, it is possible that there are other scoring systems using baseline variables which could be better than the present one.

3. CREATING SCORING SYSTEM CANDIDATES

In this section, we discuss various models and variable selection procedures to build models for creating the scoring systems. We first consider the case that (Y, G, Z) is completely observed. A general approach for modeling the subject-specific treatment difference parametrically is to model the mean for each treatment group:

$${\mu }_k(\mathit{Z})=g_k({\mathit{\beta }}_k^{\prime }\mathit{h}(\mathit{Z})),$$ (5)

where h(Z) is a known vector function of Z with the first component being 1, β_k is an unknown vector of parameters, g_k is a given link function, and k = 0, 1. To estimate β_k, one may minimize a loss function L_k(β), which may be based on a likelihood or a residual sum of squares.

An alternative approach is to utilize a single model for both treatment groups:

$$E(Y\mid \mathit{Z},G)=g({\mathit{\beta }}^{\prime }\mathit{h}(G,\mathit{Z})),$$ (6)

where h(G, Z) is a known vector function of (G, Z) with the first component being 1, β is an unknown vector of parameters, and g is a given link function. Note that h(G, Z) may include G, Z, and G × Z interaction terms. In the presence of G × Z interaction terms, the results of variable selection procedures will depend on the coding of the treatment indicator G. To this end, we code treatment group 0 and treatment group 1 using -1 and +1, respectively. Again, one may obtain an estimator β̂ for β by minimizing a loss function L(β). Under this setting, D̂(Z) = g(β̂′ h(1, Z)) − g(β̂′ h(−1, Z)).

For Model (5) or (6), one may also use an estimation procedure for β with a built-in variable selection algorithm. For instance, for (6), let β̂_λ be a minimizer of

$$L(\mathit{\beta })+\mathrm{\lambda }{\Vert \mathit{\beta }\Vert }_d,$$ (7)

where L(β) may be the negative log of the likelihood function for (6) or the residual sum of squares, and λ > 0 is the regularization parameter. Note that for the lasso procedure (Tibshirani, 1996), d = 1 and for ridge regression (Hoerl and Kennard, 1970), d = 2. One may select the regularization parameter λ̂ based on the standard cross-validation procedure (Tibshirani, 1996). With the resulting β̂_λ̂, let D̂(Z) be the score.

Note that with a procedure using (7), it can be shown that, when the dimension of the covariate vector p is fixed and λ̂ = o(n), β̂_λ̂ converges to a constant vector as n → ∞ (Knight and Fu, 2000). This is an important property to guarantee that we will have a unique, well-defined limiting working model when repeating the algorithm with different training sets discussed in the next section. Similarly, we may use the above variable selection algorithms with the model described in (5) separately for each treatment group. Similar to the L_d penalized estimator, the regression parameter estimator based on the standard stepwise variable selection procedure also has this stabilization property under more rigorous regularity conditions.

Now, consider the case that Y may not be observed completely due to censoring of the event time T. A common approach is to relate the event time to the covariates with a Cox proportional hazards model (Cox, 1972). For example, one may combine the data from two treatment groups and consider a working model:

$$\mathrm{pr}(T>t\mid \mathit{Z},G)=g(\log \mathrm{\Lambda }(t)+{\mathit{\beta }}^{\prime }\mathit{h}(G,\mathit{Z})),$$ (8)

where g(x) = e^−ex, h(G, Z) is a known vector function of (G, Z), Λ(·) is an unknown baseline cumulative hazard function, and β is an unknown vector of parameters. Again h(G, Z) may include G, Z, and G × Z interaction terms. To estimate β, one may use the partial likelihood estimate. Here the loss function L(β) is the negative log of the partial likelihood. An alternative is to utilize a corresponding (7) to obtain β̂_λ̂. Now, suppose Y = I(T ≥ t₀), where t₀ is a given time point. Then one may use (Kalbfleisch and Prentice, 2002)

$$\widehat{D}(\mathit{Z})=g(\log \widehat{\mathrm{\Lambda }}(t_0)+{\widehat{\mathit{\beta }}}_{\widehat{\mathrm{\lambda }}}^{\prime }\mathit{h}(1,\mathit{Z}))-g(\log \widehat{\mathrm{\Lambda }}(t_0)+{\widehat{\mathit{\beta }}}_{\widehat{\mathrm{\lambda }}}^{\prime }\mathit{h}(-1,\mathit{Z})),$$ (9)

where

$$\widehat{\mathrm{\Lambda }}(t)=\sum _{i=1}^n{\mathit{\int }}_0^t\frac{d{N}_i(s)}{{\sum }_{j=1}^n{Y}_j(s)e^{{\widehat{\mathit{\beta }}}_{\widehat{\mathrm{\lambda }}}^{\prime }\mathit{h}(G_j,{\mathit{Z}}_j)}},$$

with N_i(t) = I(X_i ≤ t)Δ_i and Y_i(t) = I(X_i ≥ t), i = 1, … , n.

If we are interested in the restricted mean event time, that is, Y = min(T, τ₀), the resulting score from Model (8) is

$$\widehat{D}(\mathit{Z})={\mathit{\int }}_0^{{\tau }_0}\left\{g(\log \widehat{\mathrm{\Lambda }}(t)+{\widehat{\mathit{\beta }}}_{\widehat{\mathrm{\lambda }}}^{\prime }\mathit{h}(1,\mathit{Z}))-g(\log \widehat{\mathrm{\Lambda }}(t)+{\widehat{\mathit{\beta }}}_{\widehat{\mathrm{\lambda }}}^{\prime }\mathit{h}(-1,\mathit{Z}))\right\}\mathit{dt}.$$ (10)

Note that one may also fit a separate Cox model for each treatment group to create D̂(Z).

4. COMPARING DIFFERENT SCORING SYSTEMS

For a reasonably good scoring system, one expects that the curve $\widehat{\mathit{AD}}(c)$ is increasing with c, as in Figure 1(a). In general, different scoring systems D̂(·) will group patients differently. In order to compare two systems, say D̂₁(·) and D̂₂(·), we need to modify the scale of the x-axis for the plot in Figure 1(a). Specifically, we convert the conditional event D̂(Z⁰) ≥ c in (1) to H(D̂ (Z⁰)) ≥ q, where H is the empirical cumulative distribution function of D̂ (Z⁰). The resulting estimate corresponding to (2) is denoted by $\stackrel{\sim }{\mathit{AD}}(q)$. Note that $\stackrel{\sim }{\mathit{AD}}(q)=\widehat{\mathit{AD}}(H^{-1}(q))$. Given 0 ≤ q ≤ 1, $\stackrel{\sim }{\mathit{AD}}(q)$ is simply an estimated average treatment difference for the subgroup of subjects with scores exceeding the qth quantile, which representing an approximation to 100(1 − q)% of the study population. For example, with this new scale for the x-axis, the curve in Figure 1(a) becomes the solid curve ${\stackrel{\sim }{\mathit{AD}}}_1(q)$ in Figure 2. The subgroup of patients with an average CD4 count treatment difference of 100, as described in Section 2, represents the patients with scores in the top 52% of the study population. Now, since RNA is relatively expensive to measure in resource-limited regions, one question is whether we can use the baseline log(CD4) only to construct a similarly useful scoring system D̂₂(·). By fitting separate linear regression models for each of the two treatment groups using only log(CD4), the resulting score is D̂₂(Z) = 40.57+8.27 log(CD4). Note that this new score indicates that a patient with a large baseline CD4 value tends to benefit more from the new treatment. The corresponding ${\stackrel{\sim }{\mathit{AD}}}_2(q)$ is given in Figure 2 (dashed curve). This new curve is not an increasing function. Moreover, this curve is uniformly lower than ${\stackrel{\sim }{\mathit{AD}}}_1(q)$, indicating that if we use ${\stackrel{\sim }{\mathit{AD}}}_1(q)$ and ${\stackrel{\sim }{\mathit{AD}}}_2(q)$ to select any given proportion 100(1 − q)% of patients from the study population, the overall treatment benefit of the selected subpopulation using ${\stackrel{\sim }{\mathit{AD}}}_1(·)$ would be always larger than that using ${\stackrel{\sim }{\mathit{AD}}}_2(·)$. Thus the addition of baseline RNA into the regression models provides substantial improvement in the ability to select the subgroup of patients with a desirable level of overall treatment benefit. In general, the higher the curve $\stackrel{\sim }{\mathit{AD}}(·)$ is, the better the scoring system is. It is interesting to note that if we were able to use the score D̂(Z) = D(Z), the true treatment difference, the resulting curve $\stackrel{\sim }{\mathit{AD}}(·)$ would be uniformly the largest among all working models for treatment differences based on Z (see Supplementary Materials Appendix A for details). Note that the performance of a scoring system only depends on the ranks of its scores. If any strictly monotone increasing transformation of the true treatment difference D(Z) is used as the scoring system, the resulting curve $\stackrel{\sim }{\mathit{AD}}(·)$ would be identical to the one induced by D(Z).

Figure 2.

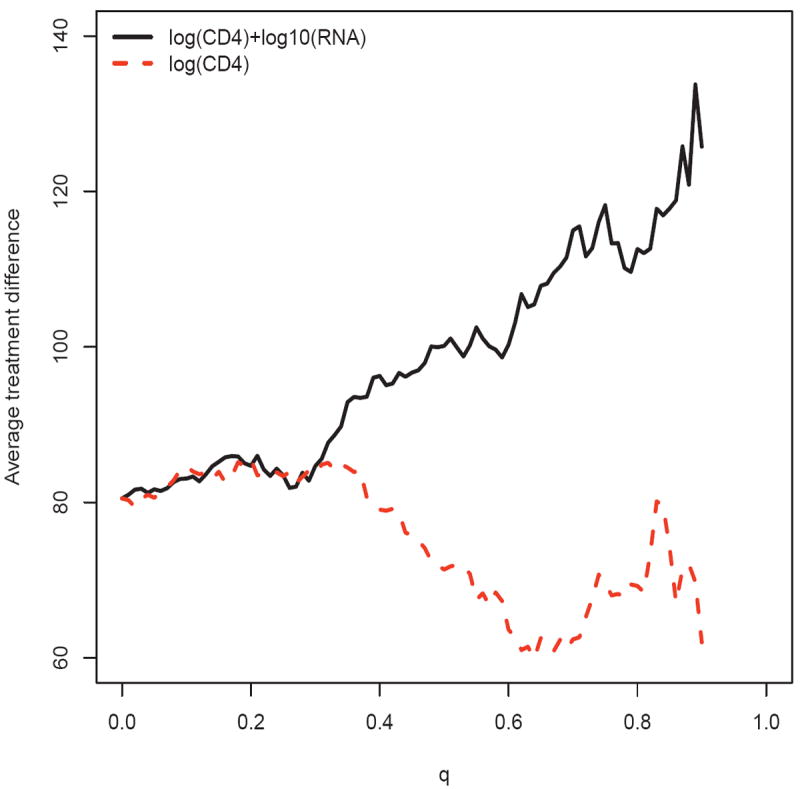
Comparing the two estimated average treatment differences for patients with largest 100(1 − q)% scores using the systems built with and without log₁₀(RNA) for the ACTG 320 data

When the dimension of Z is greater than one, it is difficult, if not impossible, to estimate D(Z) well nonparametrically. Thus it is likely that the treatment difference curve $\stackrel{\sim }{\mathit{AD}}(·)$ resulting from one model may not dominate that from another model over the entire interval of interest. If we are interested in identifying a subpopulation with a specific treatment difference, one may choose a scoring system which gives us the largest subset of patients satisfying this criteria among all candidate models. If there is no specific proportion of study population or specific level of treatment difference that is of particular clinical interest, one may use a summary measure of the curve to select the “best” model. For example, a possible metric is the area under the curve (AUC) of $\stackrel{\sim }{\mathit{AD}}(·)$. Let H̄(·) denote the cumulative distribution function of D̄(Z⁰). In Supplementary Materials Appendix B, we show that the AUC is a consistent estimator for

$$E(D({\mathit{Z}}^0)\log \{{[1-\overline{H}(\overline{D}({\mathit{Z}}^0))]}^{-1}\left\}\right),$$ (11)

which is the expected value of the product of the true subject-specific treatment difference D(Z⁰), given the individual patient’s covariate vector Z⁰, and a strictly increasing transformation of the rank of the patient’s limiting score D̄(Z⁰). The quantity (11) is a measure of the concordance between the true treatment difference and its empirical counterpart. Therefore, a higher AUC indicates a better fit of the working model. Furthermore, the area between the curves (ABC) of $\stackrel{\sim }{\mathit{AD}}(·)$ and the horizontal line $y=\stackrel{\sim }{\mathit{AD}}(0)$, estimates the corresponding covariance of two random quantities in (11). Note that this covariance is ρσ₀, where ρ is the correlation of the two terms in (11) and σ₀ is an unknown constant which does not depend on any specific scoring system. It follows that to compare two scoring systems, one may use the ratio of two ABCs to examine the relative improvement from one model to the other.

Since the upper tail of the curve $\stackrel{\sim }{\mathit{AD}}(·)$ may not be stable, one may use a partial AUC (by integrating the curve up to a specific constant η) as a metric for model evaluation and comparison. For the two models in Figure 2, with η = .90, the aforementioned AUCs are 97.8 and 75.4 for the models with and without baseline RNA, respectively. The corresponding ABCs are 17.3 and -5.1, respectively. Note that the ABC using the scoring system with baseline log(CD4) alone is negative, indicating that the overall performance of this scoring system is worse than a scoring system which groups the patients at random.

Now, if one considers the area under a weighted version of the curve, $(1-q)\stackrel{\sim }{\mathit{AD}}(q)$, this quantity consistently estimates

$$E(D({\mathit{Z}}^0)\overline{H}(\overline{D}({\mathit{Z}}^0))).$$ (12)

The expected value given in (12) directly measures the concordance of the subject-specific true treatment difference and the rank of the limiting score. This quantity may be easier to interpret heuristically than (11). Moreover, the corresponding area between this curve and the straight line $y=(1-q)\stackrel{\sim }{\mathit{AD}}(0)$ is the covariance associated with the quantities given in (12) (see Supplementary Materials Appendix B for details). Also note that there are no existing procedures in the literature which can estimate such concordance measures at the patient level. Furthermore, if we could use the true treatment difference D(Z) as the score, each of these concordance scores would attain its maximum value among all possible models derived from Z (see Supplementary Materials Appendix A for details).

When the dimension of the covariate vector Z is not small, it may not be appropriate to use the same data set to build a score via a complex variable selection algorithm and then use the same set to obtain $\stackrel{\sim }{\mathit{AD}}(·)$ for model evaluation. Rather, one may randomly divide the data set into two independent pieces, the training and the evaluation sets, to avoid potential bias due to overoptimism in assessing the adequacy of the model. When the data set is not large, an alternative approach is to use a random cross-validation procedure. Specifically, consider a class of models for the response Y and covariate vector Z. For each variable selection and estimation algorithm for this class of models, we randomly split the data set into two pieces, use the training set to obtain the scoring system D̂(Z), and construct the corresponding estimate $\widehat{\mathit{AD}}(·)$ using the evaluation set. Here the sizes of both the training and evaluation sets are of order n. We repeat this process M times.

Now, for the mth iteration, m = 1, ⋯, M, let D̂_m(Z), ${\widehat{\mathit{AD}}}_m(c)$ and H_m(c) be the corresponding aforementioned D̂(Z), $\widehat{\mathit{AD}}(c)$ and H(c), respectively. Let ${\widehat{D}}_a(\mathit{Z})=\frac{1}{M}{\sum }_{m=1}^M{\widehat{D}}_m(\mathit{Z})$, ${\widehat{\mathit{AD}}}_a(c)=\frac{1}{M}{\sum }_{m=1}^M{\widehat{\mathit{AD}}}_m(c)$, and $H_a(c)=\frac{1}{M}{\sum }_{m=1}^M{H}_m(c)$. Then ${\stackrel{\sim }{\mathit{AD}}}_a(q)={\widehat{\mathit{AD}}}_a(H_a^{-1}(q))$. The comparisons among all the candidate models can be made via ${\stackrel{\sim }{\mathit{AD}}}_a(q)$. We then use the corresponding ${\widehat{\mathit{AD}}}_a(c)$ of the best model to select the desirable subpopulation. Note that the score of a future subject with the covariate vector Z⁰ is D̂_a(Z⁰). This cross-training-evaluation averaging process is similar to bagging (Breiman, 1996).

If for each of the model selection algorithms, its D̂(Z⁰) converges in probability to a deterministic quantity, say D̄(Z⁰), uniformly in Z⁰, as n → ∞, then in Supplementary Materials Appendix C we show that ${\widehat{\mathit{AD}}}_a(·)$ is uniformly consistent in the sense that

$$\underset{c\in (-\infty ,c_0)}{\sup }|{\widehat{\mathit{AD}}}_a(c)-\mathit{AD}(c)|=o_p(1),$$

for any c₀ such that $\mathrm{pr}(\overline{D}({\mathit{Z}}^0)\ge c_0)>0$. For most algorithms, the resulting D̂(Z⁰) would be stabilized, for example, using lasso or ridge regression procedures discussed in the previous section. However, with an extensive search for the best scoring system, it is not clear how to make further inference about AD(c) with the same data set. On the other hand, if there is only a single pre-specified working model in our analysis, we show in Supplementary Materials Appendix D that $W_a(c)=n^{1/2}\{{\widehat{\mathit{AD}}}_a(c)-\mathit{AD}(c)\}$ converges weakly to a mean zero Gaussian process. Furthermore, in Supplementary Materials Appendix E, we present a novel perturbation resampling method to obtain such an approximation in practice. We also conducted an extensive numerical study to examine the appropriateness of such a distribution approximation. The details of the results of this simulation study is given in the Remarks Section. As an example, in Figure 1(b), for the HIV data with baseline CD4 count and RNA value, we used 500 random cross-validations with 4/5 of the data as the training set to obtain the estimate ${\widehat{\mathit{AD}}}_a(c)$, which is presented by the solid line. The dashed lines and the shaded region in Figure 1(b) are the pointwise and simultaneous 95% confidence intervals, respectively. These interval estimates are quite useful to decision making on the choice of “c” beyond utilizing point estimates only.

We have conducted an extensive simulation study to examine the performance of the above cross-training-evaluation process. We find that under various practical settings, for each fitted model to create the scoring system, the empirical average of ${\widehat{\mathit{AD}}}_a(·)$ is nearly identical to AD(·). Moreover, the average score D̂_a(Z⁰) to be utilized for selection of future study subjects gives us, for example, almost the same average treatment difference $E((Y_{(1)}^0-Y_{(0)}^0)\mid {\widehat{D}}_a({\mathit{Z}}^0)\ge c)$as AD(c). More details of our numerical study results are given in the Remarks Section.

5. EXAMPLES

First, we illustrate our proposal using the data from the ACTG 320 HIV study described in the Introduction, using the nine baseline covariates listed in Table 1 of Hammer et al. (1997). This set of covariates includes the baseline CD4 and RNA values. There are 870 patients who had complete information with respect to these 9 covariates. Again, we used week 24 CD4 value as the response variable Y, as in Section 2. Here, we consider two classes of models to construct various scoring systems. The first one, as in (5), uses an additive linear model for each treatment group with all nine of the covariates. The second one, as in (6), uses a single model with main covariate effects and interactions between the treatment indicator and other covariates. For each of the two classes of models, we used four variable selection procedures to build candidate scoring systems. For the first procedure, we used the full model with all the baseline covariates. For the second one, we used a stepwise variable selection based on Akaike information criterion (AIC) (Akaike, 1973). We then used lasso and ridge regression as the third and fourth variable selection procedures, respectively. The tuning parameters were selected by the standard cross-validation procedure built in the R package glmnet. For comparison, we also considered the simple two-variable model, discussed in Section 2, which uses only baseline CD4 and RNA.

Figure 3 summarizes the treatment difference curves ${\stackrel{\sim }{\mathit{AD}}}_a(·)$ based on the averages over M = 500 replications of a cross-validation procedure, where each replication resulted from the random selection of 4/5 of the data as the training set. The results from these two classes of models are quite similar, except when using the lasso variable selection procedure. The model using only CD4 and RNA without variable selection performs well. On the other hand, the scoring systems using 9 covariates with the standard variable selection algorithms do not perform as well.

Figure 3.

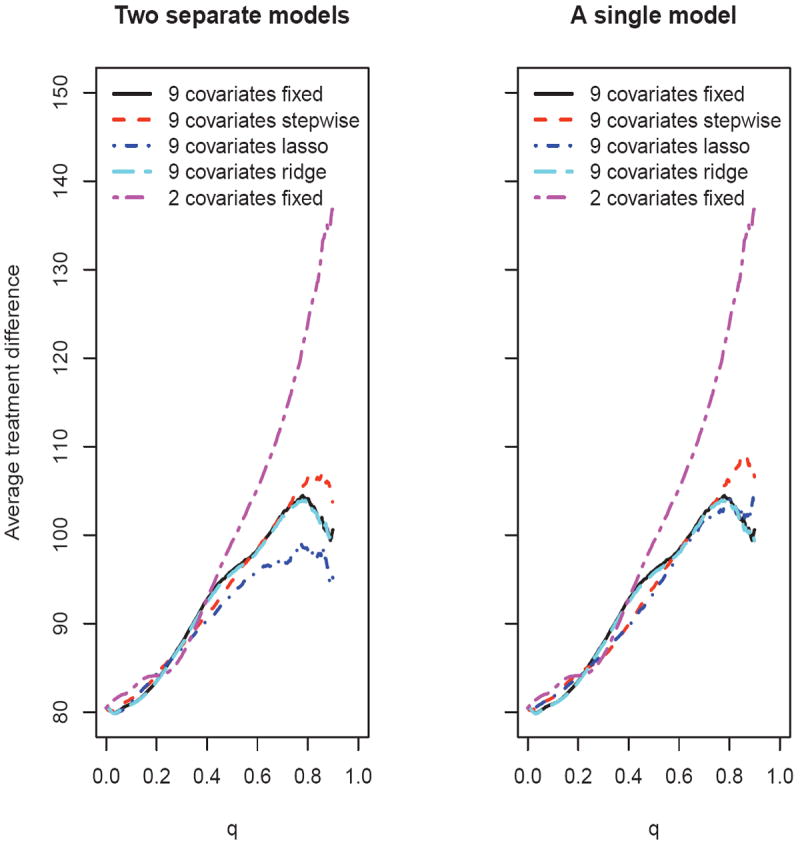
Comparing the estimated average treatment difference curves using various scoring systems based on 500 replicates of cross-validation for the ACTG 320 data (left panel: two separate models; right panel: a single interaction model)

Now, if one wants to identify a subpopulation with an average CD4 count treatment difference of 100 cells/mm³, then clearly the scoring system built with CD4 and RNA, which gives us the largest target subset of patients among all the candidate models, is the most favorable. In fact, using the two-variable model, 52% of the patients meet this criteria, while no more than 30% of the patient population is identified via any of the other candidate models. If this specific level of treatment difference is not of particular clinical interest, one may use the AUC and ABC discussed in Section 3 to compare the scoring systems. For example, with two separate models and η = .90, the ABC for the scoring system built using nine covariates with the lasso procedure is 9.1, compared with 17.3 for the simple model built using only CD4 and RNA.

As a second example, we considered a recent clinical trial “Prevention of Events with Angiotensin Converting Enzyme Inhibition” (PEACE) to study whether the ACE inhibitors (ACEi) are effective for reducing certain future cardiovascular-related events for patients with stable coronary artery disease and normal or slightly reduced left ventricular function (Braunwald et al., 2004). In this study, 4158 and 4132 patients were randomly assigned to the ACEi treatment and placebo arms, respectively. The median follow-up time was 4.8 years. One main endpoint for the study was the patient’s survival time. By the end of the study, 334 and 299 deaths occurred in the control and treatment arms, respectively. Under a proportional hazards model, the estimated hazard ratio is 0.89 with a 0.95 confidence interval of (0.76, 1.04) and a p-value of 0.13. Based on the results of this study, it is not clear whether ACEi therapy would help the overall patient population with respect to mortality. However, with further analysis of the PEACE survival data, Solomon et al. (2006) reported that ACEi might significantly prolong survival for the subset of patients whose kidney functions at the study entry time were not normal (for example, those with estimated glomerular filtration rate, eGFR, < 60). This finding could be quite useful in practice. On the other hand, such a subgroup analysis has to be executed properly and the results of such analysis have to be interpreted cautiously (Rothwell, 2005; Pfeffer and Jarcho, 2006; Wang et al., 2007).

For this example, we considered the time-to-event endpoint, T, the time to all-cause mortality. To build a candidate scoring system, we first used the 7 covariates previously identified as statistically and clinically important predictors of the overall mortality in the literature (Solomon et al., 2006). These covariates are eGFR, age, gender, left ventricular ejection fraction (lveejf), history of hypertension, diabetes, and history of myocardial infarction. For comparison, we also used two scoring systems built using eGFR alone and lveejf alone, which are two conventional predictive markers for cardiovascular diseases. In addition, we considered the scoring systems built with various variable selection procedures using the baseline covariates listed in Table 2 of Braunwald et al. (2004). However, we did not use three of the variables listed: race, country, and serum creatinine, which were not available in our database from the US National Institutes of Health. Moreover, we omitted four binary variables due to lack of variability (i.e., over 95% of patients exhibited the same covariate value). These excluded variable are: use of Digitalis, use of antiarrhythmic agent, use of anticoagulant, and use of insulin. On the other hand, an extra variable eGFR, which is a function of age, gender, race, and serum creatinine, was available in our database. To this end, we considered the remaining 20 variables from Table 2 of Braunwald et al. (2004) in addition to eGFR, resulting in a total of 21 covariates. In our analysis, we included all patients (n = 7460) who had complete information concerning these 21 covariates. To estimate the score for the treatment differences, we considered two classes of models: a separate Cox model for each of the two treatment groups, and a single Cox model which includes treatment-covariate interaction terms. For each of the two classes of models, we used the same four variable selection procedures as in the previous example to build candidate scoring systems.

First, suppose that one is interested in survival probability at month 72. We let Y = I(T ≥ 72). Figure 4 summarizes the treatment difference curves for various scoring systems based on 500 random cross-validations with 4/5 of the data as the training set. The treatment difference curve with the 7 clinically meaningful covariates and the one with eGFR alone are similar. Both perform uniformly better than any of the scoring systems which use all 21 covariates. When using two separate models, as shown in the left panel of Figure 4, the performance of the scoring systems constructed via variable selection procedures appears similar to the full model. Using a single interaction model (right panel), the stepwise and lasso variable selection procedures appear inferior to the one with all 21 covariates. It is interesting to note that the scoring system based on lveejf alone performs quite poorly, indicating that this conventional marker for cardiovascular diseases by itself is not helpful in identifying patients who would benefit from ACEi. To further quantify the relative performance among the candidate scoring systems, one may use the AUC and ABC discussed in Section 3. For example, with two separate models and η = .90, the ABC for the scoring system built with 7 covariates is 0.015, which is the largest among all candidates. The estimated ratio of correlations between the true treatment difference D(Z⁰) and log{[1 − H̄ (D̄(Z⁰))]⁻¹} using this scoring system is 1.21 relative to that using eGFR alone, 1.65 relative to the one using all 21 covariates, and 4.11 relative to that using lveejf alone.

Figure 4.

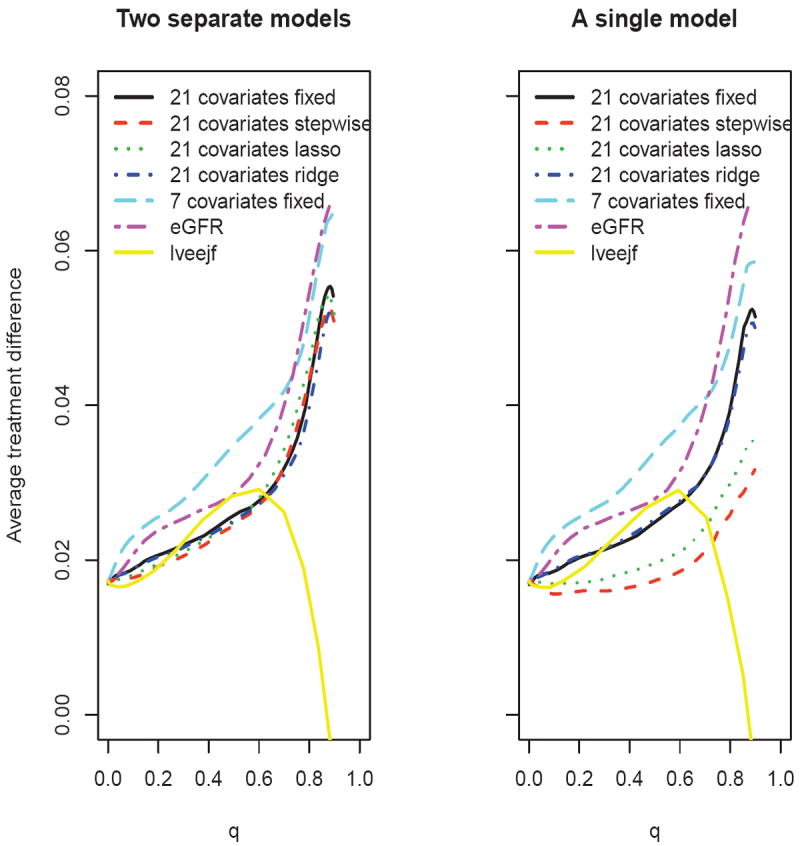
Comparing the estimated average treatment difference curves using different scoring systems with respect to 72-month survival rate, based on 500 replicates of cross-validation for the PEACE data (left panel: two separate models; right panel: a single interaction model)

Next, suppose that one is interested in the restricted mean event time up to month 72. To this end, we let Y = min(T, 72). Figure 5 presents the results based on 500 random cross-validations with 4/5 of the data as the training set. The scoring system built with the 7 covariates appears to outperform the others. Again it appears that the scoring systems created using the variable selection procedures with 21 covariates perform similarly or inferior to the one with the full model, and the system based on lveejf only performs poorly. It is interesting to note that the model with eGFR alone does not perform particularly well for this endpoint.

Figure 5.

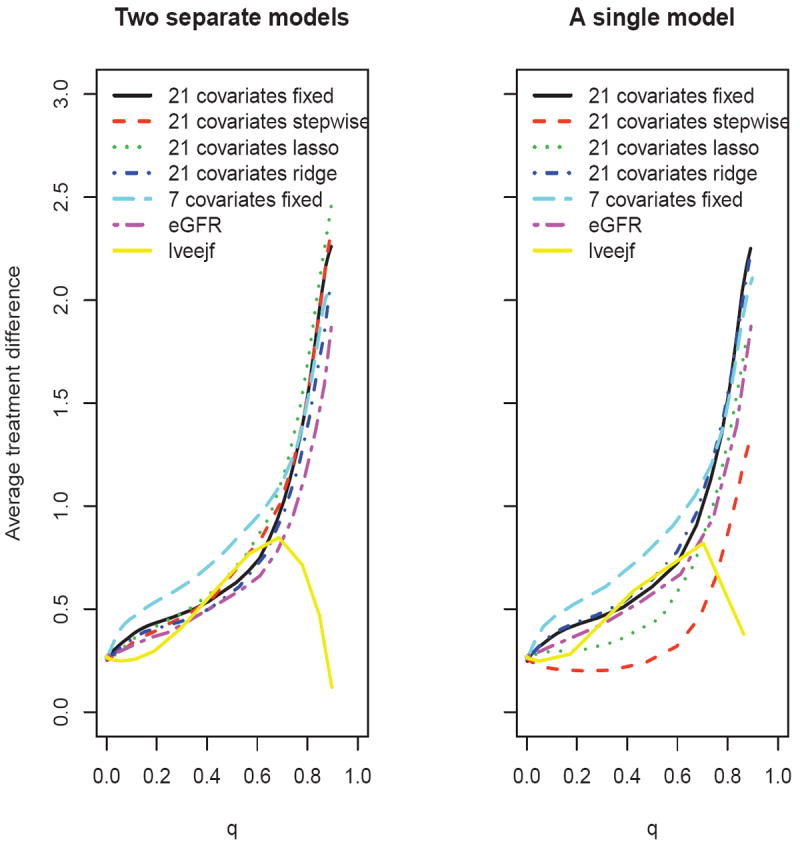
Comparing the estimated average treatment difference curves using different scoring systems with respect to restricted mean survival time up to 72 months, based on 500 replicates of cross-validation for the PEACE data (left panel: two separate models; right panel: a single interaction model)

Based on the partial AUC and ABC, the scoring system using two separate models with 7 covariates is the best among the candidate models for the survival probability at month 72. This model also gives the best scoring system among the candidate models for the restricted mean event time up to month 72. Figure 6 provides the estimated average treatment differences ${\widehat{\mathit{AD}}}_a(c)$ over a range of values c for both endpoints. From this figure, one can easily identify the subgroup of patients with any desired level of treatment benefit. For example, if we desire a 72-month survival rate benefit of 0.05, since $\widehat{\mathit{AD}}(0.038)=0.05$, we can identify the subset of patients with Z⁰ such that D̂(Z⁰) ≥ 0.038. If we desire a treatment benefit of 1.5 months for the restricted mean event time up to month 72, the corresponding subset would consist of patients with Z⁰ such that D̂(Z⁰) ≥ 2.23.

Figure 6.

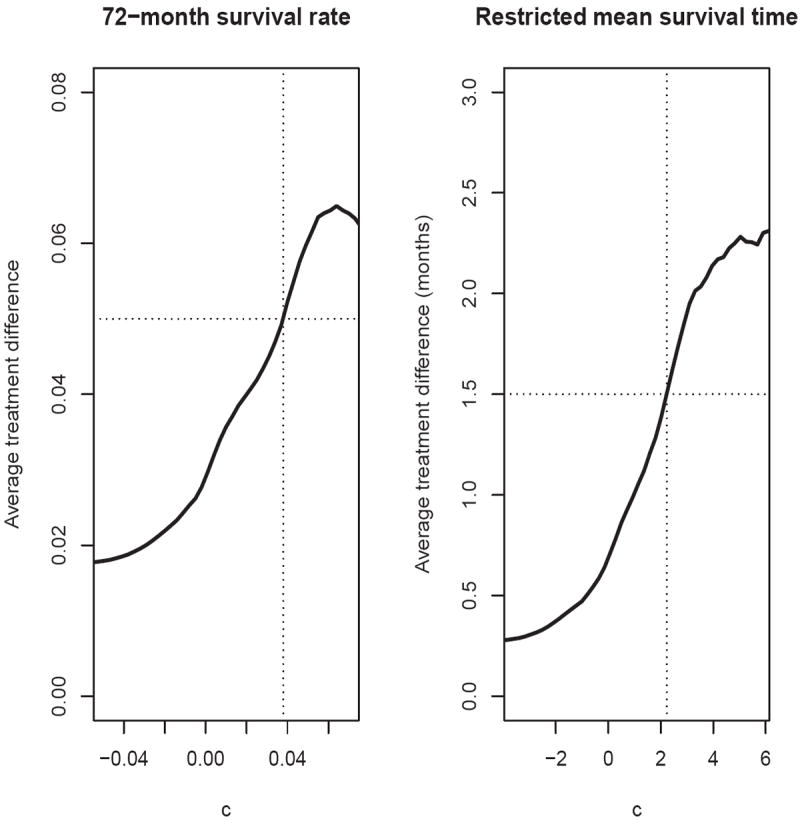
Estimated average treatment difference for patients with D̂(Z) ≥ c using the scoring system built with two separate models and 7 covariates for the PEACE data (left panel: 72-month survival rate; right panel: restricted mean survival time up to 72 months)

6. REMARKS

Note that the typical subgroup analysis strategy, which tries to identify a target population for future study by dichotomizing one or more baseline variables, may not be efficient, especially when the dimension of the covariate vector Z is large. That is, the resulting population selected by this strategy can be quite small, which is not practically useful. Our proposed procedure attempts to select the largest population whose subjects would have a desired overall treatment benefit, among all candidate scoring systems.

We conducted an extensive numerical study to examine the performance of the new proposal under various practical settings. We find that the estimator ${\widehat{\mathit{AD}}}_a(c)$ via the random cross-validation procedure is practically unbiased for its theoretical counterpart AD(c) in (1) when c is not very large (the upper tail of ${\widehat{\mathit{AD}}}_a(·)$ may not be stable). On the other hand, if we use the entire data set to fit a model for creating a scoring system, and use the same data set to estimate AD(c), the resulting estimator $\widehat{\mathit{AD}}(·)$ can be substantially overly optimistic. As an example, in our study we mimicked the HIV example to generate the data from a single linear model with response Y being the week 24 CD4 count and independent variables being the treatment indicator, the nine baseline covariates discussed in Section 5, and the treatment-covariate interactions. The error of the model was assumed to be normal with mean zero. We fitted the HIV study data using this model and then used this model to generate responses repeatedly. To simulate a data set with sample size n = 870, we first sampled 870 vectors of the discrete covariates from their empirical joint distribution from the original study database. We then sampled 870 vectors of the continuous covariates from a multivariate normal distribution with mean and covariance equal to the empirical mean and covariance matrix from the original data. Then we generated a week 24 CD4 count using the above “true” model. For each simulated data set of n = 870 patients, we fitted two separate linear models (one each for the control and treatment group) using the above 9 covariates additively, and used the resulting parameter estimates to construct a scoring system D̂(Z). We then generated 100,000 new independent observations (Y, G, Z) from the same distribution described above, and used these fresh samples to estimate the mean value of the treatment difference $Y_{(1)}^0-Y_{(0)}^0$, given D̂(Z) > c. We repeated this process 1000 times and used the empirical average to approximate AD(c). The resulting curve (solid) is given in Figure 7(a). Now, to obtain an empirical average of ${\widehat{\mathit{AD}}}_a(c)$, we used the above 1000 simulated data sets with sample size n. The random cross-validation procedures were repeated 500 times for each simulated data set. The dashed curve in Figure 7(a) is the resulting empirical average of ${\widehat{\mathit{AD}}}_a(c)$ with a 4:1 ratio of training and evaluation samples. The dotted curve in Figure 7(a) is the corresponding empirical average of $\widehat{\mathit{AD}}(·)$, where the same data set is used for both training and evaluation. Note that the dotted curve is markedly higher than the solid one, indicating that the procedure using the entire data set for model building and evaluation can be quite misleading.

Figure 7.

Comparisons between the estimation procedures with and without cross-validation with n = 870; (a) and (b) are based on simulation with the 9 covariates mimicking the HIV example; (c) and (d) are based on simulation with the 9 covariates plus 50 noise variables. The (a) and (c) present the average treatment difference curves, the solid curve is the “truth”, the dashed curve is the empirical average using cross-validation procedure with a 4:1 ratio of training and evaluation samples, and the dotted curve is the empirical average without using cross-validation. In (b) and (d), the solid and dashed lines are the coverage probabilities of the 95% confidence intervals without and with cross-validation, respectively.

We repeated the above simulation procedure with the same true model for the response variable, but this time added 50 random standard normal covariates to our analysis, representing pure noise. We used all the 59 covariate to fit the models and constructed the scoring systems. In Figure 7(c), the empirical average of the naive $\widehat{\mathit{AD}}(·)$ is dramatically higher than its true counterpart, while the empirical average of ${\widehat{\mathit{AD}}}_a(·)$ obtained via cross-validation is still quite close to the truth. From our extensive numerical study, we find that the estimation procedure for AD(·) performs well with a random K-fold cross-validation when 5 ≤ K ≤ 10 (i.e., repeatedly using K − 1 subsets as training data and 1 as evaluation data).

As indicated in Section 4, when an extensive model selection process is involved, it is difficult, if not impossible, to make further inference about the average treatment difference curve AD(·) associated with the final scoring system using the same data from which it was constructed. If there is an independent data set generated from a similar population, the techniques for analyzing standard empirical processes may be utilized for constructing the interval estimates by treating the scores as being fixed (Song and Pepe, 2004; Song and Zhou, 2011). On the other hand, if there is only a single pre-specified working model in our analysis, one may be able to construct interval estimates with the same data set after model fitting. Based on our extensive numerical study with the aforementioned simulation setup, we find that the coverage levels of such interval estimators (pointwise and simultaneous) based on ${\widehat{\mathit{AD}}}_a(·)$ are quite close to their nominal values. For example, Figures 7(b) and 7(d) present the empirical coverage probabilities of the pointwise 95% confidence interval estimator for AD(c) under the above two simulation settings. The dashed and solid lines are based on ${\widehat{\mathit{AD}}}_a(c)$ and $\widehat{\mathit{AD}}(c)$, respectively. The empirical pointwise coverage probabilities are very close to 0.95 for the interval estimators based on ${\widehat{\mathit{AD}}}_a(c)$. Moreover, the 95% simultaneous confidence interval estimators based on ${\widehat{\mathit{AD}}}_a(c)$ have empirical coverage probabilities of 98.4% and 97.6% under the two simulation settings.

In Cai et al. (2011), under a single pre-specified model for creating a scoring system, a nonparametric smooth functional estimator for the treatment difference is provided for any fixed score D̂(Z). Their procedure can be quite useful at the individual level for the treatment selection. However, the nonparametric estimator can be unstable even with data from a moderately sized study. The approach taken for the management of future patients, as discussed in this paper, is similar to the approaches proposed by Song and Pepe (2004) and Song and Zhou (2011) in which the score was simply a univariate biomarker. Such a cumulative stratification strategy can be quite useful for the treatment selection with a utility function defined at a population level.

The average treatment difference curve AD(c) is defined conditionally on the study patient population. For the patient management of a general patient population, one needs to generalize the scoring system from the study population to the general population. If the score is derived from a single true regression model for both populations, then a weighted scheme based on the density functions of the covariate vectors for the two treatment groups may be utilized to make such an adjustment of the score from the study population to the general population (in practice, this is very difficult for the case with high dimensional covariate vectors). The general issues have been discussed, for example, by Frangakis (2009) and Cole and Stuart (2010).

The average treatment difference curve AD(c) is related to the tail-oriented STEPP plot (Bonetti and Gelber, 2000), which is based on a single covariate U. Similar to the tail-oriented STEPP plot which considered both subgroups with U ≥ u and U < u, one may construct a corresponding plot for our proposal with the score D̂(Z) less than c for selecting the study population. Note that this plot can also be constructed with the score in the “>” direction by using a new scoring system −D̂(Z).

From a risk-benefit perspective for evaluating the new treatment, one may additionally collect toxicity information and then construct a set of corresponding treatment contrast measures using the same efficacy score D̂(Z). The resulting two sets of curves can be quite useful for selecting a proper target population who may be expected to experience relatively large treatment benefits without excessive toxicity. For comparing multiple treatment arms with a control, we may construct pair-wise treatment-control difference curves ${\stackrel{\sim }{\mathit{AD}}}_a(·)$. It follows from our proposal that the treatment with the highest treatment difference curve or a function thereof may be selected to be the candidate for the future studies.