Relative stability of different DNA guanine quadruplex stem topologies derived using large-scale quantum-chemical computations

Abstract

We provide theoretical predictions of the intrinsic stability of different arrangements of guanine quadruplex (G-DNA) stems. Most computational studies of nucleic acids have applied Molecular Mechanics (MM) approaches using simple pairwise-additive force fields. The principle limitation of such calculations is the highly approximate nature of the force fields. In this study we for the first time apply accurate QM computations (DFT-D3 with large atomic orbital basis sets) to essentially complete DNA building blocks, namely, seven different folds of the cation-stabilized 2-quartet G-DNA stem, each having more than 250 atoms. The solvent effects are approximated by COSMO continuum solvent. We reveal sizeable differences between MM and QM descriptions of relative energies of different G-DNA stems, which apparently reflect approximations of the DNA force field. Using the QM energy data, we propose correction to earlier free energy estimates of relative stabilities of different parallel, hybrid and antiparallel G-stem folds based on classical simulations. The new energy ranking visibly improves the agreement between theory and experiment. We predict the 5′-anti-anti-3′ GpG dinucleotide step to be the most stable one, closely followed by the 5′-syn-anti-3′ step. The results are in good agreement with known experimental structures of 2, 3 and 4-quartet G-DNA stems. Besides providing specific results for G-DNA, our study highlights basic limitations of force field modeling of nucleic acids. Although QM computations have their own limitations, mainly the lack of conformational sampling and the approximate description of the solvent, they can substantially improve quality of calculations currently relying exclusively on force fields.

Introduction

Nucleic acids adopt a wide variety of structures and possess diverse dynamical behavior, both of which are essential for their biological functions. Beyond experiments, structural dynamics of nucleic acids can be studied by computational techniques. The most common computational method for this purpose is classical (molecular mechanics based,^1–7 MM) atomistic molecular dynamics (MD) simulation.^8–12 Molecular simulations allow explicit inclusion of solvent and a rather large sampling of conformational space, with contemporary simulations reaching easily beyond the microsecond time scale. Both solvent and sampling of conformational space are essential for proper description of the structural dynamics. However, classical simulations of nucleic acids are limited by the approximate nature of the empirical force fields.^6,13,14

Modern electronic structure (quantum chemical, QM) computations offer inherently more accurate description of a studied system compared to force fields.^15–17 However, the applicability of QM methods to nucleic acids is limited by the size of the systems that can be handled, difficulties in inclusion of solvent and essentially lack of any sampling. Thus, QM calculations in studies of nucleic acids have mostly been used for benchmark computations to derive the basic picture of molecular interactions such as base stacking^18–20 or to provide data for verification and parameterization of the simulation force fields.^6,14 Among studies related to this work, calculations on guanine-quartet (G-quartet) systems should be noticed.^21–28 QM computations have also characterized specific local molecular interactions seen in experimental nucleic acids structures,^29,30 while hybrid quantum-chemical/molecular mechanical (QM/MM) approaches have been used to address reaction mechanisms of RNA enzymes.^31–33 However, in general it is not easy to achieve biochemical relevance in QM computations of nucleic acids.¹⁷ Reliable QM descriptions have been limited to only small fragments of the nucleic acids molecules (dozens of atoms when considering QM methods of quality comparable to the approach used in this study, e.g., up to ~60 atoms in studies of two stacked base pairs).

Considering the approximate nature of the simulation force fields, inclusion of accurate large-scale (hundreds of atoms) QM calculations into the portfolio of computational techniques to study nucleic acids is desirable. In the present work we for the first time apply such computations to a system that represents a sufficiently complete DNA fragment. Specifically, we study seven distinct folds of the cation-stabilized 2-quartet guanine quadruplex stem.³⁴

The ability to apply large-scale QM computations to nucleic acids reflects method advances, such as development of fast and accurate computations capable of including the dispersion energy.^35–38 This allows a major increase in the size of the studied systems while retaining the accuracy of the structure-energy mapping.³⁹ Still, applications of the QM methodology to nucleic acids remain difficult. Even inclusion of hundreds of atoms does not always provide a complete enough system. Moreover, the conformational space accessible by nucleic acids and their fragments is complex, mainly due to the dihedral space of the backbone.⁴⁰ Optimization techniques do not allow its unambiguous characterization. The calculations may be easily trapped in local minima of unclear significance and/or be biased by spurious interactions not observed in complete solvated nucleic acids. Additionally, the negative charge associated with each phosphate group necessitates inclusion of a solvent. The solvent screening effects in QM calculations can only readily be incorporated using approximate continuum solvent models, which neglect specific hydration. Thus, even with the improved methods, QM computations of nucleic acids are not straightforward. However, despite these caveats, such computations can be very useful to address many specific questions, especially in combination with experimental and simulation data. We anticipate that large-scale QM computations will become a common tool to study nucleic acids in the near future.

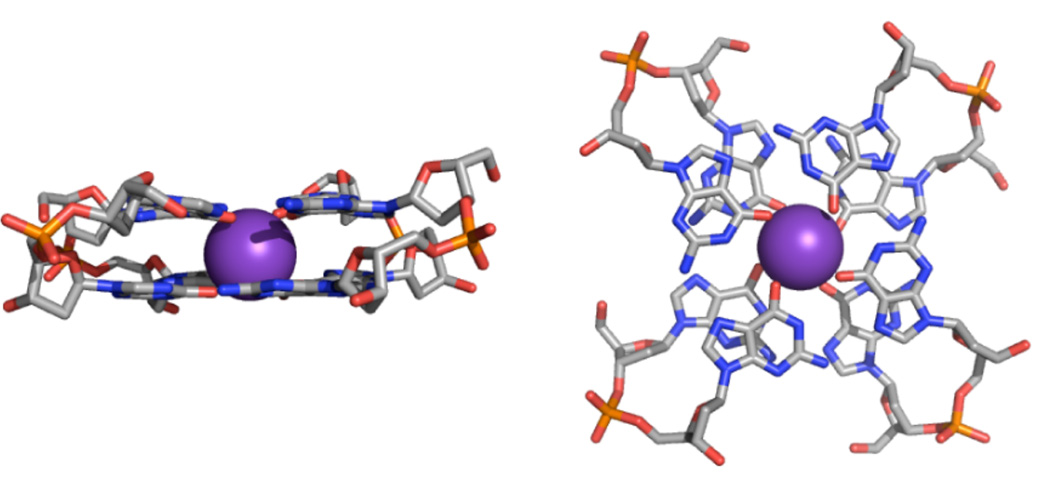
Guanine quadruplex molecules (G-DNA) are the most important non-canonical DNA structures.^41–50 G-DNA is formed by nucleic acids sequences containing short G-tracts, i.e., two or more consecutive guanines in the strand. The basic structural unit of G-DNA is a planar quartet of cyclically bound guanines stabilized by monovalent ions. Several consecutive quartets stack together to form the G-DNA stem consisting of four G-tracts with the monovalent ions lining up in its inner channel (Figure 1). The G-DNA molecule can consist of four or two separate sequences, or a single sequence, that come together with the G-tracts that make up the G-DNA stem in various combinations of parallel and anti-parallel strand orientations. The biochemically most relevant are single-stranded (monomer) topologies. Monomeric and dimeric quadruplexes need single-stranded loops to connect their G-tracts. The G-DNA molecules can adopt different topological variants that often are very sensitive to the base sequence and the surroundings.^{41,43,51–54} One of the specific features of G-DNA topology is alternation of syn and anti (defined by glycosidic torsion χ) nucleotides in the individual quartets, which is imposed by orientation of the G-tracts.⁵⁵ In a given quartet (Figures 2 and 3, Supporting Information Figure S1), guanines belonging to G-tracts (G-strands) running anti-parallel with respect to each other must have opposite orientation of the bases along the glycosidic bond while guanines that belong to parallel strands must have identical χ orientation.⁵⁵ Supporting Information Figure S1 depicts all quadruplex topologies and types of G-tracts mentioned in this study.

Figure 1.

2-quartet G-DNA stem in the 5′-anti-anti-3′ (AA) arrangement.

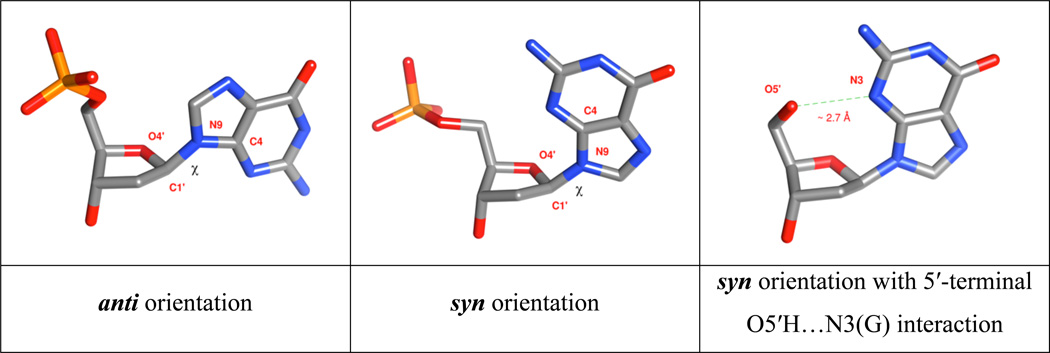
Figure 2.

Two orientations of the glycosidic torsion angle χ: anti (left) and syn (center and right). χ torsion angle is defined as O4′-C1′-N9-C4 and O4′-C1′-N1-C2 for purines and pyrimidines, respectively. The O5′H…N3(G) hydrogen bond typical for 5′-terminal syn guanosines in the G-DNA is depicted right.³⁴

Figure 3.

Two-quartet G-DNA stems used in our computations. From left to right: AA, AS, 3AA+1SS, SA-aabb, SA-abab, SA-aaab and SA-aaaa structures. Each stem consists of four 5′-GG-3′ dinucleotide steps (strands); S and A stand for syn and anti guanines. The notation ‘a’ and ‘b’ is used to distinguish SA stems with different relative 5’-3’ orientation of the adjacent strands around the structure; a is used for strands oriented upward in our Figure while b for strands oriented downward; c.f., the names of the structures with the relative orientation of the arrows showing the 5’-3’ directionality of the strands. White rectangle marks syn and grey anti nucleosides. The channel cation (K⁺) is not shown. The first six arrangements were considered in the preceding MD simulation study,³⁴ the seventh arrangement has been added in the course of this study.

G-DNA molecules have been often studied by simulation techniques.^34,56–72 Our recent study utilized post-processing MM-PBSA free energy computations to address the basic rules governing the topological preference of G-DNA stems.³⁴ The simulations were carried out for six two-quartet [d(GG)]₄ stems, which included different strand orientations (Figure 3). The calculations predicted that the four possible 5′-GpG-3′ steps (dinucleotides) show the following relative stability order: 5′-syn-anti-3′ (SA) > anti-anti (AA) > anti-syn (AS) > syn-syn (SS). This subsequently determines the basic rules governing the preferred quadruplex stem topologies and their dependence on the number of consecutive G-quartets.³⁴ The data suggest that anti-parallel G-quadruplexes tend to maximize the number of syn-anti 5′-GpG-3′ steps and avoid the unfavorable anti-syn and syn-syn steps. This rule is consistent with observed topologies of most of the monomeric and dimeric anti-parallel G-quadruplex structures.³⁴ Nevertheless, the computations were not capable to explain why tetrameric quadruplexes experimentally tend to form all-parallel stems with all-anti orientation of nucleobases.^41,55 Thus, we suggested that some force field bias may affect the calculated balance of all-parallel all-anti stems versus the antiparallel stems.³⁴

In this study, we re-investigate the 2-quartet G-DNA stems geometries using modern QM dispersion-corrected density functional theory (DFT-D3) methods.^73,74 The DFT-D3 method obviously does not allow carrying out QM MD simulations for solvated nucleic acids. However, small but already complete DNA structures can be gradiently optimized while using continuum solvent model such as COSMO^75,76 to screen the electrostatic interactions. Such computations can then be compared with equivalent molecular mechanics optimizations with inclusion of Poisson-Boltzmann (PB) continuum solvent model that has been used in the earlier MM-PBSA free energy computations.³⁴ Provided the QM and MM optimized structures are similar, we can compare relative energies of the different stem topologies (Figure 3) as predicted by the MM and QM methods. One of the genuine requirements, a constraint that allows unambiguous comparison, is the similarity of the sugar-phosphate backbone conformations. Specifically, the backbone conformations should belong to the same rotameric family (e.g. the combined set of all the backbone dihedrals)^40,77 in both the QM and MM structures. Our computations reveal surprisingly large differences between the MM and QM descriptions, leading to a major revision in the predicted energy order of different G-DNA stem arrangements.³⁴

Methods

Initial structures

We have created eight starting structures. Six correspond to those investigated in the earlier MD free energy study (Figure 3).³⁴ In the AA (i.e., anti-anti) model, all the guanines have anti glycosidic bond orientations, and the structure has four parallel anti-anti steps. The coordinates were taken from the second and the third G-quartets of the first molecule (strands A-D) of the parallel tetrameric quadruplex [d(TG4T)]4 0.95 Å X-ray structure (PDB ID 352D).⁷⁸ This differs from the preceding MD study³⁴ where an NMR structure was used. The X-ray structure is more accurate than the NMR structure so it is more reliable for QM gradient geometry optimization. Due to genuine sampling of MD simulations, both starting structures are equally suitable for MD simulations. Three syn-anti (SA) models (SA-aabb, SA-abab and SA-aaab - Figure 3) were built as in ref ³⁴. They all have four SA steps but with different strand orientations (‘a’ and ‘b’ denote the strand directions around the G-quartet). The SA-aabb model was constructed using coordinates of the first and the second quartets obtained from the crystal structure of the diagonal antiparallel G-quadruplex [d(G4T4G4)]2 (PDB 1JPQ; 1.9 Å).⁷⁹ The SA-abab structure was built from the first model in the NMR structure of the thrombin-binding DNA aptamer d(G2T2G2TGTG2T2G2), PDB: 148D.⁸⁰ The SA-aaab stem was built from the first two quartets in the first model of the NMR structure of the human telomere G-quadruplex d(T2G3T2AG3T2AG3T2AG3A), PDB: 2GKU.⁸¹ The AS model was built from the second and the third quartets of 1JPQ. The ‘3AA+1SS’ model, with three AA steps and one SS step, was obtained from the second and third quartets of 2GKU while using the first NMR model with α/γ g-/g- backbone topology (refer to reference³⁴ for further discussion).

We have further prepared a second variant of the SA-abab fold (SA-abab-2) using the first and second quartet of the 1.5 Å 2AVH X-ray structure of [d(G4T3G4)]2 edge-loop quadruplex.⁸² Finally, entirely new 1.08 Å 3TVB crystal structure of parallel stranded tetrameric [d(G4)]4 quadruplex appeared recently.⁸³ This structure, in contrast to all preceding parallel stranded structures, yet in line with our simulation predictions,³⁴ shows the first (5′-) quartet being all-syn while the remaining quartets are all-anti. The first quartet is converted to syn due to the absence of any additional nucleotide at the 5′-end of the strands in this structure.¹¹ This facilitates formation of syn-specific stabilizing terminal intra-nucleotide O5′… N3(G) H-bonds (see below).³⁴

All structures contained a single K⁺ ion between the quartets, added manually in case of solution structures. The formal charge on the models is -3 (four phosphates and one cation). Our calculations do not require neutralization, since no periodic boundary conditions are used.

Optimization of AA and AS structures with a subset of X-ray water molecules

The X-ray structures of AA and AS steps reveal bridging water molecules positioned ~3.0 Å from N2(G) of the 5′ anti guanine and ~2.8 Å from O4′ of the following 3′ nucleotide (see below). We prepared additional structures of AA and AS systems with one such bridging water molecule per each GpG dinucleotide. Initial positions of oxygen atoms were taken from the experimental structures while the water molecules were oriented to serve as H-bond donor to O4′(G+1) and acceptor to N2(G).

O5′H…N3(G) H-bonds in 5′-terminal syn G nucleosides

In G-DNA, we need to distinguish between guanines that are the 5′-terminal ones in the sequences and all the other guanines that are preceded by any stem, loop or flanking nucleotide.^11,34 The 5′-terminal guanine is the first nucleotide of the whole molecule and thus possesses free O5’-H termini. When such guanine adopts syn geometry in the G-tract it can form intramolecular O5′H…N3(G) H-bond (Figure 2). Such H-bonds substantially affect the syn vs. anti energy difference in computations as well as in experiments.¹¹ These H-bonds indeed form in experimental structures possessing 5’-terminal guanines. These H-bonds cannot form if there is any nucleotide preceding (in the 5’-direction, i.e., upstream) the syn guanosine since the O5’ is not free. In computations, care is needed with models having 5′-terminal syn guanosines, including cases when the model structure is created by truncation of the experimental structure, since several scenarios can occur.

All X-ray structures with 5′-terminal syn guanosines indicate O5′…N3(G) H-bonds with ~3.0 Å heteroatom distances. However, subsequent formation of these H-bonds in either MM or QM geometry optimizations may be influenced by the initial orientation of the H5T terminal hydrogen, depending also on the optimization protocol (see below). The geometry may be less well defined in NMR structures (see below).

If the syn guanosine is not the 5′ terminal one in the experimental structure, then the backbone adopts different conformation with the O5′…N3(G) distance 4.5–5.0 Å (Figure 2,Supporting InformationTable S1). Even after truncation of a structure leading to a free 5′-terminus, the H-bonds do not form upon QM optimization using such starting structures.

In MD simulations these H-bonds form in all cases with 5′-terminal guanosines irrespective of the starting geometry due to the genuine sampling of the MD method.³⁴

In our starting structures, there are four short O5′…N3(G) distances in the SA-aaaa model and one in the SA-aabb and SA-abab-2 models. They all correspond to presence of 5’-terminal H-bond in the template part of the experimental structures. A specific case is the SA-abab structure where we observed an alternative O5′…N2(G) H-bond with the terminal O5′H group serving as acceptor. This was a result of the initial NMR structure used for optimization. Note that the 148D NMR structure is somewhat ambiguous as its different models display a full spectrum of different positions for the terminal O5′H group of the G1 nucleotide.

The interaction is absent in the experimental structures used as templates for the remaining 5′ terminal syn nucleotides in our 2-quartet stems due to presence of other upstream nucleotides. No terminal H-bonds form in these nucleotides using any minimization protocol, but they still form in simulations.

QM methods

All ab initio QM calculations were performed with the TURBOMOLE 6.3 suite of programs.⁸⁴ The structures were fully optimized using the meta-GGA functional TPSS⁸⁵ and the D3 London dispersion correction with Becke-Johnson damping^73,74 (dubbed DFT-D3(BJ), or as shorthand in the manuscript as DFT-D3). This method has also been used to get the energy data. To estimate reliability of the calculations, a few single point calculations were reevaluated at higher PW6B95-D3(BJ) level.⁸⁶

All geometries optimized in this study were obtained with inclusion of the continuum solvent, although in some analyses we evaluated their energies without the solvent contributions.

In general, the large all-electron Gaussian AO def-TZVP basis set^87,88 was used in the optimizations. In one case, enlargement of the polarization part of the AO basis to def2-TZVP was applied to understand the influence of the methods choices. All of the QM calculations employ the resolution of the identity (RI) approximation^89–91 for the two-electron Coulomb integrals and also apply the numerical quadrature grid m4 ⁹² for the integration of the exchange-correlation contribution.

Bulk solvation effects were represented by the COSMO continuum solvation model^75,76 assuming the bulk dielectric constant of 78.5 for water. The atomic van der Waals radii for the molecular cavity construction in COSMO are taken as their defaults in TURBOMOLE (in Å for H: 1.3, C: 2.0, N: 1.83, O: 1.72, P: 2.11, K: 2.22).

Single-point gas phase energies of individual 5′-GpG-3′ dinucleotides were evaluated at the same level of theory as the QM optimizations.

The choice of the density functional is key aspect in DFT studies and we have worked intensely in recent years to clarify this issue by extensive benchmarking ranging from thermochemistry to molecular interactions.⁹³ Structure optimizations are less sensitive and we are using the TPSS-D3 level as very reliable default for several years. The method is sufficient also for relative energies (see also below).

MM methods

MM calculations were carried out with AMBER9⁹⁴ and the AMBER12 codes using parmbsc0¹⁴ and parmbsc0+parmχ_OL4⁴ force fields, which are recent refinements of the original Cornell et al. force field¹. Parmχ_OL4 is a parameterization of the χ torsion of DNA refining the description of the χ syn region.⁴ Dang’s parameters were used for the description of K⁺ ions.⁹⁵ Two implicit solvation models were employed namely the Poisson-Boltzmann (PB) procedure used in the preceding MM-PBSA study³⁴ and the latest AMBER version of the generalized-Born (GB) method.

The PB optimization procedure included minimization (1000 steepest descent cycles followed by a variable number of conjugate gradient cycles with the convergence criterion for the energy gradient set to 10⁻⁴ kcal/mol/Å) using the Poisson-Boltzmann (PB) procedure with the default AMBER9 settings (dielectric constants of 1.0 and 80.0 for the solute and the solvent, respectively, zero ionic strength, 1.6 Å probe radius, no cutoff for van der Waals and Coulombic interactions, 0.5 Å grid spacing). Atom-type/charge-based radii by Tan et al.⁹⁶ were applied. In our PB calculations, the nonpolar solvation interactions were separated into the attractive and repulsive terms⁹⁷ and the reaction field energy was computed using dielectric boundary surface charges.

GB optimization was carried out with AMBER12 using the Hawkins et al.^98,99 pairwise generalized Born model. The applied minimization methods were based on the LBFGS (Limited-memory Broyden-Fletcher-Goldfarb-Shanno quasi-Newton)¹⁰⁰ algorithm. Other parameter settings were left default (convergence criterion for the energy gradient 10⁻⁴ kcal/mol/Å, zero ionic strength, no inclusion of the surface area in the solvation term).

There is a significant difference between the PB and GB optimization protocols. While the GB optimizations often resulted in visible geometrical changes due to jumping to nearby local minima, the PB minimization in the current AMBER version is inefficient, likely due to errors associated with inexact forces. The PB optimizations did not significantly depart from the starting structure and essentially only relaxed the bond lengths and angles.

Estimation of errors in the QM treatment

Below we present a set of large-scale QM calculations on different topologies of 2-quartet G-DNA stems with inclusion of the sugar-phosphate backbone. Because the systems studied are large for a QM treatment with current hardware resources (250+ atoms, 3000–5000 basis functions) the calculations still necessarily involve some approximations. It is important to distinguish between numerical artifacts and inherent methodological problems of the basic quantum chemical approximation (DFT-D3/COSMO in our case). Note that in the QM treatment no system-specific empirical corrections are made. In our study, only relative energies of several closely related systems are important, reducing the requirement on the accuracy of the QM procedure. Further, the most important results of our study are visible from gas phase calculations of single GpG dinucleotides (see below) and are thus not affected by the solvent model.

We estimate the errors for relative energies to be on the order of a few kcal/mol. Many of the following conclusions are based on thousands of DFT-D3 benchmark calculations that we recently conducted for our GMTKN30 meta-data-base⁹³ and on other studies.^73,101 The capability of the chosen DFT-D3 method to accurately calculate intermolecular forces is documented in the literature beyond any doubt. We have shown recently that the TPSS-D3 method has excellent performance for relative energies of different DNA backbone substates with maximum and average deviations from reference CCSD(T) calculations of 0.5 and 0.2 kcal/mol for a full set of eighteen known DNA backbone families.¹⁰² TPSS-D3 belongs to the most accurate and efficient methods for evaluation of DNA backbone energies, with accuracy almost an order of magnitude better than achieved by the MM in the same test.¹⁰²

Numerical errors in the geometry optimizations are insignificant except for the molecular cavity construction/representation in the COSMO treatment. This prevents converging the QM optimizations very strictly (better than 0.1 kcal/mol).

Considering numerical issues, the RI-approximation, quadrature grid for the exchange-correlation energy and the finite AO basis set provide an estimated numerical precision of about 0.5–1 kcal/mol for relative energies compared to a non-RI, infinitely-sized grid based, and complete basis set result. The def-TZVP basis set is sufficient for structure optimization but yields basis set superposition errors (BSSE) in supermolecular interaction energy computations of 10–20%.¹⁰³ However, as we calculate primarily relative energies, the effects of intramolecular BSSE are diminished. Indeed, the test calculations using larger def2-TZVP basis set revealed only modest changes, 2.4 kcal/mol instead of 3.9 and 8.4 kcal/mol instead of 9.8 for the relative energies of the SA-aaab and SA-abab QM_opt structures, respectively. We suggest that triple-zeta type AO basis sets provide sufficiently converged properties for the present conformational/isomerism problem.

The D3 correction for long and medium range London dispersion effects^73,74 together with standard density functionals has been tested thoroughly for non-covalent interactions in many structurally very diverse, small and large systems.^73,74,93,104 Compared to accurate wave function theory results, DFT-D3 provides a solid 5–10 % accuracy for non-covalent interactions. It can be expected that this high accuracy also transfers to the relative energies which should be accurate to within 0.5 kcal/mol with D3. Another issue is the choice of the basic exchange-correlation functional in DFT. The TPSS functional is of a semi-local type which is prone to so-called self-interaction error (SIE) which can lead to significant error in large systems with localized charges (for recent examples see ref.¹⁰⁵ and, for a general overview about related challenges in DFT see¹⁰⁶). However, for relative (conformational) energies these errors mostly cancel as long as the basic electronic structure is reasonable. This is the case in our systems as exemplified by relatively large HOMO-LUMO gaps of 3–4 eV (at TPSS/def-TZVP level). As shown in Refs.^101,107 the mentioned SIE related problems more or less disappear when the electrostatic interactions are screened by COSMO. We further checked this point by performing very costly PW6B95 functional based DFT-D3 calculations. In this hybrid method part of the semi-local exchange energy is replaced by non-local Fock-exchange, which is SIE free. In these test calculations again only minor differences compared to the TPSS results were found, 2.0 kcal/mol instead of 3.9 and 8.0 kcal/mol instead of 9.8 for the relative energies of the SA-aaab and SA-abab QM_opt structures, respectively. Thus, our reported relative DFT-D3 energies should be in error by at most 2–3 kcal/mol (conservative estimate). This would have no effect on any conclusion of our study. The PW6B95-D3 method is probably the best method that can be used for such large systems. It is the overall best performing hybrid functional for our huge GMTKN30 database.⁹³ For the same reason (i.e., well documented robustness for energies) it was also recently applied for the interactions in supramolecular systems and very good results in comparison to experimental data (binding affinities) were obtained.¹⁰⁸ Thus, the agreement between the TPSS-D3 and PW6B95-D3 energies is a very important test.

The absolute accuracy of the COSMO model is difficult to estimate but of no major concern here as we merely use it to realistically describe the electrostatic interactions for a (in reality) solvated and charged system. As we are mainly interested in a comparison of MM and QM results and both methods employ conceptually similar continuum solvation models, we do not expect a big impact by the specific choice of COSMO. In test calculations employing different dielectric constants of 50.0 and 30.0, respectively, we obtained differences for the relative energy of 3AA+1SS and SA-aabb models with respect to the results for water of only 0.3 and 0.8 kcal/mol. Hence, we conclude that although the solvation model is absolutely essential for a system with several localized negative charges, its implementation details are unimportant. More importantly, the basic differences between the MM and QM results can be deduced from the gas phase computations of the 5′-GG-3′ segments (see below) and thus the results are not due to solvation model.

Results and Discussion

QM optimizations

The 2-quartet stems were initially optimized using both the MM-PB and DFT-D3 – COSMO approaches (MM_opt and QM_opt structures), each starting from the above-described initial structures. As noted in the Method section, the MM-PB optimization procedure caused only insignificant changes in the dihedral angles of the backbone and other aspects of the starting structure. The minimization merely relaxed the bond lengths and angles. In contrast, the QM optimization resulted in larger structural changes (see below). Comparison of the QM and MM relative energies using such disparate structures would be inconsistent. To overcome this, we carried out MM-PB optimizations using the QM_opt structure as the starting structure (QM→MM_opt). Since the PB MM optimization again did not change the structures significantly, the QM→MM_opt and QM_opt structures allow consistent comparison of relative energies of different stem arrangements obtained by the MM and QM energy evaluations. All starting and optimized geometries are provided in the Supporting Information.

Large energy difference between QM and MM descriptions

The first two lines of Table 1 summarize the relative energies obtained by the QM_opt and QM→MM_opt calculations, derived with respect to the AA stem (Figure 3). The values in parentheses show alternative energies after elimination of the 5’-terminal O5′…N3(G) syn intramolecular H-bonds, where relevant (see Methods). This alternative calculation is explained in details in Supporting Information text and Figure S2.

Table 1.

Relative energies (kcal/mol) of 2-quartet G-DNA stems. Solvent screening is included by the method used in the optimization.^a

Method/ Stem	AA	SA-aabb	SA-abab	SA-abab-2	SA- aaab	3AA+1SS	AS	SA-aaaa
QMoptb	0	+0.4 (+7.4)	+9.8	−4.4 (+2.6)	+3.9	+6.8	+16.7	−21.5 (+6.5)
QM→MMoptc	0	−27.0 (−20.3)	−14.8	−31.3 (−25.6)	−22.9	+2.1	−2.7	−53.9(−20.9)
Differenced	0	−27.4 (−27.7)	−24.6	−26.9 (−28.2)	−26.8	−4.7	−19.4	−32.4 (−27.4)
QM→MMoptOL4e	0	−34.0	−17.7	−39.6	−31.4	+3.7	−4.9	−58.4
Cang et al. 34f	0	−14.6(−20.2)	−14.4(−20.0)	−14.4(−20.0)	−13.4(−19.0)	+4.6(+6.0)	+ ~14	N/A

^aIntramolecular O5′H…N3(G) H-bonds in 5′-terminal syn guanosines are present in the following structures: SA-aabb, one interaction; SA-abab-2, one interaction; SA-aaaa, four interactions. All these interactions exist in the original X-ray structures. There is one O5′H…N2(G) H-bond in the SA-abab system. The H-bonds are consistently present/absent in both QM_opt and QM→MM_opt structures and thus should not systematically affect the comparison of QM and MM relative energies.

^bOptimization using the DFT-D3 COSMO approach starting from the initial structure. The estimates in parentheses were obtained by deducting 7 kcal/mol per each syn nucleotide terminal O5′H…N3(G) H-bond (see the text).

^cOptimization using the parmbsc0 force field and PB method starting from the QM_opt structure. Values in parentheses show the energies with elimination of the terminal O5′H…N3(G) H-bonds (see the text).

^dDifference between MM and QM relative energies. The estimates in parentheses were obtained when considering the deductions of the energies of the terminal O5′H…N3(G) H-bonds.

^eOptimization using the parmbsc0+χ_OL4 force field and PB method starting from the QM_opt structure.

^fMD MM-PBSA free energy computations compiled from the Table 1 by Cang et al³⁴ with −4.4 (−3.0 in parenthesis) kcal/mol correction per each 5′-terminal syn base to deduct contributions of all O5′H…N3(G) intramolecular H-bonds (for more details see the original study and the Method section).

Four points are striking: i) The differences between the QM and MM relative energies are large; ii) the variability of the G-DNA stem (i.e., two-quartet quadruplex) energies predicted by the QM approach is much smaller than obtained by the MM method, iii) there is a good correspondence between the MM and QM data when mutually comparing different SA structures but iv) the QM method systematically destabilizes the SA structures compared to the reference AA structure relative to the MM. The latter two points are essential to understand our modified prediction of relative stabilities of G-DNA stems presented below.

We suggest that the QM energies are in better agreement with known experimental data. Many G-DNA forming sequences adopt multiple and often co-existing folds, depending on details of experimental conditions.^{34,41,43,55,56} This argues against large energy differences between different stem arrangements. In addition, tetrameric quadruplexes not constrained by loops form all-parallel all-anti stems in experiments, with the specific exception of one recent structure with 5′-terminal guanines⁸³ discussed in the Methods section. The low stability of the AA stem compared to the SA stems has been noticed in the preceding MD simulation MM-PBSA study as a potential force field imbalance.³⁴ Indeed, the present QM calculations shift the balance in favor of the parallel-stranded all-anti AA arrangement.

The differences between parmbsc0 and parmbsc0+parmχ_OL4 force field computations are small (line 4 of Table 1) and we will further utilize only the parmbsc0 data. The last line of Table 1 shows that the earlier MM-PBSA free energy calculations derived from the parmbsc0 simulation trajectories³⁴ show similar, albeit muted, trends compared with the current single-point MM data. Notable also is the rather large energy difference between the two alternative SA-abab structures (14.2 kcal/mol, QM energies) favoring the SA-abab-2 model that was optimized starting from the high-resolution X-ray data. We assume that ~7 kcal/mol of this energy difference is due to the presence of a single O5′…N3(G) interaction in the SA-abab-2 structure which is absent in the SA-abab structure (see Methods and Supporting Information). The remaining part of the energy difference is due to different backbone conformations seen in the respective X-ray and NMR starting structures.

In conclusion, the most interesting result suggested by Table 1 is the large difference between the QM and MM G-stem energies. In the following parts of the paper we present a series of investigations trying to identify the origin of the QM vs. MM difference. We will investigate two possibilities i) the difference is due to the solute force field not matching the reference QM data or ii) the difference is related to the uncertainty of the solvent model. Finally, we adjust the previous MM-PBSA free energy analysis of different G-stem.³⁴

The energy differences between the QM and MM descriptions originate in intrastrand contributions

We first calculated the energetics of the four isolated 5′-GpG-3′ dinucleotides in all G-stems. The calculations were carried as single-point gas phase calculations using the 5′-GpG-3′dinucleotide geometries taken from the respective QM_opt and QM→MM_opt optimized stem structures (Table 2 and Supporting Information Table S2). These calculations include the intrinsic backbone energies, the intrastrand stacking energies and the base – backbone interactions. In contrast to Table 1, these single-strand gas phase calculations do not include the following terms: interstrand stacking, the stem-ion interactions and the solvation term. These calculations thus considerably help to understand the origin of the difference between QM and MM descriptions. Mainly, they can prove that the results are not caused by the solvent models.

Table 2.

Sum of the relative energies of the four 5′-GpG-3′dinucleotides of the 2-quartet G-DNA stems evaluated as gas phase single points (kcal/mol).^a>

Method/ Stem	AA	SA-aabb	SA- abab	SA-abab-2	SA- aaab	3AA+1S S	AS	SA-aaaa
QMoptb	0	+16.6 (+26.6)	+28.7	+4.6 (+14.6)	+19.1	+17.0	−6.3	−18.7 (+21.3)
QM→MMoptc	0	−9.9 (+5.3)	+5.7	−25.1 (−15.6)	−5.0	+17.9	−12.4	−60.3 (+1.0)
Differenced	0	−26.5 (−21.3)	−23.0	−29.7 (−30.2)	−24.1	+0.9	−6.1	−41.6 (−20.3)
T2-T1e		+0.9 (+6.4)	+1.6	−2.8 (−2.0)	+2.7	+5.6	+13.3	−9.2 (+7.1)

^aFor energies of all the individual GpG dinucleotides, see Supporting InformationTable S2. The values in parentheses are without the 5′ terminal O5′H…N3(G) H-bonds (cf. Table 1).

^bOptimization using the DFT-D3 COSMO approach starting from the initial structure.

^cOptimization using the parmbsc0 force field and PB method starting from the QM_opt structure.

^dDifference between MM and QM relative energies. The estimates in parentheses were obtained when considering the deductions of the energies of the terminal O5′H…N3(G) H-bonds.

^eDifference between predictions from Tables 2 and 1 (lines “Difference”).

The best comparison is to evaluate the QM_opt vs. QM→MM_opt relative energy differences of a given stem with respect to the reference AA G-stem, i.e., line 2 minus line 1 for both Tables 1 and 2. This result is summarized as the last line of Table 2. Clearly, the differences in the gas phase energies of the 5′-GpG-3′ steps in Table 2 explain most of the energy differences for the complete solvated G-stems in Table 1 (see also the correlation between the Table 1 and Table 2 data in Supporting Information Figure S3). Thus, the sizable difference between the QM and MM energies analyzed in our study is due to description of the intrinsic energetics of the sugar-phosphate backbone, intrastrand stacking and intrastrand base – backbone interactions. Only these terms are included in the gas phase 5′-GpG-3′dinucleotide energy calculations in Table 2. In other words, when considering the QM data as the benchmark, the differences between QM and MM data can be primarily attributed to the approximate nature of the DNA force field.

The values in parentheses in Table 2 are alternative estimates upon elimination of the O5′…N3(G) H-bonds (see Supporting Information).

Stacking calculations

Due to genuine G-DNA symmetry, the AA and 3AA+1SS stacking patterns differ from the SA and AS stacking patterns (Supporting Information).^28,109 Thus we have investigated if the difference between QM and MM descriptions could be caused by stacking many-body polarization effects.¹¹⁰ The calculations show that base stacking is described similarly by QM and MM (Supporting Information Table S3).²⁸

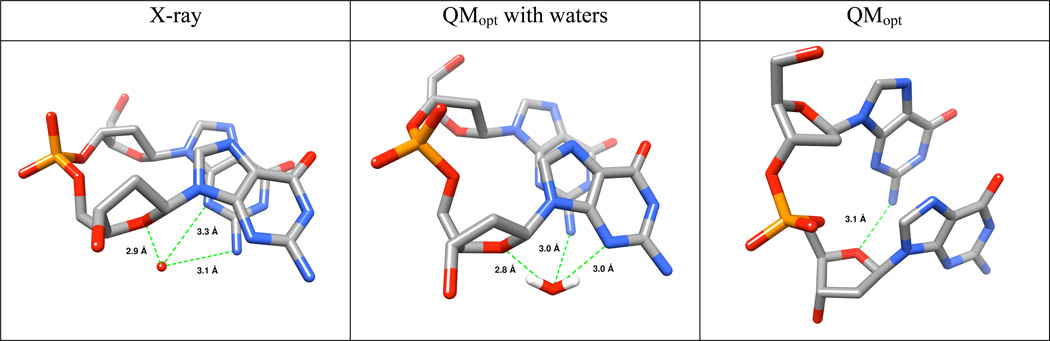
The QM COSMO optimization leads to deviation of some structures from the native geometries and formation of non-native interactions

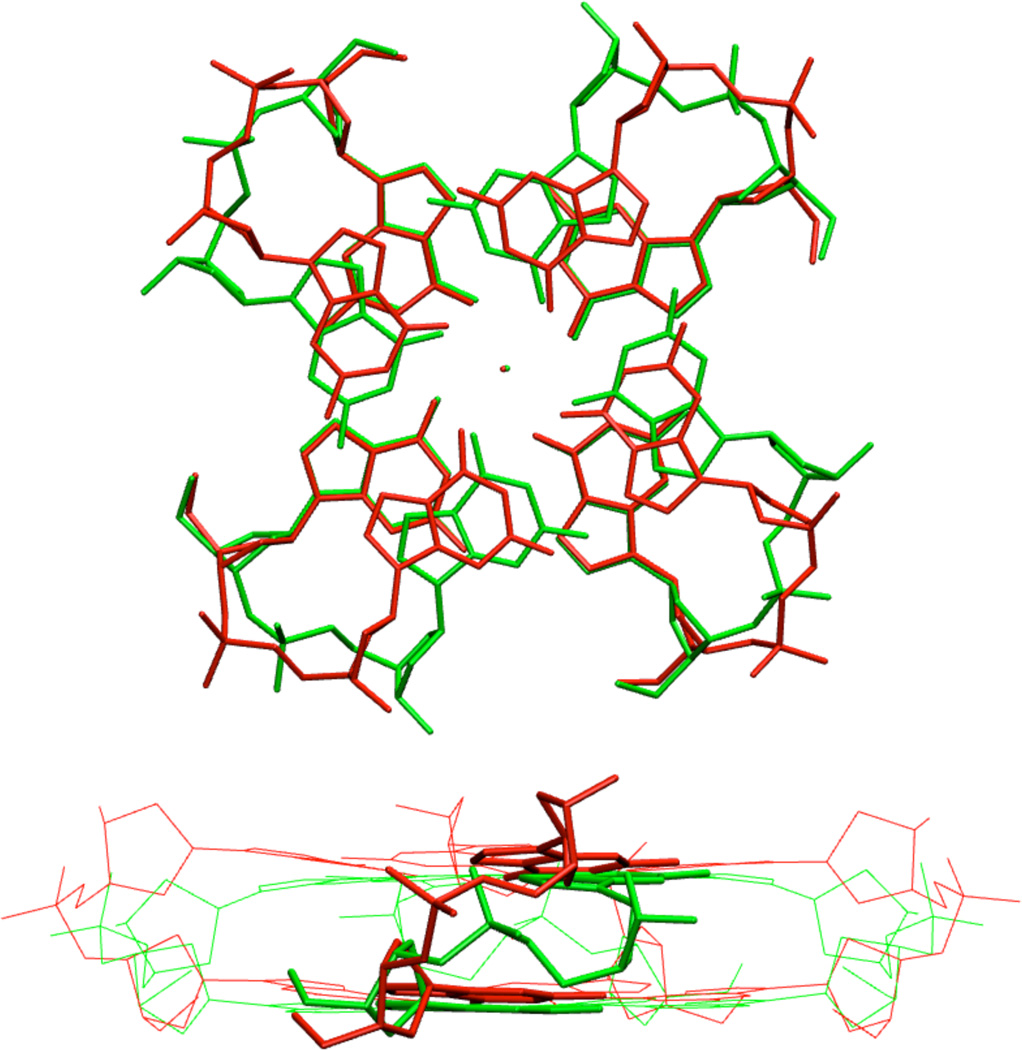
As noted above, the QM geometry minimization changes some of the studied structures. Let us first discuss the reference AA structure.⁷⁸ The QM optimization leads to visible increase of the helical twist while the quartets “buckle” towards each other (Figure 4). It is caused by formation of non-native intrastrand hydrogen bonds between N2 of the first guanine and O4’ of the second sugar (Figure 5). This is not a consequence of the truncation of the model system. Such H-bonds could form in real systems, but are prevented by explicit hydration, which is visible in the X-ray structure (see below). The N2(G)…O4′(G+1) distance drops from the experimental value of 4.5 Å to 3.1 Å upon optimization. The explicit solvent MD simulations do not change the twist of the AA stem³⁴ and the N2(G)…O4′(G+1) H-bonds are not formed.

Figure 4.

QM_opt (green) and X-ray (red) AA structures.

Figure 5.

Detailed view on the non-native N2(G) … O4′(G+1) H-bonds in the QM_opt structure of the AA model.

The geometrical change affects the backbone conformation (Figure 4,Supporting Information Table S4). The starting experimental geometry has common canonical DNA conformation, which is stretched in the course of the QM optimization, including high β values around 240°. The optimized backbone conformation looks like mere extension of the canonical backbone conformation without changing the rotameric family. (By rotameric family we mean specific combination of the backbone dihedrals, since backbone of nucleic acids adopts distinct substates due to mutual correlation of the backbone dihedrals).^18,77,102

The change of the AA structure upon QM optimization reflects lack of explicit solvent in the computations. Still, the structure can be used for comparison of QM and MM methods. We assume that the QM description of the potential energy surface (PES) is intrinsically more accurate than the MM description. We suggest that the AA QM_opt structure is correct per se, i.e., it is the right structure for the given model system and the given approximation of the solvent description. However, caution should be exerted to not over-interpret the data when using them to assess the performance of MM in explicit solvent MD simulations. It is because the comparison is made on a structure, which is shifted away from the native region to another part of the PES. For example, if the MM backbone is stiffer than the QM backbone, the over-twisted structure with stretched backbone would be penalized by the MM description more than by the QM description (see Supporting Information text and Figures S4–S6). Then the errors introduced by the force field into the explicit solvent simulations could be smaller than indicated by Tables 1 and 2, albeit the trends should be correct.

QM optimization of the 3AA+1SS stem also results in substantial increase of helical twist with formation of the non-native N2(G)…O4′(G+1) H-bonds in all three 5′-GpG-3′ AA steps. No changes of helical twist occur in the remaining structures upon QM optimization (Figure S7). There are large changes of the backbone in the AS structure, forming the non-native N2(G)…O4′(G+1) H-bonds in three out of the four strands (Supporting Information Table S4, Figure S8). SA structures show only occasional local rearrangements of the backbone upon QM optimization (Supporting Information Table S4 and the accompanying text). Note that the N2(G)…O4′(G+1) H-bond can be established only when the first guanine is in anti conformation, e.g., in the AA and AS steps, but not in the SA and SS steps.

Energy computations on the MM_opt relaxed initial structures

We have also performed MM PB and DFT-D3 COSMO single point energy computations on the MM_opt structures (Table 3), which differ only insignificantly from the starting structures due to inefficient optimization (see above). Obviously, performing QM single-point energy calculations on MM_opt structures is somewhat inconsistent. However, these calculations are not biased by any non-native features due to optimization in continuum solvent. Still, the MM description overestimates the relative stability of the SA structures (Table 3). However, the difference is smaller than when using the QM_opt structures (Table 1) with over-twisting of the AA and 3AA+1SS stems. The Table 3 reduces the energy difference between the MM and QM results for the SA stems (with exception of SA-aaaa) by ~13–15 kcal/mol, but the basic trend from the Table 1 is unchanged.

Table 3.

Relative energies (kcal/mol) calculated for the MM_opt structures.

Method/ Stem	AA	SA-aabb	SA-abab	SA-abab-2	SA- aaab	3AA+1S S	AS	SA-aaaa
QM on MMopta	0	+8.3	+40.4	+7.0	+11.3	+17.0	+14.5	+27.8
MMoptb	0	−2.0 (−7.7)c	+27.7(+4.8)d	−6.2 (−16.2)c	+1.7	+15.6	+17.6	−1.6 (−34.1)c
Difference l. 2-l. 1e	0	−10.3	−12.7	−13.2	−9.6	−1.4	+3.1	−29.4
QM, Table 3–Table 1f	0	+7.9	+30.6	+11.4	+7.4	+10.2	−2.2	+49.3
MM, Table 3–Table 1g	0	+25.0	+42.5	+25.1	+24.6	+13.5	+20.3	+52.3
Difference l. 5 - l. 4h	0	+17.1	+11.9	+13.7	+17.2	+3.3	+22.5	+3.0

^aDFT-D3 COSMO single point energy on the MM_opt structure.

^bMM_opt using the parmbsc0 force field and PB method starting from the initial (experimental) structure; the optimization procedure essentially keeps the initial structure (see Methods).

^cData in parenthesis show alternative energies when the O5′H…N3 H-bonds are formed by adjusting position of the 5′-terminal hydrogen compared to the automated Leap AMBER assignment (see the text) for those nucleotides where there is such an H-bond in the X-ray experimental structure. This allows formation of the O5′H…N3(G) H-bonds.

^dThe initial structure has one perturbed quartet which is not repaired by the MM optimization. This explains the high relative energy. The number in parentheses is for alternative structure where we established the O5′H…N3(G) H-bond by initial reorientation of the whole O5′H group.

^eDifference between lines 2 and 1, i.e., difference between the MM and QM relative energies. To be compared with line 3 of Table 1.

^fChange of the QM relative energies of the stems predicted by data from the Table 3 compared to the Table 1 (line 1, Table 3 minus line 1, Table 1).

^gChange of the MM relative energies of the stems predicted by data from the Table 3 compared to the Table 1 (line 2, Table 3 minus line 2, Table 1).

^hChange of the predicted MM - QM energy difference when Table 3 is used instead of Table 1. It can be calculated either as difference between the preceding lines 4 and 5 in this Table or as difference between lines 3 from Tables 3 and 1).

Comparison of GB and PB computations

In order to get further insights into the role of different terms, we have reevaluated the MM energies using the GB model of solvent, by performing single point calculations on the QM_opt structures (Table 4 and Supporting InformationTable S5). The GB method modestly reduces the differences between the MM and QM data compared to the PB model. Still, the difference between the QM and MM energies remains sizable. Table 4 also compares gas phase energies of complete stems as evaluated by the QM and MM for the QM_opt structures. Also this calculation confirms that the force field overstabilizes the SA structures compared to the QM level.Supporting Information text and Table S5 present some additional computations, including MM-GB optimizations. All calculations consistently point to a sizable overstabilization of the SA architectures with respect to the AA topology by the MM.

Table 4.

Single point energies (kcal/mol) for QM_opt structures (with no further relaxation) obtained using different methods.

Method/stem	AA	SA- aabb	SA- abab	SA- abab2	SA- aaab	3AA+1SS	AS	SA-aaaa
PBa	0	−24.6	−10.0	−37.2	−22.5	−0.4	+1.7	−57.8
GB	0	−16.0	−3.2	−28.3	−15.1	+5.1	+6.2	−37.7
QMb	0	+0.4	+9.8	−4.4	+3.9	+6.8	+16.7	−21.5
gas phase QM	0	+27.3	+26.1	+23.1	+30.8	+12.2	+44.6	−7.6
gas phase force field	0	+12.8	+16.6	+2.9	+17.7	+10.6	+53.6	−38.2

^aThe PB data in this Table marginally differ from the Table 1 QM→MM_opt data since additional PB relaxation has been done in the Table 1. Note that the purpose of computations in Tables 1 and 4 was slightly different. The Table 1 QM→ MM_opt calculations were done to obtain MM structures and energies using the QM_opt geometry as the start, while the purpose of Table 4 was to derive energies by all methods on entirely unprocessed QM_opt structures.

^bThe reference QM_opt data from the Table 1.

Re-optimization of the AA and AS structures with a subset of X-ray water molecules

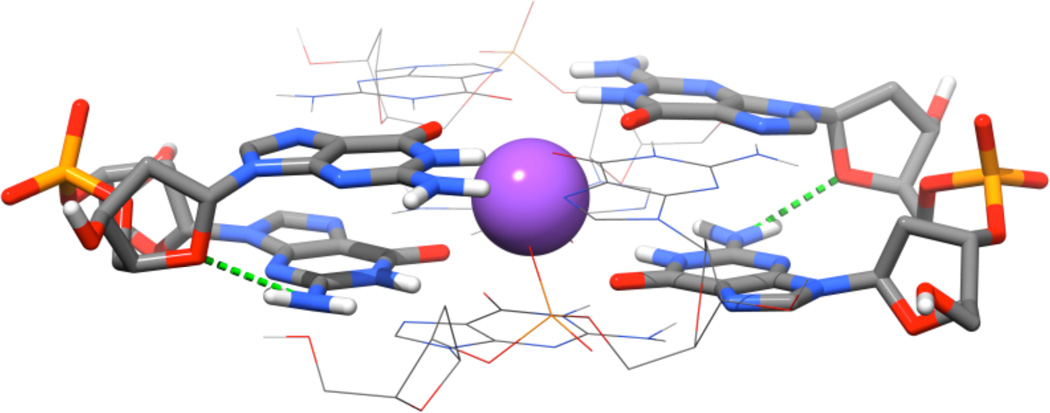
The main weakness of the above computations is over-twisting and deformation of the QM_opt AA structure due to the non-native N2(G)…O4′(G+1) H-bonds. The X-ray structure reveals that the above atoms are bridged by water molecules. Similar hydration site is visible also in MD simulations (not shown) and is almost permanently occupied with dynamical water molecules with binding times of dozens to hundreds picoseconds. Therefore, we have carried out new QM optimizations of AA and AS structures, including these four water molecules based on X-ray data (see Methods and Figure 6). The water molecules prevent formation of the non-native H-bonds and eliminate over-twisting of the AA structure. The new QM_opt structures remained in the native arrangements, although some tendency to adopt higher beta values remains visible (Supporting Information Figure S9 and Table S6). Still, even these native-like structures do not change the basic energy results of our study. Compared to the Table 1, the difference between the AA structure and the remaining structures is shifted by +7.4 kcal/mol and +0.6 kcal/mol at the QM_opt and QM→MM_opt levels, respectively (Supporting Information Table S7). Thus, the key energy difference between the MM and QM descriptions of reference AA stem and various SA structures is reduced by 6.8 kcal/mol (~25%). It is approximately at midpoint between the data from Tables 1 and 3.

Figure 6.

Explicit water molecules prevent non-native N2(G)…O4′(G+1) H-bonds in the QM_opt AA structure. Left - the X-ray water position (red ball, only oxygen is visible), which is essentially identical in all observed instances. Center - example of the water position after the QM optimization; note that the water molecule has somewhat relocated. Right - the non-native H-bond in absence of the explicit water molecule.

Significance of the energy difference between the QM and MM descriptions

The computations reveal a non-negligible difference between the internal structure-energy relation (potential energy surface) of the studied G-DNA systems as described by the MM and QM approaches. We suggest that the difference primarily reflects inaccuracy of the MM method. We are not yet able to exactly quantify the origin of the difference. However, the main part of the QM vs. MM difference is primarily attributed to the DNA force field, namely the description of the backbone and coupling between backbone and bases (cf. Table 2 and the pertinent discussion). For reasons explained above, it is not caused by the continuum solvent model. Although there is no straightforward way to use the present QM data directly for force field parametrization, they can serve as important benchmarks for testing force fields (including future polarization force fields) and fast QM methods.

We found yet another result that supports the above suggestions. During explicit solvent simulations (at ~40 ns) the simulated AA structure converts from right-handed to incorrect left-handed quadruplex.³⁴ We have taken two left-handed AA structures (taken at 50 and 55 ns) and derived their QM_opt structures. The DFT-D3/COSMO approach penalizes these structures by 18 and 23 kcal/mol compared to the reference right-handed AA structure. In contrast, the MM/PB method stabilizes these structures (QM→MM_opt data) by −14 and −21 kcal/mol. Single-strand gas phase calculations equivalent to those in Table 2 show that the QM method penalizes these two left handed structures by 15 and 23 kcal/mol relatively to the MM description.

Reevaluation of the stability order of different G-stem arrangements

The earlier MD simulation study predicted that the four possible 5′-GpG-3′ G-DNA dinucleotides have the following relative stability order: 5′-SA-3′ ~ −4 kcal/mol > AA 0 kcal/mol > AS ~ +4 kcal/mol > SS ~5 kcal/mol.³⁴ The SA and SS steps with 5′-terminal ends have estimated stabilities of ~ −8 and ~ 0 kcal/mol.

This would suggest that G-DNA stems maximize the number of SA steps, avoid AS and SS steps, and the 5-terminal Gs are syn. It gives reasonable prediction for the 2-quartet Thrombin Binding Aptamer (15-TBA), which has the SA-abab fold with one terminal syn G.⁸⁰ For the 3-quartet stems typical for the human telomeric quadruplexes, the prediction would be: hybrid 3+1 topology −9 kcal/mol, basket −5 kcal/mol, parallel all-anti 0 kcal/mol and chair 0.0 kcal/mol (see Supporting InformationFigure S1, Tables S8–S11 and the accompanying text). The calculations thus predict that the different G₃ stems have rather similar stabilities. Indeed, hybrid, parallel all-anti and basket topologies are known from atomistic experiments.^41,43,47,81 The chair topology with three G-quartets has not yet been observed but is not ruled out.¹¹¹ It is also fairly consistent with unexpected formation of 2-quartet SA G-stem of the K⁺ form of the [G₃(T₂AG₃)T] sequence. The 5′-terminal G imposes syn orientation of its first guanine while the loss of four less favorable AS steps is compensated for by the loop and flanking base interactions.¹¹² However, for the intramolecular parallel G₃ stem the energy order would incorrectly predict fold with four 5′-SAA-3′ strands (the first quartet flipped to syn) to be more stable than the observed all parallel all anti-structure with four 5′-AAA-3′ strands.¹¹³ The model fails for tetrameric G₄ stems lacking 5′-terminal Gs (e.g., (TGGGT)₄), as the parallel structures with four SAAA or SASA strands as well as anti-parallel four SASA strands structure are predicted to be considerably more stable than the observed parallel four AAAA strands structure.^78,114,115 For (GGGG)₄, the observed structure with four SAAA strands⁸³ is correctly predicted¹¹ and also the antiparallel four-tetrad stems (1JPQ and 2AVH) are correctly predicted to have four SASA strands.^79,116,117 The prediction likely overestimates stability of the SA step compared to AA step. In order to prefer all-anti arrangement for parallel stems, the SA step should be slightly less stable than the AA step.

Therefore, we have added a correction to the original data³⁴ based on present QM results. Such correction is justified, since the preceding and present study use the same force field and PB model of the solvent. The refined prediction has been obtained in the following manner. For the SA 5′-GG-3′step, we took the sum of MM-QM energy difference for the SA-aaab, SA-abab, SA-abab-2 and SA-abbb stems divided by 16 (the structures have 4×4 SA steps). We did not use the SA-aaaa structure as it was not included in the original stud y. For reasons explained above (the over-twisting and non-native interactions), we have taken average of the values from Tables 1 and 3, as the Table 1 likely overestimates and Table 3 underestimates the difference. We have taken data with eliminated 5′-terminal H-bonds (in parentheses in Table 1). Alternative calculations with inclusion of the 5′-terminal H-bonds or with inclusion of the SA-aaaa structure would not change the results dramatically. Our data give +4.7 kcal/mol correction, predicting the SA step to be by ~ +1.2 kcal/mol less stable than the AA one. Alternatively, we could use the energy data derived for the improved AA QM_opt geometry optimized with the X-ray water molecules (Supporting Information Table S7); in this case we would not need to consider Table 3 data for balancing the results. This would lead to essentially identical correction of +4.9 kcal/mol. The calculation for the remaining steps is given in Supporting Information.

We obtain the following stability order of the GpG G-DNA steps (kcal/mol): AA (0), SA (+1.2), AS (+3.5), SS (+7.8), S_5′termA (−3.2) and S_5′termS (+3.4). (“S_5’term” means 5’-terminal syn, see Supporting InformationFigure S1). Although the data were derived by studies of formally intermolecular 2-quartet stems, the prediction is applicable to any N-quartet tetrameric, dimeric and intramolecular G-DNA stem. It gives estimate of relative intrinsic G-DNA stem stability with the following factors taken into account: number of quartets, strand orientation pattern, syn-anti pattern and presence or absence of additional nucleotide at the 5’-end of the strands. The model does not take into account additional effects of loops, ion types and some other effects. The model takes into account solvation effects via the MD simulation runs³⁴ and using continuum solvent approximation for the energies. Although our stability order is only approximate, it helps separate intrinsic properties of G-stems from the remaining effects.

The adjusted energy order improves the predictions (Supporting Information Tables S8–S11). Mainly, the observed all-anti parallel topology is now correctly predicted for the tetrameric stems while four SAAA strands topology (4SAAA) remains correctly predicted for the tetrameric G₄ parallel stem with 5′-terminal guanines. All-anti pattern is also correctly predicted for the intramolecular parallel-stranded stems. The 4SASA structure is correctly predicted for the antiparallel G₄ stem, since other antiparallel variants such as 2SAAA + 2ASSS are less stable. The stability order of different G₃ topologies is now as follows: parallel all-anti 0 kcal/mol, hybrid ~ +13 kcal/mol, and basket and chair ~ +20 kcal/mol. These differences may look rather large, but as noted above, the results should be primarily considered as relative trends. In addition, the estimates of the AS and SS steps relative energies are less certain than the estimate for the SA step. Importantly, the calculation now predicts the observed syn-anti patterns for different G₃ stem topologies: all-anti for the all parallel stem, 3SAA+1SSA for the hybrid arrangement, and for chair and basket there are two variants with similar energies, namely 2SSA+2SAA and 2SAS+2ASA. The later is observed for the basket topology (See Supporting Information). The prediction is also consistent with recent NMR study showing that all-parallel all-anti form of d(TGGGT)₄ and d(TGGGGT)₄ is accompanied by minor species having 5′-end syn tetrad.¹¹⁸ This indicates that the AA step is only slightly more stable than the SA step.

Concluding remarks

Structural dynamics and energetics of nucleic acids have been traditionally studied by Molecular Mechanics (MM) approaches using simple force fields. The main limitation of the MM approaches is the highly approximate nature of the force fields. Therefore, it is tempting to include the recently developed accurate large-scale (hundreds of atoms) QM calculations into the portfolio of computational techniques to study nucleic acids. Here we apply such computations for the first time to nucleic acids. Namely, we study different folds of the cation-stabilized 2-quartet guanine quadruplex stem, complementing recent classical simulation and free energy analysis.³⁴ Our results are relevant not only for G-DNA molecules. Comparably large differences between MM and QM descriptions may be common also for other nucleic acids systems and may affect their MM-based computational studies. Before advance of large-scale QM computations, we had no appropriate tool to capture such differences.

QM calculations provide assessment of the bias introduced by force fields and include physical-chemistry effects neglected in MM description. Most notable are electronic polarization (induction) effects, which contribute the bulk of important non-additive (many-body) interactions in polar systems. The pair-additive force fields with constant atom-centered point charges neglect sensitivity of the electronic structure of the system to external electric fields while in reality the electronic structures of the individual bases and backbone units respond to their environment.¹¹⁹ The force field also does not allow sufficiently accurate description of different conformations of the flexible and highly polarizable negatively charged DNA sugar phosphate backbone. The missing contributions are unphysically compensated for by the dihedral terms of the force field.^11,40

Our study reveals large systematic differences between the MM and QM relative energy order of stability of the different G-DNA stem topologies. The MM approach underestimates the relative stability of G-DNA stems with dominant 5′-anti-anti-3′ steps (AA and 3AA+1SS folds) compared to topologies with 5′-syn-anti-3′ steps (SA-aaab, SA-aabb and SA-abab). Although the magnitude of overstabilization of the SA steps by force field varies in different sets of computations, the trend is unambiguously seen from all computations. It means that MD simulation and free energy studies of G-DNA stems are affected by systematic bias in favor of structures with antiparallel stem arrangements with SA steps. However, we would like to underline that the MM description is certainly sufficiently balanced for many analyses.¹¹ Nevertheless, combining MM and QM analyses can improve future theoretical predictions. Our study indicates that the limitations of MM methods in studies of nucleic acids may be larger than usually assumed.

When using the QM energy data as a correction to earlier free energy estimates of relative stability of different G-stem folds,³⁴ improved agreement with the experimental data is achieved. The new model uses both explicit solvent simulation MM data and QM data, with the following factors taken into account: number of quartets, strand orientation pattern, syn-anti pattern and presence or absence of additional nucleotide at the 5’-end of the strands. The remaining limitations of the model are explained above. According to the new prediction, the 5′-syn-anti-3′ G-DNA dinucleotide step is slightly less stable than the 5′-anti-anti-3′ step. We confirm the stabilizing role of 5’-terminal H-bonds of 5’-terminal syn G-DNA nucleotides.

We also illustrate difficulties facing large-scale QM computations of nucleic acids. The first issue is limited sampling, which depends on the availability of relevant starting structures. Future QM studies could profit from analysis of series of starting structures sampled by the classical explicit solvent MD simulations. The other issue is the remaining incompleteness of the studied system, which in our particular case is representation of the environment via continuum solvent model. We have observed excessive geometrical changes of some molecules including formation of non-native intramolecular interactions. We show that at least in some cases such undesired rearrangements can be prevented by including a subset of explicit water molecules. However, the difference between the MM and QM descriptions is consistently visible already from the “in vacuo” energy calculations (Tables 2 and 4). Thus our basic results are not caused by approximations of the continuum solvent models and may be considered as estimation of genuine errors inherent to the MM description. Further investigations will be needed to see if such large discrepancies between QM and MM descriptions are common also for other types of nucleic acids structures.