Abstract
Two methods of quantifying heterogeneity between studies in meta-analysis were studied. One method quantified the proportion of the total variance of the effect estimate due to variation between studies (RI), and the other calibrated the variance between studies to the size of the effect itself through a between-study coefficient of variation (CVB). Bootstrap and asymptotic confidence intervals for RI and CVB were derived and evaluated in an extensive simulation study that covered a wide range of scenarios likely to be encountered in practice. The best performance was given by asymptotic Wald confidence intervals developed for RI and CVB. The use of these heterogeneity measures together with their confidence intervals was illustrated in 5 typical meta-analyses. A new user-friendly SAS macro (SAS Institute, Inc., Cary, North Carolina) is provided to implement these methods for routine use and can be downloaded at the last author's website.
Keywords: confidence intervals, heterogeneity, meta-analysis, statistical methods
In recent decades, meta-analysis has become an essential tool for implementing the evidence-based approach to clinical practice and other areas of medicine and public health. After years of controversy, the debate on the usefulness of the meta-analytic approach has abated. Meta-analysis is now the most cited study design in the health sciences and is ranked as providing the highest level of evidence, surpassing that of individual randomized controlled trials (1).
A controversial aspect of meta-analysis methods has been how best to summarize findings in the presence of heterogeneous between-study effects. Several solutions have been suggested, including graphs (2), tests (3), use of the random-effects model (4), and descriptive statistics that quantify heterogeneity (5, 6).
Hypothesis testing as the focus of data analysis has been criticized in epidemiology, clinical research, and meta-analysis because test results are functions of both the magnitude of the underlying effect and the sample size (7). Although the number of individual subjects included in a meta-analysis is generally high, the number of studies is usually low, and tests are typically underpowered to detect heterogeneity (5). Assessing heterogeneity through graphs has been proposed as an alternative to hypothesis testing, but this approach can suffer from poor reproducibility between raters (2). Random-effects models are not always more conservative than fixed-effects models (8), and their indiscriminate use in computing pooled measures of effect in meta-analysis has thus not been universally accepted as a method for addressing heterogeneity. To address these limitations, in 1999 Takkouche et al. (5) proposed 2 quantities for quantifying the magnitude of heterogeneity in the meta-analyses: the proportion of total variance due to between-study variation (RI) and the between-study coefficient of variation (CVB). Methods were given to estimate both RI and CVB, and software (9) was developed to compute these quantities. Later, Higgins and Thompson (10) proposed a similar quantity, I2, which can also be used to estimate the proportion of the overall variance due to variation between studies.
Although 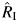 and
and 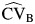 have been used in meta-analyses (e.g., 11, 12), until now confidence intervals have not been available, likely limiting their use. In the present study, we developed several asymptotic and bootstrap (13) methods for computing confidence intervals (CIs) for RI and CVB. In an extensive simulation study, we evaluated the performance of these newly proposed CIs. Finally, we made recommendations for best practice for meta-analysis that is informed by this work and presented a SAS macro that can be used to conduct a meta-analysis, including one with point and interval estimates of the recommended heterogeneity measures.
have been used in meta-analyses (e.g., 11, 12), until now confidence intervals have not been available, likely limiting their use. In the present study, we developed several asymptotic and bootstrap (13) methods for computing confidence intervals (CIs) for RI and CVB. In an extensive simulation study, we evaluated the performance of these newly proposed CIs. Finally, we made recommendations for best practice for meta-analysis that is informed by this work and presented a SAS macro that can be used to conduct a meta-analysis, including one with point and interval estimates of the recommended heterogeneity measures.
MATERIALS AND METHODS
Notation and a brief review of the meta-analysis models
The 2 primary models used in meta-analyses are the fixed-effects model, 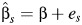 , s = 1, …, S, and the random effects model,
, s = 1, …, S, and the random effects model, 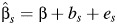 , s = 1, …, S, where β is the common effect under the fixed-effects model and an inverse-variance weighted population average under the random-effects model, bs represents the random variation between studies, es represents the sampling error around the true effect in the fixed-effects model and the sampling error around the study-specific effect in the random-effects model,
, s = 1, …, S, where β is the common effect under the fixed-effects model and an inverse-variance weighted population average under the random-effects model, bs represents the random variation between studies, es represents the sampling error around the true effect in the fixed-effects model and the sampling error around the study-specific effect in the random-effects model, 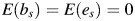 , var(bs) = τ2,
, var(bs) = τ2, 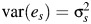 ,
, 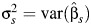 , s = 1, …, S, and S is the total number of studies included in the meta-analysis. The fixed-effects model is used to compute the common effect under the assumption that the effect is homogenous across all studies. The random-effects model is often used otherwise.
, s = 1, …, S, and S is the total number of studies included in the meta-analysis. The fixed-effects model is used to compute the common effect under the assumption that the effect is homogenous across all studies. The random-effects model is often used otherwise.
Heterogeneity tests focus on the null hypothesis that there is no heterogeneity between studies, that is, H0 : τ2 = 0. The standard heterogeneity test used in meta-analyses is the Q test (14). The test statistic, Q, is formed as a weighted sum of squared deviations of each study-specific estimate from the common effect, that is, 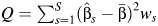 , where
, where 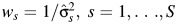 and
and 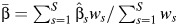 is the fixed effects estimator. DerSimonian and Laird (14) proposed the widely used estimator of the variance between studies, τ2, based on Q:
is the fixed effects estimator. DerSimonian and Laird (14) proposed the widely used estimator of the variance between studies, τ2, based on Q:
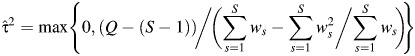 |
(1) |
In meta-analyses with data from very precise studies and/or a large number of contributing studies, the P value for the test for heterogeneity could be small (e.g., <0.05) when the magnitude of heterogeneity is also small and of no practical importance. On the other hand, if the contributing studies are small and/or there are few of them, the hypothesis of heterogeneity may fail to be rejected even when τ2 is large. Therefore, measures that represent the magnitude of heterogeneity in an intuitive form are needed to fully evaluate heterogeneity in meta-analyses.
Estimators of the magnitude of heterogeneity
As previously noted, in meta-analyses, hypothesis tests are often underpowered to detect heterogeneity (5). Furthermore, the P value does not quantify the magnitude of heterogeneity. In what follows, we consider 2 quantities for assessing the magnitude of heterogeneity that can be used as an alternative or supplement to hypothesis testing.
Takkouche et al. (5) proposed an estimator of the proportion of the total variance of the pooled effect estimate of β due to between-study heterogeneity as 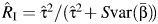 , where
, where 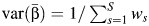 and
and 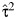 is given by equation 1. One intrinsic disadvantage of using
is given by equation 1. One intrinsic disadvantage of using 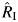 as a measure of the amount of heterogeneity between studies is that it tends toward 1, its maximum value, as
as a measure of the amount of heterogeneity between studies is that it tends toward 1, its maximum value, as 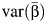 decreases. In this way, a meta-analysis based on large, precise studies would likely yield a large RI even when there is little heterogeneity between the study-specific effect estimates. To address this limitation, Takkouche et al. proposed the between-study coefficient of variation, CVB = τ/|β|, to provide further insight into the magnitude of heterogeneity in a meta-analysis (5). The estimator of CVB, which ranges in value from 0 to ∞, replaces τ with
decreases. In this way, a meta-analysis based on large, precise studies would likely yield a large RI even when there is little heterogeneity between the study-specific effect estimates. To address this limitation, Takkouche et al. proposed the between-study coefficient of variation, CVB = τ/|β|, to provide further insight into the magnitude of heterogeneity in a meta-analysis (5). The estimator of CVB, which ranges in value from 0 to ∞, replaces τ with 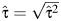 and β with
and β with 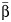 . In the present article, we slightly revised the estimator of CVB proposed by Takkouche et al. (5) so that the denominator is
. In the present article, we slightly revised the estimator of CVB proposed by Takkouche et al. (5) so that the denominator is 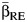 , the random-effect estimator, rather than the fixed-effect estimator,
, the random-effect estimator, rather than the fixed-effect estimator, 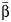 . Because CVB is the between-study coefficient of variation, it is more meaningful to estimate β as
. Because CVB is the between-study coefficient of variation, it is more meaningful to estimate β as 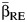 under the random-effects model when the between-study variance is nonzero; otherwise, the CVB is by definition 0 and no quantification of the magnitude of heterogeneity is needed. Later, we report on an evaluation of the empirical bias of these 2 options in an extensive simulation study. Note that CVB has the intrinsic disadvantage of increasing arbitrarily for a small β, and it is undefined when β = 0.
under the random-effects model when the between-study variance is nonzero; otherwise, the CVB is by definition 0 and no quantification of the magnitude of heterogeneity is needed. Later, we report on an evaluation of the empirical bias of these 2 options in an extensive simulation study. Note that CVB has the intrinsic disadvantage of increasing arbitrarily for a small β, and it is undefined when β = 0.
CI construction
It is widely agreed that point estimates are best considered alongside their CIs to allow for proper interpretation of results. Here, we study several approaches for calculating confidence intervals for RI and CVB, which are derived in Appendix 1. First, we consider 4 different algorithms for bootstrapped CIs for CVB and RI (13). For simplicity, we explain these algorithms for the CIs for RI. When applying these methods to the CVB, 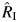 is replaced by
is replaced by 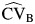 .
.
The standard bootstrap uses the empirical percentiles of the observed distribution of the resampled statistics to obtain the standard bootstrapped CI. The range-based bootstrap approximates the sample distribution of  by its resampled distribution. The bias-corrected, accelerated method for the bootstraped CIs is also based on percentiles of the bootstrap distribution, calculated using the normal distribution with an adjustment for both bias and skewness. Finally, the normal approximation method uses the normal distribution as an approximation to the distribution of RI. Details on these algorithms are given in Appendix 2.
by its resampled distribution. The bias-corrected, accelerated method for the bootstraped CIs is also based on percentiles of the bootstrap distribution, calculated using the normal distribution with an adjustment for both bias and skewness. Finally, the normal approximation method uses the normal distribution as an approximation to the distribution of RI. Details on these algorithms are given in Appendix 2.
Next, we derived 4 asymptotic methods to obtain the CIs for RI. First, the normal method is the standard Wald-type confidence interval, 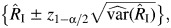 where z1−α/2 is the (1 − α/2) quantile of the standard normal distribution and
where z1−α/2 is the (1 − α/2) quantile of the standard normal distribution and 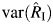 is given by equation A1. The logit method re-expresses the CI for logit(RI),
is given by equation A1. The logit method re-expresses the CI for logit(RI),
with
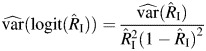 |
and uses the inverse logit transformation of the upper and lower bounds of this CI to obtain the asymmetric 95% CIs for RI. Note that if 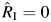 , this CI is not defined. In the Q method, the CIs for RI are obtained as
, this CI is not defined. In the Q method, the CIs for RI are obtained as
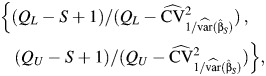 |
(2) |
where QL and QU are the lower and the upper limits of the CI for Q, equal to 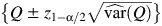 , and
, and 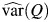 is given in equation A2, where
is given in equation A2, where
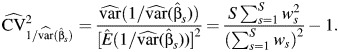 |
In the gamma method, asymmetric CIs for RI can be calculated by expression 2, where the limits of CIs of Q are based upon the percentiles of a gamma distribution (15). This gamma distribution is a scaled χ2 distribution, in which it is assumed that Q ∼ αχ2(d), where E(Q) = αd and var(Q) = 2α2d.
In addition, we derived 4 asymptotic methods for calculating the CI for CVB. The univariate delta method takes 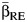 as fixed and considers only
as fixed and considers only 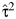 as random. This CI takes the form
as random. This CI takes the form 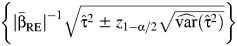 , where
, where 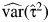 is given by equation A3. The multivariate delta method is based on equation A4 for
is given by equation A3. The multivariate delta method is based on equation A4 for 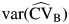 , which is then inserted into the Wald-type expression for the CI
, which is then inserted into the Wald-type expression for the CI 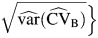
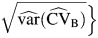 . Finally, the asymmetric log-transformed univariate delta (log-univariate delta) method and log-transformed multivariate delta (log-multivariate delta) method are logarithmic transformations of the univariate delta and multivariate delta methods, which are given by
. Finally, the asymmetric log-transformed univariate delta (log-univariate delta) method and log-transformed multivariate delta (log-multivariate delta) method are logarithmic transformations of the univariate delta and multivariate delta methods, which are given by 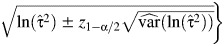
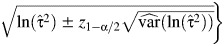 and
and 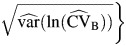
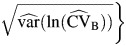 , respectively.
, respectively.
SIMULATION STUDY
Simulation study design
The simulation study was designed to assess the performance of the proposed methods for computing the CIs for RI and CVB. To cover the full range of heterogeneity that could be observed in practice, we considered values of RI equal to 0.1 (low heterogeneity), 0.3, 0.5, 0.7, and 0.9 (high heterogeneity) and values for CVB equal to 0.1 (low heterogeneity), 1, and 2 (high heterogeneity). The number of studies, S, was set equal to 10, 20, 50, and 100, and for each scenario we generated 10,000 simulated meta-analyses.
The types of studies considered in this simulation experiment are those in which a relative risk is estimated as the measure of effect and could be in the form of a rate ratio, odds ratio, or risk ratio. The relative risk (RR = exp{β}) of the studies in the simulations was set to 1 (no effect), 1.5, 2, and 4 (high effect). Note that the cases in which RR < 1 are identical to the cases in which RR > 1 and can be easily obtained by switching the coding of the exposure variable.
The variance between studies was set at τ2 = (CVB β)2 except when the RR = 1. When RR = 1, β = 0. Thus, from the definition of the CVB, once β = 0, τ2 = 0 as well, and, as a result, RI will be 0, too. Therefore, when the RR was equal to 1, we needed an alternative way to fix τ2, and we did this by solving for τ2 from the definition of 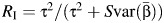 . Assuming then that the possible values of the upper bounds, UB, of the CIs for the RR were 1.1, 1.2, 1.5, and 2, for each combination of RI and S, the variance between studies could then be defined as τ2 = RIS(ln(UB)/1.96)2/(1 − RI).
. Assuming then that the possible values of the upper bounds, UB, of the CIs for the RR were 1.1, 1.2, 1.5, and 2, for each combination of RI and S, the variance between studies could then be defined as τ2 = RIS(ln(UB)/1.96)2/(1 − RI).
The variation in the study-specific weights used to construct the summary estimator depends upon the variation in the within-study variances. We thus considered values of the coefficient of variation of the reciprocal values of within-study variances, 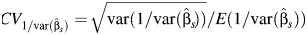 , equal to 0.1, 1, 2, and 3, representing a somewhat wider range than that observed in the meta-analyses considered as examples in this article (see the Examples of meta-analysis section below). These quantities were generated as random variables from the log-normal distribution with mean
, equal to 0.1, 1, 2, and 3, representing a somewhat wider range than that observed in the meta-analyses considered as examples in this article (see the Examples of meta-analysis section below). These quantities were generated as random variables from the log-normal distribution with mean 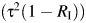
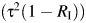 and variance defined as
and variance defined as 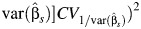
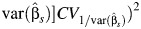 .
.
To assess the performance of the methods described above for calculating the 95% CIs, we summarized the proportion of times that the CIs covered the true value of the parameter and the mean length of the CIs. With 10,000 replications, the CIs will fail to cover the desired nominal range when the empirical coverage falls outside of 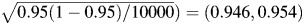
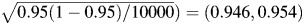 .
.
Results of the simulation study
In what follows, we present the results concerning the percent relative bias of 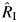 and
and 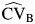 , as well as their empirical coverage probabilities. Because the results were similar for all values of the RR considered up to the third decimal place, we present the results for bias and coverage for RR = 2 only.
, as well as their empirical coverage probabilities. Because the results were similar for all values of the RR considered up to the third decimal place, we present the results for bias and coverage for RR = 2 only.
Table 1 presents the percent relative bias of 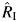 . As expected, the empirical bias decreased as the number of studies in the meta-analysis increased. For small values of RI,
. As expected, the empirical bias decreased as the number of studies in the meta-analysis increased. For small values of RI, 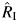 overestimated RI, and when the values of RI were bigger than 0.3, RI was modestly underestimated. The empirical bias in
overestimated RI, and when the values of RI were bigger than 0.3, RI was modestly underestimated. The empirical bias in 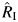 was low over a wide range of values for the coefficient of variation of the reciprocal within-study variances, although some increase in bias was observed when a large amount of variation in within-study variances was considered. When the number of studies was very large, for example, S = 100, the estimator had little bias.
was low over a wide range of values for the coefficient of variation of the reciprocal within-study variances, although some increase in bias was observed when a large amount of variation in within-study variances was considered. When the number of studies was very large, for example, S = 100, the estimator had little bias.
Table 1.
Percent Relative Bias in 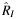 a
a
| No. of Studies by RI Value | 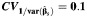 |
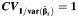 |
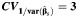 |
|---|---|---|---|
| RI = 0.1 | |||
| 10 | 50 | 56 | 167 |
| 20 | 35 | 32 | 64 |
| 50 | 16 | 16 | 19 |
| 100 | 5 | 5 | 9 |
| RI = 0.3 | |||
| 10 | −14 | −17 | 2 |
| 20 | −13 | −13 | −13 |
| 50 | −8 | −8 | −12 |
| 100 | −4 | −5 | −7 |
| RI = 0.5 | |||
| 10 | −19 | −20 | −26 |
| 20 | −10 | −12 | −20 |
| 50 | −4 | −5 | −11 |
| 100 | −2 | −2 | −5 |
| RI = 0.7 | |||
| 10 | −11 | −14 | −32 |
| 20 | −5 | −7 | −15 |
| 50 | −2 | −3 | −6 |
| 100 | −1 | −1 | −3 |
| RI = 0.9 | |||
| 10 | −3 | −5 | −19 |
| 20 | −1 | −2 | −6 |
| 50 | 0 | −1 | −2 |
| 100 | 0 | 0 | −1 |
Abbreviations: 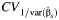 , the coefficient of variation of the reciprocal values of within-study variances; RI, proportion of total variance due to variation between studies.
, the coefficient of variation of the reciprocal values of within-study variances; RI, proportion of total variance due to variation between studies.
a Relative risk = 2, coefficient of variation between studies = 1.
The percent relative bias of the between-study coefficient of variation is presented in Table 2. When CVB was small, the bias was very small. When CVB was large (>1) but the value of RI was small, for example, RI = 0.1, 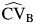 did not perform well. However, this is an unrealistic scenario because a large CVB reflects a large value of τ2 compared with the effect size, and therefore it would be expected that RI would not be small. As the value of RI increased, the bias of
did not perform well. However, this is an unrealistic scenario because a large CVB reflects a large value of τ2 compared with the effect size, and therefore it would be expected that RI would not be small. As the value of RI increased, the bias of 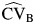 decreased. The bias of
decreased. The bias of 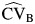 decreased when the number of studies in the meta-analysis increased. In addition, we found that when RI was greater than 0.5, in most cases considered, the
decreased when the number of studies in the meta-analysis increased. In addition, we found that when RI was greater than 0.5, in most cases considered, the 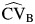 using the fixed-effects estimator of β had more bias than did the one with the random-effects estimator,
using the fixed-effects estimator of β had more bias than did the one with the random-effects estimator, 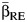 , and in many cases, substantially so (data not shown). Because these estimators of the magnitude of heterogeneity between studies are relevant only when heterogeneity between studies is evident, it follows that the estimator of β typically used when heterogeneity between studies is evident, the random-effects estimator, should be used for estimating the CVB.
, and in many cases, substantially so (data not shown). Because these estimators of the magnitude of heterogeneity between studies are relevant only when heterogeneity between studies is evident, it follows that the estimator of β typically used when heterogeneity between studies is evident, the random-effects estimator, should be used for estimating the CVB.
Table 2.
Percent Relative Bias in 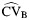 a
a
| No. of Studies by RI Value |
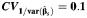 b b |
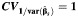 c c |
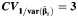 d d |
||||||
|---|---|---|---|---|---|---|---|---|---|
| CVB | |||||||||
| 0.1 | 1 | 2 | 0.1 | 1 | 2 | 0.1 | 1 | 2 | |
| RI = 0.1 | |||||||||
| 10 | 2 | 554 | 231 | 4 | 309 | 560 | 152 | 127 | 141 |
| 20 | −7 | 304 | 289 | −4 | 126 | 462 | 7 | 343 | 687 |
| 50 | −11 | 91 | 268 | −10 | 128 | 212 | −8 | 166 | 479 |
| 100 | −12 | 14 | 451 | −12 | 31 | 269 | −11 | 49 | 557 |
| RI = 0.3 | |||||||||
| 10 | −15 | 154 | 251 | −16 | 326 | 252 | 14 | 219 | 624 |
| 20 | −12 | 57 | 246 | −14 | 101 | 321 | −15 | 608 | 365 |
| 50 | −7 | 2 | 134 | −7 | 6 | 261 | −11 | 16 | 314 |
| 100 | −4 | 0 | 51 | −4 | 1 | 77 | −5 | 1 | 131 |
| RI = 0.5 | |||||||||
| 10 | −12 | 209 | 388 | −14 | 279 | 249 | −7 | 221 | 159 |
| 20 | −6 | 24 | 278 | −8 | 47 | 489 | −12 | 176 | 222 |
| 50 | −2 | 2 | 58 | −3 | 5 | 126 | −6 | 5 | 147 |
| 100 | −1 | 1 | 14 | −1 | 2 | 27 | −3 | 1 | 75 |
| RI = 0.7 | |||||||||
| 10 | −6 | 34 | 340 | −9 | 396 | 548 | −17 | 197 | 226 |
| 20 | −3 | 6 | 169 | −4 | 214 | 539 | −9 | 50 | 491 |
| 50 | −1 | 2 | 38 | −2 | 5 | 99 | −4 | 3 | 118 |
| 100 | 0 | 1 | 6 | −1 | 2 | 16 | −2 | 1 | 15 |
| RI = 0.9 | |||||||||
| 10 | −3 | 32 | 339 | −5 | 162 | 415 | −14 | 88 | 315 |
| 20 | −2 | 5 | 142 | −3 | 17 | 315 | −5 | 7 | 275 |
| 50 | −1 | 2 | 36 | −1 | 5 | 107 | −3 | 0 | 45 |
| 100 | 0 | 1 | 5 | 0 | 2 | 13 | −2 | 0 | 7 |
Abbreviations: CVB, coefficient of variation between studies; 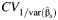 , the coefficient of variation of the reciprocal values of within-study variances; RI, proportion of total variance due to variation between studies.
, the coefficient of variation of the reciprocal values of within-study variances; RI, proportion of total variance due to variation between studies.
a Relative risk = 2.
b The mean values when the coefficients of variation between studies were 0.1, 1, and 2 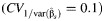 were −5 (standard deviation, 5), 75 (standard deviation, 139), and 187 (standard deviation, 140), respectively.
were −5 (standard deviation, 5), 75 (standard deviation, 139), and 187 (standard deviation, 140), respectively.
c The mean values when the coefficients of variation between studies were 0.1, 1, and 2 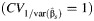 were −60 (standard deviation, 5), 108 (standard deviation, 130), and 268 (standard deviation, 185), respectively.
were −60 (standard deviation, 5), 108 (standard deviation, 130), and 268 (standard deviation, 185), respectively.
d The mean values when the coefficients of variation between studies were 0.1, 1, and 2 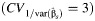 were 2 (standard deviation, 36), 114 (standard deviation, 154) and 270 (standard deviation, 205), respectively.
were 2 (standard deviation, 36), 114 (standard deviation, 154) and 270 (standard deviation, 205), respectively.
The empirical coverage probabilities for the CIs for RI are given in Table 3. When the number of studies in the meta-analysis was small, all bootstrap CIs had coverage far from the desired 95%, but when the number of studies increased, the coverage probability substantially improved. All bootstrap CIs performed poorly when heterogeneity was low. The most successful bootstrap method was the bias-corrected accelerated method, the nominal coverage of which probability improved beginning with a relatively small number of studies. The range-based bootstrap method had the worst coverage.
Table 3.
Empirical Coverage of Several 95% Confidence Intervals for RIa
| No. of Studies by RI Value |
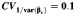 |
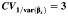 |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bootstrapb |
Asymptoticc |
Bootstrapd |
Asymptotice |
|||||||||||||
| Standard | Range-based | BCα | Normal Approximation | Normal | Logit | Q Method | Gamma Method | Standard | Range-based | BCα | Normal Approximation | Normal | Logit | Q Method | Gamma Method | |
| RI = 0.1 | ||||||||||||||||
| 10 | 100 | 35 | 99 | 97 | 95 | 81 | 100 | 100 | 100 | 13 | 99 | 91 | 84 | 65 | 100 | 100 |
| 20 | 100 | 41 | 98 | 97 | 96 | 83 | 99 | 100 | 100 | 35 | 99 | 97 | 97 | 84 | 99 | 100 |
| 50 | 99 | 50 | 98 | 97 | 96 | 86 | 97 | 99 | 100 | 49 | 98 | 98 | 99 | 90 | 97 | 100 |
| 100 | 99 | 57 | 98 | 97 | 97 | 89 | 97 | 99 | 100 | 58 | 98 | 99 | 99 | 92 | 97 | 100 |
| RI = 0.3 | ||||||||||||||||
| 10 | 100 | 47 | 99 | 98 | 96 | 94 | 96 | 100 | 100 | 18 | 99 | 99 | 86 | 86 | 100 | 100 |
| 20 | 100 | 59 | 98 | 79 | 96 | 95f | 94 | 100 | 100 | 46 | 98 | 99 | 97 | 97 | 96 | 100 |
| 50 | 98 | 73 | 96 | 87 | 97 | 96 | 93 | 99 | 100 | 66 | 97 | 81 | 98 | 98 | 91 | 100 |
| 100 | 95f | 84 | 95f | 92 | 96 | 96 | 95f | 95f | 92 | 80 | 91 | 88 | 98 | 98 | 92 | 93 |
| RI = 0.5 | ||||||||||||||||
| 10 | 100 | 61 | 98 | 81 | 96 | 98 | 85 | 100 | 100 | 26 | 98 | 100 | 87 | 95f | 99 | 100 |
| 20 | 92 | 75 | 93 | 89 | 96 | 97 | 90 | 92 | 100 | 58 | 96 | 78 | 97 | 99 | 88 | 100 |
| 50 | 94 | 89 | 95f | 95f | 95f | 97 | 93 | 94 | 90 | 80 | 89 | 89 | 97 | 99 | 88 | 90 |
| 100 | 94 | 93 | 95f | 96 | 95f | 97 | 94 | 94 | 93 | 91 | 91 | 93 | 95 | 98 | 92 | 93 |
| RI = 0.7 | ||||||||||||||||
| 10 | 89 | 77 | 93 | 93 | 96 | 99 | 86 | 89 | 100 | 38 | 98 | 73 | 90 | 98 | 94 | 100 |
| 20 | 92 | 88 | 95f | 97 | 96 | 98 | 90 | 92 | 87 | 72 | 86 | 88 | 96 | 99 | 84 | 86 |
| 50 | 94 | 93 | 95f | 97 | 95f | 96 | 93 | 94 | 92 | 90 | 91 | 95f | 95f | 99 | 89 | 92 |
| 100 | 95f | 94 | 95f | 96 | 95f | 96 | 94 | 95f | 94 | 91 | 91 | 94 | 95f | 97 | 92 | 94 |
| RI = 0.9 | ||||||||||||||||
| 10 | 89 | 86 | 94 | 99 | 96 | 95f | 86 | 89 | 85 | 68 | 86 | 88 | 93 | 100 | 80 | 85 |
| 20 | 92 | 90 | 95f | 98 | 96 | 95f | 90 | 92 | 89 | 86 | 91 | 97 | 96 | 99 | 84 | 88 |
| 50 | 94 | 92 | 95f | 97 | 95f | 95f | 93 | 94 | 93 | 89 | 92 | 96 | 96 | 97 | 90 | 93 |
| 100 | 95f | 94 | 95f | 96 | 95f | 95f | 94 | 95f | 94 | 91 | 92 | 95f | 95f | 97 | 93 | 95f |
Abbreviations: BCα, bias-corrected, accelerated; 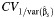 , the coefficient of variation of the reciprocal values of within-study variances; RI, proportion of total variance due to variation between studies
, the coefficient of variation of the reciprocal values of within-study variances; RI, proportion of total variance due to variation between studies
a Relative risk = 2.
b The mean values across all scenarios for the standard, range-based, BCα, and normal approximation methods 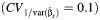 were 96 (standard deviation, 4), 74 (standard deviation, 20), 96 (standard deviation, 2), and 94 (standard deviation, 6), respectively.
were 96 (standard deviation, 4), 74 (standard deviation, 20), 96 (standard deviation, 2), and 94 (standard deviation, 6), respectively.
c The mean values across all scenarios for the normal, logit, Q, and Gamma asymptotic methods 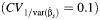 were 96 (standard deviation, 1), 94 (standard deviation, 5), 93 (standard deviation, 4), and 96 (4), respectively.
were 96 (standard deviation, 1), 94 (standard deviation, 5), 93 (standard deviation, 4), and 96 (4), respectively.
d The mean values across all scenarios for the standard, range-based, BCα, and normal approximation methods 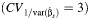 were 95 (standard deviation, 5), 62 (standard deviation, 26), 94 (standard deviation, 4), and 92 (standard deviation, 8), respectively.
were 95 (standard deviation, 5), 62 (standard deviation, 26), 94 (standard deviation, 4), and 92 (standard deviation, 8), respectively.
e The mean values across all scenarios for the normal, logit, Q, and Gamma asymptotic methods 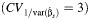 were 95 (standard deviation, 4), 94 (standard deviation, 8), 92 (standard deviation, 6), and 95 (standard deviation, 5), respectively.
were 95 (standard deviation, 4), 94 (standard deviation, 8), 92 (standard deviation, 6), and 95 (standard deviation, 5), respectively.
f The empirical coverage fell within the 95% confidence interval of the variation in the P value expected under the null hypothesis.
Overall, the empirical coverage probabilities for the CIs were closer to 95% when 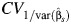 was small. In addition, the asymptotic CIs had much better coverage than the bootstrap CIs. Given a small number of studies, the most accurate empirical coverage was obtained using the normal approximation method. When the number of studies was small, the asymptotic Q and gamma methods provided insufficient coverage that worsened as heterogeneity increased. As expected, when the number of studies increased, the coverage of all asymptotic CIs improved.
was small. In addition, the asymptotic CIs had much better coverage than the bootstrap CIs. Given a small number of studies, the most accurate empirical coverage was obtained using the normal approximation method. When the number of studies was small, the asymptotic Q and gamma methods provided insufficient coverage that worsened as heterogeneity increased. As expected, when the number of studies increased, the coverage of all asymptotic CIs improved.
The empirical coverage probabilities of the CIs for CVB are given in Table 4. No method yielded uniformly good results across all values of CVB and RI that were considered, and all methods performed poorly when CVB was small or the number of studies was small. When the number of studies was small, as long as CVB was not too small, the standard and normal approximation bootstrap method and the bias-corrected, accelerated bootstrap method gave reasonable coverage. As expected, when the number of studies increased, the coverage probabilities for all CIs improved. The multivariate delta method was the best among the asymptotic methods considered. As in the case of CIs for RI, the empirical coverage probabilities for the CIs were closer to 95% when 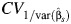 was small.
was small.
Table 4.
Empirical Coverage of 95% Confidence Intervals for the Coefficient of Variation Between Studiesa
| No. of Studies by RI Value | CVB |
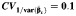 |
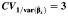 |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bootstrapb |
Asymptoticc |
Bootstrapd |
Asymptotice |
||||||||||||||
| Standard | Range-based | BCα | Normal Approximation | UD | MD | Log-UD | Log-MD | Standard | Range-based | BCα | Normal Approximation | UD | MD | Log-UD | Log-MD | ||
| RI = 0.1 | |||||||||||||||||
| 10 | 0.1 | 100 | 50 | 83 | 100 | 100 | 100 | 83 | 84 | 100 | 45 | 83 | 100 | 100 | 100 | 67 | 72 |
| 1 | 100 | 46 | 68 | 99 | 98 | 100 | 77 | 100 | 100 | 40 | 69 | 100 | 100 | 100 | 80 | 100 | |
| 2 | 99 | 40 | 59 | 99 | 85 | 99 | 83 | 100 | 100 | 39 | 68 | 100 | 97 | 100 | 90 | 100 | |
| 20 | 0.1 | 100 | 52 | 84 | 99 | 100 | 98 | 83 | 84 | 100 | 51 | 84 | 100 | 100 | 100 | 83 | 84 |
| 1 | 100 | 53 | 76 | 99 | 99 | 100 | 77 | 100 | 100 | 47 | 72 | 100 | 99 | 100 | 78 | 100 | |
| 2 | 99 | 46 | 62 | 99 | 88 | 100 | 78 | 100 | 99 | 41 | 67 | 100 | 91 | 100 | 84 | 100 | |
| 50 | 0.1 | 99 | 56 | 85 | 98 | 100 | 97 | 86 | 86 | 100 | 60 | 86 | 100 | 100 | 100 | 90 | 90 |
| 1 | 99 | 61 | 84 | 97 | 99 | 100 | 80 | 100 | 100 | 57 | 81 | 98 | 99 | 100 | 81 | 100 | |
| 2 | 99 | 56 | 72 | 99 | 90 | 100 | 78 | 100 | 99 | 53 | 73 | 99 | 89 | 100 | 80 | 100 | |
| 100 | 0.1 | 99 | 64 | 88 | 98 | 99 | 97 | 89 | 89 | 100 | 65 | 88 | 99 | 100 | 99 | 92 | 92 |
| 1 | 99 | 69 | 88 | 95f | 98 | 100 | 85 | 100 | 99 | 66 | 87 | 95f | 98 | 100 | 85 | 100 | |
| 2 | 98 | 65 | 81 | 98 | 90 | 100 | 79 | 100 | 98 | 62 | 79 | 98 | 89 | 99 | 79 | 100 | |
| RI = 0.3 | |||||||||||||||||
| 10 | 0.1 | 100 | 64 | 87 | 92 | 100 | 100 | 94 | 95 | 100 | 49 | 83 | 100 | 100 | 100 | 87 | 88 |
| 1 | 98 | 61 | 81 | 96 | 91 | 100 | 84 | 100 | 100 | 45 | 71 | 100 | 99 | 100 | 82 | 100 | |
| 2 | 96 | 54 | 71 | 98 | 78 | 97 | 82 | 100 | 100 | 39 | 69 | 100 | 90 | 100 | 90 | 100 | |
| 20 | 0.1 | 100 | 73 | 90 | 81 | 100 | 99 | 95f | 95f | 100 | 63 | 86 | 99 | 100 | 100 | 97 | 97 |
| 1 | 97 | 72 | 89 | 93 | 89 | 100 | 85 | 100 | 98 | 59 | 80 | 97 | 92 | 100 | 85 | 100 | |
| 2 | 96 | 65 | 80 | 98 | 78 | 96 | 79 | 100 | 96 | 51 | 74 | 98 | 79 | 98 | 84 | 100 | |
| 50 | 0.1 | 97 | 84 | 93 | 91 | 93 | 98 | 95f | 95f | 100 | 80 | 90 | 87 | 99 | 100 | 98 | 98 |
| 1 | 95f | 86 | 95f | 93 | 89 | 100 | 88 | 100 | 95f | 78 | 92 | 91 | 88 | 99 | 90 | 100 | |
| 2 | 96 | 82 | 90 | 96 | 76 | 94 | 77 | 99 | 94 | 71 | 84 | 96 | 78 | 95f | 80 | 100 | |
| 100 | 0.1 | 95f | 93 | 96 | 96 | 94 | 98 | 96 | 96 | 92 | 90 | 93 | 94 | 92 | 100 | 98 | 98 |
| 1 | 95f | 95f | 96 | 97 | 88 | 99 | 91 | 99 | 93 | 89 | 94 | 93 | 87 | 98 | 92 | 100 | |
| 2 | 95f | 91 | 95f | 96 | 74 | 94 | 77 | 99 | 94 | 84 | 91 | 94 | 77 | 92 | 79 | 99 | |
| RI = 0.5 | |||||||||||||||||
| 10 | 0.1 | 99 | 78 | 92 | 85 | 89 | 100 | 98 | 98 | 100 | 54 | 84 | 100 | 100 | 100 | 94 | 95f |
| 1 | 94 | 74 | 90 | 91 | 83 | 98 | 87 | 100 | 100 | 50 | 73 | 99 | 95 | 100 | 84 | 100 | |
| 2 | 94 | 67 | 81 | 96 | 73 | 93 | 78 | 99 | 98 | 43 | 70 | 99 | 82 | 99 | 88 | 100 | |
| 20 | 0.1 | 92 | 88 | 94 | 93 | 90 | 99 | 97 | 97 | 100 | 73 | 88 | 81 | 97 | 100 | 99 | 99 |
| 1 | 93 | 87 | 95f | 92 | 83 | 96 | 89 | 100 | 94 | 71 | 87 | 92 | 84 | 99 | 89 | 100 | |
| 2 | 95f | 80 | 88 | 96 | 73 | 91 | 73 | 98 | 93 | 62 | 80 | 96 | 73 | 93 | 82 | 100 | |
| 50 | 0.1 | 94 | 97 | 95f | 98 | 93 | 98 | 97 | 97 | 91 | 92 | 91 | 94 | 89 | 100 | 99 | 99 |
| 1 | 94 | 97 | 96 | 96 | 83 | 95f | 88 | 99 | 92 | 90 | 95f | 93 | 84 | 94 | 93 | 100 | |
| 2 | 95f | 88 | 95f | 94 | 65 | 90 | 65 | 96 | 94 | 82 | 90 | 95f | 76 | 89 | 76 | 98 | |
| 100 | 0.1 | 94 | 98 | 95f | 97 | 93 | 95f | 97 | 97 | 92 | 98 | 91 | 97 | 91 | 96 | 98 | 98 |
| 1 | 94 | 95f | 95f | 95f | 82 | 94 | 84 | 96 | 93 | 96 | 95f | 95f | 86 | 93 | 91 | 98 | |
| 2 | 95f | 89 | 96 | 94 | 65 | 92 | 64 | 96 | 94 | 87 | 95f | 94 | 75 | 90 | 73 | 96 | |
| RI = 0.7 | |||||||||||||||||
| 10 | 0.1 | 90 | 90 | 94 | 92 | 87 | 100 | 99 | 99 | 100 | 60 | 84 | 85 | 100 | 100 | 98 | 99 |
| 1 | 91 | 86 | 93 | 90 | 79 | 92 | 86 | 99 | 97 | 57 | 79 | 97 | 87 | 100 | 87 | 100 | |
| 2 | 93 | 76 | 86 | 95f | 70 | 86 | 67 | 96 | 95f | 50 | 74 | 98 | 76 | 96 | 87 | 100 | |
| 20 | 0.1 | 92 | 97 | 95f | 96 | 90 | 94 | 98 | 98 | 87 | 84 | 89 | 89 | 84 | 100 | 99 | 99 |
| 1 | 93 | 93 | 96 | 93 | 81 | 92 | 84 | 98 | 90 | 81 | 92 | 90 | 79 | 94 | 92 | 100 | |
| 2 | 95f | 82 | 91 | 95f | 64 | 87 | 59 | 94 | 92 | 73 | 85 | 95f | 73 | 88 | 78 | 98 | |
| 50 | 0.1 | 94 | 96 | 95f | 95f | 93 | 94 | 96 | 96 | 92 | 98 | 91 | 95f | 89 | 94 | 99 | 99 |
| 1 | 94 | 92 | 96 | 94 | 80 | 93 | 80 | 96 | 92 | 91 | 95f | 92 | 84 | 91 | 91 | 97 | |
| 2 | 94 | 85 | 95f | 94 | 57 | 90 | 56 | 94 | 94 | 83 | 93 | 94 | 76 | 88 | 73 | 95f | |
| 100 | 0.1 | 94 | 95f | 95f | 95f | 94 | 95f | 95f | 95f | 93 | 95f | 91 | 94 | 92 | 95f | 97 | 97 |
| 1 | 95f | 93 | 96 | 95f | 80 | 95f | 80 | 96 | 94 | 91 | 94 | 93 | 87 | 93 | 90 | 96 | |
| 2 | 95f | 88 | 95f | 94 | 57 | 92 | 56 | 95f | 94 | 85 | 95f | 93 | 76 | 91 | 74 | 96 | |
| RI = 0.9 | |||||||||||||||||
| 10 | 0.1 | 89 | 94 | 94 | 91 | 85 | 90 | 95f | 95f | 86 | 76 | 87 | 83 | 81 | 100 | 100 | 100 |
| 1 | 92 | 87 | 95f | 91 | 79 | 89 | 78 | 94 | 89 | 73 | 88 | 90 | 77 | 94 | 90 | 100 | |
| 2 | 93 | 75 | 87 | 94 | 68 | 84 | 53 | 91 | 91 | 64 | 81 | 95f | 69 | 88 | 82 | 99 | |
| 20 | 0.1 | 92 | 94 | 95f | 93 | 90 | 93 | 95 | 95f | 90 | 93 | 89 | 90 | 85 | 91 | 99 | 99 |
| 1 | 93 | 88 | 95f | 92 | 78 | 91 | 77 | 95f | 90 | 85 | 94 | 88 | 79 | 88 | 90 | 96 | |
| 2 | 95f | 80 | 92 | 94 | 55 | 88 | 52 | 93 | 92 | 76 | 89 | 93 | 72 | 84 | 72 | 94 | |
| 50 | 0.1 | 94 | 94 | 95f | 94 | 93 | 94 | 95 | 95f | 93 | 89 | 91 | 92 | 90 | 94 | 97 | 97 |
| 1 | 94 | 91 | 95f | 94 | 77 | 93 | 76 | 95f | 93 | 86 | 95f | 91 | 85 | 92 | 92 | 97 | |
| 2 | 94 | 85 | 96 | 93 | 52 | 91 | 51 | 94 | 93 | 81 | 95f | 91 | 78 | 89 | 77 | 95f | |
| 100 | 0.1 | 94 | 95f | 95f | 94 | 94 | 94 | 95f | 95f | 94 | 91 | 92 | 94 | 93 | 96 | 97 | 97 |
| 1 | 95f | 93 | 95f | 95f | 76 | 95f | 76 | 95f | 94 | 89 | 94 | 93 | 89 | 94 | 92 | 97 | |
| 2 | 94 | 88 | 95f | 94 | 51 | 92 | 51 | 95f | 94 | 85 | 96 | 92 | 80 | 91 | 80 | 96 | |
Abbreviations: BCα, bias-corrected, accelerated; CVB, coefficient of variation between studies; 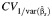 , the coefficient of variation of the reciprocal values of within-study variances; MD, multivariate delta; RI, proportion of total variance due to variation between studies; UD, univariate delta.
, the coefficient of variation of the reciprocal values of within-study variances; MD, multivariate delta; RI, proportion of total variance due to variation between studies; UD, univariate delta.
a Relative risk = 2.
b The mean values across all scenarios for the standard, range-based, BCα, and normal approximation methods 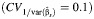 were 95 (standard deviation, 3), 79 (standard deviation, 16), 89 standard deviation, (9), and 95 (standard deviation, 3), respectively.
were 95 (standard deviation, 3), 79 (standard deviation, 16), 89 standard deviation, (9), and 95 (standard deviation, 3), respectively.
c The mean values across all scenarios for the UD, MD, Log-UD, and Log-MD asymptotic methods 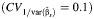 were 83 (standard deviation, 13), 95 (standard deviation, 4), 81 (standard deviation, 13), 96 (standard deviation, 4), respectively.
were 83 (standard deviation, 13), 95 (standard deviation, 4), 81 (standard deviation, 13), 96 (standard deviation, 4), respectively.
d The mean values across all scenarios for the standard, range-based, BCα, and normal approximation methods 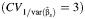 were 95 (standard deviation, 4), 73 (standard deviation, 17), 86 (standard deviation, 8), and 94 (standard deviation, 4), respectively.
were 95 (standard deviation, 4), 73 (standard deviation, 17), 86 (standard deviation, 8), and 94 (standard deviation, 4), respectively.
e The mean values across all scenarios for the UD, MD, Log-UD, and Log-MD asymptotic methods 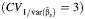 were 87 (standard deviation, 9), 96 (standard deviation, 4), 88 (standard deviation, 8), and 98 (standard deviation, 3), respectively.
were 87 (standard deviation, 9), 96 (standard deviation, 4), 88 (standard deviation, 8), and 98 (standard deviation, 3), respectively.
f The empirical coverage fell within the 95% confidence interval of the variation in the P value expected under the null hypothesis.
Examples of meta-analysis
To illustrate the use of these estimators of heterogeneity and their CIs, we considered 4 recently published meta-analyses that have been frequently cited (from 87 to 327 times as of June 2012) and one yet unpublished meta-analysis with a wide range of apparent heterogeneity (Table 5).
Table 5.
Heterogeneity Assessment in 5 Meta-Analyses
| First Author, Year (Reference) | Design | No. of Studies | No. of Citations | Mean No. of Cases | Model Used for Pooling | Pooled RR | 95% CI for the Relative Risk | P Value for H0 : β = 0 | P Value for H0 : τ2 = 0 |  |
95% CI for RI | I2 | 95% CI for I2 | CVB | 95% CI for CVB | Method(s) of Assessment of Heterogeneity |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Etminan, 2005 (11) | OS | 14 | 324 | 361 | FE | 2.13 | 1.85, 2.44 | 0.001 | 0.55 | N/A | N/A | N/A | N/A | N/A | N/A |
 , Qa , Qa
|
| Hernán, 2002 (12) | OS | 45 | 327 | 146 | FE | 0.59 | 0.54, 0.63 | 0.001 | 0.35 | 0.07 | 0.00, 0.46 | 0.07 | 0.00, 0.34 | 0.13 | 0.00, 0.54 |
 , Q , Q
|
| Millett, 2008 (17) | OS | 15 | 87 | 3571 | RE | 0.96 | 0.81, 1.11 | 0.53 | 0.001 | 0.77 | 0.44, 1.00 | 0.62 | 0.32, 0.78 | 3.86 | 0.00, 16.48 | I2 |
| Jefferson, 2002 (16) | RCT | 11 | 163 | 39 | RE | 0.39 | 0.24, 0.65 | 0.001 | 0.001 | 0.81 | 0.58, 1.00 | 0.79 | 0.62, 0.88 | 0.72 | 0.07, 1.37 | I2, Q |
| Saulyte, 2013 (unpublished data) | OS | 8 | New | 1789 | RE | 1.4 | 1.21, 1.63 | 0.001 | 0.001 | 0.93 | 0.82, 1.00 | 0.87 | 0.82, 0.94 | 0.54 | 0.05, 1.03 |
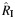 , Q , Q
|
Abbreviations: CVB, coefficient of variation between studies; FE, fixed-effects model; N/A, not applicable; OS, observational study; RCT, randomized clinical trial; RI, proportion of total variance due to variation between studies; RE, random-effects model; RI, proportion of total variance due to variation between studies; RR, relative risk.
a Test for heterogeneity based on the Q statistic.
Etminan et al. (11) investigated the risk of ischemic stroke among people with a history of migraines, with special emphasis on oral contraceptive users. Hernán et al. (12) looked at the associations of Parkinson's disease with ever smoking and with coffee consumption. Saulyte et al. focused on the relation between active smoking among children and allergic rhinitis (J. Saulyte, University of Santiago de Compostela, unpublished data, 2013). Jefferson et al. (16) conducted a meta-analysis of randomized clinical trials of amantadine and rimantadine for the prevention and treatment of influenza, restricted here to the analysis of amantadine versus placebo for the prophylaxis of influenza. Finally, Millett et al. (17) examined circumcision status in relation to infection with human immunodeficiency virus and other sexually transmitted infections among men who have sex with men.
Two of the meta-analyses provided fixed-effects estimates after confirming the absence of heterogeneity with heterogeneity test P values of 0.55 and 0.35, whereas the remainder provided random-effects estimates. The magnitude of the effect, when it existed, varied considerably from a strong protective effect (11) to a large harmful effect (16). Finally, heterogeneity as measured through 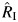 and
and 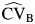 varied between total absence in the migraine study (11) to a considerable presence in the smoking study (J. Saulyte, unpublished data, 2013).
varied between total absence in the migraine study (11) to a considerable presence in the smoking study (J. Saulyte, unpublished data, 2013).
For each study, we estimated the 2 heterogeneity measures considered in this article, 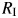 and CVB, and calculated their CIs. For comparison purposes, we also provided I2 values and their 95% CIs. When heterogeneity was small, as in the study by Hernán et al. (12), these measures were close to zero and their CIs also indicated little heterogeneity. Two studies (16; J. Saulyte, unpublished data, 2013) had a large amount of heterogeneity, as given by
and CVB, and calculated their CIs. For comparison purposes, we also provided I2 values and their 95% CIs. When heterogeneity was small, as in the study by Hernán et al. (12), these measures were close to zero and their CIs also indicated little heterogeneity. Two studies (16; J. Saulyte, unpublished data, 2013) had a large amount of heterogeneity, as given by 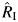 and its CI. The third study (17) had a very large value of CVB, which was probably high because the pooled
and its CI. The third study (17) had a very large value of CVB, which was probably high because the pooled 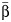 was close to zero, exemplifying the drawback of this measure. However, because
was close to zero, exemplifying the drawback of this measure. However, because 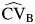 and
and 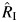 were both large and the P value for the test for heterogeneity was 0.001, it is reasonable to conclude that there was substantial heterogeneity between studies in that meta-analysis.
were both large and the P value for the test for heterogeneity was 0.001, it is reasonable to conclude that there was substantial heterogeneity between studies in that meta-analysis.
DISCUSSION
We developed several asymptotic methods for calculating CIs for RI and CVB. An extensive simulation study demonstrated that when the number of studies in the meta-analysis is small, the asymptotic CIs for RI performed much better than the bootstrap methods. Because the number of studies in meta-analyses is usually moderate, we recommend the normal approximation method given here for calculating the asymptotic CIs for RI and the multivariate delta method for the CIs for CVB. These methods are easy to calculate and have reasonably accurate coverage probability over a wide range of potential circumstances in which they may be used. Bootstrap methods are more computationally intensive and were useful only when the number of studies in the meta-analysis was very large (≥50), in which case they were no better than their asymptotic counterparts. It has been previously been reported that bootstrap methods can be unreliable in small sample size settings, which is often the case in meta-analyses (18–22).
We demonstrated that 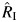 performs well as an estimator of the proportion of the total variation in the overall effect estimate that is due to heterogeneity, successfully quantifying high heterogeneity even in meta-analyses with a small number of participating studies. When the heterogeneity is low and the number of studies is small,
performs well as an estimator of the proportion of the total variation in the overall effect estimate that is due to heterogeneity, successfully quantifying high heterogeneity even in meta-analyses with a small number of participating studies. When the heterogeneity is low and the number of studies is small, 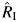 underestimates the proportion of the total variation, but because little or no heterogeneity is present, this underestimation would not likely influence the interpretation of the findings.
underestimates the proportion of the total variation, but because little or no heterogeneity is present, this underestimation would not likely influence the interpretation of the findings.
The results of the simulation study demonstrated that there is limited information to quantify the magnitude of heterogeneity between studies in meta-analyses based upon a small number of studies, but this is mitigated when S is 20 or larger. For a snapshot of the number of studies of meta-analyses published recently, we reviewed all meta-analyses printed in 2011 in the Journal of the American Medical Association and the American Journal of Epidemiology. During this time, the Journal of the American Medical Association published 19 meta-analyses with a median number of studies equal to 25 (range, 5–609), and the American Journal of Epidemiology published 13 meta-analyses with a median number of studies equal to 23 (range, 10–95), which suggests that in many meta-analyses published in high-quality journals today, the measures of heterogeneity developed in this article will perform well.
As a proportion, RI has an intuitive interpretation, but regardless of the underlying heterogeneity of the studies, it tends toward 1 as the studies participating in the meta-analysis become increasingly more precise. CVB does not have this disadvantage, but it increases rapidly to infinity as the underlying relative risk approaches the null value of one.
We saw in Table 5 that in meta-analyses (16, 17; J. Saulyte, unpublished data, 2013), there appeared to have been substantial heterogeneity. In Millett et al., the pooled effect estimate was near the null but substantial heterogeneity was evident, with 75% of overall variability in study-specific effect estimates coming from this heterogeneity (95% CI: 44, 100). The number of studies contributing to this meta-analysis was small, and the confidence limits of the heterogeneity measures were wide but consistent with considerable heterogeneity across the range of values of RI contained within the CI. Reporting a pooled effect estimate in this setting is of questionable value given the substantial heterogeneity of effects observed, as indicated by both the point and interval estimates. In the analyses by Jefferson et al. (16) and Saulyte et al. (unpublished data, 2013) the numbers of studies were somewhat greater and the estimated effects were away from the null, particularly in the study by Jefferson et al. In that analysis, 81% (95% CI: 58, 100) of the variation of the overall estimate was due to heterogeneity between studies, suggesting with reasonable confidence that substantial heterogeneity was present. However, the  was 72% (95% CI: 7, 137), which indicated that with this small number of studies, on the scale of the effect size, the heterogeneity is consistent with a relatively small amount of variation between studies (7%), as well as with a large amount (137%). In contrast, 45 studies contributed to the article by Hernán et al. (12), and the effect estimate was away from the null. With a variation between studies that was only 13% (95% CI: 0, 54) of the effect estimate and only 7% (95% CI: 0, 46) of the overall variance of the estimated effect, we can be confident that the findings of that meta-analysis can be generalized more widely.
was 72% (95% CI: 7, 137), which indicated that with this small number of studies, on the scale of the effect size, the heterogeneity is consistent with a relatively small amount of variation between studies (7%), as well as with a large amount (137%). In contrast, 45 studies contributed to the article by Hernán et al. (12), and the effect estimate was away from the null. With a variation between studies that was only 13% (95% CI: 0, 54) of the effect estimate and only 7% (95% CI: 0, 46) of the overall variance of the estimated effect, we can be confident that the findings of that meta-analysis can be generalized more widely.
An alternative estimator of the magnitude of heterogeneity between studies that is in wide use, I2, is defined as I2 = Q − S + 1/Q (10). Future research should clarify the theoretical relationship between I2 and RI; are these parameters both consistent estimates of the proportion of variance of the pooled estimate due to variation between studies, and if so, under what assumptions? In addition, the finite sample properties of the estimators of these quantities need to be compared, in terms of both bias and coverage probability, to provide guidance to analysts regarding which approach is best to use under what circumstances. A variance estimator of I2 was proposed by Higgins and Thompson (10), and it is of interest to compare its large sample and finite sample properties with that of RI. As can be seen in Table 5, there are some instances (e.g., Millett et al.) in which the results from the 2 are appreciably different.
In conclusion, along with the results from the test for heterogeneity, point and interval estimates of RI and CVB will provide the information needed to properly interpret the evidence in a meta-analysis about the extent of heterogeneity. We wish to caution that when the number of studies in a meta-analysis is small, both the test for heterogeneity (5) and point and interval estimates of the magnitude of heterogeneity may be unreliable. A publicly available SAS macro, which can be downloaded at the last author's website (http://www.hsph.harvard.edu/faculty/donna-spiegelman/software/metaanal/), performs all standard calculations for meta-analysis, including point and interval estimates of RI and CVB, so that heterogeneity can be comprehensively assessed (Appendix 3).
ACKNOWLEDGMENTS
Author affiliations: Department of Preventive Medicine, School of Medicine, University of Santiago de Compostela, Santiago de Compostela, Spain (Bahi Takkouche); Department of Epidemiology, Harvard School of Public Health, Boston, Massachusetts (Polyna Khudyakov, Donna Spiegelman); Department of Biostatistics, Harvard School of Public Health, Boston, Massachusetts (Polyna Khudyakov, Donna Spiegelman); and Department of Mathematics, Faculty of Informatics, University of A Coruña, A Coruña, Spain (Julián Costa-Bouzas).
The study was financially supported by grant PI10/01295 from Instituto de Salud Carlos III, Madrid, Spain, grant 2007-MET-001 from Centro de Investigación Biomédica en Red-Epidemiología y Salud Pública (CIBER-ESP), Madrid, Spain, and grant CA055075 from the National Institutes of Health.
Conflict of interest: none declared.
Appendix 1: Derivation of 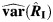 and
and 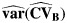
The estimator of the asymptotic 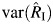 was obtained using the delta method with the reciprocal relationship between
was obtained using the delta method with the reciprocal relationship between 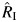 and Q, as follows
and Q, as follows
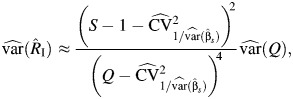 |
(rmA1) |
where the estimator for var(Q) was given by Biggerstaff and Tweedie (15) as:
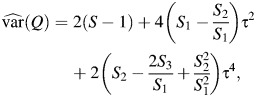 |
(rmA2) |
where 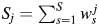 (j = 1, …, 3) and
(j = 1, …, 3) and
 |
(rmA3) |
To derive 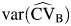 , we assumed that
, we assumed that 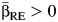 , with probability close to 1 if βRE > 0, and that
, with probability close to 1 if βRE > 0, and that 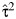 and
and 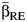 were uncorrelated as would follow asymptotically using standard normality assumptions. Noting that
were uncorrelated as would follow asymptotically using standard normality assumptions. Noting that 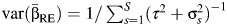 and that
and that 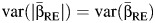 , from the multivariate delta method (17), we get
, from the multivariate delta method (17), we get
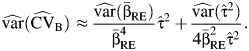 |
(rmA4) |
Appendix 2: Formulas for Bootstrap Confidence Intervals
In this appendix, we present the formulas for bootstrapped confidence intervals (CIs) for a given significance level α that were used in this paper.
The standard CI has the form 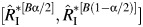 , where
, where 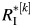 is the kth estimator of RI from B bootstrap-ordered estimators and B is the number of bootstrap samples.
is the kth estimator of RI from B bootstrap-ordered estimators and B is the number of bootstrap samples.
The range-based CI is 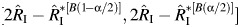 . Note that a disadvantage of this method is that a degenerate CI of (0, 0) is obtained when
. Note that a disadvantage of this method is that a degenerate CI of (0, 0) is obtained when 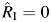 .
.
The bias-corrected, accelerated (BCα) CI can be calculated as 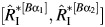 , where
, where 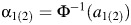 and
and 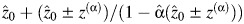
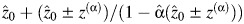 . The detailed description of this method can be found in the article by Efron and Tibshirani (13).
. The detailed description of this method can be found in the article by Efron and Tibshirani (13).
The normal approximation CI has the following form: 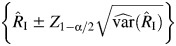 , where
, where 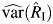 is the sample variance of
is the sample variance of  .
.
Appendix 3: The SAS macro %METAANAL
The SAS macro %METAANAL can be downloaded from http://www.hsph.harvard.edu/faculty/donna-spiegelman/software/metaanal/, along with detailed user-friendly documentation. We use the data from the smoking study (12) to illustrate the use of the macro.
%metaanal(
beta=beta, /* Input betas REQUIRED */
se or var=v,/* the standard error (s) or the variances (v) of the
coefficients */
var=var, /* Input variances */
se=se, /* Input standard errors */
data= , /* Input data set REQUIRED */
studylab = studylab, /* labels for each study REQUIRED */
name= , /* Name of variable of interest */
explabel= , /* descriptive title of exposure REQUIRED */
outcomelabel= , /* descriptive title of outcome REQUIRED */
wt=1, /* increment to scale the RR by */
outdat= , /* Output data set */
pooltype=random,
notes=nonotes,
printcoeff=F,
loglinear=t, /* whether the underlying analysis is log-linear logistic, phreg, log-binomial, poisson or not */
noprint=F);
Here is part of the input data:
obs beta std study
1 -0.82098 0.26524 ne
2 -0.44629 0.15075 ke
3 -0.30111 0.15363 ma
. . . . . . . . . . .
44 -0.52763 0.16169 will
45 -0.71335 0.17464 her
This is the main part of the output of the macro:
Statistic Value (95% CI) P Hypothesis being tested
OR/RR (F) 0.59 (0.54, 0.63) <.0001 Is OR/RR different from 1? (Fixed effects model)
OR/RR (R) 0.58 (0.54, 0.63) <.0001 Is OR/RR different from 1? (Random effects model)
Q 47.06 (27.37, 66.75) 0.3482 Is there heterogeneity among the studies?
tau2 0.0047 .
r(i) ( %) 6.6 (0.0, 46.1) .
CVB 0.127 (0.000, 0.536) .
REFERENCES
- 1.Patsopoulos NA, Analatos AA, Ioannidis JPA. Relative citation impact of various study designs in the health sciences. JAMA. 2005;293(19):2362–2366. doi: 10.1001/jama.293.19.2362. [DOI] [PubMed] [Google Scholar]
- 2.Bax L, Ikeda N, Fukui N, et al. More than numbers: the power of graphs in meta-analysis. Am J Epidemiol. 2009;169(2):249–255. doi: 10.1093/aje/kwn340. [DOI] [PubMed] [Google Scholar]
- 3.Cochran WG. The combination of estimates from different experiments. Biometrics. 1954;10(1):101–129. [Google Scholar]
- 4.National Research Council. Combining Information: Statistical Issues and Opportunities for Research. Washington, DC: National Academy Press; 1992. [Google Scholar]
- 5.Takkouche B, Cadarso-Suárez C, Spiegelman D. Evaluation of old and new tests of heterogeneity in epidemiologic meta-analysis. Am J Epidemiol. 1999;150(2):206–215. doi: 10.1093/oxfordjournals.aje.a009981. [DOI] [PubMed] [Google Scholar]
- 6.Higgins JP, Thompson SG, Deeks JJ, et al. Measuring inconsistency in meta-analyses. BMJ. 2003;327(7414):557–560. doi: 10.1136/bmj.327.7414.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ahlbom A. Biostatistics for Epidemiologists. Boca Raton, FL: Lewis Publishers; 1993. Meta analysis; pp. 145–148. [Google Scholar]
- 8.Poole C, Greenland S. Random-effects meta-analyses are not always conservative. Am J Epidemiol. 1999;150(5):469–475. doi: 10.1093/oxfordjournals.aje.a010035. [DOI] [PubMed] [Google Scholar]
- 9.Costa-Bouzas J, Takkouche B, Cadarso-Suárez C, et al. HEpiMA: software for the identification of heterogeneity in meta-analysis. Comput Methods Programs Biomed. 2001;64(2):101–107. doi: 10.1016/s0169-2607(00)00087-0. [DOI] [PubMed] [Google Scholar]
- 10.Higgins JP, Thompson SG. Quantifying heterogeneity in meta-analysis. Stat Med. 2002;21(11):1539–1558. doi: 10.1002/sim.1186. [DOI] [PubMed] [Google Scholar]
- 11.Etminan M, Takkouche B, Caamaño-Isorna F, et al. Risk of ischaemic stroke in people with migraine: systematic review and meta-analysis of observational studies. BMJ. 2005;330(7482):63. doi: 10.1136/bmj.38302.504063.8F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hernán MA, Takkouche B, Caamaño-Isorna F, et al. A meta-analysis of coffee drinking, cigarette smoking, and the risk of Parkinson's disease. Ann Neurol. 2002;52(3):276–284. doi: 10.1002/ana.10277. [DOI] [PubMed] [Google Scholar]
- 13.Efron B, Tibshirani R. An Introduction to the Bootstrap. London: Chapman & Hall; 1993. [Google Scholar]
- 14.DerSimonian R, Laird N. Meta-analysis in clinical trials. Control Clin Trials. 1986;7(3):177–188. doi: 10.1016/0197-2456(86)90046-2. [DOI] [PubMed] [Google Scholar]
- 15.Biggerstaff BJ, Tweedie RL. Incorporating variability in estimates of heterogeneity in the random effects model in meta-analysis. Stat Med. 1997;16(7):753–768. doi: 10.1002/(sici)1097-0258(19970415)16:7<753::aid-sim494>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 16.Jefferson TO, Demicheli V, Deeks JJ, et al. Amantadine and rimantadine for preventing and treating influenza A in adults. Cochrane Database Syst Rev. 2002;3:CD001169. doi: 10.1002/14651858.CD001169. [DOI] [PubMed] [Google Scholar]
- 17.Millett GA, Flores SA, Marks G, et al. Circumcision status and risk of HIV and sexually transmitted infections among men who have sex with men. JAMA. 2008;300(14):1674–1684. doi: 10.1001/jama.300.14.1674. [DOI] [PubMed] [Google Scholar]
- 18.Schenker N. Qualms about bootstrap confidence intervals. J Am Stat Assoc. 1985;80(390):360–361. [Google Scholar]
- 19.Efron B, Tibshirani R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Statist Sci. 1986;1(1):54–77. [Google Scholar]
- 20.Beran R. Bootstrap methods in statistics. Jahrb Math Ver. 1984;86:14–30. [Google Scholar]
- 21.Bickel PJ, Freedman D. Some asymptotic theory for the bootstrap. Ann Stat. 1981;9(6):1196–1217. [Google Scholar]
- 22.Singh K. On the asymptotic accuracy of Efron's bootstrap. Ann Stat. 1981;9(6):1181–1195. [Google Scholar]


