Advantages of closed-loop calibration in intracortical brain-computer interfaces for people with tetraplegia

Abstract

Objective

Brain-computer interfaces (BCIs) aim to provide a means for people with severe motor disabilities to control their environment directly with neural activity. In intracortical BCIs for people with tetraplegia, the decoder that maps neural activity to desired movements has typically been calibrated using “open-loop” (OL) imagination of control while a cursor automatically moves to targets on a computer screen. However, because neural activity can vary across contexts, a decoder calibrated using OL data may not be optimal for “closed-loop” (CL) neural control. Here, we tested whether CL calibration creates a better decoder than OL calibration even when all other factors that might influence performance are held constant, including the amount of data used for calibration and the amount of elapsed time between calibration and testing.

Approach

Two people with tetraplegia enrolled in the BrainGate2 pilot clinical trial performed a center-out-back task using an intracortical BCI, switching between decoders that had been calibrated on OL vs. CL data.

Main results

Even when all other variables were held constant, CL calibration improved neural control as well as the accuracy and strength of the tuning model. Updating the CL decoder using additional and more recent data resulted in further improvements.

Significance

Differences in neural activity between OL and CL contexts contribute to the superiority of CL decoders, even prior to their additional “adaptive” advantage. In the near future, CL decoder calibration may enable robust neural control without needing to pause ongoing, practical use of BCIs, an important step toward clinical utility.

1. Introduction

Conventional assistive devices for people with severe motor disabilities are inherently limited, often relying on residual motor function for their use. Brain-computer interfaces (BCI) and brain-machine interfaces (BMI), sometimes collectively called neural interface systems (NIS), are being developed to provide a more powerful control signal by decoding movement intentions in real time directly from neural activity (Burrow et al., 1997; Chapin et al., 1999; Serruya et al., 2002; Taylor et al., 2002; Hochberg et al., 2006, 2012; Santhanam et al., 2006; Velliste et al., 2008; Jarosiewicz et al., 2008; Kim et al., 2008; Ganguly and Carmena, 2009; Simeral et al., 2011; Hauschild et al., 2012; Collinger et al., 2013). Intracortical BCIs have permitted people with tetraplegia to control cursors on computer screens, robotic arms, and other prosthetic devices by simply imagining movements of their own arms (Hochberg et al., 2006, 2012; Kim et al., 2008; Simeral et al., 2011; Collinger et al., 2013).

Because it is not possible to map neural activity to actual arm movements in people with tetraplegia, in many previous human intracortical BCI studies the decoder has been calibrated using imagined arm movements (Hochberg et al., 2006; Simeral et al., 2011). Specifically, the participant was asked to imagine moving a mouse with his or her hand to guide a cursor that automatically moved to targets displayed on a computer screen while neuronal ensemble activity was recorded from a 96-microelectrode array implanted in the participant’s motor cortex. A decoder was then created by mapping the recorded patterns of neural activity to the computer-generated cursor movements. This decoder calibration procedure is termed “open-loop” (OL) because the participant does not receive any feedback about his or her neural activity. Subsequently, this “OL decoder” is used to infer movement intention from neural activity in real time, allowing the participant to control the motion of the cursor by simply imagining moving his or her arm. This is termed “closed-loop” (CL) neural control because the participant receives real-time visual feedback of the effect of his or her neural activity on cursor motion.

A potential shortcoming of using an OL decoder for CL neural control is that the relation between neural activity and movement intention can vary with changes in context. For example, the directional tuning of motor cortical neurons in able-bodied monkeys can differ when cursor movement is hand controlled compared to when it is neurally controlled (Taylor et al., 2002; Carmena et al., 2003; Lebedev et al., 2005; Ganguly et al., 2011). Similar context-dependent changes in neural tuning have also been reported in motor cortex of people with tetraplegia switching from a 2-cursor hybrid OL/CL decoder calibration task to purely CL neural control (Kim et al., 2008). If neural activity differs between OL decoder calibration and CL neural control, then an OL decoder will not be optimal for CL neural control. Additionally, the participant may not be as mentally engaged during OL imagination of movement as s/he would be during CL neural control, potentially further reducing the quality of a decoder calibrated on OL data.

Furthermore, the relationship between movement intention and neural activity can change over time because of physiological and/or recording nonstationarities in the neural signals (Kim et al., 2006; Wessberg and Nicolelis, 2006; Santhanam et al., 2007; Chestek et al., 2011; Perge et al., 2013). If only OL calibration were available, BCI use would have to be disrupted to recalibrate the decoder when such nonstationarities occur. Adaptive decoding has been proposed and used successfully as a solution to the signal nonstationarity problem by using data acquired during ongoing CL neural control to periodically or continuously recalibrate the decoder (for reviews, see Millán et al., 2007; Berger et al., 2010; Schlögl et al., 2010).

In continuous spike-based BCIs such as the one used in this study, various adaptive decoding methods have been tested in closed-loop neural control in able-bodied non-human primates (Taylor et al., 2002; Helms Tillery et al., 2003; Wahnoun et al., 2006; Jarosiewicz et al., 2008; Velliste et al., 2008; Shpigelman et al., 2009; Li et al., 2011; Gilja et al., 2012; Orsborn et al., 2012; Sussillo et al., 2012) and in people with tetraplegia (Hochberg et al., 2012; Collinger et al., 2013). In these studies, the decoder was initialized in OL by mapping neural activity to hand movements, to observed target presentations, or to observed effector movements. The decoder was then recalibrated using data acquired during CL neural control. In a subset of these intracortical studies (Helms Tillery et al., 2003; Shpigelman et al., 2009; Li et al., 2011; Gilja et al., 2012; Sussillo et al., 2012), the quality of neural control using the “CL decoder” was compared to the quality of neural control using the original OL decoder, and in each case, the CL decoder outperformed the OL decoder. However, none of these studies were designed to distinguish among the multiple possible contributions to the superiority of CL decoders, which could include (1) differences in neural activity during the OL vs CL calibration tasks, (2) increased mental engagement during CL than during OL, (3) the inclusion of more calibration data in the CL decoder, and/or (4) the ability of CL decoders to adapt to signal nonstationarities.

To disambiguate among these contributions to the superiority of CL decoders, we compared the quality of neural control and the strength and accuracy of the neural tuning models obtained using OL vs. balanced CL decoder calibration in people with tetraplegia performing a 2 dimensional (2D) center-out task using an intracortical spike-based BCI (Figure 1A). We found that CL decoders improved neural control relative to OL decoders even when the two decoders were balanced for the total amount of data used in their calibration, thereby excluding a possible contribution from item 3 above (the ability to include more data in CL decoder calibration). They were also balanced for the amount of elapsed time between calibration and testing, thereby excluding a possible contribution from item 4 above (the ability of CL decoders to adapt to signal nonstationarities). Directional tuning differed between OL and CL contexts, suggesting that eliminating context differences between decoder calibration and neural control (item 1 above) contributed to the performance improvement when using a CL decoder. Directional tuning was also significantly stronger during CL than during OL, suggesting an additional contribution from increased mental engagement during CL than during OL (item 2 above). Because the decoders were interleaved across blocks within each recording session, these improvements are unlikely to be attributable to uncontrolled time-varying factors. Harnessing the full adaptive potential of CL decoders by recalibrating them with additional and more recent data (i.e. including possible contributions from items 3 and 4), as could be done in practical BCI use, resulted in further improvements in tuning model accuracy and in neural control.

Figure 1. Methods and example data.

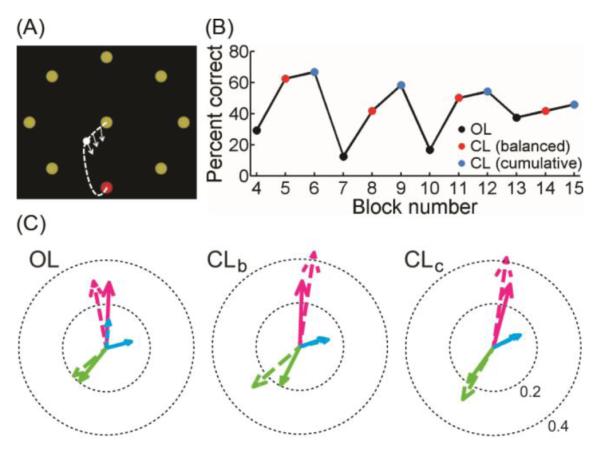
(A) The center-out-back task. Possible target locations are shown as yellow dots that turn red when they become active. After reaching a peripheral target, the participant must bring the cursor back to the center target before the next peripheral target becomes active. To obtain a tuning model from data acquired during CL control, at each moment along the cursor’s trajectory (white dotted line) toward each active target, the person’s intended movement direction is assumed to be from the current cursor location (white dot) toward the active target location (red dot). The normalized direction vectors (white arrows) were regressed against neural activity in each 100 ms bin from the initial, “ballistic” portion of each trial to obtain a model of each unit’s directional tuning. This method was used both for in-session CL decoder calibration and for post-hoc analysis. (B) Example performance data from participant S3, 1966 days post-implant, showing the percent of targets successfully acquired in each 3-5 minute CL “block” of 24 target presentations. Each dot is color-coded according to whether the decoder used in that block was an OL decoder (black), a CL_b decoder (red), or a CL_c decoder (blue). Decoder types were interleaved throughout each session to control for elapsed time since decoder calibration and other time-varying factors. (C) Examples of PDs from the same session. Each color (magenta, blue, green) represents one unit. The dashed arrow of that color represents the PD used by the decoder for that unit (H_i) and the solid arrow of the same color represents the PD obtained post-hoc for that unit from the blocks in which that decoder was used. The left plot shows 3 units in the OL decoder blocks, the middle plot shows the same 3 units in the CL_b decoder blocks, and the right plot shows the same 3 units in the CL_c decoder blocks. The length of each solid arrow represents the unit’s whole-session PD normalized modulation index (NMI) (see Methods). Similarly, the length of each dotted arrow represents that unit’s decoder NMI. As exemplified most clearly by the blue unit, the narrowing of the angle between the model and post-hoc PD in the CL blocks is a measure of improved model accuracy.

2. Methods

2.1. Participants

Permission for these studies was granted by the US Food and Drug Administration (Investigational Device Exemption ¹ ) and the Partners Healthcare/Massachusetts General Hospital Institutional Review Board. The two participants in this study (S3 and T1) were enrolled in a pilot clinical trial of the BrainGate2 Neural Interface System (http://www.clinicaltrials.gov/ct2/show/NCT00912041), and were implanted with a 96-channel intracortical silicon microelectrode array (Cyberkinetics Neurotechnology Systems, Inc., now Blackrock Microsystems, Salt Lake City, UT), as previously described (Hochberg et al., 2006; Simeral et al., 2011).

Participant S3 is a 58-year-old woman with tetraplegia and anarthria (inability to speak) resulting from a pontine stroke that occurred 9 years prior to array implantation. She retains eye movement, some head movement and facial expression, and breathes spontaneously. She has bilateral upper extremity flexor spasms that occur sporadically with many intended body movements. The array, which had electrodes 1.5 mm in length, was implanted in the hand area of her dominant motor cortex ~5 years prior to the start of this research project (See Simeral et al., 2011; Hochberg et al., 2012 for additional detail). Participant T1 was a 48-year-old woman with tetraplegia resulting from amyotrophic lateral sclerosis (ALS), diagnosed 6 years prior to array implantation. She was completely paralyzed except for some eye movement, and her breathing was assisted by a ventilator. The array, with electrodes 1.0 mm in length, was implanted in her dominant motor cortex ~9 months prior to the start of this research project.

2.2. Signal acquisition

Neural activity was detected by the 96-channel microelectrode array and monitored via a cable that was connected to a percutaneous connector during each 2-3 hour recording session. Signals were analog filtered (4^th order Butterworth band pass with corners at 0.3 Hz and 7.5 kHz) and digitized by a 96-channel NeuroPort Neural Signal Processor (Blackrock Microsystems, Salt Lake City, UT) at 30 kilosamples per second (kS s⁻¹).

In participant T1, signals were then causally filtered with a digital 4^th order 250 Hz high-pass Butterworth filter and, for each of the 96 channels, spike waveforms were manually sorted using Cerebus Central (Blackrock Microsystems, Salt Lake City, UT) into putative single neurons (‘units’) using window discriminators in 1.6 ms epochs that crossed a manually set amplitude threshold. Spike counts for each unit in each 100 ms bin were sent to custom-written software in Simulink (Mathworks, Natick, MA), where they were saved to disk and, in “closed-loop” blocks, decoded into intended movement direction for real-time neural control.

In participant S3, the 30 kS s⁻¹ signals were fed in 100 ms segments through custom software written in Simulinkx™, where they were buffered for 4 ms to avoid edge effects and then non-causally band-pass filtered using a 4^th order Butterworth filter with corners at 250 and 5000 Hz. The extracted signals were compared to an amplitude threshold set to −4.5 times the standard deviation of the filtered signals on each channel (for details on the non-causal filtering and threshold crossing methods, see Hochberg et al., 2012). The number of threshold crossing events in each 100 ms segment was saved to disk and, in CL blocks, decoded into intended movement direction for real-time neural control (see below for details).

2.3. Task design

To determine the relationship between intended movement and brain activity, we first asked the participant to watch a cursor move to targets on a computer screen in a pre-programmed 2D four-target center-out-back task and imagine that she was controlling the cursor with her own hand while her motor cortical neural activity was recorded (“open-loop”, or “OL”, decoder calibration). Participant S3 was asked to imagine bending her wrist in the desired cursor movement direction, as imagined wrist movement had previously been found to elicit robust responses in her recorded units. Participant T1 was asked to imagine that she was moving a mouse on a tabletop plane to control the movement of the cursor. Targets appeared one at a time on a 19” LCD monitor (30.5 cm high and 38 cm wide) which was placed ~56 cm in front of the participant; targets appeared at the center, at 13 cm above or below the center, or at 15 cm left or right of the center. The targets were 1.2 cm in radius (1.2 degrees visual angle) and the cursor was 0.6 cm in radius (0.6 degrees visual angle). Each of the 4 targets appeared in a random order before the set of targets was repeated. After the OL data were collected, we used these data to construct a Kalman filter (Wu et al., 2006; Kim et al., 2008) that mapped the observed patterns of neural activity to instantaneous target direction, which was assumed to be the person’s intended movement direction (for details, see 2.4., Kalman filter calibration). For participant S3, the OL decoder was calibrated on data from 24 trials, each trial consisting of a 3 second excursion of the cursor from a center to a peripheral target or a peripheral to a center target followed by a 1 second target hold period. For T1, the OL decoder was calibrated on data from 3 OL blocks of 16 trials, with each trial consisting of a 5 second excursion with a 1 second target hold period.

In subsequent blocks, the participant was asked to perform the 4-target center-out-back task under CL neural control: the participant’s intended movement direction was decoded from her neural activity, and this movement intention was used to directly control the continuous movement of the cursor in real time. For a trial to be considered successful, S3 had 8 seconds to move the cursor to the target and hold it there for at least 500 milliseconds. The target acquisition rate expected by chance in this task was near 0% because the cursor and targets were small relative to the size of the screen, continuous trajectories were decoded, and the cursor had to be held over the target for it to count as a successful acquisition. For participant T1, we simplified the task by increasing the trial time to 20 seconds and decreasing hold time to 300 milliseconds. Also, we algorithmically discarded the component of the commanded velocity vector orthogonal to the instantaneous target direction, similar to “deviation gain” used by Velliste et al (2008), which constrained the possible cursor movements at each moment in time to a single line toward and away from the current target. This effectively reduced the difficulty level of the task to that of a 1D task, while still allowing a 2D model to be generated and used for neural control. Thus, for T1, the target acquisition rate expected by chance had a theoretical range of 0% to 50%, depending on the amount and direction of bias in cursor motion. Because the baseline performance levels were expected to vary across participants and across days due to any number of uncontrolled factors, all statistical analyses were done on relative performance measures that were normalized to baseline performance on each day.

For S3, the OL decoder was used in the first CL block. After the CL block finished, a “balanced” CL (CL_b) decoder was calibrated using the neural data from the first 3 seconds of each trial of that CL block (see Figure 1A), using the same total amount of data to calibrate the decoder as was used to calibrate the OL decoder. For T1, the OL decoder was used in the first 3 CL blocks, and the first 5 seconds of each trial of these three CL blocks were used to calibrate the CL_b decoder. To test whether using CL data to train the decoder improved task performance and/or the accuracy of the decoder’s neural tuning model (even when the CL decoder was built from the same amount of data as the OL decoder), the CL_b decoder was used in the next block of neural control. To test whether more improvement would be obtained using a CL decoder that is calibrated on additional, more recent data, as could be done in practical use of the BCI, a third, “cumulative” CL (CL_c) decoder was built using all of the CL blocks acquired up to that point; this decoder was then used for decoding in the following block.

To ensure that any changes in performance and/or model accuracy that were attributed to decoder type were not influenced by any other uncontrolled time-varying factors (amount of practice, learning, fatigue, etc.), several more blocks of neural control were run, interleaving the OL, CL_b, and CL_c decoders across blocks (see Figure 1B for an example). Each time a CL_c decoder was to be used, it was first calibrated using data from all of the CL blocks that had been acquired up to that point. To control for the amount of time that elapsed since decoder calibration when comparing the OL to the CL_b decoder (whose sole difference was meant to be the context under which the calibration data were collected), the OL and CL_b decoders were never recalibrated. In S3, 12 total CL blocks were run in each session, with 24 trials per block, cycling 4 times through the OL, the CL_b, and the CL_c decoders, in that order. In T1, 10-13 total CL blocks were run in each session, with 16 trials per block, repeating each decoder type 2-5 times in random order after the initial OL, CL_b, and CL_c blocks.

2.4. Kalman filter calibration

Movement intention was decoded from spiking activity using a steady-state Kalman filter. We briefly review its properties here; full accounts can be found in other studies (Wu et al., 2006; Kim et al., 2008; Malik et al., 2011). The Kalman filter is a recursive Bayesian estimation algorithm that infers the desired cursor state from the history of spike rates. Its “observation model” assumes that the baseline-subtracted spike rates z are linearly related to the intended movement direction d at each time point t

$$z\left(t\right)=\mathit{Hd}\left(t\right)+q\left(t\right)$$ (1)

where H is the matrix relating spiking activity to movement direction and the error term, q, is drawn from a normal distribution with zero mean and covariance matrix Q Its “state model” assumes that the intended movement direction at any time evolves from the movement direction in the previous time point

$$d\left(t\right)=\mathit{Ad}(t-1)+w\left(t\right),$$ (2)

where A is the matrix relating movement directions at consecutive time points and the error term, w, is drawn from a normal distribution with zero mean and covariance matrix W

Given equations 1 and 2, the log probability of jointly observing the set of intended motion directions, D = {d(1), d(2),…,d(N)}, and the set of spike rates, Z = {z(1), z(2),…,z(N)}, can be expressed as:

$$\begin{array}{cc}\hfill \mathit{log}\left(P\right(D,Z\left)\right)=& \mathit{log}\left(p\left(d\right(1\left)\right)\right)+\sum _{t=2}^N\mathit{log}\left(p\left(d\right(t)\mid d(t-1\left)\right)\right)+\sum _{t=1}^N\mathit{log}\left(p\left(z\right(t)\mid d(t\left)\right)\right)\hfill \\ \hfill & =\mathit{log}\left(Z\right)-\frac{N-1}{2}\mathit{log}\mid W\mid -\frac{N}{2}\mathit{log}\mid Q\mid \hfill \\ \hfill & -\frac{1}{2}\sum _{t=2}^N\left(d\right(t)-\mathit{Ad}(t-1\left)\right)W^{-1}{\left(d\right(t)-\mathit{Ad}(t-1\left)\right)}^T\hfill \\ \hfill & -\frac{1}{2}\sum _{t=1}^N\left(z\right(t)-\mathit{Hd}(t\left)\right)Q^{-1}{\left(z\right(t)-\mathit{Hd}(t\left)\right)}^T\hfill \end{array}$$ (3)

where Z is a normalization factor. Usually, the Kalman filter is calibrated by finding the parameters H, Q, A, W that maximize this joint distribution. However, we found that fixing A = 0.965I and W = 0.03I where I is the identity matrix, provided a good trade-off between smoothness and responsiveness of cursor movement (Hochberg et al., 2012). Thus, for decoder calibration, we only calculated the parameters H and Q that maximized the distribution. These two parameters have the following closed-form solutions:

$$H=\left(\sum _{t=1}^{N}z\left(t\right)d{\left(t\right)}^T\right){\left(\sum _{t=1}^{N}d\left(t\right)d{\left(t\right)}^T\right)}^{-1}$$ (4)

$$Q=\frac{1}{N}\left(\sum _{t=1}^{N}z\left(t\right)-\mathit{Hd}\left(t\right)\right){\left(\sum _{t=1}^{N}z\left(t\right)-\mathit{Hd}\left(t\right)\right)}^T$$ (5)

We note that each row of H contains a 2D vector representing the Kalman filter’s model of a recorded unit’s preferred direction; its direction corresponds to the cursor direction in which the unit’s spike rate is highest (i.e. the peak of its cosine fit), and its magnitude is the unit’s modulation depth (i.e. the difference in firing rate between the peak of its cosine fit and its baseline). The modeled preferred direction vector of neuron i will be denoted as H_i.

Decoder calibration was performed in batches between blocks using data from each 100 ms bin in the first 3 seconds (for S3) or 5 seconds (for T1) of each trial after target presentation (hereafter called the decoder “calibration data”). In OL decoder calibration, this was equivalent to the cursor movement period of each trial. In CL decoder calibration, this was meant to balance the amount of time from each trial that data were used for calibrating the CL decoders with that of the OL decoders, and also to isolate the initial, “ballistic” portion of each trial, during which the participant’s intended movement direction was less likely to be influenced by error correction. For CL calibration, data from any part of the trial in which the edge of the cursor was within 1 cm (1 degree visual angle) of the edge of the target were also excluded from the decoder calibration because, as the cursor gets closer to the target, small cursor movements lead to larger angular changes in target direction, making intended movement direction more difficult to infer. The neural calibration data were shifted by a small temporal delay (200 ms for S3, 300 ms for T1) relative to the kinematic calibration data to account for a reaction time between cursor position updates and neural responses; these delays were chosen because they produced the largest directional modulation in off-line analyses of previous sessions from each participant (data not shown).

2.5. Data analysis

Performance and tuning model accuracy of the OL, CL_b, and CL_c decoders were compared as follows. For each session, data from all blocks in which a given decoder type was used were combined to obtain a single target acquisition rate (% correct) and model accuracy for that decoder type. For example, in the session shown in Figure 1B, blocks 4, 7, 10, and 13 were combined into one OL data point in Figure 2; blocks 5, 8, 11, and 14 were combined into one CL_b data point, and blocks 6, 9, 12, and 15 were combined into one CL_c data point.

Figure 2. Improvement in performance and tuning model error with CL decoder calibration.

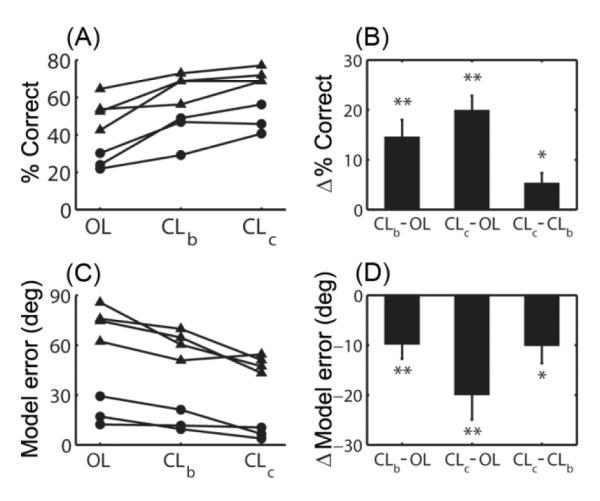
(A) Performance data from each session from both participants. The percent of targets acquired (% correct) across all blocks using the OL decoder, all blocks using the CL_b decoder, and all blocks using the cumulative CL_c decoder are shown for each session. Filled circles represent sessions from participant S3, and filled triangles represent sessions from participant T1 (whose version of the task was simplified; see Methods). (B) Changes in performance relative to OL, averaged across all sessions. There was a significant improvement in performance when using the CL_b and CL_c decoders compared to the OL decoders in the same session (Wilcoxon signed rank test, p = 0.0078). In addition, there was a significant improvement when using the CL_c decoder over using the CL_b decoder (p = 0.031). (C) Model error from each session from both participants. (D) Changes in model error relative to OL, averaged across all sessions. There was a significant decrease in model error (i.e. improvement in model accuracy) using the CL_b and CL_c decoders compared to the OL decoders (Wilcoxon signed rank test, p = 0.0078 for both CL_b and CL_c). There was also a significant improvement when using the CL_c decoder compared to the CL_b decoder (p = 0.023). Key: * = p < 0.05; ** = p < 0.01.

As stated above, the decoder is calibrated by estimating the preferred direction of each unit. Intuitively, the participant’s quality of neural control over the cursor will be influenced by the accuracy of these estimates. To assess model accuracy, we computed a “model error” defined as the angular difference between the preferred direction measured when calibrating the decoder (H_i for unit i) to the preferred direction measured during those blocks in which that decoder was used (the “post-hoc PD”). A smaller angle between the preferred directions measured when calibrating and using the decoder reflects a more accurate tuning model (Figure 1C).

Because baseline performance and model error varied across sessions and between the two participants, statistics were performed within-session on differences in performance and model error metrics relative to the OL decoder blocks (see Figure 2 B,D). P-values were obtained for these within-session comparisons using the non-parametric Wilcoxon signed rank test. Because there is more certainty in the angular error for units with stronger directional tuning, the model error of each unit was weighted (Taylor, 1996; Jarosiewicz et al., 2008, 2012b) by its whole-session “normalized modulation index” (NMI). The NMI of unit i was defined as the norm of its PD divided by the standard deviation of the residuals in the fit:

$$\frac{\Vert H_i\Vert }{\sqrt{Q_{\mathit{ii}}}}.$$ (6)

Thus, a unit with no directional tuning would have a NMI of 0, a unit whose modulation depth is equal to the standard deviation of its residuals would have a NMI of 1, and a unit whose directional modulation is larger than the standard deviation of its residuals would have a NMI greater than 1. To estimate each unit’s whole-session NMI, firing rates were baseline-subtracted within each block, and then all of the baseline-subtracted CL calibration data from the whole session were used to obtain a single PD and NMI for that unit; this NMI was used as the weight for that unit.

Model error was also compared across decoder types treating all units from all sessions as independent samples: each unit’s model error for one decoder type vs. another decoder type contributed one pair of data points in a paired weighted t-test (Goldberg et al., 2005; Jarosiewicz et al., 2008, 2012b), again weighting each unit’s contribution by its NMI.

To test whether CL neural control yields stronger directional modulation than OL imagined movements, we also compared the NMIs of the OL and CL decoder models themselves (“decoder NMIs”; see Figure 1C) as a measure of how strongly modulated the units were during the blocks on which the decoders were built. The decoder NMIs were computed the same way as the post-hoc PD NMIs (using Equation 6), but they were computed for each decoder rather than for the post-hoc PD. Because NMI is sensitive to the amount of data used in its calculation, we only applied this comparison to the OL vs. the CL_b decoders, which were created from matching quantities of calibration data; the CL_c decoders, which were created from more calibration data than the other decoder types, were excluded from the decoder NMI comparison.

3. Results

Across seven sessions from the two participants, the decoders calibrated on CL data provided a better target acquisition rate and a superior model fit than the decoders calibrated on OL data (Figure 2). In the blocks in which the CL_b decoder was used, the target acquisition rate was 14.6 ± 3.4% higher and the model error was 9.9 ± 2.9° lower than in the blocks in which the OL decoder was used (difference in target acquisition rate, p < 0.01; difference in model error, 1-tailed Wilcoxon signed rank test, p < 0.01). Recalibrating the tuning model using additional and more recent CL data resulted in further improvement of both neural control and tuning model accuracy (difference in target acquisition rate, CL_c relative to OL: 20.0 ± 2.9%; p < 0.01; difference in target acquisition rate, CL_c relative to CL_b = 5.4 ± 2.0%; p < 0.05; improvement in model error, CL_c relative to OL: 20.0 ± 4.9°; p < 0.01; improvement in model error, CL_c relative to CL_b: 10.1 ± 3.5°; p < 0.05).

Each of the above analyses treated each decoder type from each session as one data point in a pairwise analysis. To gain statistical power in comparing model accuracy across decoder types, we also computed the model error of each decoder type combining across all 251 units from all sessions (217 units from T1 and 34 units from S3), and used the difference in model error across decoder types for each cell as independent samples in a paired analysis. Across all units, the weighted mean model error was 49.9 ± 3.2° (SEM) for the OL decoders, 39.8 ± 2.6° for the CL_b decoders, and 31.8 ± 2.4° for the CL_c decoders (Figure 3A). The CL_b decoders had significantly smaller model error than the OL decoders (mean pairwise difference, CL_b – OL: 10.2 ± 3.3°, paired t-test, t = 3.12, p < 0.001). Because this improvement in model error could not be attributed to differences in the amount of calibration data or the amount of elapsed time between calibration and testing, the fact that the post-hoc PDs obtained from CL blocks were more similar to the CL_b model than they were to the OL model implies that directional tuning differs between OL and CL contexts. Furthermore, the CL_c decoders had significantly smaller model error than both the OL decoders (CL_c – OL: 18.1 ± 3.6°, t = 5.02, p < 10⁻⁷) and the CL_b decoders (CL_c – CL_b: 8.0 ± 2.8°; t = 2.85; p < 0.005), implying that even better model accuracy can be obtained by including additional and more recent data in decoder calibration. Each of these differences were also significant for each individual participant (participant S3: CL_b – OL: 6.15 ± 3.6°, p < 0.05; CL_c – OL: 13.9 ± 3.7°, p < 10⁻⁴; CL_c – CL_b: 7.79 ± 2.0°, p < 10⁻⁴. Participant T1: CL_b – OL: 13.0 ± 4.4°, p < 0.005; CL_c – OL: 21.2 ± 4.9°, p < 10⁻⁵; CL_c – CL_b: 8.12 ± 3.9°, p < 0.05).

Figure 3. Model error and decoder normalized modulation index (NMI), all units from all sessions.

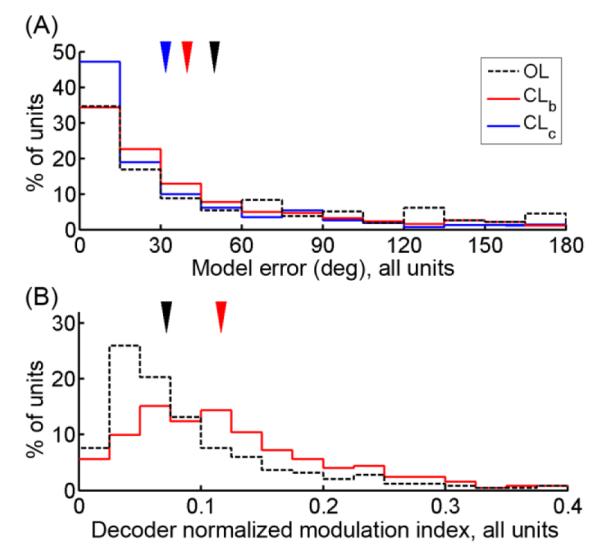
(A) Distribution of model error, combining all units from all sessions. Arrows denote the weighted mean model error for each decoder type across all units. Both the CL_b decoders (p < 0.001) and the CL_c decoders (p < 10⁻⁷) had significantly smaller model error than the OL decoders. Furthermore, the CL_c decoders had significantly smaller model error than the CL_b decoders (p < 0.005). (B) Distribution of decoder NMIs of the OL and CL_b decoders (because NMI is sensitive to the amount of data used in its calculation, the CL_c decoders were excluded from this comparison). Arrows denote the median for each group. The balanced CL decoder models had significantly higher modulation indices than the OL decoder models (p < 10⁻⁶), indicating that directional tuning was stronger during CL neural control than during OL imagination of control.

The CL_b decoders also had significantly higher decoder NMIs (median = 0.12) than the OL decoders (median = 0.07; mean pairwise difference = 0.029 ± 0.006; t = 4.67, p < 10⁻⁶), implying stronger directional modulation during the CL calibration task than during the OL calibration task (Figure 3B). This difference was also significant for each individual participant (participant S3: mean pairwise difference = 0.031 ± 0.015, t = 2.08, p < 0.05; participant T1: mean pairwise difference = 0.029 ± 0.007, t = 4.22, p < 10⁻⁵).

4. Discussion

When calibrating a decoder for a spike-based neural interface for people with paralysis, data acquired during neural control (“CL” decoder calibration) resulted in a superior decoding model and better subsequent neural control than data acquired during imagined movements without feedback (open-loop or “OL” calibration). Model error was smaller, the directional modulation was stronger, and neural control was better with CL decoders than OL decoders, even when the same amount of data were used to calibrate both decoders and when the same amount of time elapsed between each decoder’s calibration and its use. Because the decoders were interleaved across blocks within each session, the observed differences are unlikely to be attributable to time-varying factors such as practice, learning, fatigue, or elapsed time since decoder calibration.

Given that neural tuning can change across different contexts (Taylor et al., 2002; Carmena et al., 2003; Lebedev et al., 2005; Kim et al., 2008; Ganguly et al., 2011), a likely reason for the observed improvement in neural control and smaller model error using the balanced CL decoders is that CL calibration minimizes the contextual differences between decoder calibration and neural control. In BCI studies with able-bodied monkeys, if the monkeys’ arms are restrained or allowed to move differently during neural control than during OL calibration, it is perhaps not surprising that MI directional tuning differs between hand control and neural control (Taylor et al., 2002; Carmena et al., 2003; Lebedev et al., 2005; Ganguly et al., 2011) given the sensitivity of motor cortical tuning to arm kinematics, dynamics, and proprioceptive feedback (Georgopoulos et al., 1982; Schwartz et al., 1988; Fu et al., 1995; Sergio and Kalaska, 1998; Kakei et al., 1999; Churchland and Shenoy, 2007). However, in people with tetraplegia, arm movements are absent in both OL and CL contexts, so differences in arm movements cannot explain these results. Instead, these results suggest that the activity of neurons in human MI is sensitive to the subtle distinction between imagination of movement without an effect on the external world (arguably a relatively “natural” scenario) and imagination of movement with an effect on the external world (a scenario that has only become possible recently with the advent of brain-computer interfaces).

Furthermore, the stronger directional modulation that was observed during CL neural control than during OL imagination of movement is consistent with a higher level of mental engagement during CL neural control, as increased attention, motivation, and alertness are known to increase the amount of neural activation and information present in neural activity (Edeline, 2003; Reynolds and Chelazzi, 2004; Roesch and Olson, 2004; Chapman and Meftah, 2005; Zhang et al., 2011).

Another possible source of the observed differences in neural activity between OL and CL contexts might be additional feedback-enabled neural modulation in CL that corresponds to the user’s attempts to seek strategies that improve neural control (see, e.g., Fetz, 1969, 2007; Moritz et al., 2008; Chase et al., 2009; Koyama et al., 2010), which does not occur during OL because such feedback is not provided. The improvements in neural control using a CL decoder, then, might be partly attributable to the incorporation of these modified neural patterns into the CL decoding model, combined with the person’s continued use of similar strategies during subsequent CL neural control.

Regardless of the source of the observed improvements with CL decoders, if these improvements translate to practical BCI applications (e.g. increased typing speed in a point-and-click communication interface), then their functional implications are substantial. Even before taking advantage of the “adaptiveness” of CL decoder calibration (i.e., when using the balanced CL decoder), we observed a ~30% relative improvement in target acquisition rate over baseline performance using the OL decoder. Using the cumulative CL decoder, we observed a ~40% relative improvement over baseline. In a practical BCI setting, even more improvement could potentially be obtained by including more calibration data as it is collected and/or by selecting the calibration data with attention to other relevant factors such as signal nonstationarities. When neural signals are not stably recorded, the decoder could be continually recalibrated using only the most recent and relevant CL data. When the neural signals are stable over long periods of time, adding more calibration data as it is collected would continually improve the accuracy of the tuning model, and would enable more complex tuning models to be utilized that require more parameters to be fitted.

Future intracortical BCIs should provide users with control over multiple types of assistive devices over the course of a day – e.g., a computer keyboard from morning to noon, and an assistive robotic limb at mealtime. It will thus be important to understand the degree to which a decoder calibrated in one CL context (e.g., the center-out-back task) will extend to other CL contexts (e.g., a communication interface, physical devices, etc.). If neural tuning also differs across different CL contexts, a decoder created during the use of one BCI application might not be optimal for another BCI application. However, preliminary work shows that the tuning model of a CL decoder calibrated in a center-out task matches the PDs obtained in a communication interface as closely as it matches the PDs obtained from other blocks of the same center-out task (Jarosiewicz et al., 2011), suggesting that neural activity does not differ as strongly across CL contexts as between OL and CL contexts.

A crucial component of decoder calibration is knowledge of the person’s movement intention, so that its relationship with the corresponding neural data can be modeled. How will this be accomplished in practical BCI applications in which targets are not pre-specified? In most conceivable practical applications of point-and-click BCIs (such as in a neural communication interface; see Bacher et al., 2011), selections will be made by dwelling or neurally “clicking” on possible targets on the computer screen (Kim et al., 2011; Simeral et al., 2011). This allows for a possible solution to the absence of a priori knowledge of target location: if a given selection is not followed by a corrective action (e.g., “backspace” or “undo”), one could infer retrospectively that the BCI user correctly selected his or her desired target. Once that target location is known, the person’s intended movement direction during each moment of the preceding trajectory can be assumed to have been toward that target, and as before, the tuning model can be calibrated using this inference of instantaneous intended direction (Jarosiewicz et al., 2012a). With additional constraints on the assumptions of the intended movements and on the data that would be included in decoder calibration, similar approaches for retrospective target inference guiding ongoing CL calibration could conceivably be extended to multi-dimensional neural control, such as reach and grasp control of a robotic arm (Hochberg et al., 2012; Collinger et al., 2013) or functional electrical stimulation of the person’s own limbs (Moritz et al., 2008; Chadwick et al., 2011; Ethier et al., 2012).

5. Conclusions

In two people with tetraplegia enrolled in the BrainGate pilot clinical trial, neural control was superior, and the decoder had a more accurate tuning model with a higher signal-to-noise ratio, using closed-loop decoder calibration compared to open-loop decoder calibration. Closed-loop calibration was superior even when the amount of data used to calibrate the closed-loop decoder was balanced with the open-loop decoder and when the same amount of time had elapsed between each decoder’s calibration and its use. These improvements are likely attributable to differences in neural activity between open-loop and closed-loop contexts and to increased levels of mental engagement during closed-loop neural control. Recalibrating the decoder using additional and more recent closed-loop data, as could be done during practical use of the neural interface system, resulted in further improvement of both the tuning model and of neural control. These methods may enable robust neural control without needing to pause ongoing, practical use of BCIs, an important step toward clinical utility.