An application of item response theory to fMRI data: Prospects and pitfalls

Abstract

When using functional brain imaging to study neuropsychiatric patients an important challenge is determining whether the imaging task assesses individual differences with equal precision in healthy control and impaired patient groups. Classical test theory (CTT) requires separate reliability studies of patients and controls to determine equivalent measurement precision with additional studies to determine measurement precision for different levels of disease severity. Unlike CTT, item response theory (IRT) provides estimates of measurement error for different levels of ability, without the need for separate studies, and can determine if different tests are equivalently difficult when investigating differential deficits between groups. To determine the potential value of IRT in functional brain imaging, IRT was applied to behavioral data obtained during a multi-center functional MRI (fMRI) study of working memory (WM). Average item difficulty was approximately one standard deviation below the ability scale mean, supporting the task’s sensitivity to individual differences within the ability range of patients with WM impairment, but not within the range of most controls. The correlation of IRT estimated ability with fMRI activation during the task recognition period supported the linkage of the latent IRT scale to brain activation data. IRT can meaningfully contribute to the design of fMRI tasks.

1. Introduction

Over the past several decades, item response theory (IRT; Lord and Novick, 1968; Rasch, 1960) has become the preferred methodology for the study of test and item characteristics. Yet, IRT has only rarely been applied in neuropsychological research, and almost never in published functional brain imaging studies. In this paper, we discuss some of the practical issues researchers are likely to confront when applying these techniques to functional brain imaging studies. This demonstration is accomplished by applying IRT to behavioral data obtained during a multi-center functional MRI (fMRI) study of working memory. Readers wishing a more general discussion of IRT should consult introductory texts (e.g., de Ayala, 2009; Embretson and Reise, 2000), review papers (e.g., Reise and Waller, 2009; Thomas, 2011), and technical resources (e.g., Baker and Kim, 2004; van der Linden and Hambleton, 1997).

1.1. Motivation for using IRT in functional brain imaging

Although interesting fMRI studies are being performed under behaviorally unconstrained conditions (Meda et al., 2012), most of the studies in the fMRI literature have used cognitive challenge tasks to probe patterns of brain-activation. Behavioral contributions to the design of fMRI tasks have focused almost exclusively on the validity of the task as an apparent assessment of cognitive neuroscience domains of interest. Once the content validity of items is determined, item properties such as difficulty and discriminating power are assumed, often implicitly, to be equivalent across items. When item difficulty is considered, it typically enters through the manipulation of independent variables, such as memory load or stimulus visibility, that alter the marginal probability of a correct response over subgroups of items (Huang et al., 2006; Potkin et al., 2009). However, item difficulty needs to be considered when designing brain activation probes in order to avoid ceiling and floor effects, especially when studying groups of subjects who perform at different ability levels (Gur et al., 1992). Difficulty should be matched across cognitive challenge probes in order to support the attribution of differential brain response to the different neurocognitive systems that the probes were designed to evoke (Gur et al., 1992; Snyder et al., 2011; Spitzer et al., 1996).

These initial applications of psychometric ideas to the design of brain activation tasks were not developed within an explicit psychometric framework, although the principles of classical test theory (CTT) often seem to be assumed. Today, IRT offers an accessible, advanced set of tools for establishing the precision and accuracy of individual items (see Embretson and Hershberger, 1999). IRT models involve both individual person parameters and individual item parameters scaled along the same latent dimension. This focus results in an explicit model of item and person characteristics that are differentiated while remaining linked to each other through a parametric equation. Separation of person and item parameters allows for invariance of item characteristics across groups and individuals that differ in ability (Lord, 1980), and provides an explicit rationale for the use of different items to assess the same neurocognitive system in diverse groups of patients (e.g., adaptive testing methods). IRT also permits the assessment of item information (similar to the concept of reliability) and standard error at specific points along the ability spectrum, whereas CTT would require different reliability studies along arbitrarily quantitized intervals of ability. Measurement precision can be determined independently for groups and individuals with different ability levels, as often occurs in functional brain imaging studies of clinical groups (e.g., Brown and Eyler, 2006).

The primary purpose of using IRT in imaging research is to evaluate item properties in order to ensure that tests are measuring intended neurocognitive constructs with appropriate difficulty to detect individual differences in latent ability; a precise approach to the ideas advocated by Gur et al. (1992). Unfortunately, there are several obstacles to using IRT in imaging studies; most notably, the typically large subject samples required to estimate IRT parameters and questions whether or not the latent abilities estimated in IRT are related to brain activation. A test of IRT’s practical utility in imaging research is needed.

1.2. An application of IRT to an fMRI study of working memory

Data come from the East Coast Traveling Subjects (ECTS) study performed by the Function Biomedical Informatics Research Network (FBIRN). The aim of the study was to assess the multi-site reliability of functional imaging data before embarking on a larger multi-center study of schizophrenia patients. Participants were administered a working memory task (WMT) designed to detect differential patterns of brain activation of healthy volunteers and schizophrenia patients with working memory impairment. The WMT is a forced-choice delayed visual recognition memory test, permitting the separate detection of brain processes involved in stimulus encoding, memory maintenance, and target recognition. The task was presented in the magnet while images sensitive to blood oxygen level dependence (BOLD) signals were acquired (see Buxton, 2002).

To model WMT item characteristics, we consider nested versions of a general IRT model where N examinees respond to J items. Let X_ij=x_ij denote the observed response for the i^th examinee to the j^th item, where x_ij=1 if the response is correct and 0 otherwise.¹ The probability of a correct response is approximated by a logistic function of subject ability (θ_i), item difficulty (β_j), item discrimination (α_j), and item guessing (γ_j) parameters

$$P(X_{ij}=x_{ij}|{\beta }_j,{\alpha }_j,{\gamma }_j,{\theta }_i)={\gamma }_j+(1-{\gamma }_j)\frac{e^{{\alpha }_j({\theta }_i-{\beta }_j)}}{1+e^{{\alpha }_j({\theta }_i-{\beta }_j)}}$$ (1)

Eq. (1) is commonly referred to as a three-parameter logistic (3-PL; Birnbaum, 1968) model. The θ_i parameter reflects the subject’s standing on the underlying ability that is required for accurate item responding (e.g., memory). It is an unobservable characteristic of the examinee that may also be referred to as a latent factor or trait. The β_j or item difficulty parameter makes it more or less probable that an examinee of a given ability level will provide a correct response. The α_j or discrimination parameter reflects the weight or relevance of the underlying ability dimension to the probability of a correct response. The γ_j or lower-asymptote parameter conveys the probability that an examinee with infinitely low ability will correctly respond (often guessing).

IRT models range from simple to complex in both scope and ease of application. For imaging researchers hoping to use IRT in their work, it is first necessary to consider what combination of freely estimated item parameters can be viably attained from available data. The answer is due, in part, to characteristics of items, but also practical issues related to sample size. It is challenging to collect large samples in imaging research due to cost, time, and access barriers associated with scanning equipment. In the current study, for instance, item responses and imaging data were collected for 18 participants over nearly 6 months of multisite collaboration at a cost of approximately $1000 per scanning session, per site. This reduced number of examinees – which is common in cognitive and imaging research – can annul the beneficial large sample properties of maximum likelihood estimators (see Baker and Kim, 2004). It is well known, for example, that samples sizes should range from several hundred to several thousand participants for simple to complex IRT models respectively (de Ayala, 2009; Reckase, 2009). Sample sizes of ≤ 50 can result in biased parameter estimates or fail to converge, even for simple models (Lord, 1968). Unstable or biased estimates of item characteristics associated with small sample sizes are especially troublesome for maximum likelihood and least squares estimators. Later, we discuss the use of Bayesian estimators with constraining prior information to improve model convergence and fit.

As with most imaging data sets, the WMT data structure is a transpose of the typical psychometric data set. That is, whereas psychometric data are characterized by a greater number of subjects than items, the current data are characterized by a greater number of items than subjects. This is seen as a problem in IRT, because whereas subjects are typically modeled with just a single parameter, items are modeled with multiple parameters. As the ratio of subjects to items grows smaller, it becomes increasingly difficult to accurately estimate item parameters.

Fortunately, there may be characteristics of items that, when combined with certain types of estimation procedures, can overcome this challenge. It is generally known that traction in parameter estimation can be gained by constraining item characteristics to single, group values (see Wainer and Wright, 1980). This strategy works well when individual item parameters show only minor deviations from the group average, and do not significantly deteriorate model fit when held constant. A more general, less stringent framework for this strategy comes from hierarchical Bayesian modeling, where individual items are assumed to be drawn from common distributions (Levy, 2009). If the properties of these distributions (e.g., shape, mean, and variance) are known, or can be assumed based on experimental control and prior theory, limitations in the estimation of item properties from observed data can be mitigated. The WMT, like most cognitive tasks used in imaging research, makes use of highly controlled, relatively homogenous stimuli. As will be shown, this allows for greater use of Bayesian concepts in parameter estimation, and facilitates IRT modeling of behavioral data used in fMRI research.

1.3. Hypotheses and goals

This study’s aims were to: (a) determine how well IRT model parameters could be estimated from an unusual, small subject sample, large item array, multi-site data set; (b) use IRT derived test standard error functions to investigate the impact of shortening the WMT on the precision of ability estimates; and (c) determine if the latent IRT scale linking ability and item difficulty was related to brain activation.

2. Method

2.1. Participants

Nine male and nine female, right-handed volunteers were scanned five times at four magnet sites while performing the WMT (mean [range], age: 34.44 [23–53] years; education: 17.06 [12–23] years). Data obtained from these volunteers were in compliance with the requirements of each participating institution’s Institutional Review Board. Participants were recruited across a wide educational range; however, most were better educated and held higher occupation levels in comparison to the general public (Brown et al., 2011). Additional enrollment and study requirements are found in Brown et al. (2011). All participants were recruited at a single site where, with one exception, they were initially scanned, then sent to a study site for repeated scans. Scan order was randomized across the four sites. IRT analyses did not include data from the initial recruitment scan. Data from the recruitment session were excluded in order to train out task learning effects consistent with the analytic design of the complementary multi-site reliability study (Brown et al., 2011). That is, because subjects tended to develop more effective testing strategies after the initial assessment, primary response data were excluded.

2.2. Task

Each 284-s WMT run was divided into passive viewing – fixation, passive viewing – scrambled pictures, encode, maintain, and recognition periods. During the encode period, participants were asked to memorize eight line drawings of common objects presented serially at 2-s intervals. During the recognition period participants were presented every 2 s with a screen containing two pictures: one from the previous encode set and one that had not been presented to the subject during the session. During the maintain period, subjects were asked to detect the presence/absence of a human face while neutral or negative valence photographs from the International Affective Pictures System were presented in order to ensure subject attention (Lang et al., 2008; Brown et al., 2011); however, data about the impact of affective valence during the maintenance period on subsequent recognition were not included in the IRT analyses due to concerns about model complexity.

WMT items came from a population of 515 line drawings randomly assigned to study lists. In total, 256 items were presented at each site, and 1024 items were presented across all sites. However, more than half of these were repetitions of the same items administrated across multiple sites (most subjects were administered 467 total unique items).

2.3. Imaging methods

Detailed descriptions of the structural and functional imaging protocols are provided by Greve et al. (2011). Time series of the ${\mathrm{T}}_2^{*}-\text{weighted}$ images were obtained while participants performed eight runs of the WMT. A gradient echo, single shot echoplanar image sequence, axial anterior commissure–posterior commissure aligned was acquired at each site at 3.34 mm × 3.34 mm in-plane resolution and 4-mm slice thickness with 1-mm skip. The fMRI time series analysis was performed using FSL’s FEAT routine to perform a single-voxel general linear analysis of the ${\mathrm{T}}_2^{*}-\text{weighted}$ image time series (www.fmrib.ox.ac.uk/fsl/feat5/ ). See Brown et al. (2011) for further description of the fMRI processing stream. The imaging data presented below only compared the MR signal amplitude during the recognition period against the MR signal acquired during the baseline periods. A high resolution T₁-weighted image was also collected.

2.4. Item and ability parameter estimation

We used Bayesian methods of parameter estimation using OpenBUGS statistical software for Linux (Lunn et al., 2009) with Markov chain Monte Carlo methods (MCMC; for details see Fox, 2010; Patz and Junker, 1999; Swaminathan et al., 2003). From the Bayesian perspective, parameter estimates are viewed as weighted averages of information that comes from data alone (likelihoods) and information that comes from prior knowledge (prior distributions). Prior distributions can be weakly informative, in which case data have a large impact on parameter estimates, or strongly informative, in which case data have a small impact on parameter estimates. We considered three versions of the IRT model in Eq. (1); each was estimated twice, once with weakly informative priors and once with strongly informative priors. The models are listed in the left half of Table 1. Individual values for subject ability parameters were estimated in all models; however, the models are increasingly stringent with respect to the estimation of individual item parameters. The purpose of comparing weakly and strongly informative prior distributions, as well as individual versus group values for the item parameters, was to determine the degree to which prior theory was needed to overcome the small sample size problem common to fMRI.

Table 1.

Results of parameter estimation for models of varying complexity.

Model						Results
#	θ	β	α	γ	Priors	Converged	PSD θ	PSD β	PSD α	PSD γ	DIC
1	Individual	Individual	Individual	Group	Weak	No	—	—	—	—	—
2	Individual	Individual	Individual	Group	Strong	Yes	0.19	0.71	0.53	0.01	8397.82
3	Individual	Individual	Group	Group	Weak	Yes	0.23	1.60	0.38	0.01	8482.44
4	Individual	Individual	Group	Group	Strong	Yes	0.19	0.69	0.23	0.01	8483.80
5	Individual	Group	Group	Group	Weak	Yes	0.31	0.66	0.33	0.22	8729.56
6	Individual	Group	Group	Group	Strong	Yes	0.31	0.28	0.19	0.05	8730.00

Note: “Individual” refers to the estimation of unique parameter values for each subject (θ) or each item (β, α, and γ). “Group” refers to the estimation of one value for all items. “Weak” item priors allow estimates to be based on observed data without the influence of “Strong” prior beliefs. θ, subject ability parameter; β, item difficulty parameter; α, item discrimination parameter; γ, item guessing parameter; PSD, posterior standard deviation; DIC, deviance information criterion.

Ability parameters were specified with strongly informative priors in all models to identify the scale of measurement: θ ~N(0,1), which is required, in some form, for all IRT models. For item parameters, weakly informative priors were: β~uniform(−4, 4), α~uniform(0, 4), γ~uniform(0, 1); and strongly informative priors were: β~N(−1, 1), α~logN(0, 0.25), γ~beta(20, 20) I(0.40, 0.50). The choice of normal, lognormal, and beta distributions for strongly informative priors on β, α, and γ respectively are conventions in IRT that tend to accurately reflect observed data (see Fox, 2010). The hyperparameters of these priors themselves should reflect theory or previous data observations. Note that mean item difficulty was assigned a hyperparameter of negative one. This was meant to reflect the WMT’s design, which was tailored for cognitively impaired individuals (i.e., low difficulty), and the observation that participants in the study were generally well educated, which suggests above average general ability (Wilson et al., 1979). The choice of hyperparameters for discrimination simply reflects that WMT items are moderately correlated with overall performance. Hyperparameters for lower-asymptote reflect the expectation of random guessing (i.e., 0.50). However, the parameter had to be constrained to the interval between 0.40 and 0.60 to prevent improbable values.

Convergence was established by whether or not the Gibbs samplers could draw values and by monitoring the traceplots and potential scale reduction factors (PSRFs; Brooks and Gelman, 1998; Gelman and Rubin, 1992). PSRFs compare between-chain variation to within-chain variation with values near 1.00 implying that simulated values are close to the target distribution, and larger values implying poor convergence. Deviance information criterion (DIC) values (Spiegelhalter et al., 2002) were used to compare models. Smaller DIC values imply better fit. Analyses of residual item correlations (e.g., Yen, 1993) were unreliable due to the small number of subjects.

3. Results

3.1. Estimation of IRT model parameters

Results of estimation for the six models are reported in Table 1. All models employing strongly informative priors converged without difficulty. That is, the OpenBUGS software successfully returned parameter estimates and none had PSRF values greater than 1.1, suggesting good convergence. Among models with weakly informative priors, the OpenBUGS software did not successfully return parameter estimates for the model allowing individual differences in both item difficulty and item discrimination parameters (Model 1).

Average posterior standard deviation (PSD) values for the parameter estimates are also reported in Table 1 (PSD values are interpreted similarly to standard error values). The mean parameter estimates for the models are reported in Table 2. Parameter estimates are generally consistent between models (note that the absolute difference between γ and β is more important than the individual values); however, Model 3, where guessing was estimated to be 0.84, is a clear exception. The guessing parameter appears to have been overestimated in this model, causing distortion in all other parameters (a common problem for the 3-PL; see Baker and Kim, 2004). For the other models, establishing prior restrictions on guessing appears to have been sufficient to recover plausible parameter estimates.

Table 2.

Parameter estimates for models of varying complexity.

Model						Mean estimated value
#	θ	β	α	γ	Priors	θ	β	θ−β	α	γ
1	Individual	Individual	Individual	Group	Weak	—	—	—	—	—
2	Individual	Individual	Individual	Group	Strong	0.76	−1.03	1.79	1.13	0.59
3	Individual	Individual	Group	Group	Weak	−0.14	0.11	−0.25	3.43	0.84
4	Individual	Individual	Group	Group	Strong	0.57	−1.01	1.58	1.41	0.59
5	Individual	Group	Group	Group	Weak	−0.01	−1.70	1.69	1.25	0.52
6	Individual	Group	Group	Group	Strong	0.06	−1.79	1.73	1.06	0.52

Note: “Individual” refers to the estimation of unique parameter values for each subject (θ) or each item (β, α, and γ). “Group” refers to the estimation of one value for all items. “Weak” item priors allow estimates to be based on observed data without the influence of “Strong” prior beliefs. θ, subject ability parameter; β, item difficulty parameter; α, item discrimination parameter; γ, item guessing parameter.

Direct comparison of the models’ DIC values suggested that allowing individual differences in item parameters consistently improved model fit. That is, Models 3 and 4, which allowed for variation in difficulty, fit better than Models 5 and 6, and Model 2, which allowed for variation in difficulty and discrimination, fit better than Models 3 and 4.

3.2. Standard error analyses

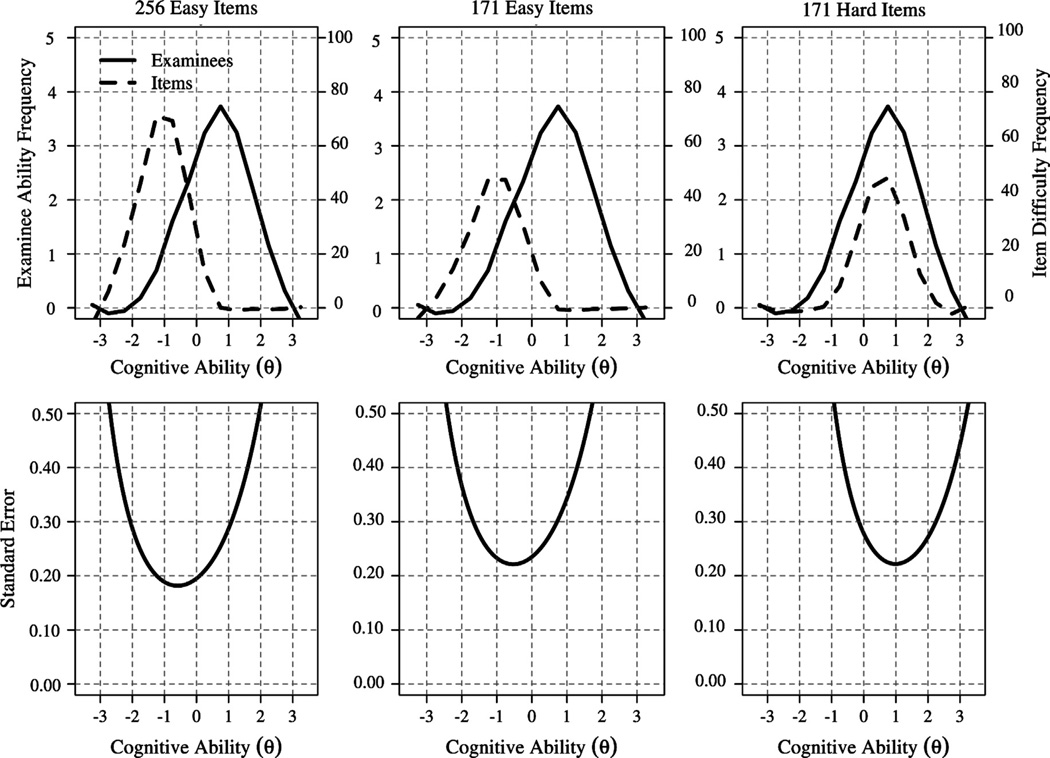
Distributions of ability and item difficult estimates for Model 4 are plotted in the top left panel of Fig. 1. The distributions are shown for a 256 item version of the WMT (the baseline for this study). As can be seen, the mode of the distribution of item difficulty is approximately 1.5 S.D.s lower than the mode of the distribution of examinee ability (the X-axis is scaled in standard deviation units). This implies that the WMT is too easy for subjects in the current sample, and is optimized for impaired examinees. This can also be seen in the corresponding standard error function shown in the bottom left panel of Fig. 1, which indicates standard error reaches a minimum near the mean of the distribution of item difficulty; far below average ability in the sample. Nonetheless, due to the high number of items administered (256), reliability² remains high at ρ_θ =0.90 in the sample (usually considered excellent).

Fig. 1.

Panels on the left are derived from acquired study data. The remaining panels are simulated data. Top: Loess fit of histograms for Working Memory Task ability (solid lines) and item difficulty (dashed lines) parameter estimates for Model 4. X-axis is scaled in standard deviation units. Bottom: standard error function for Working Memory Task ability parameter estimates in Model 4. Plots are shown for 256 easy items (left column), 171 easy items (center column), and 171 hard items (right column).

Because of the expense of long fMRI sessions, investigators prefer to use brief activation tasks. Shortening a task, however, can diminish the quality of behavioral data. To demonstrate this, the center column in Fig. 1 shows the impact of reducing the total number of items by 33% (171 total). At this level, reliability drops to ρ_θ =0.85 in the sample. This is because measurement precision is not optimized for non-impaired groups, as is shown in the bottom center panel of Fig. 1. However, by increasing average item difficulty (i.e., matching difficulty to ability), it is possible to reduce the total number of items by 33% and yet retain an overall reliability of ρ_θ =0.90 in the sample. This is because a hard version of the WMT would be optimized for non-impaired groups, as is shown in the bottom right panel of Fig. 1.

3.3. Correlations with brain images

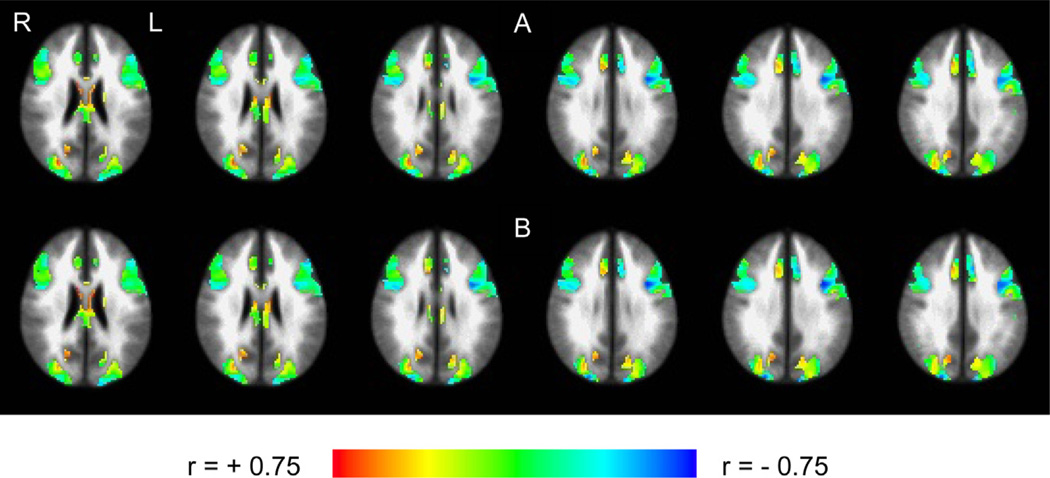
For the IRT model to be a useful guide to fMRI task design, the model’s ability domain should be related to task activation. Because the ability parameter (θ) is an estimate derived from the data, it is possible that the estimation process might introduce noise or bias into the estimates, potentially corrupting the relationship between ability and brain activation. As discussed above, accuracy of estimated parameters is a particular concern because functional brain imaging studies typically involve much smaller samples than conventional item response studies. Alternatively, because estimates of θ, unlike the observed percent correct score, have been uncoupled from item difficulty, their correlation with brain activation might be greater than correlations with percent correct scores. To investigate correlations with brain activation we averaged across the four sites the %signal change maps generated by the GLM for the recognition period in order to produce one brain activation map for each subject. A map of the voxel-wise correlations of Model 4 θ estimates with %signal change is presented in Fig. 2A for gray matter voxels where %signal change was significantly different from zero. Fig. 2B presents correlations between percent correct with %signal change. The two maps appear to be nearly identical. In both cases, moderate to large inverse correlations (−0.65 to −0.75) between ability and activation are present in some dorsolateral prefrontal cortex voxels. Alternatively, moderate to large direct correlations are observed in some occipital and parietal voxels.

Fig. 2.

(A) Voxel-wise correlations of θ with %signal change during the recognition period. (B) Voxel-wise correlations of %correct with %signal change during the recognition period. Data are presented for gray matter voxels where %signal change was greater than zero.

4. Discussion

4.1. Findings

IRT was applied to behavioral data obtained during a multi-center fMRI study of working memory. Modified 3-PL models were fit to the data, each varying in the number of parameters that were restricted versus freely estimated for all items. Several practical challenges were encountered in trying to fit the models to the data set. Most prominently, the limited number of participants, large amounts of planned missing data, and relative low difficulty of the items in comparison to subjects’ abilities complicated estimation of item parameters. To mitigate these complications, parameters were estimated using a Bayesian approach incorporating prior information into the final values. Results of estimation suggest that strongly informative priors were necessary for all but the simplest versions of the IRT model.

The study team had strong expectations about the abilities of participants, as well as item difficulties. Participants were well educated and the majority worked in business, finance and management jobs (Brown et al., 2011), which predicted above average general ability (Wilson et al., 1979). Moreover, given the unusual multi-center aspect of the study, task development was guided by the principle of tight experimental control over stimulus and item content, which led task developers to create a test composed of very similar items. Finally, because schizophrenia patients often perform about one standard deviation below the mean on delayed response types of working memory tasks, the study team focused on the development of relatively easy items (Lee and Park, 2005). The assumptions of easy item difficulty and above average ability were systematically incorporated into model priors. Given the Bayesian approach to the analysis, posterior values of these model parameters would move away from their priors if the initial model fit the data poorly. The results, however, converged with the investigators’ expectations for the selected Model 4. The mean posterior ability value was 0.57 and the mean posterior item difficulty was −1.01, values similar to the prior expectations, further validating this modeling approach.

Although not reported in this paper, adding a site parameter to the model did not improve fit. This result might be unique to the current study, where considerable effort went into avoiding site effects (e.g., removing task learning-contaminated data, avoiding repeated administration of items, using highly standardized experimental procedures, and central training of research assistants). The minimal contribution that site made to the modeling of item performance across subjects is compatible with the finding that between subject variance in fMRI data acquired during the same study was 10 or more times greater than site variance for most regions of interest (Brown et al., 2011). As with the behavioral data, minimization of site effects in the fMRI data was likely due to the standardization efforts that went into this study’s implementation. A paper by Glover et al. (2012) discusses the multiplicity of issues needing to be addressed when planning between-site fMRI studies.

Standard error functions provided guidance about the impact of altering test length and test difficulty on the test’s sensitivity to individual differences in working memory ability. Participants in the present study were administered approximately 256 items on the WMT per scan session. The test standard error function for 256 items was relatively flat across a range of approximately −2 to 1 on the ability spectrum. The 256 item task, as designed, discriminates working memory ability among 82% of the general population over an ability range where no standard error is greater than 0.25. This corresponded to an excellent reliability value in the current sample (0.90). However, because item difficulty is shifted towards the lower end of the ability distribution, the test discriminates the working memory performance of mildly to moderately impaired individuals better than more able subjects, complicating the interpretation of patient versus healthy control effects sizes and change due to treatment.

The impact of reducing the total number of items administered on standard error was shown for versions of the task with average item difficulty unmatched (easy) or matched (hard) to the average ability of the current sample. While the unmatched version of the task was associated with a drop in reliability (0.85), the matched version of the task retained the high reliability value of the full version (0.90) while reducing test administration by 33% of items. This, of course, would result in a substantial time and cost savings in fMRI studies. The results suggest that researchers should use different versions of cognitive tasks with difficulties matched to the abilities of specific sub-populations of examinees. Indeed, the optimal solution with respect to maximizing measurement precision would be to administer each examinee a potentially unique set of items based on the principle of matching item difficulty to specific ability levels through computerized adaptive testing (see van der Linden and Glas, 2010).

The IRT estimate of ability correlated as well with brain activation during the recognition period as did percent correct. The similar correlation of the IRT estimate of ability and percent correct with brain activation linked the latent ability dimension to brain activation. This linkage further implies that variations in item difficulty should be related to the evocation of brain activity as well. Using an event-related design, Bedny et al. (2007) have shown that meaningful BOLD signal responses can be detected at the individual item level. A similar event-related design could be used to directly test the hypothesis that item parameters provide meaningful information about the magnitude of brain activation. Furthermore, it is well known that standard error attenuates regression coefficients (i.e., shrinks them towards zero). To the extent that item difficulty and brain activation are directly linked, it can be assumed that regression coefficients relating brain activation to other variables of interest will be attenuated in psychometric regions of high standard error.

4.2. Limitations

Small sample size is perhaps the most critical limitation of parameter estimates reported in this study. The results provided guidance on the general distributions of ability and difficulty parameters, but are not acceptable for test calibration. The goal of this study was not to precisely calibrate individual WMT item parameters, but rather to show how IRT could be used to quantify the overall properties of a task used in fMRI. Our results suggest that with the addition of several constraints and prior theory, such quantifications can be achieved. Also, IRT analyses were conducted under the assumption that examinees’ performances on the behavioral task were due, primarily, to a single working memory dimension. The unidimensional assumption is unlikely ever to be justified unambiguously for clinical neuropsychological applications, where, even for simple tasks, lesions involving different brain systems can impair performance by disrupting any of several neurocognitive processes (Luria, 1966; Kaplan, 1988). Finally, it should again be noted that the IRT models evaluated in this study do not account for site/repeated administration effects (for a similar model see Spray, 1997). It is possible that subjects became better at the task due to repeated exposure to the stimuli, or that item parameters were not invariant to different site/list contexts. However, several analyses that attempted to incorporate or quantify site effects (not reported here) suggested that site variability was very minimal (e.g., Brown et al., 2011).

4.3. Suggestions for future research

One apparent solution to the problem of applying IRT to fMRI studies with limited data is to calibrate item parameters using larger samples in less expensive testing circumstances (e.g., participants not undergoing fMRI), and then to use these precalibrated items to estimate examinees’ abilities in the experimental imaging studies. The application of precalibrated items to samples different from those used to calibrate the items is justified by the assumed invariance of item parameters in IRT models (Lord, 1980). Nonetheless, this study does suggest that there is value to using IRT methodology in fMRI research even without precalibrated items. Researchers can use Bayesian techniques with informative prior estimates of subject and item characteristics to derive approximate parameter estimates. These estimates allow for analyses that can ensure tests are appropriately difficult.

IRT modeling can help improve precision in measurement, resulting in more robust correlations with brain activation. However, complexities are bound to arise when modern psychometric models are retroactively applied to preexisting behavioral tasks. Thorough consideration of item characteristics prior to test administration can alleviate some of these concerns. And, by combining the expertise of psychometricians with the expertise of cognitive modelers, investigators can develop improved models capable of accounting for the multifaceted aspects of brain activation tasks. This combined program of psychometric and cognitive theory will be facilitated by the continued development of multidimensional measurement models that can quantify diverse cognitive processes. Several theorists have made progress in this respect (see Batchelder, 2010; Embretson, 2010).

4.4. Conclusion

Despite the challenges associated with the application of IRT to the small samples typical of fMRI studies, the results of the present study indicated that such applications can be informative. In the present application, IRT confirmed the sensitivity of task items to the ability range targeted by task designers while producing reasonable ability estimates for the individuals studied. The study results also suggested that the latent ability scale on which item difficulty was calibrated was linked to brain activation. Together the results support the view that IRT can meaningfully contribute to the design of tasks to be used in fMRI studies.