Embodied Language Comprehension: Encoding-based and Goal-driven Processes

Abstract

Theories of embodied language comprehension have proposed that language is understood through perceptual simulation of the sensorimotor characteristics of its meaning. Strong support for this claim requires demonstration of encoding-based activation of sensorimotor representations that is distinct from task-related or goal-driven processes. Participants in three eye-tracking experiments were presented with triplets of either numbers or object and animal names. In Experiment 1, participants indicated whether the size of the referent of the middle object or animal name was in between the size of the two outer items. In Experiment 2, the object and animal names were encoded for an immediate recognition memory task. In Experiment 3, participants completed the same comparison task of Experiment 1 for both words and numbers. During the comparison tasks, word and number decision times showed a symbolic distance effect, such that response time was inversely related to the size difference between the items. A symbolic distance effect was also observed for animal and object encoding times in cases where encoding time likely reflected some goal-driven processes as well. When semantic size was irrelevant to the task (Experiment 2), it had no effect on word encoding times. Number encoding times showed a numerical distance priming effect: encoding time increased with numerical difference between items. Together these results suggest that while activation of numerical magnitude representations is encoding-based as well as goal-driven, activation of size information associated with words is goal-driven and does not occur automatically during encoding. This conclusion challenges strong theories of embodied cognition which claim that language comprehension consists of activation of analog sensorimotor representations irrespective of higher level processes related to context or task-specific goals.

Reading a word allows us to access different aspects of its meaning. On the one hand, we may understand a word that has a concrete referent by virtue of its connection to other internal symbols or associations that provide information about categories, semantic relations, or linguistic co-occurrence. On the other hand, we may understand that word’s meaning through our experience with its referent’s sensory characteristics such as color, shape and size. The role of such analog sensory representations in word meaning has been examined in contemporary cognitive psychology since the 1960s, with mental imagery recognized as playing an important role in memory (Baddeley, 1986; Paivio, 1986), thought (Kosslyn, 1980), and with spatial representations seen as crucial to the construction of mental models (Bower & Morrow, 1990; Glenberg, Meyer & Lindem, 1987; Johnson-Laird, 1983). More recently, sensorimotor experiences have been assigned a central role in language processing within the field of embodied cognition.

Embodied cognition has become an umbrella term referring to a broad and highly diverse movement within cognitive science, with the defining premise that the body and bodily action play a central role in shaping cognition (Wilson, 2002). This approach addresses the origins of knowledge as well as how knowledge is represented mentally and neurally during information processing. Knowledge of concepts is argued to emerge from perceptual experience and to be represented not in an amodal semantic faculty but in the very same sensorimotor systems that originated the experience (Barsalou, 1999; Glenberg & Robertson, 2000; Zwaan, 2004; Zwaan & Madden, 2005). The embodied approach to language processing includes a number of psychological theories proposing that words are understood through “perceptual simulation” or activation of sensorimotor representations of concepts. According to Barsalou’s perceptual symbol systems hypothesis (Barsalou, 1999), language comprehension takes place through a process of words activating simulators associated with the perceptual properties of their referents, creating a perceptual simulation of a text or utterance that preserves the analog properties of what is represented. Similarly, the immersed experiencer framework (Zwaan, 2004) describes language comprehension as a process of “vicarious experience of the described situation” (p. 36). Importantly, perceptual simulation within the embodied framework is not an optional aid to comprehension. Instead, representation of concepts is inherently perceptual, and processing language for comprehension consists of perceptual simulation or immersed experience.

Important empirical support for the embodied account of online language comprehension is provided by demonstrations of activation of sensorimotor properties of word meaning during reading and spoken language comprehension. For example, in studies of sentence processing, participants respond faster to pictured objects if the picture matches the shape or orientation of the object that was implied in a previously read sentence (the appearance-compatibility effect: Stanfield & Zwaan, 2010; Wassenburg & Zwaan, 2010; Zwaan, Stanfield & Yaxley, 2002) or when the action required to make a response matches the action that is described in the sentence (the action-compatibility effect: Glenberg & Kaschak, 2002). In addition, canonical visuospatial features of spoken words can affect eye-movements during visual search tasks (Yee, Huffstetler & Thompson-Schill, 2011) as well as performance on concurrent spatial reaction time tasks (Richardson, Spivey, Barsalou & McRae, 2003; Bergen, Lindsay, Matlock & Narayanan, 2007).

These studies and many others effectively demonstrate activation of visuospatial and motor representations during sentence or word comprehension. However, critics of the embodied account of language processing have argued against the idea that conceptual representations consist of sensorimotor information, as well as the suggestion that online language processing is mandatorily driven by activation of sensorimotor representations. Critics of the empirical evidence for activation of sensorimotor representation during online language processing have argued that some behavioral effects that have been attributed to activation of embodied representations during language processing might also be explained by symbolic processes. For example, evidence that lexical processing can be facilitated when words are presented in a way that matches their embodied perceptual experience (known as “spatial iconicity,” e.g. “ceiling” appearing above “floor”) (Zwaan & Yaxley, 2003) may also be explained by the frequency with which pairs of words occur in particular orders (Tse, Kurby & Du, 2010). This finding highlights the possibility that statistical patterns among linguistic symbols can be used in some cases to derive physical or perceptual relationships between referents (Louwerse, 2008). Additionally, recent work in perception and perceptual learning suggests that perceptual encoding involves the extraction of complex and abstract relations from the environment. As such, ‘perceptual representations’ themselves are considered abstract relational structures, while the actual basic sensory features are fleeting and do not become a part of the accessible output of the encoding process (Kellman & Massey, 2013).

Critics of the idea that conceptual representations consist of sensorimotor information have argued further that demonstrations of sensorimotor activation during conceptual processing do not provide evidence that sensorimotor representations are constitutive of the concept or even conceptually relevant (Adams, 2010; Mahon & Caramazza, 2008; Weiskopf, 2010). For example, Mahon & Caramazza suggest that the observed sensorimotor effects may arise from activation originating in abstract, disembodied representations spreading into systems capable of sensorimotor representation. This would occur not because language comprehension inherently involves activation of sensorimotor activation, but because such activation is driven by higher order task and goal-related processes.

This sort of goal-driven account of embodied activation is supported by empirical work assessing task-related influences on sensorimotor activation during language processing. Louwerse and Jeuniaux (2010) found that processing of picture pairs was more strongly affected by real-world canonical spatial relations than processing of words, especially when the task involved spatial iconicity judgments. Conversely, processing of word pairs was more strongly affected by frequency of word order, especially when the task involved semantic relatedness judgments. When the task required assessment of physical relationships, sensory information was activated and facilitated performance, but when the task involved judgment of symbolic relationships, statistical properties of language better explained reaction time patterns. Similarly, property verification judgments (e.g. “Can a moth be speckled?”) can be affected by linguistic co-occurrence as well as perceptually represented information about referent modality. However, fast judgments are more likely to be affected by linguistically encoded relationships, while slower responses were more sensitive to perceptual information (Louwerse & Connell, 2011). Assuming that goal-driven activation takes more time than encoding-based activation, this result supports a goal-driven account of perceptual properties of concepts.

Understanding the role of goals in driving activation of sensorimotor representations is important because the defining difference between the embodied cognition account of language processing and current “disembodied” accounts is precisely the idea that embodied language comprehension is driven by direct, mandatory activation of ‘experiential representations’ taking place at the word level of language comprehension (Zwaan, 2004). Accordingly, conceptual representations are argued to consist of sensorimotor information at their core, rather than activating such information peripherally through spreading activation. “Whereas such knowledge is cumbersome and brittle in amodal symbol systems…it ‘rides for free’ in perceptual symbol systems” (Barsalou, 1999, p. 604, quotations in original).

As such, the embodied cognition account of language processing predicts encoding-based activation during the reading of words irrespective of higher-level processes related to context or task-specific goals. In contrast, a disembodied account of language comprehension can explain the appearance- and action-compatibility effects by assuming that flow of activation within and between cognitive systems is largely goal-driven. Evidence for goal-driven activation of sensorimotor representations provides support for what might be called a weak (or conventional) form of embodied cognition where language-processing goals guide the flexible use of different representational formats (including embodied ones). This approach to embodiment is not weak in the sense that it characterizes sensorimotor representations as unimportant, but rather that it does not characterize them as foundational representations that necessarily have priority in processing. Such a description fits many approaches to mental representation that have developed within traditional cognitive psychology (e.g., for visual imagery see Kosslyn, 1980; for stimulus-response compatibility see Kornblum, Hasbroucq & Osman, 1990). In contrast, support for a strong (or radical) form of embodied cognition requires evidence of encoding-based activation of embodied representations irrespective of task goals, a pattern that would show that sensorimotor representations have general priority in processing.

Analog representations of magnitude

A variety of useful tasks have been developed that provide insight into the processing of representations of semantic magnitudes associated with symbols such as words and numbers. Tasks involving comparison of magnitudes have consistently shown the symbolic distance effect -- the finding that the time required to determine the larger of two visually presented numerals is an inverse function of the difference between the two numerals (Henik & Tzelgov, 1982; Koechlin, Naccache, Block & Dehaene, 1999; Moyer & Landauer, 1967; Van Opstal, Gevers, De Moor & Verguts, 2008). For example, choosing the larger number of the pair 2 and 8 takes less time than making the same choice for the pair 6 and 8. Reaction times depend more strongly on the ratio of the pair of numbers than on their absolute difference and in this way resemble a classic psychophysical function. The same effect occurs when participants compare lexical stimuli instead of numbers, such that choosing the larger or smaller of a pair of animal names is facilitated for pairs with a large difference in size (lobster – cow) compared to a small difference in size (sheep – cow). This finding is impressively robust (Banks & Flora, 1977; Dean et al., 2005; Holyoak, Dumais & Moyer, 1979; Moyer & Bayer, 1976) and occurs for a variety of other types of words and dimensions (Dean et al., 2005; Holyoak & Walker, 1976; Paivio & Te Linde, 1980; Te Linde & Paivio, 1979). The pattern of reaction times is similar to that found for actual perceptual comparisons such as choosing the longer of two lines (Johnson, 1939) or the larger of two circles (Moyer & Bayer, 1976). Therefore, the symbolic distance effect is generally thought to indicate a conversion process of abstract numbers or words into analog representations on the dimension of interest, such as numerical magnitude or animal size. The comparison decision is then made based on these analog representations, constituting an “internal psychophysical judgment” (Moyer, 1973 p.183).

While symbolic comparison effects provide insight into the way that we process symbolic stimuli, the trial-final reaction times measured in these tasks do not provide direct insight into the encoding of symbols because they are influenced by other task-relevant processes such as comparison, decision making and response selection. In contrast, distance priming tasks are thought to measure the effects of encoding-based activation. The numerical distance priming effect is the finding that responses to a numerical target are faster when it is preceded by a number that is close in magnitude than by one that is distant. For example, processing the digit 6 is facilitated when preceded by the prime 4 compared to the prime 2 (Brysbaert, 1995; Den Heyer & Briand, 1986; Marcel & Forrin, 1974; Reynvoet, Brysbaert & Fias 2002). This effect is found both when the prime requires a deliberate response and during short SOA masked priming (Koechlin, Naccache, Block, & Dehaene, 1999), and has been found with verbal numerals (four, six) as well as Arabic numerals and non-symbolic quantities such as dot patterns (Herrera & Macizo, 2008). In addition, the effect occurs even when successful execution of the task does not require activation of the number’s magnitude (Brysbaert, 1995; Van Opstal & Verguts, 2011). Importantly, comparison to letter stimuli has shown that numerical distance priming relies on activation of magnitude rather than simply order information, since the (alphabetical) order information associated with letters leads to comparison distance effects, but not distance priming (Van Opstal, Gevers, De Moor & Verguts, 2008).

Few studies have explicitly investigated whether analog representations of size associated with lexical items that refer to objects also lead to size-based priming effects during encoding. Referent size of individual words has not been found to reliably affect performance on a lexical decision task, likely because size information does not help to distinguish words from non-words (Kang, Yap, Tse & Kurby, 2011). There is some evidence that priming occurs based on overlap in perceptual properties of words’ referents, (Flores d’Arcais & Glazenborg, 1985; Schreuder, Flores d’Aracais, & Glazenborg, 1984) so that “orange” can prime “ball” by virtue of both objects being round. However, other work suggests that these effects may occur only when perceptual information is first made salient to the comprehender (Pecher, Zeelenberg & Raaijmakers, 1998), leaving an unclear picture of the role of task-related and goal-driven processes on perceptual priming with lexical items.

Current study

In the symbolic distance effect and numerical distance priming, proximity in the semantic magnitude of two stimuli have opposite effects on reaction time, and for this reason the two effects are thought to measure different levels of processing. The symbolic distance effect, or facilitation of comparison decisions for numbers that are numerically distant, takes place at the task or goal-related level of comprehension. At this level, symbolic comparison tasks with lexical items robustly show reaction time patterns similar to numbers, suggesting that both numerical and lexical symbolic comparison decisions are based on analog representations. As with other priming effects, numerical distance priming is observed at encoding, thus providing substantial evidence for the analog representation of numerical semantic magnitude at the encoding or word-meaning level. This provides the opportunity to distinguish between activation at the encoding and goal-driven stages of language comprehension based on distinct patterns of reaction time within a single task.

Brysbaert (1995) created a novel numerical-priming paradigm that is especially well-suited to the goal of distinguishing encoding-based priming from goal-driven comparison effects. Participants in an eye-tracking experiment were presented with triplets of Arabic numerals and asked to indicate whether the middle numeral was numerically in between the two outer numbers. In conjunction with eye-tracking, the use of three numbers, rather than the typical two, allowed encoding and decision processes to be isolated in a single task. Encoding of the middle number takes place before a comparison decision must be made, since all information needed to make a correct decision is available only after the third number has been processed. As such, time spent looking at the middle number provided a measure of encoding time. A gaze-contingent display technique was used in which the numbers were masked except when the participant looked at them during first-pass reading from left to right. This eliminated preview and rereading effects that might have reduced the value of looking time as a measure of encoding. Brysbaert observed a numerical distance priming effect on the middle number, such that its encoding time was reduced on trials with a small numerical difference between the first and middle number, compared to trials with a larger difference. Crucially, the same effect was observed when, instead of judging magnitude-order, participants simply encoded each triplet into memory for an immediate recognition task, demonstrating encoding-based activation of semantic magnitude associated with numbers independent of goal-based activation related to the reader’s task. The current study extends Brysbaert’s distance-priming paradigm to words referring to objects in order to assess whether activation of magnitude information about semantic size associated with lexical items is encoding- or goal-based.

Experiment 1

This experiment applied Brysbaert’s (1995) gaze-contingent triplet-comparison task to object and animal names. As illustrated in Figure 1, participants read three words (all referring either to objects or animals) and then indicated with a speeded key-press whether the size of the referent of the middle word was between the sizes of the referents of the first and last word. The three object or animal names were shown from left-to-right on a screen, and a gaze-contingent display technique was used so that each name could only be encoded during the eyes’ first-pass over that word. Triplets of words were constructed so that the distance in the semantic size of the second and first items was small, medium or large. The task provides two measures of interest: (1) Decision time is the interval between when the eyes first look at the final name in the triplet and the execution of the manual response; it includes goal-based activation of task-relevant semantic properties since it covers the time during which all information needed to perform the task is available. (2) Encoding time is the gaze duration on the middle word, a measure that is widely accepted in the eye-tracking literature as sensitive to lexical encoding (e.g., Inhoff, 1984; Morris, 1994; Rayner, 1998). In Brysbaert’s study, this measure showed distance priming for Arabic numerals indicating that it reflected encoding-based activation of numerical magnitude information.

Figure 1.

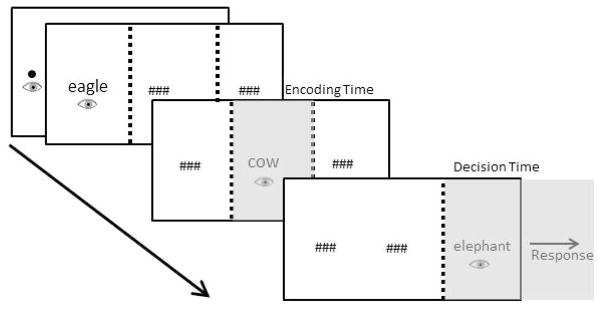
Presentation of stimuli and dependent measures in Experiment 1 and 3. Encoding time is measured as the gaze duration on the middle word. Decision time is the time from the onset of the last word until the indication of a response by a speeded key-press. A gaze-contingent display technique was used in which the words were masked except when the participant looked at them during the first reading pass from left to right. This eliminated preview and rereading of the first and middle word.

To our knowledge, theories of embodied cognition have not previously been applied to distance-priming or the symbolic distance effect. However, these theories have proposed that sensorimotor representations are the foundation of the meaning of language and that language comprehension involves perceptual simulations of the meaning of what is being understood (Barsalou, 1999; Glenberg & Robertson, 2000; Zwaan, 2004; Zwaan & Madden, 2005), rather than having sensorimotor representations activated based on task goals as critics have contended (Mahon & Caramazza, 2008; Adams, 2010). As such, we believe that the strong (or radical) embodied cognition approach leads naturally to the prediction for this task that distance priming should be found for encoding time on the middle object or animal name as Brysbaert (1995) found for numerals, because encoding a name should involve creation of a representation that captures the perceptual properties of its referent. In contrast, the goal-driven activation account suggests that the visuospatial characteristics of a word’s referent are not activated automatically during encoding but that instead this information is accessed in a goal-driven manner at a later stage of language processing. Therefore, the goal-driven activation account does not predict distance priming on encoding time and instead suggests that any effects of semantic distance should be understood in terms of how semantic distance affects the processes that are invoked by the task goals. Both the embodied-cognition and goal-driven activation approaches lead to the prediction that the decision-time measure should show a symbolic distance effect since the difficulty of comparing the size of perceptual representations is inversely related to the difference in their sizes (Moyer & Bayer, 1976; Banks & Flora, 1977; Holyoak et al., 1979; Dean et al., 2005).

Method

Participants

Twenty-four undergraduates at the University of North Carolina at Chapel Hill participated for course credit. All were native English speakers with normal or corrected-to-normal vision and were naïve about the research goals.

Stimuli

Experimental stimuli consisted of triplets of object and animal names selected from size-rating norms for animal (Dean et al., 2005) and object names (Holyoak et al., 1979). Objects and animals were selected with two constraints: (1) Across items there was a substantial range in rated size that was evenly distributed so that approximately equal numbers of items could be placed in each of three size groups (small, medium and large), and (2) the average standard deviation in size ratings for an item was low, indicating that size representations were similar across raters. Cross-individual consistency in size estimates was further validated by examining the reliability of ratings for the 21 animal names that were normed in both Dean et al. and Holyoak et al. Although the two studies used different rating scales, had different rating instructions, and were collected more than twenty years apart, the two sets of norms were highly correlated, r = .96, p < .001, R² = .91.

The stimulus triplets were constructed as follows. Twenty-one animal names referring to animals across a range of sizes served as targets appearing in the middle position of a triplet, while the remaining 25 animal names served as flankers. Triplets were constructed so that the semantic size difference between the first and the second animal was small (about 1 target standard deviation), medium (about 2 target standard deviations) or large (3 or more target standard deviations). In addition, the first item was either larger or smaller than the target item, so that there were an equal number of ascending and descending triplets, resulting in a 3(size difference) × 2(direction of the size difference) within-subjects design. The third word in the triplet was added so that for half of the trials, the size of the middle animal was in between the size of the two outer animals, resulting in a “consistent” triplet (e.g. eagle – cow – elephant). On the other half of the trials, the size of the middle item was not in between the two outer items, resulting in an “inconsistent” triplet (e.g. giraffe – cow – elephant). The same procedure was followed for the object triplets, using 21 target and 37 flanker objects. The greater number of flanker items for objects as compared to animals was possible because Holyoak et al. (1979) supplied more items that fit our criteria than did Dean et al. (2005). Flanker items were chosen so as to minimize repetition of flanker items within blocks. See Appendix A for a sample of our experimental stimuli.

A norming study was conducted to measure the semantic relatedness of all the word pairs occurring within the triplets. Thirty participants were presented with the pairs one at a time and asked to rate the association between the items in the pair (“Indicate the degree to which you feel these two items are associated. For example, how often do you think of the two items together, do they occur together in the real world, or are they mentioned in the same context?”), answering on a scale of 1 (not at all associated) to 7 (entirely associated). The order of the words in each pair was counterbalanced across participants. None of the participants in the norming study took part in any of the eye-tracking experiments reported here. Overall, the pairs were rated low on semantic relatedness, with a mean rating of 2.52 for small difference pairs (SD = .62), 2.48 for medium difference pairs (SD = .62) and 2.18 for large difference pairs (SD = .53). The slight difference in mean similarity ratings for pairs with small and medium size differences was significant by subjects but not by items, t₁(29) = 2.82, p = .009, d = .51; t₂(41) = .32, p = .749. For pairs with medium and large size differences, the difference in similarity ratings was significant, t₁(29) = 8.50, p < .001, d = 1.55; t₂(41) = 2.65, p = .011, d = .41. Previous research on semantic or associative priming suggests that words are processed more quickly when preceded by a semantically related or associated prime (Meyer & Schvaneveldt, 1971). Therefore, if the results of the experiment show reduced reading times for pairs within the small or medium size difference condition compared to the large size difference condition, it will be important to distinguish between effects caused by the size difference manipulation and differences in semantic relatedness.

Target items were counterbalanced across six lists, each consisting of six blocks of 42 trials, resulting in 252 trials per participant. In each block, all target words appeared once in random order, with animal and object triplets randomly intermixed. Unlike the targets, flanker items were occasionally repeated within blocks. Across the blocks within a list, each word appeared once in each condition, so that all participants saw each target in each condition, resulting in a total of six differently primed presentations of each target word. To control for possible effects of target repetition, each list started with a different block. Each experimental session started with twelve warm-up trials, which did not contain any of the target words used in the experimental trials. The warm-up trials were excluded from all analyses. To make sure participants fully understood the task, they were also presented with several practice triplets verbally by the experimenter before they were set up for eye-tracking.

Procedure

Eye movements were recorded from the participants’ right eye using an SR EyeLink 1000. Stimuli were presented on a 20 inch ViewSonic G225f Monitor at a distance of 61 cm with a display resolution of 1024 × 768. At the beginning of each session the tracker was calibrated using a 9-point procedure; calibration was checked between trials and the tracker was recalibrated when necessary. Participants sat in a well-lit room with a chin and a forehead rest minimizing their head movements. They were instructed to read the triplets silently and decide for each triplet whether the size of the middle object or animal was in between the two outer (first and last) objects or animals. Participants answered by indicating “yes” or “no,” using a handheld console. The experimenter monitored eye movements throughout the session.

Each trial started with a fixation point placed on the left side of the screen on the horizontal axis. Once this point was fixated, the next screen appeared, with the first word of the triplet slightly to the right of the fixation point. The middle and last word appeared in the center and on the right side of the screen on the same horizontal axis, masked by hash marks. Gaze-contingent invisible boundaries were placed approximately 120 pixels to the left of the middle and last word’s mask. Gaze contingencies were set up so that each word was visible only when the eyes entered the word’s region from left to right, and was no longer visible after the eyes left its region to the right (see Figure 1). This method of stimulus presentation prevented potential parafoveal preview or rereading of the first and middle word. When the participants moved their gaze across the invisible boundary between the first and middle word, the middle word was unmasked and the first word was masked. The same event was repeated when the eyes crossed the invisible boundary between the middle and last word, so that the middle word was masked and the third word unmasked. Once the eyes left the first or middle word to the right, these items did not become visible again upon regressive eye-movements. The last word remained visible until a response was made. Participants received feedback on their accuracy after every trial.

Analysis of eye movements

Fixations shorter than 80 ms and within 1 degree of a longer, immediately subsequent fixation were merged with the longer fixation by an automatic procedure in the Eyelink software.

Following Brysbaert (1995), gaze duration on the middle word was taken as a measure of encoding time for this item, reflecting encoding-based activation of word properties. Gaze duration is the average of the sum of all first-pass fixation durations on a word and is widely used as a measure of lexical encoding in eye-tracking studies of reading (Inhoff, 1984; Morris, 1994; Rayner, 1998). Secondary analyses of encoding time were also performed using first-fixation duration (the duration of the first fixation on a word regardless of whether the word receives other first-pass fixations) and single fixation duration (the duration of the first fixation on a word on those trials where the word only receives one first-pass fixation). These latter two measures potentially reflect earlier processes than does gaze duration, but their interpretation can be problematic. First-fixation duration depends systematically on whether the word receives subsequent first-pass fixations. Single-fixation duration measures performance only on a subset of trials and is most meaningful when a high proportion of trials receive single fixations. In addition to these standard eye-tracking measures, Decision Time was defined as the time from the onset of the third word until the button press indicating a response, reflecting goal-based activation. We also computed Middle-Last Ratio, which was the gaze duration of the middle word over the decision time. This provided a measure of the proportion of time spent on the middle word compared to the time spent on the last word and the task-decision on each trial.

Results and Discussion

The detailed data analyses reported below are based on the first three blocks performed by each participant. This is done to allow close comparison to the results of Experiment 3, where the addition of another task meant that only three blocks of data could be obtained in this part of the experiment. Analyses of all six blocks in Experiment 1 showed very similar patterns of results and all effects of interest remained significant¹. Overall accuracy was 87%, and no participant had an average accuracy below 71%. Inaccurate trials were excluded from all analyses involving response time measures, but not middle word encoding time, as gaze duration does not measure task-related responses that can be evaluated for accuracy.

Mean correct decision times are shown in the left panel of Figure 2. They showed a strong symbolic distance effect, with times decreasing as the difference in semantic size between the first and middle word increased, F₁(1,23) = 24.4, p <.001, partial η² = .52; F₂(1,41) = 17.8, p < .001, η² = .30, for the linear effect of size difference. There was no difference in decision times between ascending and descending trials, F₁(1,23) = 3.1, p = .09; F₂(1,41) = 2.2, p = .148, though there was a marginally significant tendency for the effect of size difference to be stronger for descending than ascending trials, F₁(1,23) = 4.5, p < .05, partial η² = .16; F₂(1,41) = 2.6, p = .117. Decision times were faster for consistent trials (requiring a ‘yes’ response, M = 2049 ms) than for inconsistent trials (requiring a ‘no’ response, M = 2241 ms), F₁(1,23) = 10.43, p < .01, partial η² = .31 ; F₂(1,41) = 10.39, p < .01, partial η² = .21. Consistency did not interact with size difference, F₁(1,23) = 1.1, p = .296; F₂(1,41) = .54, p = .467.

Figure 2.

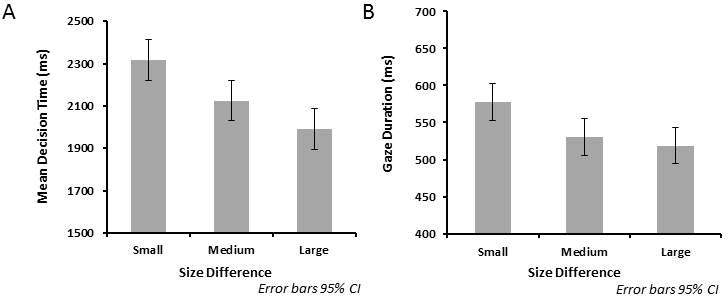
Mean decision times (A) and middle word encoding times (B) for trials with small, medium and large differences in semantic size between the middle and first item in Experiment 1. Both measures show a symbolic distance effect. Gaze duration on the middle word and decision time are shorter when the difference in semantic size between items is larger.

Mean accuracy rates followed the same pattern as decision times, with accuracy increasing as the difference in semantic size between the first and middle word increased from small (M = .83), to medium (M = .88) and to large (M = .91),, F₁(1,23) = 16.7, p <.001, η² = .43; F₂(1,41) = 21.0, p <.001, η² = .34, for the linear effect of size difference.

Only 34% of trials consisted of a single fixation, and for this reason analyses of encoding time focus on gaze duration². As shown in the right panel of Figure 2, middle word encoding times also showed a symbolic distance effect, such that mean encoding time on the middle word was shorter when the semantic size difference between the first and middle word was larger, F₁(1,23) = 11.7, p < .01, partial η² = .34 ; F₂(1,41) = 6.0, p < .02, partial η² = .13, for the linear effect of size difference. Middle word encoding time did not show a difference between ascending and descending trials, F₁(1,23) = .2 p = .663; F₂(1,41) = .002, p = .969, nor was there an interaction between size difference and direction of the difference, F₁(1,23) = .2, p = .674, F₂(1,41) = 1.0, p = .343. Observation of a symbolic distance effect on the middle words shows that the effect of size difference on encoding time for words was the opposite of the distance-priming effect that Brysbaert (1995) found for numbers. This pattern does not support encoding-based activation of size information, which we have argued leads to the prediction that distance priming should be observed for encoding times. The surprising finding of a symbolic distance effect on encoding times is analyzed below in relation to individual differences in strategies for performing the triplet comparison task.

Variation in individual strategies

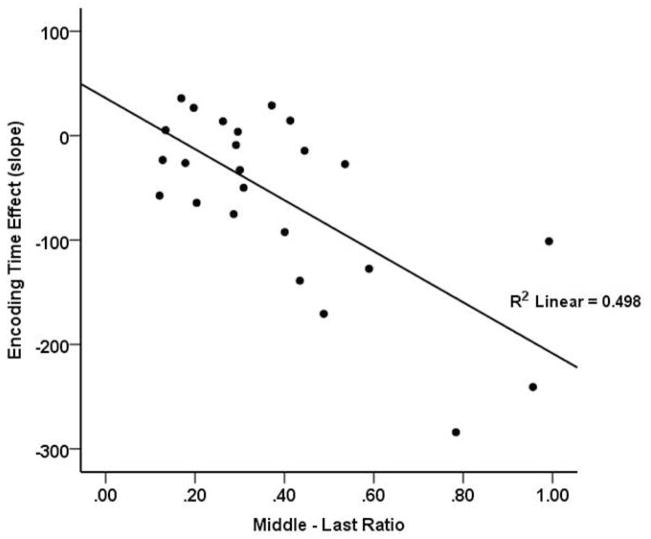
Our analysis plan followed Brysbaert (1995) in operationalizing encoding time as gaze duration on the middle word, an approach that is consistent with practice in the reading literature where systematic effects of lexical properties on gaze duration have led to its being considered a primary measure of word recognition (Inhoff, 1984; Morris, 1994; Rayner, 1998). The finding that gaze duration on the middle word showed a symbolic distance effect indicates that for this task gaze duration may reflect both lexical encoding and goal-driven processing. This possibility was tested by examining whether the magnitude of a participant’s symbolic distance effect on encoding time for the middle word was related to his or her judgment strategy. The magnitude of the symbolic distance effect on encoding time was given by the slope of the linear effect of size difference between the first and middle words on middle-word gaze duration encoding time. More negative slopes indicate stronger symbolic distance effects, while a slope of zero indicates no distance effect and a positive slope would indicate distance priming. Judgment strategy was given by the a participant’s middle-last ratio, defined as the participant’s average encoding time on the middle word divided by his or her average decision time on correct trials. Mean participant middle-last ratios ranged from .12 to .99. High ratios indicate that the participant spent a relatively long time encoding the middle word compared to the time spent on the last word until the response indicating a decision, a pattern that is consistent with the use of an incremental-judgment strategy where the semantic size of the middle word is mentally compared to that of the first word before the eyes move on to the final word. Lower ratios indicate long decision times relative to middle word encoding times, a pattern that is consistent with the use of a final-judgment strategy where mental comparison of sizes is postponed until the last word is seen.

The scatterplot in Figure 3 shows that the magnitude of a participant’s symbolic distance effect on encoding time was strongly related to his or her judgment strategy, with larger symbolic distance effects observed for participants pursuing an incremental-judgment strategy than for those pursuing a final-judgment strategy. This conclusion is supported by a robust negative correlation between participants’ middle-last ratios and the slopes of their size-difference effects, r = −.71, p < .001, R² = .50. Judgment strategy, as measured by middle-last ratio, was not related to overall speed measured by total time for trial completion, r = .12, p = .593. However, subject middle-last ratio was related to overall accuracy, with use of an incremental strategy showing a positive correlation with mean accuracy in the task, r = .49, p <.02, R² = .237. This supports the idea that individual participant strategies not only affect the extent to which participants exhibit the symbolic distance effect on the middle word, but also their level of task performance.

Figure 3.

Individuals’ mean middle-last ratio by the slope of the size-based effect on the middle word in Experiment 1. There is a strong, negative relationship between the individuals’ mean middle-last ratio and mean encoding slope. Individuals with a high middle-last ratio (incremental judgment strategy) show a strong symbolic difference effect during middle word gaze durations. Individuals with a low middle-last ratio (final judgment strategy) show no systematic effect of size difference on middle word gaze durations.

The scatterplot in Figure 3 also provides evidence about whether use of an incremental judgment strategy may have caused distance priming for the second word to be masked by mental comparison processes that occurred while the participant looked at the second word. If that were the case, then it would be expected that participant’s using a final-judgment strategy (indicated by a low middle-last ratio) might show distance priming, rather than the symbolic distance effect, on middle-word encoding time. Examination of performance for participants using a final-judgment strategy, shown toward the left in Figure 3, suggests that this was not the case. The slopes of the size-difference effect for these participants appear to be randomly distributed around zero, rather than showing a preponderance of positive slopes of the sort that would be associated with distance-priming effects. Statistical support for this conclusion comes from the absence of a significant effect of size difference on encoding time (middle-word gaze duration) for the 50 percent of participants with the lowest middle-last ratios (M = .21), F₁(1,11) = 2.7, p = .132; F₂(1,41) = .84, p = .365 (n = 12). The 50 percent of participants with the highest middle-last ratios (M = .56) showed robust symbolic distance effects on encoding time, F₁(1,11) = 12.5, p < .01, η² = .53; F₂(1,41) = 10.6, p < .01, η² = .21 (n = 12).

This experiment showed robust symbolic distance effects on decision times across participants, and on encoding times for those participants using an incremental-judgment strategy. Because the symbolic distance effect reflects difficulty of comparing the size of objects that are close in size, these effects support the idea that size information associated with lexical items was activated by the goal of size comparison. The experiment provided no evidence of distance priming as would be expected if size information were automatically activated during lexical encoding.

Experiment 2

The results of Experiment 1 did not show a size-based priming effect of the sort that would be expected if activation of semantic size occurs during lexical encoding of object and animal names in the same way that Brysbaert (1995) showed that it did for numerals. However, the results did show comparison-based activation of size information both on decision time and on middle-word encoding time, with the analysis of judgment strategy suggesting that the absence of distance priming was not due to masking by the symbolic distance effect. The current experiment examines whether distance priming between successive object and animal names is found when the task demands do not involve the semantic size of the referents. It uses Brysbaert’s memory paradigm, where participants read three words as in Experiment 1 but then judged whether a subsequently presented probe word had been among the preceding triplet. Brysbaert found numerical distance priming in this task even though the magnitude of the numbers was not relevant to performing the task. This provided evidence that the magnitude of numbers is activated automatically upon encoding even if magnitude is not relevant to task goals. Examination of whether size-based priming is found for object and animal names in this task provides a further test of whether there is encoding-based activation of semantic size that may perhaps have been masked by comparison processes in Experiment 1.

Method

Participants

Twenty-four undergraduates at the University of North Carolina at Chapel Hill participated for course credit. All were native English speakers with normal or corrected-to-normal vision and were naïve about the research goals. None had participated in Experiment 1.

Stimuli & Procedure

The object and animal names, as well as the mode of presentation, were identical to those used in Experiment 1. However, participants were instructed to move their gaze to a mask at the bottom-center of the screen after reading the third word in each triplet. Once fixated, the mask was removed to reveal a fourth word. On half of the trials, the fourth word had been among that trial’s triplet, while on the other half it was new (but could have appeared earlier in the experiment on one or more different trials). The participants’ task was to indicate whether the probe had been among the triplet or not, indicating ‘yes’ or ‘no’ on a hand-held console. The first, middle and last word of the triplet appeared as ‘old’ probes equally often. No words of the triplet were visible on the screen after the onset of the probe. The probe remained visible until a response was made. Participants received accuracy feedback after each trial.

After completing the experiment, participants were given a questionnaire with increasingly specific questions checking for any awareness of the size difference manipulation.

Analysis of eye movements

Eye movements were analyzed as in Experiment 1. Middle-last ratios were not computed since the triplet and the probe were not considered to take part in the same task process. Due to a stimulus error .9% of all trials were excluded.

Results and Discussion

Detailed results are presented for the first three blocks only as in Experiment 1³. Overall accuracy across participants was 97%, with no participant scoring below 92% accuracy. Inaccurate trials were excluded from all analyses involving fixations on the last word or the probe and response time measures.

Sixty-two percent of trials had only a single fixation, so both single-fixation duration and gaze duration were considered as measures of encoding time. Neither measure showed significant variation as a function of the distance in semantic size of the middle word from the initial one. Average single-fixation durations as a function of distance were 215 ms (small), 216 ms (medium) and 212 ms (large), F₁(1,23) = 1.0, p = .305; F₂(1,41) = .44 p = .512. Average gaze durations were 242 ms (small), 247 ms (medium) and 243 ms (large), F₁ (1,23) = .07, p = .788, F₂(1,41) = .02, p = .896. Encoding times also did not vary as a function of the direction of the difference between the first and middle words on either measure F₁(1,23) < 1; F₂(1,41) <1, nor was there a significant interaction between size difference and the direction of the difference, F₁(1,23) = 1.6, p = .213; F₂(1,41) = 2.7, p = .110.

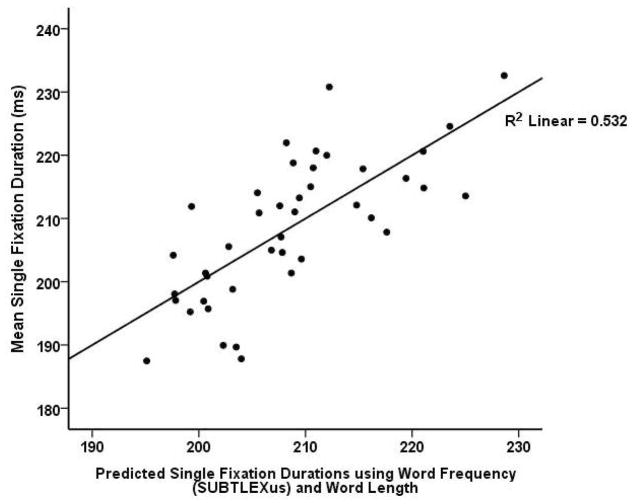
The null effect of size difference on middle-word encoding time was found for a measure that was used by Brysbaert (1995) to show distance priming with numbers and which has been widely used as a measure of lexical access as well as semantic integration in studies of reading (Inhoff, 1984; Morris, 1994; Rayner, 1998). In order to show that reading time on the middle word was a sensitive measure of lexical encoding in this experiment, we investigated its relation to word length (number of letters) and word frequency (SUBTLEXus, Brysbaert & New, 2009), factors that are strongly related to ease of lexical encoding and known to affect fixation duration during reading of continuous text for comprehension (Rayner, 1998). Multiple-regression analyses showed that on the middle-word, single-fixation duration was strongly related to word length and frequency, r = .73, R²= .532, F(2,39) = 22.2, p < .001 (see Figure 4); word length significantly predicted single fixation duration, β = .42, p < .01, as did the log of word frequency per 51 million, β = −.40, p < .01. A consistent but statistically weaker relation was found with gaze duration. Neither word length nor word frequency interacted with size difference.

Figure 4.

Multiple regression of single fixations duration, using word frequency (SUBTLEXus, Brysbaert & New, 2009) and word length as predictors. Both word frequency and length are known as robust predictors of encoding time of written words (Rayner, 1998).

In sum, this experiment showed that while reading time on the middle word was related to ease of lexical encoding, it provided no evidence of distance priming as would be expected if there were encoding-based activation of semantic size for object and animal names. This suggests that meaningful encoding of words is affected by statistical properties of words as linguistic symbols, such as word frequency, but not visuospatial properties like semantic size. However, previous results on numerical distance priming show that numerical symbols do elicit activation of magnitude information upon encoding (Brysbaert, 1995).

Experiment 3

Neither Experiment 1 nor Experiment 2 provided any evidence of distance priming in the processing of animal and object names, though Experiment 1 showed very robust symbolic distance effects for these words. This pattern supports the conclusion that representations of semantic size are not automatically activated as part of encoding these items but that activation follows instead from the processes required to achieve task goals. In contrast, research on numerals has consistently shown distance priming (Brysbaert, 1995; Den Heyer & Briand, 1986; Marcel & Forrin, 1974; Reynvoet et al., 2002) and symbolic distance effects (Brysbaert, 1995; Henik & Tzelgov, 1982; Koechlin et al., 1999; Moyer & Landauer, 1967; Van Opstal et al., 2008), a pattern indicating that representations of semantic size for numerals are automatically activated during encoding and that the use of those representations is influenced by task goals. In Experiment 3 the size-order judgment task of Experiment 1 (Brysbaert, 1995, Experiment 1) is used with both word and number trials in order to determine whether this difference in how semantic size is activated for words and Arabic numerals can be demonstrated in the same experiment.

Method

Participants

Twenty-four undergraduates at the University of North Carolina at Chapel Hill participated for course credit. All were native English speakers with normal or corrected-to-normal vision and were naïve about the research goals. None had participated in Experiment 1 or 2.

Stimuli

The animal and object triplets were identical to those in Experiment 1. However, to allow for the addition of the number block while keeping the testing session under forty-five minutes each participant was presented with each target three times, once in each size condition, rather than six times as in Experiment 1. Thus, a participant saw each item-by-size combination either in an ascending or a descending triplet, but not in both. This resulted in a total of 126 animal and object trials per participant. This is equivalent to the first 3 blocks of data which were reported for Experiment 1. The trials were presented in random order.

The number triplets were constructed by having each Arabic numeral between 14 and 97 presented as a target (middle) number once, resulting in 76 trials per participant. The first and last numbers were selected so that the numerical difference between the target and the flankers was between 1 and 19. The direction of the difference between the first and middle number was either ascending or descending, and the third number was chosen so that the triplet was either consistent (e.g. 24 – 26 – 31) or inconsistent (e.g. 24– 26 – 25), counterbalanced across four lists. Each list contained each target number once, with consistent/inconsistent and ascending/descending trials appearing equally often. Similarly, each numerical difference between 1 and 19 appeared approximately equally often per list. Each subject saw one list, preceded by eight warm-up trials which were excluded from all analyses. The number trials were presented in a separate block from the word trials, and the presentation order of these blocks was counterbalanced across participants so that half of the participants started with the number block and then completed the word block while the other half of the participants started with the word block and then completed the number block.

Procedure

The stimulus presentation and eye-tracking procedures were the same as in Experiment 1 with one exception. Whereas in Experiment 1 the first word of the triplet appeared in place of the fixation point, in Experiment 3 the fixation point and the three words were each placed on a separate vertical quarter of the screen. This allowed for more reliable measurement of the reading time on the first word, as the appearance of all three words in the triplet was triggered in the same way. A gaze-contingent invisible boundary was placed to the right of the fixation point and 80 pixels from the left boundary of the first word. Once the fixation point was fixated and the trial started, all three words appeared to the right of the fixation point masked by hash marks, with 240 pixels between the left boundaries of the masks. Gaze-contingent invisible boundaries were placed 80 pixels from the left boundary of each mask in the triplet, preventing preview and rereading of any of the words before entering and after exiting the word’s region.

As in Experiment 1, participants were asked to indicate whether the size of the middle animal or object was in between the size of the two outer items. For the number trials, the task was to indicate whether the middle number was in between the two outer numbers. All responses were made by pressing ‘yes’ or ‘no’ on a hand-held console.

There was a short break between the number and word blocks, and the eye tracker was recalibrated for all participants between the two blocks.

Analysis of eye movements

Eye movements were analyzed as in Experiment 1.

Results

Two participants whose accuracy score was below 57% on one portion of the experiment were excluded from both sets of analyses and replaced. Comparing accuracy and total trial time for the number and object-animal portion of the experiment indicates that the task was easier to perform with numbers than with object and animal names. Overall accuracy was higher for the number (93%) than for the word portion of the experiment (89%): F(1,23) = 12.0, p < .01, η² = .34, and mean total trial time was faster for the numbers (M = 2348 ms) than the object-animal names (M = 3590 ms): F(1,23) = 58.0, p < .001, η² = .72. For both the word and number tasks, inaccurate trials were excluded from all reading time analyses involving response time measures, but not analysis of the middle word encoding times. Reading time results for the word and number blocks are discussed separately below.

Object and animal names

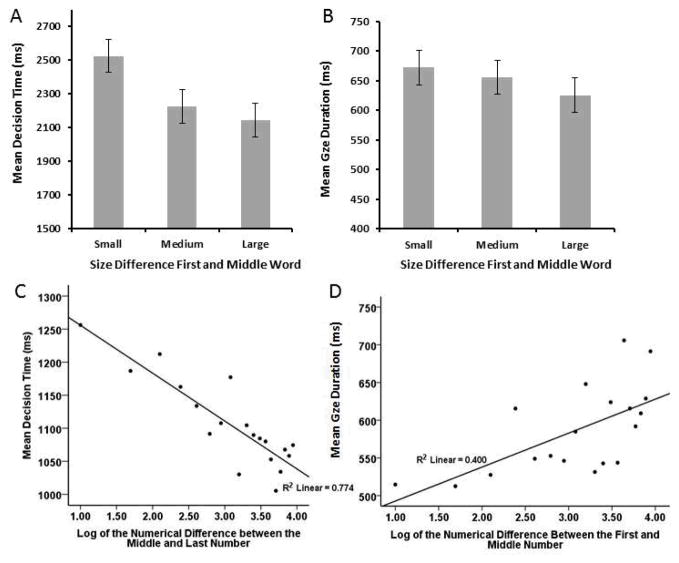
Mean decision times of correct decisions are shown in the top, left panel of Figure 5. As in Experiment 1, they showed a strong symbolic distance effect, with times decreasing as the difference in semantic size between the first and middle word increased, F₁(1,23) = 31.1, p < .001, partial η² = .58 ; F₂(1,41) = 25.5, p < .001, η² = .38, for the linear effect of size difference. There was no significant difference in decision times between ascending and descending trials, F₁(1,23) = 3.9, p = .061; F₂(1,41) = 3.4 p = .072, though there was a tendency for the effect of size difference to be stronger for descending than ascending trials, F₁(1,23) = 8.1, p < .01, partial η² = .26 ; F₂(1,41) = 5.0, p < .05, partial η² = .12. Decision times were faster for consistent than inconsistent trials, F₁(1,23) = 9.9, p < .01, partial η² = .3 ; F₂(1,41) = 14.1, p < .01, partial η² = .26, but the interaction between consistency and size difference was not significant, F₁(1,23) = 1.1, p = .299; F₂(1,41) = .9, p = .362.

Figure 5.

Encoding (as measured by gaze duration) and decision times for words and numbers in Experiment 3. The decision times (A) and middle word encoding times (B) for the words both show a symbolic distance effect. Decision as well as encoding times are shorter when the difference in semantic size between the middle and first item is larger. The number decision times (C) follow this pattern as well. Decision time decreases as the log difference between the last and middle number increases. The encoding times of the middle number (D) show the opposite pattern in the form of a numerical distance priming effect. Middle number encoding times increase as the numerical difference between the middle and first number increases.

As in Experiment 1, mean accuracy rates showed a symbolic distance effect similar to the decision times. Mean accuracy increased as the difference in semantic size between the first and middle word increased from small (M = .85), to medium (M = .90) and to large (M = .91), F₁(1,23) = 9.3, p < .01, η² = .29; F₂(1,41) = 19.5, p <.001, η² = .32, for the linear effect of size difference.

Only 32% of trials consisted of a single fixation and for this reason analyses of encoding time focus on gaze duration⁴. As shown in the top-right panel of Figure 5, encoding time on the middle word also showed a symbolic distance effect, such that mean gaze durations on the middle word decreased as the difference between the middle and first word increased, F₁(1,23) = 9.5, p < .01, partial η² = .29; F₂(1,41) = 7.4, p < .02, partial η² = .15. Middle-word encoding time did not differ significantly for ascending and descending trials, F₁(1,23) = .04, p = .850; F₂(1,41) = .1, p = .745, nor was there an interaction between size difference and direction of the difference, F₁(1,23) = .06; p = .804, F₂(1,41) = .4, p = .556.

These results for the word portion of Experiment 3 replicate Experiment 1 on all measures of interest.

Variation in individual strategies for animal and object names

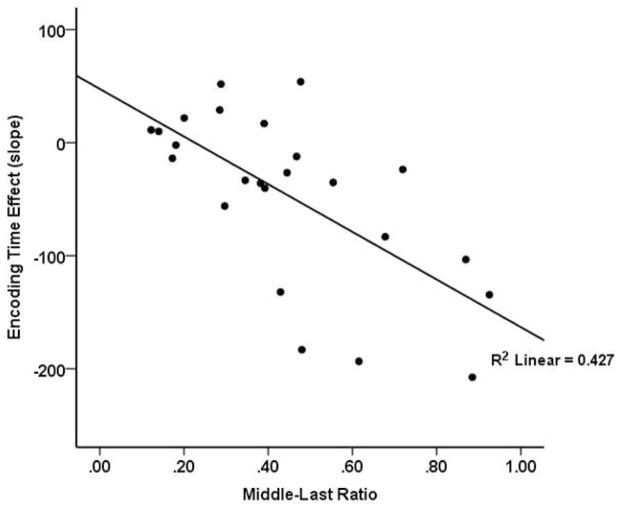
Analysis of variation in participants’ task strategies was assessed as in Experiment 1 by examining the relationship between middle-last ratio and symbolic distance effect slopes on encoding time. Individuals’ mean middle-last ratios ranged from .12 to .93. Figure 6 shows that there was a strong negative correlation between participants’ middle-last ratio on correct trials and the slopes of their size-distance effects, r = −.65, p < .01, R² = .43, just as there was in Experiment 1. Individuals with higher ratios showed more negative encoding time slopes, indicating a stronger effect of size difference. Consistent with Experiment 1, judgment strategy, as measured by middle-last ratio, was not related to overall speed as measured by total time for trial completion, r = −.12, p = .616. In contrast to Experiment 1, where higher middle-last ratios were significantly related to overall accuracy, this relationship was not significant in Experiment 2, r = .33, p = .122. However, the results of one participant were very different from the general pattern, as this person had both the lowest decision ratio (.12) and the highest accuracy rate (1.0). When this outlier was removed there was a significant correlation between middle-last ratio and accuracy that was numerically similar to the one found in Experiment 1, r = .49, p < .02, R² = .240. Removal of this participant’s data caused little change in the critical relationship between encoding time slope and middle-last ratio, r = −.64, p < .01, R² = .412.

Figure 6.

Individuals’ mean middle-last ratio by the slope of the size-based effect on the middle word in Experiment 3. These results show the same pattern as Experiment 1. There is a strong, negative relationship between the individuals’ mean middle-last ratio and mean encoding slope. Individuals with a high middle-last ratio (incremental judgment strategy) show a strong symbolic difference effect during middle word gaze durations. Individuals with a low middle-last ratio (final judgment strategy) show no systematic effect of size difference on middle word gaze durations.

As in Experiment 1, the 50% of participants with the lowest middle-last ratios (M = .27) did not show a significant effect of size difference on encoding time, F₁(1,11) = .13, p = .726; F₂(1,41) = .03, p = .855, while the 50% of participants with the highest middle-last ratios (M = .63) showed a significant effect on this measure, F₁(1,11) = 14.2, p < .01, η² = .56 ; F₂(1,41) = 7.1, p < .02, η² = .15.

These results on strategy effects for the word portion of Experiment 3 replicate those from Experiment 1 on all measures of interest.

Numbers

Whereas the design of the object-animal names study used three categories of size difference (small, medium, large), the difference in size for the numbers varied continuously from one to nineteen. Accordingly, the effects of size difference were analyzed using regression rather than ANOVA, with times regressed on the log of size difference because of evidence that the mental number line is logarithmic (Shepard, Kilpatric & Cunningham, 1975; Dehaene, 2003). Trials on which the first and last number were identical (6.2% of the trials) were excluded from all analyses involving decision time and accuracy measures as were trials where decision times were more than three standard deviations above the grand mean (2.4% of correct trials).

As seen in the bottom-left panel of Figure 5, average correct decision times decreased with the log of the difference between the middle and final numerals, r = .88, R²= .77, F(1,17) = 58.1, p < .001. The generality across participants of this symbolic distance effect on decision times was further assessed by fitting the regression model to each participant’s data individually. The slope parameters calculated this way were significantly less than zero (M = −51.1), t(23) = −3.1, p < .01, d = .64. Decision times were faster for consistent triplets (1051 ms) than inconsistent triplets (1196 ms), F(1,23) = 20.5, p < .001, η² = .47 and the effect of size difference on decision time was greater for consistent sequences than for inconsistent sequences, t(23) = 4.6, p < .001, d = .95.

Forty-five percent of trials consisted of a single fixation so analyses of encoding time focus on gaze duration. As seen in the bottom-right panel of Figure 5, average encoding times for the middle number increased with the log of the difference between the first and middle numerals, r = .63, R² = .40, F(1,17) = 11.3, p < .01. The generality across participants of this distance priming effect on encoding times was significant in a test of the slope parameters obtained from fitting the regression model to participants’ data individually, (M = 39.3), t(23) = 2.44, p < .05, d = .50. Encoding times were slightly faster for ascending (565 ms) than descending (605 ms) trials, F(1,23) = 5.5, p < .05, partial η² = .19, but the direction of the difference did not interact with size difference: t(23) = −1.95 p = .064. Size difference between the middle and final numeral did not systematically affect mean accuracy rates, r = .29, F(1,17) = 1.5, p = .237.

These results support both encoding- and goal-based activation of numerical magnitude. At the number-meaning level of comprehension, encoding-based activation results in a numerical distance priming effect on encoding times. At the task-level of comprehension, goal-based activation of numerical magnitude results in a symbolic distance effect on the comparison decision times.

Variation in individual strategies for numbers

Individual participant strategies were assessed the same as in Experiment 1 and the word portion of Experiment 3, using middle-last ratios computed by taking the encoding time on the middle word over the decision time. Participants’ mean middle-last ratios on correct number trials ranged from .20 to 1.10. In addition, the strength of the numerical distance priming effect for each individual was calculated by taking the slope of encoding time as a function of the numerical distance between the middle and first number, so that more positive slopes indicated stronger priming effects. Whereas individual strategies were related to the strength of the symbolic distance effect on encoding times for the object and animal names, individual participant strategies did not uniformly affect the strength of the numerical distance priming effect as there was no relationship between the subject’s mean middle-last ratio and their encoding time slope: r = .26, p = .213.

Judgment strategy, as measured by middle-last ratio, was related to overall speed, with use of an incremental judgment strategy showing a positive correlation with average time needed to complete each trial: r = .60, p < .01, R² = .36. This is in contrast with results on object and animal names in Experiment 1 and the word portion of Experiment 3, where decision ratio was not related to overall speed. This suggests that individuals with an incremental judgment strategy for the numbers generally processed numerical stimuli more slowly than individuals with a final judgment strategy.

Middle-last ratio was not related to accuracy: r = .23, p = .283. Again, this result is in contrast with Experiment 1 and the word portion of Experiment 3 once we removed one participant outlier, in which higher middle-last ratios were related to better task performance.

Discussion

The results Experiment 3 support our earlier results showing that representations of the size of objects and animals are not automatically activated during lexical encoding of their names, but rather that size information is activated for the comparison processes necessary to achieve task goals. Further, this pattern contrasts with that found for Arabic numerals, where representations of semantic size are automatically activated during encoding and where the use of those representations is also influenced by task goals. These conclusions are supported by the finding that object and animal names do not show a distance priming effect but do show a symbolic distance effect, while numerals show distance priming early in processing and a symbolic distance effect later in processing as previously demonstrated by Brysbaert (1995).

Analyses of individual differences in task strategies provide further evidence that semantic size is activated in different ways for object-animal names and for Arabic numerals. The two types of stimuli lead to similar variation in middle-last ratio, a measure of the time spent on the middle word or number relative to the time spent on making the decision after seeing the final word or numeral. However, the characteristics of performance associated with this variation in task strategies differ for the two types of stimuli. For object and animal names, a high middle-last ratio was associated with showing a symbolic distance effect on encoding time for the middle word, with higher accuracy and no increase in overall trial time. This suggests that participants showing high middle-last ratios made use of an incremental-judgment strategy that involved comparing the semantic size of the middle and first items before encoding and comparing the final item. This strategy is efficient in that it increased accuracy without increasing overall time to complete the trial. For numerals, variation in middle-last ratio was not related to the magnitude of distance priming during encoding of the middle number, nor was it related to performance accuracy. However, high middle-last ratios were associated with slower trial times.

Differences in the meanings associated with animal-object names and numerals suggest a reason why there are differences in the use of semantic size information for these two types of symbols. Many different types of semantic properties are associated with object and animal names. Automatically activating all of those meanings upon encoding a word may be impossible or inefficient. Accordingly, semantic size information is only activated by processes that are specifically related to task goals, in this case comparison of the size of successive items. Use of an incremental-judgment strategy is efficient because activation of the size information is difficult, making it problematic to engage in a final-judgment strategy where activation and comparison of size information is postponed until all three items have been encoded. In contrast, because little meaning beyond semantic size is inherently associated with numerals, semantic size information may be automatically activated upon encoding. Such easy, automatic activation eliminates any processing advantage of an incremental-judgment strategy relative to a final-judgment strategy where the activated size representations for the three items can be evaluated with respect to the task demand of determining whether the middle number is in between the outer ones. For this reason greater time spent looking at the middle item is not efficient and is associated with longer overall trial times.

Comparison of overall performance in the numeral and animal-object tasks provides further support for the notion that activation of size information is much easier for numerals than for animals and objects. As noted above, average completion times and error rates were substantially lower for numeral stimuli than for animal and object stimuli. It seems that semantic size information rides for free with numerals but not with words referring to concrete objects.

General Discussion

The three experiments reported here examined the way in which semantic size is activated and used to make judgments. They did so by measuring looking times and decision times as participants made judgments about three symbols (words or Arabic numerals) displayed on a screen. A gaze-contingent display technique was used so that participants only received visual information about each of the symbols during first-pass fixations on the region of the screen containing the symbol. This technique tightens the association between looking time and encoding time by preventing parafoveal preview and rereading (Brysbaert, 1995). Experiment 1 showed that decision times in a three-item, size-order judgment task increased as the distance in the semantic size of the referents of successive animal or object names decreased. This symbolic distance effect was also observed on encoding time for participants who adopted an incremental-judgment strategy of comparing the size of the first two items before proceeding to encoding of the third item. This pattern indicates that semantic size of the referent was activated in a goal-driven manner by the mental processes for comparing the size of the referents. Experiment 1 provided no evidence of distance priming (reduction of encoding time when the preceding referent was close in size); an effect that would have indicated that semantic size was activated automatically during encoding. Experiment 2 used a memory-probe task rather than an order-judgment task but also found no evidence of distance priming within the three-item sequences. If the task goal of size comparison had masked distance priming due to encoding-based activation in Experiment 1, then the absence of any size-related task goal should have unmasked the distance-priming effect. Experiment 3 replicated the pattern seen in Experiment 1 for animal and object names, indicating goal-driven activation of size representations but no automatic activation of size representations during lexical encoding. In addition, it showed that size representations were activated both in a goal-driven manner and automatically during encoding when the items in the sequence were Arabic numerals rather than words referring to concrete objects. This contrast between words and numerals suggests that size information is automatically activated on encoding when size is the dominant if not sole meaning of a symbol, as for numerals, but that it is not automatically activated on encoding symbols, such as words, that have many associated meanings.

The pattern of results for words in these experiments is not consistent with predictions derived from accounts of language comprehension as an embodied process that is fundamentally based on perceptual simulation. Models of this sort, such as perceptual symbol systems (Barsalou, 1999) or the immersed experiencer framework (Zwaan, 2004), propose that language comprehension entails reactivation of the information associated with the perceptual experience of the word’s referent. If reactivation of perceptual experience is a necessary part of language comprehension, then distance-priming should have been observed during encoding. However, our results suggest that words are encoded without such perceptual reactivation and that semantic size representations are activated in a goal-driven manner by processes necessary for successful task performance.

In contrast, numbers do appear to function as perceptual symbols. While language-processing goals guide the flexible use of different representational forms associated with the meaning of linguistic symbols, magnitude information associated with numerical symbols can be characterized as foundational to the representation of number meaning and showing a general priority in processing. This difference in the symbolic content activated upon initial processing is likely due to differences in the complexity of meaning associated with linguistic compared to numerical symbols. Arguably, analog magnitude defines the meaning of a numerical symbol more efficiently than could any symbolic connection. The meaning of linguistic symbols, on the other hand, may be more efficiently encoded as a function of its connection to other linguistic symbols. After all, our primary experience with words is among other words, rather than in direct connection with the world. These conclusions are supported by earlier demonstrations that language processing is affected by perceptual features of referents primarily when that information facilitates task performance (Louwerse & Jeuniaux, 2010; Louwerse & Connel, 2011; Kang et al., 2011).

Of course it is possible to counter that encoding a word leads to reactivation of some of the perceptual properties of its referent but that priming was not observed for semantic size because it was not a sufficiently important or salient property of the object or animal names. Priming might have been observed for other different perceptual dimensions, such as color or texture, that are more salient than size in general or that are particularly salient for some set of objects. While this line of reasoning cannot be discounted completely, we believe that it is not compelling. For the objects and animals that we studied, semantic size is a very stable property of meaning, as demonstrated by the consistency of participants’ size ratings across studies (Dean et al., 2005; Holyoak et al., 1979). Further, abundant demonstrations of the symbolic distance effect (Banks & Flora, 1977; Dean et al., 2005; Holyoak, et al., 1979; Moyer & Bayer, 1976) show that size comparisons for these words are made using the same kind of analog representations that are used for numbers (Henik & Tzelgov, 1982; Koechlin et al., 1999; Moyer & Landauer, 1967; Van Opstal et al., 2008) and for actual perceptual stimuli (Johnson, 1939; Moyer & Bayer, 1976). The symbolic distance effect has long been used to demonstrate an “internal psychophysics” (Moyer, 1973 p.183) where the relative size of the referents is processed using representations that are akin to perceptual representations. Accordingly, the characteristics of semantic size make it an excellent property in which to look for reactivation of perceptual experience as a result of encoding words.

It is also possible to counter that people create simulations rich enough to extract the relevant aspects of the meaning of words without expending more cognitive effort than strictly necessary (Gibbs & Perlman, 2010), or that the content of a simulation varies with the context in which a concept is presented (Pecher, Zeelenberg & Barsalou, 2004), and that therefore activation of perceptual properties is selective. Similarly, it has been suggested that fast activation of linguistic symbols may be sufficient for tasks that rely on linguistic associations, but that slower, more effortful activation of perceptual representations is necessary for successful execution of tasks that require conceptual information (Barsalou, Santos, Simmons & Wilson, 2008). These views readily account for the absence of distance priming in Experiment 2, where the memory task made semantic size irrelevant, though it is less clear how they would account for the results of Experiments 1 and 3, which explicitly required use of semantic size. An optimal simulation of the word meanings for this task certainly involves size information, yet there is no evidence of such a simulation during encoding. This suggests that the activation of analog, modal representations is not what constitutes language comprehension, or at least not exclusively. During encoding, comprehension may rely on activation of abstract, propositional or perceptually underspecified representations of word meaning, which in turn allow for activation of context- or task-relevant aspects of word meaning.

Moreover, goal-driven activation of perceptual information during language comprehension would fall under the weak (or conventional) form of embodied language processing, in which the activation of embodied representations is possible and potentially very important, but neither foundational to word meaning nor a mandatory component of word processing. As we have argued, this weak form of embodied language does not differ from other characterizations of language processing in a way that is problematic for either type of approach. The goal-driven activation model can account for the observation of context-dependent activation of perceptual information related to concepts by assuming flow of activation between perceptual and non-perceptual systems according to goals associated with comprehension and task performance, without assuming that the conceptual representation itself consists exclusively or primarily of sensorimotor information. This contrasts with the strong (or radical) form of embodied language processing, in which sensorimotor representations are considered to have general priority in processing.

The lack of an automatic connection between words and sensorimotor representations may be exactly what allows our linguistic system to be such a powerful representational tool. As noted earlier, words referring to concrete objects are part of a rich semantic space, which can include category information, semantic associates and linguistic co-occurrence information as well as a multifaceted perceptual representation. Based on the comprehension goals of the reader, different aspects of this complex meaning space can be activated flexibly. While explicit task demands provided the comprehension goals in the current studies, the goals that guide comprehension during everyday language use are usually implicit. Some of these goals may be implied by the demands of comprehension or conversation, while others may be aimed at guiding action in the environment in real time, as discussed by proponents of embodied cognition (Wilson, 2002). Close integration of perceptual and motor processes with other cognitive processes, including language, increases the efficiency of action in the environment, suggesting a substantial flow of goal-directed activation between linguistic, perceptual and motor processes.

Appendix A. Sample of experimental stimuli used for the animal and object conditions

Direction	Size Difference	Word 1	Target	Word 3
ascending	S	sheep	cow	monkey
	M	eagle		elephant
	L	lobster		raccoon
descending	S	giraffe		monkey
	M	hippo		elephant
	L	elephant		raccoon
ascending	S	raccoon	dog	bear
	M	iguana		lobster
	L	butterfly		horse
descending	S	ostrich		bear
	M	tiger		lobster
	L	hippo		horse
ascending	S	butterfly	rat	ostrich
	M	moth		ant
	L	ant		sheep
descending	S	iguana		ostrich
	M	eagle		ant
	L	bear		sheep
ascending	S	chair	door	head
	M	jacket		mountain
	L	head		saw
descending	S	boat		head
	M	ship		mountain
	L	mountain		saw
ascending	S	finger	apple	button
	M	acorn		man
	L	pearl		petal
descending	S	foot		button
	M	pillow		man
	L	lake		petal
ascending	S	saw	tire	boat
	M	foot		finger
	L	egg		hill
descending	S	man		boat
	M	garage		finger
	L	lake		hill