An Empirical Approach to Sufficient Similarity: Combining Exposure Data and Mixtures Toxicology Data

Abstract

When assessing risks posed by environmental chemical mixtures, whole mixture approaches are preferred to component approaches. When toxicological data on whole mixtures as they occur in the environment are not available, EPA guidance states that, toxicity data from a mixture considered “sufficiently similar” to the environmental mixture can serve as a surrogate. We propose a novel method to examine whether mixtures are sufficiently similar, when exposure data and mixture toxicity study data from at least one representative mixture are available. We define sufficient similarity using equivalence testing methodology comparing the distance between benchmark dose estimates for mixtures in both data rich and data poor cases. We construct a “similar mixtures risk indicator” (analogous to the hazard index) on sufficiently similar mixtures linking exposure data with mixtures toxicology data. The methods are illustrated using pyrethroid mixtures occurrence data collected in child care centers (CCC) and dose-response data examining acute neurobehavioral effects of pyrethroid mixtures in rats. Our method shows that the mixtures from 90% of the CCCs were sufficiently similar to the dose-response study mixture. Using exposure estimates for a hypothetical child, the 95^th percentile of the (weighted) similar mixtures risk indicator (SMRI) for these sufficiently similar mixtures was 0.20 (i.e., where SMRI< 1, less concern; >1, more concern).

1. Introduction

When assessing the human health risks posed by chemical mixtures in the environment, risk assessors prefer whole mixture approaches to those relying on component data.⁽¹⁾ Preferred whole mixture methods rely on toxicity or epidemiology data on the mixture of concern, that is the mixture to which people are exposed; however, toxicity values from a tested mixture considered “sufficiently similar” to the mixture of concern in the environment may serve as surrogates.⁽¹⁾ While some methods have been proposed to examine whether mixtures are similar^(2–5), additional methods are needed to evaluate similarity among mixtures through approaches that are objective, transparent and reproducible.

The approach for examining similarity among mixtures that is proposed here extends the work of Stork et al ⁽⁶⁾, which determines whether chemical mixtures exhibit sufficiently similar dose-response functions, comparing BMDs of the mixtures. Stork’s methodology⁽⁶⁾ uses hypothesis testing for “equivalence” and mixed model theory to define sufficient similarity in dose-response for chemical mixtures containing the same chemicals with different mixing ratios, where complete dose-response data are available on one mixture (i.e., reference mixture) and only mixing ratios are available on the candidate mixture. This approach requires that both the reference and candidate mixtures contain the same c components. Here, we extend Stork’s method allowing for the absence of chemicals in either the reference or candidate mixture, i.e., one mixture is a subset of the other. We use some of the data collected on the occurrence of multiple pesticides in the First National Environmental Health Survey of Child Care Centers (CCC Study) to illustrate the approach. ⁽⁷⁾

Each year, roughly 13 million U.S. children are placed in child care centers (CCCs) for up to 10 hours per day during work days.⁽⁷⁾ Relatively little research has been conducted to characterize children’s exposures to pesticide mixtures occurring in CCCs. Previous pesticide exposure assessments in CCCs were limited by geographic area, sample location within the facility, diversity of analytes measured and accompanying questionnaire data. ^(7–10) The CCC study was designed to address some of these limitations.

The CCC Study measured pesticide occurrence from July through October 2001 at multiple locations in 168 licensed U.S. CCCs serving children under 6 years of age. ⁽⁷⁾ The CCCs were randomly selected to provide a nationally representative sample of licensed institutional CCCs in the U.S.; survey-sampling weights were developed so that estimates are nationally representative. Here, in the context of our illustrative case study, we consider only floor wipe data for pyrethroid pesticides, a class of similar compounds used as insecticides, from the CCC study. Each of the 168 occurrence profiles for the pyrethroids in the floor wipe samples differs. That is, there is a unique mixture associated with each floor wipe sample.

Typically, pesticide risk assessments rely on exposure and dose-response information and we use this information to show how our method might be applied in the case study. Exposure information may include environmental occurrence (e.g., concentrations of pesticides measured on floors, ng/cm²) and contact information (e.g., amount of time spent playing on floor, exposed skin surface area). Such assessments may also utilize body tissue or fluid information (e.g., urinary pesticide metabolite concentrations), although we do not use such data here. Dose-response relationships between chemicals and health outcomes typically are estimated using animal bioassay data. In the U.S. EPA’s methods for non-cancer health outcomes, dose-response assessments based on bioassay data are developed through a two-step process ⁽¹¹⁾: (1) defining a point of departure (POD) based on bioassay data; and (2) extrapolating from the POD to a reference dose (RfD) by applying appropriate uncertainty factors. The RfD is an “estimate of a daily oral exposure to the human population that is likely to be without an appreciable risk of deleterious effects during a lifetime.”⁽¹²⁾ When possible, Benchmark dose (BMD) models are used to estimate PODs. The BMD_L, the lower one-sided 95% confidence limit for the dose of the chemical associated with the benchmark response (BMR; i.e., typically the change in response rate over background), typically serves as the POD. ⁽¹³⁾ Uncertainty factors are then applied; these are intended to account for the following: (i) variation in susceptibility among the human population; (ii) uncertainty in extrapolating animal toxicity data to humans; (iii) uncertainty in extrapolating from data obtained in a study with less-than-lifetime exposure; (iv) uncertainty in extrapolating from a low level of effects rather than from a dose where there are no effects; and (v) uncertainty associated with an incomplete toxicity database.

Considering our case study’s use of the CCC study data, if it were feasible, it would be ideal to perform a dose-response study for each of the 168 unique mixtures (i.e., a data-rich case) and analyze the distribution of one or more summary measures¹ for each dose-response curve, such as the benchmark dose (BMD). We present a data rich case study for comparing BMDs. If dose-response data are not available for all mixtures (i.e., a data-poor case), as is the case here, we use a tested mixture as a surrogate (termed a “reference mixture” herein) and evaluate which of the environmental mixtures (i.e., mixtures of concern termed “candidate mixtures” herein), are sufficiently similar and could be used in a risk assessment.⁽¹⁴⁾ For the environmental mixtures that are sufficiently similar to the reference mixture, we construct a ‘similar mixture risk indicator’ which links relevant occurrence data (in the numerator) to estimates of PODs (in the denominator) for the set of mixtures considered sufficiently similar to the reference mixture.

2. Methods

2.1 Data sources

2.1.1 Exposure data

In the CCC Study -, they analyzed 13 synthetic pyrethroid pesticides and pyrethrins I and II, in floor wipe samples.² We assumed these 15 compounds to comprise the whole mixture of pyrethroids/pyrethrins (and, for convenience, are referred to hereafter as pyrethroids). Values below the limit of detection (LOD) were replaced by the $\text{LOD}/\sqrt{2}$. ^{(15, 16)}

For each center, we determined the fractional surface loading (FSL) of each pyrethroid, i.e., the proportion of total pyrethroid surface residue attributed to a particular pyrethroid:

$$\text{FSL}\text{of}{\text{i}}^{\text{th}}\text{pyrethorid}=\frac{\text{surface}\text{load}\text{of}{\text{i}}^{\text{th}}\text{pyrethroid}(\text{ng}/{\text{cm}}^2)}{{\displaystyle \sum _{\text{i}=1}^{15}}\text{surface}\text{load}\text{of}{\text{i}}^{\text{th}}\text{pyrethroid}(\text{ng}/{\text{cm}}^2)}$$ Eq. (1)

By construction, for each center the 15 FSLs summed to 1. For each pyrethroid, its specific FSL was averaged across the centers to determine the pyrethroids that were present at the greatest concentrations. Many samples had non-detectable pyrethroid levels so this analysis was limited to centers with higher surface loadings. To do this, the centers were sorted by total pyrethroid surface load (ng/cm²) and the top 10% of centers (17 centers) identified. Upon limiting the analysis to the centers with highest total surface loadings, 6 pyrethroids accounted for the majority of pyrethroid load. The trend was evident when progressing from all centers, to the top 10% where 6 pyrethroids account for 96.4% of the total surface loading and the total mass. Normalized by these 6 pyrethroids, the average FSLs were: cypermethrin (28.7%), deltamethrin (3.4%), esfenvalerate (2.7%), cis-permethrin (19.8%), trans-permethrin (32.5%), and β–cyfluthrin (12.8%). In Table 1, the permethrins were combined: permethrin (52.3%).

Table 1.

Summary percentage of pyrethroids measured from floor wipes in the CCC Study in the top 10% of the centers (in terms of total loading), mixing ratios for two reference mixtures and relative potency estimates from Wolansky et al. where delta/tralomethrin was used as the index chemical.

Chemical	Average percent in top 10% of CCC Study Centers	Normalized for top 6 to sum to 100* (5 chemical mixture)	Mixing Proportions for 11 chemical mixture*	Relative Potency Estimates**
Cyfluthrin	12.4	12.8	0.49	1.136
Cypermethrin	27.8	28.7	2.34	0.235
Deltamethrin/tralomethrin	3.2	3.4	0.55	1.00
Esfenvalerate	2.6	2.7	0.26	2.092
Cis-permethrin	19.1	52.3	9.31	0.059
trans-permethrin	31.3
cis-allothrin	0.6	0	0	Set at 1.0
trans-allothrin	<1	0	0	Set at 1.0
Bifenthrin	<1	0	0.70	0.782
Cyhalothrin	1.9	0	0.29	1.902
Pyrethrin I	<1	0	0	Set at 1.0
Pyrethrin II	<1	0	0	Set at 1.0
Resmethrin	<1	0	64.10	0.009
Sumimethrin	<1	0	0	Set at 1.0
Tetramethrin	<1	0	0	Set at 1.0
S-Bioallethrin		0	19.82	0.028
Fenpropathrin		0	1.69	0.326
Telfluthrin		0	0.49	1.111

^*used by Wolansky et al in mixture dose-response study of neurotoxicity;

^**Relative potency estimates from Wolansky et al (17, 18); chemicals not evaluated by Wolansky et al have relative potency estimates set at 1.0

2.1.2 Mixtures dose-response data

Wolansky et al. ^{(17, 18)} orally dosed (in corn oil) male Long-Evans rats with a mixture (Table 1) of five environmentally relevant pyrethroids or a mixture of 11 pyrethroids with mixing proportions determined by ED₃₀ values. Two hours after a single dosing, they measured motor activity for 1 hr using figure-eight mazes. Total activity was calculated as the sum of horizontal and vertical activity photocell counts.³ We primarily focus on the environmentally relevant 5 chemical mixture; but we use data from both mixtures to demonstrate the data rich.

2.2 Test for Sufficient Similarity

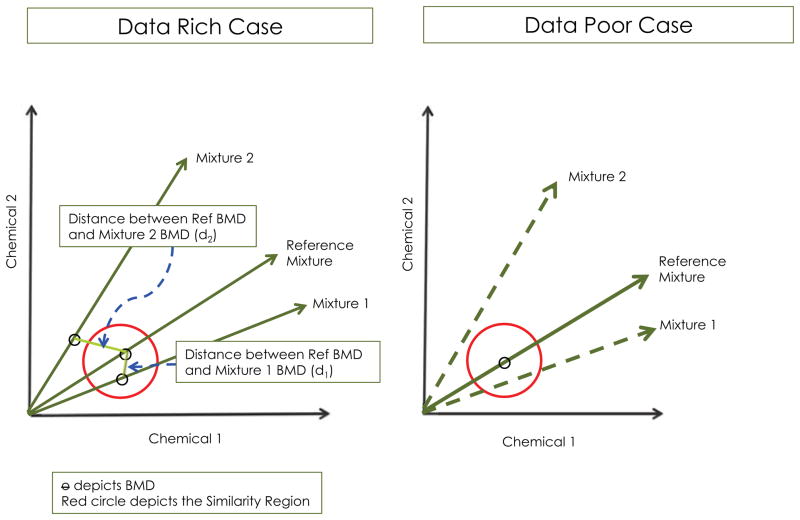
Suppose dose-response data are available for two mixtures with different and specified (i.e., fixed) mixing proportions of comparable, but not identical sets of chemicals. For convenience, let the reference mixture be comprised of k_r components and the candidate mixture be comprised of k_i components (Figure 1). Define c as the number of unique chemicals in the reference mixture and the candidate mixture (i.e., c = k_r ∪ k_i). Consider a benchmark response (BMR) is set and associated benchmark doses are estimated for both mixtures. Let θ_r^*be the BMD for the reference mixture (with defined and fixed mixing proportions from k_r components) and θ_i^* be the BMD for the i^th mixture (with defined and fixed mixing proportions from k_i components). Since we do not assume the same full set of chemicals, let θ_r be the BMD for the reference mixture using all c chemicals (i.e., with 0’s included for chemicals not included in the mixture) and θ_i be the BMD for the i^th mixture in c-dimensions.

Figure 1.

Two-dimensional schematic for testing for sufficient similarity using a similarity region (red circle). When the distance between the BMD of the reference mixture and a candidate mixture is less than the radius of the circle, the mixtures are considered sufficiently similar. In the data poor case, simplifying assumptions are necessary to estimate the distance, which is generally based on comparison of the mixing proportions between the reference and candidate mixtures (see text). The two-dimensional case is generalizable to c dimensions.

We propose to evaluate similarity between two mixtures based on the Euclidean distance (i.e., the shortest distance between any two points) between the BMDs for the two mixtures where the calculation allows for missing chemicals in either mixture by expressing their proportion as zero. A weighted version of the distance may be used to de-emphasize or magnify the effect of some components of the mixtures based on information regarding potency or other toxicologically relevant characteristics. For example, a difference in the contribution of one chemical in the estimated BMDs of, say, 10 mg/kg is not equivalent to the same difference for another chemical which is more potent by orders of magnitude. The analysis incorporates the relative potency information by increasing the weight on the difference in BMD components of more potent chemicals and down-weighting the differences from less potent chemicals in the calculation of weighted distance.

Without loss of generality, the weights are constrained to sum to the number of components as in the unweighted case (i.e., with all weights of 1.0). With c chemicals, define

$$w_j=c\times \frac{{RP}_j}{{\displaystyle \sum _{k=1}^c}{RP}_k}$$ Eq. (2)

where RP_j is the relative potency estimate for the j^th chemical. Define W as a diagonal matrix with the respective weights, w_j, as given in equation (2), subject to the constraint, $\sum _{i=1}^c{w}_i=c$. The weighted distance (d_w) is constructed in the following manner:

$$\begin{array}{l}{d}_w=\sqrt{({\mathbf{\theta }}_r-{{\mathbf{\theta }}_i)}^{\prime }\mathbf{W}({\mathbf{\theta }}_r-{\mathbf{\theta }}_i)}\\ =\sqrt{\sum _{j=1}^c{w}_j{\left({\theta }_{jr}-{\theta }_{ji}\right)}^2}\end{array}$$ Eq. (3)

Using relative potencies to calculate the weighted distance is preferred to the unweighted distance (where w_j=1 for all j=1,…,c), which may be used when relative potencies are not available.

Suppose we consider the two BMDs to be sufficiently similar when d_w ≤ Δ, where Δ is a positive number set a priori. (Note: A discussion for rationale for selecting Δ is included in section 3.1.) Using equivalence testing methodology, we test the following hypothesis:

$$\begin{array}{l}{H}_0:d_w>\mathrm{\Delta }\\ H_1:d_w\le \mathrm{\Delta }\end{array}$$

which can be tested using the principle of confidence interval inclusion ⁽¹⁹⁾, i.e., an alpha-level test rejects H₀ when the upper limit of the one-sided confidence interval on d_w does not exceed Δ. For example, assuming d̂_w has a bell-shaped distribution,

$${\widehat{d}}_w+t_{1-\alpha ;N-p}\sqrt{\mathit{Var}({\widehat{d}}_w)}\le \mathrm{\Delta }$$ Eq. (4)

where d̂_w is estimated from available dose-response data (details below), t_{1−α ;N−p} is the critical value from the t distribution, associated with α (e.g., 5%) in the upper tail, with N−p degrees of freedom (i.e., total sample size minus number of model parameters in the dose-response data for the mixtures), and Var(d̂_w) is the variance of the estimate for distance.

2.2.1. Data Rich Case: “Gold-standard” because dose-response data available for all mixtures

In the atypical scenario where dose-response data are available for all mixtures, the estimation of d_w and its variance estimate are based on dose-response modeling. That is, d_w is estimated using an assumed model for the dose-response curves along the respective fixed mixing ratios. The Var(d̂_w) can be estimated using the delta method⁴ with the estimated model parameters and corresponding covariance matrix. The t-distribution is justified for calculating the upper confidence limit with moderate to large sample sizes since d̂_w is a function of maximum likelihood estimates.

2.2.2 Data poor case: Alterations in the “gold-standard test” to determine sufficient similarity

Assume dose-response data are available for a reference mixture and that a BMR is specified. Suppose the mixing ratios of candidate mixture(s) of relevant exposures are available but dose-response data are not available for these mixing ratios (See Figure 1). As defined previously, we set c as the number of unique chemicals in both mixtures. Given the specified BMR, a BMD for the reference mixture, θ_r, can be estimated with the available dose-response data; however, the BMD for the i^th candidate mixture cannot be directly estimated without corresponding dose-response data.

To set notation, define T_r as the BMD in terms of total dose (i.e., the summed doses of each mixture component in θ_r). For the reference mixture with proportions of each chemical given in the c-dimensional vector a_r, the BMD is the proportion a_r times the total dose, T_r, for each chemical, i.e., using vector notation,

$${\mathbf{\theta }}_r=T_r{\mathbf{a}}_r.$$

In this data poor case we assume we know the mixing ratios, a_i, for the i^th mixture, but as there are no studies available to estimate the BMD (in terms of total dose) for this mixture, we cannot estimate T_i or θ_i. Thus, we cannot estimate d_w (from equation 3) without simplifying assumptions.

Without loss of generality, consider a two-chemical mixture with mixing proportions of, say, 0.3 and 0.7 and total dose for the BMD of, say, 10 units (i.e., 3 units of chemical 1 and 7 units of chemical 2). It is reasonable to expect that when the mixing proportions are, for example, 0.31 and 0.69, the total dose BMD should be close to 10 units. Thus, it is reasonable to assume that mixtures with similar mixing proportions have similar BMDs, i.e., T_i ≈ T_r. Thus in the data poor case, we propose to estimate the BMD for the i^th mixture by adjusting the total dose of the mixture to that of the reference mixture, i.e.,

$${\mathbf{\theta }}_i^{\mathit{adj}}=T_r{\mathbf{a}}_i$$ Eq. (5)

where T_r is the total dose of BMD for the reference mixture. In this scenario, the distance measure is

$$d_w=\sqrt{\sum _{i=1}^c{w}_j{({\theta }_{jr}-{\theta }_{ji}^{\mathit{adj}})}^2}=T_r\sqrt{\sum _{i=1}^c{w}_j{(a_{jr}-a_{ji})}^2}$$

which can be estimated as

$${\widehat{d}}_w={\widehat{T}}_r\sqrt{\sum _{i=1}^c{w}_j{(a_{jr}-a_{ji})}^2}$$ Eq. (6)

The distance estimate increases as the difference between corresponding mixing proportions increases. The variance of distance estimate is

$$\mathit{Var}({\widehat{d}}_w)=\mathit{Var}({\widehat{T}}_r)\left\{\sum _{i=1}^c{w}_j{(a_{jr}-a_{ji})}^2\right\}.$$ Eq. (7)

Thus, the variance is the product of a term that accounts for biological variability and the sum of weighted squared differences between the mixing proportions. The estimate for Var(T̂_r) is found using the delta method in the analysis of the mixture dose-response data for the reference mixture.

2.3 Combining exposure data and BMDs to calculate a “Similar Mixture Risk Indicator”

The Hazard Index (HI), routinely used in chemical mixtures risk assessments ^{(20, 21)}, is the sum of hazard quotients, the ratio of exposure (e.g., estimate of daily intake rate, DI) to an acceptable exposure level for a specific chemical (e.g., acceptable daily intake rate). RfDs often provide acceptable exposure rates.

$$\text{Hazard}\text{Index}(\text{HI})=\sum _{j=1}^c\frac{{DI}_{\text{j}}(\text{ng}/\text{kg}/\text{day})}{{\text{RfD}}_{\text{j}}(\text{ng}/\text{kg}/\text{day})}$$

where c is the number of chemicals in the HI. HIs exceeding 1 typically warrant further analysis.

The Similar Mixture Risk Indicator (SMRI_HI), developed here, is based on the HI method. The SMRI_HI is calculated using the BMDLs estimated from a reference mixture to articulate the single chemical BMDLs using its specified mixing proportions and BMR. These BMDLs are generally smaller than those estimated using single chemical data since they account for other chemicals in the mixture.

To distinguish them from RfDs for single chemicals, we denote the mixture BMDL adjusted by uncertainty factors as ‘mixture reference values’ (mRVs). mRV_j is the mRV multiplied by the proportion of the j^th chemical in the mixture. The SMRI_HI evaluates whether the intake for a sufficiently similar chemical mixture (i.e., DI_j for the j^th chemical in the mixture) is “close” to the externally estimated mixture reference values:

$${\text{SMRI}}_{\text{HI}}=\sum _{j=1}^c\frac{{\text{DI}}_{\text{j}}(\text{ng}/\text{kg}/\text{day})}{{\text{mRV}}_{\text{j}}(\text{ng}/\text{kg}/\text{day})}.$$ Eq. (8)

The SMRI_HI uses an additive approach to evaluate risk for the candidate. For the SMRI_HI, when the chemicals in the mixture share a common mode of action, this statistic can assume that dose-addition is in effect and the analysis has a strong biological basis. When the chemicals in the mixture cause toxicity via different modes of action, this statistic is still useful, but likely conservative. ⁽¹⁾ For the latter case, the confidence in the accuracy of the risk evaluation would be less than in the former case.

When relative potency estimates are available for the components in the mixture(s), an alternative SMRI approach to that in equation (8) is available for mixtures sufficiently similar to the reference mixture. An index chemical is identified based on the strength of the data supporting its potency and the subsequent analysis is based on the index chemical-equivalent metric. The metric of the mixtures is in terms of the index chemical (e.g., similar to the TEF approach where an index chemical equivalent dose is estimated) and the BMDL is estimated for the reference mixture on this scale, denoted mRV. In the data poor case, the exposure for the i^th candidate mixture is estimated on the same scale as:

$$\sum _{j=1}^c{w}_j{x}_{ij}$$ Eq (9)

where x_ij is the “dose” of the j^th chemical in the i^th mixture, and the reference value is based on the BMDL for the reference mixture, on this index chemical-equivalent metric, adjusted with uncertainty factors. The corresponding RPF-based SMRI is the ratio of the observed (weighted) concentrations for each mixture to the common mRV from the index-equivalent scale; i.e., for the i^th mixture,

$${\text{SMRI}}_{\text{RPF},\text{i}}=\frac{{\displaystyle \sum _{j=1}^c}{w}_j{DI}_{ij}}{\mathit{mRV}}.$$ Eq (10)

The example in the next section illustrates the approaches.

3. Illustrative CCC Case Study

A primary objective of this analysis is to combine environmental chemical mixtures occurrence data with dose-response data of a reference mixture. This motivating example uses the two data sources in calculating a SMRI for environmental mixtures that are sufficiently similar to the reference mixture.

The CCC Study was a nationally representative survey; thus, using sampling weights, occurrence information for CCCs across the contiguous U.S. states can be inferred from statistics for the surveyed centers. The sum of residue values from floor wipe samples for the 15 pyrethroids/pyrethrins is a skewed distribution with 90^th percentile of 2.21 ng/cm² (Figure 2). Residue values from 25% (n=42) of the floor wipe samples across the 168 centers were all below the limit of detection (a sum of 0.077 ng/cm²); using the survey sampling weights, the floor wipe samples from the remaining 75% of day care centers have detectable pyrethroid residues. On the other hand, the sum of pyrethroids/pyrethrins in the top 10% of the centers exceeded 2.21 ng/cm². Further, the average residues from the top six chemicals in these 17 centers (unweighted) accounted for 96% of the sum (Table 1) which was the mixing ratio used by Wolansky et al (manuscript in preparation) in a neurotoxicity study of five pyrethroids (with cis- and trans-permethrin combined). In addition, Wolansky et al ⁽¹⁸⁾ experimentally evaluated a mixture of 11 pyrethroids (Table 1) for rat neurotoxicity.

Figure 2.

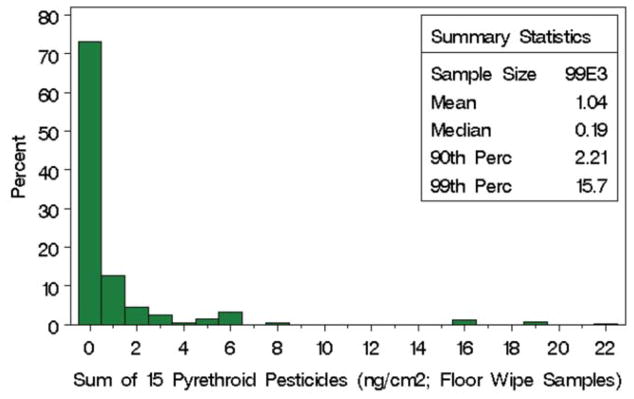
Histogram of the sum of 15 pyrethroids/pyrethrins measured from floor wipes in 168 child care centers in the CCC Study.

3.1 Testing for sufficiently similar mixtures with dose-response data available for both: the Data Rich Case

Two mixtures were experimentally evaluated for neurotoxicity using motor activity: a mixture of 11 pyrethroids ⁽¹⁸⁾ and a mixture of 5 pyrethroids based on the CCC Study. A segmented (threshold) nonlinear exponential function was used to model mean motor activity (percent control), i.e.,

$$\mu =\left\{\begin{array}{cc}100& t<\delta \\ \alpha +(100-\alpha )\text{exp}\left(\beta (t-\delta )\right)& t\ge \delta \end{array}\right\}$$

where t is total dose of each mixture, α is the maximum-effect parameter, β(<0) is associated with the slope of the mixture in a decreasing curve, and δ is the threshold parameter for the mixture. The variance of response was assumed constant across dose groups and mixtures. A Newton-Raphson iterative algorithm was used to estimate unknown model parameters (in Proc NLMIXED in SAS version 9.2). A common estimate for the maximum effect of the mixture was assumed across the two mixtures and was estimated to be 32.9% of control (Table 2). The fit of the dose-response curves was considered adequate for both mixtures (Figure 3).

Table 2.

Model parameter estimates and their standard errors from a segmented nonlinear exponential model fit to motor activity data for a 5 chemical mixture and an 11 chemical mixture in the unweighted (Figures 3A,B) and weighted case (Figure 3C,D). The BMR for the BMD was 20% (i.e., 80% of control).

	Unweighted Analysis		Weighted Analysis
Parameter	Estimate	Standard Error	Estimate	Standard Error
α	32.9	12.8	32.9	12.8
β5	−0.088	0.035	−0.26	0.10
β11	−0.024	0.020	−0.35	0.30
δ5	8.51	1.18	2.85	0.40
δ11	30.4	17.6	2.10	1.22
σ2	557.3	57.0	557.3	57.0
Functions of model parameters
BMD(5)	12.5	0.99	4.20	0.33
BMD(11)	45.4	9.1	3.13	0.63
ED40(5)	18.8	1.8	6.30	0.60
ED40(11)	68.3	8.2	4.73	0.57
d=Distance between BMDs	30.6	6.0	3.10	0.27
Upper one-sided 95% conf limit on d	40.5		3.5
Δ for combined analysis*	22.9		1.60
Δ for 5 chemical mixture analysis&	6.30		2.10

^*defined as max(ED40-BMD);

^&defined as ED40(5)-BMD(5)

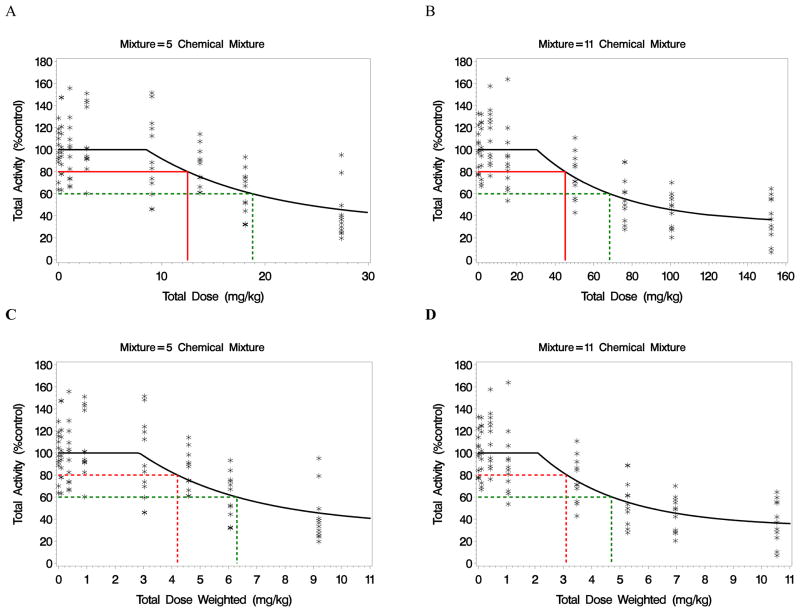
Figure 3.

Observed and model predicted motor activity for (A) the reference mixture of 5 pyrethroids using the mixing ratio determined from the CCC Study; and (B) a mixture of 11 pyrethroids with mixing ratio determined from ED30 estimates (18). The red line segments represent a BMR of 20% and corresponding BMD; the green line segments represent a 40% effect and corresponding dose. The total dose scale was transformed in figures (C) and (D) using weights based on relative potency estimates (Table 1).

Based on expert judgment, a 20% effect (BMR) was defined as a response of 80% of control (depicted in Figure 3). Expert judgment was used to determine the degree of change in the behavioral response that balanced the statistical and perceived biological significance of a change. The US EPA guidance on setting the BMR suggests using “a minimal level of change in the endpoint that is generally considered to be biologically significant…”. ⁽¹¹⁾ For the motor function endpoint used here, this expert judgment included:

• A well defined characterization of the dynamic range of the assay;

• An experimental design that includes internal replication;

• Extensive historical and positive control data ^(22,23);

• A characterization of the overall reliability of the assay ⁽²⁴⁾;

• An assumption that the choice of the BMR is a reasonable marker for determining a similarity bound for mixtures.

From these considerations, the BMR was set at 20% (i.e., 80% of control) and the similarity bound was based on the maximum change in total dose of the two mixtures between the BMD and the ED40 (i.e., 60% control) estimates. Thus, the similarity bound is 22.9, which is based on the difference between the 11 chemical mixture BMD (45.4 mg/kg) and the ED40 (68.3 mg/kg). Using this boundary, both the 5 chemical mixture and the 11 chemical mixture are sufficiently similar to themselves, by definition. Thus, we select a critical value of Δ=22.9 mg/kg to define a maximum distance from the reference BMD (i.e., θ_r) within which the mixtures will be considered sufficiently similar in the region of the BMD.

The associated benchmark doses (BMDs) for the two mixtures were 12.5 and 45.4 mg/kg/day for the 5-chemical and 11-chemical mixture, respectively (Table 2); however, this difference does not reflect the distance between the two points using all 11-dimensions for the union of 11 chemicals. A more appropriate comparison is the Euclidean distance between these point estimates, which, using equation (2), is estimated to be 30.6 (Table 2) with upper one-sided 95% confidence limit of 40.5. The two BMDs would be considered to be sufficiently similar (i.e., associated with mixtures that are sufficiently similar) if the upper 95% confidence limit is less than a critical value selected a priori. With Δ=22.9, we cannot claim the BMD from the 5 chemical mixture is sufficiently similar to that from the 11 chemical mixture as the upper one-sided 95% confidence limit on the distance between the two BMDs, i.e., 40.5, exceeds the similarity boundary of 22.9.

The 5-chemical mixture is dominated by permethrin at 52.3%, the least potent individual chemical in the mixture.⁽¹⁸⁾ A weighted analysis was conducted (described below) where the proportion of permethrin in the mixture is down-weighted, and the d_w distance measure (from equation (3)) is used in the test for similar BMDs. The unweighted case is presented for illustration of a data poor scenario where relative potencies are not available.

3.2 Connecting the reference mixture to the CCC Study occurrence data: the Data Poor Case

With dose-response data available for the reference 5-chemical mixture (Table 1), it is of interest to determine which if any of the 168 centers in the CCC Study have exposure data on candidate mixtures, which can be considered sufficiently similar to the reference mixture. In this data poor case, we base the subsequent analysis on the model of the 5-chemical reference mixture (Table 1). We first eliminate the bottom 25% (N=42) of the candidate mixtures where all sample concentrations of the 15 chemicals are less than the LOD. For each of the remaining 126 candidate mixtures, data are not available to estimate a BMD. However, from a “data poor” perspective, using equation (5), we estimate BMDs by assuming the total dose for the BMD is reasonably estimated using the reference mixture value (i.e., T̂_r) and the proportions of the 15 chemicals in the candidate mixtures. With these adjusted values, we calculate the distance (equation (6)) between the estimated reference BMD from the 5-chemical mixture and those calculated from the candidate mixtures in the occurrence data.

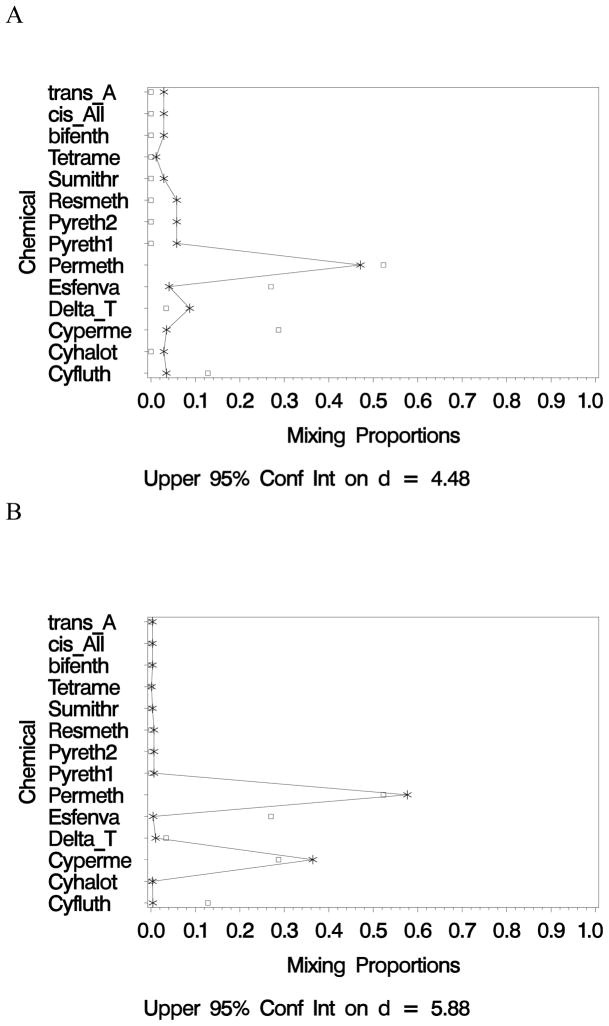
To set the critical value, using the 5 chemical reference mixture, the BMD is estimated to be 12.5 mg/kg and the ED40 is estimated as 18.8 mg/kg. Thus, using the critical value for the similarity boundary of Δ=6.3 mg/kg, candidate mixtures from 7 centers are considered sufficiently similar to the reference mixture. That is, the upper 95% confidence limit on the distance between the reference mixture BMD and the BMD “estimated” from the candidate mixtures observed from these 7 centers is less than the critical value of 6.3. Figure 4 provides a schematic for comparing the mixing proportions for the reference mixture (i.e., used in the toxicology study by Wolansky) and the observed mixing proportions from two candidate mixtures from the 7 CCCs considered to have sufficiently similar mixtures in terms of the benchmark doses. The mixture in Figure 4A, for example, is comprised primarily of permethrin (46%) with 9% from deltamethrin/tralomethrin and between 3 and 6% from 11 other chemicals.

Figure 4.

Mixing proportions for the reference mixture (squares) compared to those observed at two of the daycare centers (asterisks). The 95% confidence intervals are based on the unweighted analysis.

To evaluate the potential hazard of the 7 sufficiently similar mixtures, we calculate the SMRI_HI in equation (8), using observed exposure values and estimated BMDs as shown below. Some simplifying assumptions are made for these calculations of human intake from floor wipe samples and for the mixture BMDs from the reference mixture (see appendix for details).

Using equation (8), a SMRI_HI was calculated for each of the 7 centers with sufficiently similar mixtures to the reference mixture. Of concern is how close the daily intake is to the point of departure associated with an increase in risk for the mixture. This SMRI_HI is not generalizable to all mixtures, but pertains to mixtures which are sufficiently similar to the reference mixture. In this case, if the exposure values are similar to the corresponding mRVs, then the SMRI_HI is close to 1, and the risk assessor may conclude that the exposures need further evaluation. Here, for the 7 centers with exposures sufficiently similar to the reference mixture (where the dose-response data are available), the distribution of SMRI_HI is skewed with a median of 0.005 for an average size 3 yr old boy. The estimated 99^th percentile of the SMRI_HI is 0.028. However, this analysis assumes equal weights on all 15 chemicals and does not adjust for differences in relative potency.

3.2.1. Analysis using a Weighted Distance to Determine Sufficiently Similar BMDs

The weighted distance is included in an analysis where the BMDs are estimated using a relative potency scale for the total dose. The estimate for BMD for the 5 chemical mixture was based on adjusted total dose values using relative potencies multiplied by each component, i.e.,

$$\begin{array}{l}{t}_w=\sum _{j=1}^c{x}_j\times {RP}_j\\ =\sum _{j=1}^{c}t\times a_j\times {RP}_j\end{array}$$

where x_j is the dose of the j^th chemical, with mixing proportion a_j and total dose t. On the weighted total dose scale, the estimated BMD for the 5 chemical mixture was 4.20 using a nonlinear exponential threshold model (Table 2 and Figure 3). The critical value for the similarity region was determined by the difference in the estimated BMD and the ED40 (i.e., 6.30 mg/kg) – representing a 20% shift in response from the BMR of 20%. Thus, the critical value is Δ=2.10 in units of the weighted total dose.

In the weighted analysis, there were 114 centers with the upper confidence limit (equation 7 using weights) on the distance between BMDs below the similarity boundary of 2.10. Using the SMRI_RPF (equation (10)) with weighted components, the median SMRI_RPF calculated for a hypothetical 3-year-old boy of average size is 0.01 for the 114 centers considered sufficiently similar to the reference mixture; the 95th percentile is 0.20; and the 99^th percentile estimate is 0.68. Applying the survey sampling weights (Figure 5), the percentiles change only slightly except in the tail where the 99^th percentile is dampened to 0.37. Using the sampling weights the 114 centers represent 69,000 centers across the 48 contiguous states in the U.S.

Figure 5.

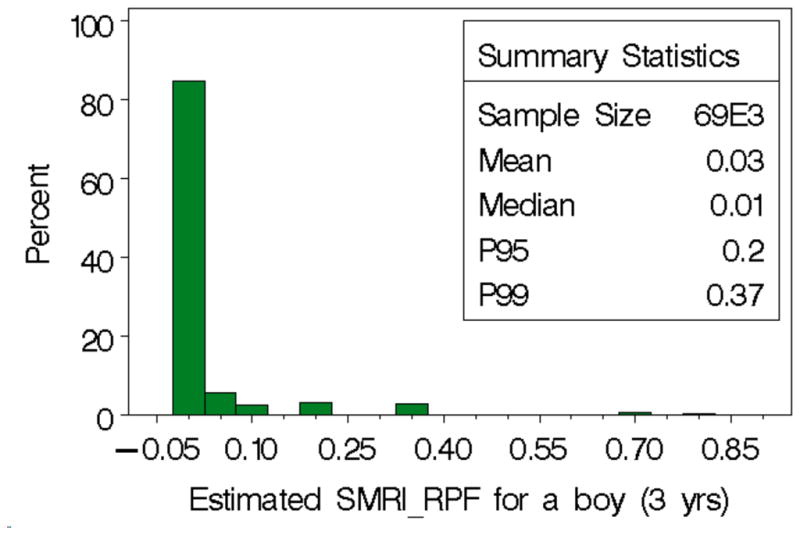
Histogram for the distribution of the SMRI_RPF estimates using exposure data considered sufficiently similar to the reference mixture (defined by a weighted distance between the BMDs of less than 2.10; selecting 114 centers) with sampling survey weights representing more than 69K day care centers in the 48 contiguous states. The index is calculated assuming a 3 year old boy, 14.2 kg and 96 cm tall. Other assumptions are in the text.

4. Discussion

Our sufficient similarity approach is based on a Euclidean distance (i.e., straight-line distance) measure between BMD estimates for a reference mixture and candidate mixture(s). Other distance measures could be considered (e.g., Mahalanobis distance; Manhattan distance; Chebyshev distance; Minkowski distance). The Euclidean distance is a basic concept related to the Pythagorean formula. ⁽¹⁶⁾ The distance calculation is based on the mixing proportions of the reference mixture and the observed candidate mixture(s). The calculation uses zeros for components not included in the constructed reference mixture and measured concentrations for the candidate mixture(s) with LOD adjustments. These zeros accurately describe components not in the constructed reference mixture while increasing the distance measure, yielding a conservative adjustment for claiming sufficient similarity. We presented both a weighted and unweighted distance measure to test for sufficient similarity. Clearly, the distance weighted by relative potency estimates is more toxicologically meaningful; the unweighted case was presented for illustration when relative potency estimates are not available.

An important part of our test for sufficient similarity is the determination of the similarity region, which we linked to the choice of the BMR and corresponding BMD; i.e., the BMR may be considered the boundary of a biological effect, and the BMD accommodates the dose-responsiveness of the mixture. We used expert judgment to set the BMR as well as the associated radius of the similarity region. While guidance exists for choosing the BMR, ⁽¹¹⁾ there is no available guidance for choosing the bounds (here, radius) of the similarity regions. Establishing reproducible and objective approaches for defining the similarity region is an area of future research; here, we have articulated initial considerations. Analogously, the Food and Drug Administration has established guidelines for bioequivalence testing for generic drugs.⁽¹⁵⁾ Future work may include an evaluation of how historical control variability could inform the boundary of an adverse effect. For example, the standard deviation estimates of the control groups (in percent control units) in the Wolansky 5-chemical and 11-chemical mixture studies were 18.9% and 18.2%, respectively. Therefore, a 20% effect (response is 80% of control) is roughly one standard deviation below the mean; therefore, in this case, both approaches result in essentially the same similarity boundary.

EPA characterizes similar mixtures based on chemical composition and component proportions, but does not provide specific methods ^(5)(25). Previously, Bull and colleagues ^{(3, 4)} described similarity among complex mixtures of drinking water disinfection by-products (DBPs). They identified variables that shifted the quantities and types of DBPs that are formed following disinfection and then identified the toxicological properties of DBP chemical classes or individual DBPs with respect to their potential for producing similar toxicity.

Environmental studies such as the CCC Study that analyze the occurrence of multiple related chemicals where humans likely contact them are critical to human health risk assessment. Such studies expand the knowledge of both the levels of chemical mixtures present in these environments and the relative proportions of each chemical comprising the various mixtures, providing insights into the differences in the quantities and composition of these mixtures across locations.

Tornero-Velez et al.⁽²⁶⁾ determined pyrethroid occurrence patterns in the CCC study. Applying community ecology methods, the occurrence of pesticides at specific locations appeared to be structured by technical, social, and economic factors, which reduced the spectrum of possible combinations. Thus, of all realized combinations in the CCC study, 98.6% were 5-way combinations or lower order. Overall, there were 38 unique combinations, 18 of these were lower order combinations (3-way or lower), and 20 were higher order combinations. The most frequent binary combination was the technical paring of cis-/trans-permethrin (46 occurrences). This pair (“A,B”) was a conspicuous component of higher order combinations; so, for example, the most frequent 3-way combination (“A,B,C”) was embedded in the two most frequent 4-way combinations (“A, B, C, D” and “A,B, C, E”) and these were realized in two of four 5-way combinations (“A,B,C, D, E” and “A,B, C, E, F”). These co-occurrence patterns suggest that toxicologists can use survey data to help target a handful of representative test mixtures to characterize a Euclidean n-space consistent with the mixtures of a “niche” such as the CCC environment.

Inferences to the CCC environment would hold as long as the processes leading to these mixtures are stationary. Thus, future longitudinal studies consisting of multiple wipe tests at the same locations over time would be valuable because they could measure changes in these mixtures over time and provide information that could be used to characterize long-term exposures from these environments, rather than exposure information at a single point in time. Complimentary mixture toxicity studies such as that of Wolansky et al. are equally important to the characterization of health risks in these environments, because they provide meaningful insights into toxicity differences in mixtures with different proportions and at different exposure levels.

Our study integrates data from CCC Study and the Wolansky studies by proposing transparent, systematic and repeatable approaches for judging which of the CCC Study pesticide mixtures are sufficiently similar to those characterized by the Wolansky dose-response study. We distinguish between mixtures where there is adequate dose-response information on the mixtures of concern and limited dose-response information on a test mixture potentially similar to the mixture of concern. Our approach is used to evaluate similarity among defined mixtures (i.e., mixtures where the components are identified and quantified) without an assumption of additivity in testing for sufficient similarity; however, additivity is assumed in the construction of the SMRI_HI and the SMRI_RPF. The approach requires the identification of meaningful biological differences in response. Here, a 20% change in total activity was judged to represent a biologically meaningful difference among responses across all changes in total activity that were lower than the total activity measured in controls. This informal expert judgment was based on one of the author’s (KC) experience with responses of the same test species in this bioassay and an understanding of typical variability in responses across individual animals that underwent the same treatment. Had the response been an increase in total activity, in the expert’s opinion a 10% change in total activity would have indicated a meaningful difference in response. We note that formal expert elicitation may provide a different answer to this question of a biologically meaningful difference among responses.

We illustrate a use of defining a sufficiently similar set of mixtures using occurrence data with toxicity data by calculating a “similar mixture risk indicator”. In risk assessment ⁽¹⁾, the HI provides an indicator of risk from exposure to a mixture of concern. HIs above 1 generally are evaluated more thoroughly. Interpretation of the SMRI defined herein follows similarly. The denominator of the SMRI used in the example is based on an acute reference value derived from a mixture BMDL. The numerator is based on an exposure scenario for a hypothetical child in a CCC. Indices well below 1 suggest that there is little risk associated with the subset of mixtures that are sufficiently similar to the reference mixture in this hypothetical example. Values at or above 1 would suggest the need for additional evaluation of the risk.

The approach used for calculating the SMRI is limited by the number of assumptions used in its calculation. The analysis estimates an acute dermal hazard posed by a subset of CCC Study mixtures that were judged to be sufficiently similar to the 5 chemical mixture evaluated by Wolansky et al. Given the limitations of these data sets, we deemed it inappropriate to extrapolate our results:

1. to exposures of longer duration than the one-day acute scenario,

2. to other exposure routes or other hypothetical individuals, and

3. to other CCC Study mixtures that were not sufficiently similar to those studied by Wolansky.

In summary, we have developed a novel approach to rigorously test for sufficient similarity using equivalence-testing methods. The approach is transparent and reproducible; however, the science-based judgment to objectively quantify “what is similar” remains a line of research inquiry. The approach allowed us to make statements in the case study such as 90% of the 126 CCCs where at least one of 15 pyrethroids was detected were sufficiently similar to the reference (5 chemical) mixture when chemicals were weighted using relative potency estimates. Thus, a conclusion from this illustrative study is that it is reasonable to use the reference dose from the mixture study as a surrogate for the RfDs for the vast majority of pyrethroid mixtures observed in CCCs from across the country. These types of conclusions provide important supplementary information to risk evaluation of chemical mixtures.

Abbreviations

BMD

benchmark dose

BMDL

lower one-sided confidence limit on the benchmark dose

BMR

benchmark response

CCC Study

First National Environmental Health Survey of Child Care Centers

DI

daily intake

EPA

U.S. Environmental Protection Agency

FDA-CDER

Food and Drug Administration – Center for Drug Evaluation and Research

LOD

limit of detection

HI

hazard index

POD

point of departure

RfD

reference dose

RV

reference value

SMRI

similar mixture risk indicator

Var

variance

APPENDIX

➢Estimating the intake of a mixture of pyrethroids

We estimate human exposure using assumptions made from a study of a different pesticide, chlorpyrifos, in children (27). In this study, mean estimates for hard floor surface wipes (0.02 ng/cm²) at home were similar to mean estimates of hand wipes at a child care center (0.02 ng/cm²). Assuming the floor wipe estimates are similar to hand wipes, the potential absorbed dose from a dermal route was calculated as (27):

$$E_{\mathit{der}}=\frac{{CA}_{t}R}{A_{h}B}$$

where E_der is the maximum potential absorbed dose (ng/kg/day) of the chemical through the skin of a child over a 24 hr period of time; C is the mass of the chemical in the hand wipe sample (ng), A_t is the exposed skin surface area (cm²) for a child based on their age and gender, A_h is the skin surface area of both hands of a child (cm²), R is the absorption rate (%/day), and B the body weight of the child (kg). Similar to Morgan et al, we assume a ~2% absorption rate per day. In the case of a hypothetical boy aged 36 months with average height (96 cm) and weight (14.2 kg) a body surface area (calculated using the Mosteller formula), $\mathit{BSA}(m^2)=\sqrt{\frac{\mathit{Height}(cm)\times \mathit{Weight}(kg)}{3600}}$ is 0.615 m²=6153cm²; assuming 37% skin area exposed (28), the exposed skin surface area is 2338 cm². Morgan et al estimated dermal exposure (as calculated from hand wipes) was only about 1% of aggregate exposure (ng/kg/day); we assume a similar percentage for the pyrethroids. Thus, for this hypothetical example using a surface wipe sample of, say, 1 ng/cm²(i.e., C/A_h=the mass in the hand wipe sample divided by the hand surface area) assuming a dermal absorption rate of 2% and that the aggregate exposure is 100 times greater than that measured from dermal exposure, the hypothetical 3 yr old boy has an aggregate exposure (i.e., DI = 100*E_der) of

$$DI=100\times \frac{1(ng/c{m}^2)\times 0.02(/\mathit{day})\times 2338(c{m}^2)}{14.2(kg)}=329.3(ng/kg/\mathit{day}).$$

➢Estimating mixture reference values for the pyrethroids

The BMD estimates are based on doses of mg/kg. We did not identify a reference value (RV) for pyrethroid mixtures; to estimate a RV in this illustrative analysis, we apply two uncertainty factors of 10 each to the BMDLs; the first, an inter-individual uncertainty factor, accounts for variation in susceptibility in the human population and the second, an animal-to-human uncertainty factor, accounts for interspecies uncertainty. The BMDLs are divided by 100 (=10×10). Thus, for example, suppose the lower 95% confidence interval on the BMD for the j^th chemical is estimated to be 30 mg/kg, we estimate the mRV_j as

$${\mathit{mRV}}_j=\frac{30(mg/kg)\times {10}^6(ng/mg)}{100}=3\times {10}^5(ng/kg)$$