Human Cortical θ during Free Exploration Encodes Space and Predicts Subsequent Memory

Abstract

Spatial representations and walking speed in rodents are consistently related to the phase, frequency, and/or amplitude of θ rhythms in hippocampal local field potentials. However, neuropsychological studies in humans have emphasized the importance of parietal cortex for spatial navigation, and efforts to identify the electrophysiological signs of spatial navigation in humans have been stymied by the difficulty of recording during free exploration of complex environments. We resolved the recording problem and experimentally probed brain activity of human participants who were fully ambulant. On each of 2 d, electroencephalography was synchronized with head and body movement in 13 subjects freely navigating an extended virtual environment containing numerous unique objects. θ phase and amplitude recorded over parietal cortex were consistent when subjects walked through a particular spatial separation at widely separated times. This spatial displacement θ autocorrelation (STAcc) was quantified and found to be significant from 2 to 8 Hz within the environment. Similar autocorrelation analyses performed on an electrooculographic channel, used to measure eye movements, showed no significant spatial autocorrelations, ruling out eye movements as the source of STAcc. Strikingly, the strength of an individual's STAcc maps from day 1 significantly predicted object location recall success on day 2. θ was also significantly correlated with walking speed; however, this correlation appeared unrelated to STAcc and did not predict memory performance. This is the first demonstration of memory-related, spatial maps in humans generated during active spatial exploration.

Introduction

The systematic encoding of spatial location by firing of neurons within a population creates a “spatial map” (Derdikman and Moser, 2010). In primates, including humans, spatial maps are driven by views of the environment (Rolls, 1999), location within the environment (Ekstrom et al., 2003; Doeller et al., 2008, 2010), or distance along a trajectory (Cornwell et al., 2008; Jacobs et al., 2010). Intracranial recording and functional imaging studies in humans, in which participants use a joystick or button pad to move through a simulated environment, have consistently shown increased activity in medial temporal lobe and posterior and medial parietal cortices during spatial navigation (Kahana et al., 1999; Bischof and Boulanger, 2003; Caplan et al., 2003; Ekstrom et al., 2005; Cornwell et al., 2008; Kaplan et al., 2012).

Commonly, cell firing during spatial navigation is organized by θ frequency local field potential oscillations. θ is critical for the synchronization and integration of diverse cell classes and cortical regions during spatial learning (O'Keefe and Recce, 1993; Sirota et al., 2008; Montgomery et al., 2009; Young, 2011). In addition, θ encourages long-term potentiation of synaptic efficacy (Larson and Lynch, 1986; Wills et al., 2010), such as occurs during “unsupervised” spatial learning (Chen et al., 2010). θ's low frequency may permit synchronization of widespread brain regions (Caplan et al., 2003), including posterior parietal cortices (Byrne et al., 2007). Posterior parietal cortices are critically involved in spatial processing (Andersen et al., 1985; Sakata and Kusunoki, 1992; Todd and Marois, 2004; Save and Poucet, 2009), maintain strong connections to the hippocampus (Clower et al., 2001; Save et al., 2005; Rushworth et al., 2006), are important nodes in brain networks constructing spatial maps (Ekstrom et al., 2005; Doeller et al., 2010; Jacobs et al., 2010), and show increased θ power during navigation (White et al., 2012). Relative to rodents, humans may rely more heavily on parietal cortex for supporting spatial map formation (Shrager et al., 2008).

The likelihood that humans use θ driven mechanisms to learn complex environments through fully active exploration has not been tested, largely because the head and body restraints required for electrophysiological recording eliminate the vestibular, somatosensory, and proprioceptive brain afferents underlying construction of spatial maps, body location, and wayfinding (Berthoz, 1997; Nitz, 2006). Recent experiments in mouse have shown a strong reduction in spatial map activity and alterations in temporal coding when animals run with their head fixed in simulated environments, compared with natural movements in the real world (Chen et al., 2013; Ravassard et al., 2013). Indeed, ambulatory and vestibular self-motion signals are the primary determinants of the total spatial information per spike of hippocampal place cells (Terrazas et al., 2005). We recorded synchronized EEG, head, and body movement from 13 participants freely moving about a large-scale virtual environment to test the hypotheses that an individual's θ activity during spatial exploration recorded over posterior parietal cortex reflects their position in allocentric space and predicts future memory performance.

Materials and Methods

Experimental design.

To test the prediction that subjects organize memory spatially, we developed a naturalistic paradigm that required multiple, complex trajectories through an extended space and placed heavy demands on memory. Synchronized recordings of 3D head, hand, and torso movements, via optoelectronic and inertial sensors, and 72 channel active electrode EEG recordings were obtained from 13 subjects (3 female; age [mean ± SD] = 25 ± 4 years) as they explored a novel virtual environment (Fig. 1) (for details of the method, see Snider et al., 2013). Subjects wore a wide field-of-view head-mounted display and moved at will in a large-scale, richly textured room (∼4 × 5 m) containing numerous objects resting on shelves, tables, and the floor (Fig. 1A1). This virtual room, located on an “aircraft carrier,” was the same size as the real world space in which subjects were walking (Fig. 1A2).

Figure 1.

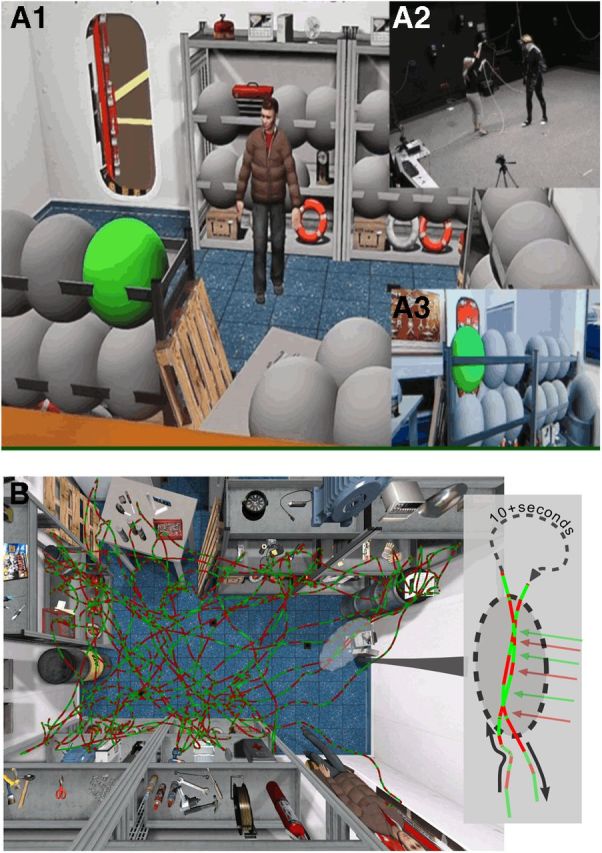
A, Experimental environment. Subjects freely explored a virtual storage room (A1, bird's eye view), matched in size (4 × 5 m) to the physical room in which the subject was present (A2). The subject walked to green bubbles, which popped when touched by the right hand, revealing the hidden object. The virtual room was presented on a head-mounted display (A3). B, Sample θ sign map. EEG data were recorded continuously while the subject walked in the virtual environment. The path from a single session is color coded by the sign of the 6 Hz Haar wavelet (θ frequency). The sign of the signal aligned across two traversals (inset, red and green arrows) that occurred at different times.

Sessions lasting 2 h were conducted on successive days. The first day was dedicated to exploration, and the second day to testing subjects' memory of the environment. By maintaining the subjects' naiveté about the memory aspect of the experiment on day 1, the knowledge of the environment on day 2 came from unsupervised learning. On day 1, subjects first investigated the room for 10 min with no instruction, except “explore the environment.” This taskless “free exploration” block was followed by five blocks with a task. Opaque virtual bubbles were placed around 39 different objects in the room. The subjects walked up to one bubble at a time (indicated by turning green in random order) and popped it by touching it with their hand, thereby uncovering the object underneath (the objects had been present during the initial exploration, but not obscured by the bubbles). As a cover task, subjects indicated their interest in the object using a virtual slider. A block ended when all the objects were uncovered and visible. For each of these five “interest” blocks, the order of bubble popping varied randomly, but the objects remained the same, thus ensuring both multiple paths through the virtual environment (VE) and opportunity for unsupervised learning of the object locations. Subjects proceeded at their own pace and could take breaks at any time, but they were encouraged to do so between blocks.

The following day (day 2), the subjects entered the same virtual room. However, the locations of 13 of the 39 objects were randomly swapped from their positions on day 1. As on day 1, subjects walked to a bubble covering an object when it turned green and touched the bubble exposing the object. Subjects then indicated how certain they were that the object was the same one that was in that location on day 1, again by adjusting the virtual slider. This process was repeated over 5 blocks of trials, with each block lasting 5–8 min. A different set of 13 objects were misplaced in each block.

Virtual environment.

The hardware supporting the VE consisted of a 24 camera PhaseSpace Impulse active infrared-emitting diode (IRED) motion capture system (www.phasespace.com), providing 3D position information of the right hand, head, and torso, an Intersense (www.intersense.com) InertiaCube3 orientation sensor for head orientation, a 20 speaker Ambisonic Auralizer Sound System (www.worldviz.com), and a Sensics (www.sensics.com) xSight 6123 head-mounted-display (HMD). The HMD provided a panoramic, stereo view of the VE (120 deg horizontal field of view and 45 deg vertical), creating a strong feeling of presence in the VE (Snider et al., 2013). A questionnaire was given to the subjects (12 of 13 subjects completed the questionnaire) to assess their engagement in the VE (Witmer et al., 2005). It specifically contained questions pertaining to “involvement,” such as “How much were you able to control events?” or “How involved were you in the virtual environment experience?” Responses to questions about haptic feedback and auditory cues, none of which was present, were disregarded. The VE was rendered via custom scripts written for Vizard 3.0 (www.worldviz.com) with a total end-to-end latency of <40 ms (Snider et al., 2013) and spatial precision on the order of millimeters. All cables (the EEG fiber optic cable, the InterCube3 RJ10 cable, and the thick 11-mm-diameter HMD cable) went up through the ceiling in the center of the room with enough free length to comfortably explore the entire space while minimizing physical interference with the wires (Fig. 1A).

The VE room had a large empty space in the middle surrounded by shelves of objects. The objects were richly detailed and textured 3D renderings, some of which were created from photographs taken on the U.S.S. Midway museum (www.midway.org). All objects were appropriate to the context of an aircraft carrier setting (i.e., there were no “blue rabbits”), but there were tools, fire extinguishers, life preservers, coffee cups, and so forth (Fig. 1B). The empty space in the center of the VE coincided with empty space in the actual room (Fig. 1), and subjects were instructed to remain in the room between the shelves. Exits were obstructed with virtual obstacles, except for an open virtual door at which all blocks began. Subjects could look through the door to see a virtual flight deck but were instructed not to go through it. Subjects appeared to move at a normal, unhurried speed and navigate very naturally through the environment. All of the interactions occurred in a manner that avoided touching any objects in the real environment to minimize the influence of haptic-vision mismatch.

The position of the subject's head, as tracked by the IRED system, and its orientation, from the inertial sensor, moved the camera rendering the VE through the environment in real time and with a one-to-one mapping of real onto virtual space. The IRED and inertial sensors were combined to maximize the responsiveness and stability of the system for improved immersion. The subjects moved through the environment as though they were really in the virtual room, as a sort of completely immersive simulation, with the VE precisely and consistently controlling the environment. The subject's hand was also tracked and rendered as a visible, 5-cm-diameter orange ball, which the subjects used to pop bubbles and indicate interest (or confidence) on a continuously variable slider that appeared in the VE after bubble popping. The main focus here is on the relation of the EEG to the subjects' spatial location within the VE during the intervals in which the subjects were walking between objects (EEG to exposing the objects will be reported separately). To isolate walking intervals we calculated the speed of the head from a least square, linear fit to a 300 ms sliding window to estimate the slope of the position. Any speed exceeding 0.2 m/s was considered walking. The resulting paths (Fig. 1B; see Fig. 4A) were composed primarily of long traversals of the room when the subject walked from bubble to bubble or to the middle of the room to find the next target bubble. These data emphasize spatial awareness of and navigation within the room over responses to individual items in the room, and, when combined with the EEG (described below), allow us to focus in on spatial map generation.

Figure 4.

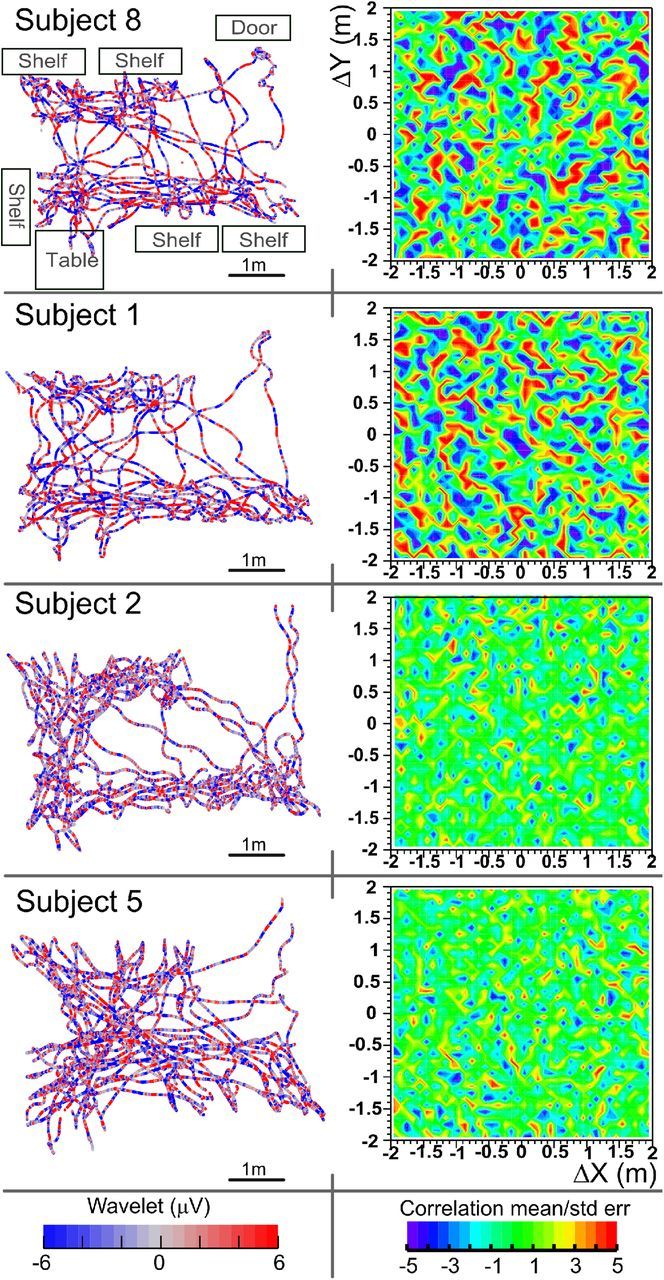
Spatial autocorrelograms. Left column, Head paths taken over a 5–10 min exploration block when subjects were interacting with objects located on the shelves and table; color represents 6 Hz Haar wavelet. The layout of the room is sketched on the top left (compare withFig. 1B). Right column, Corresponding statistical maps of autocorrelograms at each directional displacement. All data are from the first day when the task was to rate “how interesting” the object was. Red and blue represent displacements with consistent θ (|mean/SE| >3). Correlation was relatively high and structured in some subjects (top, 2, 1, and 8) but not others (bottom, 2, 2, and 5).

EEG.

Scalp EEG recordings reflect coordinated activity in large cortical assemblies, but they are also sensitive to artifacts due in large part to eye movements and muscle activity, especially from the region of the neck and face, as well as pickup of stray fields from the environment. Although these artifacts in the EEG cannot be totally prevented, they can be minimized in the following ways. First of all, we used the 64 channel BioSemi ActiveTwo system (www.biosemi.com), which features electrodes that contain individual preamplifiers, eliminating the wire from the electrode to the first amplifier, and thus minimizing the pickup of extraneous signals in the physical space and those generated by movement of the wire relative to the electrode. Eight external electromyographic (EMG) electrodes were added to help identify muscular artifacts and were placed as follows. Four electro-oculogram (EOG) electrodes were mounted on the supraorbital and infraorbital ridges of the right eye as well as lateral to the outer canthi of right and left eyes. Two electrodes were further attached to the right and left neck at the height of the seventh cervical vertebra monitoring activity of neck muscles, particularly the trapezius. Two electrodes were mounted on the left and right mastoids, the average of which was used as reference for all analyses.

Movement artifacts from muscle activity were further minimized by encouraging subjects to walk at a comfortable, steady pace (lack of time pressure) and reminding subjects to avoid excessive facial movements, such as smiling, frowning, or grimacing. Walking speed in our experiment did not exceed 1.25 m/s, and typically was much slower with mean speed during walking of 0.5 ± 0.2 m/s (mean ± SE across subjects and blocks). Also, at the start of the experiment, just after setting up the EEG, but before entering the VE, subjects were shown how shrugging their shoulder or clenching their teeth caused large, easily visible artifacts in the EEG. One experimenter monitored the EEG traces in real time during the experiment and told the subjects if muscular noise became apparent.

Any artifacts resulting from muscular and eye activity that did remain in the EEG were compensated for or removed through offline filtering and data preprocessing as follows. Initially, to be as close to the data as possible and avoid any potential nonlinear interaction with advanced signal processing, we analyzed a single electrode located over central, posterior parietal cortex (scalp site Pz, International 10–20 system). Analysis of the signal at the single electrode Pz was preplanned based on two considerations. First, Pz strongly reflects synchronized activity in parietal cortices, where we hypothesized the existence of a detectable spatial signal (as described in the Introduction). Second, Pz is minimally affected by muscular artifacts because it is relatively far away from both the neck and eyes (Goncharova et al., 2003; Schlögl et al., 2007; Nolan et al., 2011). We rereferenced recordings from Pz to the average mastoids, high-pass filtered at 0.25 Hz (Kaiser window, ripple = 10 dB, width 0.1 over Nyquist, and SciPy signal library) to eliminate static drift, and took a Haar wavelet transform at 6 Hz, which is the middle of the 4–8 Hz human θ frequency band. To maintain the maximum amount of information about the underlying signal, the entire wavelet coefficient, including amplitude and phase, was used for the analysis (for evidence for the central importance of phase as well as amplitude in scalp EEG, see Whittingstall and Logothetis, 2009; Ng et al., 2013). To be clear, we did not turn the wavelet coefficient into power (or phase) separately; instead, we analyzed the raw coefficient, the product of the signal with the 6 Hz Haar mother wavelet at all time points. The wavelet data were then aligned with the position of the subject's head in 2D space by downsampling the 1024 Hz EEG data onto each sample point from the 120 Hz position data (10 ms time-locked average). The height of the head could be ignored because it varied only ∼5 cm.

The primary analysis and planned comparisons used only data from Pz. To conduct exploratory and follow-on analyses, the high-density 70 channel EEG-EMG data were processed with extended infomax independent component analysis (ICA) (Bell and Sejnowski, 1995). ICA is a blind source separation procedure that separates the EEG into a set of statistically maximally independent components, some of which represent electrocortical sources, whereas others represent eye movements, neck and other muscle sources, and other artifacts (Jung et al., 2000). The processing steps for running ICA were as follows. First, the data were high-pass filtered at 1 Hz and low-pass filtered at 30 Hz using the default fir filter in EEGLAB (Delorme and Makeig, 2004). Second, the onset and offset of walking intervals were identified by looking for 1 s or longer intervals when subjects maintained a speed >0.2 m/s. Then, these intervals were set as events in the EEG data using custom MATLAB scripts for EEGLAB v10.2 (MathWorks) (Delorme and Makeig, 2004). To generate epochs of equal length, we covered the walking intervals by 1 s events starting 0.5 s before the onset of walking (e.g., if walking onset and offset were at 3.1 and 5 s, then the 1 s events started at 2.6, 3.6, 4.6, and 5.6 s). These data were then processed using ICA to identify independent components. Seventy such maximally independent components were thus obtained. Eye movement and muscular sources were readily identified by spatially focal scalp projection, distribution or source location outside of the brain, and/or power spectrum with high-frequency activity (Jung et al., 2000; Delorme and Makeig, 2004; Gwin and Ferris, 2012; Ma et al., 2012). The time course of these independent components (ICs) was then inspected for periods of transient noise that were marked for removal in later processing. The weight matrix for the parietal ICs was applied to the raw data, and the result was fed into the same algorithm that was used on the Pz data (0.25 Hz high-pass, 6 Hz Haar, downsampled onto position). sLoreta (Pascual-Marqui, 2002; McMenamin et al., 2009) was used to estimate the current source density of the mean IC activity.

Autocorrelograms.

A quantitative measure of the relationship between θ oscillations and relative position in space was obtained by calculating autocorrelations of Haar wavelet coefficients at all pairs of discretely sampled positions at fixed directional separations with respect to each other (Fig. 2). All pairs of position points (usually ∼30,000 samples) were binned into histograms dependent on their relative position (i.e., change in their x and y coordinates). The binning was done with a custom NVIDIA CUDA (www.nvidia.com/cuda) application to handle the large number of comparisons. There were six total histograms recording w₁, w₁², w₂, w₂², w₁w₂, and N, where subscripts 1 and 2 indicate two elements of the wavelet values from different times. These values were then used to calculate the autocorrelation at each relative position as follows:

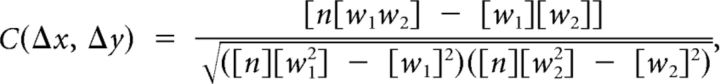where the brackets indicate histograms at each relative separation. We enforced a time delay such that Measurement 2 occurred at least 10 s after Measurement 1, so that correlations could only come from different traversals of the room. This removed a trivial peak at zero relative shift (due to the correlation of the 6 Hz signal with itself after 1/120 s) and made the autocorrelograms not necessarily mirror symmetric because Time point 2 was in all cases necessarily after Time point 1. All of these choices were made to be as conservative as possible in constructing the autocorrelograms.

Figure 2.

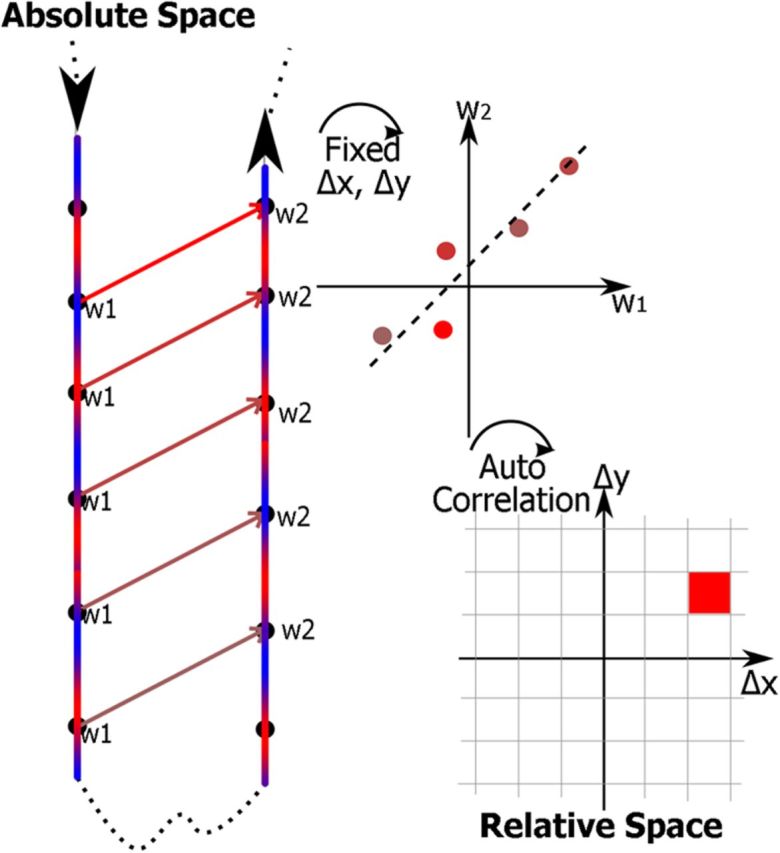
Construction of the autocorrelation maps. The two blue/red lines indicate walking trajectories that happen to pass parallel to one another. The color represents the EEG signal along the trajectory. All the points labeled w₁ are a fixed distance, in both x and y, away from the points labeled w₂. These points at the fixed separation are then plotted against each other, and their correlation is estimated. The value of the correlation is then put into a map of relative space. The procedure is then repeated for every other separation on the autocorrelation map to build the complex maps (e.g., Fig. 4B).

The above procedure for calculating the autocorrelation of a signal was taken from the literature (compare Hafting et al., 2005). However, the signal strengths we expected necessitated a more rigorous estimation of the statistical significance of the autocorrelation maps. Thus, we developed a two step rebinning procedure that first oversamples the spatial autocorrelation maps and then combines the local oversampled data to generate means and SEs. In the first analysis step, spatial autocorrelation maps were calculated as above with spatial resolution of 1 × 1 cm. Because 6 Hz activity in subjects moving with an average speed of 0.5 ± 0.2 m/s was analyzed, the signal was stationary (and thus trivially locally correlated) over length scales on the order of 0.5 m/s/6 Hz = 0.083 m or ∼10 cm. Thus, a grid size of 10 × 10 cm was chosen as the final bin size to represent local estimates of the autocorrelation. The data from the smaller 1 × 1 cm histogram were rebinned into the larger 10 × 10 cm bins to estimate both the local mean and error. To avoid edge effects at large separation, any 10 × 10 cm bins with fewer than 1000 points per bin in the larger histogram were rejected (the average number of points per bin was 2.11 × 10⁵, with SD 1.35 × 10⁵). Plots show the autocorrelogram averaged across the 100 1 × 1 cm bins within each 10 × 10 cm bin, divided by the SE across those 100 bins (see Fig. 4) plotted as statistical maps for the different relative displacements. This is helpful for presentation purposes because SEs vary across the room due to differential sampling (the space was longer in one direction than the other). The resulting numbers cannot be strictly interpreted as t scores because the autocorrelations in even the larger bins are not necessarily independent measures. Thus, conclusions regarding statistical significance are based on resampling statistics described below. However, one should note that the local error estimate obtained in this way is similar (and actually more conservative) than that obtained with bootstrapping methods applied to the same data as described below. For ease of description, the “map strength” of a spatial autocorrelogram was defined as the SD of all the values in all of the bins. Higher map strength corresponded to more spatial displacements with nonzero autocorrelation. We term this procedure “spatial displacement θ autocorrelation” or “STAcc.”

Statistical tests and control procedures.

A resampling procedure was used to estimate the level of autocorrelation that would be expected under the null hypothesis that there was no consistent relationship between θ activity and spatial displacement. Under the null hypothesis, the EEG data from any subject mapped onto the paths from any other subject would generate statistically identical autocorrelations to the actual data. The autocorrelograms were calculated as above for the resampled datasets. This procedure was performed on the 6 Hz wavelet of Pz activity, by swapping the EEG and path data across all possible pairs of subjects (∼8300 total resampled autocorrelation maps). Because block durations were not constant, the EEG from approximately the matching time across subjects was used for downsampling the EEG onto position data as described above. We verified that keeping only 10% of the swaps was sufficient and applied the technique to the eye-movement sensitive EOG data as well, using 10% of all possible pairs (∼830 total). Significance was tested by constructing histograms of all pixels of the autocorrelograms of the resampled and actual datasets and measuring the Kolmogorov–Smirnov distance between the resampled and original data (length 100,000 subsamples of both was compared 1000 times because it was not computationally feasible to use the entire dataset). The p values from the Kolmogorov–Smirnov test were averaged, resulting in an estimate of the probability of the null hypothesis. For two sequences coming from the same distribution, the Kolmogorov–Smirnov p value is evenly distributed from 0 to 1; thus, a mean p value of 0.5 would be expected if the two sequences came from the same distribution. The absolute value of the correlations was also tested with a t test. All statistics were performed in R version 2.15.2 (http://www.R-project.org), ANOVAs were run with the “ez” package, and linear mixed models (LMMs) were fit using the “lme4” package. For the LMMs, the χ² test was used to compare models with and without parameters of interest. LMMs were only used to test for a relationship between speed and wavelet power (both continuous variables).

Although the bootstrapping procedure described above was the most rigorous method to estimate the probability under the null hypothesis, it was too computationally intensive to perform for every comparison. In these other comparisons, especially across frequencies other than 6 Hz, we calculated the expected results under the null hypothesis by replacing the EEG with a constant sine wave at the frequency of interest. This presented the autocorrelogram algorithm with an oscillatory signal that had no spatial correlation, by construction, but maintained similar local correlations. The rate of change of the sine wave slowed with frequency, which lowered the effective sample rate (the number of periods of the underlying oscillation). Thus, because the path length remained the same, the baseline error increased inversely with frequency. To estimate the actual signal in the EEG data when the bootstrap procedure was impractical, the sine wave baseline was subtracted. The sinusoidal baseline procedure approximates the expected baseline for reasonably smooth data, such as filtered EEG data, but it significantly underestimates the impact of repeated punctual events, such as eye movements (Fig. 3A), and bootstrapping is the best alternative.

Figure 3.

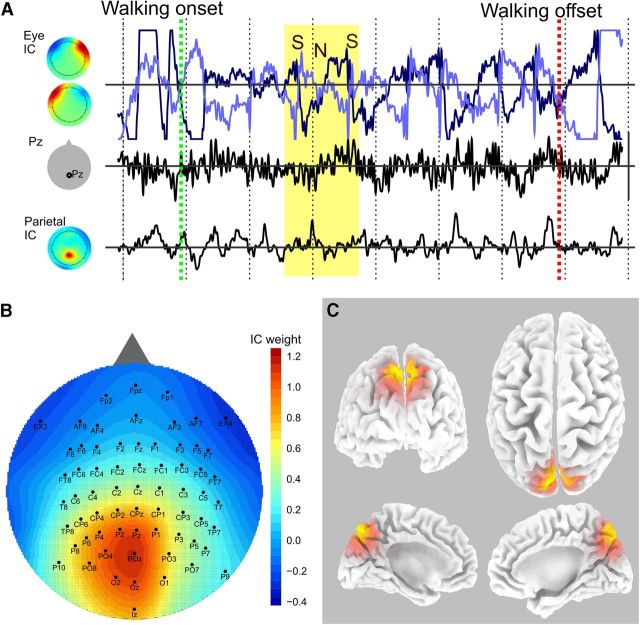
EEG activity during walking. A, Concurrent EEG traces from a 3 s walking interval from one subject. Walking onset starts at the green line and ends at the red, with 0.5 s intervals marked off by dashed vertical lines. The lines on the top row (light and dark blue) indicate eye movement-related activity with sources (left) showing left and right eye movements. The data from the Pz electrode are in the middle, and a single parietal IC is on the bottom. The yellow region represents a saccade where the eye fields suddenly switch signs (the saccade [S]) then slowly revert (head adjustment [N]) followed by another saccade (second S). The eye and neck movements do not have a noticeable effect on the Pz or parietal ICs. B, All the brain ICs from all the subjects were averaged to show the central-posterior-midline parietal localization of the activity. C, sLoreta localization of the current source density corresponding to the mean back-projected IC (B). Orange represents regions of significant activity. The estimated location of the source is the medial aspect of the superior parietal cortex (precuneus).

In cases of behavioral correlation with the memory score, there was a significant ceiling effect because some subjects had a nearly perfect memory score. Therefore, nonparametric tests were used: Spearman correlation for regression onto continuous variable or permutation testing for ordinal variables. The permutation analysis generated an expected baseline distribution of correct memory for the individual objects assuming the null hypothesis that no relationship between object and memory exists. To account for any potential subject and block variability, we shuffled the object identities within each subject and block but left the number of correct responses the same. This shuffling explicitly broke any potential dependence of memory on object identity while maintaining individual subject tendencies by block. We then used the Kolmogorov–Smirnov test to compare the distribution of fraction correct for each object calculated from the shuffled data to the distribution of fraction correct actually observed for the unshuffled objects. This was repeated 100 times to give an average probability of the null hypothesis. The permutation test was applied both to the object identities (i.e., cup or wrench) as well as the spatial locations available for the objects (i.e., shelf or table).

Results

Behavioral

We studied subjects navigating in a fully immersive, ambulatory VE consisting of a richly textured room with numerous 3D objects located on shelves, tables, and the floor. Except for an initial free exploration block on day 1, objects were covered in opaque bubbles, one of which was colored green. Subjects walked to the green bubble and touched it. The bubble then disappeared exposing the object. On day 1, subjects rated how “interesting” each object was using a virtual slider. On day 2, subsets of the objects were swapped in location on multiple blocks of trials. The subject's task was to rate whether each object had been in that location or not on the previous day. Along with head, body, and arm position data, 64 channel EEG and 8 channel EMG were recorded throughout the sessions. We evaluated memory on day 2 resulting from unsupervised learning on day 1, by asking whether the subjects recognized that the spatial locations of certain objects had been switched on day 2. Given that a large number of items were sampled, and then only briefly, this paradigm placed significant demands on memory, as evidenced by the range of retention scores across subjects on day 2: 76–96% correct (chance = 50%). Because a different 13 of the 39 objects were shuffled for each of the 5 blocks testing memory on day 2, the subjects' performance improved somewhat over blocks from an average of 79 ± 9% on block 1 to 89 ± 8% on block 5 (mean ± SD, F_(4,48) = 6.92, p = 0.0002).

Immersion in the VE was evaluated with a questionnaire (Witmer et al., 2005). Average immersion scores were 5.6 of 7 (SD 0.8), which reflects very strong immersion (Usoh et al., 2000). Additionally, qualitatively, subjects were observed to move naturally and confidently through the environment. No correlation of the judged immersion in the VE with memory performance was observed, either across all questions (r = 0.18, p = 0.59, Spearman test) or within the targeted “involvement” questions (r = 0.21, p = 0.54, Spearman test). Thus, any variations across subjects in judged immersion in the VE played an insignificant role in the performance of the task.

As a cover task on day 1, subjects rated their interest in the objects. These data also were used to verify that the objects were not individually memorable. The subjects' rated interest in the objects on day 1 showed no relation to the memory performance on day 2 (r = 0.06, p = 0.72, Spearman test). Additionally, an ANOVA was performed to measure dependence of the rated interest of the objects across subjects and showed that no object was consistently rated as either interesting or not (F_(38,468) = 0.63, p = 0.96). Furthermore, permutation testing of the object–memory relationship accepted the null hypothesis (p = 0.14), indicating that objects had similar memorability. Also, the permutation test applied to object placement location (i.e., table or shelf) accepted the null hypothesis of no relation to memory (p = 0.82). Thus, neither the individual object identities nor their placements could account for the observed memory performance.

ANOVAs showed that the following path descriptors were similar across subjects and blocks (after free exploration): total time spent walking (F_(4,60) = 0.84, p = 0.50), total distance traversed while walking (F_(4,60) = 1.7, p = 0.17), and average walking speed (F_(4,60) = 1.9, p = 0.13). Additionally, the speed along the walking intervals (when subjects maintained a speed of at least 0.2 m/s for at least 1 s) was compared at 11 positions (0–5%, 5–15%, …95–100%) along the interval and showed no variability across subjects for any of the positions (p > 0.25, familywise error corrected, Kolmogorov–Smirnov tests). Speed followed a bell-shaped curve with a peak speed of 0.63 ± 0.02 m/s ∼60% of the way along a walking interval. Thus, paths were statistically similar across subjects, and movement variability cannot explain the observed wide range of memory.

Parietal scalp EEG during movement

Figure 3A shows an example of EEG data during movement. A walking interval (speed > 0.2 m/s) initiated at the green line and continued for ∼6 s (red line). Over that time interval, eye movements and neck muscle activity were present. An example is highlighted in the yellow section and is easily visible in the eye movement-related IC (Fig. 3A, top row). The subject made a saccade (S) with an accompanying rapid change in eye potential, followed by a head movement (N) while the gaze remained fixed, and finally another saccade. This sequence of eye-neck movement was very common during this virtual exploration and could have dominated the EEG. Artifacts were accounted for initially by using the Pz electrode, which was far from the eyes and only minimally affected as seen in Figure 3A (second row) where the eye movements do not bleed through to the Pz data. The data were also cleaned with ICA, and independent components with parietal activity (Fig. 3A, bottom row) also showed little relation to the eye activity. Further, all three of eye, Pz, and parietal IC activity were analyzed separately in the main procedure below.

The ICA procedure was run on the walking intervals from all subjects, and 11 of 13 subjects had scalp ICs identifiable as parietal as determined from their power spectrum and scalp distribution (mean ± SD, 2.2 ± 0.8 ICs per subject). On average, the sources were located on the midline over posterior parietal regions (Fig. 3B,C), consistent with expectations of posterior parietal activity during spatial exploration and representation of 3D space (Andersen et al., 1985, 1995; Save et al., 2005; Sato et al., 2010; White et al., 2012) and consistent with the location of electrode Pz, over midline posterior parietal cortex. The mean activity map was analyzed using sLoreta to estimate possible localization of generating cortical sources. The estimated reconstructed source was localized in the medial aspect of the superior parietal cortex (precuneus, BA 7/31, MNI coordinates: x = 5, y = −75, z = 50) (Fig. 3C).

θ autocorrelograms are related to space

Structure was evident in plots of the subjects' location versus ongoing θ sign (Fig. 1B, highlighted region) or complete θ wavelet coefficients (Fig. 4, left column). For example, in the highlighted region of Figure 1B, the pattern of red (positive coefficient)-green-red is aligned on the two paths that happened to be parallel, even though the subject traversed these paths at very different times. The significance of the apparent spatial structure was tested by calculating the autocorrelation of the wavelet coefficient with spatial displacement (see Materials and Methods; Fig. 2). Briefly, all possible pairs of sample points with a given spatial displacement were autocorrelated with a robust procedure that resulted in both the correlation coefficient and an estimate of its error. The autocorrelation procedure was repeated for spatial separations with 10 cm step sizes (i.e., …−10, 0, 10…cm in x and …10, 0, 10… cm in y) to construct “spatial displacement autocorrelation” (STAcc) maps. For visualization, the STAcc maps were plotted as t values (mean ± SE, Fig. 4, right column). In some subjects, STAcc maps showed large regions of significant autocorrelation or anticorrelation, which appeared as mottled patterns of red and blue on the green background. There was no obvious structure to the regions of significance. These differences between subjects were quantified by measuring the SD of the autocorrelation at each separation (each pixel in the raw map) to generate a “map strength” where a higher score indicated a more highly differentiated spatial map than a lower score. An ANOVA of the map strength versus block and day across subjects showed that map strength increased from 0.022 ± 0.005 to 0.026 ± 0.007 from block 1 to 5 (F_(4,48) = 4.04, p = 0.007) but did not depend on day. Importantly, and somewhat unexpectedly, the sharpness of the maps varied markedly across subjects, despite the absence of evident differences in amount of exploration or trajectories. This variability is visually apparent in the second column of Figure 4 where the first two examples exhibited large, mottled spots of significant activity, but the last two showed almost none. The θ autocorrelograms in Figure 4 thus appear to indicate that oscillations at two locations were systematically related to the vector displacement between those locations. Further statistical tests and quantification supporting this result are presented below.

Control tests

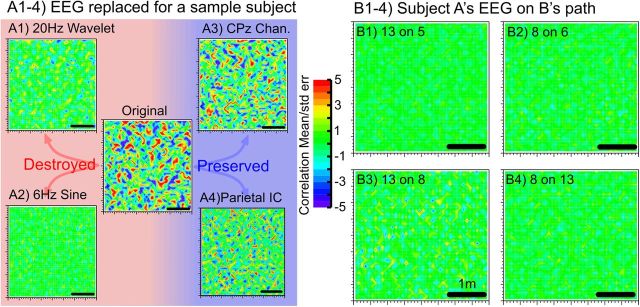
The absolute values of the correlations were small, ∼0.05, although on par with those seen in fMRI experiments (Doeller et al., 2010). Thus, we performed a further set of tests to verify that the elevated spatial autocorrelations were not artifactual. The simplest method was to replace the actual EEG data of a subject with a sine wave at 6 Hz (i.e., a false signal with no spatial information or correlation with the subject's position in space, but having the same frequency as the 6 Hz wavelet). Using the sine wave instead of an actual electrophysiological signal as recorded over medial posterior parietal cortex destroyed the correlation signal, and the autocorrelograms became flat (Fig. 5A2). This test controls for occult correlations that might be inherent in the multistep signal processing and analysis procedure.

Figure 5.

Validation tests. A, Additional tests of signal specificity, obtained in a subject with strong autocorrelations (Subject 8, day 1, block 2). The signal is decreased by (A1) analyzing with a 20 Hz instead of a 6 Hz wavelet or (A2) replacing the EEG with a pure 6 Hz sine wave. Conversely, the signal is preserved when (A3) it is calculated at a neighboring electrode (CPz) or (A4) using ICA to isolate a parietal source. B, Autocorrelograms calculated using one subject's EEG on another subject's path. B1–B4 show representative examples of all combinations EEG and path from good performers of the memory task (Subjects 6 and 8) and poor performers (Subjects 5 and 13). The lack of a signal indicates that the autocorrelograms are specific to the individual and are not artifacts of the analysis routines.

The spatial autocorrelation also was massively reduced by autocorrelating a wavelet coefficient in the β frequency band (20 Hz) with relative position in space (Fig. 5A1). Thus, if the 6 Hz θ spatial autocorrelation is artifactual, it must be an artifact that is frequency-specific. Conversely, the signal was still present at a neighboring electrode (CPz, located ∼3–4 cm anterior to Pz), which produced results comparable to those obtained at Pz (Fig. 5A3). Thus, if artifactual, the artifact extends to an adjacent electrode. Finally, similar results were obtained using ICA components with high weights of electrodes over midline parietal regions (Fig. 5A4; IC with increased weights over central, posterior parietal areas). Thus, the responsive signal appears to arise in a coherent pattern of activity over a set of electrodes. Overall, these control tests render unlikely an artifactual origin of the observed θ spatial autocorrelation.

Swap tests and resampling statistics

The most definitive verification of the autocorrelograms came from projecting the EEG from one subject onto another subject's path and then computing the autocorrelogram. Because the subjects were constrained by the task to take qualitatively similar paths walking from bubble to bubble, they had similar movements and environmental interactions, but precise details about their paths were dissimilar because object order (and thus subject trajectory, footfall time, location in the room, etc.) was different across subjects. The intersubject swapping procedure did indeed flatten the autocorrelograms (Fig. 5B1–B4). This elimination of the autocorrelations by projecting one subject's EEG onto another subject's path is a strong indication that the structure in the autocorrelograms between EEG and path within each subject, as seen in Figure 4, is unlikely to be artifactual. In addition, we performed all possible combinations of swaps of EEG and paths across subjects to generate a bootstrap estimate of the correlation that would be expected under the null hypothesis that there is no relationship between EEG and displacement (see Fig. 7A). The variance of that histogram was a bootstrap estimate of the overall SE because the larger the variance, the greater the number of higher correlation values. The bootstrap estimate, ∼0.005, agreed reasonably well with the local SE estimate of ∼0.01, indicating that a sufficient number of swaps were performed. The fact that the peak correlations were 10 times larger than the bootstrapped error emphasized the robustness of the autocorrelograms. The histogram of map strengths (SD of the bins from an autocorrelation map, methods) from actual subjects was significantly different from swaps (p < 10⁻⁴, Kolmogorov–Smirnov test), and actual subjects showed higher correlation than swapped data (3.68 ± 0.06 times larger, t = −461, df = 228462.2, p < 2.2 × 10⁻¹⁶, t test). In all subjects, the values in the spatial autocorrelograms were greater than expected by chance (Fig. 6B), and in some the mean values at most displacements were several times larger than the local SEs.

Figure 7.

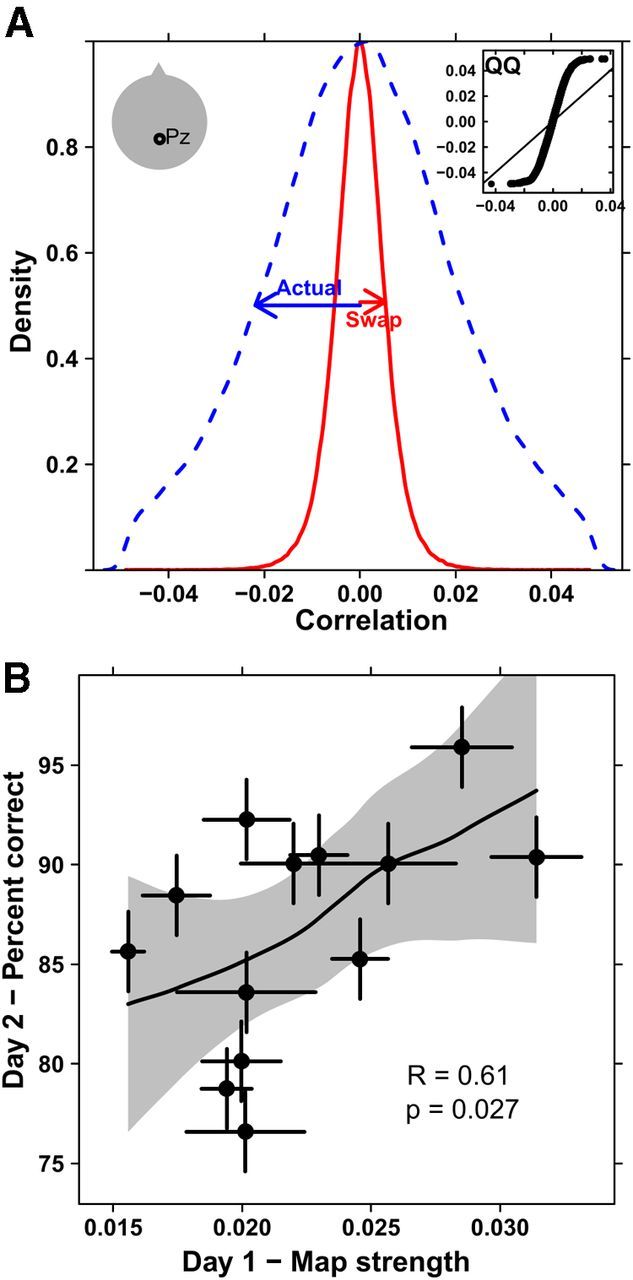
Data from an electrode placed above midline parietal (Pz). A, To quantify strength, the autocorrelation value at each relative position (10 × 10 cm bins) is binned into a histogram (blue, dashed). As a baseline estimate, we swap EEG and path across subjects (red, solid). The two histograms differ significantly (p < 1.e−4, Kolmogorov–Smirnov test) with the actual distribution ∼3.4 times wider than the swaps. For verification, the inset shows a quantile-quantile plot with points falling off the 45 degree line. B, Map strength (the SD of the autocorrelation histogram as in A, but for every block separately) is calculated for each subject. The map strength from day 1's exploration is positively correlated with the fraction of objects correctly localized on day 2 (r = 0.61, p = 0.027, Spearman), even though the subjects were naive to the memory aspect of the task on day 1. Error bars indicate SEs across blocks. The shaded region is an estimated 95% confidence interval.

Figure 6.

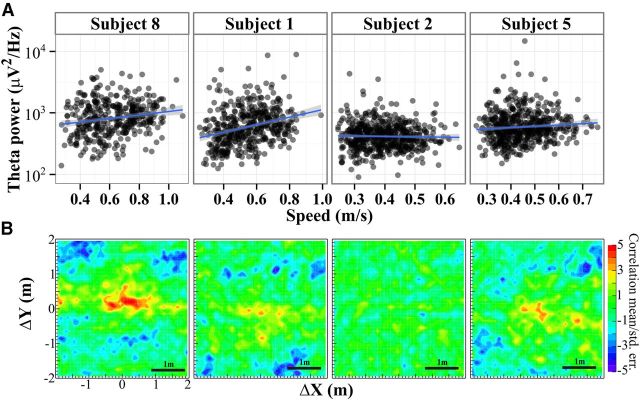
Speed during walking related to θ and space. A, The θ power over walking intervals of at least 1 s was estimated for all walking intervals on day 1. Each point corresponds to one walking interval for the subject. The line shows the least-squares line (SE shaded) for log power versus speed. θ power increases with walking speed. B, The autocorrelation calculation was used to estimate the spatial dependency of speed. Unlike θ (Fig. 4, right column), these have a strong peak at the center, indicating that, when subjects were at the same spatial location (0,0 in relative space), they tended to be moving at the same speeds. Negative correlations are observed at distances equal to about half the average distance across the room, reflecting the fact that individuals sped up and then slowed down during typical trajectories.

Speed correlates with θ power but not spatial maps

Figure 6A shows the dependence of θ power on speed for the same four subjects in Figure 4 all from day 1 data. Each point represents a walking interval in which speed was >0.2 m/s for at least 1 s. Subjects had an average of 79 ± 3 (mean ± SE) walking intervals per block. There was a significant correlation between θ power, and speed in 10 of 13 subjects over the whole interval (p < 0.05) and an LMM showed that the θ power was better modeled with speed as a factor (χ²₍₁₎ = 12.35, p = 0.00044). This relationship also held when the walking trajectories were broken up into 1 s intervals to estimate a more “instantaneous” power versus speed relationship: 11 of 13 showed significant correlation (p < 0.05) and the LMM was significant (χ²₍₁₎ = 11.57, p = 0.0007). Thus, θ power increased significantly with speed.

Figure 6B shows the spatial autocorrelation of the speed. This was calculated in exactly the same way as those for the scalp electrode data (Fig. 4, second column). Interestingly, these do show some structure with a peak near the center. In relative space, the center of the autocorrelation maps corresponds to returning to exactly the same point in absolute space. Thus, the peak near (0,0) in Figure 6B indicated that subjects tended to walk at the same speed when they returned to the same spot. This is consistent with subjects slowing down to approach objects and walking faster near the center of the room. The autocorrelation was slightly extended in the x-direction because the room was also extended in that direction. Thus, subjects approached (and stopped/started at) bubbles with more variability in the x-direction than the y-direction simply because there was more room in x than y. Negative correlations are observed at distances equal to about half the average distance across the room, reflecting the fact that individuals sped up and then slowed down during typical trajectories. These speed autocorrelation maps were completely unrelated to the θ maps, both qualitatively (i.e., the maps in Figure 6B were from the same data as those in Figure 4, right column) and quantitatively. Comparing the two maps from electrode data and speed data pixel by pixel within each subject and block, there was almost no correlation (mean p = 0.60, unadjusted; 1/77 unadjusted p <0.05; and mean ± SD, r = 0.0005 ± 0.002). Thus, the speed autocorrelation did not drive the electrode results. Furthermore, the memory on day 2 was not predicted by the speed map strength (r = 0.28, p = 0.36, Spearman), and thus did not explain the observed correlation between memory on day 2 and electrode map strength on day 1 described below.

Strength of θ autocorrelations predicts subsequent memory

As noted, synchronization at the θ frequency is thought to coordinate the hippocampal-parietal network activity underlying spatial mapping and to promote lasting synaptic modifications underlying map retention. We therefore asked whether the strength of the relationship between θ and spatial location predicted subsequent memory for the environment. Indeed, one of the most striking aspects of the autocorrelograms was that they varied from subject to subject; for example, Subject 8 in Figure 4 showed more structure in the form of regions of red and blue than did Subject 5. The greater the variation in the autocorrelations across spatial displacements, the greater was the structure in the map, as quantified by map strength (variance of each pixel in the autocorrelation map). The map strength for individual subjects on day 1 significantly predicted the subjects' percentage correct identifications on day 2 (r = 0.61, p = 0.027, Spearman test; Fig. 7B). The map strength was calculated identically for the Pz data on day 2, during the recall phase of the test, and these showed no correlation with the results of the memory test (r = 0.099, p = 0.75, Spearman test; data not shown). Thus, the unsupervised learning stage of the experiment on day 1 was the most important for developing spatial awareness for reliable object-location memory. In summary, not only were the observed autocorrelations significant, but they also predicted the subsequent memory performance of the subjects, consistent with the hypothesis that spatial maps contribute to memory performance.

Eye movements

One source of potential confound present in EEG studies is eye movements (Jung et al., 2000). To test whether eye movements were driving the spatial autocorrelations, the same autocorrelation analysis was run on an EOG electrode above the right eye. EOG detects changes in the electric field around the eye mostly resulting from eye movements and blinks. The results did show autocorrelations of similar overall strength to the Pz results; however, and most importantly, the eye movement correlations showed the same strength when swapped across subjects (p = 0.48, Kolmogorov–Smirnov test; Fig. 8A), indicating that their associated autocorrelations were artifacts of the signal itself, and not unique to the subjects. The width of the autocorrelation histograms in Figure 8A was the same regardless of swapping (t = −1.5, df = 479240.5, p = 0.13, t test). The eye movements were dominated by relatively few large deflections (Fig. 3A) that appeared as strong, punctate events in the Haar transformed signal. As the swaps of the eye movement data showed, punctate events are capable of swamping the autocorrelation regardless of where or when they occur because they are significant outliers that dominate the correlation. Also, the map strength calculated from the eye movements on day 1 did not predict the percentage correct on day 2 (r = 0.18, p = 0.55, Spearman test; Fig. 8B). Thus, we conclude that the eye movements did not produce the structure in the spatial autocorrelations.

Figure 8.

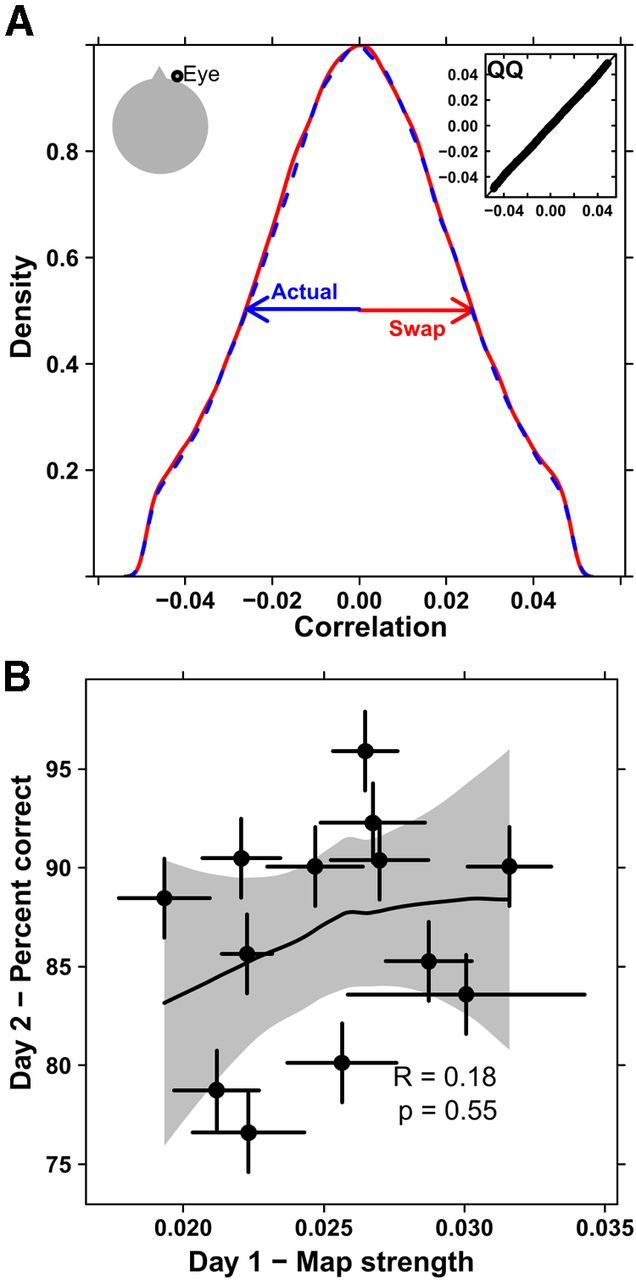
Data from an electrode placed above the right eye. A, The autocorrelation value was calculated for the actual subjects' data (blue, dashed) and swaps of eye movements and position across subjects (red, solid). There is no apparent change in the distribution of autocorrelations (p = 0.48, Kolmogorov–Smirnov test). Inset, A quantile-quantile plot with points falling on the 45 degree line, again indicating no difference between the two distributions. B, The percentage of correctly remembered responses on day 2 is uncorrelated with the map strength (SD of the autocorrelations) and shows no significant relation (r = 0.18, p = 0.55, Spearman). Error bars represent SEs across blocks. The shaded region represents an estimated 95% confidence interval.

Autocorrelograms show θ specificity and suggest parietal localization

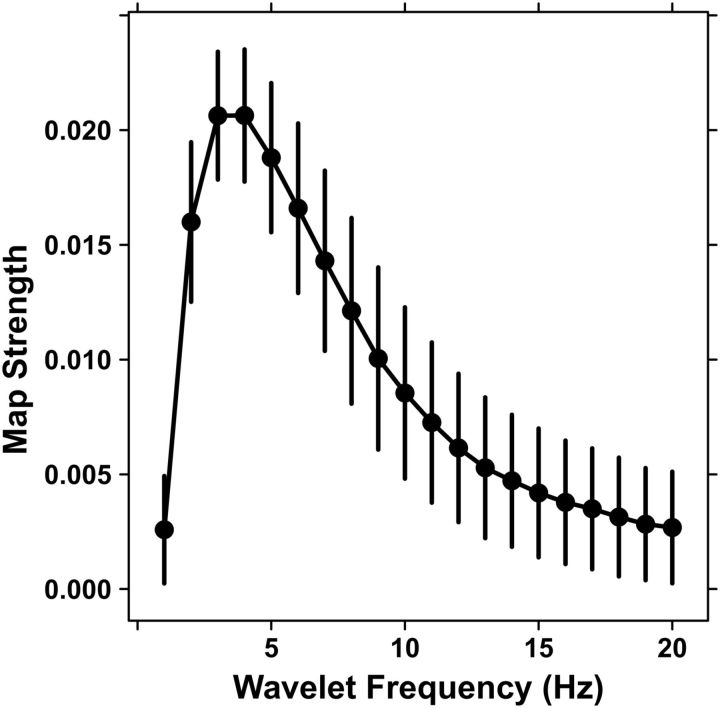
To examine the specificity of the autocorrelograms to the θ band, we recalculated the autocorrelograms for all subjects using the same procedure, but using wavelets at varying frequencies. With this larger number of points, the swapping procedure was impractical, so we estimated the baseline by replacing the wavelet of each subject at each frequency with a corresponding sine wave at the same frequency, as in Figure 5A2. This procedure gave a similar estimate of the baseline-expected correlation at 6 Hz where the bootstrap reference was available (∼0.006 for sine vs ∼0.005 for bootstrap); however, it had a larger associated random error because we combined the local error (from rebinning) for both the sine and actual data, and those values were similar as expected. Figure 9 shows that there was a peak in the map strength above baseline at 4 Hz and extending from 2 to 8 Hz (p < 0.05, Holm corrected for family-wise error), consistent with high δ and θ activity.

Figure 9.

Frequency localization. The map strength of the autocorrelograms was measured with wavelets at frequencies from 1 to 20 Hz for all subjects and compared with a sine wave baseline at the same frequency. Error bars combine SEs across all subjects and blocks with the error estimated for the baseline and the signal itself. The peak activity over ∼2–8 Hz is consistent with θ activity.

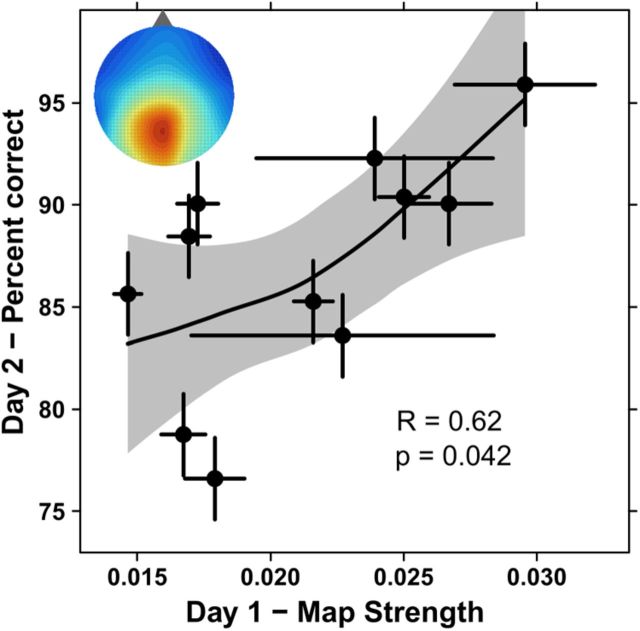
We also tested whether the ICA components, which were estimated to arise in the parietal cortex (Fig. 3B,C), contributed to the spatial autocorrelation. Like the map strength calculated from the Pz signal, map strength from these ICA components on day 1 was correlated with the fraction correctly remembered on day 2 (r = 0.62 p = 0.042, Spearman test, Fig. 10). Thus, the ICA analysis supported the spatial autocorrelation signal from Pz, its apparent generation in parietal cortex, and its prediction of subsequent memory for the environment.

Figure 10.

Parietal localization. The correlation of behavior with the map strength from the ICs by subject is maintained (r = 0.62, p = 0.042, Spearman) as in the result from Pz alone (Fig. 6B). Inset, Topography of the parietal activity during walking (compare Fig. 3B). Error bars represent SEs across blocks, and the shaded region represents an estimated 95% confidence interval.

Discussion

In the current study, we searched for cortical field potentials associated with spatial maps by recording EEG over the parietal lobe while subjects freely walked about and interacted with a simulated environment. θ was consistent across separate traversals of a given separation, and the signal from both a midline posterior parietal electrode and source activity estimated to medial, posterior parietal cortex showed significant spatial autocorrelation. Similar analyses performed on an EOG channel, used to measure eye movements, showed no significant spatial autocorrelations, ruling out eye movements as the source of the structure seen in the autocorrelograms. Moreover, projecting the EEG from one subject onto another subject's path also destroyed the spatial autocorrelation. The spatial maps were most strongly generated in the low frequency range (2–8 Hz). Importantly, the strength of the spatial maps during naive exploration significantly correlated with future memory of the spatial configuration of the objects. Subjects who had higher map strengths during exploration subsequently were better able to recognize subtle changes in the environment. θ was also correlated with walking speed, but this correlation did not explain the spatial displacement autocorrelation or predict subsequent memory.

Spatial maps in rodents, primates, and humans

The spatial correlates of θ described here in humans may be related to the spatial maps in rodents. Such maps represent space using a manifold of rapidly interacting maps formed in the hippocampus and associated temporal cortex, and extending into parietal and frontal areas (Derdikman and Moser, 2010). In rats, these internal maps are constructed using cells in the extended hippocampus (Derdikman and Moser, 2010) that fire (1) at particular locations (“place cells”) (O'Keefe et al., 1998), (2) the vertices of hexagonal grids that cover space (Hafting et al., 2005), (3) the edges of the environment (Solstad et al., 2008), or (4) head direction (Sargolini et al., 2006). Additionally, speed is a strong determinant θ power (McFarland et al., 1975) and frequency (Sławińska and Kasicki, 1998) in the rat hippocampus, and that speed-theta relationship has been observed in humans (Watrous et al., 2011).

Of particular relevance to the current study, neurons in posterior parietal cortex, a region that is strongly interconnected with the hippocampus and allied areas, are tuned to the animal's location along a given spatial route (Nitz, 2006). In primates, the parietal lobes subsume extensive spatial functions, including representation of 3D space, spatial exploration, and navigation (Andersen et al., 1985; Todd and Marois, 2004; Save et al., 2005; Sato et al., 2010). Moreover, hippocampal θ oscillations have been shown to entrain neurons in both prefrontal cortex and parietal cortex in the rat (Sirota et al., 2008). Furthermore, parietal cortex itself may be critical for establishing map-like representations when these representations must be based on the spatial arrangement of objects in an animal's navigational space (Save et al., 1992; Save and Poucet, 2000).

Although there have been few neural recordings in primates exploring their environments, a recent study demonstrated that a large proportion of neurons in the medial parietal region of monkeys are activated depending on their location in a simulated environment (Sato et al., 2010). Place-responsive neurons have also been recorded in the human hippocampus of epileptic patients performing simulated movements in virtual environments (Ekstrom et al., 2003). Moreover, neurons with spatially periodic firing fields (grid cells) have been recorded in monkey and human entorhinal cortex (Killian et al., 2012; Jacobs et al., 2013), and in human medial parietal cortex (posterior cingulate) (Jacobs et al., 2013). In addition, humans navigating a simulated environment produced specific macroscopic fMRI signals in different areas of cortex, including entorhinal cortex and medial parietal regions predicted from the coordinated activities of grid cells in rats exploring a real world space (Doeller et al., 2010; Kaplan et al., 2012). Indeed, both hippocampus and medial and lateral posterior parietal cortices increased their activity during simulated movement initiation when subjects began navigating to locate objects, and θ power, peaking at 5 Hz, also transiently increased during this period (Kaplan et al., 2012).

EEG studies also have revealed parietal cortices to be important nodes in brain networks associated with spatial navigation. White et al. (2012) found medial temporal-parietal activity to specifically be associated with navigational processes. Likewise, using a virtual tunnel spatial orientation task, Gramann et al. (2010) found that subjects who used an allocentric coding strategy showed increased EEG activations in inferior and medial parietal cortices (as well as in the occipital-temporal region). Collectively, these studies suggest that in humans, as in other mammals, spatial maps are rapidly constructed in the hippocampal-parietal system upon encountering novel, complex environments.

θ oscillations and memory

We found that the spatial autocorrelation map strength was greatest when calculated with wavelets ranging from 2 to 8 Hz, having an absolute peak at 3–4 Hz. Thus, δ/θ frequencies were more tightly locked to spatial displacements than were higher frequencies. This finding is consistent with the previously described role of θ in working memory processes (Sauseng et al., 2010). θ power during implicit learning predicts later retrieval success (Klimesch et al., 1996), increases with increasing memory load (e.g., Gevins et al., 1997; Jensen and Tesche, 2002), and may subserve memory encoding and retrieval (Klimesch et al., 1996, 2001). Moreover, θ oscillations in EEG are sensitive to spatial navigation and to individual differences in spatial (Baker and Holroyd, 2013) and navigational ability (White et al., 2012).

The autocorrelation maps reported here do not exhibit the highly symmetric structure evident in spatial maps found in single units of the entorhinal cortex of rats recorded during free exploration (Hafting et al., 2005), and we are not proposing that our scalp EEG findings represent such single-unit activity. Indeed, scalp EEG reflects the activity of large numbers of cells and is subject to spatiotemporal cancellation and smearing by the CSF, skull, and scalp intervening between cortex and electrode. Nonetheless, θ phase modulates high γ activity, which in turn is correlated with cell firing (Canolty et al., 2006; Whittingstall and Logothetis, 2009; Lachaux et al., 2012). The precise mechanism underlying the findings reported in the present paper will need to be uncovered through simultaneous recordings of surface EEG, neural firing, and LFP.

Individual variation in spatial maps and memory

Construction of spatial maps has been hypothesized not only to facilitate subsequent navigation in an environment but also to help associate particular elements with particular places (McNaughton et al., 2006). As with hippocampal place cells, entorhinal grid cell firing is in phase with the local θ rhythm (Hafting et al., 2008); and when θ is disrupted by medial septum inactivation, entorhinal grid cells are disrupted (Koenig et al., 2011) and memory is impaired (Winson, 1978). Moreover, phase-precession between spatial firing and local θ provides a mechanism whereby the same circuit can be used for memory encoding and retrieval (Burgess and O'Keefe, 2011). θ has also been associated with episodic recall in humans, but the mechanism of its involvement remains obscure (Nyhus and Curran, 2010), and θ power during learning may predict future memory performance (Gevins and Smith, 2000).

Consistent with these previous findings, we found that map strength predicted subsequent memory, posing several questions to be addressed in future investigations. One is examining the influence of proximal cues (i.e., particular objects in consistent locations) versus distal cues (i.e., the walls and general layout of the room) in generating the structure in the autocorrelations. Different subjects may have preferentially based their spatial encoding on proximal versus distal cues, and this might explain some of the variation in the strength of their spatial maps. Further experiments are needed to distinguish the relative importance of these different encoding strategies in the generation of the structure in the spatial autocorrelations. Notwithstanding these remaining questions, the results described here constitute the first evidence that correlations between θ and spatial location exist in humans and are related to the strength of memory encoding. These results strongly suggest that the θ-space relationships embedded in the EEG reflect modifications to large cortical ensembles that contribute importantly to higher-order cognitive operations.