Synaptic Input Correlations Leading to Membrane Potential Decorrelation of Spontaneous Activity in Cortex

Abstract

Correlations in the spiking activity of neurons have been found in many regions of the cortex under multiple experimental conditions and are postulated to have important consequences for neural population coding. While there is a large body of extracellular data reporting correlations of various strengths, the subthreshold events underlying the origin and magnitude of signal-independent correlations (called noise or spike count correlations) are unknown. Here we investigate, using intracellular recordings, how synaptic input correlations from shared presynaptic neurons translate into membrane potential and spike-output correlations. Using a pharmacologically activated thalamocortical slice preparation, we perform simultaneous recordings from pairs of layer IV neurons in the auditory cortex of mice and measure synaptic potentials/currents, membrane potentials, and spiking outputs. We calculate cross-correlations between excitatory and inhibitory inputs to investigate correlations emerging from the network. We furthermore evaluate membrane potential correlations near resting potential to study how excitation and inhibition combine and affect spike-output correlations. We demonstrate directly that excitation is correlated with inhibition thereby partially canceling each other and resulting in weak membrane potential and spiking correlations between neurons. Our data suggest that cortical networks are set up to partially cancel correlations emerging from the connections between neurons. This active decorrelation is achieved because excitation and inhibition closely track each other. Our results suggest that the numerous shared presynaptic inputs do not automatically lead to increased spiking correlations.

Introduction

The origin and the magnitude of correlations in cortical spiking activity remains controversial. Extracellular recordings report correlations in the range from 0.01 to 0.26 during cognitive tasks in visual and motor areas (Cohen and Kohn, 2011). Recent studies report very weak correlations in cortical input layers challenging the notion that correlations are abundant and particularly strong between nearby neurons with similar receptive fields (Ecker et al., 2010; Hansen et al., 2012; Smith et al., 2013). Similarly, low average correlations have been recorded extracellularly in the auditory cortex of anesthetized rats and analytically shown to emerge from active decorrelation in tightly coupled networks (Renart et al., 2010). Determining the intracellular signature of correlations in synaptic inputs and membrane potentials would clarify apparently contradictory results from extracellular recordings of spiking activity.

Spike count correlations quantify correlated variability between neurons (in contrast to signal correlations, which describe similar response pattern). Spike count correlations can emerge from shared presynaptic inputs, global activity modulations (Sanchez-Vives and McCormick, 2000; Renart et al., 2010), and factors that influence the neuron's mean response but are not known to the experimenter (Roelfsema et al., 2004; Cohen and Newsome, 2008; Nienborg and Cumming, 2009). Here, we focus on correlations that potentially emerge from shared presynaptic inputs (Shadlen and Newsome, 1998; Bair et al., 2001).

Recent theoretical studies of cortical networks show that shared presynaptic inputs do not necessarily lead to correlated firing (Hertz, 2010; Renart et al., 2010; Ly et al., 2012; Middleton et al., 2012; Tetzlaff et al., 2012). A network with fixed connection probability and sufficiently strong connections to enable a small fraction of excitatory inputs to evoke an action potential can actively decorrelate spikes (Renart et al., 2010). This occurs because spontaneous excitatory and inhibitory activities covary so that the highly correlated excitatory and inhibitory inputs in essence summate and cancel each other. There, an important prediction is that the excitatory (E) and inhibitory (I) inputs between neighboring neurons are correlated and together produce weakly correlated membrane potential correlations near resting potential (V_r) (Renart et al., 2010). This effect requires fast inhibitory feedback to ensure a short time lag between excitation and inhibition.

Recordings in vivo show positive correlations of the subthreshold membrane potential during quiet wakefulness and whisking (Poulet and Petersen, 2008), and in lightly anesthetized animals during spontaneous and sensory-evoked activity (Lampl and Reichova, 1999; Okun and Lampl, 2008). Importantly, E and I synaptic potentials are negatively correlated (Okun and Lampl, 2008). Similarly, in vitro experiments report instantaneous membrane potential correlations (Silberberg et al., 2004), instantaneous excitatory input current correlations (Ikegaya et al., 2004), and EPSP as well as IPSP correlations (Hasenstaub et al., 2005). How correlated synaptic inputs combine and shape membrane potential and spiking correlations between pairs of neurons has not been addressed experimentally.

Here, we examine, through intracellular recordings of synaptic inputs and membrane potentials, the extent to which the auditory cortex complies with the conditions required for active decorrelation. Unlike in simulations, the in vitro preparation involves a variety of cell types with different intrinsic properties, heterogeneous synaptic connection footprints, different temporal dynamics for synaptic transmission, and different short-term synaptic depression/facilitation (Oswald et al. 2009; Oswald and Reyes, 2011; Levy and Reyes, 2012). We performed simultaneous recordings from pairs of neurons in the auditory cortex of mice in activated thalamocortical slices. As predicted, excitation and inhibition are correlated and combine to decorrelate the membrane potential to produce weak spiking correlations. Moreover, we show that the delay between excitation and inhibition is short and activity dependent, consistent with the theory of decorrelation in a strongly coupled network.

Materials and Methods

Slice preparation.

Acute thalamocortical slices from postnatal day 11–22 of Swiss Webster or G42 mice of either sex were prepared as described in Cruikshank et al. (2002) and in accordance with guidelines of the New York University Animal Welfare Committee. Mice were anesthetized with halothane and decapitated. The brain was removed and two coronal cuts were made to remove the anterior 25% of the brain and the cerebellum. The brain was then removed from the skull and immersed in ice-cold (0–4°C) standard artificial CSF (ACSF) containing the following (in mm): 125 NaCl, 25 NaHCO₃, 25 glucose, 2.5 KCl, 1.25 NaH₂PO₄, 2 CaCl₂, and 1 MgCl₂) bubbled with 95% O₂ and 5% CO₂. Slices with 300 μm thickness were cut at a 15° angle from the horizontal plane using a vibratome (Campden Instruments). Recordings were made from the “primary” slice (Cruikshank et al., 2002), chosen based on distance from the ventral surface and visual inspection. The primary slice contains intact projections from the ventral division of medial geniculate nucleus (MGv) to the primary auditory cortex (Cruikshank et al., 2002). Slices were maintained in standard ACSF at 37°C for 30 min and subsequently at room temperature (20–22°C) until transferred to the recording chamber.

Electrophysiology.

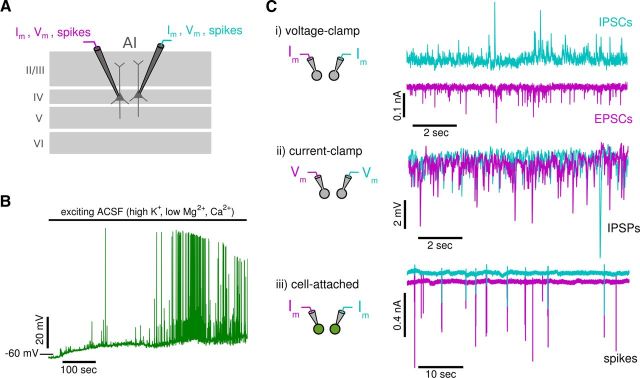
Recordings were from pyramidal neurons in layer IV in the primary auditory cortex identified electrophysiologically and morphologically with the aid of infrared differential interference contrast microscopy (Olympus; Stuart et al., 1993, see Fig. 1A). To increase activity, slices were perfused at 29–33°C with ACSF (termed exciting ACSF) modified to contain high potassium, low calcium, and low magnesium concentrations (6.25 mm KCl, 1.5 mm CaCl₂, and 0.5 mm MgCl₂ instead of 2.5 mm, 2 mm, and 1 mm; Silberberg et al., 2004; Neubauer and Berger, 2008). Perfusion of the exciting ACSF depolarizes the membrane and induces spontaneous activity (Fig. 1B). Induced firing rates range between 0 and 2 spikes per second and show a large variability in interspike intervals (coefficient of variations between 0 and 10; see Fig. 7).

Figure 1.

Recordings from pairs of neurons. A, Schematic of paired recordings of spiking and subthreshold activities from pyramidal neurons in layer IV of the primary auditory cortex. B, Perfusion with exciting ACSF depolarizes neurons and induces spontaneous activity (see Materials and Methods). Top bar marks application of exciting ACSF. C, The experimental protocol consists of three types of paired recordings: (i) input currents recorded in voltage-clamp mode (shown for IPSCs and EPSCs), (ii) subthreshold membrane potentials recorded in current-clamp mode (shown for IPSPs), and (iii) the trans-membrane currents associated with spikes recorded in cell-attached mode (large inward currents indicate spikes). All recordings (except in B) are done with voltage-clamp internal solution to block action potentials and improve space clamp (see Materials and Methods).

Figure 7.

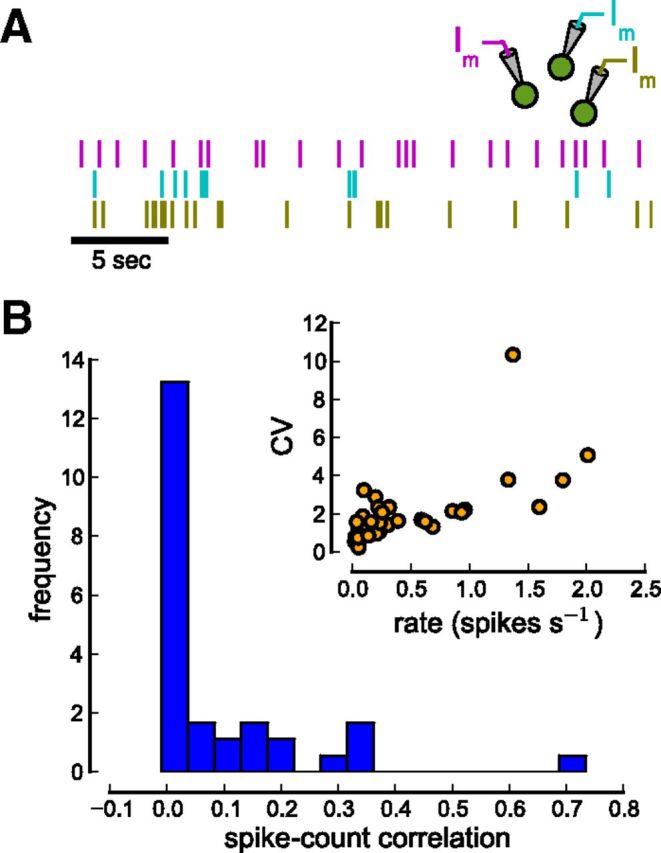
Spike count correlations between neurons. A, Spike output of cells is recorded in cell-attached mode. The raster plot shows the spiking of three simultaneously recorded cells. B, Distribution of spike count correlation coefficients. The histogram is plotted for the spike count window T = 50 ms (N_pairs = 39). The inset shows firing rate and CV for all individual cells. Recorded cells fire at low discharge rates (mean firing rate 0.517 ± 0.541 spikes per second) and firing is very irregular (mean CV 2.12 ± 1.88).

Electrodes, pulled from borosilicate pipettes (1.5 OD) on a Flaming/Brown micropipette puller (Sutter Instruments), had resistances in the range of 5–10 MΩ when filled with 100 mm Cs-gluconate, 20 mm KCl, 4 mm ATP-Mg, 10 mm phosphocreatine, 0.3 mm GTP, 10 mm HEPES, and 5 mm QX-314, pH 7.3 (chemicals from Sigma). Note that the internal solution contained cesium to improve space clamp and QX-314 to block sodium channels. Control experiments, where spiking was not blocked, were performed with the same internal solution except that K-gluconate was substituted for Cs-gluconate and QX-314 was omitted (Fig. 1B).

Simultaneous whole-cell voltage-clamp, current-clamp, and cell-attached recordings were made from up to four neurons using BVC-700A amplifiers (Dagan), digitized at 10 kHz using an ITC-18 interface (Instrutech). Data were stored on a computer using Igor software (WaveMetrics) in combination with the NeuroMatic package (http://www.neuromatic.thinkrandom.com/).

Data analysis.

Using the records obtained from each neuron pair, we calculated the correlations in continuous variables such as the membrane potential and synaptic currents, as well as in the discrete spiking activities.

The normalized cross-correlation of two continuous variables, x(t) and y(t), was calculated according to the following:

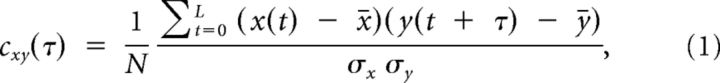where the sum runs over the total recording time, L, at steps of size dt. σ_x and σ_y are the SDs, and x̄ and ȳ are the means of both variables. The SDs in the denominator normalize the cross-correlation. Thus, c_xy(τ) for two identical signals (or scaled versions of one another) will have a value of 1 at zero time lag. Nonidentical traces result in values between −1 and 1 indicating negative and positive correlations, respectively (Lampl and Reichova, 1999; Silberberg et al., 2004; Renart et al., 2010). Note that c_xy at zero time lag, τ = 0, is identical to the Pearson product-moment correlation coefficient, which is a measure of the instantaneous correlation between both variables.

Recorded membrane potentials and synaptic currents are nonstationary and fluctuate over a wide range of timescales. Changes in the overall excitability of the local circuit and/or slow electrode drift can result in changes over long timescales (tens to hundreds of milliseconds), which would distort the correlation measures. These distortions were suppressed using detrending of the continuous variables. For detrending, we performed x′(t) = x(t) − ({x(t)}_t-w/2,t+w/2 − <x>_L), were x′(t) is the detrended data point at time t, x(t) is the raw data point at time t, <x>_L is the average of the whole recording of length L, and {x(t)}_t-w/2,t+w/2 is the median of a window of width w = 3 s centered at each data point.

We separated epochs of low- and high-amplitude activity in our recordings by searching for excursions that exceeded the overall detrended recording average by 5 mV in current-clamp recordings or 0.15 nA in voltage-clamp recordings (see text). All excursions including 100 ms before and 200 ms after the threshold crossing were removed from the trace and the cross-correlation (Eq. 1) was calculated for the remaining trace (termed low-amplitude correlations). The excluded excursions were stacked and the cross-correlation was calculated (termed high-amplitude correlations). Low-amplitude voltage traces where not included in the analysis if they were interrupted by >60 high-amplitude excursions during a 5 min recording and if the total length fell <200 s to increase the reliability of the cross-correlation. Note that this thresholding was performed after detrending.

We extracted estimates of individual postsynaptic potential (PSP) amplitudes by considering the difference between maxima and minima of the membrane potential recording. First, we smoothed the raw traces and the first derivative of the membrane potential recordings using a symmetric Savitzky–Golay filter with a third-order polynomial and a window size of four data points. We then identified the location of maxima and minima through the negative and positive slope zero-crossings of the smoothed first derivative, respectively. EPSP amplitudes were estimated as the difference between the maxima and the minima of the smoothed membrane potential for recordings at −80 mV. IPSP amplitudes were calculated as the difference between the minima and the maxima for recordings at 0 mV. We identified the onset of high-amplitude epochs through PSP amplitudes larger than 15 mV that were preceded by PSPs < 15 mV for at least 600 ms (see Fig. 4C). Our amplitude analysis only considers PSP larger than 0.4 mV to limit the impact of noise.

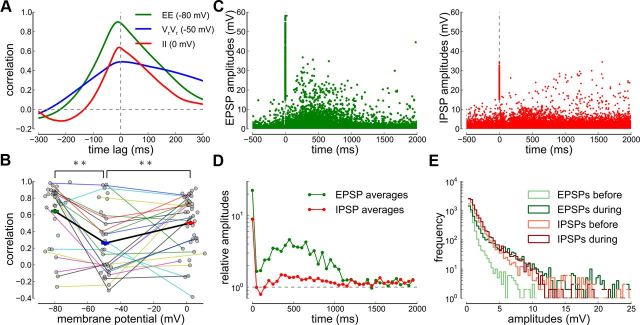
Figure 4.

Correlations and EPSP/IPSP amplitude dynamics during high-amplitude epochs. A, Cross-correlograms during high-amplitude epochs at three different holding potentials. The cross-correlations are shown for IPSPs (II, red, recorded at 0 mV), resting membrane potentials (V_rV_r, blue, recorded at −50 mV), and EPSPs (EE, green, recorded at −80 mV) of one example cell pair. B, Pearson correlation coefficients versus average membrane potential during high-amplitude epochs for all neuron pairs. Recordings from the same cell pair are connected. The average EE, V_rV_r, and II correlations are marked by green, blue, and red bars (mean ± SEM) connected by the thick black line. C, EPSP and IPSP amplitudes before and during high-amplitude epochs. Individual EPSP (left) and IPSP (right) amplitudes are aligned with respect to the onset of a high-amplitude epoch (see Materials and Methods). Data from all recordings are overlaid. D, Relative EPSP and IPSP amplitudes during high-amplitude epochs. Average EPSP (green) and IPSP (red) amplitudes in 50 ms bins during the high-amplitude epoch (onset at t = 0 ms) with respect to the average EPSP and IPSP amplitude during the 5 s before the high-amplitude epoch. E, EPSP and IPSP amplitude histograms before and during high-amplitude epochs. Amplitudes during the high-amplitude epoch include EPSP/IPSP occurring during the (0, 1000) ms interval from onset.

Spiking correlations were quantified using the standard expression for the spike count correlation coefficient of the activities of two cells i and j as follows:

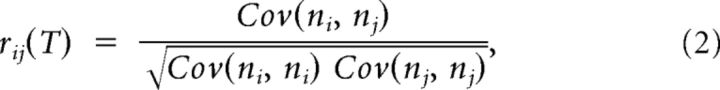where Cov(n_i, n_j) is the covariance between the activity of two cells Cov(n_i, n_j) = 〈(n_i(t) − v_i)(n_j(t) − v_j)〉 = $\frac{1}{L}{\displaystyle {\sum }_{t=0}^L\left(n_i\left(t\right)-v_i\right)\left(n_j\left(t\right)-v_j\right)}$. n_i(t) and n_j(t) are the convolutions of the spike trains of neuron i and j with a normalized square kernel of length T. T defines the timescale of the correlations quantified by r_ij(T) and values between T = 10 and 300 ms are considered here. The mean firing rate of neuron i is defined as the average of n_i(t) over its whole length of the recording L, i.e., ν_i = <n_i(t)>_L. r_ij(T) measures the degree to which fluctuations in the activity of the two cells (at temporal resolution T), measured with respect to their temporal average across the whole duration of the spike trains, are predictive of each other.

Significance levels are marked as follows throughout the manuscript: *p < 0.05 and **p < 0.01.

Recurrent network simulations and spatially extended neurons.

Simulations were performed using a conductance-based integrate-and-fire network (Renart et al., 2010). Briefly, the network is composed of excitatory (N_E = 4000), inhibitory (N_I = 1000), and external (N_X = 4000) neurons. The membrane potential V_i^∝ of the ith neuron (i = 1, …, N_α) from population α = E, I evolves according to the following:

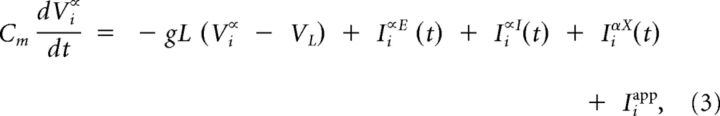where C_m = 0.25 nF is the membrane capacitance, g_L = 16.7 nS is the leak conductance (membrane time constant C_m/g_L = 15 ms), V_L = −70 mV is the resting potential, and θ = −50 mV is the firing threshold. After a spike, V_i^∝ was reset to V_L during an absolute refractory period of 2 and 1 ms for E and I cells, respectively.

The synaptic input currents to neuron i, I_i^αβ(β = E, I, X), are given by the product of a conductance change (time course given by the difference of two exponentials) and the driving force, determined by the reversal potential of V_rev = 0 mV for excitatory inputs (from E and external populations) and V_rev = −80 mV for inhibitory inputs. Cell j in population β = E, I, X is connected with cell i in population α = E, I with a probability of p = 0.2. The injected current, I_app, was adjusted to isolate EPSPs (at −80 mV), IPSPs (at 0 mV), or a combination of both at intermediate potentials. Neurons in the external network fire with Poisson statistics with a constant rate of 2.5 spikes per second (Renart et al., 2010).

Compartmental neuron model.

The “ball-and-stick” neuron model used to simulate spatially extended neurons consisted of a cylindrical soma compartment (soma diameter d_s = 85.5 μm, length l_s = 85.5 μm), connected to a linear chain of 12 cylindrical dendritic compartments for a total length of 600 μm (compartment diameter is d_d = 1.5 μm, compartment length is l_d = 50 μm). The membrane capacitance is 1 μF · cm⁻², the leak conductance is 0.0666 mS/cm², and the cytoplasmic resistance is R_i = 160 Ω · cm. The membrane time constant (15 ms) is the same as for the point neurons in the network simulation (see above). The space constant of the compartmental model is 0.6 mm and the electrotonic length of the dendritic compartments is 1.0 (length/space constant), which is a typical value to simulate large pyramidal cells. The membrane potential of each compartment is described by Equation 3, where the capacitance and the leak current are multiplied by the total area of the soma or each dendritic compartment plus two extra terms for the axial currents, (V_m^k−1 − V_m^k)/R_α^k−1 + (V_m^k+1 − V_m^k)/R_α^k. The axial resistance between dendritic compartments is given by R_a = 4l_dR_i/(πd_d²) and between the soma and the first dendritic compartment by R_a = 2l_dR_i/(πd_d²) + 2l_sR_i/(πd_s²). We adjusted the geometry of the soma and the dendrite such that the compartmental model exhibits the same input resistance as the point neurons in the recurrent network above. In other words, a step current injection of 0.5 nA at the soma produces a 30 mV depolarization in the point neuron and in the spatially extended neuron. Simulations of the recurrent network and the compartmental model were performed using the Python-based simulator BRIAN (Goodman and Brette, 2008).

Results

To characterize the correlations in the subthreshold and suprathreshold range, we performed simultaneous whole-cell patch-clamp recordings from two to four layer IV neurons in an in vitro thalamocortical slice preparation of the primary auditory cortex (Fig. 1). We measured (1) isolated EPSCs and IPSCs; (2) isolated EPSPs and IPSPs, and the composite EPSPs and IPSPs at membrane potentials near resting potential; and (3) spiking activities (Fig. 1C). To facilitate measurements of correlations, we increased spontaneous activity by bathing the slice in extracellular solution containing high potassium, low magnesium, and low calcium concentrations (Silberberg et al., 2004; Neubauer and Berger, 2008; Fig. 1B).

Correlated synaptic inputs to pairs of neurons

We recorded from two nearby (<200 μm) neurons and measured correlations in excitatory and inhibitory synaptic inputs. To isolate EPSPs or IPSPs, we held the membrane potentials at the reversal potentials of inhibitory (−80 mV) and excitatory inputs (0 mV), respectively. We then measured their combined effects on correlations by holding the membrane potentials near rest (approximately −50 mV).

Membrane potential recordings can be separated into epochs with low-amplitude PSPs and epochs with high-amplitude PSPs (Fig. 2). Low-amplitude PSPs occur irregularly in pairs of neighboring cells (Fig. 2A–C, lower right, orange bars), occasionally occurring synchronously (stars). In contrast, PSPs during high-amplitude epochs occur very synchronously (Fig. 2A–C, lower left, gray bars).

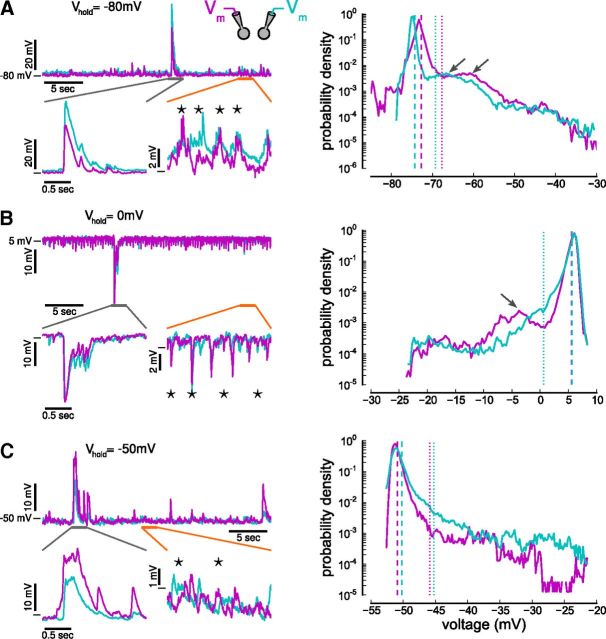
Figure 2.

Simultaneously recorded membrane potentials. A–C, Left, Simultaneous whole-cell current-clamp recordings from pairs of layer IV pyramidal cells both held at approximately −80, 0, and −50 mV. Holding cells at −80 mV reveal EPSPs (A), at 0 mV IPSPs (B), and at −50 mV a mixture of both (C). Note periods of low-amplitude (<5 mV) and high-amplitude (>5 mV) activity (orange and gray lines mark magnified regions of low- and high-amplitude epochs, respectively). During high-amplitude epochs, neurons receive highly correlated inputs. During low-amplitude epochs, neurons receive only occasional, simultaneous inputs (stars). A–C, Right, Voltage histograms from simultaneously recorded neurons at the three holding potentials. Secondary peaks in the histograms are marked by arrows. For convenience, membrane potentials that are >5 mV (dotted lines) above the mean (dashed lines) are classified as high-amplitude epochs (see text for more details).

Histograms of excitatory and inhibitory synaptic potentials and resting membrane potentials (Fig. 2A–C, right) have distinct peaks followed by a long tail, which may be accompanied by an additional, smaller peak at ∼10 mV above the histogram mean (Fig. 2A,B, right, arrows): these represent low- and high-amplitude epochs. The synchronous inputs during high-amplitude epochs produce prolonged depolarizations when recording EPSPs or hyperpolarizations when recording IPSPs. Such epochs give rise to a large skew of the membrane potential distribution (mean skew of membrane potentials recorded at −80 mV: 5.58, at −50 mV: 5.39, and at 0 mV: −4.42). Bimodality of the membrane potential has also been observed during UP and DOWN states in slow-wave sleep (Timofeev et al., 2001), in slices (Sanchez-Vives and McCormick, 2000), and in anesthetized (Lampl and Reichova, 1999; DeWeese and Zador, 2006) and awake animals (DeWeese and Zador, 2006; Hromádka et al., 2013). Similar to the brief UP states recorded in the auditory cortex in vivo (DeWeese and Zador, 2006; Hromádka et al., 2013), high-amplitude epochs occur rarely (mean rate of occurrence 0.11 ± 0.07 Hz) and nonperiodically (coefficient of variation of interepoch intervals 0.92 ± 0.45) in our preparation. The mean duration a high-amplitude epoch is 704 ± 535 ms (mean ± SD for all measures).

Initially, we confined analyses to low-amplitude epochs (high-amplitude epochs are examined separately below). From the bimodal membrane potential histogram, we designated membrane potential excursions smaller than a fixed amplitude of 5 mV to be low amplitude (see Materials and Methods). We then calculated the cross-correlation between membrane potential traces recorded in both cells at 0 mV, −80 mV, and −50 mV (Fig. 3A; shown for one example cell pair). The positive peaks at around zero time lag in the cross-correlograms of excitatory inputs, inhibitory inputs, and membrane potentials near rest (approximately −50 mV) indicate synchronous inputs to the pair of neurons (correlation 0.328 for EPSPs at zero time lag; correlation 0.372 of IPSPs; resting membrane potential correlation at −50 mV is 0.184; Fig. 3A). In this example, EPSPs and IPSPs both show stronger correlations than the membrane potential traces recorded near resting potential.

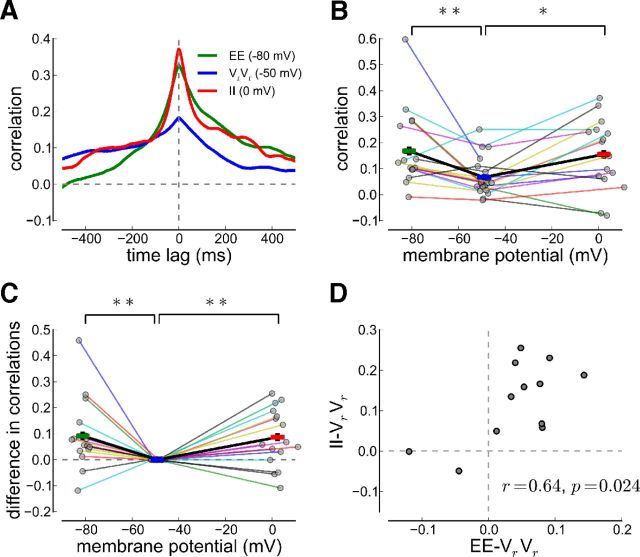
Figure 3.

Excitatory and inhibitory synaptic input and resting membrane potential correlations. A, Cross-correlograms at three different holding potentials. The voltage cross-correlogram is shown for one example cell pair. In all panels, correlations are shown for IPSPs (II, red, recorded at 0 mV), resting membrane potentials (V_rV_r, blue, recorded at −50 mV), and EPSPs (EE, green, recorded at −80 mV). B, Pearson correlation coefficients versus average membrane potential for recordings from cell pairs for which EE and/or II correlations have been measured together with resting membrane potentials correlations (N_EE = 17, N_VrVr = 21, N_II = 16). C, Same plot as in B but the correlations are shifted vertically such that the resting membrane potential correlations are equal to zero. EE (II) correlations are larger than V_rV_r correlations in most cell pairs (15 of 17 for EE, 12 of 16 for II). The average EE, V_rV_r, and II correlations are marked by green, blue, and red bars (mean ± SEM) connected by the thick black line. Recordings from the same neuron pair are connected by a thin, colored line in B and C. D, Difference in II correlations and resting membrane potential correlations versus difference in EE correlations and resting membrane potential correlations. All points represent neuron pairs for which correlations at all three membrane potentials have been recorded.

A difference in EPSP, IPSP, and resting membrane potential correlations is apparent for all recordings from individual neuron pairs. To avoid possible distortions in the population data, we included correlations only from neuron pairs where EE and/or II correlations have been measured together with resting membrane potential correlations (Fig. 3B, correlations from the same cell pair are connected; each point is connected by a line). The Pearson correlation coefficients (measured at zero time lag) of neuron pair recordings are distributed broadly for the EE and II correlations (Fig. 3B). Despite that variability, the correlation coefficients of both EPSPs (at −80 mV) and IPSPs (at 0 mV) are significantly larger than those of the resting membrane potential recordings (Fig. 3B; one-way ANOVA, EE vs V_rV_r: F = 7.93, p = 0.0078; II vs V_rV_r: F = 6.58, p = 0.015).

The reduction in correlations at resting membrane potential in the population data (above) is also present in individual neuron pairs. To visually assess the difference between EE/II and resting membrane potential correlations per neuron pair, we vertically shifted all correlation coefficients per neuron pair such that the resting membrane potential correlations are zero (Fig. 3C). The EE correlations are larger than resting membrane potential correlations in 15 of 17 cell pairs, and the II correlations are larger than resting membrane potential correlations in 12 of 16 cell pairs. The EE-V_rV_r and the II-V_rV_r correlation differences are significantly greater than zero for all neurons pairs (p = 0.0099 for EE-V_rV_r; p = 0.0068 for II-V_rV_r; Fig. 3C). Furthermore, there is a significant correlation between the EE-V_rV_r difference and the II-V_rV_r difference (r = 0.64 p = 0.024; Fig. 3D).

These data suggest that the vast majority of recorded cell pairs receive correlated EPSPs and IPSPs. In these cell pairs, the resting membrane potential correlations are significantly smaller, consistent with the hypothesis that correlated EPSPs and IPSPs cancel each other to reduce resting membrane potential correlations (Renart et al., 2010). Moreover, our analysis shows that the strength in excitatory input correlations correlates with the strength in inhibitory input correlations in each cell pair (Fig. 3D; see Discussion).

To ensure the measured correlations emerge from synaptic inputs, we blocked synaptic transmission by perfusion of a mixture containing the selective NMDA receptor antagonist d-AP5, AMPA and kainate receptor antagonist DNQX, and the GABA_A receptor antagonist bicuculline (data not shown). Correlations measured before drug application (mean EPSP correlations 0.25 ± 0.04, mean IPSP correlations 0.25 ± 0.03) were significantly reduced (EPSP correlations 0.01 ± 0.04; resting membrane potential correlations 0.03 ± 0.01; IPSP correlations 0.09 ± 0.08) after drug application and partially recovered after washout (EPSP correlations 0.13 ± 0.1; IPSP correlations 0.22 ± 0.12; resting membrane potential correlations 0.07 ± 0.08). The resting membrane potential correlations before synaptic block (0.09 ± 0.01) were significantly smaller than EPSP and IPSP correlations (EE and V_rV_r: F = 11.65, p = 0.0066; II and V_rV_r: F = 20.70, p = 0.0011). This demonstrates that the above measured correlations stem from synchronous synaptic inputs rather than some unspecific global sources of correlations.

Large amplitude events

We now turn to investigate input correlations and PSP amplitude dynamics during the high-amplitude epochs. In particular, we extract single EPSP and IPSP amplitudes before and during high-amplitude epochs and examine their relative time course.

The high degree of synchrony in excitatory inputs, inhibitory inputs, and membrane potentials at rest during high-amplitude epochs (Fig. 2, left column) is reflected in cross-correlograms with a large peak at zero time lag (shown for one example cell pair in Fig. 4A; EE correlations at zero time lag 0.888, V_rV_r correlations 0.489, II correlations 0.632).

The Pearson correlation coefficients of high-amplitude epochs from individual cell pairs are highly variable (Fig. 4B). However, the majority of pairs exhibit strong IPSP and EPSP correlations with values >0.5. Membrane potential correlations near resting potential are significantly reduced, due to summation of EPSPs and IPSPs and cancellation, but there is a considerable number of pairs (9 of 31) showing high correlations (>0.5) at resting potential (Fig. 4B).

To determine why cancellation of excitatory and inhibitory inputs is incomplete during high-amplitude epochs, we estimated individual EPSP and IPSP amplitudes from our recordings (see Materials and Methods) and followed their temporal evolution during the high-amplitude epochs (Fig. 4C,D). The onset of the high-amplitude epoch is marked by a large EPSP and IPSP followed by a short recovery period and a subsequent peak of high-amplitude inputs 500 ms after onset (Fig. 4C,D).

During the low-amplitude regime, the IPSP amplitudes were larger than EPSP amplitudes on average (Fig. 4E) and were, nevertheless, sufficient to weaken membrane potential correlations (Fig. 3). However, during the high-amplitude epochs, the amplitudes of the EPSPs increased more than those of the IPSPs (Fig. 4D,E). This suggests that, even though the EPSPs and IPSPs are highly correlated, the disproportionate increase in EPSP amplitude negates the cancellation effect of IPSPs, giving rise to strong correlations even at resting membrane potentials (Fig. 4B; see Discussion).

Inhibition tracks excitation with short delays

To further test whether weak membrane potential correlations at rest were due to cancellation between strongly correlated excitatory inputs and strongly correlated inhibitory inputs, we measured directly the correlations and the relative delays between excitatory inputs in one cell and inhibitory inputs in the other. To more precisely record the timing of synaptic inputs, we performed the recordings under voltage-clamp and measured EPSCs and IPSCs.

We held both cells at 0 mV to isolate inhibitory currents and at −80 mV to isolate excitatory currents. In addition, we directly measured correlations between excitatory currents in one cell and inhibitory currents in the other by holding one cell at −80 mV and the other at 0 mV, respectively (Fig. 5A). After removing high-amplitude excursions from the current traces (>0.15 nA, see above and Materials and Methods), we calculated the cross-correlations between the current traces (Fig. 5B). The EPSCs and the IPSCs were correlated as in the current-clamp experiments (maximal EE correlation 0.299, maximal II correlation 0.284 for the example cell pair shown in Fig. 5B).

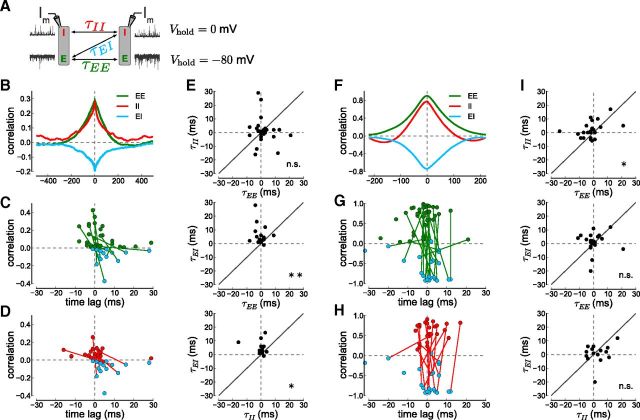
Figure 5.

Synaptic input current correlations and time lags. A, Schematic of experimental procedures for measuring delays between E and I inputs. Delays (τ_EE, τ_II, τ_EI) between cells are obtained from the cross-correlograms of excitatory, inhibitory, or combined excitatory–inhibitory inputs to both cells. B, Cross- correlograms of low-amplitude excitatory and inhibitory current inputs. EPSC correlations (EE, green, recorded at −80 mV), IPSC correlations (II, red, recorded at 0 mV), and EPSC with IPSC correlations (EI, light blue, recorded when holding one cell at −80 mV and the other at 0 mV) are shown for an example cell pair. C, Plot of correlations versus time lag. Each point shows the location and value of the maximal EE correlation (green) and minimal EI correlation (light blue) per recorded cell pair (N_cell-pairEE = 12, N_cell-pairEI = 15). Points from the same cell pair are connected, if both recordings exist. D, Similar to C but for II (red) and EI (light blue) correlations (N_cell-pairII = 32, N_cell-pairEI = 15). E, Input delays per cell pair. II versus EE delays (top), EI versus EE delays (middle), and EI versus II delays (bottom). Each point stems from a cell pair in which both correlations have been obtained and the points depict the time lag where the correlogram peaks. F–I, The right side shows the same analysis but for high-amplitude events (>0.15 nA; see Materials and Methods). F, The cross-correlograms shown for an example cell pair with high-amplitude epochs during the three recording conditions. G–I, Each point shows the maximum and location of the correlogram per cell pair (N_cell-pairEE = 39, N_cell-pairII = 25, N_cell-pairEI = 21).

An important theoretical prediction is that excitatory and inhibitory synaptic currents are directly correlated (Renart et al., 2010). Indeed, EPSCs in one cell are negatively correlated with IPSCs in the other cell (minimal EI correlation for the example cell pair in Fig. 5B, −0.196, light blue; average minimal EI correlations: −0.057 ± 0.015, N = 26). The negative peak in the cross-correlogram indicates that excitatory currents in one cell are synchronous with inhibitory currents in a neighboring cell. The peak is negative since excitatory and inhibitory currents have opposite signs (see Eq. 1). A negative deflection in the current trace (due to an EPSC) occurs nearly simultaneously (see below) with a positive deflection in the current trace of another cell (due to an IPSC), which by definition is a negative correlation.

The width of the cross-correlogram indicates that synchronous excitatory and inhibitory currents occur within a ±200 ms time window (Fig. 5B). To quantify the time delay between synchronous excitatory and inhibitory inputs (τ_EE, τ_II, τ_EI; Fig. 5A), we determined the magnitude and the location of the peak (for EE and II) or trough (for EI) of the cross-correlogram for individual cell pairs. A peak or trough at 0 ms indicates simultaneously occurring events while an off-center peak or trough indicates that inputs to one cell are consistently delayed with respect to inputs to another cell.

The EI correlogram peak location, τ_EI (Fig. 5C, light blue), is at more positive time lags than the EE correlogram peak, τ_EE (green), for individual cell pairs. Similarly, the EI correlogram peak location, τ_EI, is at more positive time lags than the II correlogram peak, τ_II (Fig. 5D, red). To further quantify the input delays on a cell pair by cell pair basis, we plotted the delays versus each other. Plotting τ_EI versus τ_EE (Fig. 5E, middle) or versus τ_II (bottom) shows that most points were above the unity line and we found that EE and II delays were significantly smaller than EI delays (τ_EE < τ_EI in 12 of 14; τ_II < τ_EI in 9 of 11 cell pairs). In contrast, there was no tendency in the plot of τ_II versus τ_EE indicating that excitatory and inhibitory inputs each arrive simultaneously in cell pairs (Fig. 5E, top; 8 of 23 were above the unity line).

High-amplitude epochs exhibit a tighter excitation–inhibition coupling

The presence of high-amplitude events (Fig. 2) may represent instances where inhibition temporarily fails to track excitation, resulting in strong correlations. Without the countering effects of inhibition, excitation would spread rapidly through the network (so-called runaway excitation). However, applying the correlation analysis to the high-amplitude excursions revealed that inhibition, though relatively smaller, actually tracks excitation with a shorter time delay than during to the low-amplitude epochs (Fig. 5F–I).

Large amplitude events were strongly synchronous across all cells (Figs. 2, 4B) as reflected in large measured correlations in synaptic input currents (EE peak correlation 0.903, II peak correlation 0.777, and EI trough correlation −0.739 for the example cell pair in Fig. 5F). In contrast to low-amplitude synaptic currents, the individual cell pair data indicate a more synchronous arrival of excitation and inhibition in nearby cells. There were no clear differences in the EE and EI time lags (Fig. 5G). The II and EI time lags were also similar in cell pairs for which both correlations were measured (Fig. 5H). The tighter coupling between excitation and inhibition is apparent when plotting τ_EI versus τ_EE (Fig. 5I, middle) and τ_EI versus τ_II (bottom). In contrast to the low-amplitude data, there is no significant trend of excitation leading inhibition (Fig. 5, compare E and I); instead, excitation and inhibition appear to occur with a shorter or no time lag.

Thus, the highly synchronous high-amplitude epochs do not arise from an increase in the time lag between excitation and inhibition. On the contrary, the temporal coupling between excitation and inhibition appears to be tighter during the high-amplitude epochs. A short-lasting excess in the magnitude of excitation not counterbalanced by inhibition gives rise to the high-amplitude epochs (Fig. 4C,D; see Discussion).

Underestimation of correlations by poor space clamp

Layer IV pyramidal neurons in mouse auditory cortex have dendrites that can span a few hundred micrometers (Richardson et al., 2009; Levy and Reyes, 2012). As a consequence, there is poor space clamp and the holding voltage imposed at the soma is not maintained in the dendrites. It is therefore unlikely that we were able to completely isolate excitatory and inhibitory inputs even when the somatic membrane potentials were held at their respective reversal potentials. We therefore investigated the impact of space clamp on the measured correlations of synaptic inputs and membrane potentials using a compartmental neuron model. We found that we most likely underestimate excitatory and inhibitory input correlations and therefore the impact of decorrelation due to poor space clamp.

The compartmental model consisted of a soma and 12 dendritic compartments with a total length of 600 μm. To better understand how the synaptic input location affects membrane potential correlations, we distributed synaptic inputs in three different ways along the dendritic tree (Fig. 6A, left): (1) all synaptic inputs arrive at the soma, (2) excitatory and inhibitory inputs are homogeneously distributed across soma and dendritic compartments, and (3) inhibitory inputs linearly decrease with the distance from the soma with excitatory inputs constant. The latter case appears to be the most realistic input distribution scenario for a large class of interneuron inputs (Somogyi et al., 1983; Kubota and Kawaguchi, 2000). For comparison, we run the same simulations with point neurons receiving all excitatory and inhibitory inputs at the one equipotential compartment.

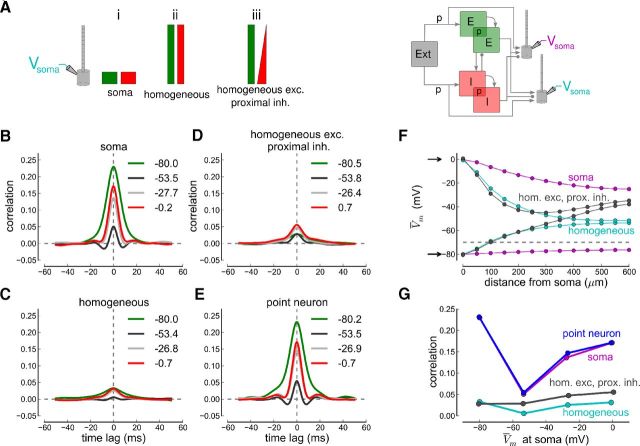
Figure 6.

Effects of space clamp on correlations examined with simulations. A, Left, Synaptic input distributions along the somatodendritic axis of the compartmental neuron model. The excitatory (green) and inhibitory (red) inputs from the recurrent network are such that (i) all synaptic inputs arrive at the soma, (ii) excitatory and inhibitory inputs are distributed homogeneously across soma and dendrite, and (iii) inhibition linearly decreases with distance from the soma with excitation constant. Right, Synaptic inputs from a recurrent network simulation are delivered to two spatially extended neurons. The recurrent network consists of 4000 E and 1000 I cells receiving uncorrelated excitatory input from an external pool of 4000 neurons (Ext). The connection probability for external to E and I neurons, as well as between and within the E and I neuron population, is constant, p = 0.2 (see Materials and Methods). B–E, Cross-correlograms of the membrane potential at different holding potentials for the three different input distributions and for point neurons. The average membrane potential (in mV) during the simulation is given for each cross-correlogram. F, Plot of average membrane potential versus distance from the soma while holding the somatic membrane potential at 0 mV (upper arrow) or at −80 mV (lower arrow). G, Pearson correlation coefficients at different average potentials for the three input regimes and point neurons. Each correlation coefficient is from a simulation injecting a different amount of current into the soma resulting in the respective average membrane potential at the soma.

We use a recurrent network consisting of 4000 excitatory, 1000 inhibitory conductance-based integrate-and-fire neurons, and 4000 external Poisson neurons to generate the synaptic inputs (Fig. 6A, right; see Materials and Methods; Renart et al., 2010). Excitatory neurons fire spontaneously at ∼ 1.1 spikes per second and inhibitory neurons at ∼ 3.8 spikes per second (Renart et al., 2010). The average number of excitatory, inhibitory, and external inputs to the extended neurons is 800, 200, and 800 (total number of each neuron population times the connection probability, p · N_E,I,X), respectively, on average (connections are drawn randomly) in all the four cases. Note that the distribution of inputs from external neurons resembles that for recurrent excitatory neurons. To facilitate simulations, only two “recorded” neurons had multiple compartments; the remaining were point neurons. These two neurons do not project to others (Fig. 6A, right). As in our recordings, we injected a constant current at the soma to impose the average membrane potential during recordings of membrane potential dynamics (through I_app in Eq. 3). We adjusted the current to isolate EPSPs at −80 mV and IPSPs at 0 mV and at intermediate potentials. We then computed the cross-correlograms of the EPSPs, IPSPs, and membrane potentials for each injected current (Fig. 6B–E).

Synaptic inputs distributed over the dendritic tree deflect the dendritic membrane potential away from the potential imposed at the soma. Inhibitory inputs, for example, hyperpolarize the dendrite such that the depolarizing current injected at the soma is unable to sustain the depolarization (e.g., at 0 mV to record inhibition only) in the dendrites (Fig. 6F). As a consequence, the driving force for excitatory synaptic input at the dendritic tree is not zero and IPSPs are not well isolated. This effect varies largely with the distribution of synaptic inputs across the somatodendritic structure (Fig. 6F). Proximal inhibition and homogeneous excitation, for example, results in strongly depolarized distal dendrites due to the prevalence of excitation there (Fig. 6F, gray lines). These simulations show that it is not feasible to completely separate excitation and inhibition due to the spatial extent of pyramidal neurons.

Because of poor space clamp, the correlations in the two spatially extended model neurons were underestimated (Fig. 6G). Even when attempting to isolate excitatory and inhibitory inputs, excitation and inhibition interact along the dendritic tree in spatially extended neurons and add to partially cancel each other. This interaction reduces correlations, similar to what occurs near resting potential. Note that there is no difference in measured correlations in point neurons and in spatially extended neurons with all inputs arriving at the soma (case i in Fig. 6A,G).

These simulations therefore suggest that because of poor space clamp, the experimentally measured correlations in vitro are an underestimate of the true values. Importantly, membrane potential correlations at −50 mV are affected less by poor space clamp in the realistic case of proximal inhibition and homogeneous excitation (the correlation coefficient is reduced by a factor 8.2 at −80 mV and by a factor 3.1 at 0 mV, but by 1.77 at −54 mV; Fig. 6G). Altogether, the poor space clamp leads to an underestimation of the differences between EPSP/IPSP correlations and resting membrane potential correlations (Fig. 6G).

Weak spike-output correlations

To determine how membrane potential correlations translate into spike-output correlations, we performed cell-attached recordings from pairs of neurons. These recordings were from different cell pairs than the whole-cell recordings above because the internal solution contained QX-314, which blocked voltage-activated sodium channels underlying action potentials (see Materials and Methods). As expected from the weak membrane potential correlations, spike count correlations are small.

During cell-attached recordings we observed a range of small firing rates (mean ± SD: 0.517 ± 0.541 spikes per second; Fig. 7A,B, inset). Firing is highly irregular possibly due to the nonstationary conditions in the activated slice (coefficient of variation; CV mean ± SD: 2.12 ± 1.88; Fig. 7B, inset). Spike count correlations are weak and positive across all firing rates (median: 0.0168 for a count window of T = 50 ms; Fig. 7B). Furthermore, correlations are independent of the firing rate (Pearson correlation coefficient r = 0.129, p = 0.432) suggesting that the rate-correlation dependence is weak at low firing rates (de la Rocha et al., 2007; Cohen and Kohn, 2011). We observed consistently small spike count correlations across a large range of time windows (10 ≤ T ≤ 300 ms, median largest at T = 50 ms; results not shown).

Consistent with the weak membrane potential correlations measured above, spike count correlations between pairs of neurons are weak. However, the small firing rates may, along with the active decorrelation, contribute to low spike count correlations. Unfortunately, we could not drive the neurons to fire at higher rates under physiological conditions. These results are therefore consistent with the weak membrane potential correlations measured but not conclusive in terms of the strength of spiking correlations in our preparation.

Discussion

We recorded from pairs of neurons in layer IV of the auditory cortex to determine the correlation structure between excitatory and inhibitory inputs in networks with realistic connections. We showed that excitation and inhibition are correlated leading to mutual cancellation. We further demonstrated that the net effect is to weaken membrane potential correlations at rest, which in turn would reduce spike count correlations. Our results suggest that correlations from shared presynaptic inputs are actively suppressed in cortical networks, as has been previously proposed in a theoretical study (Renart et al., 2010). Our findings from layer IV neurons are in agreement with recent results of weak spiking correlations in cortical input layers (Hansen et al., 2012; Smith et al., 2013).

Similar to our findings, recordings from pairs of cortical neurons in vivo showed correlations between excitatory and inhibitory inputs with inhibition tightly tracking excitation (Okun and Lampl, 2008). Other in vivo studies have reported strong membrane potential correlations at resting potential in the barrel cortex of awake mice (0.72 ± 0.11 during quiet periods, 0.33 ± 0.17 during active whisking; Poulet and Petersen, 2008) and the visual cortex of anesthetized cats (0.40 ± 0.02, Lampl and Reichova, 1999). Whether these studies are consistent with our findings would require direct comparison of correlations of isolated synaptic inputs with those of composite inputs at resting potential. Interestingly, the correlations decrease in the presence of sensory stimulations (visual stimulation; Lampl and Reichova, 1999 and whisking; Poulet and Petersen, 2008). This decrease in correlations might be due to the fact that the resting potential in quiescence is near the reversal potential for IPSPs (which emphasizes correlations between excitatory inputs) but increases, during sensory stimulation, to a level where decorrelation would occur (Fig. 3). The relatively high correlations observed during quiescence and sensory stimulation might be due to other sources not compensated for by active decorrelation of shared presynaptic inputs (see Introduction).

During the recordings, we observed distinct low- and high-amplitude epochs. Membrane potential decorrelation occurred during low-amplitude epochs and partially during high-amplitude epochs where correlations were high for isolated synaptic inputs and for their composite near resting potential (Figs. 4B, 5F). Furthermore, tracking between excitation and inhibition is tighter during the high-amplitude epochs (Fig. 5). It would be of interest to determine whether the low/high correlations in stimulated/nonstimulated conditions (Lampl and Reichova, 1999; Poulet and Petersen, 2008), or the DOWN/UP state dynamics in cortical slices (Sanchez-Vives and McCormick, 2000) and in the auditory cortex in vivo (DeWeese and Zador, 2006; Hromádka et al., 2013) correspond to the low/high-amplitude epochs in our experiments. As in the in vivo and in vitro studies, we observed that weak membrane potential correlations are accompanied by an increase in the small amplitude, high-frequency component of the voltage traces. Together, these results suggest that the same cortical network can show decorrelated and highly synchronous activity regimes.

The mechanism underlying the transition from low- to high-amplitude epochs is unknown. We showed that the increase in EPSP amplitudes was disproportionately greater than the increase in IPSP amplitudes (Fig. 4C,D). This excess of excitation could stem from a change in overall tonic excitatory external drive (e.g., from the thalamus), depression of inhibitory synaptic transmission, or neuromodulatory action overwhelming inhibition due to the substantially smaller number of inhibitory cells in cortex. However, neural network simulations indicate that transient input changes increase the correlations in excitatory and inhibitory inputs but membrane potential decorrelation remains effective, making it unlikely that sudden input changes alone cause high-amplitude epochs (results not shown).

Our data suggest that the strength of excitatory input correlations covaries with the strength of inhibitory input correlations (Fig. 3D). This result indicates that the heterogeneity of synaptic input correlations are not independent; rather, they are comodulated on a pair-by-pair basis to ensure low membrane potential correlations. Plasticity mechanisms would be required to give the system this fine architectural structure.

The match in the EE and II input correlation magnitude may be due to hard-wired connections between neuron pairs. Spike count correlations have been reported to be high for pairs of neurons that are near each other (Smith and Kohn, 2008) and have similar tuning properties or receptive fields (Zohary et al., 1994; Kohn and Smith, 2005; Ecker et al., 2010). Correspondingly, neuron pairs from different functional columns (Oviedo et al., 2010) or different auditory receptive fields might show weaker input correlations compared with neurons with similar properties. Alternatively, some of the variability in the input correlations could be attributed to nonstationary spiking activity in the slice, that is, the same cell pairs might enter different states through fluctuations in the induced spontaneous activity.

We observe correlations in excitation and inhibition between pairs of cells emerging from shared presynaptic inputs in vitro. It should, however, be noted that the absence of long-range connections and neurotransmitters alters the activity state (Hasselmo, 1995) and could potentially influence interneuron correlations. Furthermore, reducing the driving force for the hyperpolarizing potassium current renders each neuron intrinsically more excitable. The resulting activity state could therefore be more asynchronous than spontaneous cortical activity in vivo mostly driven by synaptic inputs.

In summary, our results indicate that correlations from shared presynaptic inputs in densely connected cortical networks do not contribute to observed correlations in membrane potentials and spiking activity. Rather cortical networks seem to be organized to partially cancel correlations emerging from shared presynaptic inputs. Further investigations of synaptic input and membrane potential correlations in vivo with respect to receptive fields and network activity state are necessary to complete our understanding of how input correlations translate into membrane potential correlations and in turn into spike count correlations. We suggest that overall network activity modulations but not shared synaptic inputs are the dominant source of observed correlations. The variability of cortical activity states could furthermore explain the large range of reported spike count correlations from extracellular multiunit recordings.