Tuning Your Priors to the World

Abstract

The idea that perceptual and cognitive systems must incorporate knowledge about the structure of the environment has become a central dogma of cognitive theory. In a Bayesian context, this idea is often realized in terms of “tuning the prior”—widely assumed to mean adjusting prior probabilities so that they match the frequencies of events in the world. This kind of “ecological” tuning has often been held up as an ideal of inference, in fact defining an “ideal observer.” But widespread as this viewpoint is, it directly contradicts Bayesian philosophy of probability, which views probabilities as degrees of belief rather than relative frequencies, and explicitly denies that they are objective characteristics of the world. Moreover, tuning the prior to observed environmental frequencies is subject to overfitting, meaning in this context overtuning to the environment, which leads (ironically) to poor performance in future encounters with the same environment. Whenever there is uncertainty about the environment—which there almost always is—an agent's prior should be biased away from ecological relative frequencies and toward simpler and more entropic priors.

1. The mind and the world

Among the founding dogmas of cognitive science is that in order for the mind to make sense of world, it must incorporate constraints and regularities inherent in the environment. This idea has been expressed in many forms, all sharing a common emphasis on how structure in the environment informs the mind. One influential proposal is Shepard's (1994) notion of internalization, in which the mind incorporates implicit knowledge about the environment. Another is Marr's (1982) notion of constraints, thought of as regularities of the natural world that allow the many potential interpretations of perceptual data to be pruned down to a single unique solution. Barlow (1961, 1974, 1990, 1994) has long argued that neural coding should reflect the statistical regularities and redundancies latent in the sensory signal. Also related is Richards' “Principle of Natural Modes” (Richards, 1988; Richards & Bobick, 1988), which relates perceptual inference to the regularities in the natural world. The common thrust of all these proposals is that the inference procedures embodied by the mind work well because they embody tacit knowledge about the world. If such knowledge is absent or inaccurate—if the mind's assumptions are “mistuned” to its environment—its tricks will not work or will work poorly.

Several modern lines of reasoning have strengthened the argument, traditionally made by nativists and rationalists, that inference cannot usefully proceed without biases that are in some sense tuned to the world. One well-known line of reasoning stems from the “no free lunch” theorems of Wolpert (1996) and Wolpert and Macready (1997). These theorems imagine the space of possible worlds (problems) and the space of possible learning or search algorithms probabilistically, and show that no algorithm is uniformly better than all others over the entire ensemble of possible worlds. Even an apparently universally useful procedure like gradient descent, for example, is no better than an apparently useless one like random search in some possible worlds. It is actually easy to imagine such a world: Consider a world with mostly random structure but in which optimal solutions are densely scattered throughout the search space. In such a world, random search would occasionally happen upon a good solution, while gradient descent would be practically useless. Of course, such a random world bears little resemblance to (any reasonable model of) the actual world, but that is precisely the point. To be more useful than average in our world, algorithms must make nontrivial tacit assumptions about its structure. For example, assuming that solution surfaces are usually continuous in the search space—not true in all possible worlds, but often true in ours—makes gradient descent useful. But generic assumptions about the properties of “realistic problems” do not generally favor any one class of algorithms; instead more specific knowledge must be brought to bear (Sharpe, 1998). That is, the brain must be tuned to the world. But what does this mean exactly?

This article raises this question in the context of Bayesian inference. Bayesian models, which assume that the mind estimates the structure of the world via a rational probabilistic procedure, have become increasingly influential in perceptual and cognitive theory (Chater & Oaksford, 2008; Knill & Richards, 1996). Because Bayesian models represent demonstrably optimal inference procedures, they make a particularly natural setting in which to ask what it means for the brain to be tuned to the world. In fact, a fairly simple conception of tuning has become a cliché of cognitive science: The brain is suitably tuned to its environment when it adopts priors that are empirically correct—that is, that are in fact true in the environment. Perhaps surprisingly, though, this seemingly simple idea is actually contrary to a core epistemological tenet of Bayesian theory. This is a rather strange clash of philosophical positions that is difficult to appreciate without delving into conflicting historical views about the nature of probability. In the next section, I briefly review the historical controversy, showing the modern common wisdom about probabilities—that their true values can estimated by tabulating frequencies of events in the world—contradicts Bayesian philosophy, and thus cannot provide a consistent basis for understanding how a Bayesian observer can be tuned to its environment.

2. The Lord's prior

The conception of “tuning” that is tacitly adopted in many modern treatments is that the optimal Bayesian observer is correctly tuned when its priors match those objectively in force in the environment (the “Lord's prior”). In Bayesian probability theory, priors represent the knowledge brought to bear on a decision problem by factors other than the data at hand, that is, the state of beliefs “prior to” (really, separate from) any consideration of the evidence. (Gauss's term was ante eventum cognitum: “before the cognitive act”; see D'Agostini, 2003.) In the Lord's prior view, priors are said to match the world when each event class h, which objectively occurs in the environment with probability p(h), is assigned a prior of p(h). A simple extension replaces the discrete event h with the continuous parameter x, in which case we would want the prior on x, p(x), to be equal to the objective probability density function p(x). This condition defines what is referred to in the perception literature as an ideal observer, that is, an agent that makes optimal decisions based on assumptions that are in fact true in the environment, and which thus whose decision that are optimal in that environment.

This conception also underlies some of the enthusiam for natural image statistics in the literature, in which Bayesian inference is endowed with priors drawn from statistical summaries of the world, or proxies thereof such as databases of natural images. In a natural image statistics framework, the best way to set a prior is canvass the world and ask what its prior is. Indeed, in many treatments, setting priors empirically is held up as a desirable aspiration, self-evidently superior to alternatives which are derided as arbitrary or “subjective.” A recent example is Jones and Love (2011), who criticize Bayesian models on a number of fronts but comment (p. 173) that “the prior can be a strong point of the model if it is derived from empirical statistics of real environments” and later (p. 180) lament that “[u]nfortunately, the majority of rational analyses do not include any measurements from actual environments.”

Associated with this view is the idea that natural selection will put adaptive pressure on agents to adopt the “true” prior—that over the course of generations, it will nudge innate priors toward their true environmental values (Geisler & Diehl, 2002). Implicit in this idea is an assumption that having true probabilistic beliefs is maximally beneficial to the organism. This assumption has been criticized because the utility function may well favor something other than truth (Hoffman, 2009; Mark, Marion, & Hoffman, 2010). But even if one improves this view by coupling it with a suitable loss function (Maloney & Zhang, 2010), the central dictum is that inference benefits by having priors that are “empirically correct.”

3. Frequentist versus epistemic views of probability

But this viewpoint, agreeable as it may seem to modern ears, is actually at odds with traditional Bayesian philosophy of probability. The distinction revolves around competing views of what “probability” means, generally involving the distinction between the frequentist and subjectivist (or epistemic or Bayesian) conceptions of probability. Frequentists (e.g., Fisher, 1925; Venn, 1888; von Mises, 1939) define probability strictly in terms of some “infinitely repeated random experiment,” such as an infinite sequence of coin tosses. The probability of h (e.g., “heads”) is defined as the ratio of number of trials on which h occurs to the total number of trials in such a thought experiment. Most psychologists are so accustomed to this way of looking at probability that we struggle to think about it any other way. (The common use of the term “base rate” as a synonym for “prior probability” reflects this attitude.) But the frequentist conception is extremely limiting. For example, it automatically means that probabilities can only be assigned to stochastic events that are, in principle, capable of being repeated many times with different outcomes. For example, a frequentist cannot assign a probability to a scientific hypothesis, say the existence of gravitons, because the proposition that gravitons exist is presumably either true or false and cannot be assessed by repeated sampling (e.g., tabulating universes to assess the fraction in which gravitons exist). Historically, frequentists have been willing to accept this limitation, restricting probability calculations to properties of random samples and other plainly stochastic events.

But Bayesians, beginning with Laplace (1812) and continuing with influential twentieth-century theorists such as Jeffreys (1939/1961), Cox (1961), de Finetti (1970/1974), and Jaynes (2003), wanted to use the theory to support inferences about the probability of the (fixed, not random) state of the world based on the (random) data at hand, a paradigm referred to historically as “inverse probability.” In the frequentist view, the state of the world does not have a probability, because it has a fixed value and cannot be repeatedly sampled with different outcomes. (It is not a “random variable”.) Hence, instead of thinking of p(h) as the relative frequency of h, Bayesians think of it as the degree of belief that h is true, referred to as the subjectivist, epistemic, or Bayesian view.¹ In the epistemic view, the uncertainty expressed by a probability value relates only to the observer's state of knowledge (not randomness in the world) and changes whenever this knowledge changes. Epistemic probabilities are not limited to events that can be repeated, and thus can be extended to propositions whose truth value is fixed but unknown, like the truth of scientific hypotheses. A Bayesian would happily assign a probability to the proposition that gravitons exist (e.g., p(gravitons exist) = 0.6), reflecting a net opinion about this proposition given the ensemble of knowledge and assumptions he or she finds applicable. To Bayesians, frequencies (counts of outcomes) arise when the world is sampled, but they do not play a foundational role in defining probability. Indeed, Bayesians have often derided the “infinitely repeated random experiment” upon which frequentism rests as a meaningless thought experiment—impossible to observe, even in principle, in reality.²

As a consequence of this divergence in premises, frequentists tend to view probabilities as objective characteristics of the outside world, while Bayesians regard them as strictly mental constructs. To frequentists, probabilities are real facts about the environment, about which observers can be right or wrong. But to Bayesians, probabilities simply describe a state of belief. To put it perhaps too coarsely: To frequentists, probabilities are facts, while to Bayesians they are opinions.³

This point was put perhaps most strikingly by Bruno de Finetti, a key figure in the twentieth-century renaissance of Bayesian inference, who began his Theory of probability with the phrase “PROBABILITY DOES NOT EXIST,” a sentence he insisted be typeset in all capital letters (see de Finetti, 2008). Why would a probability theorist make such a peculiar remark? What De Finetti meant was simply that probability is not an objective characteristic of the world, but rather a representation of our beliefs about it.⁴ Actual events, if we record them and tabulate the proportion of the time they occur (e.g., the number of heads divided by the number of tosses), are frequencies, not probabilities, and are only related to probabilities in a more indirect way (which Bayesians then debate at great length). The mathematical rules of probability theory are about these beliefs and how they relate to each other and to evidence, not about frequencies of events in the outside world. Ipso facto, probabilities in general, and prior probabilities in particular, cannot be assessed by tabulating events. As Jaynes (2003) put it (p. 916): “the phrase ‘estimating a probability ’ is just as much a logical incongruity as ‘assigning a frequency ’ or ‘drawing a square circle.’” Jeffreys (1939/1961), who first laid out the logic of modern Bayesianism, put it bluntly: “A prior probability is not a statement about frequency of occurrence in the world or any portion of it.”

4. What is the true value of a probability?

These sentiments are so at odds with the contemporary common wisdom in cognitive science about probabilities—that they simply represent relative frequency of occurrence in the world—that the modern reader struggles to understand what was meant. But the core of the epistemic view is simply that probabilities are not objective characteristics of the outside world that have definite values. Consider the simple example of baseball batting averages. What is the probability a given baseball player will get a “hit” at his next at-bat? By baseball convention, this probability is approximated by a tabulation of the player's past performance: hits divided by at-bats. But now the player steps up to the plate. What is the probability he will get a hit at this at-bat? The pitcher is left-handed, so we can improve our estimate by limiting the calculation to previous encounters with left-handed pitchers. It is a home game, so we can refine the estimate still further; a runner is on base; today is Sunday; and so forth. Every additional factor further refines the estimate to a more comparable set of circumstances but also reduces the quantity of relevant data upon which to base our estimate. In the limit, every at-bat is unique, at which point the entire notion of generalizing from past experience breaks down. But even if we had infinite data, and plenty of data for each subcondition we might imagine, which of these subconditions is the right one—which ones gives the “true” probability of a hit today?

A moment's thought suggests that there is no objectively correct answer to this question. It depends on what factors are considered causally relevant, which depends on the observer's model of the situation, as causal influences cannot be definitively determined on the basis of experience alone. More notationally careful Bayesians (e.g., Jaynes, 2003, or Sivia, 2006) often acknowledge this point by notating the prior on h as p(h|a), rather than simply p(h), with a representing the ensemble of background knowledge or assumptions believed by the agent to be relevant to the prior probability of h. (The prior is not “unconditional” as it is often described in informal treatments.) What you think about the prior on h depends on your model. And as in any inductive situation, there is no deductively certain model, but only a (perhaps infinite) collection of models that are inductively persuasive to various degrees—each of which potentially assigns a different probability to h. There is no right answer, only a range of plausible answers.

The baseball problem is a variant of a problem discussed by the early frequentist John Venn (1888) (glossed by Howie, 2004 as the “tubercular authoress from Scotland” problem). As a frequentist, Venn's solution was to insist that probabilities were only definable with respect to large ensembles of “similar” cases, never individual events—a restriction that severely limits the scope of probability theory, and which Bayesians do not accept. For example, to meet Venn's criteria for determining the probability of hitting safely, the batter would have to be tested over a long sequence of trials under identical conditions, much as Fisher (an even more dogmatic frequentist) was to propose several decades later as a method of carrying out experiments. But such a procedure would plainly preclude determining the probability of a hit from tabulations of past performance in actual baseball games.

But the normal way of computing baseball averages is perfectly coherent in the epistemic view. Previous performance (such as the proportion of hits in previous at-bats) is simply evidence influencing the observer's degree of belief that the batter will hit safely in his next at-bat—not, as in the frequentist view, an estimate of the “true” probability of a hit, which they would regard as meaningless. The Bayesian observer is free to take more factors into account, or fewer, depending on the chosen model of the situation, which determines which factors are believed relevant. In this view, the adopted probability of a hit, whether the batting average or some more refined estimate, is simply an estimate and not the “truth.” Probabilities are not true or false but simply characteristics of models (not of reality). It is perfectly reasonable to regard a coin as having heads probability 0.5, but what this really means is that our model of the coin is as a p = .5 Bernoulli process, and we believe, but cannot be sure, that our model is right. There is no ground truth. Probabilities do not have “true” values in the environment, and the Lord's prior does not exist.

It is important to understand that the epistemic view of probability is essential to the Bayesian program, and it cannot be lightly set aside without making inverse probability effectively impossible. Only if probabilities relate to degrees of belief can they be associated with nonrepeatable hypotheses, like “gravitons exist,” or “an earthquake will strike Los Angeles in the next decade,” or even “it will rain tomorrow.” The issue is especially acute in cognitive science, where many of the hypotheses to which we wish to assign probabilities are themselves intrinsically subjective, like “the best parse of this sentence is …” or “the best perceptual grouping of this image is ….” These events obviously cannot be objectively tabulated, as the underlying condition cannot itself be objectively confirmed. One can of course substitute various approximations and proxies, such as tabulations of subjective evaluations of them (e.g., Elder & Goldberg, 2002; Geisler, Perry, Super, & Gallogly, 2001), though this necessarily introduces an element of circularity (because a supposedly objective estimation procedure is being grounded in a tabulation of subjective conclusions). Such estimates are extremely interesting and informative but cannot be thought of as probability ground truth—not simply because they are approximations, but because in the Bayesian approach, frequency tabulations, no matter how extensive and objective, do not determine probability in the first place.

As mentioned above (footnote 2), some (e.g., Popper, 1959) have argued for a view of probability as propensity, meaning an objective tendency for an event to occur in a particular way (see Mellor, 2005). This interpretation aims to establish an objective status for probabilities, based on the physical properties of the situation, without the need for infinite repeatability inherent in the frequentist view. Bayesians generally reject any view in which probabilities are not states of belief and point to numerous demonstrations that probabilities can change when only knowledge has changed without a change in physical state (see Jaynes, 1973 for numerous examples). But for purposes of the current paper, the main point is that propensities, like epistemic probabilities, are not defined by relative frequencies of events, meaning that tabulations of events in the real world do not play an especially central role in defining them.

5. The contemporary zeitgeist

With the ideological dichotomy between frequentist and epistemic probabilities in mind, it is evident that contemporary attitudes reflect an historically anomalous combination of assumptions from competing camps. On one hand, an increasingly large fraction of the field adheres to a Bayesian model of inference. On the other hand, many researchers evince what can only be described as a frequentist attitude toward the setting of prior probabilities: that they are most properly set by direct objective measurement of relative frequencies in the world. Purves (2010, p. 227), in explaining Bayesian inference for purposes of perception, defines the prior as “the frequency of occurrence in the world of surface reflectance values, illuminants, distances, object sizes, and so on.” Jones and Love (2011), while criticizing Bayes, likewise assume that priors ought to be based on “measurements from actual environments.” This viewpoint echoes that of the devout frequentist Egon Pearson (the son of the eminent statistician Karl Pearson, and co-inventor of the Neyman–Pearson school of frequentist statistics), who remarked in 1929: “prior distributions should not be used, except in cases where they were based on real knowledge” (Lehmann, 2011)—by which he meant to dismiss Bayesian inference, not to define it. The idea that Bayesian priors can only properly set by measurement of recurring stochastic properties of the world was, after all, a central reason why frequentists such as Fisher and E. Pearson wholly rejected Bayesian inverse probability—recognizing that by that standard most priors cannot be meaningfully set at all (because the conditions are unrepeatable). That is, the notion of grounding priors in empirical base rates—essentially a contradiction in terms, and rejected (for different reasons) by both sides—has now become a cliché of the field.

And perhaps most important, the dissonance between the epistemic view of probability historically adopted by Bayesians and the widespread emphasis on naturalistic (frequentist) setting of priors does not seem to be widely recognized. As contemporary perceptual theorist Qasim Zaidi⁵ has quipped, many contemporary perceptual theorists could be described as “frequentist Bayesians.”

As suggested above, such attitudes are especially common among “consumers” of Bayesian theory, who may be less steeped in its intellectual history. “Producers” of Bayesian cognitive theory are far more likely to consistently adopt an epistemic view, invoking the phrase “degree of belief” in defining probability and contrasting it with the frequentist view (e.g., Oaksford & Chater, 2009). Work in the hierarchical Bayesian paradigm (e.g., see Goodman, Ullman, & Tenenbaum, 2011; Salakhutdinov, Tenenbaum, & Torralba, 2010) shows how priors can be set “subjectively” but in a way that still respects prior knowledge (see discussion below). Similarly my own work on the structure of visual contours invokes a simple subjective prior, the von Mises prior on turning angle, which is informed by but not defined by the empirical structure of natural contours (Feldman, 1995, 1997, 2001; Feldman & Singh, 2005). All these approaches, broadly speaking, fall into the mainstream Bayesian tradition of using priors to represent the observer's prior beliefs, and not supposedly objective characteristics of the environment.

But does not one want, if possible, to base one's prior as faithfully as possible on data from past experience? As is often emphasized in Bayesian theory, prior probabilities do not have to derive solely from prior observations; they can and should reflect all prior knowledge, including knowledge not easily expressed in terms of frequencies—for example, symmetries of the problem (Jaynes, 1973) or a preference for simple hypotheses (Jeffreys, 1939/1961). This is the reasoning behind the well-known maximum-entropy principle (Jaynes, 1982), which says that one should choose the prior that maximizes the Shannon entropy consistent with all the knowledge one has. The max-ent prior imposes the minimum amount of additional structure or information over what is actually known, and thus “most honestly” or most generically encodes that knowledge. For example, if one knows that a parameter has mean μ and variance σ², the maximum-entropy prior is a Gaussian N(μ, σ²), and in practice such a prior often works better than a prior cobbled more “faithfully” from environmental tabulations.

But again, if one has detailed information about frequencies in the world, should not one use it? First, of course, Bayesian theory already has a perfectly “epistemic” way of incorporating past observations into the prior: conventional Bayesian updating, in which the posterior derived from past data becomes the prior with respect to future data. The question is not whether observations of the environment are relevant: They are, on either account. The question is whether they are constitutive of the prior (the “frequentist Bayesian” view) or simply evidence about what it should be (the Bayesian). But still, the difference in attitude leads to a difference in procedures. For example, observation may tell us that the frequency does not appear to be perfectly Gaussian. Would we not do better to use the observed frequency distribution as our prior? Counter-intuitively, the answer in practice is often no. Jaynes (2003) directly addresses the question of why Gaussian priors so often out-perform more detailed priors based on frequency tabulations. (He refers to this as the “ubiquitous success” of Gaussian priors, p. 710, and the “near-irrelevance of sampling frequency distributions,” p. 712.) Often, the answer is that the “details” are just noise rather than reliable properties of the environment. So whether one wants to be influenced by these details in setting one's prior depends on how much one believes them. Setting priors entirely empirically, as often done in natural image statistics, means choosing to be influenced exclusively by past experience and nothing else. This argument will be developed below.

6. What else, if not the “truth?”

To summarize the argument so far: Frequentists think of events in the world as having definite objective probabilities. Many contemporary researchers, adopting Bayesian techniques but frequentist attitudes, consider the observer ideally tuned when it adopts as its prior the empirically “true” prior—a concept that does not, in fact, play any role in Bayesian theory. From a Bayesian point of view, priors are simply beliefs, informed by the observer's model and assumptions along with previously observed data, and are not, in principle, subject to empirical validation.

Of course, while in Bayesian theory priors cannot literally be true or false, they certainly can influence the decisions the observer makes and thus the outcomes it enjoys. So what prior should the observer adopt? One of the benefits of viewing probabilities epistemically is that it frees us from assuming that the answer to this question is automatically “the true one.” Instead, we are at liberty to consider the choice of prior in a more openended way. From an epistemic viewpoint, there may well be choices of prior that work better than the one that matches environmental relative frequencies. In the epistemic tradition, the observer is free to adopt whatever prior he or she wants for whatever reasons he or she wants—not just as the result of tabulation or measurement—and so we can ask which choice actually works best.

Thus, it is quite conceivable that an observer under adaptive pressure to be “tuned” to the environment would do well not to adopt what we normally think of as the “true” prior. In a very concrete sense, posterior beliefs may be optimized with another prior. This may sound extremely counterintuitive, because it suggests the existence of a class of observers superior to ideal observers. But the mathematical argument is extremely straightforward, and indeed all its main elements are familiar from the Bayesian literature. In what follows I develop this argument, showing that the choice of prior should be influenced by more than just the fit between the prior and the world.

7. Quantifying the match between the head and the world

From here on we denote by p(h) the “true” prior of h in the world, bearing in mind as discussed above that this really means that p(h) is the prior on h in the model of the world that we are working with. Expectations taken relative to this prior should be thought of as reflecting not ground truth but a particular hypothetical model that we wish evaluate. Given that, we would like to quantify the discrepancy between p (the world) and a given prior q adopted by a particular observer (the head). A conventional quantification of this match, adopted nearly universally in information-theoretic statistics (see Burnham & Anderson, 2002), is the Kullback-Leibler distance or divergence D(p║q), defined as

$$D(p\Vert q)=\sum _{i}p(h_i)log\frac{p(h_i)}{q(h_i)},$$ (1)

which can be thought of as the expectation (under p, ranging over hypotheses h_i) of the log of the ratio between p and q. The divergence⁶ is useful measure of the discrepancy between two priors because it quantifies the inefficiency of assuming q when p is in fact true. That is, it measures the number of extra bits required to encode the world via the observers' model q compared to the Shannon optimal code under p (Cover & Thomas, 1991).

I conducted a simple Monte Carlo simulation designed to measure the performance of observers with various priors q in a world actually governed by p. In this situation, an observer that assumes prior q equal to the true prior p is an “ideal observer” and has maximum probability of classifying observations correctly. The aim of the simulation is to see how performance varies as q is varied over the space of possible priors. The simulation assumes a simple classification task with data x ∈ R² generated by one of two sources A and B, each of which is circular Gaussian density with distinct means μ_A, μ_B ∈ R², and common variance σ². All these parameters are known to the observers except the priors. Classes A and B occur in fact with probability p(A) and p(B) = 1 − p(A), respectively. Tested priors q run the full range of possible priors in step sizes of 0.2, with each prior evaluated 10,000 times and the results averaged.

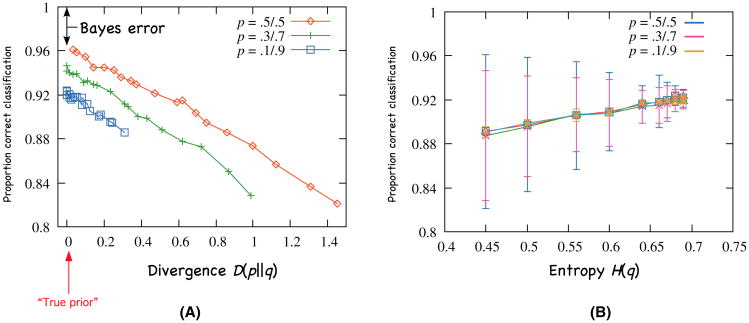
Fig. 1A shows performance (classification proportion correct) as a function of the divergence D(p ║ q) ranging over choices of q. As one would expect, performance decreases linearly with divergence from the true prior: The ideal observer (D(p ║ q)=0) is best, and others degrade as their assumptions increasingly diverge from that of the ideal. In the evolutionary simulacrum imagined by Geisler and Diehl (2002), adaptive pressure would urge organisms up this slope, minimizing divergence from the environment.

Fig. 1.

Results of the Monte Carlo simulation, showing that classification performance (A) decreases linearly with divergence of the observers's choice q from the true prior p but (B) increases with the entropy of the chosen prior q. Results are plotted for three different choices of “true” priors: high entropy (p₁ = 0.5; p₂ = 0.5), lower entropy (p₁ = 0.3; p₂ = 0.7), and very low entropy (p₁ = 0.1; p₂ = 0.9). The residual error when the true prior is used (divergence = 0, far left) is the Bayes error.

However, there is another factor affecting performance, shown in Fig. 1B: the influence of the entropy H(q) of the chosen prior. Entropy of a probability distribution p, defined by Shannon's formula

$$H(p)=-\sum _{i}p(h_i)logp(h_i),$$ (2)

can be thought of as a measure of the symmetry of the probabilities and is maximized when they are all equal. The plot in Fig. 1B shows that—collapsing over divergence—more entropic priors actually perform better. This is true for all three tested true priors, that is, regardless of their entropy. This effect is thus independent of the degree to which the prior is tuned to the environment; assuming equal degree of tuning (i.e., divergence), the more entropic the prior, the more accurate the resulting classifications. The conventional intuition is that the “true” ecological prior provides ideal performance, but this simulation shows that this is not all there is to it. Regardless of the degree of tuning—and even for ideally tuned (zero divergence) observers—more entropic priors are better.

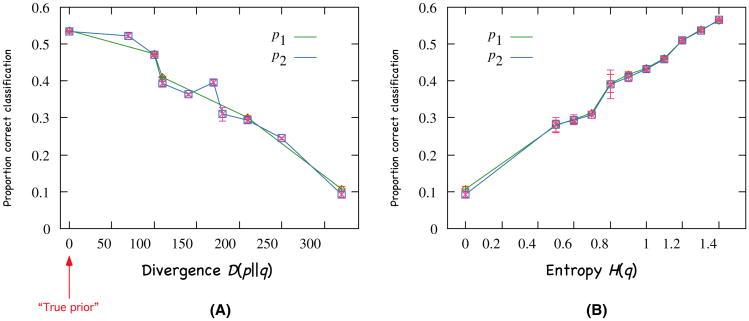
Fig. 2 shows a slightly more complex simulation with four classes instead of two. (This makes the prior space three-dimensional instead of one-dimensional, cubing the number of priors tested, so in this version only 5,000 trials were run per prior.) The influence of divergence is as before, and the effect of entropy is more clear than before. Note that the larger number of classes is inherently more confusable, meaning that absolute ideal performance is worse than before (Bayes error is greater). But again ranging over the space of priors, more entropic priors lead to objectively superior performance.

Fig. 2.

Results of the Monte Carlo simulation for four classes, again showing that classification performance (A) decreases linearly with divergence from the true prior, but (B) increases with the entropy of the chosen prior. Here, in higher dimensions, the effect of entropy is stronger, with a steeper slope and smaller error bars. Results are shown from two choices of prior with different entropies (p₁ = {.1, .3, .3, 3}, p₂ = {.1, .2, .3, .4}). Note with a larger number of classes, the classes are more confusable, leading to a larger Bayes error.

8. Bias and variance

This suggests that tuning an organism to its environment involves somewhat more than collecting statistics from the environment, interpreting them as the true priors, and endowing the organism with them. Historical Bayesians raised a philosophical objection to this idea, and the above analysis provides a more tangible one. Mere tuning does not, in fact, optimize performance.

Another way of looking at this is in terms of the degree to which we “believe” the data that the environment has provided us in the past. If we have a small amount of data, the data are likely to include a fair amount of noise along with the signal. Even with the large data sets often used in the natural image statistics literature, the wobbles and wiggles of an empirically tabulated database are plainly visible in the plots. Do we think that each of these wobbles and wiggles represents a genuine and robust elevation or depression in the probability of conditions in the world?

Common sense suggests not, and in this case, common sense is backed up by standard theory in the form of what is referred to as bias/variance or complexity/data-fit trade-off (Geman, Bienenstock, & Doursat, 1992; Hastie, Tibshirani, & Friedman, 2001). The bias/variance tradeoff is a simple consequence of the fact that more complex models (e.g., with more parameters or fudge factors) can generally fit data better than simpler ones, simply because the extra parameters can always be fit so that the loss function is reduced. In the limit, a sufficiently complex model (e.g., a high enough dimension polynomial) can fit any data, even if the model is completely wrong. Fitting the data “too well” in this sense is called overfitting. At the opposite extreme, fitting the data too coarsely, with a model that is too simple, is called underfitting. Somewhere in the middle is a perfect balance, which, unfortunately, there is no general way of finding, because there is no absolute way of deciding what is signal and what is noise.

But generally to avoid overfitting, one must be willing to allow the data to be fit imperfectly, leaving some variance unexplained. Indeed, in any realistic situation, one does not really want to fit the data perfectly, because some of the data are noise—random fluctuations unlikely to be repeated. Overfitting thus inevitably leads to poor generalization, because some aspect of the learning was predicated on data that were unrepresentative of future data. For this reason, virtually every working inference mechanism includes (implicitly or explicitly) a damping process to restrain the complexity of models, sometimes referred to as regularization (see Briscoe & Feldman, 2011; Hastie et al., 2001).

9. Overtuning to the environment

In the context of fitting our observer to the world, what this means is that setting priors to match observed frequencies risks overfitting the world, or what might be called “overtuning” to environment. The conventional view is that one cannot “overtune”; the optimal observer is one whose prior matches the Lord's prior exactly, and the closer one can come to it, the better. But in view of the bias/variance tradeoff, one would be unwise to fit one's prior too closely to any finite set of observations about how the world behaves, because inevitably the observations are a mixture of reliable and ephemeral factors.

One may object that with a sufficiently large quantity of prior data, perhaps on evolutionary time scales and with learning encoded genetically, the prior can be estimated with arbitrarily high precision. But this conception assumes a fixed, repeating Bernoulli sequence with a static prior—a fishbowl with an infinitely repeated probabilistic matrix. In practice, environmental conditions are not singular, perfect, and unchanging. In reality, probabilities vary over time, space, and context, in potentially unknown and unpredictable ways. The environment inevitably contains uncertainty, not only about the classification of items on individual trials but about the nature of the probabilistic schema itself. To fit past experience perfectly is to overtune.

10. Uncertainty about the environment

For concreteness, one can imagine that the observer believes him- or herself to be in an environment where the true prior is p(h), but that he or she might be in an alternative (counterfactually nearby) environment with a slightly different true prior, whose value is randomly distributed about p(h). Equivalently, one can simply imagine that the prior is believed to be p(h) but that this belief is tempered by some uncertainty; in this conception, the true prior is a fixed but unknown value, and the prior distribution captures the observer's uncertainty about its value. The former scenario is more frequentist in “feel,” and the latter more subjectivist, but they are mathematically equivalent: Both can be cast mathematically in terms of a distribution of environments, with the priors governing them centered on a “population mean” plus some error distribution. In either conception, our observer must contend with a prior whose value cannot be regarded as a fixed value but rather as a probability distribution over possible values.

I modeled this situation in another Monte Carlo simulation by assuming that the “true” prior is itself chosen stochastically. First, we choose an imaginary prior p₀ (the “population mean” about which environments are chosen), and a vector e of probabilistic noise (components e_i chosen uniformly from (0,1), then normalized). We then create the actual environmental prior p by mixing the mean with a quantity ε of noise,

$$p=(1-\in )p_0+\in e.$$ (3)

The noise coefficient ε modulates the magnitude of uncertainty about the true nature of the environment. Five levels of e were used, .1, .2, .3, .4, and .5. Zero noise ε = 0 corresponds to the previous simulation, results of which are included here for comparison. All other parameters are as before. Once the true prior has been chosen, we again evaluate priors q ranging over the space of possible priors and evaluate their performance in the chosen environment.

Fig. 3 shows the results. The decrease in performance with divergence from the true prior is again visible, as is the increase with the entropy of the subjective prior. The novel element here is the modulation of this latter effect by ε, the magnitude of noise or uncertainty about the meta-environmental mean. The more uncertainty, the better mean performance in this new (and more uncertain) environment. More specifically, given a fixed level of divergence from the true prior, the more uncertainty the observer's prior contains, the better its performance (see inset). In this sense, having a more “random” prior works better, even at a fixed level of ostensible tuning (divergence).

Fig. 3.

Results of the simulation with various levels of uncertainty added to the true prior, showing (A) decrease in performance with divergence and (B) increase in performance with entropy, separated by the level ε of noise. Inset shows mean performance as a function of ε.

This plot suggests performance that is, in a very literal sense, superior to that of an ideal observer of the same environment. The well-versed reader will recoil at this characterization, because by definition performance cannot exceed that of the ideal. But the classical ideal observer presumes a perfectly well-defined environment, whose governing probabilities are fixed and invariant; indeed, the entire point of the construct is to model optimal performance given such knowledge. (Nothing proposed here involves performance superior to the ideal observer in the classical situation.) But in real circumstances, there is almost always uncertainty about the environment, outside of the imaginary world of the well-defined and infinitely repeated random experiment. Real environments exhibit uncertainty, not only about the outcomes of individual trials but also about the underlying governing probabilistic schema. In such environments, an “overlyidealized” ideal observer lacks robustness and can perform poorly when conditions stray from the assumptions.

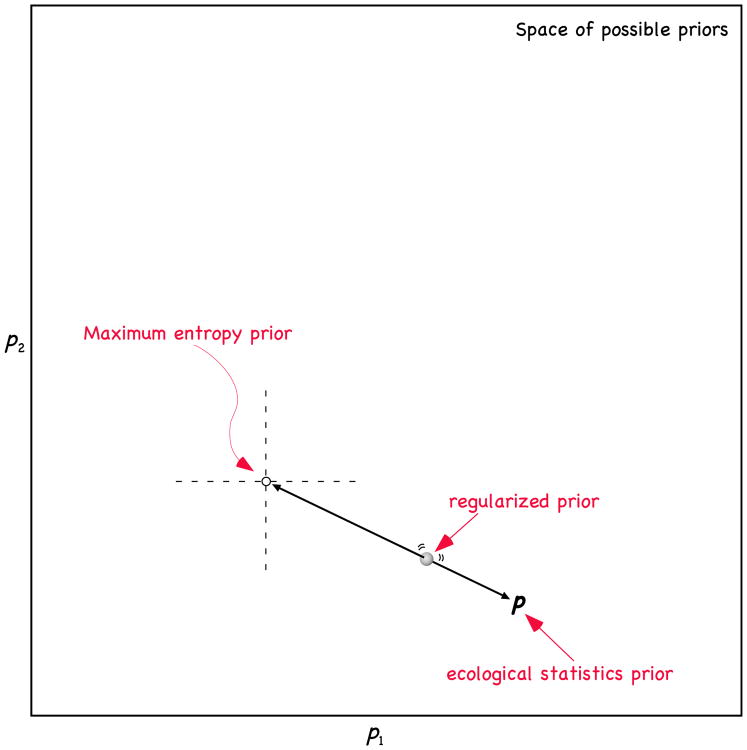
11. The regularized ideal observer

This leads to the idea of the regularized ideal observer, illustrated graphically in Fig. 4. The regularized ideal observer is really a spectrum of possible priors, with the classical ideal observer having D(p║q) = 0 (i.e., p = q) at one pole and a completely entropic prior at the other. (This is not Jaynes' maximum-entropy prior, which already incorporates everything that is known, but the prior with maximum entropy given the hypothesis space alone—e.g., equal priors on all hypotheses.)

Fig. 4.

The class of regularized priors, depicted as a “bead on a string” connecting the ecological prior to the point of maximum entropy. Sliding the bead all the way to the maximum-entropy point ignores past experience; sliding it all the way to the ecological prior sacrifices robustness against uncertainty.

As a concrete example, imagine you have a coin that has been flipped some large number of times and come up heads 57% of the time. What prior should one use in the future? The “frequentist prior” is p(h) = .57. The answer based on symmetry considerations alone (two apparently similar sides, treat them equally) is p(h) = 0.5. The regularized ideal prior is the class of priors in between, that is, 0.5 < p(h) < 0.57. The regularized prior can be thought of as a “bead on a string” connecting these two poles (Fig. 4).

Why would one choose to disregard, or partly disregard, empirical evidence that the truth is .57? That is, why would one push one's bead away from the ecological prior? Again, the answer is uncertainty about the model of the environment. If the environment from which the prior data were drawn were really a fixed stochastic source, with all nuisance variables randomized (as in a Fisherian experiment), then conventional methods of estimating the heads probability would apply, leading to an estimate that balanced the influence of the data and the influence of the prior according to Bayes' rule. But if the environment is not assumed fixed, then no matter how much data one has in support of the model in which h has probability p(h), there is residual uncertainty about whether that model will continue to apply identically in the future. Conventional estimation procedures designed to robustly estimate the prior, such as cross-validation, are aimed at stabilizing the estimate of the (presumed fixed) generating distribution of past performance. But as per Hume, the future is not guaranteed to resemble the past. The uncertainty is not statistical but ontological. How do we know that future observations will reflect, so to speak, the same coin? And how will we perform with different but similar coins? Believers in the Lord's prior assume that future observations of the same environment will, by definition, represent ever more flips of the same coin. But for an organism in a natural environment, subject to inevitable change, this assumption is baseless—an implicit invocation of the “frequentist fantasy” of infinitely repeated random experiments. To assume a fixed, repeating probabilistic model is essentially wishful thinking, lacking evidential support, and impossible even in principle to support empirically. Instead of assuming that the world will continue identically into the future, an intelligent observer ought to guard against the inevitable modification of conditions. To accomplish this, the prior must, to some degree, be regularized away from past data.

So we can remedy the situation by assuming that the prior has some uncertainty, that is, noise, around it. Fortunately, it is easy to predict, at least in a general way, how probability distributions change when noise is added to them: Their entropy increases. This point is illustrated schematically in Fig. 5, which shows how a particular prior (here, a distribution of p over hypotheses) generally increases in entropy when random probability noise (another distribution chosen independently) is added. This is essentially the second law of thermodynamics. Technically, we would say that entropy function is concave, meaning that for independent distributions p (here, the prior) and e (here, the noise), entropy is superadditive, H(p + e) ≥ H(p) + H(e).

Fig. 5.

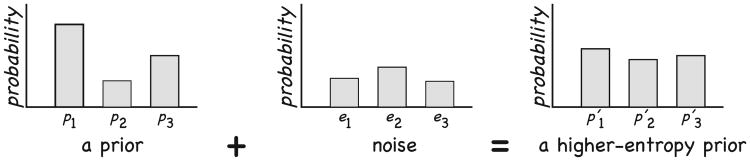
When probability noise is added to a prior, the result is (usually) a higher-entropy prior.

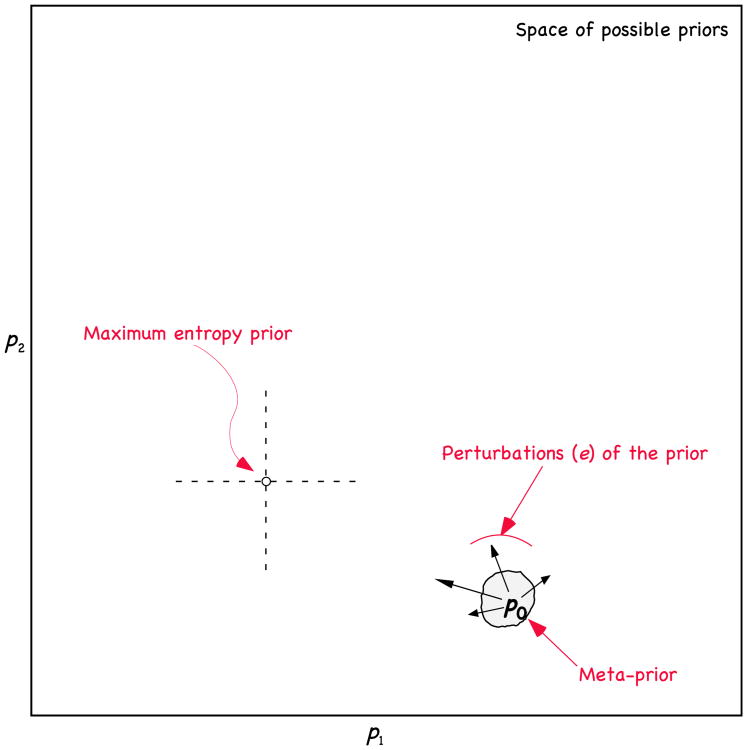
Fig. 6 illustrates the same idea in “prior space,” the space of possible priors p (here depicted two-dimensionally, but the same applies in higher dimensions). If the true prior p is perturbed, the prior tends to move in the direction of maximum entropy. Our coin with observed frequency 57% heads might actually have higher than 57% probability of heads, but it is more likely to have less (i.e., closer to 50%), giving it higher entropy. This effect becomes more extreme the higher the dimension; the more degrees of freedom in the prior, the more likely they will blur when noise is added, resulting in greater entropy.

Fig. 6.

A probability space {p₁,p₂} (with p₃ = 1 − p₁ − p₂; the prior with maximum entropy is at {1/3,1/3}). The figure illustrates what happens when probability noise is added to a given “meta-prior,” or population mean from which priors are drawn. Noise can move the prior in any direction, but it usually moves it in a direction that increases entropy.

If there is any uncertainty about the true prior, or (equivalently) any doubt that future instances will be drawn from the same distribution as past ones, then a regularized ideal observer is superior to a classical ideal observer. In this sense, the regularized ideal observer might reasonably be called “super-ideal,” or perhaps more accurately “robust-ideal.” It is robust in a number of senses: against noise, against faults in the assumptions about the environment, and against actual changes in the nature of the environment; and for all these reasons is more portable into moderately different environments. From an epistemic or subjectivist perspective, these are all essentially equivalent conditions: They all reflect subjective uncertainty about the priors governing future generation of data.

Naturally, there are many ways to construct a suitably regularized prior; the above construction is intended only as an instructive illustration. The main constraints are (a) that the prior should be understood as a state of belief rather than an objective fact about the environment, and (b) that beliefs about the environment are uncertain. These constraints imply, contrary to widespread intuition, that there is no one true prior (i.e., the Lord's), but rather a family of possibilities from which to choose. As mentioned above, one well-developed approach that accommodates these constraints is hierarchical Bayes (Gelman, Carlin, Stern, & Rubin, 2003; Goodman et al., 2011; Salakhutdinov et al., 2010). In these models, priors are drawn from analytical families that are themselves parameterized by higher level parameters (hyperparameters) which themselves have prior distributions. In this way, the prior can be adapted flexibly to the environment, estimated in a suitably regularized manner based on environmental data. Critically, this approach entails that while some values of the parameters might work better than others, there is no one “true” prior.

12. Conclusion

The idea that perceptual and cognitive mechanisms derive their success in part from a meaningful connection to the statistics of the natural world, perhaps first suggested by Brunswik (1956), and greatly extended by many more recent authors, is a profound insight. An agent's choice of priors, implicitly entailed by its decisions and behavior, has tangible implications; if they are misset, performance is materially diminished. But how exactly do you set the priors to achieve optimal performance? The argument in this article is that the contemporary fashion of setting them from tabulations in the environment has deep conceptual problems, invoking a hodgepodge of conflicting ideas from Bayesian and frequentist camps that would be accepted by neither. As Jorma Rissanen, the founder of Minimum Description Length theory, remarked about setting the prior: “[o]ne attempt is to try to fit it to the data, but that clearly not only contradicts the very foundation of Bayesian philosophy but without restrictions on the priors disastrous outcomes can be prevented only by ad hoc means” (Rissanen, 2009, p. 28).

This article develops techniques for conceptualizing the prior that (a) avoid contradictions with the foundations of Bayesian inference, and (b) suitably restrict—or, more properly, regularize—its relation to the environment. In the Bayesian tradition, the observer's prior may legitimately be based on any kind of knowledge or beliefs, including but not limited to data about frequencies. Of course, some subjective priors are better than others. From an evolutionary point of view, the best prior is one that maximizes adaptive fitness, not one that happens to agree with a relative frequencies in the environment (cf. Hoffman, 2009; Mark et al., 2010). The main point of this article is that “Bayesian frequentist” attitudes—faith in the Lord's prior—are not only epistemologically naive but, moreover, risk overtuning. Overtuning, in turn, leads to a fragility of performance in future encounters with the same class of environments, which is maladaptive. Priors must be suitably regularized to truly optimize the fit between mind and world.