The force-frequency relationship: insights from mathematical modeling

Abstract

The force-frequency relationship has intrigued researchers since its discovery by Bowditch in 1871. Many attempts have been made to construct mathematical descriptions of this phenomenon, beginning with the simple formulation of Koch-Wesser and Blinks in 1963 to the most sophisticated ones of today. This property of cardiac muscle is amplified by β-adrenergic stimulation, and, in a coordinated way, the neurohumoral state alters both frequency (acting on the sinoatrial node) as well as force generation (modifying ventricular myocytes). This synchronized tuning is needed to meet new metabolic demands. Cardiac modelers have already linked mechanical and electrical activity in their formulations and showed how those activities feedback on each other. However, now it is necessary to include neurological control to have a complete description of heart performance, especially when changes in frequency are involved. Study of arrhythmias (or antiarrhythmic drugs) based on mathematical models should incorporate this effect to make useful predictions or point out potential pharmaceutical targets.

You have made my heart beat faster with a single glance of your eyes

Song of Solomon 4: 9–10

in this essay, we review the different attempts that have been made to understand the force-frequency relationship from a quantitative point of view. This intrinsic property of cardiac muscle results in increased force at higher frequencies. Additionally, this property is modulated by the neurohumoral state. We clarify the concept that heart frequency and force development are not independent entities; rather, they are consequences of the neurohumoral state, and, as such, it cannot be overlooked in the development of mathematical models of the heart.

In 1871, Bowditch observed that, in the frog heart, the force of contraction was markedly influenced by the frequency of stimulation with a positive correlation. Bowditch's staircase phenomenon (“treppe”) was later reproduced in 1902, when Woodworth worked with the perfused apex of a dog heart. He also verified the all-or-none principle (the “law of maximal contraction”) and put forward the optimal interval concept. The all-or-none principle states that once a stimulus reaches the threshold to elicit a contraction, further increasing the stimuli's amplitude will not result in a bigger contraction. The optimal interval concept establishes that there is an specific temporal separation between stimuli that produces maximum force. Although Bowditch had already postulated that this effect was the result of two opposing influences, Woodworth expressed it in a more articulated way: “The length of the optimum interval is governed by the interplay of two opposing factors . . . the stimulating effect of a rapid succession of contractions and the recuperative effect of a long pause” (60). While those findings were of primary importance, they were not recognized for a long time. One explanation is that they were overshadowed by Starling's discovery in 1918 of the regulation of the heart through fiber length. This new concept seemed to explain almost all the phenomena involving cardiac force regulation, including the interval-force relationship.

Attention to the staircase effect was revived by a publication by Hadju and Szent-Gyorgyi in 1952 (15), where the authors explored the effect of temperature and ion composition on the treppe from a frog heart. They were assisted by the advancements in technology at that time, which rendered it possible to do isometric recordings. Ten years later, Koch-Weser and Blinks, in a encompassing review (24), presented a quantitative approach to the phenomena. According to these authors, changes in the force by altering the interval between contractions could be explained by the interplay of three factors: the negative effect of activation (NIEA), the positive effect of activation (PIEA), and the rested state contraction (RSC). Every time the heart contracts, it produces changes in the muscle that are unfavorable for the development of force in the subsequent beats (NIEA). This would be the reason why one contractions obtained right after another have smaller amplitudes. In the same way, a contraction also induces a set of modifications that favor the development of force in the following beats (PIEA). This explains the gradual increase in force when switching from low to high pacing. These two accumulative effects have different persistence on the muscle. If there was a pause long enough, both effects would disappear, and the heart would produce a contraction independent of the previous beats: the RSC. Following the rationale of Koch-Weser and Blinks, the amount of contraction at a given time would be equal to the RSC minus the accumulation of NIEA plus the accumulation of PIEA.

Both effects followed an exponential decay. NIEA had a strong effect but disappeared quickly, whereas PIEA was small but long lasting. Differences in the kinetics and amplitude of these effects were responsible for the diverse shape of force-frequency plots reported at the time (positive, negative, or biphasic). These parameters varied between species and even between atria and ventricles of the same heart. No physical counterpart was assigned to either component of their theory, but it was the first attempt for a quantitative analysis of the force-frequency relationship (Fig. 1).

Fig. 1.

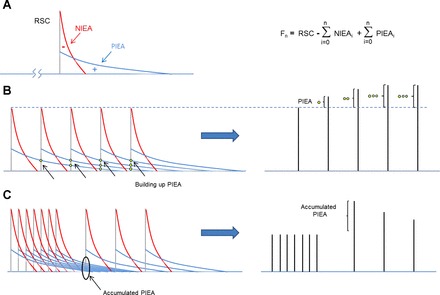
Koch-Wesser and Blinks proposal to calculate the effects of intervals between beats on force generation. A: every contraction can be characterized by the following three elements: the rested state contraction (RSC; gray line), the negative inotropic effect of activation (NIEA; red line), and the positive effect of activation (PIEA; blue line). At any beat (n), force (F_n) can be calculated as the RSC minus the accumulated NIEA (NIEA_i) plus the accumulated PIEA (PIEA_i). B: as the frequency of stimulation increases, more PIEA is accrued, explaining the gradual increase in force when switching from low to high pacing. C: changing from high to low frequency will build up PIEA, which gradually decreases, explaining “postrest potentiation.”

Although Alexander Sandow had already coined the term “excitation-contraction coupling” (E-C coupling) by that time (53), the role of Ca²⁺ as the link (coupling) between the stimuli (excitation) and muscle activation (contraction) was still controversial. The importance of Ca²⁺ in contraction was clear since 1883, from work by Ringer (51), and roles of sarcoplasmic reticulum (SR) Ca²⁺ transport and Ca²⁺ current were identified in the 1960s. However, the development and improvement of Ca²⁺-imaging techniques allowed more full understanding of the phenomenon. A key confirmation of the crucial function of this ion came in 1978, with the work of Allen and Blinks, who measured intracellular Ca²⁺ concentrations with aequorin. They showed that standard inotropic interventions were consequences of increasing intracellular Ca²⁺ (1). Ca²⁺ has now gained a central place in the field of E-C coupling. The standard description of the events that take place after a stimulus is as follows (3): at every depolarization, voltage-sensitive Ca²⁺ channels open and generate an influx of this ion into the cardiac cell. This Ca²⁺ partly goes to the cytosol, but, most importantly, induces an additional Ca²⁺ release from the SR in a process termed “Ca²⁺-induced Ca²⁺ release.” This increase in cytosolic Ca²⁺ levels makes this ion bind to the myofilaments and generates a contraction. For the cell to relax, Ca²⁺ levels have to return to their original values. This is achieved by means of Ca²⁺ pumps located in the SR [sarco(endo)plasmic reticulum Ca²⁺-ATPase (SERCA pump)] as well as in the membrane (sarcolemmal Ca²⁺ pump). The former resequesters Ca²⁺ back to the SR, whereas the latter extrudes Ca²⁺ from the cell. An additional contribution to remove Ca²⁺ is provided by the Na⁺/Ca²⁺ exchanger (NCX) and mitochondrial Ca²⁺ uptake, but SERCA and NCX are the dominant processes (3).

In a simplified view, we can consider NIEA as the result of SR Ca²⁺ refilling kinetics, SR Ca²⁺ content, and, importantly, the refractoriness of the release process. After a stimulus, enough time has to elapse for the Ca²⁺ reuptake process to be complete and for the release process to recover from the prior beat (4). If the interval between twitches is too short, the SR Ca²⁺ content may not have recovered, and even then the release process may not have yet recovered. The result is a smaller contraction will ensue (i.e., NIEA). On the other hand, PIEA can be attributed to the facilitation property of the L-type Ca²⁺ channel and to increased SR Ca²⁺ content. The former is due to positive feedback via Ca²⁺/calmodulin-dependent phosphorylation of the L-type Ca²⁺ channel (8), although larger Ca²⁺ transients also exert negative feedback via Ca²⁺-dependent inactivation of Ca²⁺ channels. The increased SR Ca²⁺ loading is due to enhanced SR Ca²⁺ uptake during the Ca²⁺ transient, which is facilitated by a frequency-dependent acceleration of SERCA function and contributes to frequency-dependent acceleration of relaxation (8). The SR can also lose Ca²⁺ during diastole (Ca²⁺ leak), so the shorter diastolic interval at higher heart rate also limits the loss of SR Ca²⁺ between beats, thereby contributing to PIEA. Notably, the rate of SR Ca²⁺ leak can also vary in different species and conditions (31). It is clear now that any maneuver that increases the intracellular Ca²⁺ transient will have a positive inotropic effect. Likewise, procedures that decrease the transient will produce a negative effect on the contraction. All the mechanisms involved in cardiac E-C coupling possess intrinsic dynamics, such as inactivation, recovery, and refractoriness. There is a finite time for the processes to be completed and return to the starting conditions. There is also a modulatory effect of intracellular Ca²⁺ on the Ca²⁺ current itself: Ca²⁺-dependent inactivation (5) and the Ca²⁺-dependent facilitation mentioned above. When there is a change in the interval between stimuli, the ensuing Ca²⁺ transient will be the result of the new settings for each of the systems (e.g., refractoriness of the SR release, how many channels have returned from the inactivated to close state, and levels of intracellular Ca²⁺ and Na⁺ at that moment). To follow these multiple paths is not an easy task, and sometimes the results are counterintuitive (and thus the need of mathematical models to track the interactions among the different mechanisms involved in the generation of a cardiac contraction).

Such a task started in the early 1960s, when mathematical modelers adapted Hodgkin and Huxley formalism to reproduce the cardiac action potential (AP) (46). In 1962, Dennis Noble published the first reconstruction of the AP of pacemaker Purkinje fibers (36); furthermore, he improved it in 1975 with the inclusion of Ca²⁺ current in the McAllister, Noble, and Tsien model (33). However, this new current's main purpose was restricted to generate the typical plateau phase of the cardiac AP. Beeler and Reuter were the first to explicitly model the so-called slow inward current, as a link between the electrical activity of the membrane and the contractile response of the myocyte (2). This description was enhanced by DiFrancesco and Noble with the incorporation of newly described mechanisms in addition to ionic currents: electrogenic pumps and exchangers and buffers inside the cytoplasm. More importantly, this novel formulation incorporated the presence of the SR as an intracellular compartment with two functions: uptake and release of Ca²⁺ (9). We can consider the DiFrancesco-Noble model as the minimum representation to simulate Ca²⁺ fluxes in the myocyte. It comprised routes of Ca²⁺ entry through Ca²⁺ channels (and NXC), intracellular compartments for release, resequestration and accumulation, and finally Ca²⁺ extrusion via the exchanger and pumps. In the 1990s, Yoram Rudy published a series of papers describing an expanded model of the guinea pig ventricular myocyte (29, 30, 61). These included a comprehensive list of new ionic currents in addition to novel formulations of the existing ones. Buffers were included in the cytoplasm (troponin and calmodulin) as well as in the SR (calsequestrin). By that time, there was a clear shift from general models that integrated voltage-clamp data from several species to particular models based on data gathered from a single species. Models for different species started to be published, e.g., rat models from Pandit et al. (40, 41), canine models from Winslow and colleagues (ventricular myocyte) (14, 59) and Nattel and colleagues (atrial model) (23, 47), and rabbit models from Bers and coworkers (45, 56). Among all these species-specific models, the most sought after was the human one, which was no trivial task due to the lack of experimental data for validation. Although there were several models published in the late 1990s, such as those by Nygren et al. (38), Courtemanche et al. (7), and Priebe and Beuckelmann (44), the most influential was the one developed by Ten Tuscher et al. in 2004 (58). More recently, Bers and colleagues (11) published a formulation with realistic repolarizing K⁺ currents and Ca²⁺ handling, which was followed by one by O'Hara et al. (39) that used undiseased human ventricular data.

However, the final player in E-C coupling, the contraction, was still missing in the models. A major impediment was that the interactions between actin and myosin were not very well understood (49), and researchers were content to use Ca²⁺ as a surrogate for force (32, 55). Simulations of the Ca²⁺ transient versus stimulus interval were considered equivalent to the force-frequency relationship. The resulting inotropy can be thought as a consequence of increased Ca²⁺ availability to myofilaments at higher frequencies. During fast pacing rates, more APs create more sarcolemma Ca²⁺ fluxes via Ca²⁺ channels, increasing the SR Ca²⁺ load combined with a reduced time at diastole for Ca²⁺ to be extruded by NCX. A transit time from SR uptake to the release sites (“translocation step”) was instituted to create a delay in Ca²⁺ releasibility at high frequencies (18), although we now know that this delay is predominantly due to the time required for Ca²⁺-release channel restitution (4). Ultimately, mechanical models of the cardiac myocyte started to appear. The original proposal developed by Huxley for skeletal muscle consisted of two states, rested and activated (21), and was now expanded to three (48, 50), four (16, 20), or five (42) or more states (35). These models focused primarily on the myofilaments' interactions, with little attention paid to the events that take place on the membrane; some even used a synthetic Ca²⁺ waveform. This was in part a reflection of how experiments were carried out. Laboratories working with myofilaments did not investigate the effects on sarcolemma Ca²⁺ fluxes, and researchers that focused their work on ionic channels or membrane transporters considered the myofilaments as just passive components. The importance of interactions between the mechanical environment and the electrophysiology of the cell began to be appreciated in the early 1980s (27). It took 10 yr for modelers to start incorporating myofilaments into comprehensive descriptions of the cardiac cell (25, 37), a tendency that was firmly established only recently with the development of the Kyoto model (26, 57), the Rice model (50), the E-C coupling/mitochondrial energetics model (6, 43), or LabHEART 5.3.¹ Finally, it was possible to simulate mechanistically based force-frequency plots.

Parallel to the development of force models, other laboratories started to simulate the results of β-adrenergic stimulation on AP and Ca²⁺ transients. The known effects of isoproterenol on ionic currents and pumps (namely, augmented L-type Ca²⁺ current, delayed rectifier K⁺ current, and SERCA pump activity) were now included in standard formulations (13, 54). These modifications produced higher Ca²⁺ transients (inotropic effect) with faster relaxation rates (lusitropic effect) and shorter APs. These changes allowed the myocyte to accommodate more contractions in less time as well as stronger contractions. It was clear that the heart was adjusting itself to beat at a faster rate and with augmented force; indeed, β-adrenergic stimulation was tuning the heart to develop stronger force at higher frequencies. Again, there was a positive correlation between contraction and stimulation rate, but that was not the effect that Woodworth had observed! The staircase phenomena reported by Woodworth did not involve altering the neurohumoral state. Treppe is an intrinsic characteristic of the heart muscle, and while in vivo, the cardiac system amplifies this property via neurotransmitters to match new systemic metabolic demands (Fig. 2).

Fig. 2.

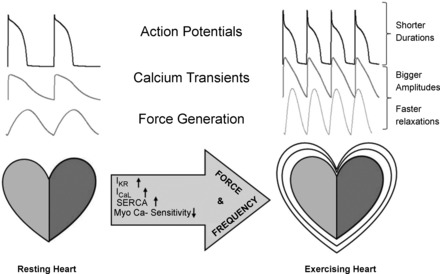
To meet the energetic demands of exercise, the autonomic system alters heart frequency at the level of the sinoatrial node and concomitantly modifies the cell machinery of ventricular cells by altering ionic channels, pumps, and myofilament sensitivity to produce a stronger contraction with faster relaxation. Shown is a simulation of rabbit action potentials, Ca²⁺ transients, and force obtained with LabHEART 5.3. I_Kr, delayed rectifier K⁺ current; I_CaL, L-type Ca²⁺ current; SERCA, sarco(endo)plasmic reticulum Ca²⁺-ATPase.

Force and heart rate go hand in hand.

Using the terms “frequency of stimulation” and “heart rate” indistinguishably causes a subtle misunderstanding. While the former refers to the parameter that researchers modify in their setup to observe alterations in force development by the cardiac cell (or tissue), heart rate is the result of the cardiovascular neurohumoral state. If there is a need for a greater O₂ supply, a chain of modifications is set in motion to cope with the increased demand. Those modifications alter the heart rhythm and force production of each cell of the cardiac muscle, producing changes in frequency and stroke volume. If we consider the heart simply as an oscillator that pumps blood regularly, it is straightforward to show that increasing the frequency alone will not be sufficient to achieve the new metabolic demands. In humans, the number of beats could change from 60 to 180 beats/min (about threefold) while the O₂ requirement increases between 7 and 10 times. Likewise, the range of variation in force production (or stroke volume) is approximately twofold, and this alone also is not sufficient. It is only by the combined increase in frequency and stroke volume that the heart manages to meet the new energetic requirements. β-Adrenergic stimulation, on one hand, accelerates the sinoatrial node in the atrium and, on the other hand, prepares the ventricle to accommodate this higher rate. A ventricular cell beating at 3 Hz has a different “set point” from the one beating at 1 Hz. This fact should make us cautious to extrapolate results obtained in isolated cells or muscle strips where frequency has been independently changed. Modelers should be careful to speculate about the consequences that certain modifications (e.g., channel mutations) have on the behavior of the cardiac cell at different frequencies. To make it more realistic, we should incorporate concomitant modifications that happen in real life, such as an increase in both L-type Ca²⁺ and K⁺ currents with decreased myofilament Ca²⁺ sensitivity. Furthermore, frequency of stimulation and cell machinery need to vary in concordance, and the failure to do so has deleterious consequences. The most obvious case is trying to pace the heart at higher frequencies without the modifications induced by β-adrenergic stimulation in the ventricle. AP durations are not short enough to accommodate the necessary contractions in the given time (Fig. 3A). However, the opposite is also hazardous, for if we apply isoproterenol on an isolated cardiomyocyte and prepare it for a high demanding task but stimulate it at very low frequency, early afterdepolarizations can arise. These abnormal depolarizations occur during phase 2 or phase 3 of the AP and can lead to arrhythmias, but they disappear when the cardiomyocyte is paced at shorter intervals (Fig. 3B). There has to be a concordance between the settings of the cell and the task at sight. This concordance is mediated by the autonomic nervous system.

Fig. 3.

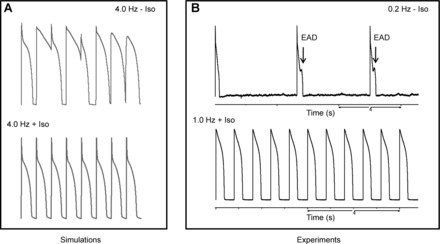
β-Adrenergic stimulation and frequency have to be in agreement. A: simulations of rabbit action potentials. Pacing the cell at a high rate without the modifications induced by β-adrenergic stimulation generated alterations on the action potential waveform. These variations disappeared after the inclusion of isoproterenol (Iso)-induced effects. B: experiments with guinea pig ventricular myocytes. Application of Iso to the cells and pacing at a very low frequency (0.2 Hz) caused early afterdepolarizations (EADs). These afterdepolarizations disappeared when the frequency of stimulation was increased.

This has been elegantly demonstrated in a series of experiments performed in conscious dogs by Ross and colleagues in 1990. They verified the dose-dependent action of β-adrenergic stimulation to enhance the force-frequency response (22, 34). This group also showed that in heart failure, the intrinsic force-frequency response is depressed; however, most importantly, the amplification effect was lost because there was a failure to enhance the force-frequency relationship (10). This lack of concordance explained the impaired exercise performance observed in heart failure (52). Physiological force-frequency plots should be positive and incorporate sympathetic effects on channels, transporters, and myofilaments because this is part of how the heart rate increases physiologically. Indeed, the reason for the heart to beat faster is to pump more blood. A negative correlation is incompatible with the intended outcome.

Conclusions.

Mathematical models capable of simulating the force-frequency relationship have come a long way since the Koch-Wesser and Blinks proposal. With the new knowledge of Ca²⁺ fluxes and signaling pathways, a more accurate picture has emerged, e.g., the effect of Ca²⁺/calmodulin-dependent protein kinase II has been subjected to intense research and modeling (12, 17, 19). Contrary to skeletal muscle, where more fibers are recruited as the load increases, all of the heart's fibers are engaged in every beat. The mechanism by which the heart copes with the higher load is to amplify the intrinsic force-frequency relationship of each myocyte, achieved through neurological stimulation. The fact that models can now simulate β-adrenergic effects, pacing them at different frequencies, allows us to see that these two factors are intertwined. β-Adrenergic effects and frequency need to accompany each other or else harmful effects could ensue, as frequency is not an independent variable in the heart. The results obtained by researchers where the pacing of stimulation is altered but without the addition of β-adrenergic agonist can now be complemented by mathematical models to depict a more realistic scenario. Plots like rate adaptation or AP duration versus cycle length should be mapped into the neurohumoral state. In this way, models will provide richer information about cardiac performance in a continuously adapting environment. Mathematical models will need to include the neurohumoral state, at least in a stepwise fashion, to provide important insights about arrhythmias (or antiarrhythmic drugs). While cardiac modelers have already linked the mechanical with electrical systems in their formulations, we now need to add neurological modulation. To properly reproduce the convergence of cardiac chronotropy and inotropy (28), the new generation of models, of which we have already seen examples (13, 54), will have to include neurological control on the intrinsic feedback of the cardiac cell. Conceivably, we could finally simulate one important fact of life: that our heart beats faster (and stronger!) with the adrenaline rush from the glance of our lover's eyes.

GRANTS

This work was supported by National Institutes of Health Grants R37-HL-30077 and P01-HL-80101 (to D. M. Bers) and R03-AG-031944 and R01-HL-90880 (to Y. Chen-Izu).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.L.P., J.A.N., and Y.C.-I. conception and design of research; J.L.P. prepared figures; J.L.P. and J.A.N. drafted manuscript; J.L.P., J.A.N., and Y.C.-I. edited and revised manuscript; J.A.N., Y.C.-I., and D.M.B. approved final version of manuscript.