Folding and Binding of an Intrinsically Disordered Protein: Fast, but Not ‘Diffusion-Limited’

Abstract

Coupled folding and binding of intrinsically disordered proteins (IDPs) is prevalent in biology. As the first step toward understanding the mechanism of binding, it is important to know if a reaction is ‘diffusion-limited’ as, if this speed limit is reached, the association must proceed through an induced fit mechanism. Here, we use a model system where the ‘BH3 region’ of PUMA, an IDP, forms a single, contiguous α-helix upon binding the folded protein Mcl-1. Using stopped-flow techniques, we systematically compare the rate constant for association (k₊) under a number of solvent conditions and temperatures. We show that our system is not ‘diffusion-limited’, despite having a k₊ in the often-quoted ‘diffusion-limited’ regime (10⁵–10⁶ M^–1 s^–1 at high ionic strength) and displaying an inverse dependence on solvent viscosity. These standard tests, developed for folded protein–protein interactions, are not appropriate for reactions where one protein is disordered.

Introduction

It has long been assumed that the specific, folded, three-dimensional structure of a protein was a prerequisite for its function in the cell. More recently, it has been recognized that many of Nature’s proteins have no fixed structure,¹ instead occupying an enormous number of rapidly interconverting conformations.² These intrinsically disordered proteins (IDPs) are widespread in biology³ and, despite their lack of structure, perform many important functions in the cell.⁴ One of the ways Nature has utilized this disorder, and maintained it in evolution, is in the form of ‘coupled folding and binding’ whereby an unstructured IDP gains structure only when bound to a target protein.⁵ This mode of protein–protein interaction presents an alternative to that between the typically large, flat interfaces between two already folded proteins. There are many potential advantages for these protein–protein interactions⁶ which could explain the high abundance of IDPs in signaling processes and their abundance in eukaryotic cells that rely more on complex signaling pathways.³

Protein–protein interactions do not lead to static complexes, as might be inferred from the thousands of structures in the protein data bank. The cell does not rest at equilibrium and the association and dissociation of proteins plays a major role in the complex pathways of life. Acquiring kinetic rate constants is vital to building up models of these pathways.^6,7 Understanding the mechanisms of binding, the structural changes to get to the final structure, sheds light on the molecular principles Nature uses to tune these rate constants. Due to their recent recognition, relatively few kinetic studies of IDP binding have been conducted⁸ and even fewer have had any mechanistic details probed.⁹⁻¹² A central question has been whether only lowly populated states of an IDP, similar in structure to the bound form, can bind their target (the conformational selection mechanism), or whether disordered protein chains gain structure and ‘fold’ upon contact with their partner protein (the induced fit mechanism).¹³

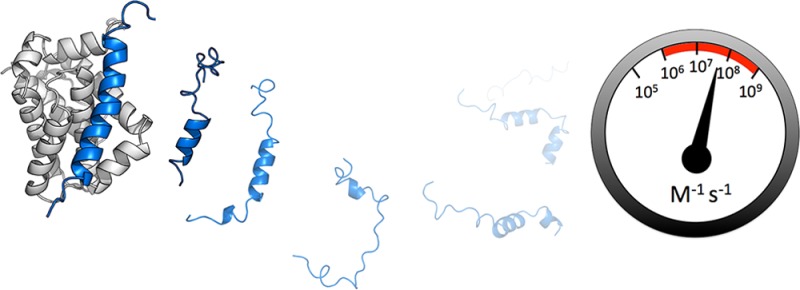
The maximum rate that two proteins can come together is physically limited by the speed that, through perpetual random collisions with solvent molecules, they diffuse and rotate through solution before colliding with the correct orientation. This speed limit for association has been labeled the ‘diffusion-limit’ and, when applied to two folded proteins interacting, is traditionally characterized by an association rate constant in the order of 10⁵–10⁶ M^–1 s^–114 and a predictable (inverse) dependence on solvent viscosity.^15,16 For two folded proteins, since there are clear binding sites and defined unbound states, the ‘diffusion-limited’ association rate constant can be predicted.¹⁷ However, a similar predictor for ‘diffusion-limited’ IDP association is significantly more difficult due to the highly dynamic nature of the unbound IDP. This is unfortunate, since the issue of the ‘diffusion-limit’ is of particular importance in IDP coupled folding and binding as it has a mechanistic interpretation. Hammes et al.¹⁸ describe how it is insufficient to consider just the rate constants for the induced fit and conformational selection mechanisms and ‘flux’ through both pathways must be considered. However, in a hypothetical ‘diffusion-limited’ reaction, every correctly oriented collision between protein partners successfully leads to the final bound complex. For an IDP association to be ‘diffusion-limited’ all collisions with structured and unstructured chains must be successful and, given that (by definition) most of the conformations of an IDP are unstructured, essentially all flux must be through the induced fit mechanism.^13,19 Experimentally, this regime could be detected if the overall rate constant for association (i.e., grouping all unbound states together and following this group’s conversion to the final bound complex) is consistent with that of a ‘diffusion-limited’ reaction.

One cellular process that relies heavily on these coupled folding and binding reactions is that which controls apoptosis, programmed cell death.²⁰ The mammalian Bcl-2 family contains a number of homologous proteins that fold to a globular, helical structure with a deep groove on the surface.²¹ This groove can accept a conserved protein sequence (labeled the BH3 region) from another Bcl-2 family member.²⁵ Many proteins that contain this BH3 region are predicted to have significant stretches of disorder, and peptides corresponding to this region are shown to be unstructured in isolation, forming an α-helix only upon binding this groove.²⁰ The Bcl-2 family’s control of apoptosis depends on the different expression level, cell localization and binding affinities of these ‘coupled folding and binding reactions’. Through a complex balance of sequestering and release of the lethal proteins BAX and BAK, these protein–protein interactions control the permeabilization of the mitochondrial outer membrane and consequently, cell death.²⁵

This study examines the association of two components from the Bcl-2 family, the folded protein Mcl-1 and a peptide mimic of the unstructured, ‘BH3-only’ protein PUMA. In the bound structure (Figure 1A), PUMA folds to form a long α-helix with six complete turns when bound to Mcl-1.²⁶ This single, contiguous element of secondary structure makes this an ideal model system to investigate the mechanism of IDP coupled folding and binding. Given the small size and the simple topology of the bound peptide,²⁷ is it possible that the ‘folding’ is sufficiently fast that the speed limit for association is reached and the reaction be described as ‘diffusion-limited’? We assess this question experimentally by systematically determining the rate constants for association in a number of solvent conditions and temperatures. In the process, we critically assess the appropriateness of current methods and assumptions, previous developed for folded proteins, in the labeling of an IDP coupled folding and binding as ‘diffusion-limited’.

Figure 1.

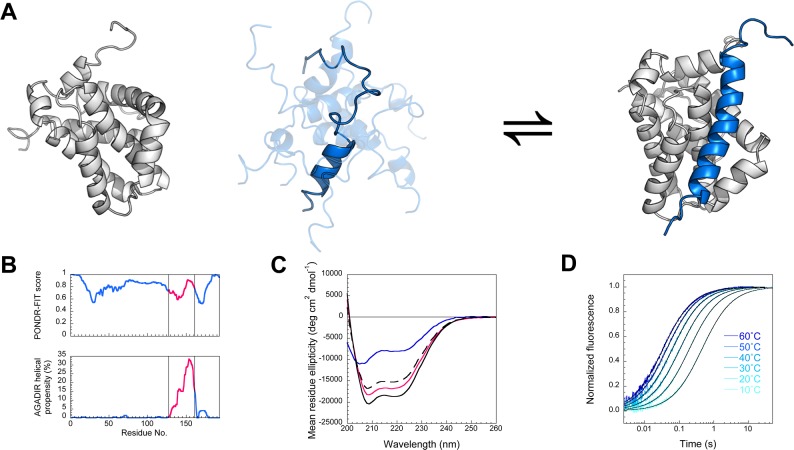
(A) Cartoon depicting Mcl-1 (gray) binding PUMA peptide (blue). Unbound Mcl-1 is based on pdb 1WSX, ensemble of structures of unbound PUMA peptide built using Chimera (UCSF)²² and bound structure is based on pdb 2ROC. Figure prepared using PyMol. (B) Full-length PUMA is predicted to be entirely disordered, producing a PONDR-FIT²³ score 0.5–1.0, and has residual helicity only in the BH3 region used in this study (magenta), as predicted by the helical propensity predictor AGADIR.²⁴ (C) Consistent with a coupled folding and binding reaction, PUMA peptide binds Mcl-1 with an increase in helicity, as shown by circular dichroism. The 1:1 complex (black solid line) has a greater α-helical signal than the spectrum predicted for no interaction (dashed line), which is the sum of the PUMA alone (blue) and Mcl-1 alone (magenta) spectra. (D) Kinetics of association between Mcl-1 and PUMA peptide could be followed by stopped-flow fluorescence. An increase in temperature accelerates association. Fits for irreversible association (eq 3) are shown as black lines.

Results

Spectroscopic Studies Reveal Coupled Folding and Binding

NMR structures have been solved for Mcl-1 in isolation (pdb 1WSX)²⁸ and bound to a 27 aa PUMA peptide (pdb 2ROC)²⁶ (Figure 1A and Figure S1). The backbone atoms for Mcl-1 in these two structures overlay with an RMSD of 1.78 Å, consistent with only minor conformational changes in Mcl-1: a slight opening of the surface groove, upon binding the PUMA peptide (Figure S1). Full-length PUMA is 193 aa long (Figure S2B) and is predicted to be entirely disordered²³ (Figure 1B). For this study, a longer PUMA peptide than that used in the NMR structure was chosen, 34 aa (Figure S2A), and the termini were acetylated/amidated to remove the terminal NH₃⁺ and COO^– charges. This longer, capped, PUMA peptide was chosen as a better mimic of the peptide in the context of the full length PUMA protein. Further, studies have shown that residues outside the canonical BH3 binding region can significantly affect the binding strength of peptide mimics.²⁹

Circular dichroism (CD) spectroscopy is a convenient bulk measurement to quantify secondary structure in peptides and proteins.^4,24 Consistent with a coupled folding and binding reaction, CD spectra reveal that our PUMA peptide binds to Mcl-1 to form a complex with increased α-helicity relative to the two proteins in isolation (Figure 1C). From the CD spectrum, it can be calculated that the PUMA peptide has ∼20% residual helicity in the unbound state (in 50 mM PO₄, pH 7.0, 25 °C),²⁴ consistent with the high predicted helicity of the BH3 region in the context of the full-length PUMA protein (Figure 1B). Unexpectedly (at concentrations above 2 μM), this particular PUMA construct also undergoes reversible oligomerization to a highly α-helical structure, as demonstrated by concentration dependent CD spectra, size-exclusion chromatography and denaturing SDS-PAGE (Figure S3). To examine only the monomeric peptide, all other experiments were conducted at PUMA concentrations below 1 μM.

Intrinsic tryptophan fluorescence was also used to probe the structural changes in these proteins upon association. Upon excitation at 280 nm PUMA showed a fluorescence emission spectra characteristic for a solvent exposed tryptophan, producing an emission maximum at 360 nm (Figure S4).³⁰ In contrast, Mcl-1 had a typical fluorescence spectrum for a folded protein, with the buried/quenched tryptophans showing an emission maximum at 330 nm. There was a significant increase in overall fluorescence upon complex formation (Figure S4).

Kinetics of Binding

The large change in intrinsic fluorescence was utilized to follow the kinetics of PUMA associating with Mcl-1 using rapid mixing, stopped-flow techniques. The protein and peptide were mixed at similar concentrations and the fluorescence traces fit well to equations describing irreversible association (eq 3, Methods), with a single association rate constant (k₊) (representative traces are shown in Figure 1D). Traces were also collected under pseudo-first-order conditions⁹ (Supplementary Methods, Figure S5). Only one kinetic phase was seen in all experiments. The fitting of all traces gave a concentration independent estimate of the rate constant of association ⟨k₊⟩ = 1.59 (±0.06 s.e.m.) × 10⁷ M^–1 s^–1.

No solvent conditions could be found where preformed Mcl-1 PUMA complex could be observed to dissociate without unfolding the structured Mcl-1. These included using chemical denaturants, lowering the total protein concentration, and altering the temperature. This suggested very tight binding for the complex, consistent with the previously reported equilibrium binding constant (K_d) for the peptide used in the NMR structure, determined by isothermal titration calorimetry (ITC), (0.69 nM).²⁶ As described above, our PUMA construct undergoes oligomerization and, due to the high concentrations required for the technique, precludes accurate determination of the K_d by ITC. Instead, to estimate the K_d, Mcl-1 and PUMA solutions were manually mixed at nanomolar concentrations and the fluorescence followed (Supplementary Methods, Figure S6). At these lower concentrations, closer to the estimated K_d, kinetic traces should no longer fit to the equations that describe irreversible association.³¹ This was indeed observed: by fitting instead to a model including both the association and dissociation reactions (Supplementary Methods), the dissociation rate constant (k_–), and therefore equilibrium binding constant, could be obtained ⟨k_–⟩ = 1.6 (±0.5 s.e.m.) × 10^–3 s^–1, ⟨K_d⟩ = 0.10 (±0.03 s.e.m.) nM.

Magnitude of k₊, Ionic Strength, and Viscosity Dependence Are Consistent with ‘Diffusion-Limited’ Association

The association rate constant (k₊) for a ‘diffusion-limited’ reaction can be predicted using a simple model.^15,32 Modeling the proteins as two, uniformly reactive, spheres diffusing in solution, these will collide with a rate constant described by Smoluchowski-Stokes’ equation (eq 1),

1

where T is the temperature, R the gas constant, η the viscosity of the solution, and r_A and r_B are the hydrodynamic radii of the two proteins. For two proteins of equal radii, in water at 25 °C, this gives k₊ = 7.4 × 10⁹ M^–1 s^–1. This is the upper limit for k₊; indeed, in the absence of electrostatic effects, no protein–protein association rate constant has been measured that breaks this limit.¹⁷ This k₊ estimate is relatively size independent, and using estimates for the hydrodynamic radii R_h (Supplementary Methods) for Mcl-1 and PUMA gives k₊ = 7.7 × 10⁹ M^–1 s^–1. These are overestimates of the ‘diffusion-limited’ rate constant as proteins tend to not be uniformly reactive over their entire surface and must, through rotational diffusion, collide with the correct orientation e.g. Mcl-1 has a clear binding site for the PUMA peptide. Such reactions can still be ‘diffusion-limited’ but this orientation requirement can reduce k₊ by many orders of magnitude. Many theoretical studies introduce a constant (e.g., A) in front of eq 1 to account for this^33,34 (eq 2),

2

This gives the quoted range (10⁵–10⁶ M^–1 s^–1) for a ‘diffusion-limited’ reaction¹⁴ and these are confirmed by experimental data on folded protein–protein interactions.¹⁷ The experimental k₊ for Mcl-1 PUMA appears, at first sight, to exceed this ⟨k₊⟩ = 1.59 (±0.06 s.e.m.) × 10⁷ M^–1 s^–1.

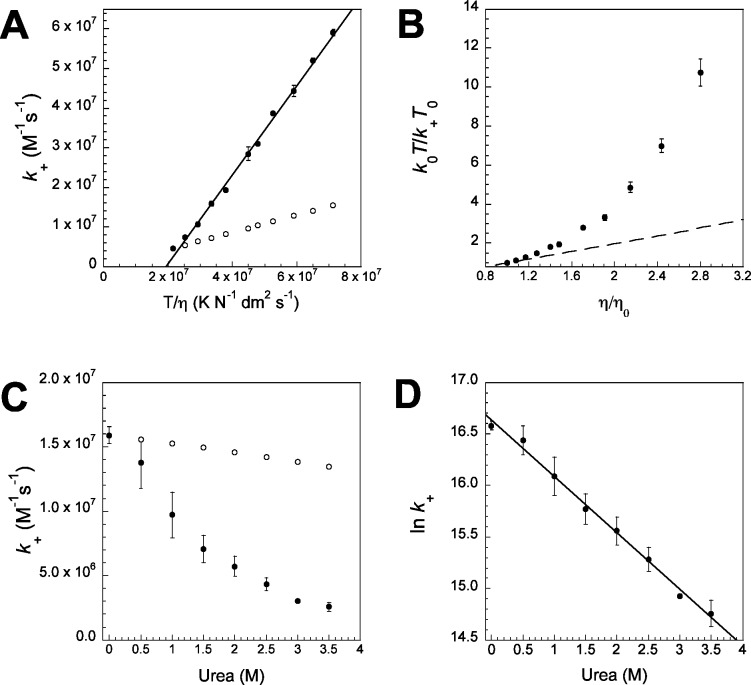
This apparent discrepancy can be explained by long-range electrostatic interactions which have been shown to significantly influence protein–protein association³⁵ and are not taken into account in the model above. At pH 7.0, PUMA and Mcl-1 are estimated to have opposite net charges³⁶ and, to compare with the Smoluchowski result above, these potentially favorable interactions must be taken into account. Salt can be used to screen these interactions and k₊ was measured in solutions with different concentrations of NaCl and therefore, varying ionic strengths (I) (Figure 2A). The results were fit to an empirical relationship between I and k₊(14) (eq 4) (Figure 2A and Figure S7) and the rate constant in the absence of long-range electrostatics (k_+basal) could be estimated k_+basal = 6 (±1) × 10⁵ M^–1 s^–1, that is, comfortably inside the ‘diffusion-limited’ range of 10⁵–10⁶ M^–1 s^–1.

Figure 2.

(A) Association is partly driven by electrostatic interactions between PUMA and Mcl-1 and k₊ is highly dependent on the ionic strength of the solution. Where repeat measurements were made standard errors are shown as error bars. The fit of the data to eq 4 is shown (black line) (see also Figure S7). No buffer specific effects are seen as the rate constant in the standard biophysics buffer (50 mM PO₄, pH 7, I = 109 mM, ○) matches that in the MOPS buffer with I corrected using NaCl (●). (B) k₊ is highly dependent on the solvent viscosity; there is good agreement between the experimental k₊ (●) and the predicted k₊ (k₊ = k₀η₀/η, ○). (C) The standard viscosity plot for relative rate constant vs relative viscosity has a slope close to unity 1.13 ± 0.02 (shown as a black line), for comparison a slope of 1 is shown as a dashed line.

Given that the rate constant, in the absence of electrostatics, k_+basal, suggested a ‘diffusion-limited’ reaction, we sought to confirm this using another assay. If ‘diffusion-limited’, k₊ should be inversely proportional to solvent viscosity (η) (as suggested by eqs 1 and 2)^15,16 and k₊ should be predicted by k₀η₀/η where k₀ and η₀ are, respectively, the rate constant and solvent viscosity in the absence of a viscous cosolvent. We measured k₊ in varying concentrations of the small-molecule viscogen glucose and the observed k₊ did indeed match the predicted rate constant (k₀η₀/η) (Figure 2B) and produce the standard viscosity plot³⁷ (k₀/k₊ vs η/η₀) with the expected slope for a ‘diffusion-limited’ reaction, ∼1 (Figure 2C).

The association of Mcl-1 and PUMA appears to satisfy the two criteria for a ‘diffusion-limited’ reaction: an inverse dependence on viscosity and k_+basal in the range 10⁵–10⁶ M^–1 s^–1. On the basis of these measurements alone, the conclusion could be drawn that the reaction mechanism is induced fit. However, the k₊ range 10⁵–10⁶ M^–1 s^–1 is based on the orientation constraints for two folded proteins associating, and as stated earlier, due to the dynamic unbound state of the IDP, there is no reason to assume this calculated range is appropriate for these ‘coupled folding and binding’ reactions. Also, the use of viscous cosolvents to label a reaction ‘diffusion-limited’ has been criticized.^37,38 To address these issues, we sought further evidence before drawing any mechanistic interpretation.

Temperature and Denaturant Dependence of k₊ Are Not Consistent with ‘Diffusion-Limited’ Association

Continuing to use the simplest spherical model (eq 2), which essentially only considers whole-protein translation and rotation, it was predicted that as temperature (T) was raised k₊ would increase. Higher T facilitates faster diffusion, both through the T term in eqs 1 and 2 and through the reduced viscosity (η) of the aqueous solvent. k₊ does indeed increase with temperature and association is accelerated (see Figure 1D).

In an attempt to determine the orientation constant A in eq 2, k₊ was plotted against T/η (Figure 3A, filled circles). If the reaction was adequately modeled by colliding spheres, and followed eq 2, k₊ should be directly proportional to T/η (e.g., Figure 3A, open circles). This is clearly not the case and a straight line fit of k₊ versus T/η has a non-zero intercept (Figure 3A, filled circles). Alternatively, these data can be plotted in an analogous way to the standard viscosity plot³⁷ (such as the one shown in Figure 2C) providing both sources of temperature dependence are taken into account. If eq 2 were satisfied, then a plot of k₀T/k₊T₀ versus η/η₀ should be linear, with a slope of 1 (dashed line, Figure 3B); however, curvature is observed (filled circles, Figure 3B).

Figure 3.

(A) The experimental association rate constant k₊ (●) is not directly proportional to T/η, as would be predicted for a ‘diffusion-limited’ reaction according to eq 2 (○, arbitrarily drawn through the 10 °C data point). Where repeat measurements were made, standard errors are shown as error bars. (B) Temperature corrected viscosity plot shows clear nonlinearity, in contrast to what is expected for a ‘diffusion-limited’ reaction (gradient of 1 shown as a dashed line). (C) k₊ is reduced by increasing the concentration of the denaturant urea (●) and this effect is not accounted for by the slower diffusion due to changes in solvent viscosity (k₊ = k₀η₀/η, ○). (D) The log of the rate constant is linearly dependent on urea concentration, suggesting that a structured state is being energetically disfavored.

These results suggest that large-scale, whole-protein motion (i.e., modeling as spheres) is not sufficient to explain the temperature dependence of k₊ and, unless the orientation constant A has a strong temperature dependence, the reaction is unlikely to be ‘diffusion-limited’. Simply colliding with the correct orientation is not sufficient for complex formation and the conformations or energetics of the proteins are, in some way, preventing this ‘diffusion-limit’ from being reached. It is interesting to note that as the temperature is raised, the reaction is faster than expected (i.e., in Figure 3A, filled circles have a larger gradient than the open circles). Either higher temperatures are favoring conformations of PUMA that are more binding competent (vide infra) or Arrhenius behavior is occurring and there is an enthalpic barrier to this association reaction.

Urea is a denaturing cosolvent used in protein folding studies to energetically disfavor structured states. Empirically it has been found that the Gibbs free energy of such a state is linearly increased by urea concentration by a constant termed an m-value.³⁹ However, increasing urea concentrations also makes solutions more viscous. If the reaction between PUMA and Mcl-1 is purely ‘diffusion-limited’, and the conformations of the peptide do not affect the speed of the reaction, then k₊ should decrease with concentration of urea in a similar way to glucose, inversely with relative viscosity (N.B. Mcl-1 remains folded, Figure S8). Interestingly, k₊ (filled circles, Figure 3C) decreased by significantly more than what would be expected due to viscosity effects alone (open circles, Figure 3C). Further, the natural log of k₊ against concentration of urea is linear, with a gradient of m = 0.55 (±0.02) M^–1 (Figure 3D). Similar to the temperature dependence, this urea dependence suggests that the conformations and energetics of the proteins are important to the reaction and are, in some way, preventing the ‘diffusion-limit’ from being reached. Further, the linear dependence of ln(k₊) would suggest that a structured state, vital along the binding reaction coordinate, is being energetically disfavored by the addition of urea.

Changes in IDP Ensemble with Solvent Composition and Temperature

Association (at 1–0.25 μM) was effectively irreversible for all solvent conditions. If the reaction were truly ‘diffusion-limited’ the helicity of PUMA should not affect the speed of the reaction as all conformations, if colliding with the correct orientation, would successfully lead to the final complex. Given that the temperature and urea dependence of k₊ suggest that this is not the case, then the conformations of the IDP must be examined. Due to the complications of the peptide oligomerizing at concentrations greater than 2 μM, many experimental techniques to quantify residual structure were not feasible. However, CD could still be used to give a measure of the α-helical content in the unbound state. Qualitatively, the peptide was less helical at higher temperatures (Figure S9). This ‘melting’ of PUMA’s helicity could alter the effective radius of the PUMA peptide and could complicate the analysis of the temperature dependence. However, as mentioned above, eq 1 and eq 2 are relatively insensitive to the radii of the proteins and this effect is unlikely to explain the results seen above (see Supporting Information). The intrinsic helicity of PUMA showed little ionic strength dependence but was reduced in the presence of urea (Figure S9). It is interesting to note that at higher temperatures association was faster than expected, despite the reduced helicity of the peptide, whereas the reverse was true for the peptide in the presence of denaturant. Thus, there is no clear relationship between solvent induced changes in helicity and association rate constant.

Attaching a Molecular ‘Ball and Chain’ Does Not Affect Association

To further investigate the effect of diffusion on the association reaction, an artificial fusion protein was constructed: a 90 aa chain containing a soluble GB1 domain⁴⁰ was fused to the N-terminus of the 34 aa PUMA peptide (GB1-PUMA) (Figure 4A and Figure S2D) to act as a molecular ‘ball and chain’. This extension is likely to exert its effect on the binding through the association rate constant; with slower diffusion than the smaller peptide it was predicted to have a reduced k₊. The association could also be hindered by steric clashing from the extra protein chain, alter the conformations of the unbound BH3 region or even accelerate the reaction by enhancing the capture radius.⁴¹ GB1-PUMA bound Mcl-1 with a similar increase in fluorescence and the kinetics of their interaction could be followed in a similar manner to the PUMA peptide. Surprisingly, the k₊ of the PUMA BH3 binding region is largely unaffected by the presence of extra protein chain, GB1-PUMA ⟨k₊⟩ = 1.29 (±0.03 s.e.m.) × 10⁷ M^–1 s^–1 and PUMA peptide 1.59 (±0.06 s.e.m.) × 10⁷ M^–1 s^–1 in the standard biophysics buffer (see Methods). The GB1-PUMA construct also showed essentially identical k₊ temperature dependence (Figure 4B). Interestingly, despite the number of extra charged amino acids, k₊ also shows similar ionic strength dependence. When fit to eq 4, GB1-PUMA and PUMA have similar values of rate constant in the absence of electrostatic effects (Figure S7), k_+basal= 2.0 (±0.4) × 10⁵ M^–1 s^–1 (Figure 4C) and k_+basal= 6 (±1) × 10⁵ M^–1 s^–1, respectively.

Figure 4.

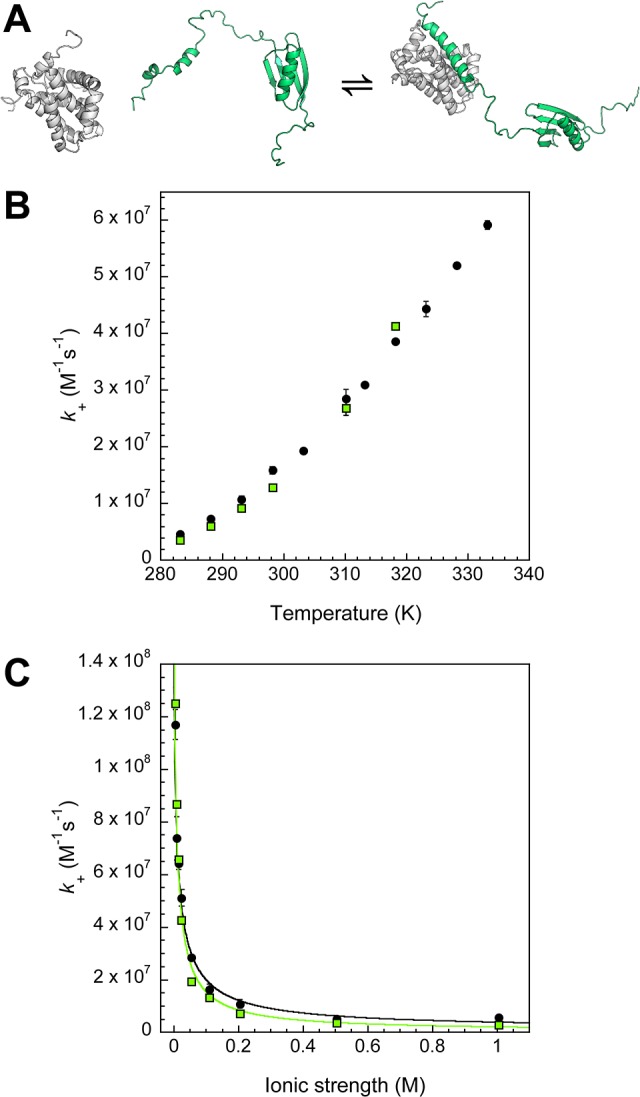
(A) Cartoon depicting Mcl-1 (gray) binding GB1-PUMA peptide (green). Unbound Mcl-1 is based on pdb 1WSX, cartoon of unbound GB1-PUMA peptide is based on pdb 3GB1, built using Chimera (UCSF),²² and bound structure is based on pdb 2ROC. Figure prepared using PyMol. (B) The rate constant for GB1-PUMA (green □) Mcl-1 association has a very similar temperature dependence to the smaller PUMA peptide (●). Where repeat measurements were made standard errors are shown as error bars. (C) GB1-PUMA (green □) k₊ is very dependent on ionic strength and shows very similar behavior to the PUMA peptide (black circles). The fit to the data shown here (black line) is obtained from a plot of ln(k₊) vs 1/(1 + κa) (Figure S7, Methods).

Discussion

The binding of BH3 regions to folded Bcl-2 family members is, due to their important physiological role and the large number of homologues, one of the most heavily studied coupled folding and binding reactions, particularly with respect to equilibrium binding constants obtained and structures solved.^21,29 BH3 peptides have potential therapeutic value and have been the focus for the design of peptide-based mimics, including hydrocarbon staples,⁴² α/β-peptides,⁴³ miniature proteins⁴⁴ and photoswitchable peptides.⁴⁵ To understand the general principles of binding, knowledge of kinetics, not just thermodynamics, is essential. Here, we report the first solution phase kinetics for BH3 peptide association and demonstrate the utility of stopped-flow experiments in the study of these interactions. We also show how careful kinetic analysis can be used to obtain a K_d when binding is tight and other techniques are not accessible. Consistent with the low, subnanomolar, K_d value obtained, PUMA has been shown to bind the folded Bcl-2 members with greater affinity than most other BH3 peptides.²⁹ This ties in with the main function of PUMA, which, upon cellular DNA damage and its expression,⁴⁶ is to compete with and displace proteins whose release eventually leads the cell to apoptosis.²⁵

The micromolar oligomerization of the PUMA BH3 region, if physiologically relevant, is unlikely to affect its nanomolar binding to Mcl-1 and other Bcl-2 members. Although, of course, this would depend on the relative and absolute concentrations of all species involved. The helical propensity of the PUMA peptide and its amphipathic nature are likely responsible for the formation of these α-helical oligomers. This study reiterates the need to check for these second order effects when using similar amphipathic peptides or their peptide-based mimics. Finally, the relative insensitivity of the PUMA peptide association rate constant to being part of a larger protein (GB1-PUMA) is also important for peptide binding studies. Many laboratories use BH3 peptides as mimics of the presumably exposed BH3 region as part of a larger protein chain.^21,29 This result, at least, suggests that this is an appropriate strategy.

The Data Do Not Allow Us To Determine the Mechanism of Binding

We show that Mcl-1 and PUMA association is not ‘diffusion-limited’ and, therefore, does not necessarily go through the induced fit mechanism. However, the data presented here cannot be used to determine whether association occurs through induced fit or conformational selection or, if both are occurring, to determine their respective fluxes.¹⁸ The temperature and denaturant dependence of k₊ suggests that there is an energy barrier component to k₊ and that some structured state is critical along the reaction coordinate. Importantly, this could support either mechanism: the structured state could be a structured, binding competent state of the unbound peptide (i.e., conformational selection), or the transition state/encounter complex in the folding of the peptide upon the surface of Mcl-1 (i.e., induced fit). We note that, as there is no correlation between the helicity of the peptide and the association rate, it is unlikely that association goes via a pure conformational selection mechanism, where the entire PUMA peptide has to be folded before binding.

Conclusions

Many studies have described a fast protein–protein association reaction as ‘diffusion-limited’, or nearly ‘diffusion-limited’, based on the magnitude of the measured association rate constant,^47,48 and/or its inverse dependence on solvent viscosity.^49,50 Here, we show, in the case of IDP coupled folding and binding, that this behavior is necessary but not sufficient to confidently label a reaction as ‘diffusion-limit’. For the binding of PUMA and Mcl-1, further experiments are required to tease out details of the binding mechanism and understand why such an important function, the regulation of programmed cell death, is under the control of disordered proteins.

Methods

Protein Expression and Purification

The synthetic genes for truncated mouse Mcl-1 (UniProt P97287) with 151 N-terminal residues and 23 C-terminal residues removed (Figure S2C) and GB1-PUMA (Figure S2D) were obtained from Genscript. The genes were inserted into a modified version of the pRSET A vector that encodes an N-terminal hexahistidine tag with a thrombin cleavage site between the tag and the protein. Due to the cleavage of thrombin, a GS is added at the N-termini of Mcl-1. Protein expression was carried out in Escherichia coli C41 (DE3) grown in LB media at 37 °C. Expression was induced, once the cells reached an optical density at 600 nm of 0.4–0.6 AU, by adding IPTG to a final concentration of 0.1 mM and reducing the expression temperature to 18 °C. The cells were grown overnight and harvested by centrifugation. The harvested cells were sonicated and centrifuged, and the protein purified from the soluble fraction by affinity chromatography on Ni²⁺-agarose resin. Bound protein was removed by thrombin cleavage for Mcl-1, elution with 250 mM imidazole for GB1-PUMA, and further purified by gel filtration using Superdex G75. All proteins were stored at 4 °C. Identity was confirmed using mass spectrometry, the concentration of GB1-PUMA was determined by the method of Gill von Hippel,³⁶ and the concentration of Mcl-1 was determined using amino acid analysis.

Peptide Synthesis and Purification

Mouse PUMA peptide, residues 128–161 (Uniprot Q99ML1) with the M144I mutation used in the NMR structure 2ROC²⁶, together with N-terminal acetylation and C-terminal amidation, was synthesized by Selleck Chemicals. Peptide was reconstituted using H₂O, then further purified using gel filtration using Superdex G30. Peptides were filtered before freezing using N_2(l), and storage at −80 °C. Peptide concentration was determined using amino acid analysis and identity confirmed using mass spectrometry.

Buffers

Unless otherwise stated, experiments were carried out in 50 mM sodium phosphate, pH 7.0. For the ionic strength dependence of association protein and peptide were exchanged to the low ionic strength 10 mM MOPS, pH 7.0, buffer (I = 0.004 M) and then ionic strength was controlled using [NaCl]. NaOH was titrated to maintain neutral pH upon addition of NaCl.

Circular Dichroism

CD scans were taken in an Applied Photophysics Chirascan, using 10 to 2 mm path length cuvettes. Percentage helicity calculated using the mean residue ellipticity at 222 nm.²⁴

Kinetics

Association kinetics were monitored by following the change in intrinsic fluorescence on an SX18 or SX20 stopped-flow spectrometer (Applied Photophysics). All PUMA solutions were incubated at 25 °C for 30 min before use to allow for dissociation of oligomers. Because of mixing artifacts, data collected before the first 5 ms were removed before fitting. Proteins were mixed at near equal (1–0.25 μM) concentrations. Association kinetics were analyzed using eq 3(51) that describes irreversible association of two proteins at initial concentrations [A]₀ and [B]₀:

3

where F is fluorescence, F₀ the initial fluorescence, ΔF is the fluorescence amplitude of the reaction, [A]₀ is the initial concentration of one protein, [B]₀ the other, x = [B]₀/[A]₀, k₊ is the association rate constant, and t is time. Where repeat measurements were made, standard errors are shown as error bars. Errors were propagated using standard equations.

Ionic Strength analysis

Empirically is has been shown that the variation of association rate constant with ionic strength can be fit to a Debye–Hückel-like approximation (eq 4).¹⁴

4

where k₊ is the association rate constant, k_+basal the basal association rate in absence of electrostatic effects, R the gas constant, T the temperature, κ the inverse of the Debye length, a the minimal length of approach (set to 6 Å) and U the electrostatic energy of interaction.¹⁴

Abbreviations

IDP, intrinsically disordered protein; Mcl-1, induced myeloid leukemia cell differentiation protein; PUMA, p53 upregulated modulator of apoptosis; BH3, Bcl-2 homology domain 3;aa, amino acids; ITC, isothermal titration calorimetry; CD, circular dichroism.

Supporting Information Available

Supplementary methods and figures. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.